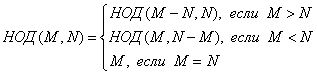Способы записи алгоритма
ПОНЯТЬ
Алгоритм – это описание последовательности действий. Следовательно, прежде чем разрабатывать алгоритм, надо выбрать язык и способ описания.
Существуют следующие основные способы записи алгоритма: словесный, словесно-пошаговый, табличный, графический, формульный, блок-схемы, программы.
Рассмотрим особенности их использования на примере одного алгоритма, возможно, самого древнего из известных – алгоритма Евклида.
Постановка задачи.
Пусть даны два натуральных числа. Нужно найти их наибольший общий делитель (НОД).
На уроках математики Вы решали эту задачу методом разложения чисел на простые множители. Сначала для каждого из чисел находятся все его простые множители. Затем выбираются одинаковые для обоих чисел множители и находится их произведение. Именно оно и будет результатом решения.
Пример
Обозначим натуральные числа M и N. Пусть M = 70, N = 112. Разложим их на множители:
| 70 35 7 1 | 2 5 7
| 112 56 28 14 7 1 | 2 2 2 2 7
|
Общими множителями являются 2 и 7. Следовательно НОД(M,N) = 14.
Чтобы использовать данный метод, надо знать, что такое простой множитель, какие числа являются простыми, нужно уметь находить общие элементы в двух множествах. Формализовать всё это крайне трудно. Метод хорош для «ручного» применения да и то для небольших чисел, но сложен для алгоритмизации.
(Рисунок - изображение Евклида) Евклид (3 в. до н.э.) – древнегреческий математик, автор первого из дошедших до нас трактатов по математике - предложил следующий способ нахождения наибольшего общего делителя.
Словесный способ записи алгоритма Евклида.
Большее из чисел заменяем разностью большего и меньшего, пока числа не станут равными. Полученное значение и будет НОД.
Исполним этот алгоритм для M = 70 и N = 112, сведя действия в таблицу.
| № шага | М | N | M N ? | M = N ? |
| 1 | 70 | 112 |
|
|
| 2 |
|
|
| нет |
| 3 |
|
| нет |
|
| 4 |
| 42 = 112-70 |
|
|
| 5 |
|
|
| нет |
| 6 |
|
| да |
|
| 7 | 28 = 70-42 |
|
|
|
| 8 |
|
|
| нет |
| 9 |
|
| нет |
|
| 10 |
| 14 = 42-28 |
|
|
| 11 |
|
|
| нет |
| 12 |
|
| да |
|
| 13 | 14 = 28 – 14 |
|
|
|
| 14 |
|
|
| Да |
Содержимое этой таблицы можно рассматривать как табличный способ записи алгоритма Евклида (для конкретных значений).
Словесно-пошаговый способ записи составляется, конечно же, на основе словесного, но может существенно отличаться от него, поскольку здесь важно явное указание последовательности действий–шагов.
Словесно-пошаговый способ записи алгоритма Евклида:
Шаг 1. Ввести значения M и N.
Шаг 2. Если М = N, то перейти к шагу 8.
Шаг 3. Если М N, то выполнить шаг 4, иначе выполнить шаг 6.
Шаг 4. М заменить на М – N.
Шаг 5. Перейти к шагу 2.
Шаг 6. N заменить на М – N.
Шаг 7. Перейти к шагу 2.
Шаг 8. Сообщить М.
На языке математики алгоритм Евклида будет иметь следующий формульный способ записи:
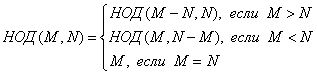
Заметим, что функция, которая при вычислении «обращается» к себе же (НОД вычисляется через НОД, но с другими значениями параметров), называется рекурсивной.
Наиболее ярким примером графического способа записи алгоритма является последовательность рисунков (без единого слова) в инструкциях по сборке игрушек в Киндер-сюрпризах.
(рисунок)
Поскольку Евклид был геометром (в школе изучается именно евклидова геометрия), то этот алгоритм он придумывал для определения общей меры двух отрезков. И описан это алгоритм Евклидом был именно в геометрической (графической) форме. Суть такова: с помощью циркуля определяем, какой из отрезков меньше. С помощью же циркуля измеряем длину этого отрезка и откладываем её от конца большего отрезка. Тем самым уменьшаем больший отрезок на разницу большего и меньшего. Продолжаем эти действия, пока отрезки не станут равными.
Пример
Проделаем эти действия для отрезков длиной 112 и 70.
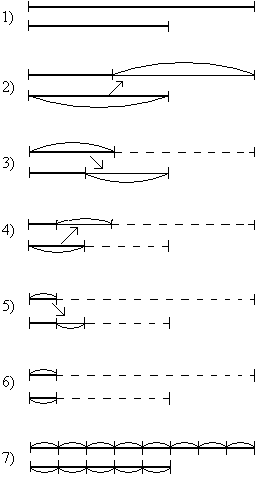
На 6 шаге отрезки сравнялись – это и есть их общая мера. В первом отрезке таких мер 8, во втором – 5.
В информатике основными способами записи алгоритма являются блок-схемы и программы.
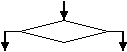
Блок-схему можно рассматривать как объединение графического и пошагового способов. В ней представлены все возможные шаги, последовательность которых указывается стрелками, а вместо названий действий используются графические фигуры.
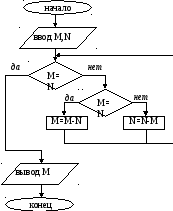
Для указания начала и конца алгоритма используется овал с выходящей/входящей стрелкой. Ввод/вывод данных обозначается параллелограммом с одной входящей и одной выходящей стрелкой. Вычисления, присваивания значений переменным обозначаются прямоугольником с одной входящей и одной выходящей стрелкой. Ромб с одной входящей и двумя выходящими стрелками используется для обозначения проверки условия, причем выходы соответствуют случаям, когда условие истинно или ложно. Для того чтобы показать, что некоторые действия нужно повторить, используется стрелка, ведущая к предыдущим блокам, или шестиугольник с двумя входами и выходами. Если блок-схема не умещается на одном листе, то переходы между блоками принято указывать в небольших пятиугольниках. В каждом блоке есть пояснительная надпись, разъясняющая над какими данными производится действие. Если блок-схема большая, то блоки принято нумеровать.
Блок-схема алгоритма Евклида будет иметь следующий вид.
Программа (от греч. pro – вперёд, gramma – писание; дословно – «нечто, написанное для будущего») – это алгоритм, записанный на каком-либо языке программирования.
У каждого языка программирования есть свои правила и особенности. Возможности современных языков программирования таковы, что один и тот же алгоритм может быть представлен разными способами даже в рамках одного языка.
На школьном алгоритмическом языке алгоритм Евклида записывается так:
величины М, N : целые;
начало
ввод М, N;
пока М N повторять
начало цикла
если MN то M := M - N иначе N := N – M
конец цикла;
вывод М;
конец
На языках Basic и Pascal алгоритм Евклида будет записан следующим образом.
| Программа на языке Basic | Программа на языке Pascal |
| 10 input M, N 20 if M=N then goto 50 30 if MN then M = M - N else N = N - M 40 goto 20 50 print M 60 end | var M, N : integer; begin read (M, N); while M N do if MN then M := M - N else N := N - M; write (M); end. |
Существование разных способов записи алгоритмов позволяет в каждом конкретном случае использовать тот из них, который наиболее удобен в данный момент для данного исполнителя.
ЗНАТЬ
Существуют следующие способы записи алгоритмов: словесный; словесно-пошаговый; формульный; графический; табличный; блок-схема; программа.
Блок-схема - совокупность геометрических фигур, каждая из которых обозначает определенное действие; порядок выполнения действий указывается стрелками, соединяющими блоки; фигуры снабжены поясняющими надписями.
Основные блоки:
| Геометрическая фигура | Пояснение | Действие алгоритма |
| 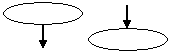
| Овал с выходящей или входящей стрелкой | Начало или конец алгоритма |
| 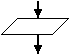
| Параллелограмм с одной входящей и одной выходящей стрелкой | Ввод данных и вывод результатов |
| 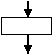
| Прямоугольник с одной входящей и одной выходящей стрелкой | Вычисления, присваивание значений |
| 
| Ромб с одной входящей и двумя выходящими стрелками | Проверка условия |
| 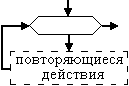
| Шестиугольник с двумя входами и двумя выходами | Повторение действий заданное число раз |
| 
| Пятиугольник с входящей или выходящей стрелкой и указанием номера блока | Переход между удалёнными блоками |
| 
| Прямоугольник с двойными боковыми линиями и указанием имени алгоритма | Вспомогательный алгоритм (подпрограмма) |
Программа - это алгоритм, записанный на каком-либо языке программирования.
Один и тот же алгоритм можно реализовать различными способами, используя разные конструкции одного языка или разные языки программирования. Алгоритм является более общим понятием, чем программа.
УМЕТЬ
1. Объясните, в чём состоит разница между алгоритмом и процессом решения задачи согласно этому алгоритму (исполнением алгоритма). Все ли возможные действия следует предусмотреть при разработке алгоритма? Все ли возможные действия придётся выполнить при исполнении алгоритма?
2. Объясните, чем вызвано существование многих способов записи алгоритмов? Объясните, в каких случаях и какой способ записи алгоритма будет наиболее удобным. Приведите примеры.
3. Кроме метода разложения на множители и метода последовательных вычитаний существуют и другие методы нахождения НОД двух натуральных чисел, например, метод целочисленного деления (иногда именно его называют алгоритмом Евклида).
По словесной записи алгоритма, реализующего данный метод, составьте словесно-пошаговую запись и блок-схему.
Пусть М и N – натуральные числа, причём МN. Найдём Х - остаток от деления нацело М на N. М сделаем равным N, N сделаем равным Х, и будем повторять деление и изменение значений М и N до тех пор, пока не получим Х=0. Наибольшим общим делителем будет последний ненулевой остаток.
4. По внешнему виду блок-схемы, не снабжённой пояснительными надписями, определите, какие ошибки есть в данной последовательности действий. На этом примере объясните, почему блок-схемы считаются наиболее наглядным способом записи алгоритмов.

ПРАКТИКУМ
Проанализируйте систему команд и среду исполнителя Робот и составьте алгоритмы для решения задач.
Исполнитель Робот действует на прямоугольном клеточном поле. Между некоторыми клетками, а также по периметру поля находятся стены. Основная цель Робота – закрасить указанные клетки и переместиться в конечную клетку.
Исполнитель Робот и поле, на котором он работает, отображаются следующим образом:

Здесь большой круг изображает Робота, маленький квадрат в левом верхнем углу поля - конечное положение Робота, черными точками помечены клетки, которые надо закрасить.
Команды исполнителя Робот:
Направо – перемещает Робота вправо;
Налево – перемещает Робота влево;
Вверх – перемещает Робота вверх;
Вниз – перемещает Робота вниз;
Закрась – закрашивает текущую ячейку;
Условный оператор: если условие то команда1 иначе команда2
Оператор цикла: пока условие повтори нц команда1 команда2 … кц
Логические условия:
стенаслева – возвращает True если слева от Робота стена и False если слева стены нет;
стенасправа – возвращает True если справа от Робота стена;
стенавверху – возвращает True если сверху от Робота стена;
стенавнизу – возвращает True если снизу от Робота стена;
клетказакрашена – возвращает True если ячейку, в которой находится Робот, нужно закрасить.
| 1 | Обойти препятствие для любого из случаев, представленных на рисунках. 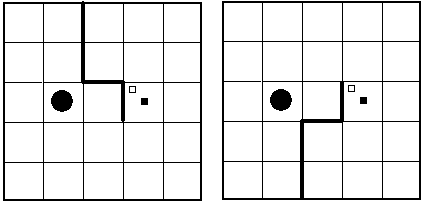
|
| 2 | Закрасить клетки у стены. Стены могут быть расположены случайным образом слева, справа, сверху и снизу от Робота, как это показано, например, на рисунках. 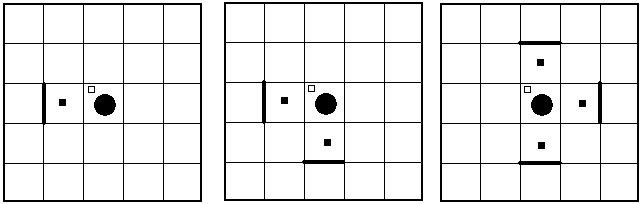
|
| 3 | Закрасить клетки под стенами. Примеры случайного расположения стен показаны на рисунках. 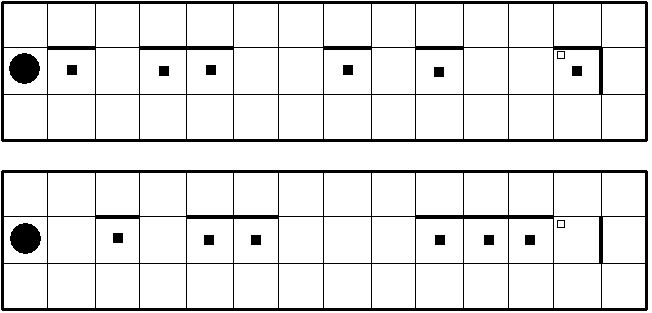
|