МКОУ «Шапихская СОШ»
Открытый мастер-класс урока геометрии в 7-ом классе на районном семинаре учителей математики на тему:
«Свойства прямоугольных треугольников. Признаки равенства прямоугольных треугольников»
Мастер-класс провел учитель математики
Алибахарчиев Аслудин Абдулмажидович
Дата 11.03.2019 год.
2019 год
Тема: Решение задач по теме «Свойства прямоугольных треугольников. Признаки равенства прямоугольных треугольников.
Тип урока: Урок когнитивного типа. Урок обобщения знаний по теме.
Форма урока: Урок исследования объекта, постановки проблемы и ее решения.
Учебно-методическое обеспечение: Л.С. Анастасян «Геометрия 7 – 9 кл.»
Время реализации: 45 мин.
Компьютерные медиапродукты. Наглядная презентация учебного материала, сделанная в среде Power Point.
Данный медиапродукт построен непосредственно на сопровождении сценария урока и содержит необходимые иллюстрации для объяснения материала.
Цель урока: Показать учащимся применение теоретических знаний на практике, умение переносить их и пользоваться ими в нестандартной ситуации.
Задачи урока:
-
Образовательные – обобщение теоретических знаний учащихся по теме «Прямоугольные треугольники», показать практическое применение свойств и признаков равенства прямоугольных треугольников;
-
Развивающие – развитие умений сравнивать, анализировать, обобщать, делать выводы; формировать исследовательскую культуру; развивать интерес к знаниям; переносить теоретические знания на практику;
-
Воспитательные – формирование умений работать в группах; принимать совместные решения; уверенности в своих силах.
Необходимое оборудование и материалы для занятия: компьютер, проектор, экран, табель – календари различных лет, карточки для практического задания, карточки для доказательства задачи, треугольники для работы в группах.
План урока:
| Этапы занятия | Временная реализация |
| I. Организационный момент: приветствие, объявление темы урока. | 2 |
| II. Актуализация опорных знаний учащихся: фронтальный опрос по теории, решение задач на готовых чертежах. | 8 |
| III. Создание проблемной ситуации. Выдвижение гипотез. Проверка гипотез при помощи измерений. Работа в группах. Обсуждение гипотез. | 10 |
| IV. Формулировка и доказательство задачи. Проверка гипотезы при помощи доказательства. | 8 |
| V. Совместная работа учителя и учащихся над проблемными вопросами учителя. | 10 |
| VI. Домашнее задание. | 3 |
| VII. Рефлексия урока. | 4 |
Учить не мыслям, а мыслить.
Кант
Сценарий урока.
Предварительно класс делится на 3 группы.
I этап: Организационный момент: Приветствие, сообщение порядка работы, выбор лидера групп.
Учитель: Ребята, на прошлом уроке мы решали задачи по теме «Прямоугольные треугольники». Сегодня я вам предложу еще одну задачу на эту тему. Вы обратили внимание на то, что у вас на столе лежат табель-календарики. Задача, которую я вам предложу сегодня для исследования будет связана с календарем. Геометрия в календаре! Необычно? Сегодня у нас много будет необычного. Но это впереди, а пока мы повторим пройденный материал.
II этап: Актуализация опорных знаний учащихся. (По ходу урока идет просмотр презентации)
1. Фронтальный опрос. (слайд №3). Повторение теоретических знаний.
-
Какой треугольник называется прямоугольным? Как называются его стороны?
-
Какие признаки равенства прямоугольных треугольников вы знаете?
-
Перечистлите свойства прямоугольных треугольников.
2. Решение задач на готовым чертежам с целью повторения свойств прямоугольного треугольника и признаков равенства прямоугольных треугольников. (Рисунки к задачам готовятся заранее на планшетах.) . (Слайды № 4, 5).
1). Устно. Определить вид треугольника. ( ∆АВС – прямоугольный.)
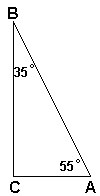
Какое свойство прямоугольного треугольника это подтверждает?
Проверим это свойство практически. Свернем у красных прямоугольных треугольников острые углы к прямому (если есть затруднения показать, как это сделать).
Сделайте вывод (В прямоугольном треугольнике сумма острых углов равна 90°).
2). Устно. Докажите, что треугольники АВС и NKM равны.

(В=35°; N=55°. Против равных углов лежат равные стороны. Значит, СВ=КМ, АС=МК. ∆АВС= ∆NKM по двум катетам.)
3). Письменно у доски. Определить вид треугольника ВМС (данная задача готовит учащихся к доказательству проблемной задачи в календаре).

Решение.
1=55°, 2=35°, против равных углов лежат равные стороны, значит
АВ = МD, АМ = СD.
∆АВМ=∆МСD (по двум катетам), следовательно ВМ=МС, ∆ВМС – равнобедренный.
Учитель: Докажите, что ∆ВМС – прямоугольный.
Углы 1 и 2 дополняют угол 3 до развернутого. 1+2+3=180°. 1+2=90°, следовательно 3=90°. ∆ВМС – прямоугольный.
Вывод: ∆ВМС – равнобедренный прямоугольный.
III этап. Создание проблемной ситуации. Выдвижение гипотез. Проверка гипотез.
1. Учитель: Ребята, у вас на столе лежат табель–календари за 2006 г. Соедините в январе этого года числа 10, 20, 30. Какую фигуру получили? (Треугольник). Чтобы в дальнейшем было легче работать с календарем, сделали его на клетчатой бумаге. Возьмите такой календарь за январь 2006 г. и соедините центры клеток с числами 10, 20, 30. Получили треугольник. (слайд № 6.) Назовите его (10–20–30). Необычно? Да. Но сегодня будем обозначать треугольники, отрезки и углы числами. Назовите стороны треугольника и его углы.
Как вы думаете, какой получился треугольник? Нам предстоит сейчас решить эту проблему. (слайд № 7)
2. Выдвижение гипотезы учащимися: (слайд № 8.)
а) равнобедренный;
б) прямоугольный;
в) равнобедренный прямоугольный.
Учитель: Для того, чтобы доказать или опровергнуть вашу гипотезу у вас имеются чертежные прямоугольные треугольники, линейка и вырезанный треугольник 10–20–30. В группах обсудите, как, используя эти инструменты, определить вид треугольника 10–20–30.
3. Работа в группах. (учащиеся при помощи измерений определяют вид треугольника. У каждой группы имеются необходимые инструменты для каждого ученика).
4. Обсуждение гипотез. Разбираются представленные гипотезы. Один человек от группы презентует классу свое решение.
4.1. Измерили линейкой и треугольником стороны и угол 10 . Получили равнобедренный прямоугольный треугольник 10–20–30 с прямым углом 10.
4.2. Измерили углы в данном треугольнике. Они равны 45°, 45°, 90°. Треугольник 10–20–30 – прямоугольный. Так как углы при основании равны, то он еще и равнобедренный.
4.3. Угол 10 – прямой. Проверили чертежным треугольником Свернем острые углы к углу 10. Сумма острых углов в треугольнике равна прямому т.е. 90°. Это свойство прямоугольных треугольников.
Треугольник 10–20–30 – равнобедренный прямоугольный.
Вывод: Треугольник 10–20–30 – равнобедренный прямоугольный.
(слайд № 9.)
IV этап. Формулировка и доказательство задачи. (Проверка гипотезы при помощи доказательства).
Учитель: Вид треугольника мы определили при помощи измерений. Мы уже говорили с вами, что измерениям доверять нельзя из-за возможных погрешностей. Любые экспериментальные данные в геометрии требуют доказательства.
Давайте сформулируем задачу, которую нам надо решить.
Задача. Если в календаре на январь за 2006 г соединить числа 10, 20, 30, то получится равнобедренный прямоугольный треугольник. Доказать.
(слайд № 10)
 5. Совместная работа учителя и обучающихся. (Учащиеся работают с карточками января 2006 г, сделанными на клетчатой бумаге, где имеется доказательство с пропусками) (приложение 1).
5. Совместная работа учителя и обучающихся. (Учащиеся работают с карточками января 2006 г, сделанными на клетчатой бумаге, где имеется доказательство с пропусками) (приложение 1).
Доказательство. (слайд № 11).
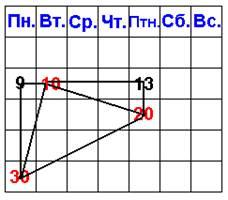
Учитель: Соединим центры клеток, соответствующих чисел. Сделаем дополнительные построения: проведем отрезки 30 – 9,
9 –13 и 13–20. Получили два треугольника: 30–9–10 и 10–13–20. Докажите, что:
а). треугольники 30–9–10 и 10–13–20 равны;
б). стороны 10–30 и 10–20 равны.
(Углы 9 и 13 прямые, стороны 9–30 и 10–13 равны соответственно сторонам 13–20 и 10–13. Значит, треугольники равны по двум катетам. Так как треугольники равны, то равны и их гипотенузы. Стороны 30–10 и 10–20 равны.)
Учитель: Определите вид треугольника 10–20–30 (равнобедренный).
Докажите, что угол 30–10–20 – прямой.
(Из равенства треугольников 30–9–10 и 10–13–20 следует, что углы 9–30–10 и 20–13–10 равны углам 30–9–10 и 10–13–20 соответственно. В прямоугольном треугольнике сумма острых углов 9–10–30 и 13–10–20 равна 90°. Углы 9–10–30 и 13–10–20 дополняют угол 30–10–20 до развернутого, значит угол 30 –10–20 равен 180–90=90°.)
Вывод: треугольник 10–20–30 – равнобедренный прямоугольный.
(слайд № 12)
V этап. Совместная работа учителя и учащихся над проблемными вопросами учителя.
Учитель: Ребята, как вы думаете, такой результат будет только для января 2006 г.? А верно ли это утверждение для января любого года? (да).
Давайте проверим вашу гипотезу.
1. Работа в группах. (учащиеся работают с табель–календарями, соединяют центры клеток чисел 10–20–30 в январях различных лет). (приложение 2).
1 группа: январь 2008, 2003, 2007.
2 группа: январь 2009, 2001.
3 группа: январь 2010, 2011.
2. Обсуждение результатов. (рисунки вывешены на доске). (слайды № 13-15).


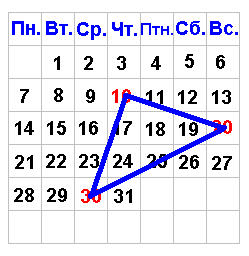
2006 2007 2008



2003 2009 2010


2011
Вопросы учителя:
-
Проанализируйте рисунки. Какой вывод вы можете сделать? (получаются 6 прямоугольных равнобедренных треугольников и отрезок);
-
Отчего зависит расположение треугольников? (от расположения чисел в январе месяце);
-
Сколько существует различных вариантов расположения дат в январском календаре. (Семь. Это зависит оттого, каким днем недели будет 1 января);
-
Когда получается отрезок? (когда центры клеток чисел 10, 20, 30 лежат на одной прямой);
-
Сколько различных треугольников получилось? (два: с прямым углом 10 и прямым углом 30).
-
Для ситуации, когда прямым углом является угол 10, мы провели доказательство. По образцу классной работы докажите дома, что и во втором случае (угол 30 прямой) получится равнобедренный прямоугольный треугольник. Рассуждения будут аналогичными.
3. Учитель: Как вы думаете, каков будет результат, если мы соединим числа 10, 20, 30 в любом месяце одного года? (получатся равнобедренные прямоугольные треугольники и отрезок).
Проверьте это на табель–календаре 2009 г. (учащиеся работают с календариками 2009 г.).
Какой сделаете вывод? (получили семь различных ситуаций расположения чисел 10, 20, 30 в году, два различных вида треугольников и отрезок). (слайд № 16)
4. Учитель: А какие еще числа в календарике можно соединить и получить равнобедренные прямоугольные треугольники? (числа 10, 20, 30 отстоят друг от друга на 10 единиц. Попробуем соединить числа, отстоящие друг от другу на 10 единиц:
1, 11, 21; 2, 12, 22; 3, 13, 23; 4, 14, 24; 5, 15, 25; 6, 16, 26; 7, 17, 27; 8, 18, 28; 9, 19, 29; 11, 21, 31).
Проверьте это на табель–календарях за 2011 г.
I группа соединяет числа 1, 11, 21; 2, 12, 22; 3, 13, 23;
II группа соединяет числа 4, 14, 24; 5, 15, 25; 6, 16, 26;
III группа соединяет числа 7, 17, 27; 8, 18, 28; 9, 19, 29; 11, 21, 31).
Сделайте вывод. (Предполагаем, что получится такой же результат, как и при соединении чисел 10–20–30). (слайд № 17, 18.)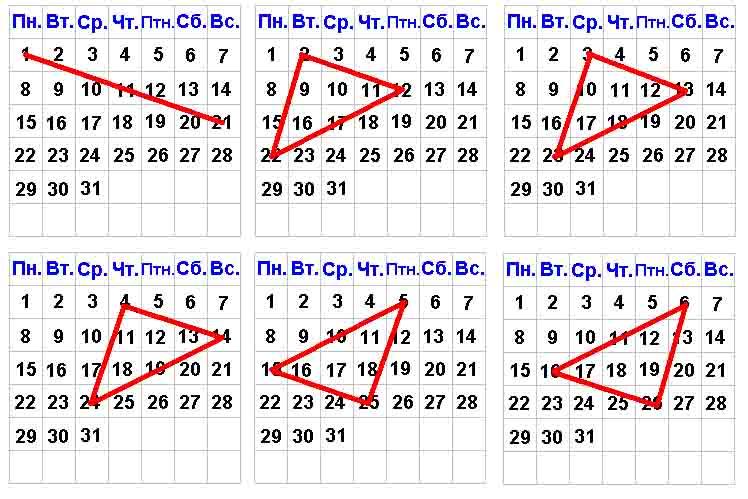

Учитель: Дома докажите, что и в этих случаях получается равнобедренный прямоугольный треугольник.
VI этап. Домашнее задание. Предлагается по выбору. (слайд № 19)
1. решение задачи для чисел 10, 20, 30 (2 случай);
2. Составить и решить задачу с другими данными.
VII этап. Рефлексия урока.
Учитель:
-
Какие знания помогли вам исследовать такую нестандартную задачу? (Свойства и признаки прямоугольных треугольников; свойства развернутого угла; свойства треугольника; умение измерять углы).
-
Проанализируйте свою работу на уроке. Оцените работу группы и отметьте в бланке наиболее активных учащихся.
Группа 1
Оценка группы ____
Работали активно:
1. _________
2.__________
3.__________
-
Поднимите руки те, кому было на уроке трудно, но интересно?
-
Поднимите руки те, кому было на уроке понятно, но остались вопросы?
-
Поднимите руки те, кому было все понятно.
Сегодня на уроке вы увидели необычное в привычном. Вы замечательно работали! Всем спасибо за урок!
ЛИТЕРАТУРА:
1. Ю.П.Дудницын, В.Л. Кронгауз «карточки по геометрии 7 класс».
НПО «Образование» 1998 г
2. Нетрусова Н. «Про календарь и треугольники»
Математика: приложение к газете «1 сентября» 2000 № 14.
Приложения:
Приложение 1
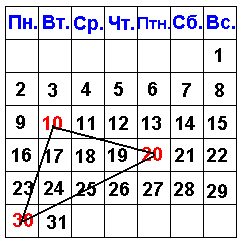
Задача. Если в календаре на январь за 2006 г соединить числа 10, 20, 30, то получится равнобедренный прямоугольный треугольник. Доказать.
Доказательство
Проведем отрезки 30–9, 9–13 и 13–20. Получили два треугольника 30–9–10 и ________. Углы 9 и __ прямые. Отрезки 9–10 и _____ равны. Отрезки ______ и 13-20 равны. Треугольники ______ и ______ равны по ___________________.
Из равенства треугольников 30–9–10 и 13–20–10 следует, что равны и гипотенузы _____ и _____. Треугольник 10–20–30 – равнобедренный.
Из равенства треугольников 30–9–10 и 13–20–10 следует, что углы 9–10–30 и 13–20–10; 9–10–30 и 13–20–10 равны (лежат против равных сторон). Углы ___ и ___ дополняют угол 30–10–20 до развернутого.
Сумма углов 9–10–30 и 13–10–20 равна 90° по свойству прямоугольного треугольника.
Значит, угол 30–10–20 равен 180° – ___ = ___, то есть треугольник 10–20–30 – ____________________.
Вывод: треугольник 10–20–30 – равнобедренный, прямоугольный.
Приложение 2
Календарь январей разных лет.










 5. Совместная работа учителя и обучающихся. (Учащиеся работают с карточками января 2006 г, сделанными на клетчатой бумаге, где имеется доказательство с пропусками) (приложение 1).
5. Совместная работа учителя и обучающихся. (Учащиеся работают с карточками января 2006 г, сделанными на клетчатой бумаге, где имеется доказательство с пропусками) (приложение 1).






























