Открытый урок по геометрии 11 класс "Конус"

СЛЕДСТВЕННЫЙ КОМИТЕТ РОССИЙСКОЙ ФЕДЕРАЦИИ

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ КАЗЕННОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ «КАДЕТСКИЙ КОРПУС СЛЕДСТВЕННОГО КОМИТЕТА РОССИЙСКОЙ ФЕДЕРАЦИИ ИМЕНИ АЛЕКСАНДРА НЕВСКОГО»

109462, г. Москва, ул. Маршала Чуйкова, дом 26 корп.1 тел./факс:(495)734-79-60; email:sk_fgkouku@mail.ru

Методическая разработка

урока геометрии

11 класс

Тема:

(задачи практического содержания)

Учитель математики

Петрунина

Ирина Валентиновна

14.12. 2017г.

Цель: формирование навыков решения практических задач по теме

Задачи:

Образовательная: Сформировать понятия: конической поверхности, сечений конуса и его элементов; формировать навыки решения задач на нахождение элементов конуса, навыки использования формул вычисления боковой и полной поверхности конуса, навыки решения прикладных задач; показать связь теории с практикой

Развивающая: способствовать развитию логического мышления учащихся и расширению кругозора; развивать пространственное воображение учащихся, умение применять формулы планиметрии при решении стереометрических задач; развивать и совершенствовать умения применять накопленные знания в измененной ситуации; развивать грамотную математическую речь, навыки самоконтроля.

Воспитательная: Воспитывать аккуратность при оформлении работ в тетрадях, ответственность за результат своего труда. Формировать навыки и умения коммуникативного общения.

Средства обучения: компьютер, мультимедийный проектор, экран, классная доска, учебник «Геометрия 10-11» Л.С. Атанасян, рабочая тетрадь, чертёжные инструменты.

Формы организации учебной деятельности: фронтальная, индивидуальная, диалог, работа с материалом слайда, учебника; самостоятельная и исследовательская работа.

Методы: наглядный, словесный, условно-символический, исследовательский.

Приложение: слайдовая презентация в программе PowerPoint

Девиз урока: «Дорогу осилит идущий, а математику – мыслящий».

После завершения урока учащиеся -

должны знать:

• основные понятия: конической поверхности, сечений конуса и его элементов,

• формулы и методы для нахождения основных компонентов конуса,

• формулы площади боковой и полной поверхности конуса;

должны уметь:

• строить чертежи по условию задачи,

• решать практические задачи на нахождение элементов конуса,

• видеть фигуры вращения.

1 этап: Организационный.

Приветствие. Проверка готовности к уроку.

2 этап: Определение темы урока.

Создание проблемной ситуации с «удивлением». (слайд 1) Прием мотивации: рассмотрите очень внимательно картину - она соответствует нашей теме урока. Какова по вашему мнению тема нашего урока? Определили, записали. (слайд 2)

3 этап: Актуализация опорных знаний.

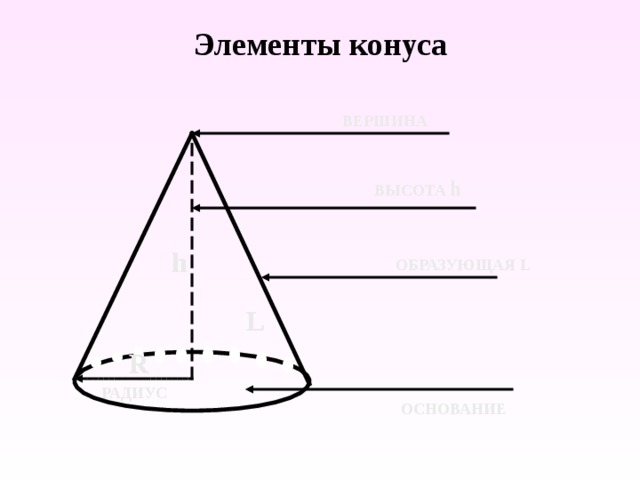
Для успешного решения задач повторим элементы конуса. (слайд 3)

4 этап: Практическая работа.

«Тяжело в учении, легко на ЕГЭ» Работа в парах (8мин)

А сейчас давайте прорепетируем ЕГЭ.  Главное на ЕГЭ- не теряя времени, выбрать правильный способ решения задачи, которую вам обязательно предложат решить на экзамене. (слайд 4)

Перед вами 8 задач. Каждая пара учащихся должна:

- определите тип решения каждой задачи;

- в каждую колонку своей таблицы записать номера задач, соответствующих указанному типу;

- отметить в условиях задач признаки, на основании которых вы произвели распределение.

На выполнение задания даётся 5 минут.

 Задачи.

1) Радиус основания конуса равен 3, образующая равна 4. Найдите площадь полной поверхности конуса, деленную на π. 1

2) Образующая конуса равна 10, высота конуса 6. Найдите радиус конуса.2

3) Осевое сечение конуса равносторонний треугольник со стороной 10см. Найти площадь боковой поверхности конуса.3

4) Диагональ осевого сечения цилиндра равна 48. Угол между этой диагональю и образующей равен 30. Найдите радиус цилиндра.2

5) Во сколько раз увеличится площадь боковой поверхности конуса, если его образующую увеличить в 3 раза?1

6) Осевое сечение конуса равносторонний треугольник со стороной 10см. Найти радиус основания и высоту конуса.2

7) Радиус основания цилиндра равен 6, высота равна 3. Найдите площадь боковой поверхности цилиндра, деленную на π. 1

8) Высота конуса 12 см, образующая – 13 см. Найти боковую поверхность конуса.3

На экране таблица. (слайд 5)

 Резюме учителя:

У: - А за какие слова вы «зацепились», чтобы поместить задачу в ту или иную колонку?

-  в первой колонке – помогают слова конус, радиус, высота.

- во второй – образующая конуса, угол наклона.

- в третьей – площадь боковой поверхности.

Учитель: Ребята, а вы знаете, что латинское слово «conus» заимствовано из греческого языка (konos - втулка, сосновая шишка) … С конусом люди знакомы с глубокой древности. В книге Архимеда (287 – 212гг. до н.эры) «О методе» приводятся решения практических задач, связанных с конусом.

5 этап: Знакомство с практическим применением.

Учитель: Ребята, на прошлом уроке вы затруднялись при перечислении предметов, имеющих форму конуса. Сегодня мы посмотрим, как разнообразно его использование и практическое применение.

Конус можно рассмотреть в различных предметах, начиная с обычного мороженого и заканчивая техникой.

В детстве многие ваши игрушки, или их составляющие имели форму конуса… А как часто его можно встретить в природе.

Это формы деревьев, рельеф земной поверхности: горы и холмы. Их можно найти и на дне океана.

Формы конуса могут принимать и природные явления, и космические объекты.

А без конусов архитектурные сооружения не были бы так привлекательны и великолепны.

Решение задач практического содержания. (слайды 6 – 25).

Задачи:

Задача № 1. Верхняя часть башни имеет форму конуса, радиус основания которого ,

а образующая 9 м. Боковую поверхность конуса планируется покрыть мозаикой. Сколько мешков клея потребуется купить для выполнения этой работы, если расход клея 5 кг на 1

и в одном мешке 25 кг клея?

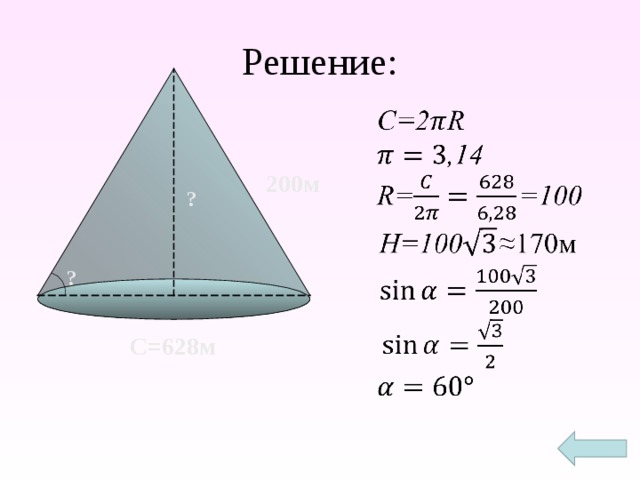
Задача № 2. Расстояние от вершины холма до основания – 200м. Длина основания холма – 628м. Найти высоту холма и крутизну спуска.

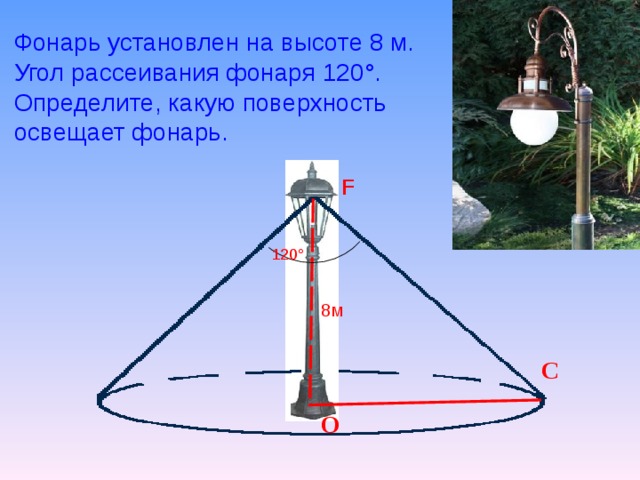
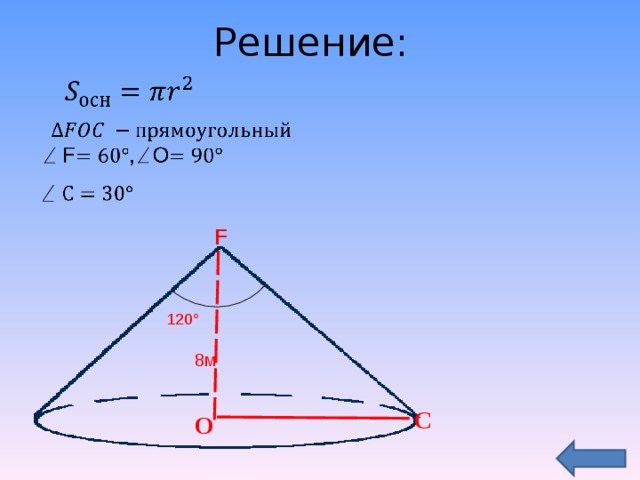
Задача № 3. Фонарь установлен на высоте 8 м. Угол рассеивания фонаря 120°. Определите, какую поверхность освещает фонарь.

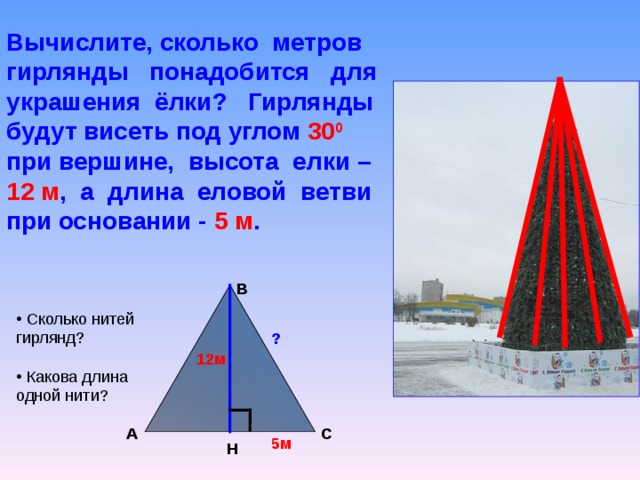
Задача № 4. Вычислите, сколько метров гирлянды понадобится для украшения ёлки? Гирлянды будут висеть под углом 30⁰ при вершине, высота елки – 12 м, а длина еловой ветви при основании - 5 м.

Задача № 5. Сколько квадратных метров брезента потребуется для сооружения палатки конической формы высотой 4 метра и диаметром основания 6 метров? На подгиб и швы необходимо добавить 5%.

Задача № 6. Вычислите высоту молниеотвода, если радиус "защищенного" круга 15 м, а угол между молниеотводом и образующей конуса безопасности 60 º.

Задача № 7. Пусть окружность конической кучи щебня 12 м. Длина двух образующих – 4,6 м. Найти площадь поверхности кучи щебня.

Задача № 8. Какова площадь воронки, образовавшейся при взрыве бомбы, если длина окружности основания воронки: С= 12м, а глубина по склону: ℓ=1,5 м.

Задача № 9. Слайд с игрушками – домашнее задание: придумать задачу по теме.

6 этап: Выполнение самостоятельной работы.

Учитель: Проверим ваши знания. Выберите из оставшихся задач любую и решите её в тетради.

Тетради собираются на проверку.

7 этап: Подведение итогов. Рефлексия.

Сегодня мы хорошо поработали. Что нового узнали? Что понравилось? Что удивило?

Попробуйте понять, для чего лично Вам может пригодиться сегодняшнее занятие.

8 этап: Домашнее задание.

Одну задачу выбрать из оставшихся. Вторую задачу составить и решить по теме «Детские игрушки».

Двузначность проблемного урока: с одной стороны, учащиеся осуществляют поисковую деятельность; с другой - овладевают обобщенными знаниями и общими принципами решения учебных задач.

Здесь же уместно включить строки из трагедии «Скупой рыцарь».

Читал я где-то,

Что царь однажды войнам своим

Велел снести земли по горсти в кучу,

И гордый холм возвысился

Царь мог с высоты с весельем озирать

И дол, покрытый белыми шатрами,

И море, где бежали корабли.

Далее следует вопрос: какой высоты мог быть такой холм? На сколько километров может увеличиться панорама для наблюдения, поднявшегося с подножия холма к его вершине.

Это одна из немногих легенд, в которой при кажущемся правдоподобии нет и зерна правды. Докажите геометрически, что если бы какой-нибудь древний деспот вздумал осуществить такую затею, он был бы обескуражен мизерностью результата. Перед ним высилась бы настолько жалкая куча земли, что никакая фантазия не смогла бы раздуть ее в легендарный «гордый холм».

горсть литра 0,2 дм.

Войско в 100 000 воинов считалось очень внушительным.

V = 0,2∙100 000 = 20 000 дм3 = 20 м3.

Угол откоса

Итак,

конус V = 20 м3 а = 45° Найти. Н конуса

Решение.

Так как Н = R, то

Надо обладать очень богатым воображением, чтобы земляную кучу в 2,7 м ( 1,5 человеческих роста) назвать «гордым холмом». Сделав расчет для меньшего угла, мы получили бы еще более скромный результат.

У Аттилы было самое многочисленное войско, которое знал древний мир. Историки оценивают его в 700 000 человек. К сведению, Аттила - предводитель гуннов, кочевого народа, сложившегося в Приуралье из многих племен. Массовое передвижение гуннов на запад (с 70-х гг. IV в.) дало толчок «великому переселению народов». Наибольшего могущества гуннская держава достигла при Аттиле (7-453 гг.), который возглавил опустошительные походы в Восточно-Римскую империю (413 г., 447 г., 448 г., 451 г.). Но в 451 году на Каталаунских полях (равнина в северо-восточной Франции к западу от города Труа) войска Западно-Римской империи в союзе с франками, вест-готами, бургундами, аланами и др. разгромили гуннов во главе с Аттилой, что привело к распаду гуннской державы.

Если бы все воины Аттилы участвовали в насыпании холма, образовалась бы куча повыше вычисленной нами, но не очень. Советую вам самим дома вычислить высоту кургана и подумать, удовлетворила бы такая высота честолюбие Аттилы или нет.

ЛИТЕРАТУРА

1. «Программы общеобразовательных учреждений. Геометрия. 10-11 классы». Составитель Т.А. Бурмистрова. Издательство Москва. «Просвещение». 2009г.

2. «Геометрия 10-11Л.С. Атанасян, В.Ф. Бутузов, С.Б. Кадомцев, Э.Г. Поздняк, И.И. Юдина». Издательство: Москва. Просвещение. 2010г.

3. «Математика. Типовые тестовые задания. ЕГЭ-2012» Под редакцией А.Л. Семенова, И.В. Ященко» Рекомендовано МИОО Издательство: Москва. Экзамен.2012 г.

4. «Математика. 2011. Самое полное издание типовых тестовых вариантов заданий ЕГЭ» Рекомендовано ФИПИ. Под редакцией А.Л. Семенова, И.В. Ященко» Издательство: Москва. АСТ. Астрель .2011 г.

5. «Поурочные планы. Геометрия 10» Т.Л. Афанасьева.Л.А. Тапилина Издательство «Учитель». г.Волгоград . 2005г.

(см.слайд 45)

ИНТЕРНЕТ-РЕСУРСЫ

1. http://www.youtube.com/watch?v=zcTM0A8rMX4

2. http://www.youtube.com/watch?v=DGn6fXsHQx0

3. http://www.youtube.com/watch?v=o1LGLUcU5O0

4. http://www.youtube.com/watch?v=aY1uVp4EoRI

5. http://ru.wikipedia.org/wiki/%D0%9C%D0%BE%D0%BB%D0%BD%D0%B8%D0%B5%D0%BE%D1%82%D0%B2%D0%BE%D0%B4

6. http://ru.wikipedia.org/wiki/%D0%A4%D1%80%D0%B0%D0%BD%D0%BA%D0%BB%D0%B8%D0%BD,_%D0%91%D0%B5%D0%BD%D0%B4%D0%B6%D0%B0%D0%BC%D0%B8%D0%BD

7. http://ru.wikipedia.org/wiki/%D0%9E%D1%81%D0%B2%D0%B5%D1%89%D1%91%D0%BD%D0%BD%D0%BE%D1%81%D1%82%D1%8C

8. http://festival.1september.ru/articles/589969/

9. http://www.uchportal.ru/load/24-1-0-21426

10. http://festival.1september.ru/articles/413311/

11. http://uztest.ru/abstracts/?idabstract=523545

12. http://festival.1september.ru/articles/505914/

УТВЕРЖДАЮ

Начальник учебно – методического отдела

__________________ /Г.Е.Штырев/

«____» _________________20___ г.

ПЛАН-КОНСПЕКТ УРОКА

Урок № 22\3.

Тема Конус. Решение задач практического содержания.

1. ФИО (полностью): Петрунина Ирина Валентиновна

2. Место работы: ФГКОУ Кадетский корпус Следственного комитета Российской Федерации имени А. Невского

3. Должность: учитель математики

4. Предмет: геометрия

5. Базовый учебник: «Геометрия 10-11», авторы Атанасян Л.С., Бутузов В.Ф., издательство «Просвещение» 2016г.

6. Класс: 11в.

7. Планируемая дата проведения урока: «_14__» декабря___2017г.

8. Цель урока: формирование навыков решения практических задач по теме.

9. Планируемые результаты урока:

Знать: основные понятия: конической поверхности, сечений конуса и его элементов; формулы и методы для нахождения основных компонентов конуса, формулы площади боковой и полной поверхности конуса.

Уметь: применять изученную теорию при решении задач.

1. Тип урока: комбинированный урок.

2. Формы работы учащихся: фронтальная, индивидуальная, парная.

3. Необходимое техническое оборудование: ПК учителя, мультимедийный проектор.

Содержание урока:

Преподаватель: Петрунина И.В.

1) Радиус основания конуса равен 3, образующая равна 4. Найдите площадь полной поверхности конуса, деленную на π.

2) Образующая конуса равна 10, высота конуса 6. Найдите радиус конуса.

3) Осевое сечение конуса равносторонний треугольник со стороной 10см. Найти площадь боковой поверхности конуса.

4) Диагональ осевого сечения цилиндра равна 48. Угол между этой диагональю и образующей равен 30. Найдите радиус цилиндра.

5) Во сколько раз увеличится площадь боковой поверхности конуса, если его образующую увеличить в 3 раза?

6) Осевое сечение конуса равносторонний треугольник со стороной 10см. Найти радиус основания и высоту конуса.

7) Радиус основания цилиндра равен 6, высота равна 3. Найдите площадь боковой поверхности цилиндра, деленную на π.

8) Высота конуса 12 см, образующая – 13 см. Найти боковую поверхность конуса.

1) Радиус основания конуса равен 3, образующая равна 4. Найдите площадь полной поверхности конуса, деленную на π.

2) Образующая конуса равна 10, высота конуса 6. Найдите радиус конуса.

3) Осевое сечение конуса равносторонний треугольник со стороной 10см. Найти площадь боковой поверхности конуса.

4) Диагональ осевого сечения цилиндра равна 48. Угол между этой диагональю и образующей равен 30. Найдите радиус цилиндра.

5) Во сколько раз увеличится площадь боковой поверхности конуса, если его образующую увеличить в 3 раза?

6) Осевое сечение конуса равносторонний треугольник со стороной 10см. Найти радиус основания и высоту конуса.

7) Радиус основания цилиндра равен 6, высота равна 3. Найдите площадь боковой поверхности цилиндра, деленную на π.

8) Высота конуса 12 см, образующая – 13 см. Найти боковую поверхность конуса.

Конус. Решение задач

Учитель

Петрунина И.В.

Элементы конуса

ВЕРШИНА

ВЫСОТА h

h

ОБРАЗУЮЩАЯ L

L

R

РАДИУС

ОСНОВАНИЕ

Задачи, решаемые

с помощью формулы площади боковой поверхности.

Задачи, решаемые

с помощью т. Пифагора.

Задачи, решаемые

с помощью т. Пифагора и формулы площади боковой поверхности.

1, 5, 7

2,4, 6

3, 8

Slide 2-Category Selection

This slide is the main game board. You go here to begin the game, and you return here after each Question/Answer slide. This is where the “contestant” selects one of the five categories and a dollar value for the question. The higher the value, the more difficult the question. When you open this slide, the categories appear one at a time, and the dollar values appear at random with an accompanying laser beep. Here’s how it works: if the contestant selects the first category for $300, you would click on the $300 text under

Башни - конусы

Конус выноса

Воронка взрыва

the 1st category (i.e., the 3rd dollar box in column one). As a result, the corresponding Question/Answer slide will automatically appear. Once the question, and then the answer, for that slide have been shown, you will click on the arrow in the bottom right of that slide to return to this main slide. When you return to this slide, the dollar amount for the box you selected will have changed from white to blue to show that that particular question has already been used. Below, you will see how to tailor the game for your particular categories.

Гирлянда

Холм

Колпак клоуна

To tailor this slide, follow these instructions:

Five different categories are used in the game. The category names appear at the top of the columns on this slide and on the five associated Question/ Answer slides (one for each dollar value). Rather than changing all of these separately, you will use the Replace command to change each placeholder category name only once.

Палатка

Фонарь

Конус

безопасности

1. Under Edit , choose Replace

• Type the placeholder name for category 1 as shown in the pop-up at the right. Type in your category name (e.g., Mixed Numbers) under Replace with:
• Type the placeholder name for category 1 as shown in the pop-up at the right.
• Type in your category name (e.g., Mixed Numbers) under Replace with:

The Replace pop-up should now look like the one on the right, only with your category name.

• The Replace pop-up should now look like the one on the right, only with your category name.

• Click the Replace All button to make the changes.
• Click the Replace All button to make the changes.

You will then see this pop-up

• You will then see this pop-up

• Click the OK button. This replaces the six occurrences of the specified placeholder category name with your category name. After this, the top of the slide will look like this:
• Click the OK button. This replaces the six occurrences of the specified placeholder category name with your category name. After this, the top of the slide will look like this:

Notice that in this case, “Mixed Numbers” doesn’t fit on the line. To fix this, simply click on the text right before the “N” and press Backspace followed by Enter. Now it’s on two lines:

2. Now, repeat Step 1 for the remaining four category placeholder names:

Большую угрозу для жизни и деятельности человека представляют разряды молний.

Конус, образованный в пространстве около молниеотвода, носит название «конуса безопасности».

Вычислите высоту молниеотвода.

60 º

15 м

Конус безопасности

В

Решение:

Из ВНС

tg60° =

ВН = ≈ 8,5 (м)

60 º

?

С

А

15м

Н

Ответ: высота молниеотвода должна быть не менее 8,5 м

Расстояние от вершины холма до основания – 200м. Длина основания холма – 628м. Найти высоту холма и крутизну спуска.

Решение:

200м

?

?

С=628м

Фонарь установлен на высоте 8 м.

Угол рассеивания фонаря 120 °.

Определите, какую поверхность освещает фонарь.

F

120 °

8м

C

О

Решение:

F

120 °

8м

C

О

Вычислите, сколько метров гирлянды понадобится для украшения ёлки? Гирлянды будут висеть под углом 30 0 при вершине, высота елки – 12 м , а длина еловой ветви при основании - 5 м .

В

• Сколько нитей гирлянд?
• Какова длина одной нити?

?

12м

А

С

5м

Н

Решение:

Сколько нитей гирлянд?

В

360° : 30° = 12 (нитей )

Как найти длину одной нити?

?

12м

Она равна образующей

конуса.

А

С

5м

Н

Сколько квадратных метров брезента потребуется для сооружения палатки конической формы высотой 4 метра и диаметром основания

6 метров ?

На подгиб и швы необходимо добавить 5%.

Дано : конус, h =4 м, d =6 м

Найти : S =?

B

l

4

H

3

3

А

6

C

Ответ: 79,2м 2 брезента

Решение:

Sбок.= πRℓ

9м

Ответ: 20 мешков.

Пусть окружность конической кучи щебня 12 м. Длина двух образующих – 4,6 м. Найти площадь поверхности кучи щебня.

Решение:

Sбок.= πRℓ

l=4,6 : 2=2,3(м)

l

l

C=12м

Детские игрушки

Домашнее задание:

составить задачу про игрушку

по теме «Конус».

Для решения задачи

надо измерить:

Длину окружности основания воронки: С= 12м

и глубину по склону: ℓ=1,5 м

Найти: Sбок.=?

Решение:

Sбок.= πRℓ

С= 2πR

R=С:2π

Sбок.= πRℓ= πСℓ:2π=Сℓ:2

Sбок.=12*1,5:2= 9м²

Ответ: 9 м²

С=12м

ℓ =1,5м