Открытый урок по математике в 6-ом классе
Тема урока: «Тренируем мышление»
Учитель: Шехинаева Светлана Агубекировна
Владикавказ, 2018
Тема урока: «Тренируем мышление»
Задачи урока: 1. Формирование и развитие мыслительных
операций, форм мышления, умозаключений по
индукции и аналогии.
2. Формирование навыков решения линейных
уравнений с параметром.
3. Формирование интереса к математике.
Оборудование: презентация, тесты.
Ход урока.
«Уравнение – это золотой ключ, открывающий все математические сезамы»
С. Коваль
1. Кто и когда придумал первое уравнение? Ответить на этот вопрос невозможно. Представь себе, что первобытная мама по имени … впрочем, у неё наверное, и имени то не было, сорвала с дерева 12 яблок, чтобы дать каждому из своих 4 детей.
Вероятно, она не умела считать не только до 12, но и до 4, и уж несомненно не умела делить 12 на 4. А яблоки она поделила, наверное так: сначала дала каждому ребенку по яблоку, потом еще по яблоку, потом еще по яблоку и тут увидела, что яблок больше нет и дети довольны.
Если записать эти действия на современном математическом языке, то получаем 4*х=12, т.е. мама решила задачу на составление уравнения.
Задачи, приводящие к решению простейших уравнений, люди решали на основе здравого смысла с того времени, когда они стали людьми. Еще за 3 - 4 тыс. лет д.н.э. египтяне и вавилоняни умели решать уравнения, вид которых и прием решения были не похожи на современные. Греки унаследовали знания египтян и пошли дальше. Наибольших успехов достиг греческий ученый …, имя которого вы узнаете после решения нескольких уравнений.
1. 5y + 3 = 36 – y 2. 7y – 2 – 2y = 10
y = ? ( A) y = ? ( Ф )
3. 9,3y – 25 – (1.7y + 37) = 14 4. 7(x – 8.2) = 3x + 19
y = ? ( Н ) х = ? ( Т )
5. 0.2(5x – 6) + 2x = 0.8 6. –(7y + 0.6) = 3.6 – y
x = ? ( O ) y = ? ( Д )
7. 15(x + 2) – 30 = 12x
x = ? ( И )
Каждому корню уравнения соответствует буква. Расположите корни в порядке возрастания и вы узнаете имя ученого ( Диофант).
Большой вклад в изучение уравнений внес среднеазиатский математик Мухаммед аль Хорезми ( 9 в.). В дальнейшем многие математики занимались проблемами уравнений. Одним из них был французский математик, имя которого вы узнаете, если выполните задания, предложенные для самостоятельной работы. Ответы к этим заданиям зашифрованы на координатном луче.
0 1 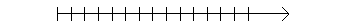
О Р И К В Т Е Ж
1. 34 – 3x = 27 – 2x 2. 40 – (x + 8) = 28
3. 5 + 8x = 14x – 67 4. (y – 35) + 32 = 7
2. Сегодня мы совершим путешествие на один из «загадочных островов». Это путешествие связано с решением уравнений, которые тренируют мышление: надо внимательно « посмотреть » как построена известная часть задачи, « увидеть » принцип её построения, выявить связи между числами, объектами, рисунками, а затем этот принцип применить по аналогии к другой части.
Аналогия в переводе с греческого языка означает сходство.
1. Найдите неизвестное число:
Математика 10
Алгебра ?
2. Продолжите ряд уравнений:
x + 1 = 2 x – 1 = 2
x + 1 = 6 x – 1 = 6
………………………………
3. Найдите неизвестное число:
корень x – 6 = 0
уравнение 3x - ? = 0
4. Найдите неизвестную букву:
3x + 11 = x + 23 5x – 7 = 13
( Е ) ( ? )
5. Исключите одно из чисел:
12 33


 x
x  2x + 13 = 19
2x + 13 = 19
21 13
3. Творческое задание (об уравнениях с параметрами).
Рассмотрим уравнение 6x -1 = x + 6 . Если в этом уравнении заменить 6 на другое число, то получим 5x – 1 = x + 5 или 4x – 1 = x + 4 и т. д. Каждое из этих уравнений решаем тем же способом, что и первое уравнение, а чтобы не решать несколько однотипных уравнений одним и тем же способом, решим задачу в общем виде, заменив изменяемое число (параметр) буквой:
ax – 1 = x + a
ax – x = a + 1
(a – 1)x = a + 1
Только не будем торопиться с делением на (а – 1) для нахождения х, так как при а = 1 это выражение обращается в 0, а на 0 делить нельзя. Случай а = 1 надо рассмотреть отдельно.
Если а = 1, то 0х = 2 – это уравнение корней не имеет.
Если а ≠ 1, то х = 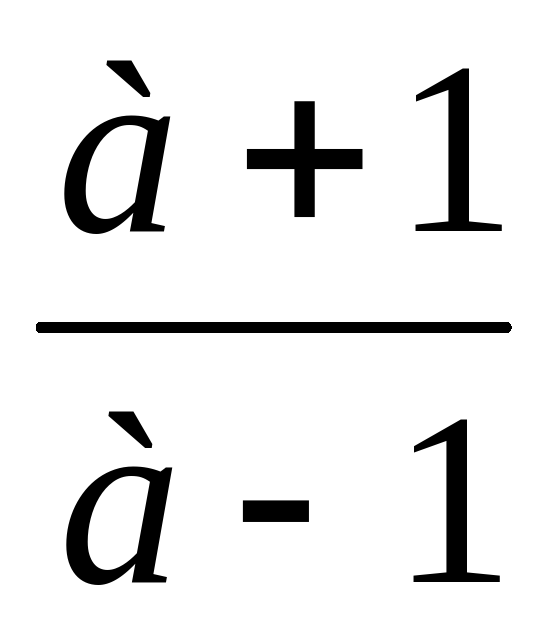 .
.
Задание, которое мы выполнили, обычно формулируется так: для всех значений параметра а решить уравнение (а – 1)х = а + 1. Ответ к этому заданию можно записать так: при а равном 1 – уравнение корней не имеет; при а ≠ 1 - х = 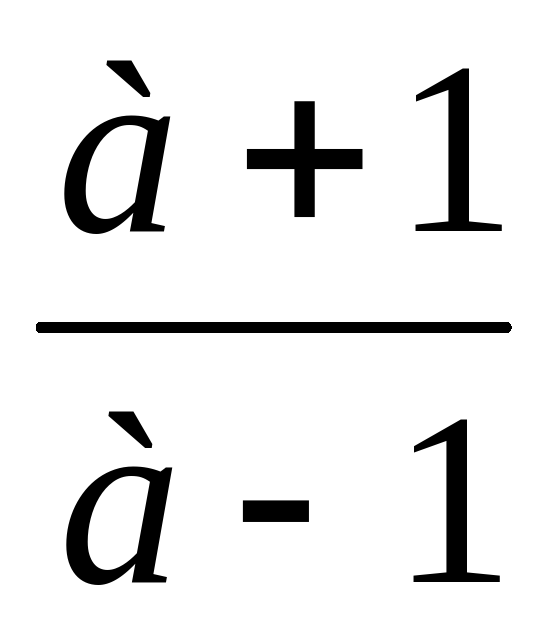 .
.
Примеры:
1) При каком значении параметра а уравнение а(х – 1) = 2х + 5 не имеет корней;
2) Для всех значений параметра а решить уравнения: ах = 7,
5х = в.
Итак, что значит решить линейное уравнение содержащее параметр (под параметром мы понимаем, входящие в алгебраические выражения величины, численные значения которых явно не заданы, однако считается принадлежащими определенным числовым множествам):
1) выразить х;
2) выяснить, при каких значениях параметра уравнение имеет корни;
3) выяснить, при каких значениях параметра уравнение корней не имеет.
4. Тестовые задания.
1 вариант
1) 3х + 1 = 8
2) 3х = 1
3) 0х = 5
4) 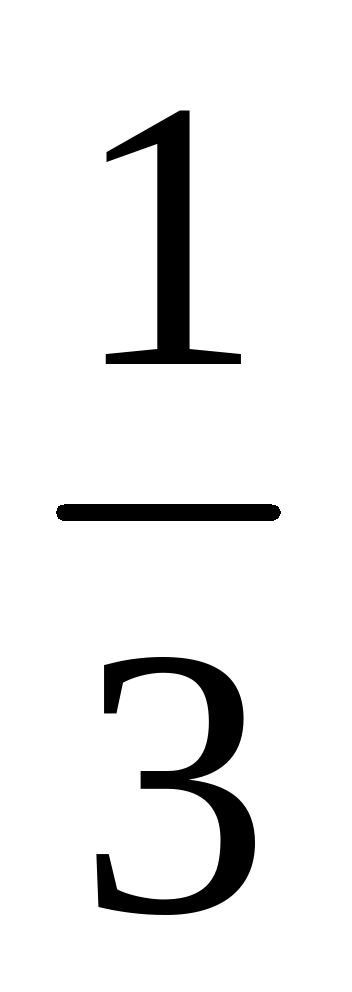 х =5
х =5
5) 2(х-0,5) = 3
6) 2х – (2х + 1) = -1
7) 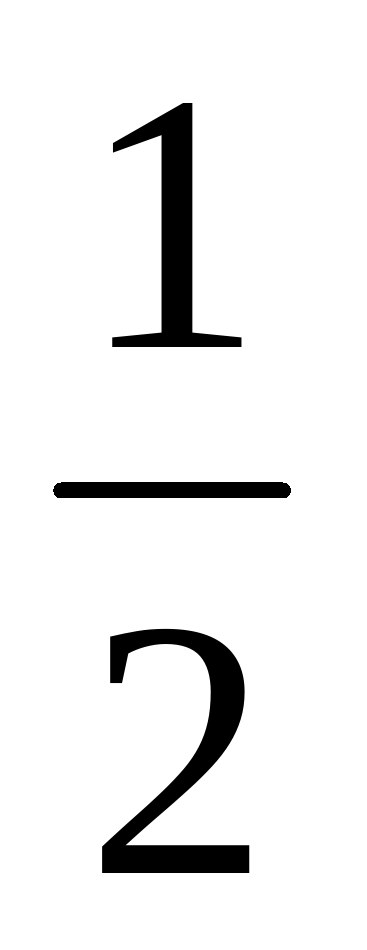 х -
х -  = 0
= 0
8) │х│= 3
9) (х – 3)(х +3) = 0
2 вариант
1) 3х – 1 = 8
2) -3х = 1
3) 0х =0
4) 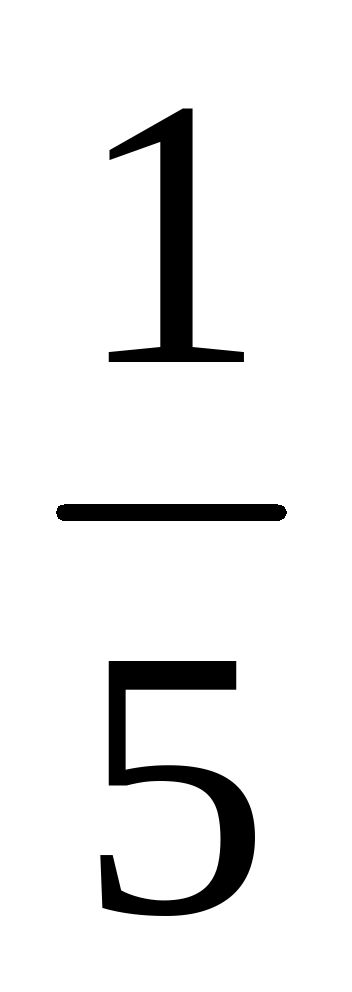 х = 3
х = 3
5) 2(х + 0,5) = 3
6) 2х – (2х – 1) = -1
7)  -
- 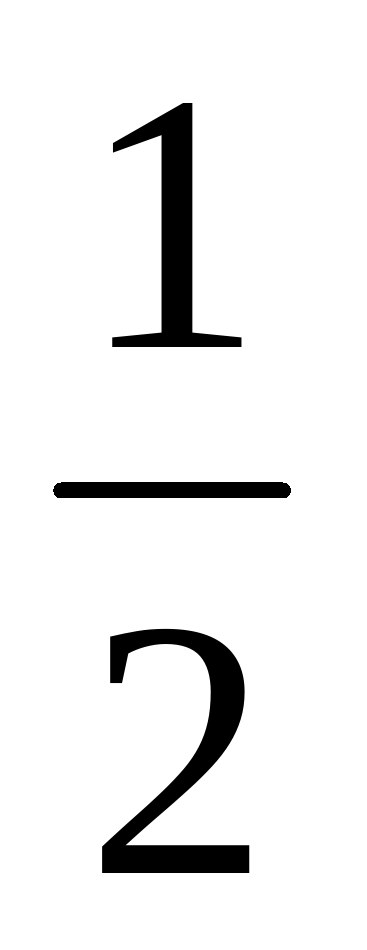 х = 0
х = 0
8) │х│=9
9) х(х-3) = 0
5. Заключение.
Старинная задача.
В папирусе Ахмеса есть специальный раздел «Исчисление кучи». Под словом «куча» подразумевается неизвестная величина. Вот одна из тех задач: «Куча. Ее 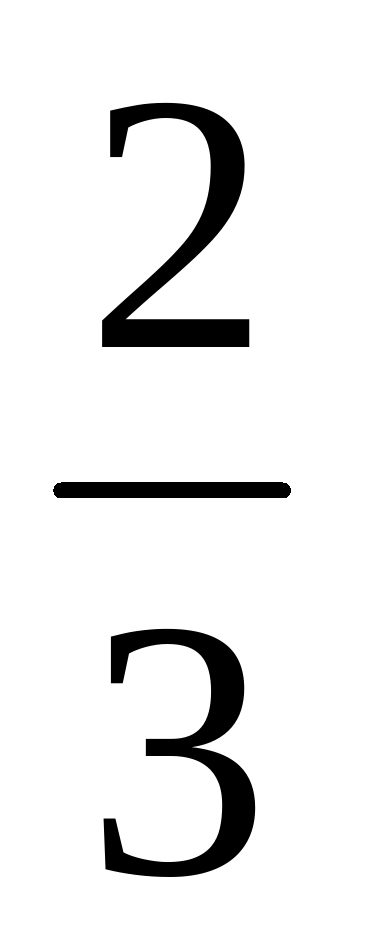 , ее
, ее 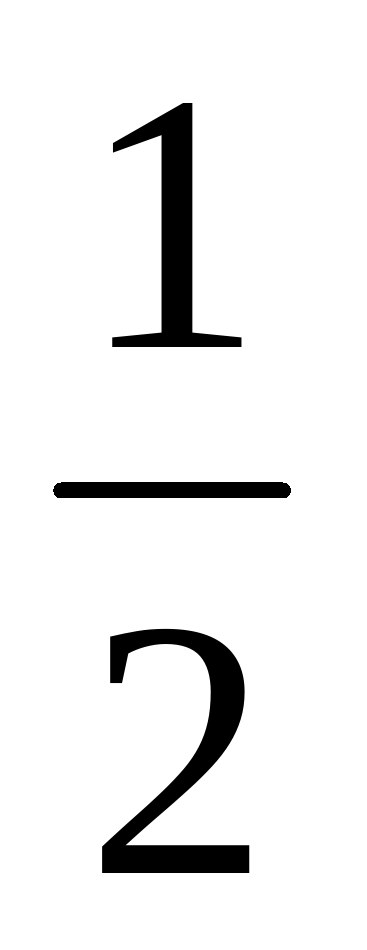 , ее
, ее 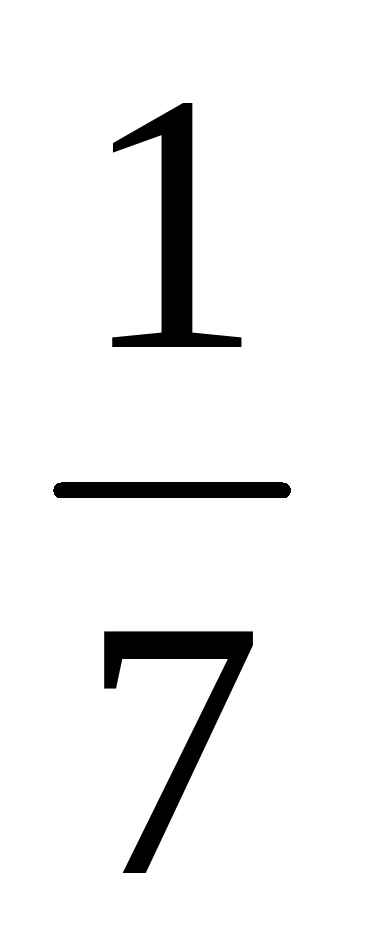 и ее целое. Это 33».
и ее целое. Это 33».
Если куча – х, то получаем уравнение:
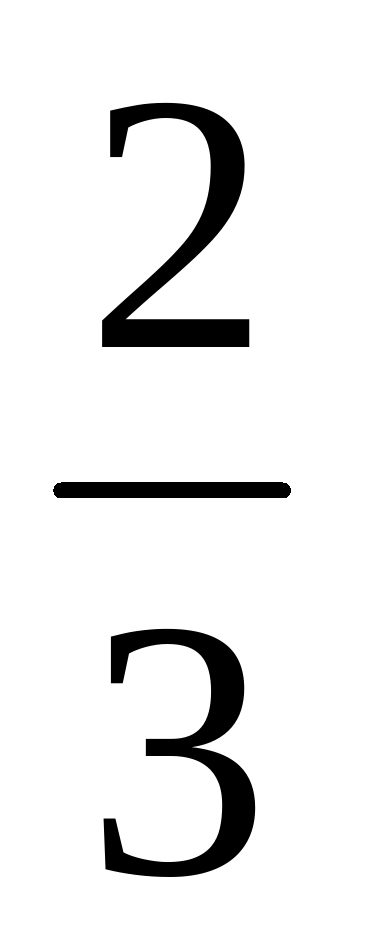 х +
х + 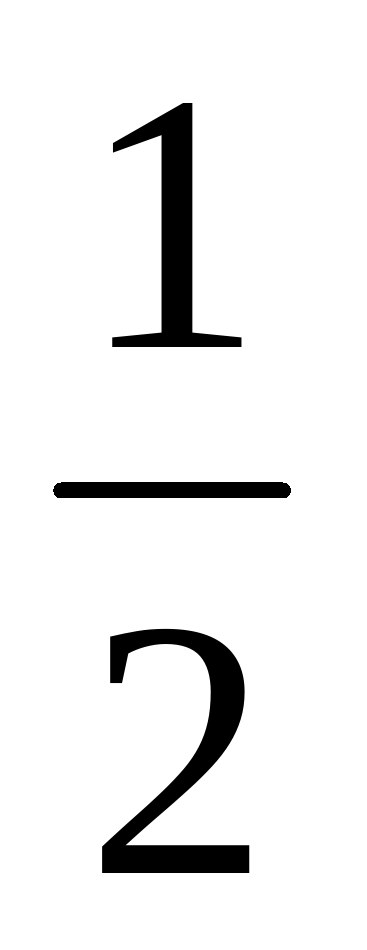 х +
х +  х + х = 33.
х + х = 33.






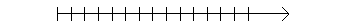



 x
x  2x + 13 = 19
2x + 13 = 19









