Просмотр содержимого документа
«1. Опорный конспект - Виды неравенств и их решение»
Просмотр содержимого документа
«4. Опорный конспект -Логарифмы »
Просмотр содержимого документа
«Технологическая карта»
Просмотр содержимого документа
«2. Опорный конспект - Равносильные преобразования»
Просмотр содержимого документа
«3. Опорный конспект - Методы решения неравенств»
Просмотр содержимого документа
«Лист самоконтроля»
Просмотр содержимого документа
«Самоанализ урока»
Просмотр содержимого презентации
«Презентация к уроку»

Секрет успеха – в мелочах
Успешно пройти ГИА
- качественная теоретическая подготовка
- качественная практическая подготовка (владение рациональными методами решения)
- самоконтроль, саморегуляция
- точное распределение времени на выполнение задания
- правильное оформление экзаменационной работы
- эмоциональный настрой
ЕГЭ 2015 (профиль)
Средний балл по России – 49, 6
Средний балл по Пермскому краю – 47
Средний балл по Пермскому району –
Подготовка к ЕГЭ 2016
Средний балл тренировочных работ 11 класса – 50, 52, 58

Тема: «Решение логарифмических неравенств»
Цели:
- повторить теоретический материал;
- выполнить практическую работу, вспомнить методы решения логарифмических неравенств;
- научиться находить рациональные способы решения;
- строить алгоритм решения неравенства;
- распределять время для выполнения работы;
- правильно оформлять работу;
- выработать волевую саморегуляцию (умение мобилизировать себя на решение проблемы).

Решение неравенств
Основные виды неравенств и способы их решения
Равносильные преобразования неравенств
Методы решения неравенств
Определение и свойства логарифма
Логарифмическая функция, её свойства и график

Задания для повторения
№ 1
Преобразуйте выражения, используя свойства логарифмов

Задания для повторения
№ 2
Представьте число в виде логарифма с основанием 2
№ 3
Вычислите:

Задания для повторения
№ 4
Выясните, при каких значениях Х существует логарифм
 1 функция __________, знак неравенства _______ при 0 монотонность логарифмической функции возрастает не меняем убывает меняем" width="640"
1 функция __________, знак неравенства _______ при 0 монотонность логарифмической функции возрастает не меняем убывает меняем" width="640"
Решение простейших логарифмических неравенств
При решении простейших логарифмических неравенств
необходимо учитывать ___________________________
- при а 1 функция __________, знак неравенства _______
- при 0
монотонность логарифмической функции
возрастает
не меняем
убывает
меняем

Решите неравенства
Работа в группах: составьте план решения неравенства
Метод подстановки
?
Решите неравенства самостоятельно
Свойства логарифмической функции
Метод интервалов
Свойства логарифма
Переход к равносильной системе

Проверка
1
65
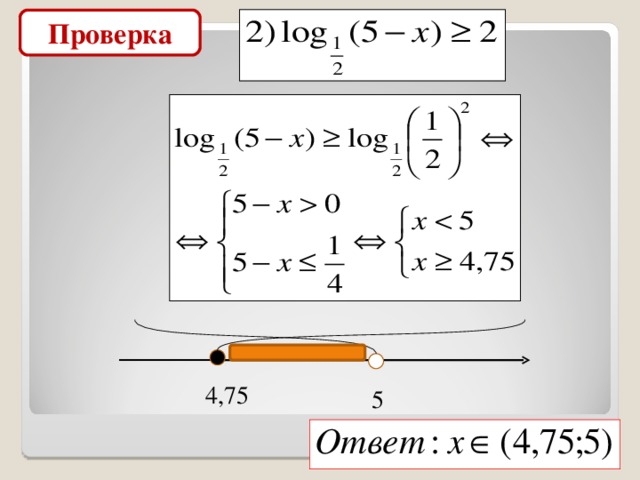
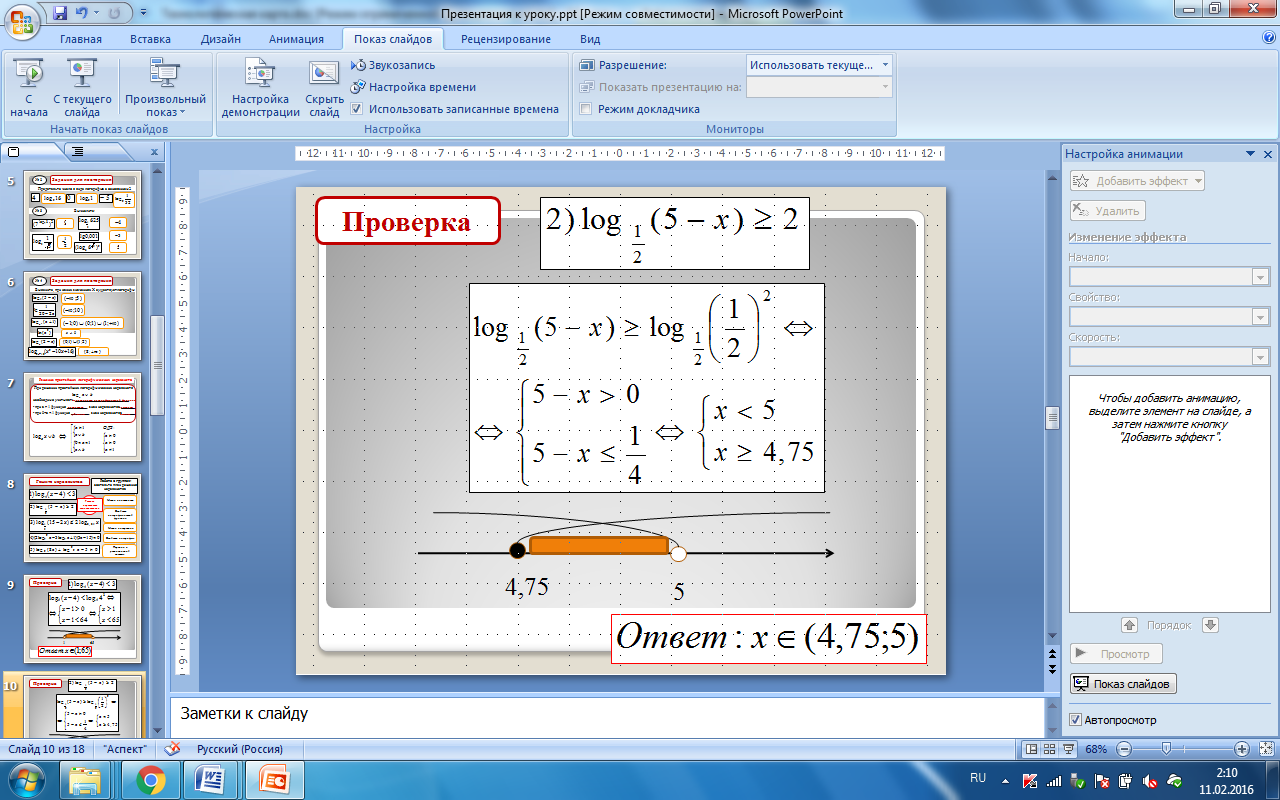
Проверка
4,75
5

Проверка
0
7,5
5
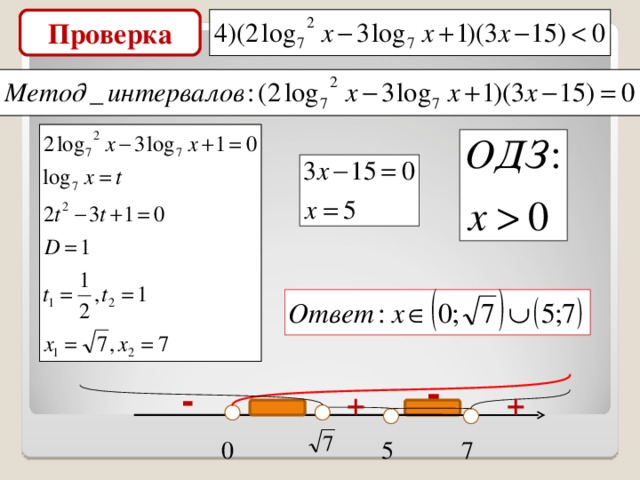
Проверка
-
-
+
+
7
5
0
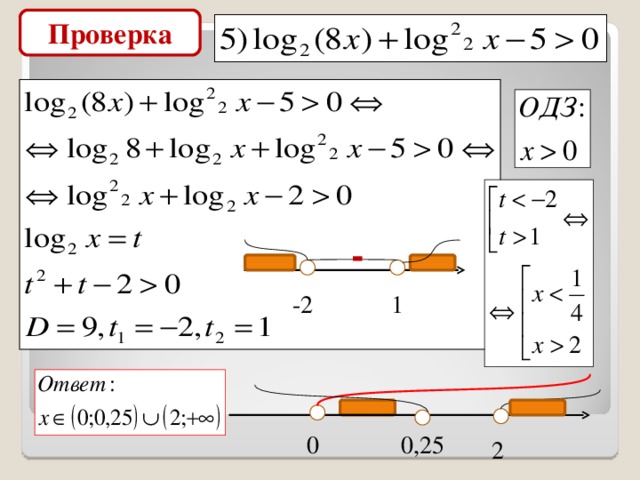
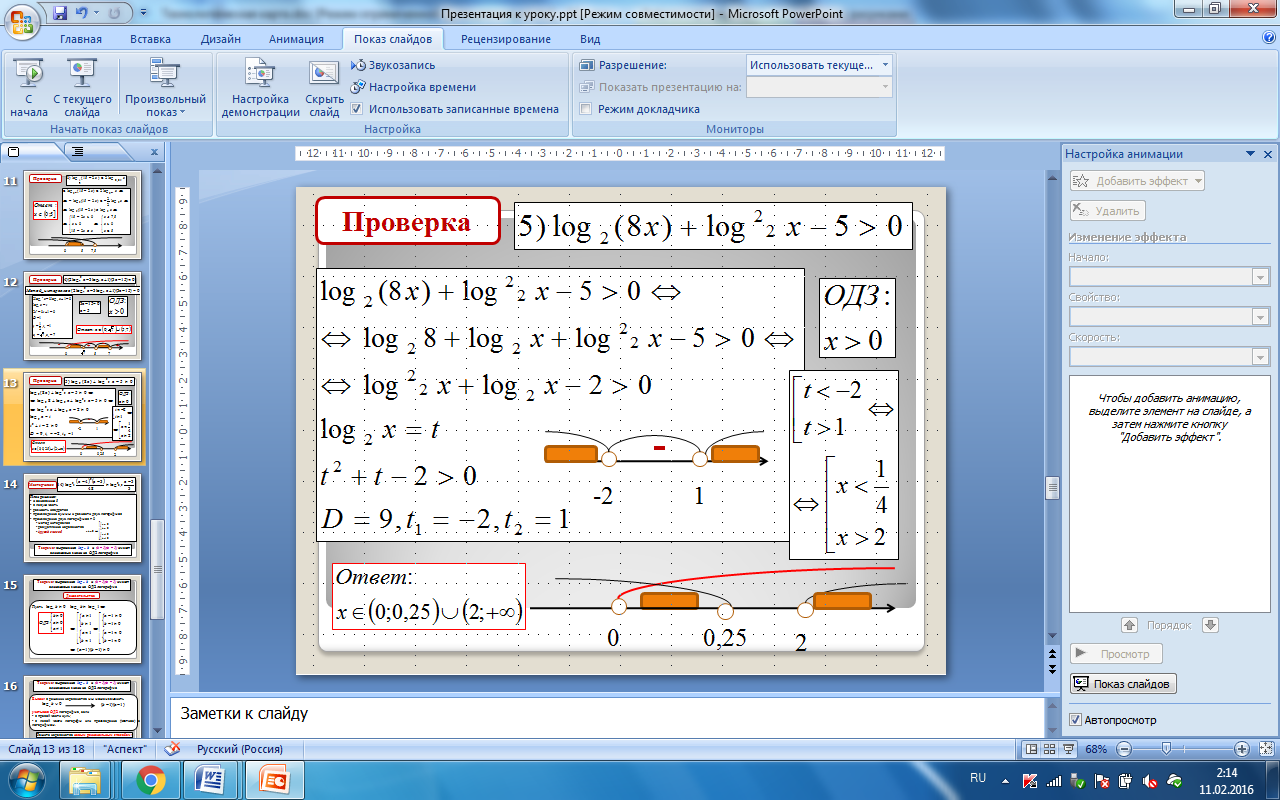
Проверка
-
-2
1
0,25
0
2
 0 метод интервалов расщепление неравенства другой способ метод интервалов расщепление неравенства другой способ к основанию 5 в левую часть разность квадратов произведение суммы и разности двух логарифмов произведение двух логарифмов 0 метод интервалов расщепление неравенства другой способ – метод интервалов расщепление неравенства другой способ – метод рационализации метод рационализации Теорема : выражения log а b и ( b – 1)(а – 1 ) имеют одинаковые знаки на ОДЗ логарифма" width="640"
0 метод интервалов расщепление неравенства другой способ метод интервалов расщепление неравенства другой способ к основанию 5 в левую часть разность квадратов произведение суммы и разности двух логарифмов произведение двух логарифмов 0 метод интервалов расщепление неравенства другой способ – метод интервалов расщепление неравенства другой способ – метод рационализации метод рационализации Теорема : выражения log а b и ( b – 1)(а – 1 ) имеют одинаковые знаки на ОДЗ логарифма" width="640"
Мастер-класс
План решения:
План решения:
- к основанию 5
- в левую часть
- разность квадратов
- произведение суммы и разности двух логарифмов
- произведение двух логарифмов 0 метод интервалов расщепление неравенства другой способ
- метод интервалов
- расщепление неравенства
- другой способ
- к основанию 5
- в левую часть
- разность квадратов
- произведение суммы и разности двух логарифмов
- произведение двух логарифмов 0 метод интервалов расщепление неравенства другой способ –
- метод интервалов
- расщепление неравенства
- другой способ –
метод рационализации
Теорема : выражения log а b и ( b – 1)(а – 1 ) имеют одинаковые знаки на ОДЗ логарифма

Теорема : выражения log а b и ( b – 1)(а – 1 ) имеют одинаковые знаки на ОДЗ логарифма
Доказательство
Пусть
13

Теорема : выражения log а b и ( b – 1)(а – 1 ) имеют одинаковые знаки на ОДЗ логарифма
Вывод: в решении неравенства мы можем заменить
учитывая ОДЗ логарифма, если
- в правой части нуль;
- в левой части логарифм или произведение (частное) с логарифмом.
Решите неравенства новым рациональным способом :

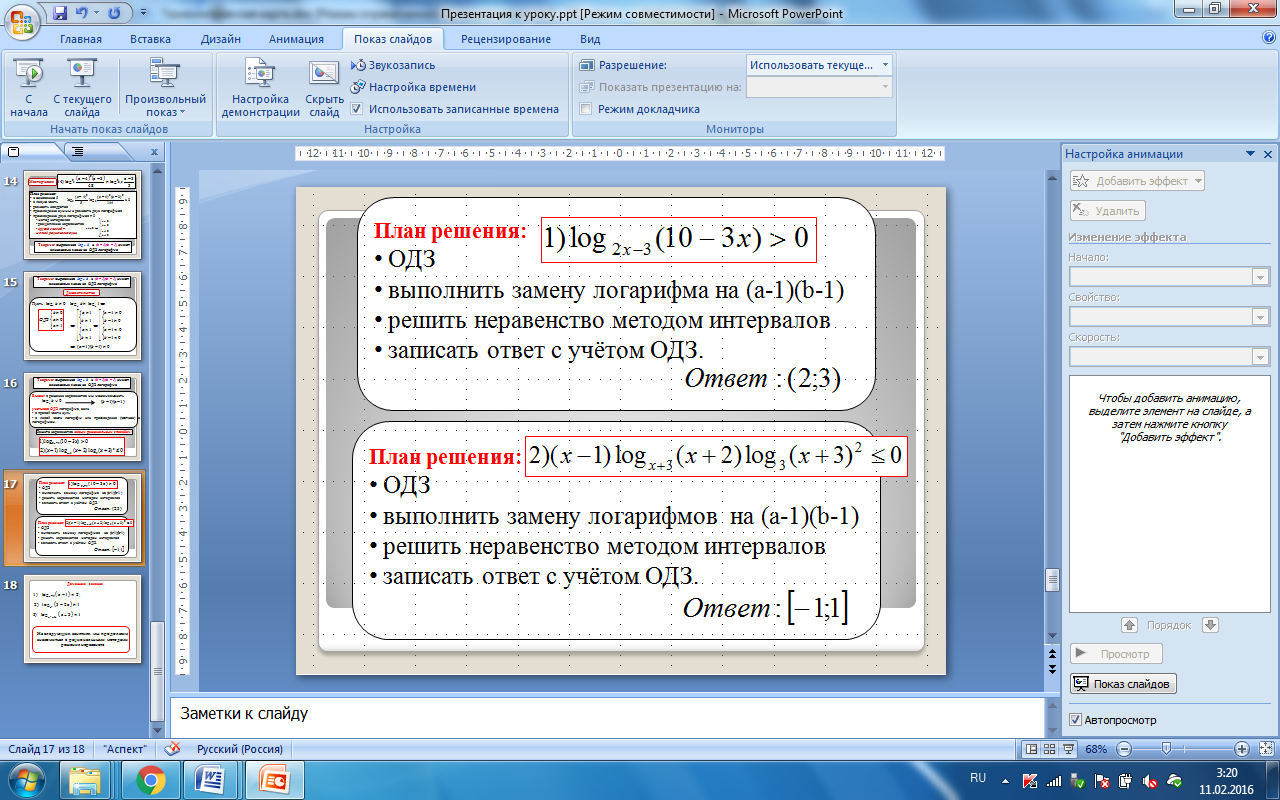
План решения:
- ОДЗ
- выполнить замену логарифма на ( a -1) (b-1)
- решить неравенство методом интервалов
- записать ответ с учётом ОДЗ.
План решения:
- ОДЗ
- выполнить замену логарифмов на ( a -1) (b-1)
- решить неравенство методом интервалов
- записать ответ с учётом ОДЗ.
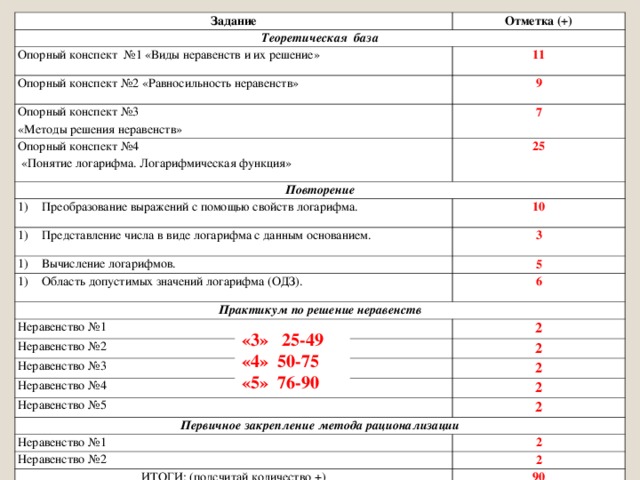
Задание
Отметка (+)
Теоретическая база
Опорный конспект №1 «Виды неравенств и их решение»
Опорный конспект №2 «Равносильность неравенств»
11
9
Опорный конспект №3
«Методы решения неравенств»
Опорный конспект №4
«Понятие логарифма. Логарифмическая функция»
7
25
Повторение
- Преобразование выражений с помощью свойств логарифма.
- Представление числа в виде логарифма с данным основанием.
10
3
- Область допустимых значений логарифма (ОДЗ).
5
6
Практикум по решение неравенств
Неравенство №1
Неравенство №2
2
2
Неравенство №3
Неравенство №4
2
Неравенство №5
2
2
Первичное закрепление метода рационализации
Неравенство №1
2
Неравенство №2
ИТОГИ: (подсчитай количество +)
2
90
«3» 25-49
«4» 50-75
«5» 76-90

Домашнее задание
Какие цели урока выполнили ?
На следующих занятиях мы продолжим знакомиться с рациональными методами решения неравенств







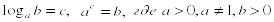 огарифмом положительного числа b по положительному и не равному единице основанию а называется показатель степени, в который нужно возвести число а, чтобы получить b.
огарифмом положительного числа b по положительному и не равному единице основанию а называется показатель степени, в который нужно возвести число а, чтобы получить b. войства логарифмов:
войства логарифмов: 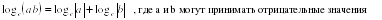
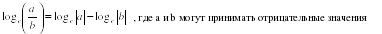
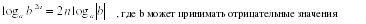

 адание: дополните предложение:
адание: дополните предложение: абота в парах
абота в парах
 роверка: сл. № 9 – 13.
роверка: сл. № 9 – 13.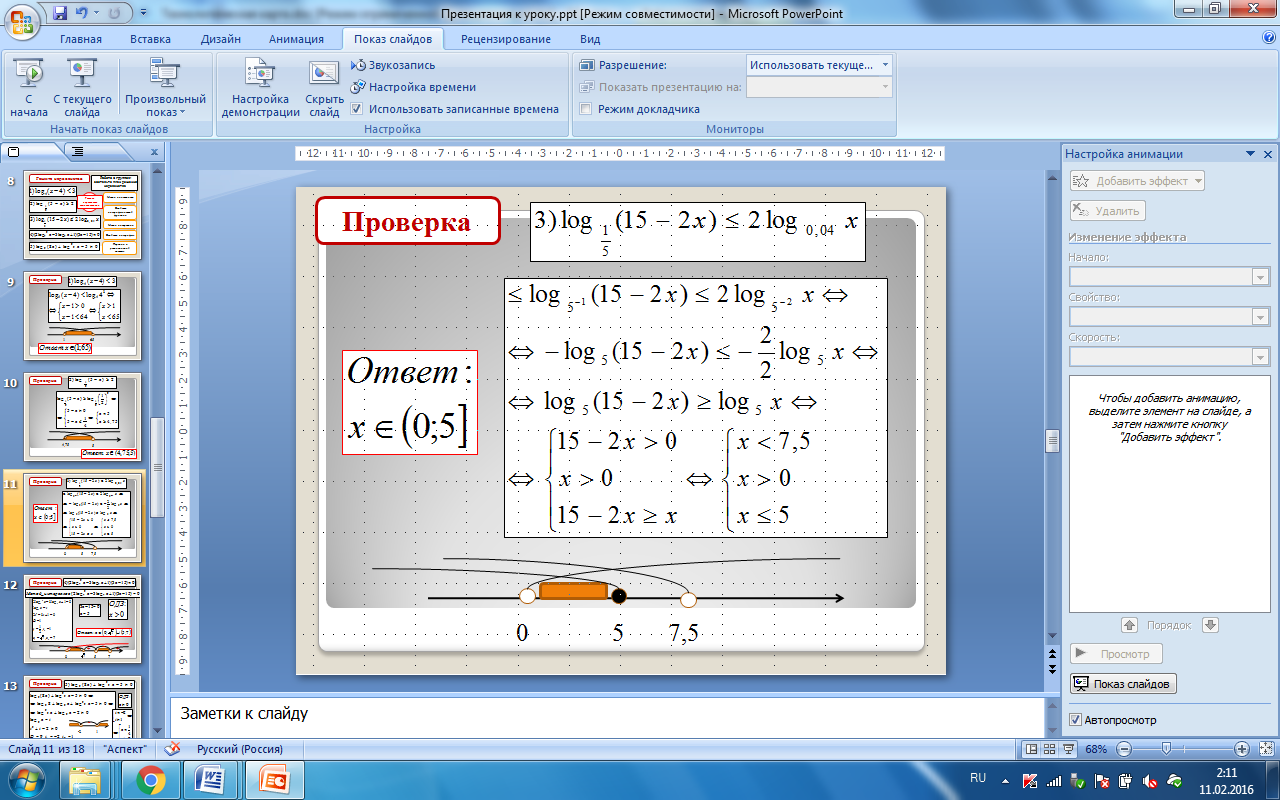


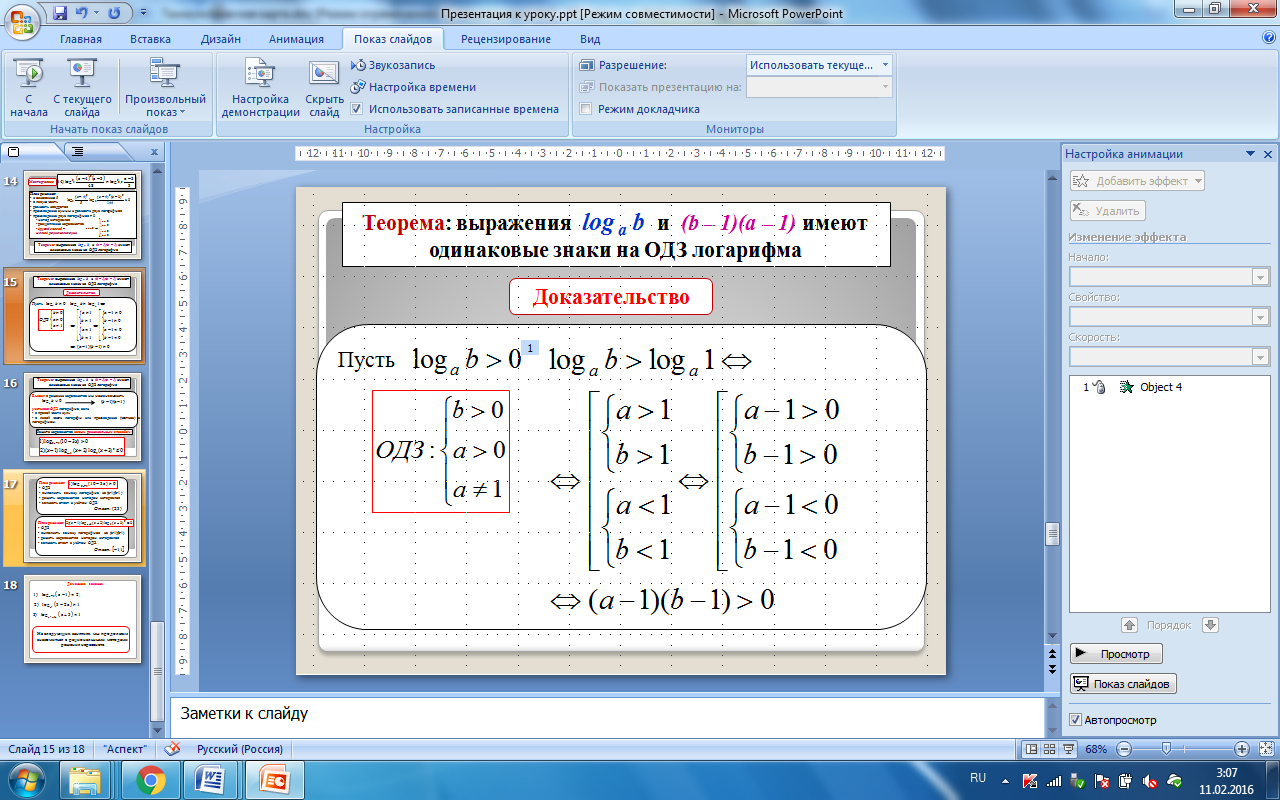 сделайте вывод, для чего мы доказали эту теорему?
сделайте вывод, для чего мы доказали эту теорему?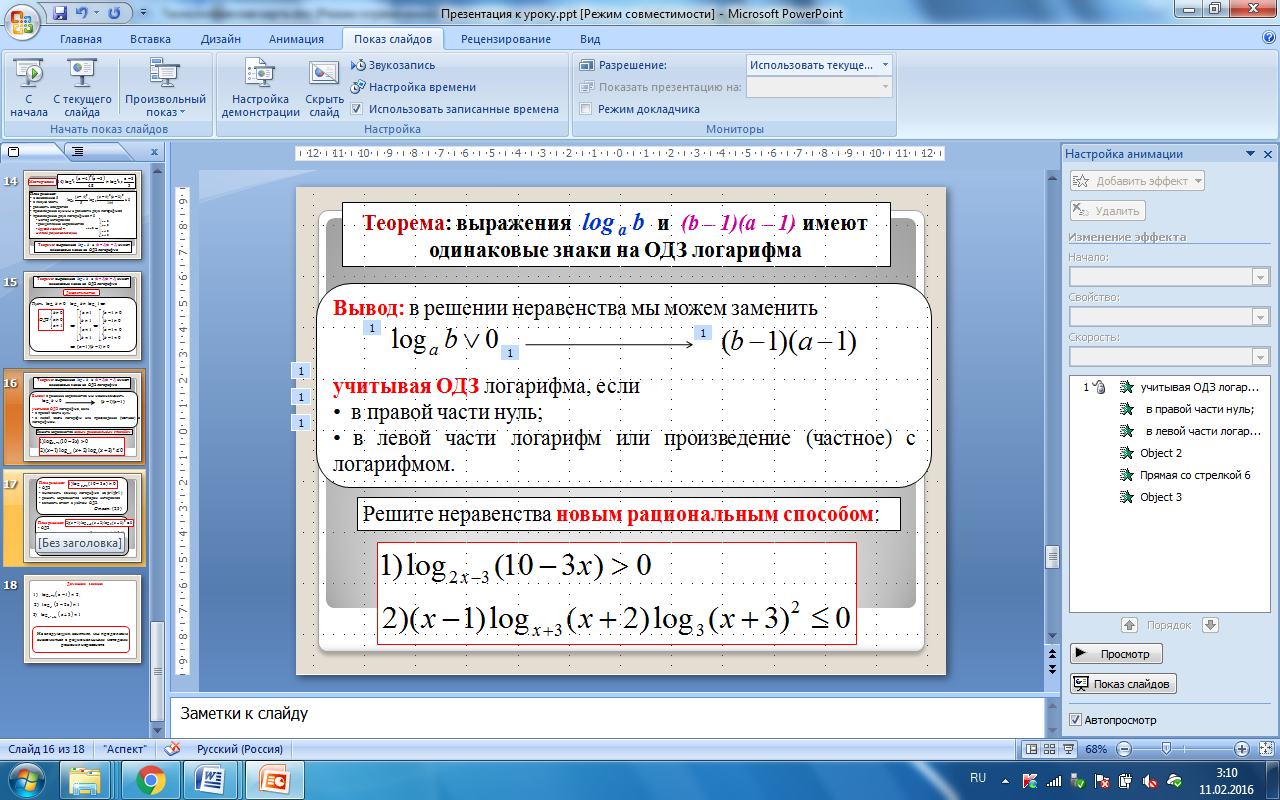
 аполняют лист самоконтроля (блок «Первичное закрепление метода рационализации»).
аполняют лист самоконтроля (блок «Первичное закрепление метода рационализации»).


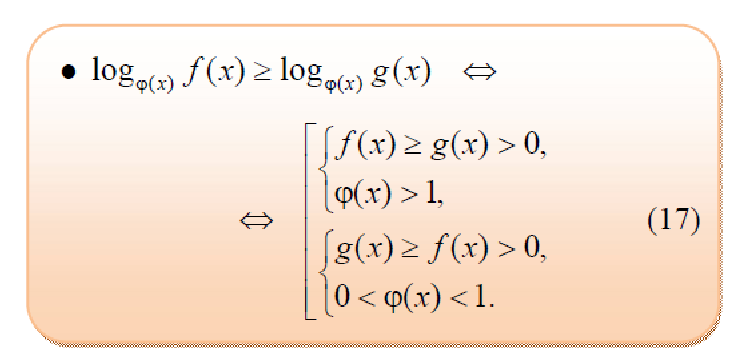




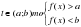
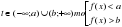






 1 функция __________, знак неравенства _______ при 0 монотонность логарифмической функции возрастает не меняем убывает меняем" width="640"
1 функция __________, знак неравенства _______ при 0 монотонность логарифмической функции возрастает не меняем убывает меняем" width="640"






 0 метод интервалов расщепление неравенства другой способ метод интервалов расщепление неравенства другой способ к основанию 5 в левую часть разность квадратов произведение суммы и разности двух логарифмов произведение двух логарифмов 0 метод интервалов расщепление неравенства другой способ – метод интервалов расщепление неравенства другой способ – метод рационализации метод рационализации Теорема : выражения log а b и ( b – 1)(а – 1 ) имеют одинаковые знаки на ОДЗ логарифма" width="640"
0 метод интервалов расщепление неравенства другой способ метод интервалов расщепление неравенства другой способ к основанию 5 в левую часть разность квадратов произведение суммы и разности двух логарифмов произведение двух логарифмов 0 метод интервалов расщепление неравенства другой способ – метод интервалов расщепление неравенства другой способ – метод рационализации метод рационализации Теорема : выражения log а b и ( b – 1)(а – 1 ) имеют одинаковые знаки на ОДЗ логарифма" width="640"















