Оценочные и методические материалы к образовательной программе основного общего образования 9 класс, геометрия.
| Класс, предмет | Учебник | Методические рекомендации, оценочные материалы (КИМЫ) |
| 9класс, геометрия | Геометрия 7-9 классы Учебник для общеобразовательных организаций Москва «Просвещение», 2017 | Контрольные работы по геометрии под редакцией Атанасяна |
Перечень контрольных работ за год по календарно-тематическому планированию
Входная контрольная работа
Контрольная работа №1 по теме: «Векторы»
Контрольная работа №2 по теме: «Метод координат»
Контрольная работа №3 по теме: «Соотношения между сторонами и углами треугольника. Скалярное произведение векторов»
Контрольная работа №4 по теме: «Длина окружности, площадь круга и кругового сектора»
Контрольная работа №5 по теме: «Движение»
Контрольная работа№6 по теме: «Начальные сведения из стереометрии»
Административная контрольная работа за первое полугодие
Административная контрольная работа за второе полугодие
Итоговая контрольная работа№10
Входная контрольная работа
Вариант 1
А1. В прямоугольном треугольнике найдите гипотенузу с, если его катеты равны: а=5 см, b=12 см.
А2. В треугольнике АВС 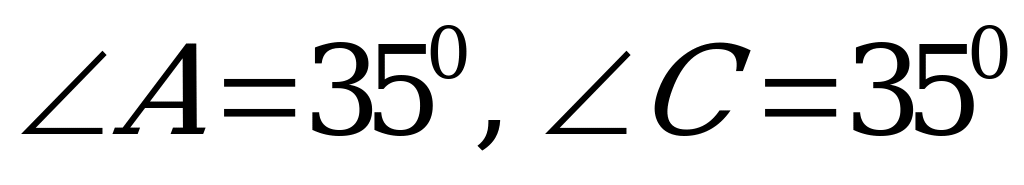 . Найдите
. Найдите 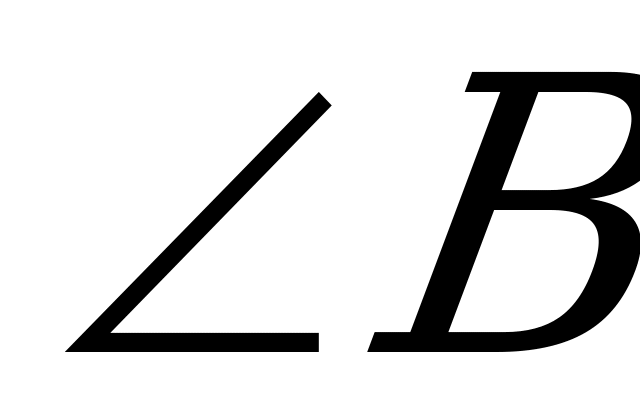 .
.
А3. В равнобедренном треугольнике боковая сторона равна 10 дм и основание равно 12 см. Найдите: а)высоту треугольника, проведенную к основанию треугольника; б) площадь треугольника.
А4. Постройте равнобедренный треугольник по боковой стороне и углу при основании.
__________________________________________________
В1. Около остроугольного треугольника АВС описана окружность с центром О. Расстояние от точки О до прямой АВ равно 6 см, 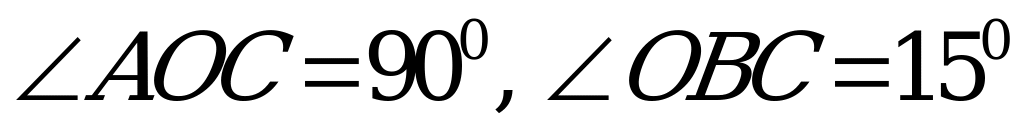 .
.
Найдите: а) угол АВО; б) радиус окружности.
Вариант 2
А1. В прямоугольном треугольнике гипотенуза с=25 см, один из его катетов: а=24 см. Найдите другой катет b.
А2. В прямоугольном треугольнике АВС 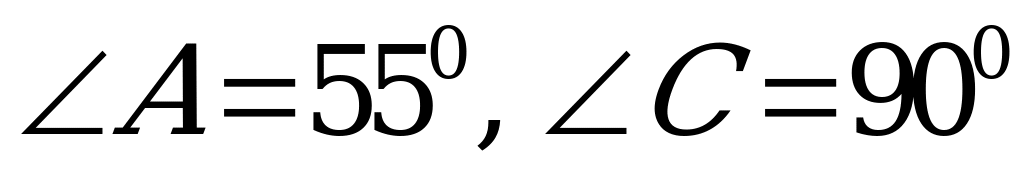 . Найдите
. Найдите 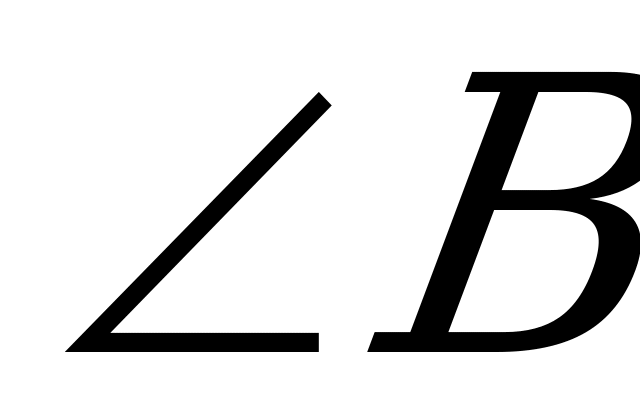 .
.
А3. В равнобедренном треугольнике боковая сторона равна 13 дм и основание равно 10 см. Найдите: а)высоту этого треугольника, проведенную к основанию треугольника; б) площадь треугольника.
А4. Постройте окружность данного радиуса, проходящую через две данные точки.
__________________________________________________
В1. В треугольник АВС с прямым углом С вписана окружность с центром О, касающаяся сторон АВ, ВС и СА в точках DE и F соответственно. Известно, что 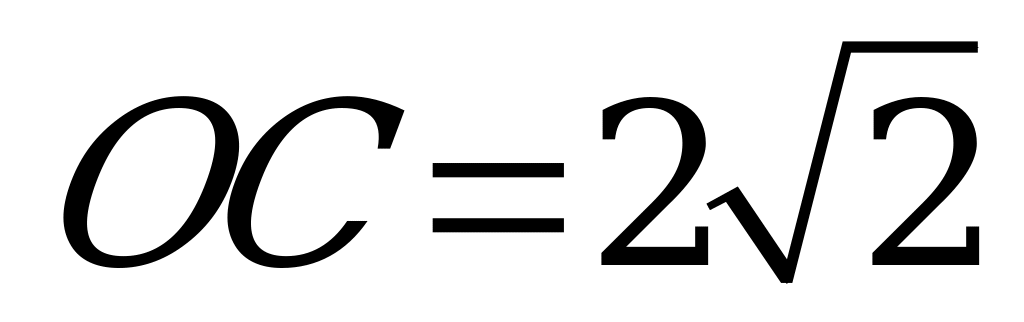 .
.
Найдите: а) радиус окружности; б) углы EOF и EDF.
Критерии оценивания
За верное выполнение каждого задания части А обучающийся получает 2 балла. За верное выполнение заданий части В – 5 балла. За неверный ответ или его отсутствие выставляется 0 баллов.
Максимальная сумма, которую может получить учащийся, – 13 балла.
Обучающийся получает оценку «3», набрав не менее 50% баллов (6 баллов); от 61 до 82% (от 7 до 11 баллов) – «4»; от 83 до 100% (12 до 13) - «5».
Контрольная работа №1 по теме: «Векторы»
|
|
| Вариант 1. |
|
1. ABCD – параллелограмм, 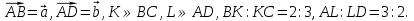 Найдите разложение вектора Найдите разложение вектора 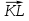 по неколлинеарным векторам по неколлинеарным векторам 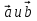 . .
2. Дана трапеция ABCD с основаниями AD=20 и BC=8, О -точка пересечения диагоналей. Разложите вектор 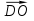 по векторам по векторам 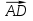 = =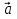 и и 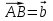 . .
3. Диагонали ромба АС = а, BD = b. Точка K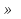 BD и BK : KD = 1 : 3. Найдите величину | BD и BK : KD = 1 : 3. Найдите величину |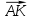 |. |.
4. В равнобедренной трапеции острый угол равен 60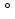 , боковая сторона равна 12 см, большее основание равно 30 см. Найдите среднюю линию трапеции. , боковая сторона равна 12 см, большее основание равно 30 см. Найдите среднюю линию трапеции.
5. В прямоугольнике ABCD известно, что AD=a, DC=b, O точка пересечения диагоналей. Найдите величину 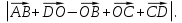 Вариант 2 |
1. ABCD – параллелограмм, 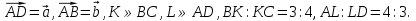 Найдите разложение вектора
Найдите разложение вектора 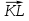 по неколлинеарным векторам
по неколлинеарным векторам 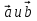 .
.
2. Дана трапеция ABCD с основаниями AD=15 и BC=10, О -точка пересечения диагоналей. Разложите вектор 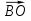 по векторам
по векторам 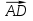 =
=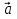 и
и 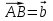 .
.
3. Диагонали ромба АС = а, BD = b. Точка K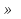 AC и AK : KC = 2: 3. Найдите величину |
AC и AK : KC = 2: 3. Найдите величину |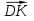 |.
|.
4. В равнобедренной трапеции острый угол равен 60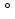 , боковая сторона равна 10 см, меньшее основание равно 14 см. Найдите среднюю линию трапеции.
, боковая сторона равна 10 см, меньшее основание равно 14 см. Найдите среднюю линию трапеции.
5. В прямоугольнике ABCD известно, что AB=a, BC=b, O точка пересечения диагоналей. Найдите величину 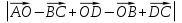 .
.
Критерии оценивания:
Каждое задание оценивается в 1 балл.
На «5» -5 баллов
На «4»- 4 балла
На «3» - 3 балла
Контрольная работа №2 по теме: «Метод координат»
Вариант 1
1. Четырехугольник имеет вершины с координатами А (1;1), В (3;5), С (9;-1), D(7;-5). Определите вид четырехугольника (с обоснованием) и найдите его диагонали.
2. Напишите уравнение окружности с центром в точке С (-3;1), проходящей через точку А (2;3).
3. Прямая l проходит через точки А (-3;1) и В (1;-7). Напишите уравнение прямой m, проходящей через точку С(5;6) и перпендикулярной прямой l.
Вариант 2
1. Четырехугольник имеет вершины с координатами А (-6;1), В (2;5), С (4;-1), D(-4;-5). Определите вид четырехугольника (с обоснованием) и найдите его диагонали.
2. Напишите уравнение окружности с центром в точке С (2;-3), проходящей через точку А (-1;-2).
3. Прямая l проходит через точки А (2;-1) и В (-3;9). Напишите уравнение прямой m, проходящей через точку С(3;10) и перпендикулярной прямой l.
Критерии оценивания:
Каждое задание оценивается в 1 балл.
На «5» -3 баллов
На «4»- 2 балла
На «3» - 1 балла
Контрольная работа №3 по теме: «Соотношения между сторонами и углами треугольника. Скалярное произведение векторов»
Вариант 1.
1) В треугольнике АВС 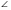 А = 450,
А = 450, 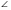 В = 600, ВС =
В = 600, ВС = 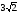 Найдите АС.
Найдите АС.
2). Две стороны треугольника равны 7 см и 8 см, а угол между ними равен 1200. Найдите третью сторону треугольника.
3) Найдите косинус угла М треугольника KLM, если К (1; 7), L (-2; 4), М (2; 0).
Вариант 2
1). В треугольнике СDE 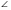 С = 300,
С = 300, 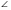 D = 450, СЕ =
D = 450, СЕ =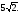 Найдите DE.
Найдите DE.
2). Две стороны треугольника равны 5 см и 7 см, а угол между ними равен 600. Найдите третью сторону треугольника.
3) Найдите косинус угла А треугольника ABC, если А (3; 9), В (0; 6), С (4; 2).
Критерии оценивания:
Каждое задание оценивается в 1 балл.
На «5» -3 баллов
На «4»- 2 балла
На «3» - 1 балла
Контрольная работа №4 по теме: «Длина окружности, площадь круга и кругового сектора»
Вариант №1
1. Длина окружности равна 8П см. Найти площадь круга.
2. Найти длину дуги окружности радиуса
6 см, если ее градусная мера равна 300.
3.Хорда окружности равна 6 и стягивает дугу 600 .Найдите длину дуги и площадь соответствующего сектора.
4.Найти площадь заштрихованной фигуры.
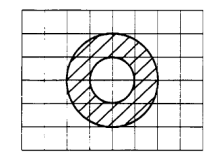
Размер клетки 1×1 см.
Вариант №2
1. Длина окружности , описанной около квадрата 16 П. Найти периметр квадрата.
2. Найти площадь круга, вписанного в треугольник со сторонами 10,13,и13 см.
3. Найти длину дуги окружности радиуса
4 см, если ее градусная мера равна 450.
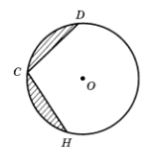
4.На рисунке хорды СD и СН стягивают дуги в 900.Радиус окружности R.Найти площадь заштрихованной фигуры.
Критерии оценивания:
Каждое задание оценивается в 1 балл.
На «5» -4 балла
На «4»- 3 балла
На «3» - 2 балла
Контрольная работа №5 по теме: «Движение»
Вариант 1
Начертите ромб ABCD. Постройте образ этого ромба:
При симметрии относительно точки С;
При симметрии относительно прямой АВ;
При параллельном переносе на вектор 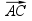 ;
;
При повороте вокруг точки D на 300 по часовой стрелке;
При повороте вокруг точки А на 600 против часовой стрелки.
Вариант 2
Начертите ромб ABCD. Постройте образ этого ромба:
При симметрии относительно точки С;
При симметрии относительно прямой АВ;
При параллельном переносе на вектор 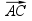 ;
;
При повороте вокруг точки D на 300 по часовой стрелке;
При повороте вокруг точки А на 600 против часовой стрелки.
Критерии оценивания:
Каждое задание оценивается в 1 балл.
На «5» -5 баллов
На «4»- 4 балла
На «3» - 3 балла
Контрольная работа№6 по теме: «Начальные сведения из стереометрии»
Вариант 1
1.а) Как могут быть взаимно расположены в пространстве прямая и плоскость?
б) Как надо понимать утверждение: «Прямые а и b не параллельны»?
2. Основание прямой призмы – параллелограмм со
сторонами 7 и 10 см и углом 30º, высота призмы равна
9 см. Найти площадь поверхности и объем призмы.
3. Сторона основания правильной четырехугольной
пирамиды равна 6 см, высота 4 см, апофема 5 см. Найти
площадь поверхности и объем пирамиды.
4.Найти площадь поверхности и объем цилиндра, радиус
которого равен 5 см, высота 9 см.
5.Прямоугольный треугольник с катетами 15 и 8 см
вращают вокруг оси, содержащей катет 15 см. Найти
площадь поверхности и объем конуса.
6.Найти площадь сферы и объем шара радиуса 9 см.
Хватит ли металлического бруска в форме прямоугольного параллелепипеда со сторонами 10,15, 20 см, чтобы выплавить такой шар?
Вариант 2
1.а) Как могут быть взаимно расположены в пространстве две плоскости?
б) Через две прямые нельзя провести плоскость. Как они расположены?
2. Основание прямой призмы – ромб со стороной 12 см и
углом 30º, высота призмы равна 7 см. Найти площадь
поверхности и объем призмы.
3. Сторона основания правильной четырехугольной
пирамиды равна 12 см, высота 8 см, апофема 10 см.
Найти площадь поверхности и объем пирамиды.
4.Найти площадь поверхности и объем цилиндра, радиус
которого равен 3 см, высота 5 см.
5.Прямоугольный треугольник с катетами 12 и 5 см
вращают вокруг оси, содержащей катет 12 см. Найти
площадь поверхности и объем конуса.
Найти площадь сферы и объем шара радиуса 6 см. Хватит ли металлического бруска в форме прямоугольного параллелепипеда со сторонами 9,10, 11 см, чтобы выплавить такой шар?
Критерии оценивания:
Каждое задание оценивается в 1 балл.
На «5» -5 баллов
На «4»- 4 балла
На «3» - 3 балла
Контрольная работа по геометрии за I-е полугодие
Вариант 1.
Часть 1
1. В трапеции ABCD, основания которой равны 5 и 8 см, MN – средняя линия.
Отрезок BE параллелен стороне CD. Найдите длину отрезка MK.
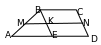
Ответ:__________________
2.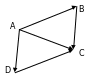 Какие из равенств являются верными? Укажите в ответе их номера.
Какие из равенств являются верными? Укажите в ответе их номера.
1. 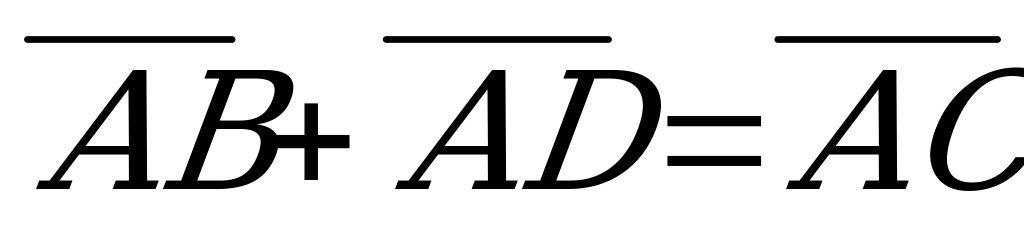 2.
2. 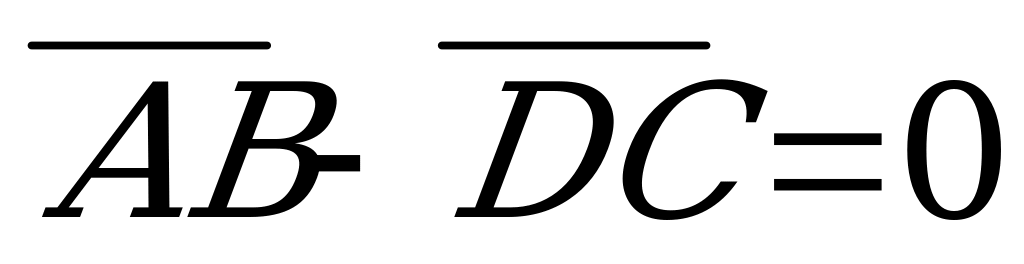 3.
3. 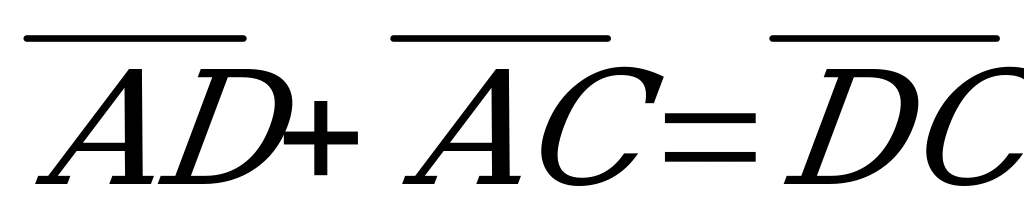
Ответ:__________________
3. Выберите верные утверждения, запишите их номера без пробелов и запятых:
1) Вектор — это направленный отрезок, для которого указано, какая из его точек является началом, а какая концом.
2) Векторы называются противоположными, если они сонаправлены и длины их равны.
3) Средняя линия трапеции — это отрезок, соединяющий середины её оснований
4) Каждая координата суммы двух и более векторов равна сумме соответствующих координат этих векторов
5) Вычисление длины вектора по его координатам вычисляется по формуле |a|= 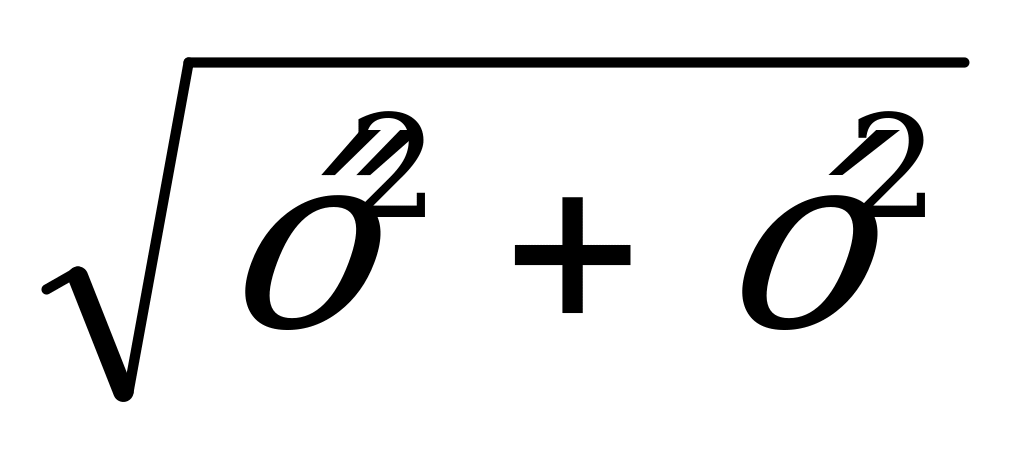
Найдите координаты центра окружности (х - 2)2 + (у + 1)2 = 16
1) (-2; 1) 2) (2; -1) 3) (1; -2) 4) (-1; 2)
Часть 2
(запишите подробное решение задач)
Радиус окружности равен 4. Центр окружности принадлежит оси Оу и имеет отрицательную координату. Окружность проходит через точку (0; -2). Напишите уравнение окружности.
Вариант 2
Часть 1
1. В трапеции ABCF, основания которой равны 7 и 10 см, MN – средняя линия.
Отрезок BE параллелен стороне CF. Найдите длину отрезка MK.
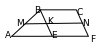
Ответ:__________________
2. Какие из равенств являются верными? Укажите в ответе их номера.
Какие из равенств являются верными? Укажите в ответе их номера.
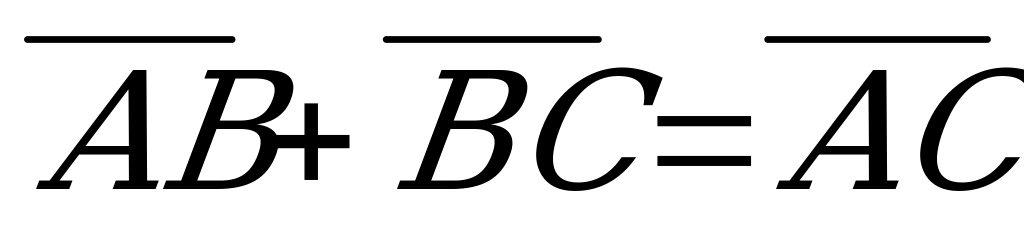 2.
2. 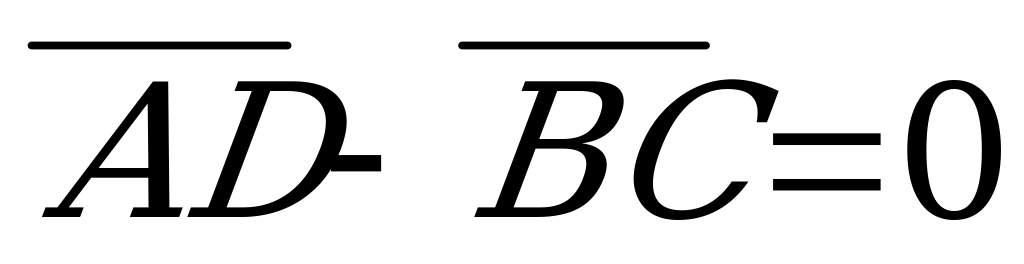 3.
3. 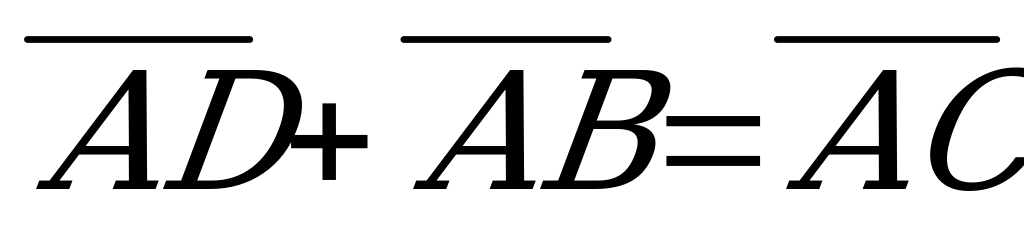
Ответ:__________________
3.Выберите верные утверждения, запишите их номера без пробелов и запятых:
1) От любой точки можно отложить вектор, равный данному и притом только один.
2) Векторы называются равными, если они сонаправлены
3) Средняя линия трапеции параллельна его основаниям и равна их полусумме
4) каждая координата суммы двух и более векторов равна разности соответствующих координат этих векторов.
5) Каждая координата середины отрезка равна полусумме соответствующих координат его концов.
Найдите координаты центра окружности (х + 4)2 + (у - 3)2 = 9
1) (3; 4) 2) (-3; 4) 3) (-4; 3) 4) (4; -3)
Часть 2
(запишите подробное решение задач)
Напишите уравнение прямой, проходящей через две точки А(-3;-3) и В(3;5)
Вариант 1
1. В треугольнике АВС точка D – середина стороны АВ, точка М – точка пересечения медиан.
а) Выразите вектор  через векторы
через векторы 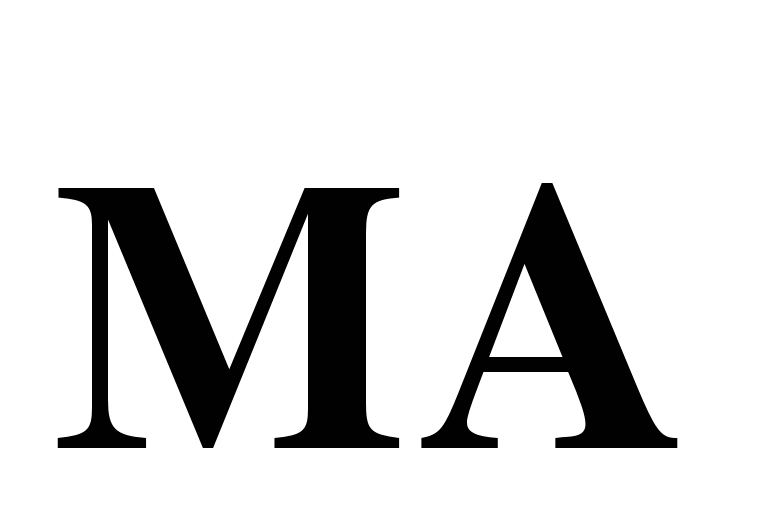 и
и 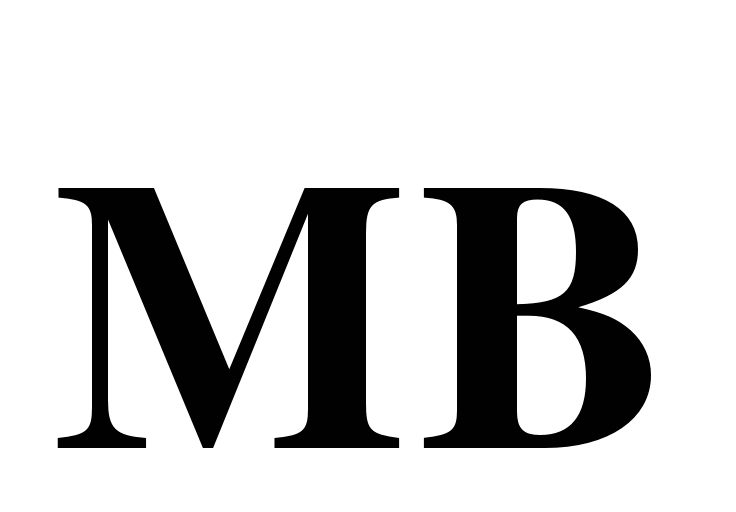 и вектор
и вектор 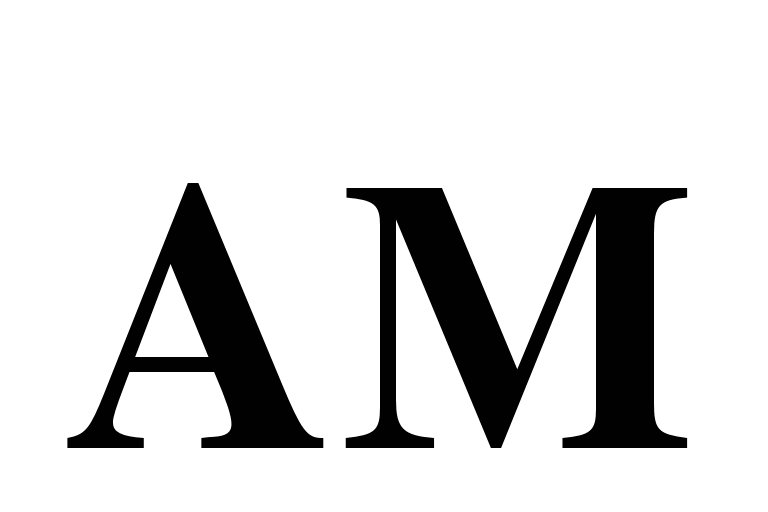 через векторы
через векторы 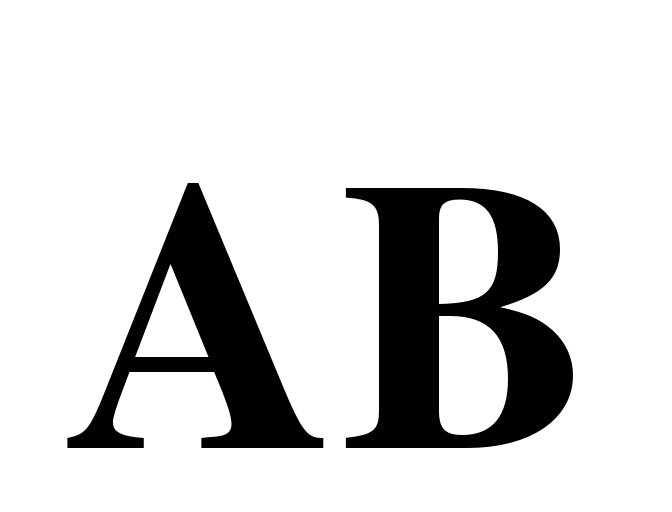 и
и 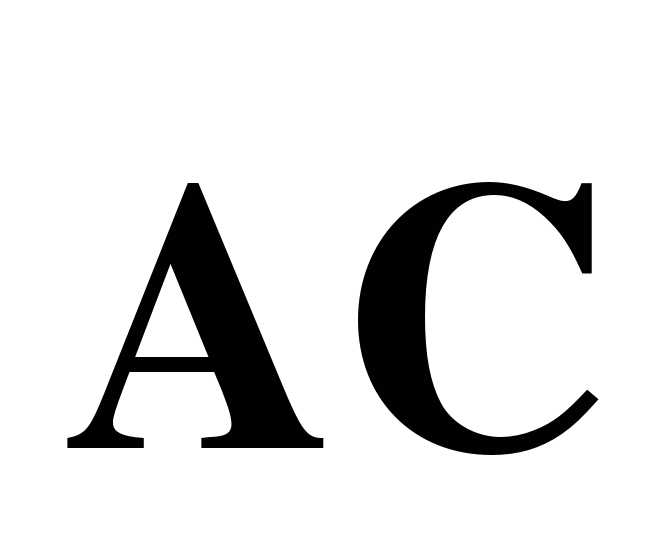 .
.
б) Найдите скалярное произведение 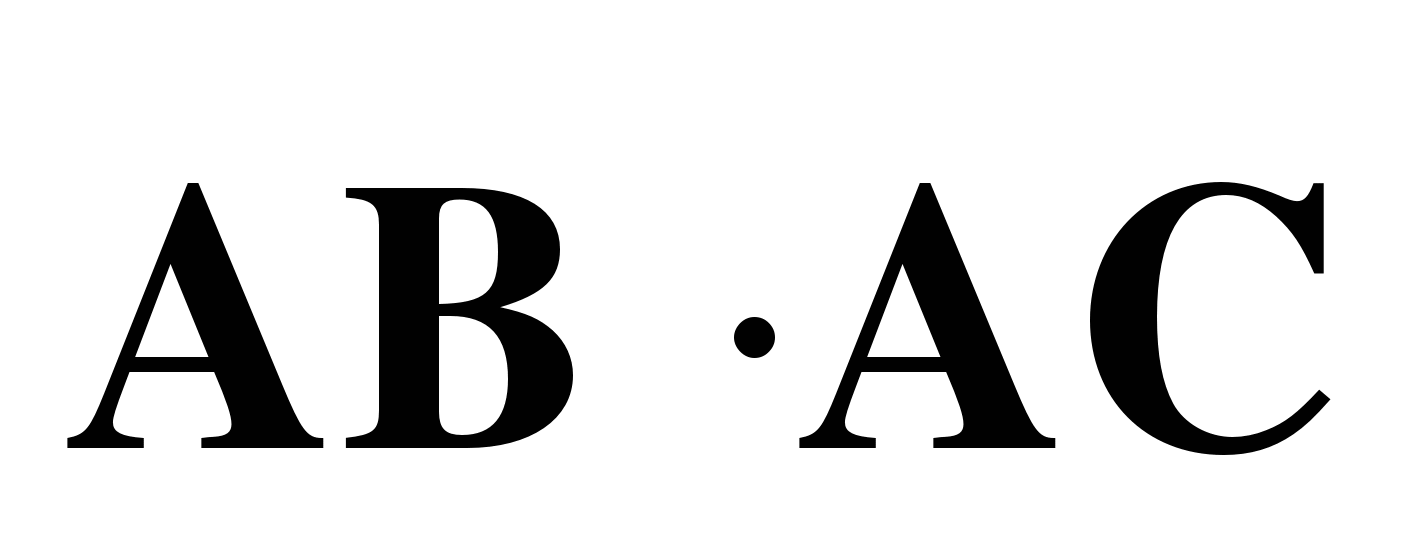 , если
, если 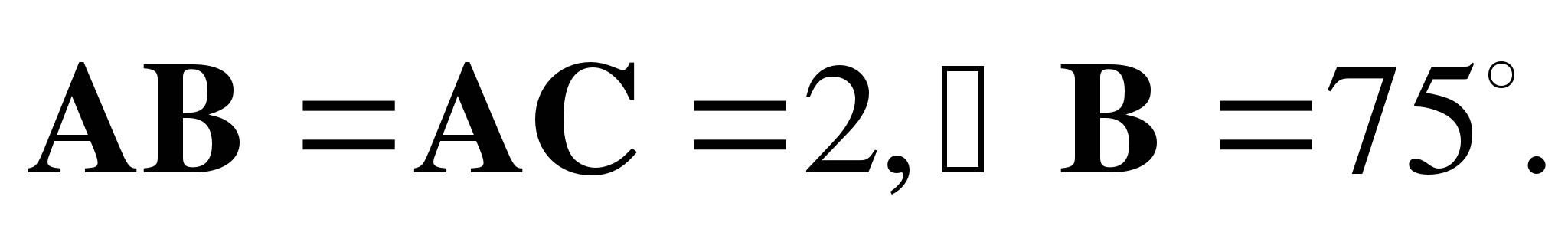
2. Даны точки А(1; 1), В(4; 5), С(-3; 4).
а) Докажите, что треугольник АВС равнобедренный и прямоугольный.
б) Найдите длину медианы СМ.
3. В треугольнике АВС 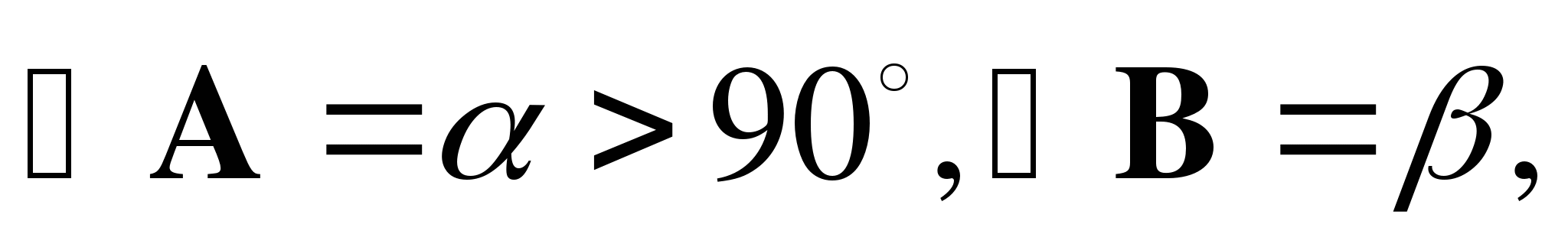 высота ВD равна h.
высота ВD равна h.
а) Найдите сторону АС и радиус R описанной окружности.
б) Вычислите значение R, если 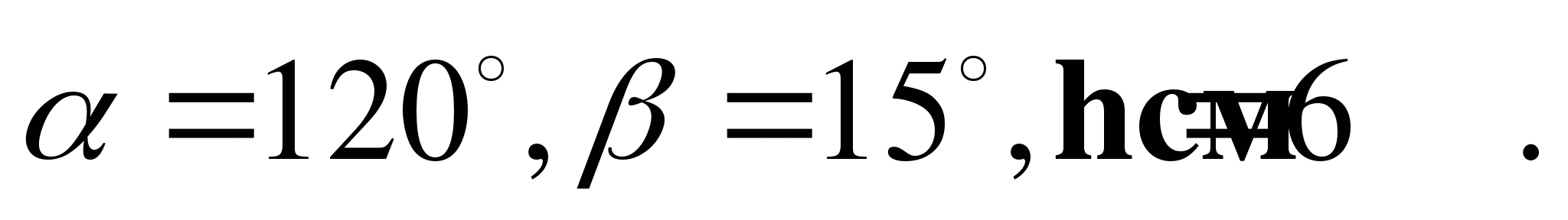
4. Хорда окружности равна а и стягивает дугу в 120о. Найдите: а) длину дуги; б) площадь сектора, ограниченного этой дугой и двумя радиусами.
Критерии оценивания:
Каждое задание оценивается в 1 балл.
На «5» -5 баллов
На «4»- 4 балла
На «3» - 3 балла
Контрольная работа за второе полугодие
1 вариант
1). В треугольнике АВС  А = 450,
А = 450,
 В = 600, ВС =
В = 600, ВС = 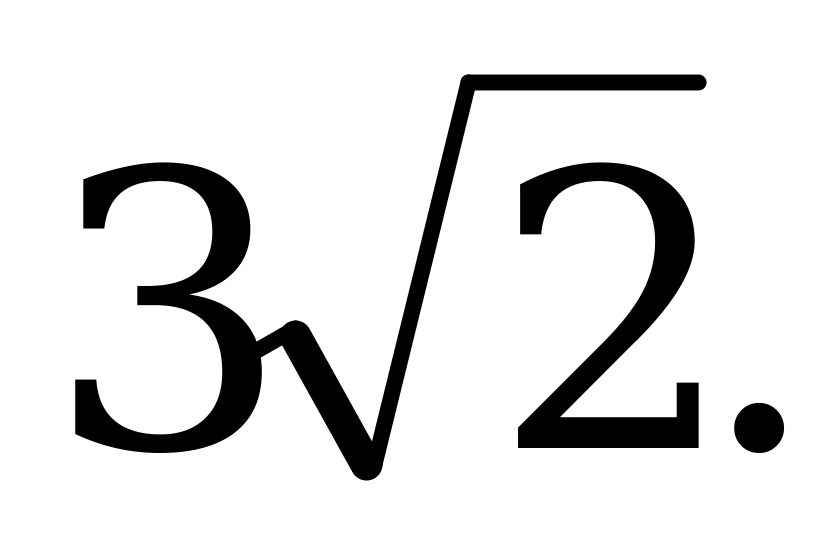 Найдите АС.
Найдите АС.
2). Две стороны треугольника равны
7 см и 8 см, а угол между ними равен 1200. Найдите третью сторону треугольника.
3). Определите вид треугольника АВС, если
А ( 3;9 ), В ( 0; 6 ), С ( 4; 2 ).
4). * В ΔАВС АВ = ВС, 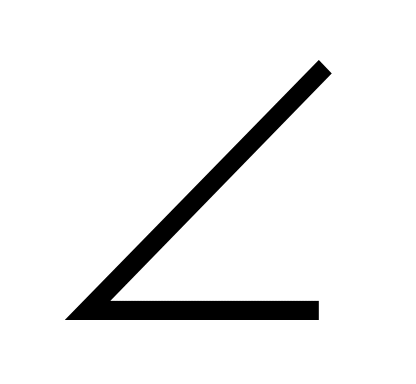 САВ = 300, АЕ – биссектриса, ВЕ = 8 см. Найдите площадь треугольника АВС.
САВ = 300, АЕ – биссектриса, ВЕ = 8 см. Найдите площадь треугольника АВС.
2 вариант
1). В треугольнике СDE 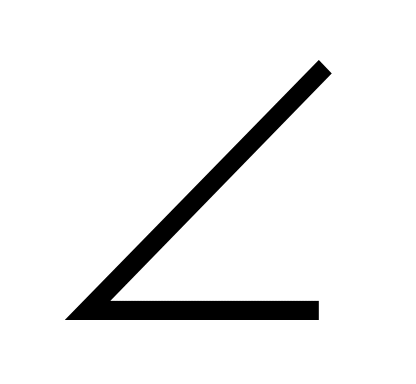 С = 300,
С = 300,
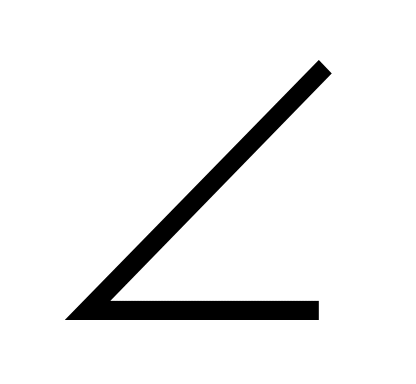 D = 450, СЕ =
D = 450, СЕ =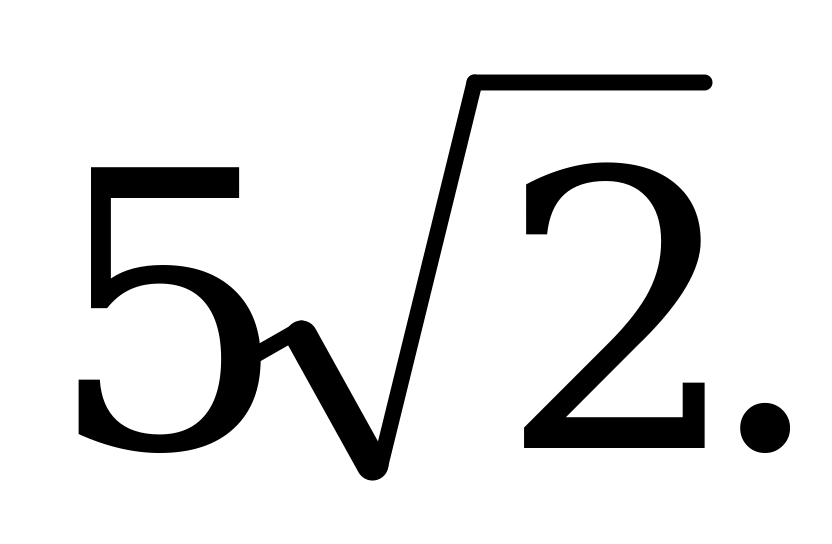 Найдите DE.
Найдите DE.
2). Две стороны треугольника равны
5 см и 7 см, а угол между ними равен 600. Найдите третью сторону треугольника.
3). Определите вид треугольника АВС, если
А ( 3;9 ), В ( 0; 6 ), С ( 4; 2 ).
4). * В ромбе
АВСD АК – биссектриса угла
САВ, 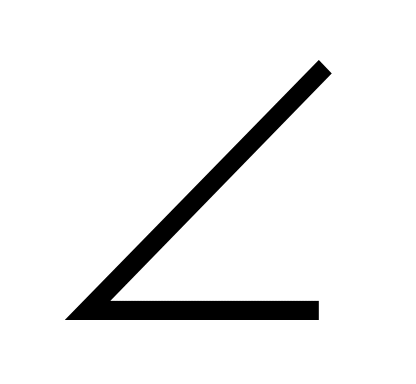 ВАD = 600, ВК = 12 см.
ВАD = 600, ВК = 12 см. Найдите площадь ромба.
Критерии оценивания:
Каждое задание оценивается в 1 балл.
На «5» -4 балл
На «4»- 3 балла
На «3» - 2 балла
Итоговая контрольная работа
Вариант 1
1. Сумма двух углов равнобедренной трапеции равна 140°. Найдите больший угол трапеции. Ответ дайте в градусах.
2. Отрезки AB и CD являются хордами окружности. Найдите длину хорды CD, если AB = 20, а расстояния от центра окружности до хорд AB и CD равны соответственно 24 и 10.
3. Периметр ромба равен 24, а синус одного из углов равен 1/3. Найдите площадь ромба.
4. На рисунке изображена трапеция . Используя рисунок, найдите cosHBA.
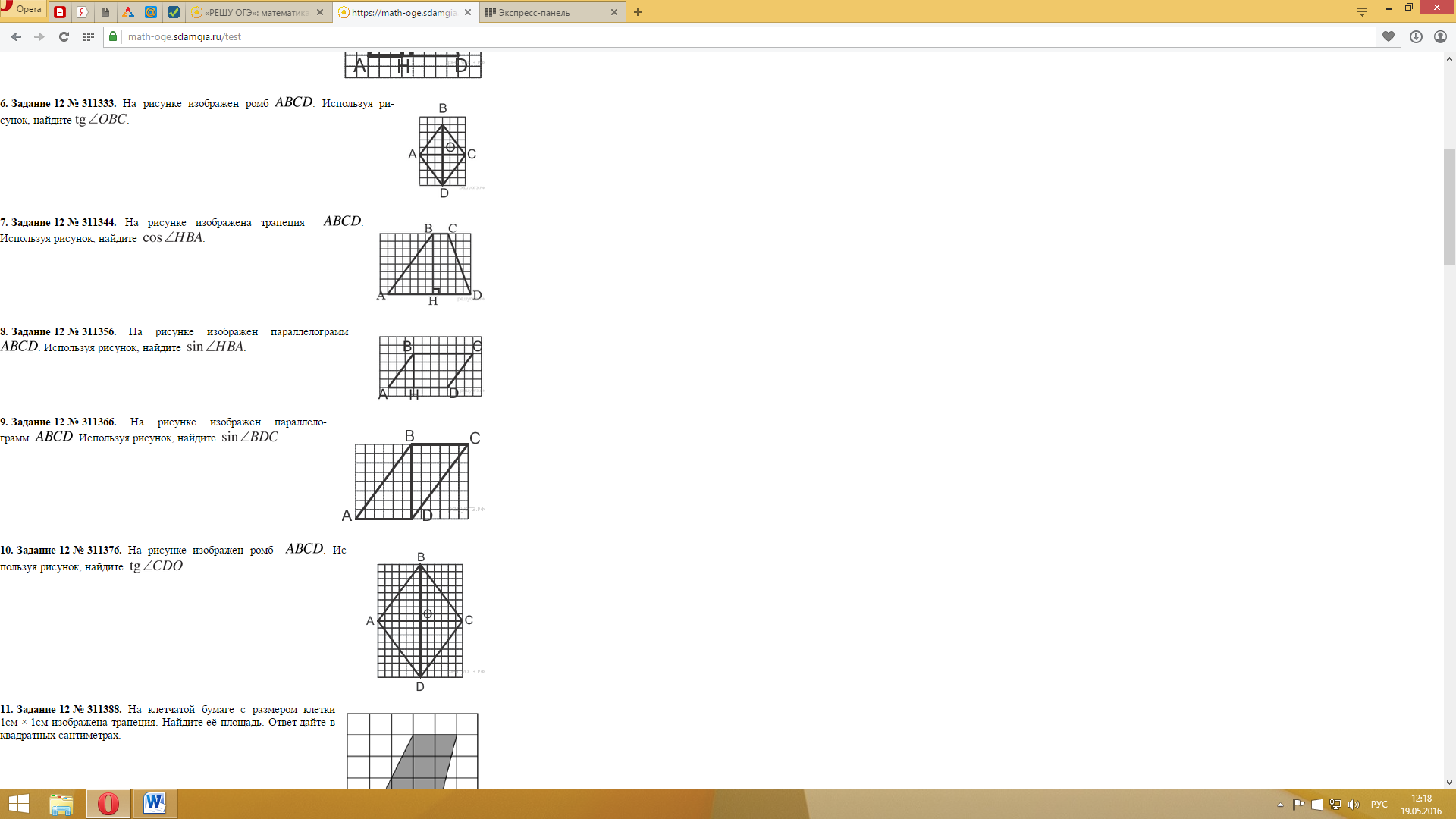
Вариант 2
1. Сумма двух углов равнобедренной трапеции равна 220°. Найдите меньший угол трапеции. Ответ дайте в градусах.
2. Отрезки AB и CD являются хордами окружности. Найдите расстояние от центра окружности до хорды CD, если AB = 18, CD = 24, а расстояние от центра окружности до хорды AB равно 12.
3. Одна из сторон параллелограмма равна 12, а опущенная на нее высота равна 10. Найдите площадь параллелограмма.
4. На рисунке изображен параллелограмм. Используя рисунок, найдите sinHBA.

Критерии оценивания:
Каждое задание оценивается в 1 балл.
На «5» -4 баллов
На «4»- 3 балла
На «3» - 2 балла







 Какие из равенств являются верными? Укажите в ответе их номера.
Какие из равенств являются верными? Укажите в ответе их номера.