Российская Федерация, Элиста
СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до 07.06.2025
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока
Была в сети 04.12.2018 21:13
Манджиева Девяля Чудеевна
Преподаватель математики
64 года
1 388
43 595 
Местоположение
Параллельный перенос
Категория:
Математика
04.12.2018 20:57
Просмотр содержимого документа
«Параллельный перенос»
Параллельный перенос
- Наглядно параллельный перенос определяется как преобразование, при котором точки смещаются в одном и том же направлении на одно и то же расстояние
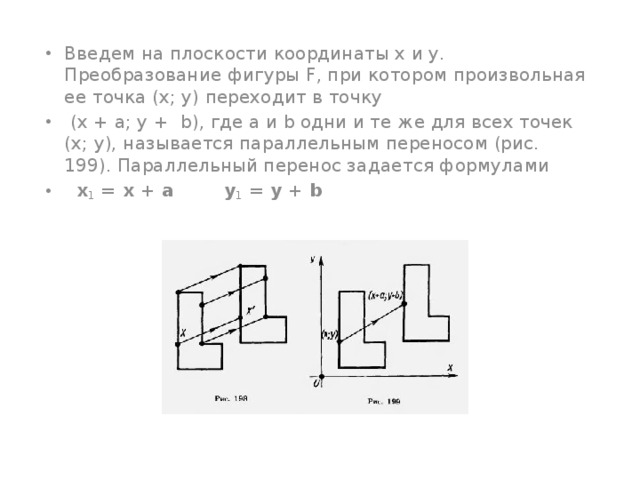
- Введем на плоскости координаты х и у. Преобразование фигуры F, при котором произвольная ее точка (х; у) переходит в точку
- (х + а; у + b), где а и b одни и те же для всех точек (х; у), называется параллельным переносом (рис. 199). Параллельный перенос задается формулами
- x 1 = x + а у 1 = у + b
Свойства параллельного переноса
Две произвольные точки А(х 1 ; у 1 ) и В (х 2 ; у 2 ) переходят при параллельном переносе в точки А 1 (х 1 +а; у 1 + b), В 1 (х 2 + а; y 2 +b). Поэтому АВ 2 =(х 2 -х 1 ) 2 + (у 2 -у 1 ) 2
A 1 B 1 2 =(х 2 -х 1 ) 2 + (у 2 -у 1 ) 2
Отсюда АВ=А 1 В 1 . Таким образом, параллельный перенос сохраняет расстояния, а значит, является движением, что и требовалось доказать.
- Пусть точки A (x 1 ; y 1 ) и В (x 2 ; y 2 ) переходят в точки A 1 (x 1 +а; y 1 + b) и В 1 (х 2 + а; y 2 + b) (рис. 200). Середина отрезка АВ 1 имеет координаты
Те же координаты имеет и середина отрезка А 1 В. Отсюда следует, что диагонали четырехугольника АА 1 В 1 В пересекаются и точкой пересечения делятся пополам. Значит, этот четырехугольник — параллелограмм. А у параллелограмма противолежащие стороны А А 1 и ВВ 1 параллельны и равны.
Заметим, что у параллелограмма АА 1 В 1 В параллельны и две другие противолежащие стороны — АВ и А 1 В 1 . Отсюда следует, что при параллельном, переносе прямая переходит в параллельную прямую.
- В предыдущем доказательстве предполагалось, что точка В не лежит на прямой АА 1 . В случае, когда точка В лежит на прямой АА 1 , точка В 1 тоже лежит на этой прямой, так как середина отрезка АВ 1 совпадает с серединой отрезка ВА 1 (рис. 201). Значит, все точки А, В, А 1 , В 1 лежат на одной прямой.
Таким образом:
В таком случае точки А и В смещаются по прямой АВ на одно и то же расстояние
Примеры параллельного переноса можно найти в архитектуре, живописи
Примеры параллельного переноса:
Примеры параллельного переноса:
Примеры параллельного переноса:
- Спасибо за внимание!
© 2018, Манджиева Девяля Чудеевна 1093 2
Рекомендуем курсы ПК и ППК для учителей
Похожие файлы
Вебинар для учителей
Свидетельство об участии БЕСПЛАТНО!
Полезное для учителя
Реализация образовательных программ осуществляется с применением исключительно электронного обучения и ДОТ
