Параллелограмм.
Приступаем к изучению разных видов четырёхугольников.
Определение. Параллелограммом называется выпуклый четырёхугольник, у которого стороны попарно параллельны.
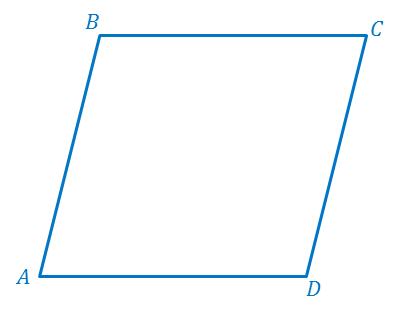
 – параллелограмм. У него
– параллелограмм. У него  .
.
Рассмотрим свойства параллелограмма.
ТЕОРЕМА. У параллелограмма противолежащие стороны и углы равны.
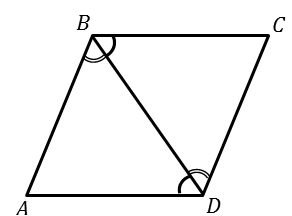
Дано:  – параллелограмм
– параллелограмм
Доказать: 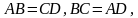
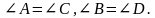
Доказательство.
1. Проведём диагональ 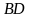 . Рассмотрим
. Рассмотрим 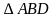 и
и 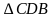 .
.

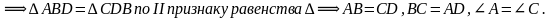
2. 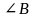 и
и 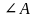 ;
; 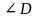 и
и 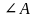 – внутренние односторонние при параллельных прямых, значит,
– внутренние односторонние при параллельных прямых, значит,
 .
.
3. Итак,  , ч.т.д.
, ч.т.д.
ТЕОРЕМА. Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам.
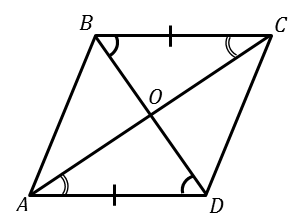
Дано:  – параллелограмм
– параллелограмм
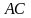 и
и 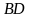 – диагонали
– диагонали
Доказать: 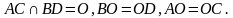
Доказательство.
1. Т.к. параллелограмм является выпуклым четырёхугольником, то, по свойству выпуклых многоугольников, его диагонали пересекаются, т.е. 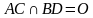 .
.
2. Рассмотрим 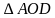 и
и  .
.
по II признаку равенства треугольников , ч.т.д.
Итак, параллелограмм обладает двумя свойствами:
Противолежащие стороны и углы параллелограмма равны.
Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам.
Признаки параллелограмма.
Часто бывает ситуация, когда известны какие-то свойства четырёхугольника, а какой вид имеет этот четырёхугольник неизвестно. В этом случае помогут признаки параллелограмма.
ТЕОРЕМА (I признак параллелограмма).
Если в четырёхугольнике две стороны равны и параллельны, то такой четырёхугольник является параллелограммом.
Дано:  – четырёхугольник
– четырёхугольник

Доказать:  – параллелограмм.
– параллелограмм.
Доказательство.
Проведём диагональ 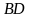 и рассмотрим
и рассмотрим 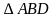 и
и 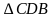 .
.
. Эти углы являются внутренними накрест лежащими при прямых  и
и  , значит, по признаку параллельности прямых,
, значит, по признаку параллельности прямых,  .
.
Итак, в четырёхугольнике  , т.е. стороны попарно параллельны, значит,
, т.е. стороны попарно параллельны, значит,  – параллелограмм (по определению), ч.т.д.
– параллелограмм (по определению), ч.т.д.
ТЕОРЕМА (II признак параллелограмма).
Если в четырёхугольнике противоположные стороны попарно равны, то этот четырёхугольник является параллелограммом.
Дано:  – четырёхугольник
– четырёхугольник

Доказать:  – параллелограмм.
– параллелограмм.
Доказательство.
Проведём диагональ 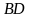 и рассмотрим
и рассмотрим 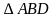 и
и 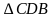 .
.
 и
и  . А эти пары углов являются внутренними накрест лежащими. По признаку параллельных прямых: «если внутренние накрест лежащие углы равны, то прямые параллельны», делаем вывод, что
. А эти пары углов являются внутренними накрест лежащими. По признаку параллельных прямых: «если внутренние накрест лежащие углы равны, то прямые параллельны», делаем вывод, что  , а
, а  . По определению параллелограмма, данный четырёхугольник является параллелограммом, ч.т.д.
. По определению параллелограмма, данный четырёхугольник является параллелограммом, ч.т.д.
ТЕОРЕМА (III признак параллелограмма).
Если в четырёхугольнике диагонали пересекаются и точкой пересечения делятся пополам, то такой четырёхугольник является параллелограммом.
Дано:  – четырёхугольник,
– четырёхугольник,
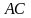 и
и 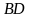 – диагонали,
– диагонали,  ,
,

Доказать:  – параллелограмм.
– параллелограмм.
Доказательство.
Рассмотрим  и
и  .
.
по I признаку равенства треугольников  и
и  . А эти углы являются внутренними накрест лежащими при прямых
. А эти углы являются внутренними накрест лежащими при прямых  и
и  , значит,
, значит,  .
.
Мы доказали, что в четырёхугольнике  две стороны параллельны и равны (
две стороны параллельны и равны ( ), значит, по I признаку, этот четырёхугольник является параллелограммом, ч.т.д.
), значит, по I признаку, этот четырёхугольник является параллелограммом, ч.т.д.
Начертите параллелограмм  . Проведите в нём диагонали
. Проведите в нём диагонали 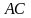 и
и 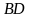 . Обозначьте их точку пересечения буквой
. Обозначьте их точку пересечения буквой  .
.
Найдите длину отрезка  , если известно, что диагональ
, если известно, что диагональ  см.
см.
Чему равна диагональ 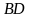 , если известно, что отрезок
, если известно, что отрезок  см?
см?
Найдите периметр треугольника  , если сторона
, если сторона  равна
равна  см, а диагонали
см, а диагонали 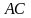 и
и 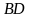 равны
равны  см и
см и  см соответственно.
см соответственно.
Две стороны параллелограмма равны  см и
см и  см. Найдите периметр параллелограмма.
см. Найдите периметр параллелограмма.
Сумма двух противолежащих углов параллелограмма равна  . Чему равны эти углы?
. Чему равны эти углы?
Периметр параллелограмма равен  см. Одна из его сторон равна
см. Одна из его сторон равна  см. Определите остальные стороны параллелограмма.
см. Определите остальные стороны параллелограмма.
Найдите углы параллелограмма, если известно, что один из них равен сумме двух других углов параллелограмма.
Одна из сторон параллелограмма равна  см, а другая – в
см, а другая – в  раза меньше. Найдите периметр параллелограмма.
раза меньше. Найдите периметр параллелограмма.
Высоты параллелограмма равны  см и
см и  см. Найдите расстояние от точки пересечения диагоналей параллелограмма до одной из меньших сторон.
см. Найдите расстояние от точки пересечения диагоналей параллелограмма до одной из меньших сторон.
В параллелограмме  сторона
сторона  см, диагонали равны
см, диагонали равны  см и
см и  см, точка
см, точка  – точка пересечения диагоналей. Чему равен периметр треугольника
– точка пересечения диагоналей. Чему равен периметр треугольника  ?
?
В параллелограмме один угол равен  . Найдите остальные углы параллелограмма.
. Найдите остальные углы параллелограмма.
В треугольнике  . Из точки, взятой на стороне
. Из точки, взятой на стороне  , проведены две прямые, параллельные сторонам
, проведены две прямые, параллельные сторонам  и
и 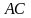 . Определите вид получившегося четырёхугольника и все его углы.
. Определите вид получившегося четырёхугольника и все его углы.
Четырёхугольник  – параллелограмм, отрезки равны. Докажите, что
– параллелограмм, отрезки равны. Докажите, что  также является параллелограммом.
также является параллелограммом.
Диагональ 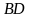 параллелограмма
параллелограмма  продолжена на равные отрезки
продолжена на равные отрезки  и
и  . Докажите, что
. Докажите, что  также является параллелограммом.
также является параллелограммом.
В параллелограмме  биссектриса угла
биссектриса угла  пересекает сторону
пересекает сторону  в точке
в точке  , причём,
, причём,  . Найдите периметр параллелограмма.
. Найдите периметр параллелограмма.
Диагональ параллелограмма составляет со сторонами параллелограмма углы в  и
и  . Найдите углы параллелограмма.
. Найдите углы параллелограмма.
Стороны параллелограмма относятся как  , а его периметр равен
, а его периметр равен  см. Найдите стороны параллелограмма.
см. Найдите стороны параллелограмма.
В четырёхугольнике . Диагонали четырёхугольника пересекаются в точке  . Найдите периметр
. Найдите периметр  .
.
Из вершины  параллелограмма
параллелограмма  с острым углом
с острым углом  проведён перпендикуляр
проведён перпендикуляр  к прямой . Найдите
к прямой . Найдите  и
и 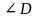 .
.
В выпуклом четырёхугольнике . Докажите, что  .
.
Середина отрезка 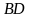 является центром окружности с диаметром
является центром окружности с диаметром 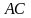 , причём, точки
, причём, точки  не лежат на одной прямой. Докажите, что
не лежат на одной прямой. Докажите, что  .
.
Постройте параллелограмм по большей стороне, меньшей диагонали и углу между ними.
В четырёхугольнике – точка пересечения диагоналей. Периметр треугольника  равен
равен  см,
см,  см,
см,  см. Найдите
см. Найдите  .
.
Дан параллелограмм  с острым углом
с острым углом  . Из вершины
. Из вершины  опущен перпендикуляр
опущен перпендикуляр  к прямой
к прямой  . Найдите
. Найдите  и
и 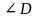 .
.
В выпуклом шестиугольнике  все стороны равны,
все стороны равны,  . Докажите, что
. Докажите, что  .
.
Дан параллелограмм  . На продолжении диагонали
. На продолжении диагонали 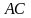 за вершины
за вершины  и
и  отмечены точки
отмечены точки  и
и  соответственно так, что
соответственно так, что  . Докажите, что
. Докажите, что  .
.
Постройте параллелограмм по меньшей стороне, острому углу и углу между этой стороной и меньшей диагональю.
Одна сторона параллелограмма втрое больше другой стороны. Найдите стороны параллелограмма, если его периметр равен  см.
см.
В параллелограмме  с острым углом
с острым углом  из вершины
из вершины  проведён перпендикуляр
проведён перпендикуляр  к прямой
к прямой  . Найдите углы параллелограмма, если
. Найдите углы параллелограмма, если  .
.
Один из углов параллелограмма на  меньше другого. Найдите углы параллелограмма.
меньше другого. Найдите углы параллелограмма.
В параллелограмме  с острым углом
с острым углом  из вершины
из вершины  проведён перпендикуляр
проведён перпендикуляр  к прямой
к прямой  . Найдите углы параллелограмма, если
. Найдите углы параллелограмма, если  .
.
Докажите, что четырёхугольник, имеющий центр симметрии, является параллелограммом.
На диагонали 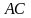 параллелограмма
параллелограмма  отмечены две точки
отмечены две точки  и
и  так, что
так, что  . Докажите, что четырёхугольник
. Докажите, что четырёхугольник  – параллелограмм.
– параллелограмм.
На сторонах  и
и  параллелограмма
параллелограмма  вне его построены правильные треугольники
вне его построены правильные треугольники  и
и  . Докажите, что треугольник
. Докажите, что треугольник  равносторонний.
равносторонний.
Докажите, что выпуклый четырёхугольник  является параллелограммом, если
является параллелограммом, если  .
.
Угол  параллелограмма
параллелограмма  меньше угла
меньше угла  . Докажите, что
. Докажите, что  .
.
В параллелограмме  проведена биссектриса угла
проведена биссектриса угла  , которая пересекает сторону
, которая пересекает сторону  в точке
в точке  .
.
Докажите, что треугольник  равнобедренный.
равнобедренный.
Найдите сторону  , если
, если  см, а периметр параллелограмма равен
см, а периметр параллелограмма равен  см.
см.
На стороне  параллелограмма
параллелограмма  взята точка
взята точка  так, что
так, что  .
.
Докажите, что  – биссектриса угла
– биссектриса угла  .
.
Найдите периметр параллелограмма, если  см,
см,  см.
см.
В выпуклом четырёхугольнике  диагонали
диагонали 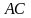 и
и 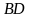 пересекаются в точке
пересекаются в точке  .
.  – медиана треугольника
– медиана треугольника  ,
,  – медиана треугольника
– медиана треугольника  . Докажите, что
. Докажите, что  – параллелограмм.
– параллелограмм.
Прямая  параллельна стороне
параллельна стороне  параллелограмма
параллелограмма  и пересекает стороны
и пересекает стороны  и
и  в точках
в точках  и
и  соответственно. Докажите, что
соответственно. Докажите, что  – параллелограмм.
– параллелограмм.
В  проведена медиана
проведена медиана  . На её продолжении за точку
. На её продолжении за точку  отложен отрезок
отложен отрезок  , равный
, равный  . Докажите, что четырёхугольник
. Докажите, что четырёхугольник  является параллелограммом.
является параллелограммом.
С тороны  и
и  треугольника
треугольника  продолжены на точку
продолжены на точку  так, что
так, что 
 . Докажите, что четырёхугольник
. Докажите, что четырёхугольник  – параллелограмм.
– параллелограмм.
 – параллелограмм, . Найдите
– параллелограмм, . Найдите  .
.
Одна из сторон параллелограмма на  см больше другой. Периметр параллелограмма равен
см больше другой. Периметр параллелограмма равен  см. Найдите стороны параллелограмма.
см. Найдите стороны параллелограмма.
В параллелограмме  диагональ
диагональ  перпендикулярна стороне
перпендикулярна стороне  и равна ей. Найдите углы параллелограмма.
и равна ей. Найдите углы параллелограмма.
Периметр параллелограмма равен  см. Найдите длины сторон, если известно, что диагональ параллелограмма делит угол на части
см. Найдите длины сторон, если известно, что диагональ параллелограмма делит угол на части  и
и  .
.
В параллелограмме  из вершины тупого угла
из вершины тупого угла  проведена высота
проведена высота  к стороне
к стороне  так, что
так, что  . Найдите углы параллелограмма.
. Найдите углы параллелограмма.
Найдите длины высот параллелограмма, если известно, что стороны  см и
см и  см, а углы относятся как
см, а углы относятся как  .
.
Найдите углы параллелограмма, если известно, что один из них в  раз меньше суммы всех остальных углов параллелограмма.
раз меньше суммы всех остальных углов параллелограмма.
В треугольнике  проведена медиана
проведена медиана  и продолжена на свою длину
и продолжена на свою длину  за точку
за точку  . Найдите периметр четырёхугольника
. Найдите периметр четырёхугольника  , если периметр треугольника
, если периметр треугольника  равен
равен  см,
см,  см.
см.
Биссектриса угла параллелограмма пересекает его сторону, образуя с ней угол  . Найдите углы параллелограмма.
. Найдите углы параллелограмма.
Биссектриса угла  параллелограмма
параллелограмма  пересекает сторону
пересекает сторону  в точке
в точке  . Найдите периметр параллелограмма, если
. Найдите периметр параллелограмма, если  см,
см,  см.
см.
Биссектриса угла параллелограмма пересекает его сторону, образуя с ней угол  . Найдите углы параллелограмма.
. Найдите углы параллелограмма.
Периметр параллелограмма  равен
равен  см. Биссектрисы углов
см. Биссектрисы углов  и
и  пересекаются на стороне
пересекаются на стороне  . Найдите длины сторон параллелограмма.
. Найдите длины сторон параллелограмма.
Биссектриса угла  параллелограмма
параллелограмма  пересекает сторону
пересекает сторону  в точке
в точке  . Найдите углы параллелограмма, если известно, что .
. Найдите углы параллелограмма, если известно, что .
Периметр параллелограмма  равен
равен  см. Биссектриса
см. Биссектриса  угла
угла  и биссектриса
и биссектриса  угла
угла  делят сторону
делят сторону  на три равные части так, что точка
на три равные части так, что точка  лежит между точками
лежит между точками  и
и  . Найдите длины сторон параллелограмма.
. Найдите длины сторон параллелограмма.
Биссектриса угла  параллелограмма
параллелограмма  пересекает сторону
пересекает сторону  в точке
в точке  . Найдите углы параллелограмма, если известно, что .
. Найдите углы параллелограмма, если известно, что .
Биссектриса угла  параллелограмма
параллелограмма  пересекает сторону
пересекает сторону  в её середине
в её середине  . Периметр треугольника
. Периметр треугольника  равен
равен  см, а длина отрезка
см, а длина отрезка  больше стороны
больше стороны  на
на  см. Найдите периметр параллелограмма.
см. Найдите периметр параллелограмма.
5








 – параллелограмм. У него
– параллелограмм. У него  .
.
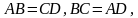
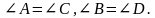
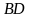 . Рассмотрим
. Рассмотрим 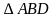 и
и 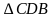 .
.
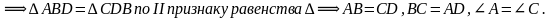
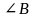 и
и 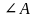 ;
; 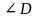 и
и  .
.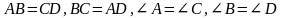 , ч.т.д.
, ч.т.д.
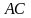 и
и 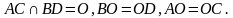
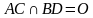 .
.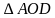 и
и 









