Переход к новому основанию логарифма

Черноволова Е.В.

Севастопольский кадетский корпус Следственного комитета РФ имени В.И. Истомина

Переход к новому основанию логарифма

Черноволова Е.В. Севастопольский кадетский корпус Следственного комитета РФ имени В.И. Истомина

Основные свойства логарифмов:

Если − положительные числа, причем , то справедливы равенства:

, для любого

, для любого

Черноволова Е.В. Севастопольский кадетский корпус Следственного комитета РФ имени В.И. Истомина

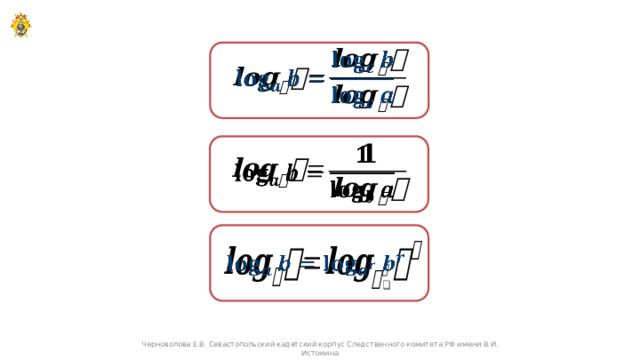
Теорема. Если , , – положительные числа, причем , , то имеет место равенство

Формула перехода к новому основанию логарифма

Черноволова Е.В. Севастопольский кадетский корпус Следственного комитета РФ имени В.И. Истомина

Следствие 1. Если , – положительные числа, причем , , то справедливо равенство

Черноволова Е.В. Севастопольский кадетский корпус Следственного комитета РФ имени В.И. Истомина

Следствие 2. Если , – положительные числа, причем , то для любого числа справедливо равенство

Черноволова Е.В. Севастопольский кадетский корпус Следственного комитета РФ имени В.И. Истомина

Пример:

Вычислить .

Решение:

Ответ: .

Черноволова Е.В. Севастопольский кадетский корпус Следственного комитета РФ имени В.И. Истомина

Пример:

Известно, что . Найти .

Решение:

Ответ: .

Черноволова Е.В. Севастопольский кадетский корпус Следственного комитета РФ имени В.И. Истомина

Пример:

Решить уравнение .

Решение:

Ответ: .

Черноволова Е.В. Севастопольский кадетский корпус Следственного комитета РФ имени В.И. Истомина

Пример:

Вычислить .

Решение:

Ответ: .

Черноволова Е.В. Севастопольский кадетский корпус Следственного комитета РФ имени В.И. Истомина

Черноволова Е.В. Севастопольский кадетский корпус Следственного комитета РФ имени В.И. Истомина