ГД 114 законспектировать лекцию, разобрать задачи и выполнить домашнее задание! Прислать на почту [email protected]u
Тема: ПЕРПЕНДИКУЛЯРНОСТЬ ПРЯМОЙ И ПЛОСКОСТИ
Цели: - сформировать у обучающихся понятие перпендикулярности прямых в пространстве, прямой перпендикулярной плоскости; изучить лемму о перпендикулярности двух параллельных прямых третьей; теоремы в которых устанавливается связь между параллельностью прямых и их перпендикулярностью к плоскости.
-продолжить формирование навыков самостоятельности у обучающихся в процессе самоконтроля и при изучении нового материала;
-воспитывать познавательный интерес к предмету.
Теоретический материал
1. Перпендикулярные прямые в пространстве
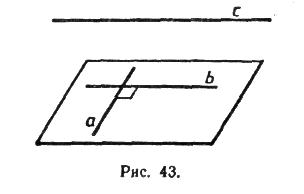
Определение: Две прямые в пространстве называются перпендикулярными (взаимно перпендикулярными), если угол между ними равен 90°. Перпендикулярность прямых а и b обозначается так: аb. Перпендикулярные прямые могут пересекаться и могут быть скрещивающимися. На рисунке1 перпендикулярные прямые а и b пересекаются, а перпендикулярные прямые а и с скрещивающиеся.
Лемма (о перпендикулярности двух параллельных прямых к третьей прямой): Если одна из двух параллельных прямых перпендикулярна к третьей прямой, то и другая прямая перпендикулярна к этой прямой.
2. Параллельные прямые, перпендикулярные к плоскости Определение: Прямая называется перпендикулярной к плоскости, если она перпендикулярна к любой прямой, лежащей в этой плоскости.
Перпендикулярность прямой а и плоскости обозначается так: a^a. Говорят также, что плоскость a, перпендикулярна к прямой а.
Если прямая а перпендикулярна к плоскости a, то она пересекает эту плоскость. В самом деле, если бы прямая а не пересекала плоскость a, то она или лежала бы в этой плоскости, или была бы параллельна ей. Но тогда в плоскости a имелись бы прямые, не перпендикулярные к прямой а, например прямые, параллельные ей, что противоречит определению перпендикулярности прямой и плоскости. Значит, прямая а пересекает плоскость a.
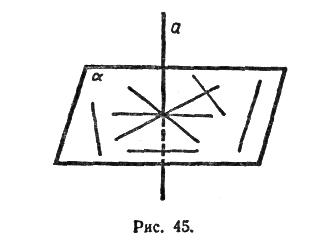
На рисунке 2 изображена прямая а, перпендикулярная к плоскости a.
Окружающая нас обстановка дает много примеров, иллюстрирующих перпендикулярность прямой и плоскости. Не покосившийся телеграфный столб стоит прямо, т. е. перпендикулярно к плоскости земли. Так же расположены колонны здания по отношению к плоскости фундамента, линии пересечения стен по отношению к плоскости пола и т. д.
Рассмотрим две теоремы, в которых устанавливается связь между параллельностью прямых и их перпендикулярностью к плоскости.
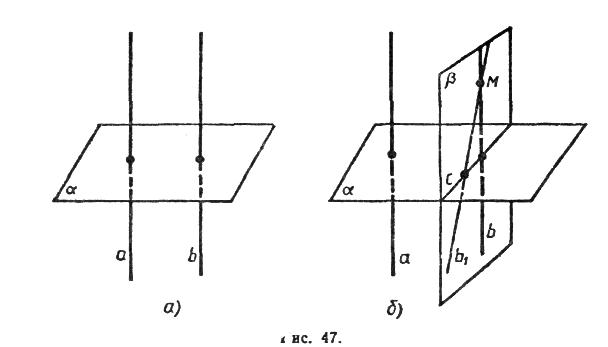
Теорема: Если одна из двух параллельных прямых перпендикулярна к плоскости, то и другая прямая перпендикулярна к этой плоскости. Теорема (обратная): Если две прямые перпендикулярны к плоскости, то они параллельны.
 3. Признак перпендикулярности прямой и плоскости
3. Признак перпендикулярности прямой и плоскости
Теорема (признак перпендикулярности прямой и плоскости): Если прямая перпендикулярна двум пересекающимся прямым, лежащим в плоскости, то она перпендикулярна и самой плоскости
Историческая справка «Провешивание прямой» (прочитать)
Для проведения длинных отрезков прямых (при прокладывании трассы шоссейной или железной дороги, линий электропередач и т.д.) применяется способ, называемый провешиванием прямой, который заключается в использовании всех - шестов, имеющих длину около 2 м., заостренных с одного конца для того, чтобы их можно было воткнуть в землю. Если нужно провести прямую линию между двумя точками А и В, положение которых дано, то сначала в этих точках ставятся вехи; затем между ними устанавливается промежуточная веха С так, чтобы веха А и С закрывали веху В. Необходимо, чтобы все вехи стояли вертикально. Правильность вертикального направления проверяется с помощью отвеса. Отвес - это шнур, на конце которого укреплен небольшой груз. Казалось бы, в этой простой процедуре провешивания прямой все ясно. Но и здесь есть много вопросов, о которых следует подумать, а ответы на них дают изучение нашего курса и других дисциплин. Во-первых, почему все отвесы мира смотрят в центр Земли, а с точки зрения геометрии- определяют прямую, перпендикулярную ее поверхности? Во-вторых, веха должна быть параллельна отвесу, и тогда она также будет перпендикулярна поверхности Земли. Таким образом, все вехи перпендикулярны поверхности Земли и, значит, параллельны между собой.
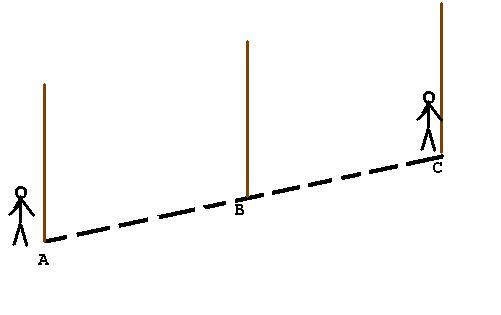
Такой способ получил название провешивание прямой на местности. Слово "провешивание" - производное от слова "веха".
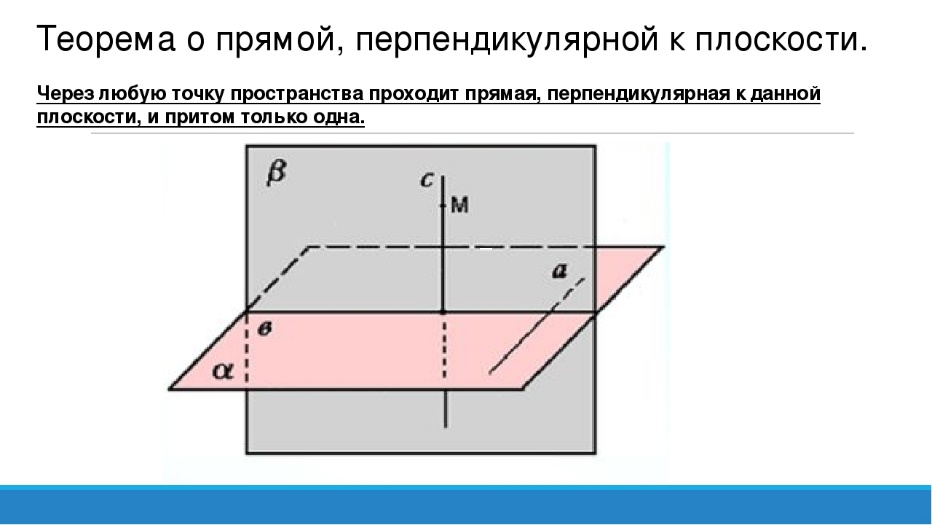
4. Теорема о прямой, перпендикулярной к плоскости
Теорема: Через любую точку пространства проходит прямая, перпендикулярная к данной плоскости, и притом только одна.
Практическая часть (Геометрия, Атанасян и др. стр.38-40)
№ 116 (а).

Дано: 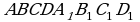 - параллелепипед,
- параллелепипед, 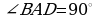
Доказать: 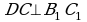 ,
, 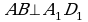
Доказательство: A1D1AD AB A1D1 (лемма);
ABDC, B1C1AD DCB1C1 (лемма).
№ 117.
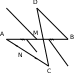
Дано: DABC - тетраэдр, BCAD, MAB, AM = MB, NAC, AN = NC
Доказать: ADMN
Доказательство: MNBC, (как средняя линия ABC);
BCAD MNAD (лемма).
№ 118.
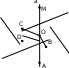
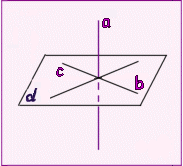
Дано: a, A,M, O a, O,B,C,D
Найти: прямые углы
Решение: a aCO, a DO, aBO (по определению перпендикулярности прямой и плоскости) AOB = 90º,
MOC = 90º, DOA = 90º
№ 121.
В треугольнике ABC дано: 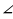 С = 90, AC = 6 см, BC = 8 см, СМ – медиана. Через вершину С проведена прямая СК, перпендикулярная к плоскости треугольника АВС, причем СК = 12 см. Найдите КМ.
С = 90, AC = 6 см, BC = 8 см, СМ – медиана. Через вершину С проведена прямая СК, перпендикулярная к плоскости треугольника АВС, причем СК = 12 см. Найдите КМ.

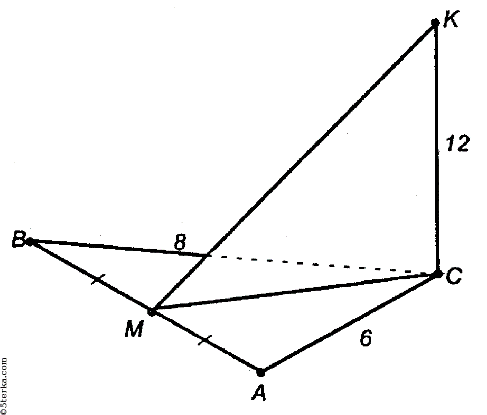
Ответ: 13 см.
№ 125.
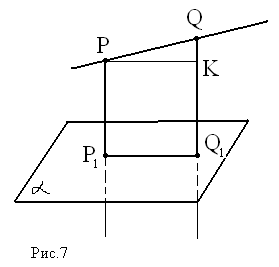
Через точки P и Q прямой РQ проведены прямые, перпендикулярные к плоскости α и пересекающие её соответственно в точках P1 и Q1. Найдите P1Q1, если PQ = 15 cм; PP1 = 21,5 cм; QQ1 = 33,5 cм.
Решение:
1) PP1 ⊥ α и QQ1 ⊥ α по условию ⇒ PP1 ∥ QQ1;
2) PP1 и QQ1 определяют некоторую плоскость β, α ⋂ β = P1Q1;
3) PP1Q1Q – трапеция с основаниями PP1 и QQ1, проведём PK ∥ P1Q1;
4) QK = 33,5 – 21,5 = 12 (см)
| P1Q1 = PK = | 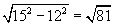
| = 9 см. |
Ответ: P1Q1 = 9 см.
Домашнее задание: повторить теоретический материал по изученной теме, решить № 122
Геометрия 10-11 класс, Атанасян и др. https://yadi.sk/i/ckDEkttw2JDKDw









 3. Признак перпендикулярности прямой и плоскости
3. Признак перпендикулярности прямой и плоскости


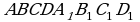 - параллелепипед,
- параллелепипед, 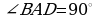
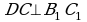 ,
, 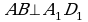


 С = 90, AC = 6 см, BC = 8 см, СМ – медиана. Через вершину С проведена прямая СК, перпендикулярная к плоскости треугольника АВС, причем СК = 12 см. Найдите КМ.
С = 90, AC = 6 см, BC = 8 см, СМ – медиана. Через вершину С проведена прямая СК, перпендикулярная к плоскости треугольника АВС, причем СК = 12 см. Найдите КМ.












