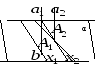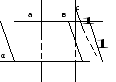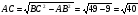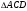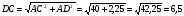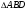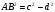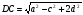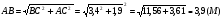Инструкционная карта № 25
Тақырыбы/ Тема: Решение задач по теме: «Перпендикулярность прямых и плоскостей в пространстве».
Мақсаты/ Цель:
Уметь применять определения, признаки и свойства перпендикулярных прямых и плоскостей в пространстве при решении задач.
Создать условия для развития умения устанавливать единые общие признаки и свойства целого, составлять план деятельности при решении задач.
Воспитание личностных качеств посредством развития индивидуальных познавательных интересов и способностей.
Теоретический материал:
Определение: Две прямые называются перпендикулярными, если они пересекаются под прямым углом.
Определение: Прямая, пересекающая плоскость, называется перпендикулярной этой плоскости, если она перпендикулярна любой прямой, которая лежит в данной плоскости и проходит через точку пересечения.

Определение: Две пересекающиеся плоскости называются перпендикулярными, если третья плоскость перпендикулярная прямой пересечении этих плоскостей пересекает их по перпендикулярным прямым.
Теорема: (признак перпендикулярности прямых в пространстве) Если две пересекающиеся прямые параллельны соответственно двум перпендикулярным прямым, то они тоже перпендикулярны.
Теорема: ( признак перпендикулярности прямой к плоскости в пространстве) Если
прямая перпендикулярна двум пересекающимся прямым, лежащим в плоскости,
то она перпендикулярна данной плоскости.
Свойства перпендикулярности прямой и плоскости.
1 Если плоскость перпендикулярна одной из двух параллельных прямых, то она
Если плоскость перпендикулярна одной из двух параллельных прямых, то она
перпендикулярна к другой.
2 Две прямые, перпендикулярные одной и той же плоскости, параллельны.
Две прямые, перпендикулярные одной и той же плоскости, параллельны.
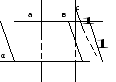
Теорема: (признак перпендикулярности плоскостей в пространстве) Если плоскость
проходит через прямую, перпендикулярную другой плоскости, то эти плоскости
перпендикулярны.
Задача: Прямые АВ,АС и АD попарно перпендикулярны. Найдите отрезок CD, если 1) АВ=3см., ВС=7см.,AD=1,5см. 2) BD=c., BC=a., AD=d.
1) Рассмотрим 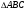
Рассмотрим 
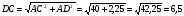
2) 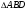
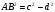
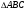

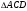
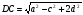
Задача: Верхние концы двух вертикально стоящих столбов, удаленных на расстоянии 3,4м соединены перекладиной. Высота одного столба 5,8м., а другого 3,9м. найдите длину перекладины.
А
АС= АА1 –СА1 =5,8-3,9=1,9
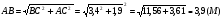
В

![]()
С
![]()
![]()
3,9
5,8

![]()
![]()
3,4
В
А


![]()
![]()
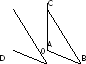
Задача: Из точек А и В, лежащих в двух перпендикулярных плоскостях, опущены перпендикуляры АС и ВD на прямую пересечения плоскостей. Найдите длину отрезка АВ, если АD=ВС=5м, СD=1м.
α

![]()
D
A



5
β


![]()
![]()
Дано: α β AC
β AC  CD
CD
A
 ВD
ВD CD
CD
B
![]() А
А α, B
α, B β
β
5
C
AD=BC=5м
CD=1м
Найти: АВ
 Решение:
Решение:
1) рассм. ACD,  =90◦
=90◦
AC=
 2)рассм. ACD,
2)рассм. ACD, 
AB=
Задача: Найдите расстояние от середины отрезка АВ до плоскости, не пересекающей этот отрезок, если расстояние от точки А и В до плоскости равны 7,4 см и 6,1 см.
Дано:AB¢α C AB, AC=CB,
AA׀=6,1см, BB׀=7,4см.
Найти:CC׀=?

Решение:
Рассмотрим AA׀BB׀-трапеция, т.к. AA׀┴α, BB׀┴α, то AA׀║BB׀
CC׀- средняя линия трапеции
CC׀= (см)
(см)
Задача: Точка А находится на расстоянии от вершины равностороннего треугольника со стороной а. Найдите расстояние от точки А до плоскости треугольника.
Дано: ∆ АВС
АВ=ВС=АС=а; SA=SB=SC=a
Найти: SO-?
Решение:
ОВ=R= Рассмотрим ∆ SOB ˂О=900 SO=
Рассмотрим ∆ SOB ˂О=900 SO=
Практическая часть:
| 1 вариант | 2 вариант | 3 вариант | 4 вариант |
Прямые АВ,АС и АD попарно перпендикулярны. Найдите отрезок CD, если: |
| АВ=6см, ВС=14см, АD=3см. | ВD=9см, ВС=16см, АD=5см. | ВС=8см, АD=2,5см, ВD=4,5см. | ВС=6,5см. АВ=1,5см, АВ=3см. |
Через точки А и В проведены прямые, перпендикулярные плоскости  , пересекающие ее в точках С и , пересекающие ее в точках С и D соответственно. Найдите расстояние между точками А и В , и отрезок АВ не пересекает плоскость  |
| АС=3м, ВD=2м,СD=2,4м . | АС=6м, ВD=3м,СD=4м | АС=10м, ВD=5м,СD=12м | АС=9м, ВD=3м,СD=8м |
Найдите расстояние от середины отрезка МN до плоскости, не пересекающей этот отрезок, если расстояние от точки M и N до плоскости равны: |
| MM1=4,5; NN1=5,5 | MM1=7,4; NN1=5,6 | MM1=2,8; NN1=6,8 | MM1=4,3; NN1=5,8 |
Из точек А и В, лежащих в двух перпендикулярных плоскостях, опущены перпендикуляры АС и ВD на прямую пересечения плоскостей. Найдите длину отрезка АВ, если: |
| АС=6м, ВD=7м, СD=7м | АС=3м,ВD=4м, СD=12м | АD==4м, ВС=7м, СD=1м | АD=13м, СD=СВ=5м |
| 5.Стороны равностороннего треугольника равны а. Найдите расстояние до плоскости треугольника от точки, которая находится на расстоянии в от каждой из его вершин. | 5.Расстояния от точки А до вершин квадрата равны а. Найдите расстояния от точки А до плоскости квадрата. Если сторона квадрата равна в. |
| а=3м, в=2м. | а=2 м, в=5м. м, в=5м. | а=10м, в=2 м. м. | а=5м, в=2м. |
Контрольные вопросы:
Какие прямые в пространстве называются перпендикулярными?
Верно ли утверждение. Что «перпендикулярные прямые лежат в одной плоскости»?
В каких условиях прямая перпендикулярна к плоскости?
В окружающей обстановке найдите примеры на свойства перпендикулярности прямой и плоскости.
Какие плоскости называются перпендикулярными?








 Если плоскость перпендикулярна одной из двух параллельных прямых, то она
Если плоскость перпендикулярна одной из двух параллельных прямых, то она