Россия, с.Каскара
СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до 02.06.2025
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока
Была в сети 21.05.2025 05:39
Крымова Татьяна Анатольевна
учитель математики и информатики
39 лет
10 950
3 675 
Местоположение
Специализация
Первый признак подобия треугольников
Категория:
Геометрия
12.02.2020 08:25
Просмотр содержимого документа
«Первый признак подобия треугольников»
Первый признак подобия треугольников
Вспомним подобные треугольники :
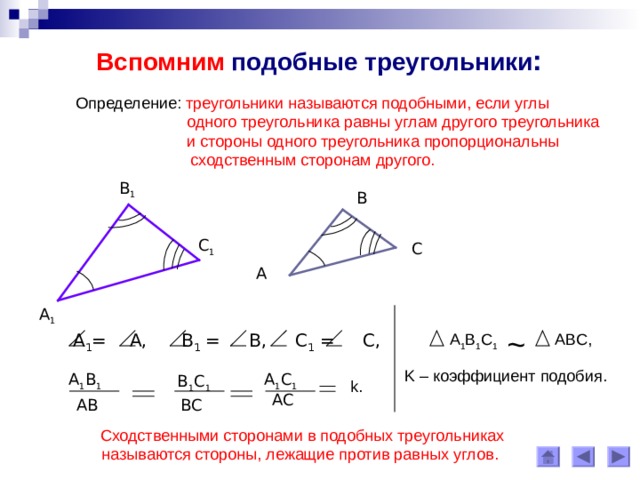
Определение: треугольники называются подобными, если углы
одного треугольника равны углам другого треугольника
и стороны одного треугольника пропорциональны
сходственным сторонам другого.
В 1
В
С 1
С
А
А 1
~
А 1 = А, В 1 = В, С 1 = С ,
A 1 B 1 C 1 ABC,
K – коэффициент подобия .
А 1 В 1
А 1 С 1
В 1 С 1
k.
АС
ВС
АВ
Сходственными сторонами в подобных треугольниках
называются стороны, лежащие против равных углов .
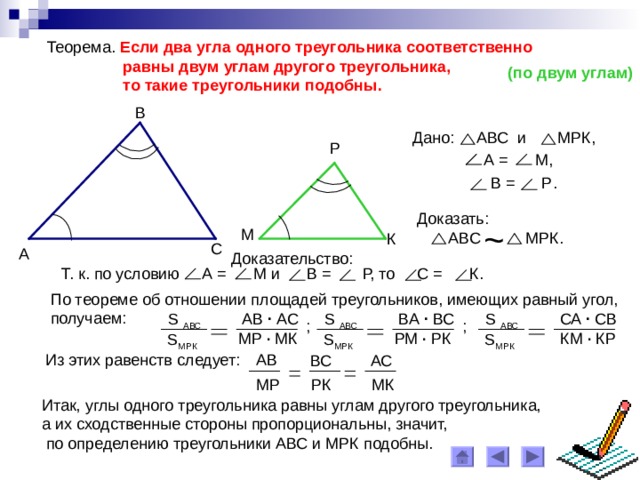
Теорема. Если два угла одного треугольника соответственно
равны двум углам другого треугольника,
то такие треугольники подобны.
(по двум углам)
B
Дано: АВС и МРК ,
Р
А = М ,
В = Р .
Доказать:
АВС МРК .
~
М
К
C
A
Доказательство:
Т. к. по условию А = М и В = Р, то С = К .
По теореме об отношении площадей треугольников, имеющих равный угол,
получаем:
S АВС
СА ∙ СВ
S АВС
АВ ∙ АС
ВА ∙ ВС
S АВС
;
;
РМ ∙ РК
МР ∙ МК
КМ ∙ КР
S МРК
S МРК
S МРК
АВ
Из этих равенств следует:
ВС
АС
МР
МК
РК
Итак, углы одного треугольника равны углам другого треугольника,
а их сходственные стороны пропорциональны, значит,
по определению треугольники АВС и МРК подобны .
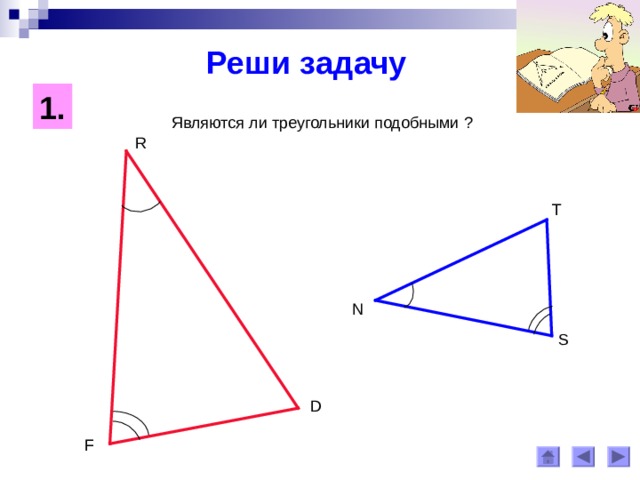
Реши задачу
1.
Являются ли треугольники подобными ?
R
T
N
S
D
F
Реши задачу
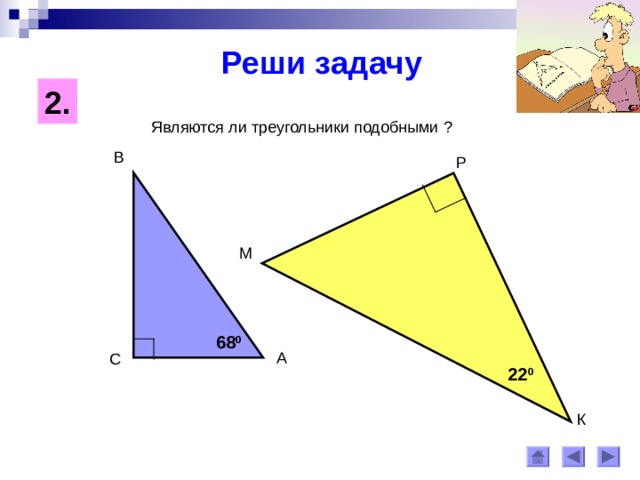
2.
Являются ли треугольники подобными ?
В
Р
М
68 0
А
С
22 0
К
Реши задачу
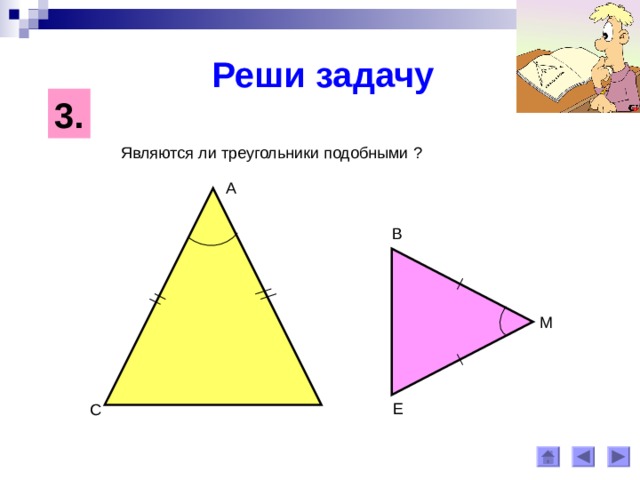
3.
Являются ли треугольники подобными ?
А
В
М
Е
С
Реши задачу
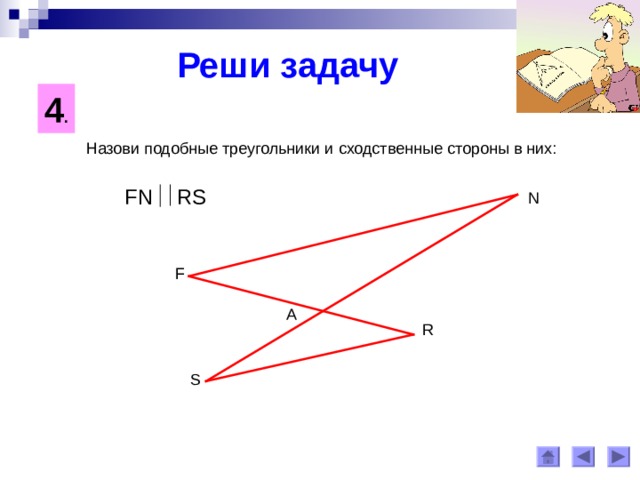
4 .
Назови подобные треугольники и сходственные стороны в них:
FN RS
N
F
A
R
S
Реши задачу
5.
Назови подобные треугольники и сходственные стороны в них:
D
HZ CK
H
Z
K
C
Реши задачу
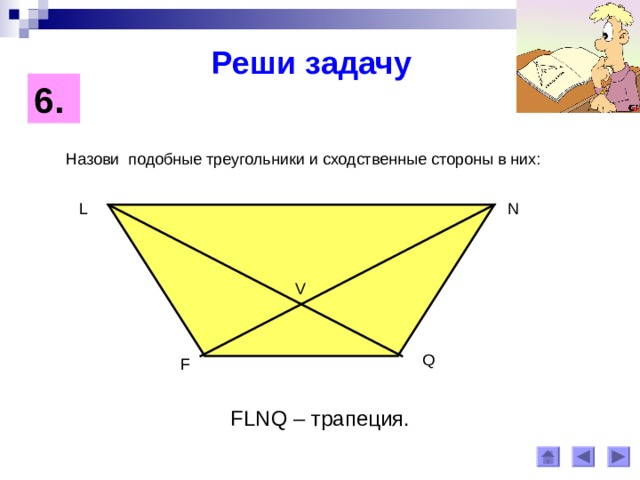
6 .
Назови подобные треугольники и сходственные стороны в них:
L
N
V
Q
F
FLNQ – трапеция .
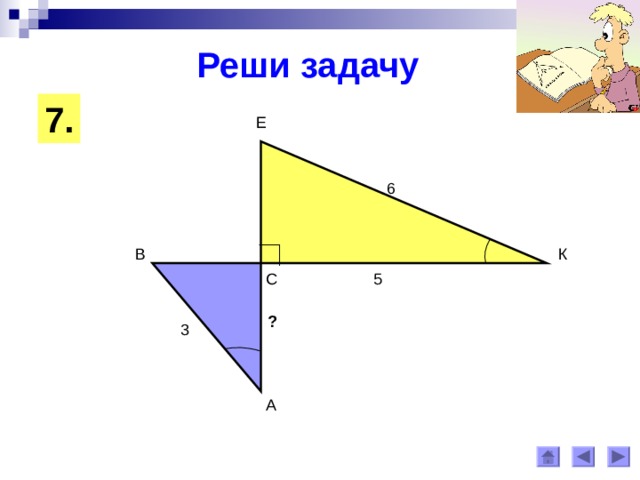
Реши задачу
7 .
Е
6
В
К
5
С
?
3
А
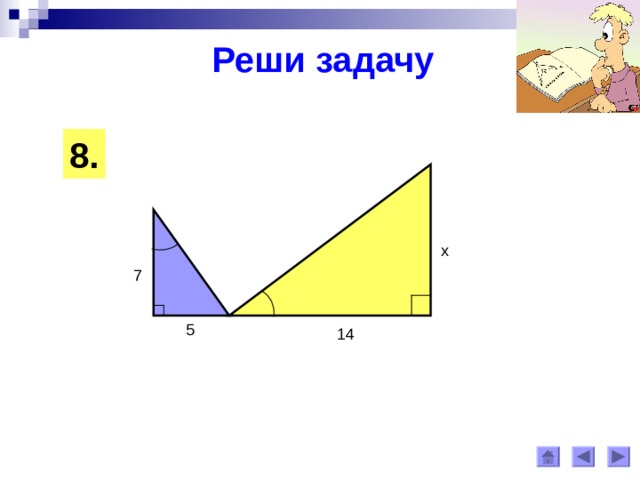
Реши задачу
8 .
x
7
5
14
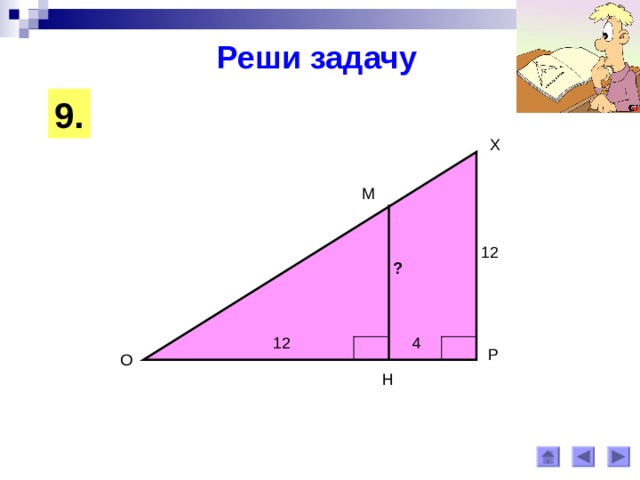
Реши задачу
9 .
Х
М
12
?
12
4
Р
О
Н
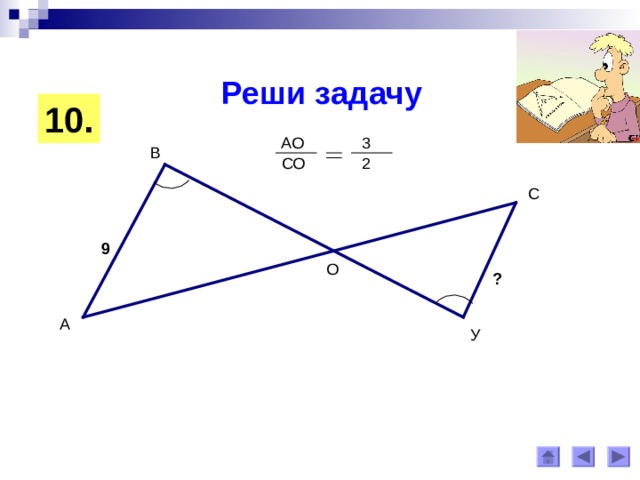
Реши задачу
10 .
АО
3
В
СО
2
С
9
О
?
А
У
Реши задачу
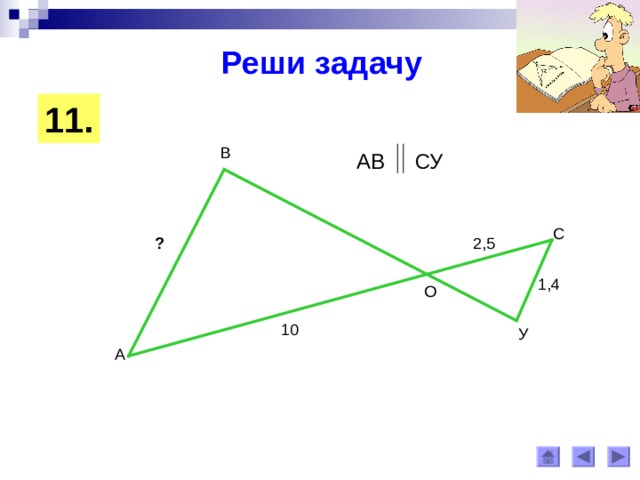
11 .
В
АВ СУ
С
?
2,5
1,4
О
10
У
А
О
Решение задачи
Диагонали трапеции АВСК пересекаются в точке О. Площади треугольников ВОС и АОК относятся как 1: 9. Сумма оснований ВС и АК равна 4,8 см. Найдите основания трапеции.
В
С
Дано: АВСК – трапеция, ВС + АК = 4,8 см ,
S СОВ : S АОК = 1 : 9 .
Найти: ВС, АК.
Решение:
К
А
АВСК – трапеция, значит, ВС АК, следовательно, САК = АСВ , как накрест лежащие (секущая – АС), аналогично АКВ = СВК .
Значит, по двум углам треугольники СОВ и АОК подобны, следовательно,
S СОВ : S АОК = k 2 , а по условию S СОВ : S АОК = 1 : 9, т. е. k 2 = 1/9; k = 1/3 .
По доказанному треугольники СОВ и АОК подобны, следовательно,
ВС : АК = k , т. е. ВС : АК = 1/3, значит, ВС = 1/3 АК или АК = 3 ВС .
А по условию ВС + АК = 4,8 см, значит, ВС + 3 ВС = 4,8; 4 ВС = 4,8 .
Получаем: ВС = 1,2 см, АК = 4,8 – 1,2 = 3,6(см).
Ответ: ВС = 1,2 см, АК = 3,6 см.
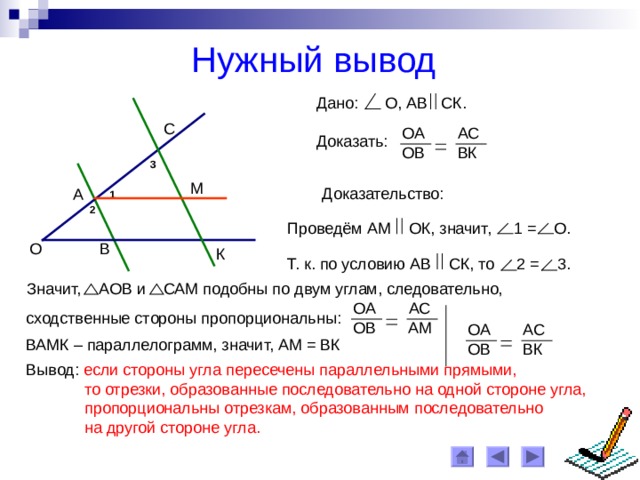
Нужный вывод
Дано: О, АВ СК .
Доказать:
С
АС
ОА
ВК
ОВ
3
М
Доказательство:
А
1
2
Проведём АМ ОК, значит, 1 = О.
О
В
К
Т. к. по условию АВ СК, то 2 = 3.
Значит, АОВ и САМ подобны по двум углам, следовательно,
ОА
АС
сходственные стороны пропорциональны:
ОВ
АМ
АС
ОА
ВАМК – параллелограмм, значит, АМ = ВК
ВК
ОВ
Вывод: если стороны угла пересечены параллельными прямыми,
то отрезки, образованные последовательно на одной стороне угла,
пропорциональны отрезкам, образованным последовательно
на другой стороне угла.
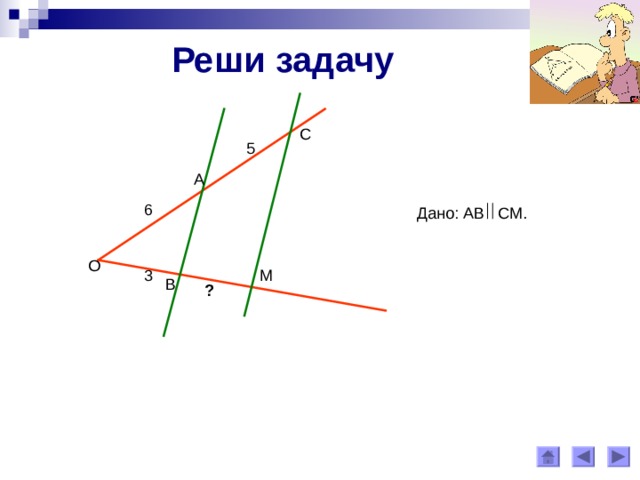
Реши задачу
С
5
А
6
Дано: АВ СМ .
О
М
3
В
?
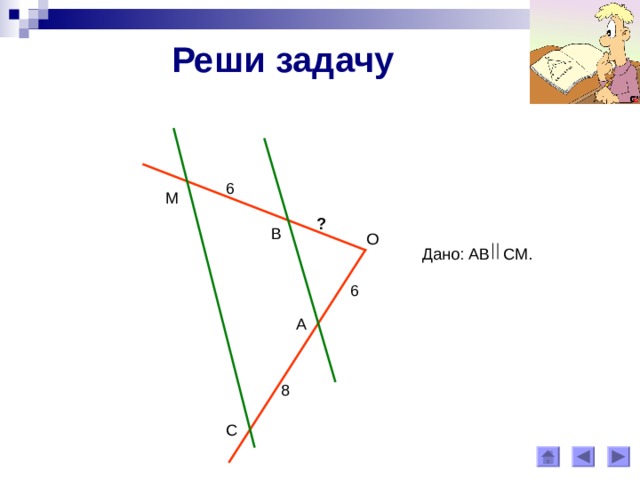
Реши задачу
6
М
?
В
О
Дано: АВ СМ .
6
А
8
С
.
Вебинар для учителей
Свидетельство об участии БЕСПЛАТНО!
Полезное для учителя
Реализация образовательных программ осуществляется с применением исключительно электронного обучения и ДОТ
