Перевод целых чисел в 2, 8, 16-ую системы счисления

0123456789 ABCDEF

0123456789

01234567

01

шестнадцатеричная

десятичная

двоичная

восьмеричная

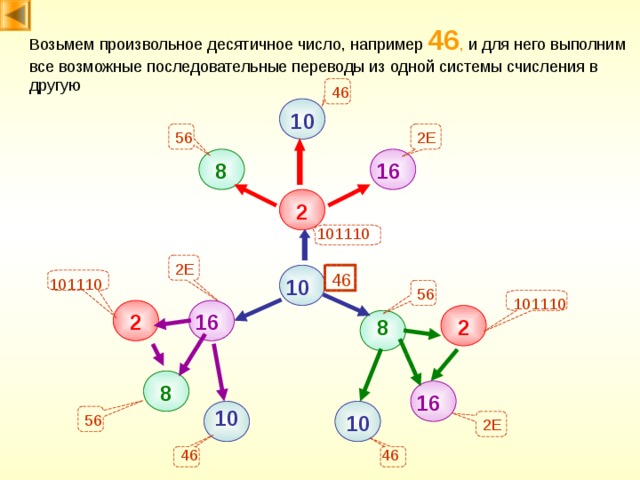
Возьмем произвольное десятичное число, например 46 , и для него выполним все возможные последовательные переводы из одной системы счисления в другую

46

10

56

2E

16

8

2

101110

2E

46

10

101110

56

101110

16

2

2

8

8

16

10

10

56

2E

46

46

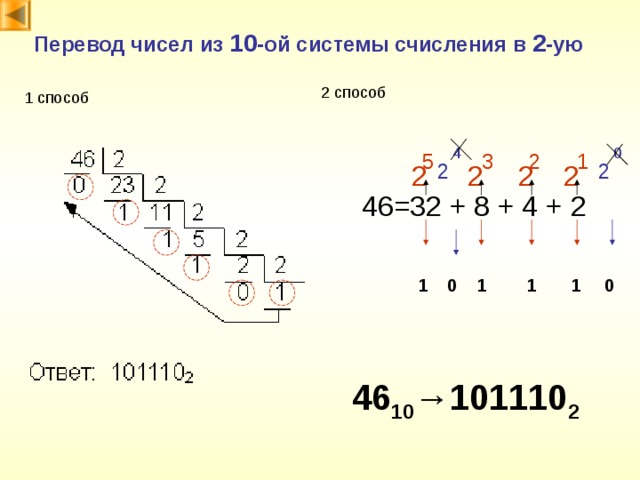
Перевод чисел из 10 -ой системы счисления в 2 -ую

2 способ

1 способ

0

4

5 3 2 1

2

2

2

2

2

2

46=32 + 8 + 4 + 2

1 0 1 1 1 0

46 10 →101110 2

Перевод чисел из 10 -ой системы счисления в 8 -ую

46 10 →56 8

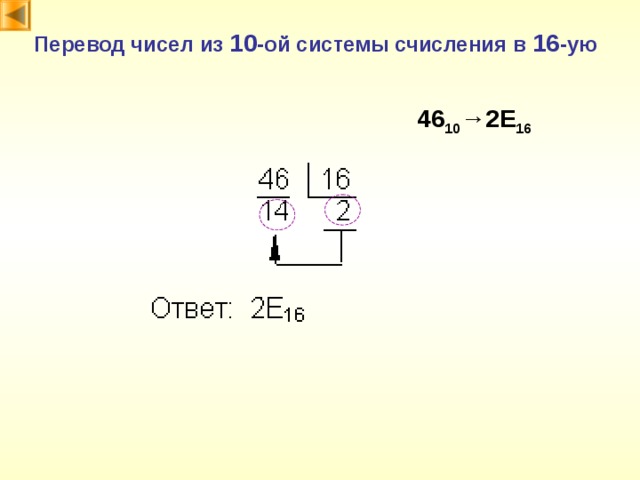
Перевод чисел из 10 -ой системы счисления в 16 -ую

46 10 →2 E 16

Перевод чисел из 2 -ой системы счисления в 8 -ую

101110 2 → 56 8

Перевод чисел из 2 -ой системы счисления в 10 -ую

32

8

4

2

32+8+4+2

101110 2 → 46 10

Перевод чисел из 2 -ой системы счисления в 16 -ую

14 (E)

101110 2 → 2E 16

Перевод чисел из 8 -ой системы счисления в 2 -ую

6

5

56 8 → 101110 2

Перевод чисел из 8 -ой системы счисления в 10 -ую

56 8 → 46 10

Перевод чисел из 8 -ой системы счисления в 16 -ую

56 8 → 2E 16

Перевод чисел из 1 6 -ой системы счисления в 2 -ую

2E 16 → 101110 2

Перевод чисел из 8 -ой системы счисления в 2 -ую

56 8 → 101110 2

Перевод чисел из 16 -ой системы счисления в 10 -ую

2E 16 → 46 10

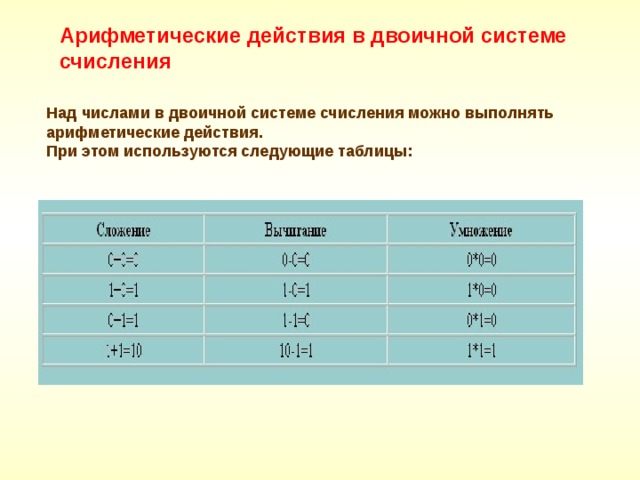
Арифметические действия в двоичной системе счисления

Над числами в двоичной системе счисления можно выполнять арифметические действия. При этом используются следующие таблицы:

Перевод дробных чисел из 10 -ой системы в 2 -ую

Перевод дробного числа из десятичной системы счисления в двоичную осуществляется по следующему алгоритму:

Вначале переводится целая часть десятичной дроби в двоичную систему счисления;

Затем дробная часть десятичной дроби умножается на основание двоичной системы счисления;

В полученном произведении выделяется целая часть, которая принимается в качестве значения первого после запятой разряда числа в двоичной системе счисления;

Алгоритм завершается, если дробная часть полученного произведения равна нулю или если достигнута требуемая точность вычислений. В противном случае вычисления продолжаются с предыдущего шага.

Пример: Требуется перевести дробное десятичное число 206,116 в дробное двоичное число.

Перевод целой части дает 206 10 =11001110 2 по ранее описанным алгоритмам; дробную часть умножаем на основание 2 , занося целые части произведения в разряды после запятой искомого дробного двоичного числа:

. 116 • 2 = 0 .232

.232 • 2 = 0 .464

.464 • 2 = 0 .928

.928 • 2 = 1 .856

.856 • 2 = 1 .612

.612 • 2 = 1 .224

.224 • 2 = 0 .448

.448 • 2 = 0 .456

.456 • 2 = 0 .912

.912 • 2 = 1 .82 и т.д.

Получим: =11001110,0001110001 2