Первый признак равенства треугольников
Приветствие. Один мудрец сказал: «Высшее проявление духа - это разум. Высшее проявление разума - это геометрия. Клетка геометрии - треугольник. Он так же неисчерпаем, как и Вселенная». Треугольник - уникальная единица познания геометрии. Он обладает множеством свойств, присущих исключительно ему, и одновременно его исследование привело учёных к многочисленным обобщениям для многоугольников.
Задание 1. Работа в группах с карточками.
Учитель: Мы с вами уже вспомнили, что два треугольника называются равными, если их можно совместить наложением. Сколько элементов треугольников при наложении должно совместиться? (6) Всегда ли нам удобно и возможно совместить треугольники наложением? Например, сравнить треугольные крыши разных домов? Почему? Выясняется, что не всегда можно наложить одну треугольную конструкцию на другую из-за их массивности, удалённости. Учитель подчеркивает, что это реальная жизненная ситуация и просит сформулировать её на математическом языке. Ученики замечают, что не всегда можно установить равенство треугольников путём наложения.
Возникает необходимость выяснить: «Существуют ли другие способы установления равенства двух треугольников?»
Задание 2. Практическая работа.
На каждой парте лежат три конверта, с вырезанными из бумаги разного цвета треугольниками. Конверт № 1. Пары треугольников с одним равным элементом (по одной равной стороне или по одному равному углу). Вы берёте треугольники из конверта №1 и пробуете наложением их совместить. Достаточно ли одного равного элемента у треугольников, чтобы сделать вывод, что они равны? Конверт № 2. Пары треугольников с двумя равными элементами (по двум равным сторонам, по двум равным углам, по одной равной стороне и одному равному углу). Вы берёте треугольники из конверта № 2 и пробуете наложением их совместить. Достаточно ли двух равных элементов у треугольников, чтобы сделать вывод, что они равны? Конверт № 3. Пары треугольников с тремя равными элементами (по двум равным сторонам и углу между ними, по стороне и двум прилежащим к ней равным углам, по трём равным сторонам, по трём равным углам). Способом наложения треугольников (из каждого конверта по порядку) обучающие должны будут ответить на вопрос учителя. Вы берете треугольники из конверта № 3 и пробуете наложением их совместить. Достаточно ли трёх равных элементов у треугольников, чтобы сделать вывод, что они равны? Какое минимальное количество равных элементов в треугольниках достаточно, чтобы они совместились при наложении?
Предлагает сформулировать признаки равенства двух треугольников Внимательно рассмотрите пары равных треугольников из конверта № 3 и скажите какие три равных элемента необходимы, для того чтобы сделать вывод о равенстве треугольников? Будут ли равны треугольники, если три угла равны, а стороны не равны? Давайте сформулируем признаки, по которым можно сделать вывод о равенстве треугольников. Начинаем со слова «Если»…( учитель демонстрирует пары треугольников).
Если две стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
Если сторона и два прилежащих к ней угла одного треугольника соответственно равны стороне и двум прилежащим к ней углам другого треугольника, то такие треугольники равны.
Если три стороны одного треугольника соответственно равны трем сторонам другого треугольника, то такие треугольники равны.
Историческая справка о признаках равенства треугольников.
Признаки равенства треугольников имели издавна важнейшее значение в геометрии, так как доказательства многочисленных теорем сводилось к доказательству равенства тех или иных треугольников. Доказательством признаков равенства треугольников занимались ещё пифагорейцы. По словам Прокла, Евдем Родосский приписывает Фалесу Милетскому доказательство о равенстве двух треугольников, имеющих равными сторону и два прилежащих к ней угла (второй признак равенства треугольников). Эту теорему Фалес использовал для определения расстояния от берега до морских кораблей. Доказательство основывается на втором признаке равенства треугольников, который мы подробно рассмотрим позже, а сегодня мы остановимся на первом признаке равенства треугольников.
Совместно с учениками учитель формулирует тему урока.
Произносят первый признак равенства треугольников. Это утверждение, справедливость которого устанавливается путём рассуждений, называется теоремой, а сами рассуждения называются доказательством теоремы. Далее ученикам сообщается, что в структуре любой теоремы есть «условие» и «заключение». Если рассматривать теорему как задачу, то «условие» - это то, что дано, то, чем можно пользоваться. «Заключение» же - неизвестный факт, требующий доказательства. Рассматривается простой пример: «если ученик не сделал домашнее задание, то учитель его не похвалит» и демонстрируется, что это утверждение состоит из двух частей -«условия» и «заключения». Вспоминаются в устной форме утверждения о равенстве вертикальных углов, обоснованные ранее. Делается замечание, что это утверждение фактически является теоремой, а его обоснование доказательством. Ученики пробуют переформулировать это утверждение по заданной схеме.
Задание 3. Ученикам предлагается самим доказать теорему. Затем учитель доказывает теорему, после чего ученики записывают доказательство в тетради.
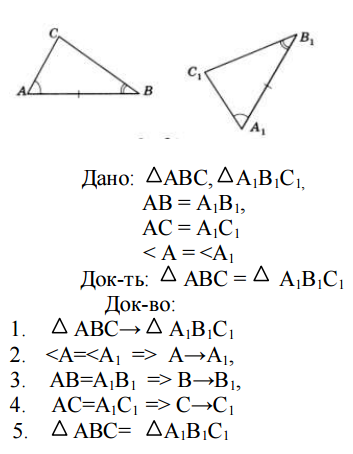
Задание 4. Две стороны и угол одного треугольника соответственно равны двум сторонам и углу другого треугольника. Следует ли из этого, что треугольники равны?
Послушайте одну старинную историю.
Это произошло в те времена, когда на улицах городов ещё не было освещения. Как-то ночью мэр столкнулся с горожанином. Это было неприятно и больно.
Тогда мэр отдал приказ, чтобы никто не выходил ночью на улицу без фонаря. Следующей ночью мэр опять столкнулся с тем же горожанином.
- Вы не читали моего приказа? — спросил мэр сердито.
- Читал, — ответил горожанин. — Вот мой фонарь.
- Но в фонаре у вас нет ничего.
- В приказе об этом не упоминалось.
Наутро появился новый приказ, обязывающий вставлять свечу в фонарь при выходе ночью на улицу. Вечером мэр опять налетел на того же горожанина,
- Где фонарь?! — закричал мэр.
- Вот он.
- Но в нём нет свечи!
- Нет, есть. Вот она.
- Но она не зажжена!
- В приказе ничего не сказано о том, что надо зажигать свечу.
И мэру пришлось издать ещё один приказ, обязывающий граждан зажигать свечи в фонарях при выходе ночью на улицу.
Математика наука точная, поэтому чтобы применить теорему нужно, чтобы выполнялись все условия.
Задание 5. Доказать равенство треугольников (устно).
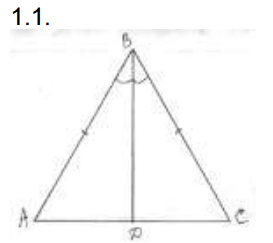
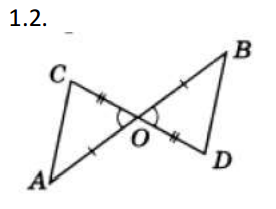
Задание 6. Самостоятельно решают №93 (Атанасян Л.С., Бутузов В.Ф., Кадомцев и др. Геометрия, 7-9 классы).
ДЗ №№ 94-96. Учитель даёт комментарий к его выполнению.
Рефлексия. Что такое теорема? Сформулируйте теорему о первом признаке равенства треугольников, укажите условие и заключение. Что запомнилось на уроке? Что на уроке было самым интересным?