Пирамида 10 класс

• Многогранник, составленный из

двух равных n -угольников, лежащих

в параллельных плоскостях и n

параллелограммов.

П

1

Р

З

М

А

И

А

Р

Я

П

И

Л

Н

А

В

Ь

2

Ь

Н

А

Р

Г

3

О

Н

А

Н

Н

Я

А

Л

К

2. Прямая призма, основания

4

которой правильные много -

угольники.

3 . AA 1 D 1 D.

4. Призма, боковые ребра

которой не равны высоте.

П

Р

М

А

Я

Я

5

Н

А

Е

И

6

О

С

Н

О

В

О

Г

А

И

Д

Н

Ь

7

А

Л

А

Т

О

С

Ы

8

В

B 1

A 1

5. Призма, боковые ребра которой перпендикулярны основаниям.

6. ABCD.

7. DB 1 .

8. D 1 H.

C 1

D 1

B

A

C

D

H

• Из истории развития и применения пирамид

• Определение пирамиды
• Элементы пирамиды
• Виды пирамид, их особенности
• Площадь поверхности и объем пирамиды
• Решение задач

ЦЕЛИ УРОКА:

• Познакомиться с историей развития пирамид и их применением;
• Сформулировать определение пирамиды и её элементов через сравнение и обобщение;
• Рассмотреть виды пирамид, их особенности.
• Познакомится с формулами площади боковой и полной поверхности пирамиды..

НЕМНОГО ИСТОРИИ

«Пирамида» - от греческого

слова «пюрамис», которым

греки называли египетские

пирамиды.

Египетские пирамиды

Мексиканская пирамида Солнца

Гора Кайлас на Тибете

Торговый центр в Илинге, Лондон

Новый вход в Лувр, Париж

Александровский маяк

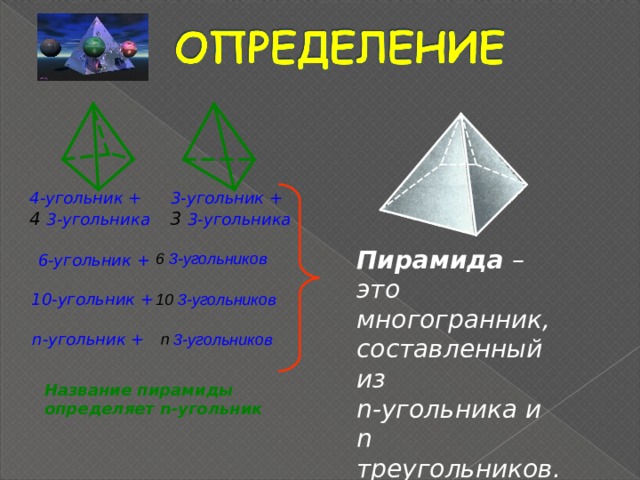
4-угольник +

3-угольник +

4 3-угольника

3 3-угольника

Пирамида – это многогранник,

составленный из

n- угольника и

n треугольников .

6 3-угольников

6-угольник +

10-угольник +

10 3-угольников

n -угольник +

n 3-угольников

Название пирамиды

определяет n -угольник

ЭЛЕМЕНТЫ ПИРАМИДЫ

Из чего состоит пирамида ?

Основание

Боковые грани

Боковые ребра

Вершина

Высота

Можно ли в пирамиде провести диагональ ?

1)Дайте определения всем элементам пирамиды (в случае затруднения

воспользуйтесь учебником).

2)Начертите треугольную пирамиду PABC, выпишите её элементы.

ПРОВЕРЬ СЕБЯ

многоугольник .

Основание -

P

ABC

Боковые грани -

треугольники .

ABP, BCP, ACP

Вершина -

общая точка всех

боковых граней .

.

P

Боковые ребра -

отрезки,

соединяющие вершину с

вершинами основания .

B

AP, BP, CP

H

Высота -

перпендикуляр,

проведенный из вершины к плоскости основания .

A

C

PH

ПИРАМИДЫ

Неправильная пирамида

Правильная пирамида

ПРАВИЛЬНАЯ ПИРАМИДА

Пирамида называется правильной, если в основании

лежит правильный многоугольник, а отрезок,

соединяющий вершину пирамиды с центром её

основания, является высотой пирамиды.

• Боковые ребра равны

• Боковые грани – равные

равнобедренные треугольники

P

P

C

C

B

B

B

C

C

B

K

H

H

H

A

D

D

A

D

A

D

A

Апофема правильной пирамиды –

высота ее боковой грани, проведенная

из вершины.

PK - апофема

S бок. = P осн. * l

где P осн. – периметр основания,

l –апофема правильной пирамиды.

S полн . = S бок . + S осн .

где S осн. – площадь основания.