Пирамида, основные свойства, характеристики

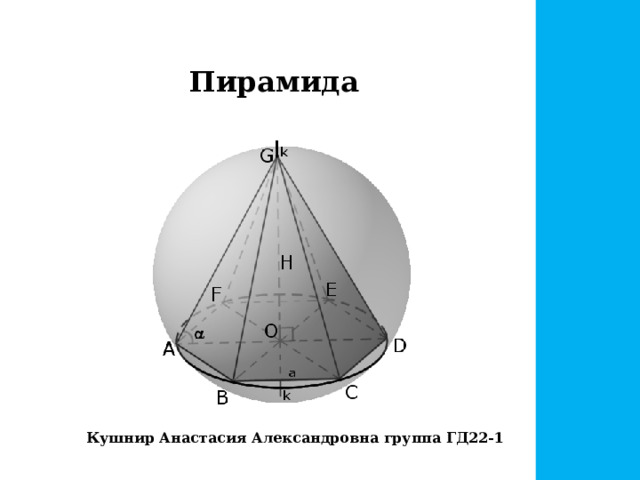
Пирамида

Кушнир Анастасия Александровна группа ГД22-1

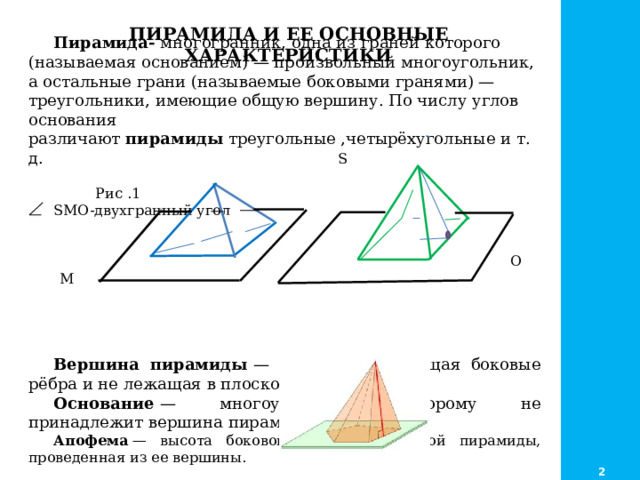
Пирамида-  многогранник, одна из граней которого (называемая основанием) — произвольный многоугольник, а остальные грани (называемые боковыми гранями) — треугольники, имеющие общую вершину. По числу углов основания различают  пирамиды  треугольные ,четырёхугольные и т. д. S

Рис .1

SMO-двухгранный угол

O М

Вершина пирамиды  — точка, соединяющая боковые рёбра и не лежащая в плоскости основания.

Основание  — многоугольник, которому не принадлежит вершина пирамиды.

Апофема  — высота боковой грани правильной пирамиды, проведенная из ее вершины.

ПИРАМИДА И ЕЕ ОСНОВНЫЕ ХАРАКТЕРИСТИКИ

ПИРАМИДА И ЕЕ ОСНОВНЫЕ ХАРАКТЕРИСТИКИ

Высота  — отрезок перпендикуляра, проведённого

через вершину пирамиды к плоскости её основания

(концами

этого отрезка являются вершина пирамиды и

основание перпендикуляра).

Боковая грань  - это треугольник, у которого один угол лежит в

вершине пирамиды, а противоположная ему сторона совпадает со

стороной основания (многоугольника).

Боковые ребра  - это общие стороны боковых граней. У пирамиды столько ребер сколько углов у многоугольника.

- Если все боковые ребра равны, то вокруг основания пирамиды можно описать окружность, а центр основания совпадает с центром окружности. Также перпендикуляр, опущенный из вершины, проходит через центр основания (круга).

- Если все боковые ребра равны, то они наклонены к плоскости основания под одинаковыми углами.

-Боковые ребра равны тогда, когда они образуют с плоскостью основания равные углы или если вокруг основания пирамиды можно описать окружность.

-Если боковые грани наклонены к плоскости основания под одним углом, то в основание пирамиды можно вписать окружность, а вершина

пирамиды проектируется в ее центр.

- Если боковые грани наклонены к плоскости основания под одним углом, то апофемы боковых граней равны.

ПИРАМИДА И ЕЕ ОСНОВНЫЕ СВОЙСТВА

ВИДЫ ПИРАМИД

  Существует несколько факторов, определяющих тип пирамиды. Основание пирамиды будет, конечно, основопалагающим фактором.  Вид пирамиды будет зависеть от основания пирамиды. Также зависит от количества сторон, которые пирамида имеет, от  ориентации вершины пирамиды относительно основания то есть вершина, расположенная над геометрическим центром основания, или она смещена на некоторое расстояние в определенном направлении. Наиболее известная форма пирамиды, которая имеет квадратное основание и вершину, расположенную непосредственно над геометрическим центром основания. Вот некоторые виды пирамид, которые наиболее часто  встречаются в геометрии.

Правильная треугольная пирамида

( в основании правильный треугольник АВС,

т.N- центр треугольника и одновременно- основание высоты DN)

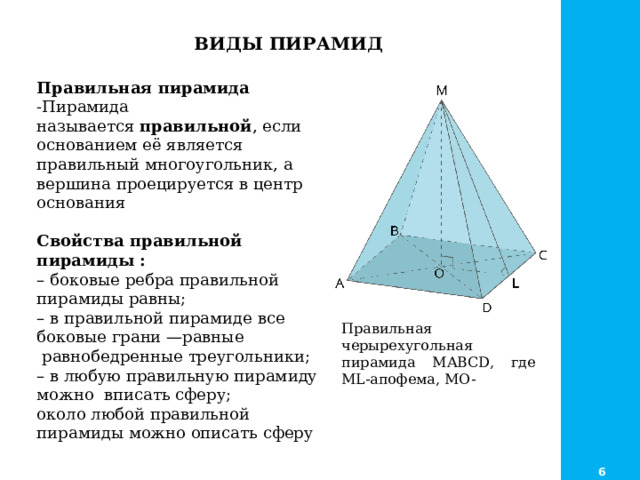
ВИДЫ ПИРАМИД

Правильная пирамида

-Пирамида называется  правильной , если основанием её является

правильный многоугольник, а вершина проецируется в центр основания

Свойства правильной пирамиды :

– боковые ребра правильной пирамиды равны;

– в правильной пирамиде все боковые грани —равные  равнобедренные треугольники;

– в любую правильную пирамиду можно  вписать сферу;

около любой правильной пирамиды можно описать сферу

Правильная черырехугольная пирамида MABCD, где ML-апофема, MO-

ВИДЫ ПИРАМИД

Шестиугольная правильная пирамида

Пятиугольная правильная пирамида

Тупоугольная пирамида  - это пирамида в которой апофема меньше половины длины стороны основания.

Правильный тетраэдр  - четырехгранник у которого все четыре грани - равносторонние треугольники. Он является одним из пяти правильных многоугольников. В правильного тетраэдра все двугранные углы (между гранями) и трехгранные углы (при вершине) равны.

Если в пирамиде провести параллельное основанию сечение, то оно разделить фигуру на две части. Пространство межу нижним основанием и сечением, ограниченное гранями, называется  усеченной пирамидой .

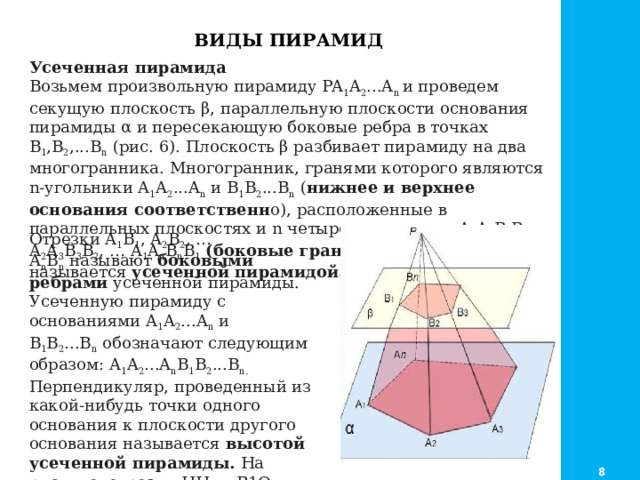
ВИДЫ ПИРАМИД

Усеченная пирамида

Возьмем произвольную пирамиду PA 1 A 2 ...A n  и проведем секущую плоскость β, параллельную плоскости основания пирамиды α и пересекающую боковые ребра в точках В 1 ,В 2 ,...В n  (рис. 6). Плоскость β разбивает пирамиду на два многогранника. Многогранник, гранями которого являются n-угольники A 1 A 2 ...A n  и В 1 В 2 ...В n  ( нижнее и верхнее основания соответственн о), расположенные в параллельных плоскостях и n четырехугольников A 1 A 2 B 2 B 1 , A 2 A 3 B 3 B 2 , … A 1 A n B n B 1   (боковые грани ), называется  усеченной пирамидой .

Отрезки A 1 B 1 , A 2 B 2 , … A n B n  называют  боковыми ребрами  усеченной пирамиды.

Усеченную пирамиду с основаниями A 1 A 2 ...A n  и В 1 В 2 ...В n  обозначают следующим образом: A 1 A 2 ...A n В 1 В 2 ...В n.

Перпендикуляр, проведенный из какой-нибудь точки одного основания к плоскости другого основания называется  высотой усеченной пирамиды.  На рисунке отрезки HH 1  и В1O –высоты усеченной пирамиды

ВИДЫ ПИРАМИД

Усеченная пирамида

Для площади боковой поверхности усеченной пирамиды верна следующая теорема

Теорема.  Площадь боковой поверхности правильной усеченной пирамиды равна произведению полусуммы периметров оснований на апофему.

Примеры и разбор решения заданий тренировочного модуля

Задание 1.  В пятиугольной пирамиде все боковые грани равны между собой. Площадь основания равна 42, а площадь боковой грани на 15 меньше. Чему равна площадь полной поверхности пирамиды?

Решение

Поскольку в пирамиде все боковые грани

равны, то и площади их будут равны.

Знаем, что площадь боковой грани на

15 меньше площади основания, значит

она равна 27. В пятиугольной пирамиде

боковых граней 5. Таким образом площадь

полной поверхности равна

27*5+42 = 177 .

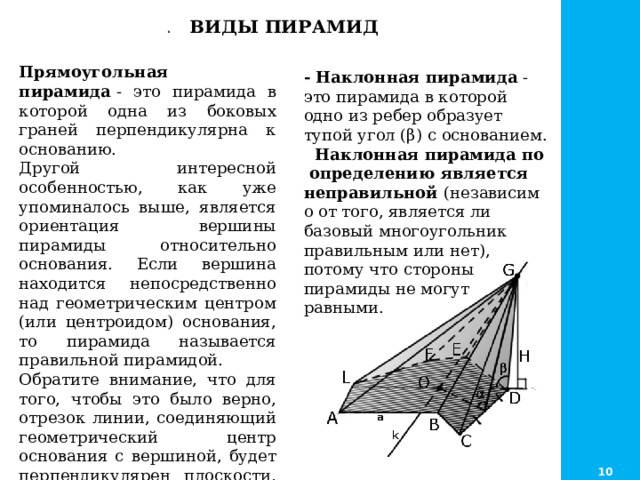
ВИДЫ ПИРАМИД

.

.

Прямоугольная пирамида  - это пирамида в которой одна из боковых граней перпендикулярна к основанию.

Другой интересной особенностью, как уже упоминалось выше, является ориентация вершины пирамиды относительно основания. Если вершина находится непосредственно над геометрическим центром (или центроидом) основания, то пирамида называется правильной пирамидой. Обратите внимание, что для того, чтобы это было верно, отрезок линии, соединяющий геометрический центр основания с вершиной, будет перпендикулярен плоскости, в которой лежит основание.

- Наклонная пирамида  - это пирамида в которой одно из ребер образует тупой угол (β) с основанием.

Наклонная пирамида по определению является неправильной  (независимо от того, является ли базовый многоугольник правильным или нет), потому что стороны пирамиды не могут равными.

ПЛОЩАДЬ ПИРАМИДЫ

Треугольной пирамидой  называется многогранник, в основании которого лежит правильный треугольник.В такой пирамиде грани основания и ребра боковых сторон равны между собой. Боковая поверхность пирамиды  - это совокупная площадь всех боковых граней пирамиды.

Соответственно площадь боковых граней находится из суммы площадей трех одинаковых треугольников. Необходимо найти их площадь Найти площадь боковой поверхности правильной пирамиды можно по формуле площади равностороннего треугольника.

Равносторонним, или правильным, называется треугольник, в котором все стороны одинаковой длины, а все три угла равны 60°. Учитывая, что все стороны равны и зная их длину, можно легко найти значение по формуле площади правильного треугольника:

Эта формула выводится из обычной формулы площади треугольник через синус угла.

ПЛОЩАДЬ ПИРАМИДЫ

А можно произвести расчет в несколько раз быстрее. Для этого необходимо применить формулу площади боковой поверхности треугольной пирамиды : Площадь боковой поверхности правильной пирамиды равна половине произведения периметра основания на апофему.

Sбок=½Pосн·d

где:

Pосн- периметр основания пирамиды,

d - апофема

Полная поверхность пирамиды состоит из поверхности боковой, то есть площади всех боковых граней, и площади основания:

S полн  = S бок  + S осн

Задача: Задача: пусть дана правильная треугольная пирамида. Сторона основания равна  b  = 4 см, апофема  a  = 6 см. Найдите полную площадь

пирамиды. Для начала найдем площадь боковой поверхности по уже известной формуле. Рассчитаем периметр:

Росн=3·4=12 см

S бок= 1/2·12·6=36 кв. см

ПЛОЩАДЬ ПИРАМИДЫ

Теперь найдем площадь основания: 

Зная площадь основания и боковой поверхности, найдем полную площадь пирамиды

ПИРАМИДЫ МИРА

Пирами́да Хеопса, Великая пирамида Гизы — крупнейшая из египетских пирамид, памятник архитектурного искусства Древнего Египта; первое и единственное из «Семи чудес света», сохранившееся до наших дней, и самое древнее из них: её возраст оценивается примерно в 4500 лет.

Г. Калининград- памятник немецким воинам, погибшим в годы Первой мировой войны 1914-1918 годов. Монумент скульптора Пауля Борхерта, представляющий собой пирамиду с барельефом "Умирающий боец", расположен на улице Малоярославской.

ПИРАМИДЫ МИРА

: 

Пирамиды майя

Пирами́да Кукулька́на  — храмовое сооружение, уцелевшее среди руин древнего города майя Чичен-Ица на полуострове Юкатан в Мексике.

Источники

: 

https ://ru.onlinemschool.com/math/formula/pyramid/

https://resh.edu.ru/subject/lesson/5866/conspect/221575/

https://www.yaklass.ru/p/geometria/10-klass/

https://myalfaschool.ru/articles/vidy-piramidhttps:// 2mb.ru/matematika/geometriya/

https://regnum.ru/news/society/1710532.html