Площадь и объем конуса, цилиндра, шара

Министерство здравоохранения Кузбасса

Новокузнецкий филиал

Государственного бюджетного профессионального образовательного учреждения

«Кузбасский медицинский колледж»

Шилепина Н. И., преподаватель

г. Новокузнецк, 2020

КОНУС

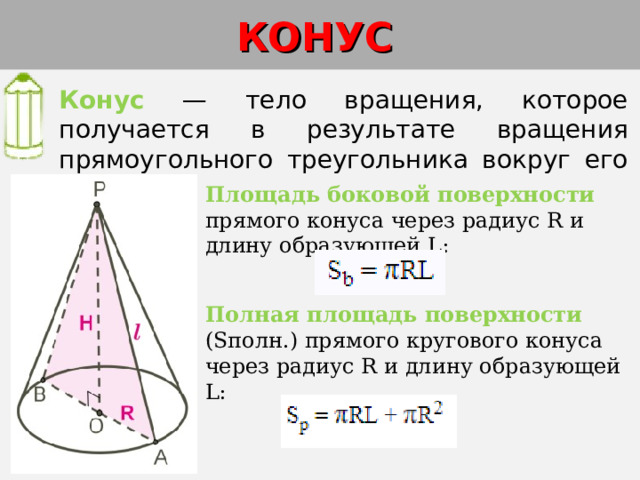
Конус — тело вращения, которое получается в результате вращения прямоугольного треугольника вокруг его катета.

Площадь боковой поверхности прямого конуса через радиус R и длину образующей L:

Полная площадь поверхности (Sполн.) прямого кругового конуса через радиус R и длину образующей L:

КОНУС

• Объём кругового конуса:

где r - радиус основы, а h - высота конуса.

Косой (наклонный) конус - это конус у которого ось не перпендикулярна основе. У такого конуса ось не совпадает с высотой.

Прямой конус

Наклонный конус

УСЕЧЕННЫЙ КОНУС

• Усеченный конус - это часть конуса, которая находится между основанием конуса и плоскостью сечения, параллельная основе.

ЗАДАЧА

ЗАДАЧА

ЦИЛИНДР

Цилиндр — это геометрическое тело, ограниченное цилиндрической поверхностью и двумя плоскостями (основами цилиндра).

Косой цилиндр

Прямой цилиндр

Наклонный цилиндр

ПЛОЩАДЬ ЦИЛИНДРА

Площадь боковой поверхности цилиндра

Полная площадь поверхности цилиндра

ОБЪЕМ ЦИЛИНДРА

ЗАДАЧА

Объем цилиндра равен 64π, а площадь боковой поверхности равна 32π. Найдите площадь полной поверхности цилиндра, деленную на π.

Выразим радиус

Площадь полной поверхности складывается из площади боковой поверхности и площадей двух оснований:

Осталось разделить полученный объем на π, тогда окончательно получаем 64. Ответ: 64

СФЕРА И ШАР

Сфера (поверхность шара) — это совокупность всех точек в трехмерном пространстве, которые находятся на одинаковом расстоянии от одной точки, называемой центром сферы (О).

Шар — это совокупность всех точек в трехмерном пространстве, расстояние от которых не превышает определенного расстояния до точки, называемой центром шара (О) (совокупность всех точек трехмерного пространства ограниченных сферой).

ПЛОЩАДЬ И ОБЪЕМ

Площадь поверхности сферы через радиус

Объём шара

ЗАДАЧА

Решение:

Радиус нового шара равен:

Тогда найдем площадь поверхности:

Ответ: 324

СПАСИБО ЗА ВНИМАНИЕ!!!