Площадь кругового сектора. Решение задач.
Подпишите работу
ФИО _______________________________________________________ класс_______________
Задание: Изучите теоретический материал. Разберите приведенные примеры задач по теме.
Выполните задание для самостоятельного решения.
Выучите определение.
О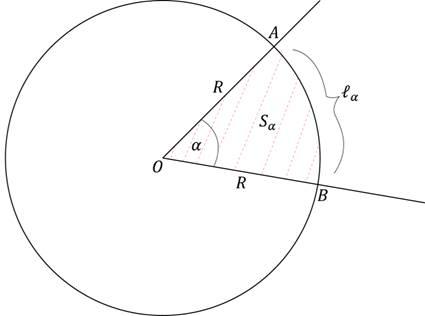 пределение: Круговой сектор – это часть круга, ограниченная дугой и двумя радиусами, соединяющими концы дуги с центром круга.
пределение: Круговой сектор – это часть круга, ограниченная дугой и двумя радиусами, соединяющими концы дуги с центром круга.
Площадь сектора – это часть площади круга.
Запомните формулу.
Площадь кругового сектора:
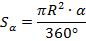 , значение числа π (пи) примерно равно π ≈ 3,14
, значение числа π (пи) примерно равно π ≈ 3,14
Здесь: α – центральный угол, измеряемый в градусах, R – радиус окружности.
Разберите решение приведенных примеров.
Пример 1.
Вычислите площадь кругового сектора, если центральный угол равен α = 30°, а радиус окружности равен R = 3 см.
Решение:
Применим формулу для вычисления площади кругового сектора:
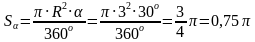
Ответ: Sα = 0,75π см2.
Пример 2:
Окружность вписана в квадрат со стороной 4 см. Найдите площадь кругового сектора (деленную на π), ограниченного половинами диагоналей квадрата.
Решение:
Составим рисунок к задаче:
О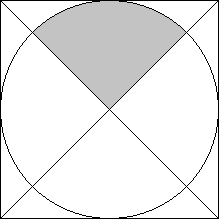 пределим угол кругового сектора. Диагонали квадрата пересекаются под прямым углом, следовательно, центральный угол α равен α = 90°.
пределим угол кругового сектора. Диагонали квадрата пересекаются под прямым углом, следовательно, центральный угол α равен α = 90°.
Определи радиус окружности. Поскольку окружность вписана в квадрат, то её диаметр D (D = 2R) равен стороне квадрата. Тогда радиус окружности R, вписанной в квадрат, вдвое меньше стороны квадрата:
R = 4/2 = 2 см.
Применим формулу для вычисления площади кругового сектора:

Разделив полученное выражение на π, получим: Sα = 1.
Ответ: Sα = 1.
Задачи для самостоятельного решения:
Выполните решение задач на отдельном листочке, обведите в кружок правильный ответ.
1. Вычислите площадь кругового сектора, если центральный угол равен α = 45°, а радиус окружности равен R = 5 см.
а) 3,14π см2 б) 3,125π см2 в) π см2 г) 0,8π см2
2. Окружность вписана в квадрат со стороной 6 см. Найдите площадь кругового сектора (деленную на π), ограниченного половинами диагоналей квадрата.
а) 1,25 б) 5,25 в) 2,25 г) 3,75






 пределение: Круговой сектор – это часть круга, ограниченная дугой и двумя радиусами, соединяющими концы дуги с центром круга.
пределение: Круговой сектор – это часть круга, ограниченная дугой и двумя радиусами, соединяющими концы дуги с центром круга.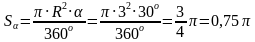
 пределим угол кругового сектора. Диагонали квадрата пересекаются под прямым углом, следовательно, центральный угол α равен α = 90°.
пределим угол кругового сектора. Диагонали квадрата пересекаются под прямым углом, следовательно, центральный угол α равен α = 90°.


















