Площадь параллелограмма и треугольника

Урок 19: «Площадь параллелограмма и треугольника»

Проверка домашнего задания

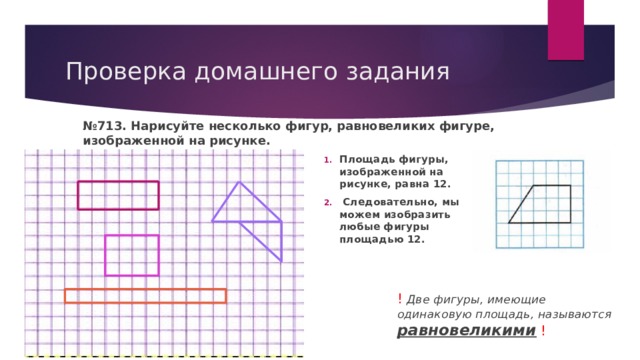
№ 713. Нарисуйте несколько фигур, равновеликих фигуре, изображенной на рисунке.

• Площадь фигуры, изображенной на рисунке, равна 12.
• Следовательно, мы можем изобразить любые фигуры площадью 12.

! Две фигуры, имеющие одинаковую площадь, называются равновеликими !

Вспомним прошлый урок

• Какие фигуры равновелики?

(Две фигуры, имеющие одинаковую площадь, называются равновеликими)

• Какие фигуры называются равносоставленными?

(Равносоставленными называют фигуры состоящие из одинаковых частей)

• Будут ли две равносоставленные фигуры равновеликими?

(Равносоставленные фигуры равновелики)

Перекройка

• На прошлом уроке мы говорили о равносоставленных фигурах. Обратите внимание на две фигуры, изображенные на рисунке.

• Оказывается, эти столь непохожие друг на друга фигуры можно разрезать на одинаковые части.

• Значит, они равновелики. Благодаря этому свойству, мы можем находить площади любых фигур. Этот прием заключается в перекраивании данной фигуры в другую, площадь которой мы вычислять умеем.

Площадь параллелограмма

• Используем прием перекройки, для нахождения площади параллелограмма

• Разрежем наш параллелограмм вдоль пунктира.
• Переложим отрезанный треугольник к другой стороне параллелограмма.
• Нам удалось перекроить параллелограмм в прямоугольник, а способ вычисления площади прямоугольника известен:

S = a · b

Площадь треугольника

• Пользуясь приемом перекройки, можно найти и площадь треугольника.

• Треугольник легко достроить до параллелограмма, проведя прямые, параллельные двум его сторонам.
• Очевидно, что площадь нашего треугольника составляет половину площади построенного параллелограмма. А как найти площадь параллелограмма, вы уже знаете.

Площадь треугольника равна половине площади параллелограмма

На странице 215 учебника МАТЕМАТИКА. Арифметика. Геометрия. Автора Е.А. Бунимович, вы ещё раз можете ознакомиться с темой «Площадь параллелограмма и треугольника».

Задание 1. Перенесите рисунок в тетрадь и покажите, как параллелограмм можно перекроить в прямоугольник. Чему равна площадь параллелограмма?

Перенеся рисунок в тетрадь и показав, как параллелограмм можно перекроить в прямоугольник, мы можем посчитать площадь прямоугольника. Так как равносоставленные фигуры по площади равны, то площадь прямоугольника равна площади параллелограмма.

S=5*5=25

Ответ: 25

Задание 2. а) Найдите площади закрашенных треугольников на рисунке 11.33. б) Достроив каждый треугольник, изображенный на рисунке 11.34, до прямоугольника, определите площадь треугольника.

а) Площадь треугольника равна половине площади прямоугольника.

1)7*4=28(см 2 )- площадь прямоугольника 1)3*3=9(см 2 )- площадь прямоугольника

2) 28:2=14 (см 2 )- площадь треугольника 2)9:2=4,5(см 2 )- площадь треугольника

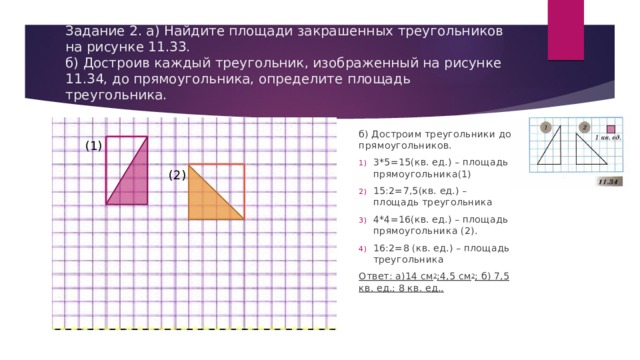
Задание 2. а) Найдите площади закрашенных треугольников на рисунке 11.33. б) Достроив каждый треугольник, изображенный на рисунке 11.34, до прямоугольника, определите площадь треугольника.

б) Достроим треугольники до прямоугольников.

• 3*5=15(кв. ед.) – площадь прямоугольника(1)
• 15:2=7,5(кв. ед.) – площадь треугольника
• 4*4=16(кв. ед.) – площадь прямоугольника (2).
• 16:2=8 (кв. ед.) – площадь треугольника

Ответ: а)14 см 2 ;4,5 см 2 ; б) 7,5 кв. ед.; 8 кв. ед..

(1)

(2)

Задание 3. Найдите площадь закрашенного треугольника (рис. 11.36)

• Для начала мы должны найти площади трех не закрашенных треугольников.

• Достроим каждый треугольник до прямоугольника.
• (3*6):2=9 (кв. ед.) – площадь треугольника 1.
• (2*5):2=5 (кв. ед.) – площадь треугольника 1.
• (1*5):2=2,5 (кв. ед.) – площадь треугольника 1.
• 9+5+2,5= 16,5 (кв. ед.) – площадь всех не закрашенных треугольников.
• 5*6= 30(кв. ед.) – площадь всего прямоугольника
• 30-16,5=13,5 (кв. ед.) – площадь закрашенного треугольника

Ответ: 13,5 кв. ед.

1

2

3

Продолжите одну из фраз

• "На сегодняшнем уроке я понял, я узнал, я разобрался…";
• "Я похвалил бы себя…";
• "Особенно мне понравилось…";
• "После урока мне захотелось…";
• "Я мечтаю о …";
• "Сегодня мне удалось…";
• "Я сумел…";
• "Было интересно…";
• "Было трудно…";
• "Я понял, что…";
• "Теперь я могу…";
• "Я почувствовал, что…";
• "Я научился…";

Домашнее задание

• К следующему уроку: параграф 46; №718, №721, №723.
•   На следующем уроке мы обязательно проверим правильность выполнения домашнего задания.​