Площадь (подготовка к ОГЭ)

Подготовила: учитель математики

МБОУ «Школа №54» г.Курск

Горбунова Л.А.

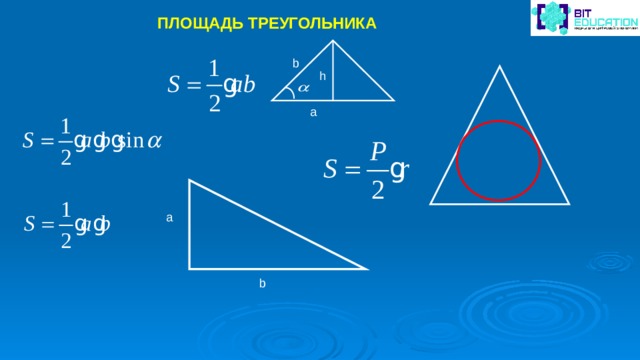
ПЛОЩАДЬ ТРЕУГОЛЬНИКА

b

h

a

a

b

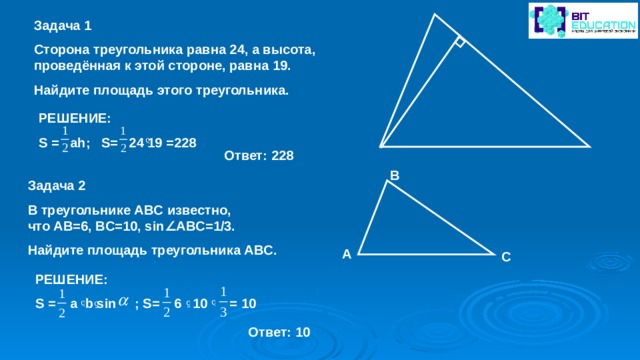
Задача 1

Сторона треугольника равна 24, а высота, проведённая к этой стороне, равна 19.

Найдите площадь этого треугольника.

РЕШЕНИЕ:

S = ah ; S= 24 19 =228

Ответ: 228

B

Задача 2

В треугольнике ABC известно, что AB=6, BC=10, sin∠ABC=1/3.

Найдите площадь треугольника ABC.

A

C

РЕШЕНИЕ:

S = a b sin ; S= 6 10 = 10

Ответ: 10

Задача 3

Два катета прямоугольного треугольника равны 6 и 7. Найдите площадь этого треугольника.

РЕШЕНИЕ:

S = a b S = 6 7 = 21

Ответ: 21

Задача 4

Периметр треугольника равен 33, одна из сторон равна 7, а радиус вписанной в него окружности равен 2.

Найдите площадь этого треугольника.

РЕШЕНИЕ:

S = r S = 33

Ответ: 33

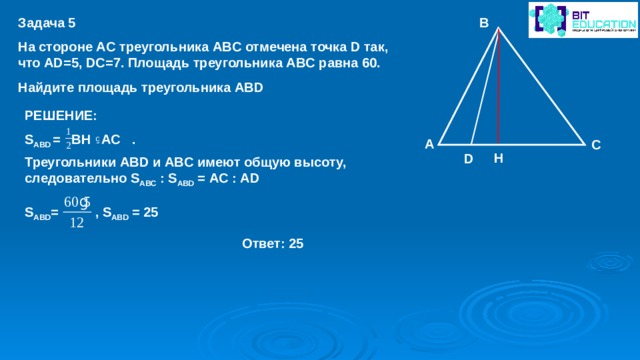
Задача 5

На стороне AC треугольника ABC отмечена точка D так, что AD=5, DC=7. Площадь треугольника ABC равна 60.

Найдите площадь треугольника ABD

B

РЕШЕНИЕ:

S ABD = BH AC .

A

C

H

D

Треугольники ABD и ABC имеют общую высоту, следовательно S ABC : S ABD = AC : AD

S ABD = , S ABD = 25

Ответ: 25

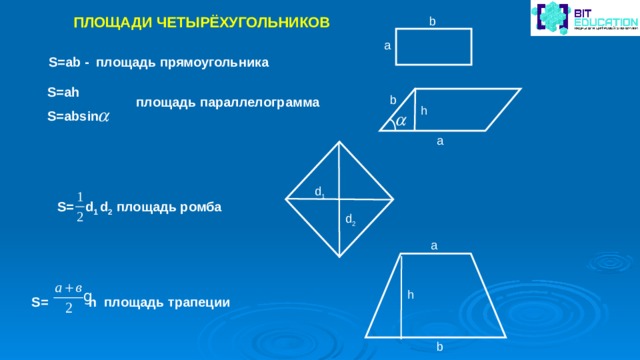
ПЛОЩАДИ ЧЕТЫРЁХУГОЛЬНИКОВ

b

S=ab - площадь прямоугольника

S=ah

S=absin

b

площадь параллелограмма

h

d 1

S= d 1 d 2 площадь ромба

d 2

a

h

S= h площадь трапеции

b

Задача 6

Сторона квадрата равна 3√2. Найдите площадь этого квадрата

РЕШЕНИЕ:

S= a 2 , S= ( 3√2 ) 2 = 18

Ответ: 18

Задача 7

Найдите площадь квадрата, описанного около окружности радиуса 40

РЕШЕНИЕ:

S= a 2 , a= √2 R , S= (40 √2 ) 2 = 3200

Ответ: 3200

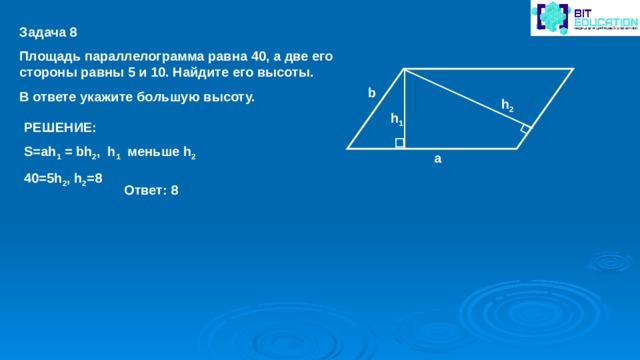
Задача 8

Площадь параллелограмма равна 40, а две его стороны равны 5 и 10. Найдите его высоты.

В ответе укажите бо л ьшую высоту.

b

h 2

h 1

РЕШЕНИЕ:

S=ah 1 = bh 2 , h 1 меньше h 2

40=5h 2 , h 2 =8

a

Ответ: 8

Задача 9

Площадь параллелограмма ABCD равна 140. Точка E — середина стороны AB.

Найдите площадь треугольника CBE.

B

C

E

M

РЕШЕНИЕ:

Проведём EM параллельно ВС,

A

D

ЕМ делит параллелограмм ABCD на два равных параллелограмма AEMD и EBCM .

S EBCM = 140 :2=70, S CBE = S EBCM :2 = 70:2=35

Ответ: 35

Задача 10

Площадь параллелограмма ABCD равна 28. Точка E — середина стороны AB.

Найдите площадь трапеции  DA E C .

B

C

РЕШЕНИЕ:

Проведём EM параллельно ВС,

E

AEMD = EBCM , S EBCM = 28:2=14, S CBE = S ECM = 14:2=7.

M

S DAEC =S AEMD +S ECM , S DEAC =14+7=21

A

Ответ: 21

D

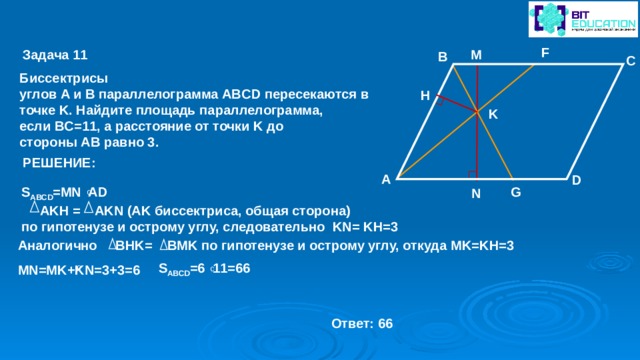
F

Задача 11

M

B

C

Биссектрисы углов A и B параллелограмма ABCD пересекаются в точке K. Найдите площадь параллелограмма, если BC=11, а расстояние от точки K до стороны AB равно 3.

H

K

РЕШЕНИЕ:

S ABCD =MN AD

AKH = AKN (AK биссектриса, общая сторона)

по гипотенузе и острому углу, следовательно KN = KH =3

A

D

G

N

Аналогично BHK= BMK по гипотенузе и острому углу, откуда MK=KH=3

MN=MK+KN=3+3=6

S ABCD =6 11=66

Ответ: 66

Задача 12

Найдите площадь ромба, если его диагонали равны 14 и 6

РЕШЕНИЕ:

Ответ: 42

Задача 13

Периметр ромба равен 20, а один из углов равен 30 0 .

Найдите площадь ромба

РЕШЕНИЕ:

Р=4а; а=20:4=5

Ответ: 12,5

Задача 14

В равнобедренной трапеции основания равны 2 и 6, а один из углов между боковой стороной и основанием равен 45°.

Найдите площадь этой трапеции

2

C

B

РЕШЕНИЕ:

ABH- прямоугольный равнобедренный, ABH = 45 0

AH=BH , AH=(6-2) : 2 =2

S= BH

S= =8

45 0

D

A

H

6

Ответ: 8

Задача 15

На средней линии трапеции ABCD с основаниями AD и BC выбрали произвольную точку E. Докажите, что сумма площадей треугольников BEC и AED равна половине площади трапеции

H

C

B

Доказательство:

По условию задачи точка E лежит на отрезке MN – средней линии трапеции. Проведем через эту точку высоту HL трапеции. Тогда по свойству средней линии, отрезки EH=EL=1/2∙HL. Используя данные обозначения, выразим площади треугольников BEC и AED следующим образом:

E

M

N

A

D

L

S BEC + S AED =

S AED =

S BEC =

= S ABCD , то получаем S BEC + S AED = S ABCD = S AEB +S CED

Так как