Площадь треугольника. Теоремы синусов и косинусов.

Теорема о площади треугольника

• Площадь треугольника равна половине произведения двух его сторон на синус угла между ними .

А

y

b

h

x

H

С

В

а

Следствие 1

• Площадь параллелограмма равна произведению двух его смежных сторон на синус угла между ними

Диагональ параллелограмма , делит его на два равновеликих

треугольника : S Δ = a b sin , S пар = a b sin

Следствие 2

• Площадь параллелограмма равна половине произведения диагоналей на синус угла между ними

ABCD- параллелограмм,

BD=d 1 , AC=d 2 , AOB= α

В

С

O

180 °- α

D

А

S AOB =S COD

S BOC =S AOD

4 ·S Δ

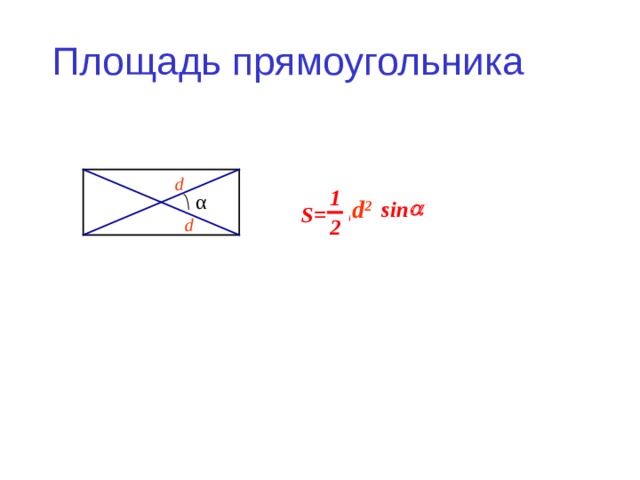
Площадь прямоугольника

d

α

d 2

d

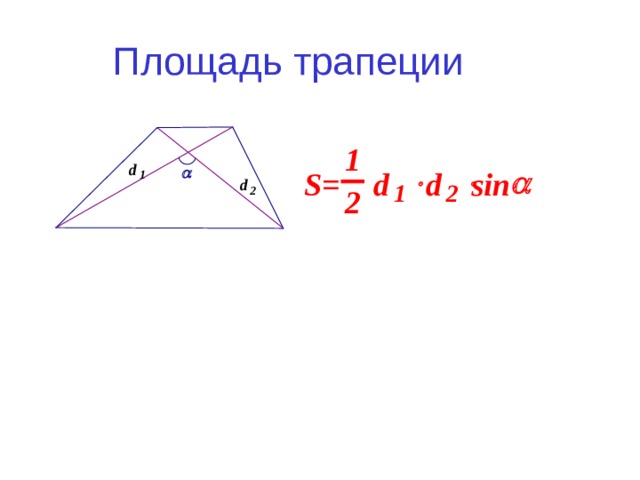
Площадь трапеции

Задания по готовым

чертежам

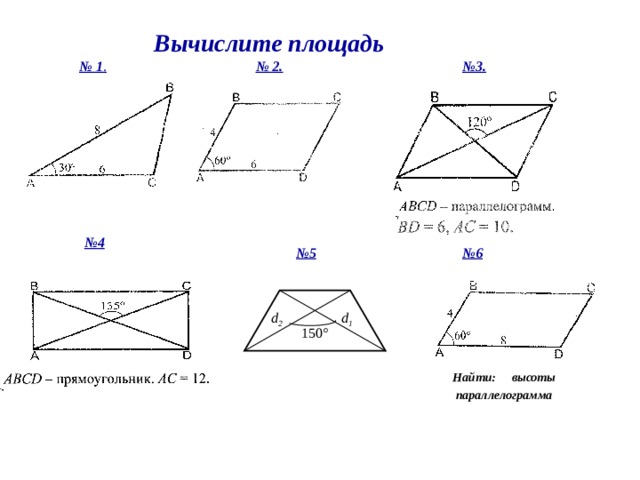
Вычислите площадь

№ 1 .

№ 3.

№ 2.

№ 4

№ 5

№ 6

d 2

d 1

d 1

150 °

Найти: высоты

параллелограмма

Теорема синусов

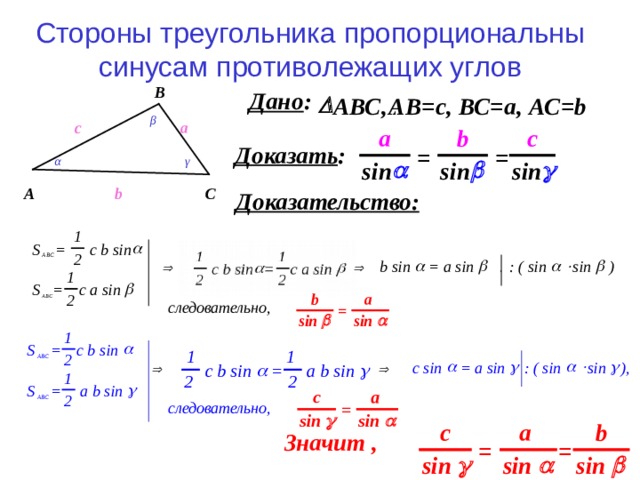
Стороны треугольника пропорциональны синусам противолежащих углов

B

β

a

c

α

γ

b

C

A

Следствие 1

Отношение стороны треугольника к синусу противолежащего угла равно двум радиусам (диаметру) описанной окружности.

ω

А

α

α

А 1

О

В

а

С

1 случай

ВА 1

Следствие 2

• Площадь треугольника можно вычислить по формуле

• a, b, c – стороны треугольника ,

R – радиус окружности , описанной около треугольника .

( докажите самостоятельно, используя теорему о площади треугольника и следствие из теоремы синусов )

с

Значит,

Задания по готовым чертежам

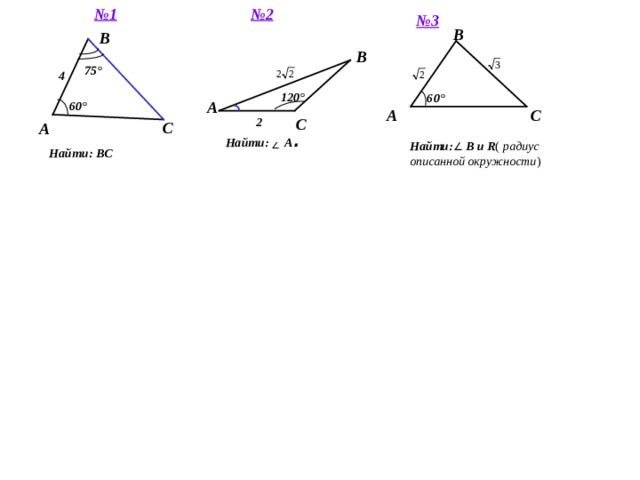
№ 1

№ 2

№ 3

B

В

B

75 °

4

120 °

6 0 °

A

60 °

C

A

2

C

С

Найти: A .

А

Найти : В и R ( радиус описанной окружности )

Найти : ВС

Теорема косинусов

• Квадрат стороны треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними .

у

С

b

a

α

х

c

(с;0)

В

(0;0)

А

По формуле расстояния между двумя точками получаем:

- 2bc cos α

+b 2 sin 2 α

b 2 cos 2 α

=

=

+b 2 sin 2 α

BC 2 = a 2 = (b cos α –c) 2

+c 2

b 2 (cos 2 α + sin 2 α )+c 2 - 2bc cos α

=

b 2 +c 2 - 2bc cos α

=

1

Задания по готовым чертежам

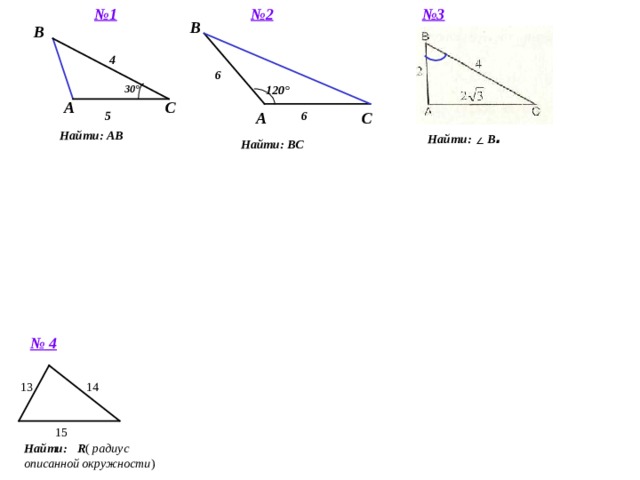
№ 2

№ 3

№ 1

B

B

4

6

120 °

30 °

A

C

С

6

А

5

Найти: B .

Найти : АВ

Найти : ВС

№ 4

14

13

15

Найти : R ( радиус описанной окружности )