Подготовка к ЕГЭ базового уровня. Задачи № 19, 20.

Подготовка к егэ по математике (Базовый уровень): Задачи № 19,20

МАОУ «Многопрофильный лицей №1» г. Магнитогорска, учитель математики- Пупкова Т.В.

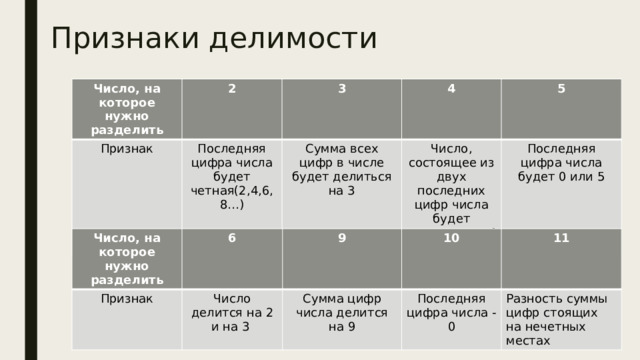
Признаки делимости

Число, на которое нужно разделить

2

Признак

3

Последняя цифра числа будет четная(2,4,6,8…)

4

Сумма всех цифр в числе будет делиться на 3

5

Число, состоящее из двух последних цифр числа будет делиться на 4

Последняя цифра числа будет 0 или 5

Число, на которое нужно разделить

Признак

6

9

Число делится на 2 и на 3

10

Сумма цифр числа делится на 9

11

Последняя цифра числа - 0

Разность суммы цифр стоящих на нечетных местах

Алгоритм решения

• Найдите трёхзначное число, кратное 25, все цифры которого различны, а сумма квадратов цифр делится на 3, но не делится на 9. В ответе укажите какое-нибудь одно такое число.

Так как наше число должно быть кратно 25, то его последние цифры должны быть или 25, или 50, или 75.

Цифры 00 на конце числа нам не подходят, так как по условию все цифры должны быть различны.

• Выпишем все трёхзначные числа, заканчивающиеся на 25, 50 или 75, все цифры которых различны, найдём сумму квадратов их цифр, проверим, делится ли она на 3 и на 9.

Покажу на примере первых пяти чисел:

• 125: 1 2 + 2 2 + 5 2 = 30. Сумма квадратов цифр делится на 3, но не делится на 9. Значит это искомое число
• 150: 1 2 + 5 2 + 0 2 = 26. Сумма квадратов цифр не делится на 3. Это число нам не подходит
• 175: 1 2 + 7 2 + 5 2 = 75. Сумма квадратов цифр делится на 3, но не делится на 9. Значит это искомое число
• Числа 200 и 225 мы не рассматриваем, так как в них присутствуют повторяющиеся цифры.
• 250: 2 2 + 5 2 + 0 2 = 29. Сумма квадратов цифр не делится на 3. Это число нам не подходит
• 275: 2 2 + 7 2 + 5 2 = 78. Сумма квадратов цифр делится на 3, но не делится на 9. Значит это искомое число

По такой же схеме нужно продолжить считать сумму квадратов цифр в числах, оканчивающихся на 25,50 или 75, исключая числа, в которых будут присутствовать одинаковые числа ( такие как 225, 525, 550, 575…)

Возможные ответы: 125, 175, 275…

Следуя из того, что искомое число делится на 4 , то можно сказать что 10с+d делится на 4. Можно заметить, что если среди цифр есть хотя бы три единицы, то равенство невозможно, так как сумма будет больше произведения. Если единица только одна, то произведение будет слишком большое. Таким образом, среди цифр есть ровно две единицы. Рассмотрим двузначные числа, которые делятся на 4, две их последние цифры образуют число, делящееся на 4. Нельзя брать числа с нулём, так как в этом случае произведение будет равно нулю.

12: тогда оставшиеся числа 1 и 4, сумма цифр равна 1+2+1+4=8, произведение цифр равно 1*2*1*4= 8.

16: тогда оставшиеся числа 1 и больше никакое не подойдет.

24: тогда оставшиеся числа 1 и 1. сумма цифр будет равна 1+1+2+4= 8, произведение равно 1*1*2*4= 8.

Остальные числа будут давать слишком большое произведение на нечетную сумму.

Возможные ответы : 1412, 4112, 1124

• Приведите пример четырёхзначного натурального числа, кратного 4, сумма цифр которого равна их произведению. В ответе укажите ровно одно такое число. Можно записать наше число как abcd. Тогда, по условию задачи, получим уравнение

a+b+c+d = a*b*c*d.

• Найдите четырёхзначное число, кратное 9, но не кратное 6, произведение цифр которого равно 1960. В ответе укажите какое-нибудь одно такое число, а лучше все.

• Если разбить число 1960 на множители, то получим числа 5, 7, 7, 8.
• Число делится на 9, если сумма цифр в нем будет делится на 9.

5+7+7+8=27. Значит любое число, составленное из этих чисел будет делиться на 9

3) Число делится на 9 и не делится на 6, если оно нечетное. Тогда в ответ можно подать любое нечетное число, составленное из этих цифр.

Возможные ответы: 7785, 7875, 8775, 8757, 8577, 5877, 5787, 7587, 7857

Остатки от деления

Приведите пример трехзначного натурального числа, большего 600, которое при делении на 4, на 5 и на 6 дает в остатке 3, и цифры которого расположены в порядке убывания слева направо. В ответе укажите ровно одно такое число .

• Чтобы число делилось одновременно на 4, 5 и 6 найдем его наименьшее общее кратное:

4*5*6=60.

2) Чтобы в остатке получилось число 3, запишем искомое число формулой 60n+3.

3) Начнем подставлять числа в формулу, пока не выполнится условие задачи.

При n=10 число 603. Условие не выполняется

При n=11 число 663. Условие не выполняется

При n=12 число 723. Условие не выполняется

При n=13 число 783. Условие не выполняется

При n=14 число 843. Условие выполняется. Это искомое число

Ответ: 843

• Цифры четырёхзначного числа, кратного 5, записали в обратном порядке и получили второе четырёхзначное число. Затем из первого числа вычли второе и получили 4536. Приведите ровно один пример такого числа.

• Так как первое число кратное 5, то оно должно кончаться на 5 или 0. Значит это abc5 или abc0
• Так как цифры второго числа записали в обратном порядке, можно записать

это число 5cba либо 0cba. Отсюда делаем вывод, что второе число 5cba , так как

0cba уже трехзначное число.

3) Исходя из условия задачи можно составить уравнение abc5=5cba+4536.

4)Отсюда делаем вывод, что a=9, получаем следующее уравнение:

9bc5 = 5cb9 + 4536.

36+9=45, значит, с=b+4 или с = b +4 –10 = b –6

5)Если с=b+4, то в следующий разряд ничего не переносится и получается b =с+5, чего быть не может

с =b – 6 (единица переносится в следующий разряд), тогда b = c+5+1, что совпадает с предыдущим условием.

6) Осталось выбрать b и с, например, b = 6; c=0.

Ответ: 4536.

• На шести карточках написаны цифры 2, 3, 5, 6, 7, 7 (по одной цифре на каждой карточке). В выражении

Задачи с карточками

 ++

вместо каждого квадратика положили карточку из данного набора. Оказалось, что полученная сумма делится на 10, но не делится на 20. В ответе укажите какую-нибудь одну такую сумму.

1) Чтобы сумма делилась на 10 она должна заканчиваться на 0. Чтобы сумма не делилась на 20, вторая цифра с конца не должна быть четной. Чтобы в конце суммы получить 0, можно выбрать следующие цифры: 2, 3, 5 и 6, 7, 7. Рассмотрим каждую из двух комбинаций.

Случай 2: комбинация 6, 7, 7.

Случай 1: комбинация 2, 3, 5.

6+□7+□□7 

2+□3+□□5 

Среди оставшихся цифр 2, 3, 5 — две нечетные и одна четная. Чтобы получить вторую цифру нечетную, нужно взять одну четную (2) и одну нечетную цифры (3 или 5) во втором разряде (к нечетной сумме будет добавляться 2 от суммы цифр в 1 разряде). Тогда получаем: 6 + 27 + 537 = 570 и 6 + 27 + 357 = 390.

Среди оставшихся цифр 6, 7, 7 — две нечетные и одна четная. Чтобы получить вторую цифру нечетную, нужно взять две чётных цифры или две нечётных цифры Тогда получаем: 2 + 73 + 675 = 750.

Ответ:  390, 570 или 750.

Задание №20

Задачи на смекалку

1. Задачи на распиливание и разрезание

• На палке отмечены поперечные линии красного, жёлтого и зелёного цвета. Если распилить палку по красным линиям,  то получится  15 кусков, если по жёлтым – 5 кусков, а если по зелёным – 7 кусков. Сколько кусков получится, если распилить палку по линиям всех трёх цветов?

Если распилить палку по красным линиям, то получится 15 кусков, следовательно, линий — 14.

Если распилить палку по желтым — 5 кусков, следовательно, линий — 4.

Если распилить по зеленым — 7 кусков, линий — 6.

Всего линий: 14 + 4 + 6 = 24 линии, следовательно, кусков будет 25.

Ответ: 25.

• Взяли несколько досок и распилили их. Всего сделали 11 поперечных распилов, в итоге получилось 16 кусков. Сколько досок взяли?

Так как нам не сказано, что все доски были распилены, то берем одну доску, пилим ее 11 раз, получаем 12 кусков.

Затем берем еще 4 целые доски и в итоге получаем 12+4 = 16 кусков

Получается одна распиленная и 4 целых доски. 1+4=5.

Ответ: 5

Параллели и меридианы

• На глобусе фломастером проведены 17 параллелей (включая экватор) и 24 меридиана. На сколько частей проведённые линии разделяют поверхность глобуса? Меридиан — это дуга окружности, соединяющая Северный и Южный полюсы. Параллель — это окружность, лежащая в плоскости, параллельной плоскости экватора.

• Для начала мы видим, что 24 меридианы разобьют глобус на 24 части. Затем рассмотрим сектор, который образовался между двумя меридианами. Если провести одну параллель, она разделит каждый сектор на 2 части. Проведение еще одной параллели разделит глобус на 3 части. Таким образом, 17 параллелей разделят один сектор на 18 частей. Тогда весь глобус будет разделен на 24*18=432.

Ответ: 432.

Квартиры, подъезды, номера домов

• Во всех подъездах дома одинаковое число этажей, а на каждом этаже одинаковое число квартир. При этом число этажей в доме больше числа квартир на этаже, число квартир на этаже больше числа подъездов, а число подъездов больше одного. Сколько этажей в доме, если всего в нём 455 квартир?

Заметим, что число 455 делится на 5, 7 и 13. Тогда, используя условие задачи делаем вывод, что в доме 13 этажей, 7 квартир на этаже и 5 подъездов.

Ответ: 13.

В доме, в котором живет Женя, 17 этажей и несколько подъездов. На каждом этаже находится по 3 квартиры. Женя живет в квартире №76. В каком подъезде живет Женя?

Мы знаем, что на каждом этаже 3 квартиры и всего 17 этажей в доме. Исходя из этого, делаем вывод, что

В одном подъезде 17*3= 51 квартира.

Соответственно, в первом подъезде квартиры с 1 по 51, во втором с 52-102 квартиру. Соответственно Женя живет во втором подъезде.

Ответ: 2.

Плата за колодец

Хозяин договорился с рабочими, что они копают колодец на следующих условиях: за первый метр он заплатит им 3500 рублей, а за каждый следующий метр — на 1600 рублей больше, чем за предыдущий. Сколько денег хозяин должен будет заплатить рабочим, если они выкопают колодец глубиной 9 метров?

Последовательность цен за метр — арифметическая прогрессия с первым элементом a1=3500 и разностью d=1600. Тогда, по формуле, сумма первых элементов прогрессии –

Если подставить в формулу наши значения, то получится:

Ответ: 89100

Спуск и подъем на высоту

• Улитка за день заползает вверх по дереву на 4 м, а за ночь сползает на 3 м. Высота дерева 10 м. За сколько дней улитка впервые доползёт до вершины дерева?

За день улитка заползёт на 4 метра, а за ночь — сползёт на 3 метра. Итого за сутки она заползёт на метр. За 7 суток она поднимется на высоту семи метров.

Ответ: 7

• Нефтяная компания бурит скважину для добычи нефти, которая залегает, по данным геологоразведки, на глубине 3 км. В течение рабочего дня бурильщики проходят 300 метров в глубину, но за ночь скважина вновь «заиливается», то есть заполняется грунтом на 30 метров. За сколько рабочих дней нефтяники пробурят скважину до глубины залегания нефти?

3 км = 3000 метров. За одни сутки нефть опускается на 300-30=270 метров.

Соотвественно 270 * 10 = 2700 метров. На следующий день они пробурят еще 300 километров и достанут до глубины залегания нефти .

Ответ: 11

Координатная прямая

• Кузнечик прыгает вдоль координатной прямой в любом направлении на единичный отрезок за прыжок. Сколько существует различных точек на координатной прямой, в которых кузнечик может оказаться, сделав ровно 5 прыжков, начиная прыгать из начала координат?

Обозначим через 1 прыжок кузнечика в одну сторону координатой прямой, а через -1 в противоположную сторону этой прямой. Общее число вариантов его перемещений будет равно 2 5 =32 , а различных точек:

1+1+1+1+1=5

1+1+1+1-1=3

1+1+1-1-1=1

1+1-1-1-1=-1

1-1-1-1-1=-3

-1-1-1-1-1=-5

то есть ровно 6.

Ответ : 6

Корзина с грибами

В корзине лежит 50 грибов: рыжики и грузди. Известно, что среди любых 28 грибов имеется хотя бы один рыжик, а среди любых 24 грибов хотя бы один груздь. Сколько груздей в корзине?

В корзине точно лежит 27 груздей и 23 рыжика, так как взять 28 груздей, как и 24 рыжика, не получится.

Ответ: 27

Монеты

В обменном пункте можно совершить одну из двух операций:

1) за 4 золотых монеты получить 5 серебряных и одну медную;

2) за 7 серебряных монет получить 5 золотых и одну медную.

У Николая были только серебряные монеты. После нескольких посещений обменного пункта серебряных монет у него стало меньше, золотых не появилось, зато появилось 90 медных. На сколько уменьшилось количество серебряных монет у Николая?

Последовательно получаем:

Если Николай за 1 серебряную получил 3 медных, а у него появилось 90 медных, то он истратил 30 серебряных (т. к. 90 : 3 = 30 серебряных).

Таким образом, у него количество монет уменьшилось на 30.

Ответ: 30

Прямоугольник и его части

• Прямоугольник разбит на четыре меньших прямоугольника двумя прямолинейными разрезами. Периметры трёх из них, начиная с левого верхнего и далее по часовой стрелке, равны 24, 28 и 16. Найдите периметр четвёртого прямоугольника.

Представим условие задачи в виде рисунка:

Введём обозначения, как показано на рисунке. Периметр верхнего левого прямоугольника равна 24, поэтому

2(a+c) = 24,  аналогично 2(a+d)=28 и 2(b+d)=16

Из третьего уравнения получаем : b+c=6

Следовательно, периметр равен 2 * 6 = 12

Ответ: 12