Россия, Омская область Тюкалинский район с.Троицк
СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока
Была в сети 24.04.2025 17:52
Терещенко Евгения Викторовна
учитель математики
36 лет
640
83 720 
Местоположение
Подготовка к ОГЭ 2023 (задание №13) Неравенства, системы неравенств
Категория:
Алгебра
10.10.2023 15:46
Просмотр содержимого документа
«Подготовка к ОГЭ 2023 (задание №13) Неравенства, системы неравенств»
Подготовка к ОГЭ 2023 ( задание №13) Неравенства, системы неравенств
Числовые неравенства
Вся числовая ось:
Интервал:
Отрезок:
Закрытый луч:
Открытый луч:
Объединение лучей :
Решением неравенства с одним неизвестным называется то значение неизвестного, при котором это неравенство обращается в верное числовое неравенство.
Решить неравенство – найти все его решения или установить, что их нет.
Свойства неравенств
1. Любой член неравенства можно перенести из одной части неравенства в другую с противоположным знаком, при этом знак неравенства не меняется.
2. Обе части неравенства можно умножить или разделить на одно и то же число, не равное нулю. Если число положительно, то знак неравенства не ме- няется, если отрицательно – знак неравенства меняется на противоположный.
Линейные неравенства
Общий вид:
Алгоритм решения неравенств, сводящихся к линейным:
1) перенести члены, содержащие неизвестное, в левую часть, а члены, не содержащие неизвестное, в правую (свойство 1);
2) приведя подобные члены, разделить обе части неравен-ства на коэффициент при неизвестном, если он не равен нулю (свойство 2).
≤ ≥ 1. Все действия на слайде – последовательно щелчком мышки. " width="640"
Решаем неравенства.
Решить неравенство – найти значение переменной,
которое обращает его в верное числовое неравенство.
Правила:
≤
≥
1.
Все действия на слайде – последовательно щелчком мышки.
2. ≥ Все действия на слайде – последовательно щелчком мышки. " width="640"
Решаем неравенства.
Решить неравенство – найти значение переменной,
которое обращает его в верное числовое неравенство.
Правила:
: а
≤
2.
≥
Все действия на слайде – последовательно щелчком мышки.
Решаем неравенства.
Решить неравенство – найти значение переменной,
которое обращает его в верное числовое неравенство.
Правила:
: а
2.
Все действия на слайде – последовательно щелчком мышки.
Решаем неравенства.
1.
Все действия на слайде – последовательно щелчком мышки.
х
-3
Ответ:
10
2.
Ответ:
Системы двух линейных неравенств
Решением системы неравенств с одним неизвестным называется то значение неизвестного, при котором все неравенства системы обращаются в верные числовые неравенства.
Решить систему неравенств – найти все решения этой системы или установить, что их нет.
Алгоритм:
1) решить оба неравенства;
2) изобразить на числовой оси множество решений первого и второго неравенств системы;
3) определить значения неизвестного, которые одновременно принадлежат обоим интервалам.
Ответ:
Ответ:
Ответ:
Квадратные неравенства:
Общий вид:
Способы решения:
1) сведение к системе линейных неравенств;
2) с помощью графика квадратичной функции;
3) метод интервалов.
Сведение к системе линейных неравенств (1 способ)
Алгоритм:
- разложить квадратный многочлен на множители:
2) составить и решить совокупность двух систем :
3) объединить решения обеих систем.
Пример : Решите неравенство
Пример : Решите неравенство
Ответ:
С помощью графика квадратичной функции (2 способ)
Алгоритм:
1) найти действительные корни квадратного уравнения или установить, что их нет;
2) определить направление ветвей параболы
3) изобразить эскиз графика квадратичной функции, используя точки пересечения (касания) с осью Ox , если они есть;
4) по графику определить промежутки, на которых функция принимает нужные значения.
0 ветви вверх Ответ: " width="640"
Решить неравенство:
a =10 ветви вверх
Ответ:
Решить неравенство:
a =−1
Ответ:
0 ветви вверх Ответ: решений нет " width="640"
Решить неравенство:
a =10 ветви вверх
Ответ: решений нет
Метод интервалов (3 способ)
Алгоритм:
1) найти нули функции решив квадратное уравнение ;
2) отметить положение нулей на оси Ox ;
3) определить знаки функции в промежутках между нулями;
A. вычислить значение функции в точке x=0 (или, например x=1 ), отметить знак в соответствующем промежутке
B. определить знаки в остальных промежутках по правилу:
(2 корня)
знаки чередуются
(1 корень)
знаки совпадают
(нет корней)
функция сохраняет
знак на всей числовой оси
4) выбрать промежутки, на которых функция принимает нужные значения.
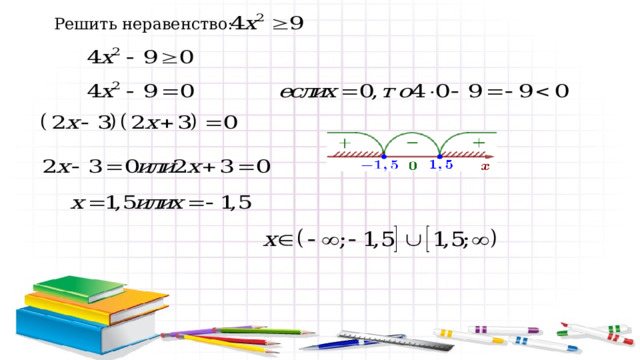
Решить неравенство:
0 ветви вверх (нет корней) функция сохраняет знак на всей числовой оси Ответ: решений нет " width="640"
Решить неравенство:
a =10 ветви вверх
(нет корней)
функция сохраняет
знак на всей числовой оси
Ответ: решений нет
0 ветви вверх (нет корней) функция сохраняет знак на всей числовой оси Ответ: x-любое число или " width="640"
Решить неравенство:
a =10 ветви вверх
(нет корней)
функция сохраняет
знак на всей числовой оси
Ответ: x-любое число или
0 ветви вверх Решение совпадает с изображенным на рисунке, в ином случае верным было бы неравенство №4. Ответ: 3 " width="640"
Укажите неравенство, решение которого изображено на рисунке:
Решим неравенство №1:
Корни не совпадают с данными рисунка.
Такие же корни даст неравенство №2, поэтому его тоже можно проигнорировать.
Решим неравенство №3:
a =10 ветви вверх
Решение совпадает с изображенным на рисунке, в ином случае верным было бы неравенство №4.
Ответ: 3
Вебинар для учителей
Свидетельство об участии БЕСПЛАТНО!
