Подготовка к ОГЭ, Задание 16.

Задание №16

Задача №1

Четырехугольник АВСD вписан в окружность. ∠ АВС равен 38°, ∠ САD равен 33°. Найдите угол АВD. Ответ дайте в градусах.

Дано: ∠АВС = 38°, ∠САD = 33°.

Найти: ∠АВD.

Решение:

1) ∠DBC = ∠CAD = 33°, так как вписанные углы, опирающиеся на одну и ту же дугу DC .

2) ∠АВD = ∠AВC – ∠DBC = 38° – 33° = 5°

Ответ: 5.

Задача №2

Площадь круга равна 69. Найдите площадь сектора этого круга, центральный угол которого равен 120°.

Дано: S круга = 69, угол кругового сектора равен 120°.

Найти: S сектора .

Решение:

Ответ: 23.

Задача №3

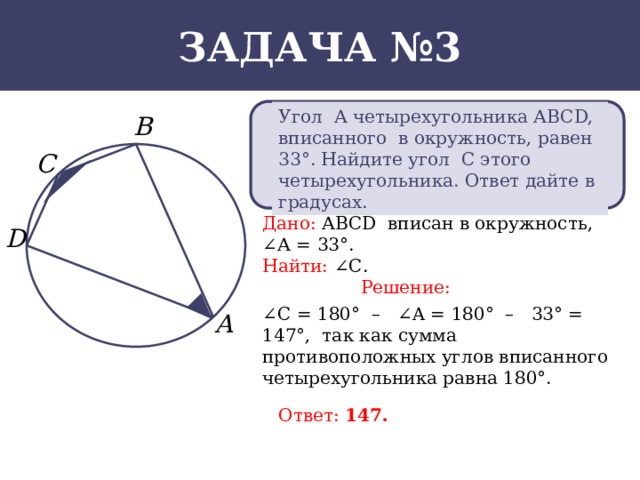
Угол А четырехугольника АВСD, вписанного в окружность, равен 33°. Найдите угол С этого четырехугольника. Ответ дайте в градусах.

Дано: АВСD вписан в окружность, ∠А = 33°.

Найти: ∠С.

Решение:

∠ C = 180° – ∠A = 180° – 33° = 147°, так как сумма противоположных углов вписанного четырехугольника равна 180°.

Ответ: 147.

Задача №4

Отрезки АС и BD – диаметры окружности с центром О. Угол АСВ равен 53°. Найдите угол АОD. Ответ дайте в градусах.

Дано: АС и BD – диаметры окружности,

∠ АСВ = 53°.

Найти: ∠ АОD.

Решение:

1) АCВ = 53° – вписанный угол, опирающийся

на ᴗ АВ, поэтому ᴗ АВ = 53°  2 = 106°, так как вписанный угол измеряется половиной дуги, на которую он опирается.

2) BD – диаметр, значит ᴗ ВАD = 180°.

3) ∠ АОD – центральный угол, опирающийся на ᴗ АD, следовательно ∠ АОD = ᴗ АD = 180° – 106° = 74°.

Ответ: 74.

Задача №5

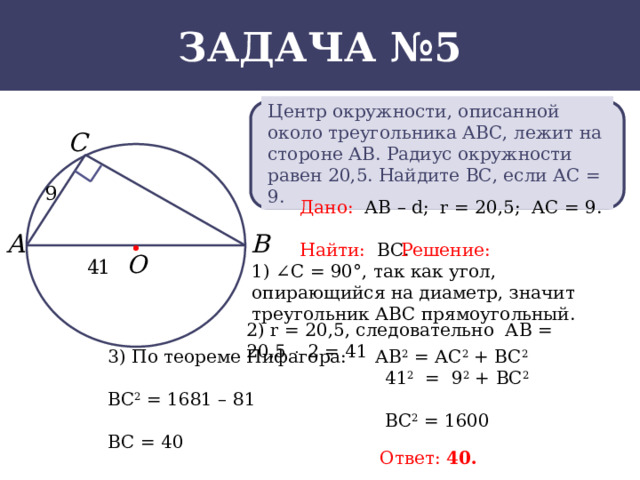
Центр окружности, описанной около треугольника АВС, лежит на стороне АВ. Радиус окружности равен 20,5. Найдите ВС, если АС = 9.

Дано: АВ – d; r = 20,5; АС = 9.

Найти: ВС.

Решение:

1) ∠C = 90°, так как угол, опирающийся на диаметр, значит треугольник АВС прямоугольный.

2) r = 20,5, следовательно АВ = 20,5  2 = 41

3) По теореме Пифагора: АВ 2 = АС 2 + ВС 2

41 2 = 9 2 + ВС 2 ВС 2 = 1681 – 81

ВС 2 = 1600 ВС = 40

Ответ: 40.

Задача №6

Точка О – центр окружности, на которой лежат точки А, В и С. Известно, что ∠АВС = 61° и ∠ОАВ = 8°. Найдите угол ВСО. Ответ дайте в градусах.

Дано: ∠АВС = 61°, ∠ОАВ = 8°.

Найти: ∠ ВСО.

Решение:

1) Проведем радиус ОВ, АО = ВО = СО = r.

2) Треугольник АОВ – равнобедренный, значит ∠А = ∠АВО = 8°.

3) Треугольник ВОС – равнобедренный, значит

∠ ВСО = ∠ОВС= 61° – 8° = 53°.

Ответ: 53.

Задача №7

На окружности с центром О отмечены точки А и В так, что : ∠АОВ = 45°. Длина меньшей дуги равна 91. Найдите длину большей дуги.

Дано: ∠АОВ = 45°, длина меньшей дуги

равна 91.

Найти: длину большей дуги.

Решение:

Ответ: 637.

Задача №8

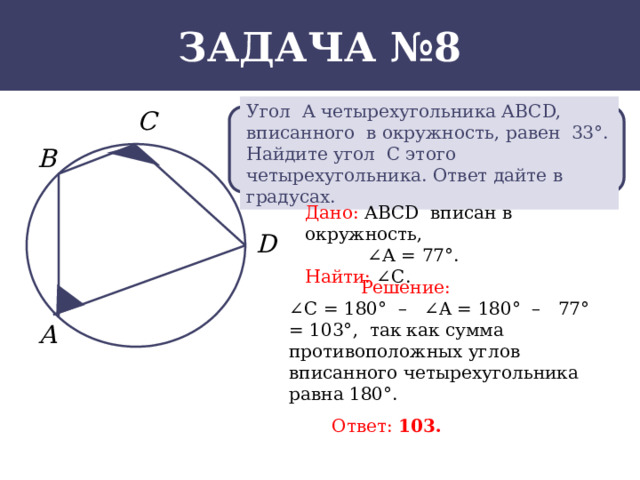
Угол А четырехугольника АВСD, вписанного в окружность, равен 33°. Найдите угол С этого четырехугольника. Ответ дайте в градусах.

Дано: АВСD вписан в окружность,

∠ А = 77°.

Найти: ∠С.

Решение:

∠ C = 180° – ∠A = 180° – 77° = 103°, так как сумма противоположных углов вписанного четырехугольника равна 180°.

Ответ: 103.

Задача №9

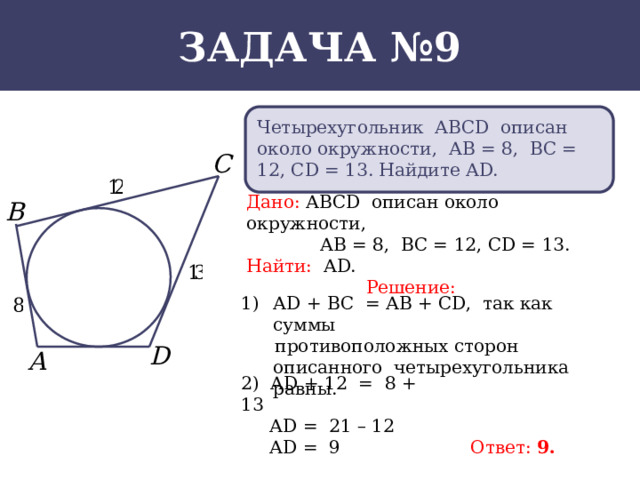
Четырехугольник АВСD описан около окружности, АВ = 8, ВС = 12, СD = 13. Найдите АD.

Дано: АВСD описан около окружности,

АВ = 8, ВС = 12, СD = 13.

Найти: АD.

Решение:

• АD + ВС = АВ + СD, так как суммы

противоположных сторон описанного четырехугольника равны.

2) АD + 12 = 8 + 13

АD = 21 – 12

АD = 9

Ответ: 9.

Задача №10

Треугольник АВС вписан в окружность с центром О. Точки О и С лежат в одной полуплоскости относительно прямой АВ. Найдите угол АСВ, если угол АОВ равен 73°.

Дано: треугольник АВС вписан в

окружность, ∠АОВ = 73°.

Найти: ∠АСВ.

Решение:

• ∠ АОВ = 73° – центральный угол, опирающийся на ᴗ АВ, следовательно ᴗ АВ = 73°.

2) ∠АСВ = 73° : 2 = 36, 5° , так как вписанный

угол измеряется половиной дуги, на которую он

опирается.

Ответ: 36,5.

Задача №11

Радиус окружности, вписанной в трапецию, равен 12. Найти высоту этой трапеции.

Дано: трапеция вписана в окружность, r = 12.

Найти: h.

Решение:

Высота трапеции равна диаметру вписанной

окружности, поэтому h = 2  r = 2  12 = 24 .

Ответ: 24.

Задача №12

Сторона АВ треугольника АВС проходит через центр описанной около него окружности . Найдите ∠ А, если ∠В = 44°. Ответ дайте в градусах.

Дано: треугольник АВС вписан в окружность,

∠ В = 44 °.

Найти: ∠А.

Решение:

1)∠C = 90°, так как угол, опирающийся на диаметр, значит треугольник АВС прямоугольный.

2)По теореме о сумме углов треугольника

∠ А = 180° – (90° + 44°) = 46°

Ответ: 46.

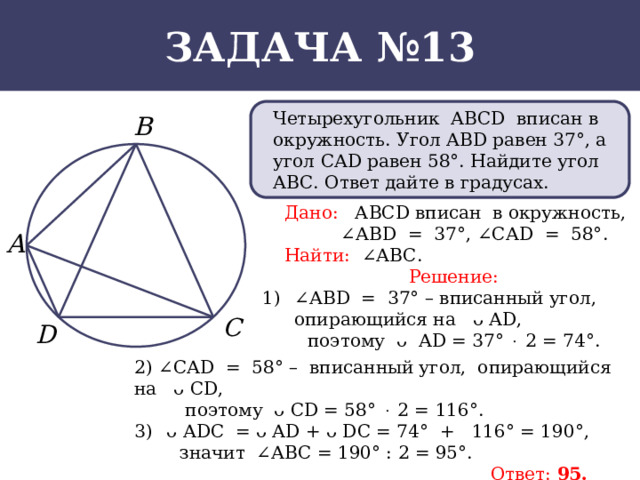
Задача №13

Четырехугольник АВСD вписан в окружность. Угол АВD равен 37°, а угол САD равен 58°. Найдите угол АВС. Ответ дайте в градусах.

Дано: АВСD вписан в окружность,

∠ АВD = 37°, ∠САD = 58°.

Найти: ∠АВС.

Решение:

• ∠ АВD = 37° – вписанный угол, опирающийся на ᴗ АD,

поэтому ᴗ АD = 37°  2 = 74°.

2) ∠САD = 58° – вписанный угол, опирающийся на ᴗ СD,

поэтому ᴗ СD = 58°  2 = 116°.

• ᴗ АDС = ᴗ АD + ᴗ DС = 74° + 116° = 190°,

значит ∠АВС = 190° : 2 = 95°.

Ответ: 95.

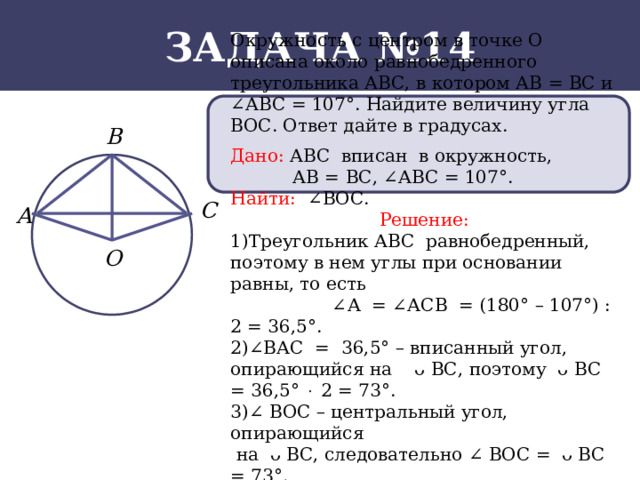
Задача №14

Окружность с центром в точке О описана около равнобедренного треугольника АВС, в котором АВ = ВС и ∠АВС = 107°. Найдите величину угла ВОС. Ответ дайте в градусах.

Дано: АВС вписан в окружность,

АВ = ВС, ∠АВС = 107°.

Найти: ∠ВОС.

Решение:

1)Треугольник АВС равнобедренный, поэтому в нем углы при основании равны, то есть

∠ А = ∠АСВ = (180° – 107°) : 2 = 36,5°.

2)∠ВАС = 36,5° – вписанный угол, опирающийся на ᴗ ВС, поэтому ᴗ ВС = 36,5°  2 = 73°.

3)∠ ВОС – центральный угол, опирающийся

на ᴗ ВС, следовательно ∠ ВОС = ᴗ ВС = 73°.

Ответ: 73.

Задача №15

Радиус окружности, вписанной в равносторонний треугольник, равен 6.

Найдите высоту этого треугольника.

Дано: треугольник АВС описан около окружности, r = 6.

Найти: h.

Решение:

1) В равностороннем треугольнике любая высота является медианой и биссектрисой и все они пересекаются в одной точке, которая является центром вписанной и описанной окружности.

2) Медианы треугольника точкой пересечения делятся в отношении 2: 1, считая от вершины,

значит h = 6  3 = 18.

Ответ: 18.

Задача №16

Через точку А, лежащую вне окружности, проведены две прямые. Одна прямая касается окружности в точке К.

Другая прямая пересекает окружность в точках В и С, причем АВ = 2, АК = 4. Найдите АС.

Дано: АК – касательная, АС – секущая,

АВ = 2, АК = 4

Найти: АС.

Решение:

АК 2 = АВ  АС

4 2 = 2  АС

АС = 16 : 2

АС = 8

Ответ: 8.

Задача №17

Касательные в точках А и В к окружности с центром О пересекаются под углом 82°. Найдите угол АВО. Ответ дайте в градусах.

Дано: касательные в точках А и В пересекаются под углом 82°.

Найти: ∠АВО.

Решение:

1)Обозначим точку пересечения касательных буквой С .

2)Отрезки касательных СА и СВ равны, значит треугольник АСВ равнобедренный,

∠ САВ = ∠СВА = (180° – 82°) : 2 = 49°.

3)Радиус окружности, проведенный в точку касания, перпендикулярен касательной, поэтому ∠АВС = 90°.

4)∠АВО = 90° – 49° = 41°

Ответ: 41.