Подготовка к ОГЭ. Задание 17.

A content placeholder. Use for text, graphics, tables and graphs. You can change this text or delete it.

Here is a placeholder for more text. You may delete this text

Here is a placeholder for more text. You may delete this text

ЗАДАНИЕ №17

.)

Диагональ прямоугольника образует угол 47° с одной из его сторон. Найдите острый угол между диагоналями этого прямоугольника.

Ответ дайте в градусах.

Задача №11

.)

Диагональ прямоугольника образует угол 47° с одной из его сторон. Найдите острый угол между диагоналями этого прямоугольника.

Ответ дайте в градусах.

Задача №11

Решение:

.)

Диагональ прямоугольника образует угол 47° с одной из его сторон. Найдите острый угол между диагоналями этого прямоугольника.

Ответ дайте в градусах.

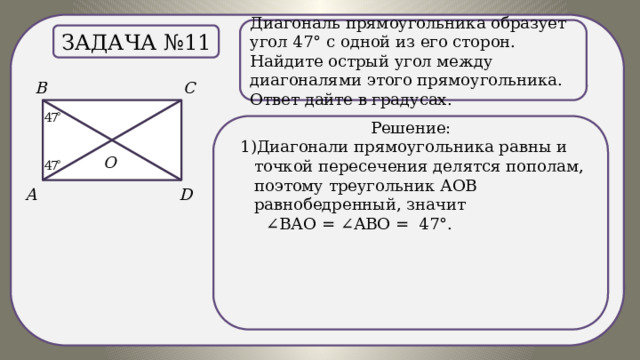
Задача №11

Решение:

1)Диагонали прямоугольника равны и точкой пересечения делятся пополам, поэтому треугольник АОВ равнобедренный, значит

∠ ВАО = ∠АВО = 47°.

.)

Диагональ прямоугольника образует угол 47° с одной из его сторон. Найдите острый угол между диагоналями этого прямоугольника.

Ответ дайте в градусах.

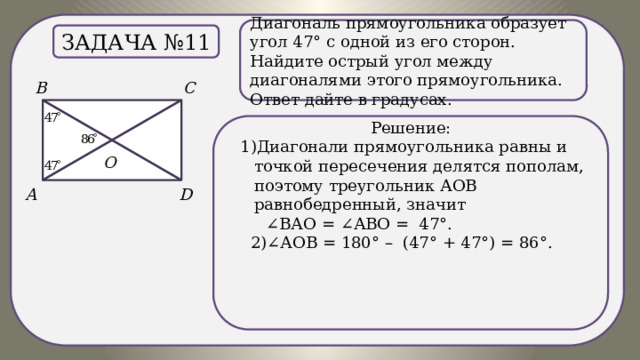
Задача №11

Решение:

1)Диагонали прямоугольника равны и точкой пересечения делятся пополам, поэтому треугольник АОВ равнобедренный, значит

∠ ВАО = ∠АВО = 47°.

2)∠АОВ = 180° – (47° + 47°) = 86°.

.)

Диагональ прямоугольника образует угол 47° с одной из его сторон. Найдите острый угол между диагоналями этого прямоугольника.

Ответ дайте в градусах.

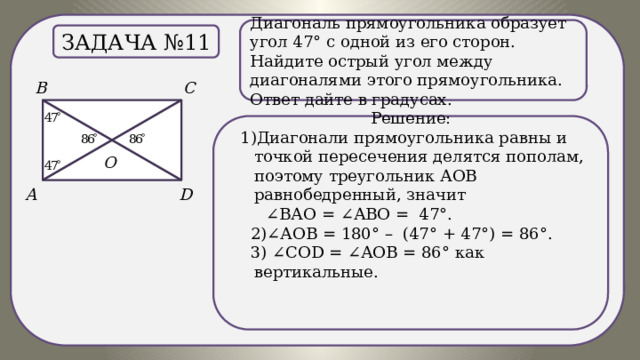
Задача №11

Решение:

1)Диагонали прямоугольника равны и точкой пересечения делятся пополам, поэтому треугольник АОВ равнобедренный, значит

∠ ВАО = ∠АВО = 47°.

2)∠АОВ = 180° – (47° + 47°) = 86°.

3) ∠СОD = ∠АОВ = 86° как вертикальные.

.)

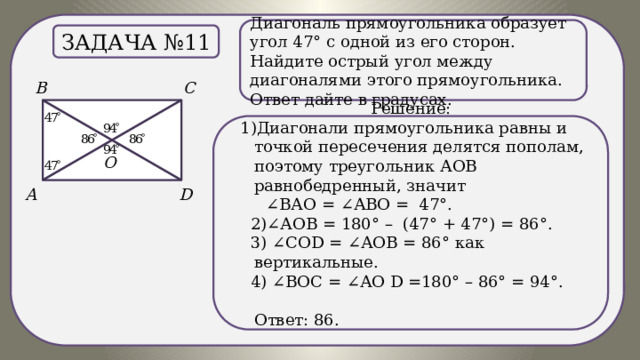
Диагональ прямоугольника образует угол 47° с одной из его сторон. Найдите острый угол между диагоналями этого прямоугольника.

Ответ дайте в градусах.

Задача №11

Решение:

1)Диагонали прямоугольника равны и точкой пересечения делятся пополам, поэтому треугольник АОВ равнобедренный, значит

∠ ВАО = ∠АВО = 47°.

2)∠АОВ = 180° – (47° + 47°) = 86°.

3) ∠СОD = ∠АОВ = 86° как вертикальные.

4) ∠ВОС = ∠АО D =180° – 86° = 94°.

Ответ: 86.

.

Диагонали параллелограмма равны 7 и 24, а угол между ними равен 30°. Найдите площадь параллелограмма.

Задача №12

.

Диагонали параллелограмма равны 7 и 24, а угол между ними равен 30°. Найдите площадь параллелограмма.

Задача №12

Решение:

Площадь параллелограмма равна половине произведения длин его диагоналей на синус угла между ними.

.

Диагонали параллелограмма равны 7 и 24, а угол между ними равен 30°. Найдите площадь параллелограмма.

Задача №12

Решение:

Площадь параллелограмма равна половине произведения длин его диагоналей на синус угла между ними.

Ответ: 42.

.

Периметр ромба равен 12, а один из углов равен 30°. Найдите площадь ромба.

Задача №13

.

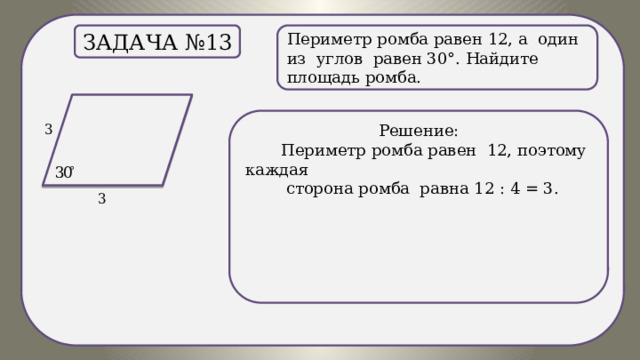
Периметр ромба равен 12, а один из углов равен 30°. Найдите площадь ромба.

Задача №13

Решение:

Периметр ромба равен 12, поэтому каждая

сторона ромба равна 12 : 4 = 3.

.

Периметр ромба равен 12, а один из углов равен 30°. Найдите площадь ромба.

Задача №13

Решение:

Периметр ромба равен 12, поэтому каждая

сторона ромба равна 12 : 4 = 3.

Ответ: 4,5.

.

Сторона ромба равна 6, а один из углов равен 150°. Найдите площадь ромба.

Задача №14

.

Сторона ромба равна 6, а один из углов равен 150°. Найдите площадь ромба.

Задача №14

Решение:

Если один из углов ромба равен 150°,

то другой угол, прилежащий к той же

стороне, равен 30° .

.

Сторона ромба равна 6, а один из углов равен 150°. Найдите площадь ромба.

Задача №14

Решение:

Если один из углов ромба равен 150°,

то другой угол, прилежащий к той же

стороне, равен 30° .

Ответ: 18.

.

Сторона ромба равна 5, а расстояние от точки пересечения диагоналей ромба до нее равно 2. Найдите площадь ромба.

Задача №15

.

Сторона ромба равна 5, а расстояние от точки пересечения диагоналей ромба до нее равно 2. Найдите площадь ромба.

Задача №15

Решение:

В ромбе диагонали взаимно перпендикулярны и точкой пересечения делятся пополам, поэтому

диагонали делят ромб на четыре равных прямоугольных треугольника.

Ответ: 20.

.

Диагонали ромба равны 21 и 6. Найдите площадь ромба.

Задача №16

.

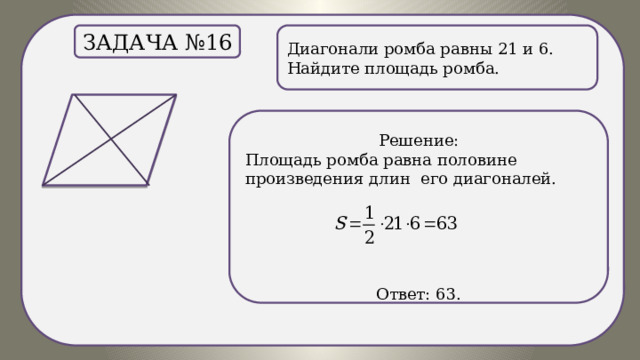
Задача №16

Диагонали ромба равны 21 и 6. Найдите площадь ромба.

Решение:

Площадь ромба равна половине произведения длин его диагоналей.

Ответ: 63.

.

Сторона ромба равна 14, а один из углов равен 150°. Найдите высоту ромба.

Задача №17

.

Сторона ромба равна 14, а один из углов равен 150°. Найдите высоту ромба.

Задача №17

Решение:

Если один из углов ромба равен 150°,

то другой угол, прилежащий к той же

стороне, равен 30° .

.

Сторона ромба равна 14, а один из углов равен 150°. Найдите высоту ромба.

Задача №17

Решение:

Если один из углов ромба равен 150°,

то другой угол, прилежащий к той же

стороне, равен 30° . В прямоугольном

треугольнике катет, лежащий против угла

в 30° равен половине гипотенузы, поэтому

Ответ: 7.

.

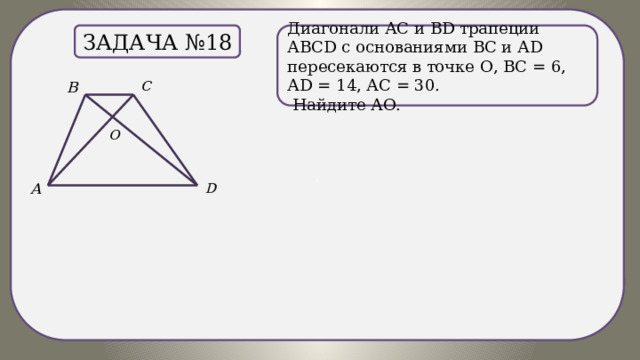
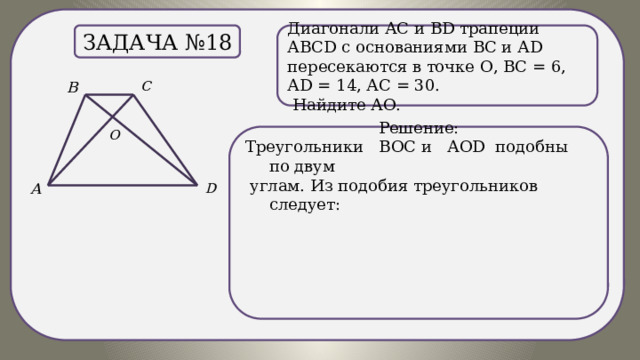
Диагонали АС и ВD трапеции АВСD c основаниями ВС и АD пересекаются в точке О, ВС = 6, АD = 14, АС = 30.

Задача №18

Найдите АО.

.

Диагонали АС и ВD трапеции АВСD c основаниями ВС и АD пересекаются в точке О, ВС = 6, АD = 14, АС = 30.

Задача №18

Найдите АО.

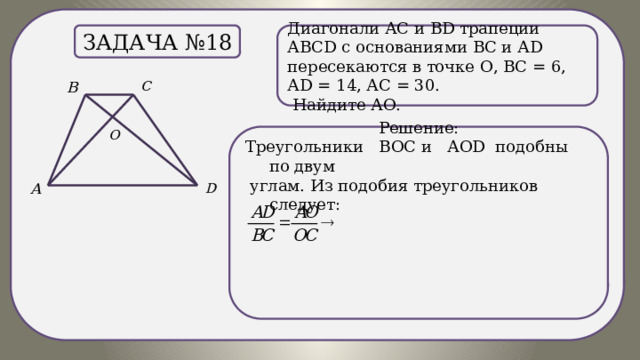
Решение:

Треугольники ВОС и АОD подобны по двум

углам. Из подобия треугольников следует:

.

Диагонали АС и ВD трапеции АВСD c основаниями ВС и АD пересекаются в точке О, ВС = 6, АD = 14, АС = 30.

Задача №18

Найдите АО.

Решение:

Треугольники ВОС и АОD подобны по двум

углам. Из подобия треугольников следует:

.

Диагонали АС и ВD трапеции АВСD c основаниями ВС и АD пересекаются в точке О, ВС = 6, АD = 14, АС = 30.

Задача №18

Найдите АО.

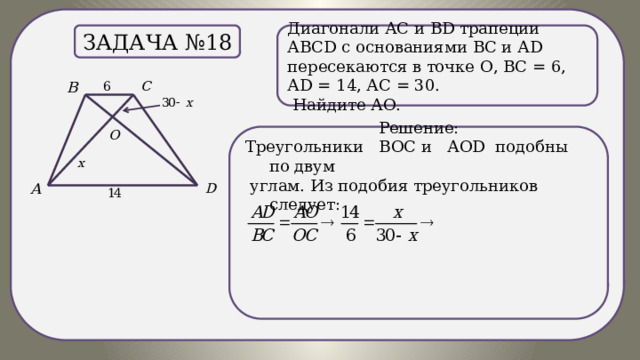
Решение:

Треугольники ВОС и АОD подобны по двум

углам. Из подобия треугольников следует:

.

Диагонали АС и ВD трапеции АВСD c основаниями ВС и АD пересекаются в точке О, ВС = 6, АD = 14, АС = 30.

Задача №18

Найдите АО.

Решение:

Треугольники ВОС и АОD подобны по двум

углам. Из подобия треугольников следует:

.

Диагонали АС и ВD трапеции АВСD c основаниями ВС и АD пересекаются в точке О, ВС = 6, АD = 14, АС = 30.

Задача №18

Найдите АО.

Решение:

Треугольники ВОС и АОD подобны по двум

углам. Из подобия треугольников следует:

.

Диагонали АС и ВD трапеции АВСD c основаниями ВС и АD пересекаются в точке О, ВС = 6, АD = 14, АС = 30.

Задача №18

Найдите АО.

Решение:

Треугольники ВОС и АОD подобны по двум

углам. Из подобия треугольников следует:

Ответ: 21.

.

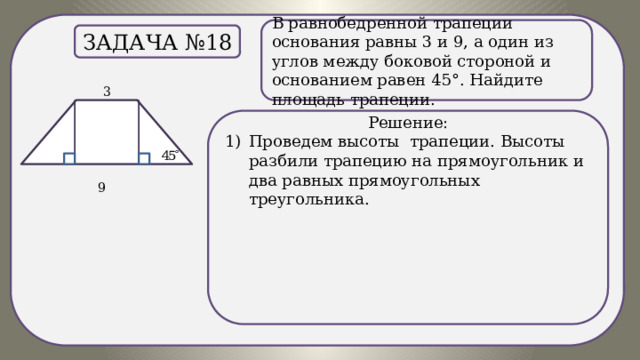
В равнобедренной трапеции основания равны 3 и 9, а один из углов между боковой стороной и основанием равен 45°. Найдите площадь трапеции.

Задача №19

.

В равнобедренной трапеции основания равны 3 и 9, а один из углов между боковой стороной и основанием равен 45°. Найдите площадь трапеции.

Задача №18

Решение:

• Проведем высоты трапеции. Высоты разбили трапецию на прямоугольник и два равных прямоугольных треугольника.

.

В равнобедренной трапеции основания равны 3 и 9, а один из углов между боковой стороной и основанием равен 45°. Найдите площадь трапеции.

Задача №19

Решение:

1) Проведем высоты трапеции. Высоты разбили трапецию на прямоугольник и два равных прямоугольных треугольника.

2) Нижнее основание разделилось на отрезки 3,3 и 3.

.

В равнобедренной трапеции основания равны 3 и 9, а один из углов между боковой стороной и основанием равен 45°. Найдите площадь трапеции.

Задача №19

Решение:

1) Проведем высоты трапеции. Высоты разбили трапецию на прямоугольник и два равных прямоугольных треугольника.

2) Нижнее основание разделилось на отрезки 3,3 и 3.

3) Каждый из прямоугольных треугольников

является равнобедренным, поэтому высота равна 3.

.

В равнобедренной трапеции основания равны 3 и 9, а один из углов между боковой стороной и основанием равен 45°. Найдите площадь трапеции.

Задача №19

Решение:

1) Проведем высоты трапеции. Высоты разбили трапецию на прямоугольник и два равных прямоугольных треугольника.

2) Нижнее основание разделилось на отрезки 3,3 и 3.

3) Каждый из прямоугольных треугольников

является равнобедренным, поэтому высота равна 3.

Ответ: 18.

.

Площадь параллелограмма равна 40, а две его стороны равны 5 и 10. Найти большую высоту параллелограмма.

Задача №20

.

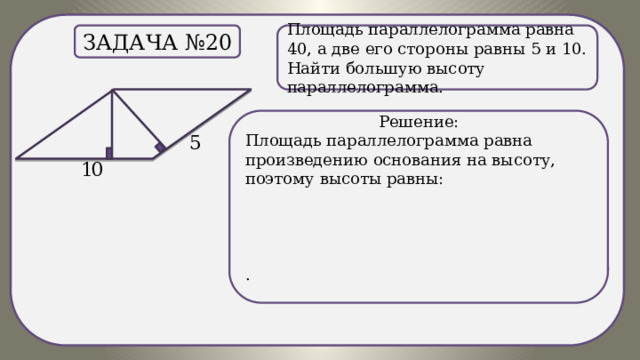
Задача №20

Площадь параллелограмма равна 40, а две его стороны равны 5 и 10. Найти большую высоту параллелограмма.

Решение:

Площадь параллелограмма равна произведению основания на высоту, поэтому высоты равны:

.

.

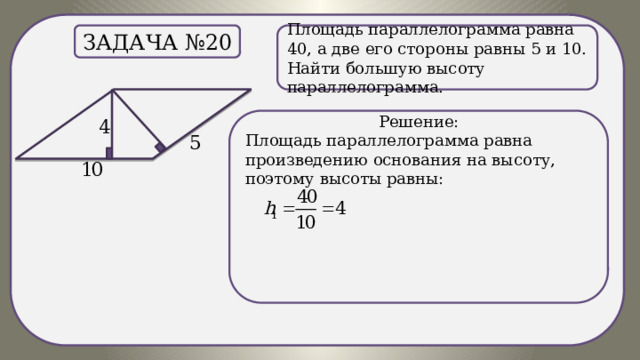
Площадь параллелограмма равна 40, а две его стороны равны 5 и 10. Найти большую высоту параллелограмма.

Задача №20

Решение:

Площадь параллелограмма равна произведению основания на высоту, поэтому высоты равны:

.

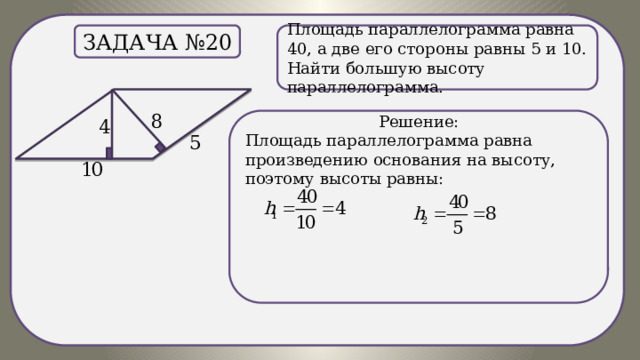
Площадь параллелограмма равна 40, а две его стороны равны 5 и 10. Найти большую высоту параллелограмма.

Задача №20

Решение:

Площадь параллелограмма равна произведению основания на высоту, поэтому высоты равны:

.

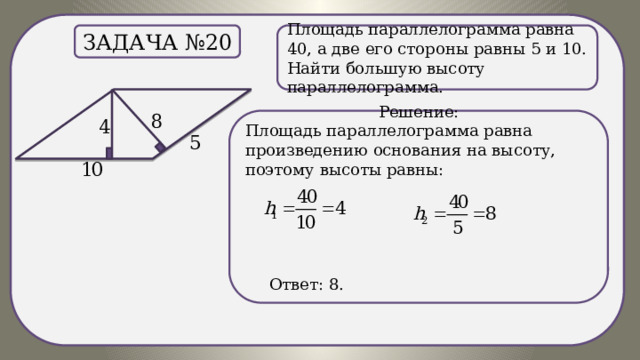
Площадь параллелограмма равна 40, а две его стороны равны 5 и 10. Найти большую высоту параллелограмма.

Задача №20

Решение:

Площадь параллелограмма равна произведению основания на высоту, поэтому высоты равны:

Ответ: 8.

.

Периметр квадрата равен 68. Найдите площадь этого квадрата.

Задача №21

.

Периметр квадрата равен 68. Найдите площадь этого квадрата.

Задача №20

Решение:

Периметр квадрата равен 68, поэтому каждая его сторона равна 68 : 4 = 17.

.

Периметр квадрата равен 68. Найдите площадь этого квадрата.

Задача №21

Решение:

Периметр квадрата равен 68, поэтому каждая его сторона равна 68 : 4 = 17.

Площадь квадрата равна квадрату его стороны, значит S = 17 2 = 289

.

Периметр квадрата равен 68. Найдите площадь этого квадрата.

Задача №21

Решение:

Периметр квадрата равен 68, поэтому каждая его сторона равна 68 : 4 = 17.

Площадь квадрата равна квадрату его стороны, значит S = 17 2 = 289

Ответ: 289.