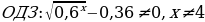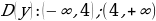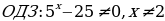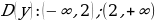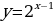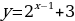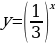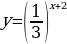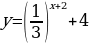Урок «Показательная функция, её свойства и график»
Конспект урока
Учебник: Мордкович А.Г. Математика: алгебра и начала математического анализа, геометрия. Алгебра и начала математического анализа. 11 кл. В 2 ч. Ч. 1. Учебник для учащ. общеобр. уч. (базовый и углублённый уровни). – М.: Мнемозина, 2014. — 307 с., § 11.
Тема урока: «Показательная функция, её свойства и график».
Тип урока: урок-практикум.
Учебная задача урока: отработать решение различных видов задач по теме «Показательная функция, её свойства и график».
Диагностируемые цели:
В результате урока ученик:
Знает:
- определение показательной функции, ее свойства и вид графика;
- подходы к решению показательных уравнений вида 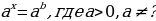 , и неравенств вида
, и неравенств вида 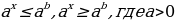 ,
, 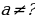 .
.
Умеет:
- строить график показательной функции и исследовать ее на свойства;
- решать простейшие показательные уравнения и неравенства.
Понимает:
- что вид графика показательной функции зависит от степени в показателе;
- как решать простейшие показательные уравнения вида 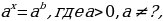 и неравенства вида
и неравенства вида 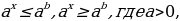
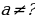 .
.
Учебные действия, формируемые на уроке:
-
Личностные: умение учащегося устанавливать связи между целью учебной деятельности и её мотивом, т.е. между результатом учения, и тем, что побуждает деятельность, ради чего она осуществляется, таким образом должна осуществляться осмысленная организация собственной деятельности ученика
-
Регулятивные: целеполагание как постановка учебной задачи на основе соотнесения того, что уже известно и усвоено учащимся, и того, что ещё неизвестно, планирование - определение последовательности промежуточных целей с учётом конечного результата, оценка - выделение и осознание учащимся того, что уже усвоено и что ещё подлежит усвоению, осознание качества и уровня усвоения;
-
Коммуникативные: планирование учебного сотрудничества с учителем и сверстниками, т. е. определение цели сотрудничества, функций участников, способов взаимодействия, умение с достаточно полнотой и точностью выражать свои мысли в соответствии с задачами и условиями коммуникации, владение монологической и диалогической формами речи в соответствии с грамматическими и синтаксическими нормами родного языка, умение доказывать собственное мнение;
-
Познавательные: анализ объектов с целью выделения признаков (существенных, несущественных); выдвижение гипотез и их обоснование; построение логической цепи рассуждений, доказательство; подведение под понятие; выведение следствий; установление причинно-следственных связей.
Методы обучения: репродуктивный, частично-поисковые, УДЕ.
Форма работы: фронтальная, групповая.
Средства обучения: традиционные, презентация.
Структура урока:
-
Мотивационно-ориентировочная часть (5 мин.)
-
Операционно-познавательная часть (38 мин.)
-
Рефлексивно-оценочная часть (2 мин.)
Ход урока
| Деятельность учителя | Деятельность ученика |
-
Мотивационно-ориентировочная часть. -
Актуализация имеющихся знаний и умений учащихся |
| Задание 1: Какие из представленных функций являются показательными? А) 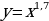 Б) 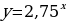 В) 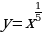 Г) 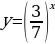 Задание 2: Возрастает или убывает показательная функция и почему? А) 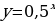 Б) 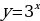
Задание 3: Какова область определения функции 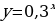 Задание 4: Каково множество значений функции y=3x? Задание 5: Из предложенных графиков функций выберите график функции: 1) 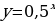 2) 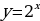 . . 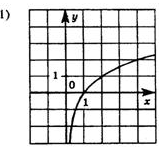
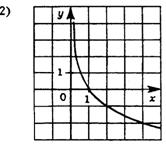
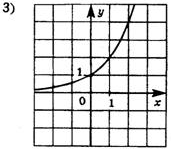
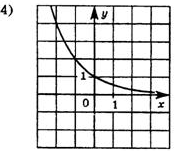
Задание 6: Решить уравнение (неравенство): А) 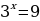 Б) 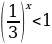 В) 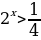 | Решение: Б), Г).
Решение: А) Убывает, т.к. основание степени 0 Б) Возрастает, т.к. основание степени 31. Решение: множество всех действительных чисел. Решение: у0 - множество всех положительных чисел. Ответ: 1) 4, 2) 3.
Решение: А) 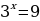 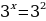
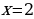
Б) 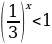 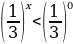
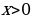
В)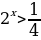 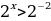
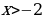
|
-
Мотивация учебной деятельности учащихся. Проблемная ситуация. |
| Итак, на предыдущих уроках вы изучили теорию по теме «Показательная функция, её свойства и график» и рассмотрели решение основных задач по теме |
-
Постановка цели урока. Поэтому сегодня на уроке вы должны отработать решение основных задач по теме «Показательная функция, её свойства и график» |
| 2. Операционно-познавательная часть. |
| Групповая работа (по 4 человека). Примерное содержание карточки для групп: Задание 1: Сравнить m и n если: А)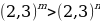 Б) 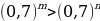 Задание 2: Найдите область определения функции: А) 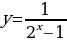 Б) 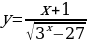
Задание 3: Найдите область значений функции 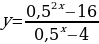
Задание 4: Найдите наибольшее и наименьшее значения указанной функции на заданном промежутке: А) 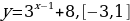 Б) 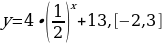 B) 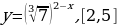
Задание 5: Построить графики функций и исследовать функции на свойства: А) 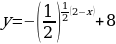 Б) 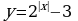
Задание 6: Решите уравнение (неравенство): А) 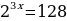 Б) 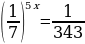 В) 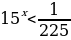 Г) 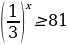 |
Решение: А) mn; т.к. 2,31 Б) mn; 0 Решение: А) 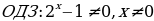 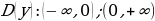
Б) 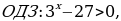  , ,
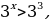
Т.к. 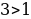 , то , то 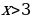 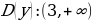
Решение: 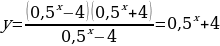 , при , при
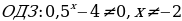
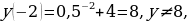
Т.к. 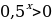 , то , то 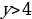 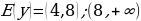
Решение: А) Т.к. функция 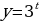 возрастает (a1), возрастает (a1), 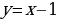 – возрастает, то функция – возрастает, то функция 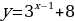 – возрастает. Значит: – возрастает. Значит: 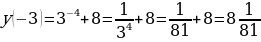 – наименьшее значение функции на – наименьшее значение функции на 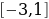 . .
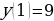 – наибольшее значение функции на – наибольшее значение функции на 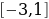 . .
Б) Т.к. функция 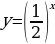 убывает (0a убывает (0a 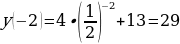 – наибольшее значение функции на – наибольшее значение функции на 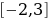 . .
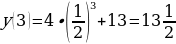 - наименьшее значение функции на - наименьшее значение функции на 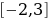 . .
В) Т.к. 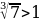 , то , то 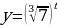 возрастает, но возрастает, но 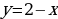 – убывает, то функция – убывает, то функция 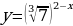 - убывает. Значит: - убывает. Значит: 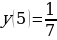 - наименьшее значение функции на - наименьшее значение функции на 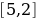 . .
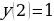 - наибольшее значение функции на - наибольшее значение функции на 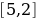 . .
Решение: А) Преобразуем выражение, задающее функцию: 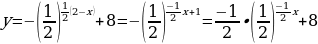
Исходная показательная функция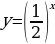 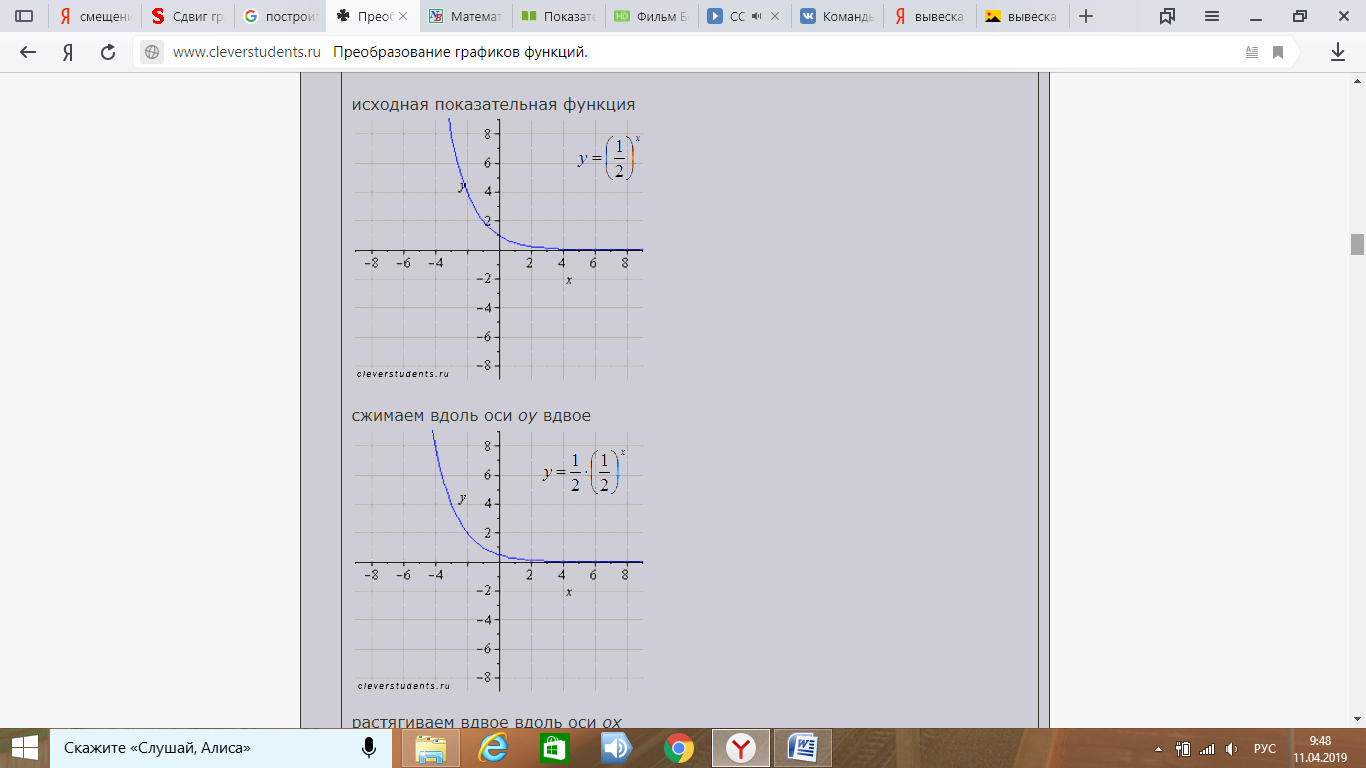
Сжимаем вдоль оси Оу вдвое: 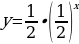 
Растягиваем вдоль оси Ох вдвое: 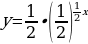 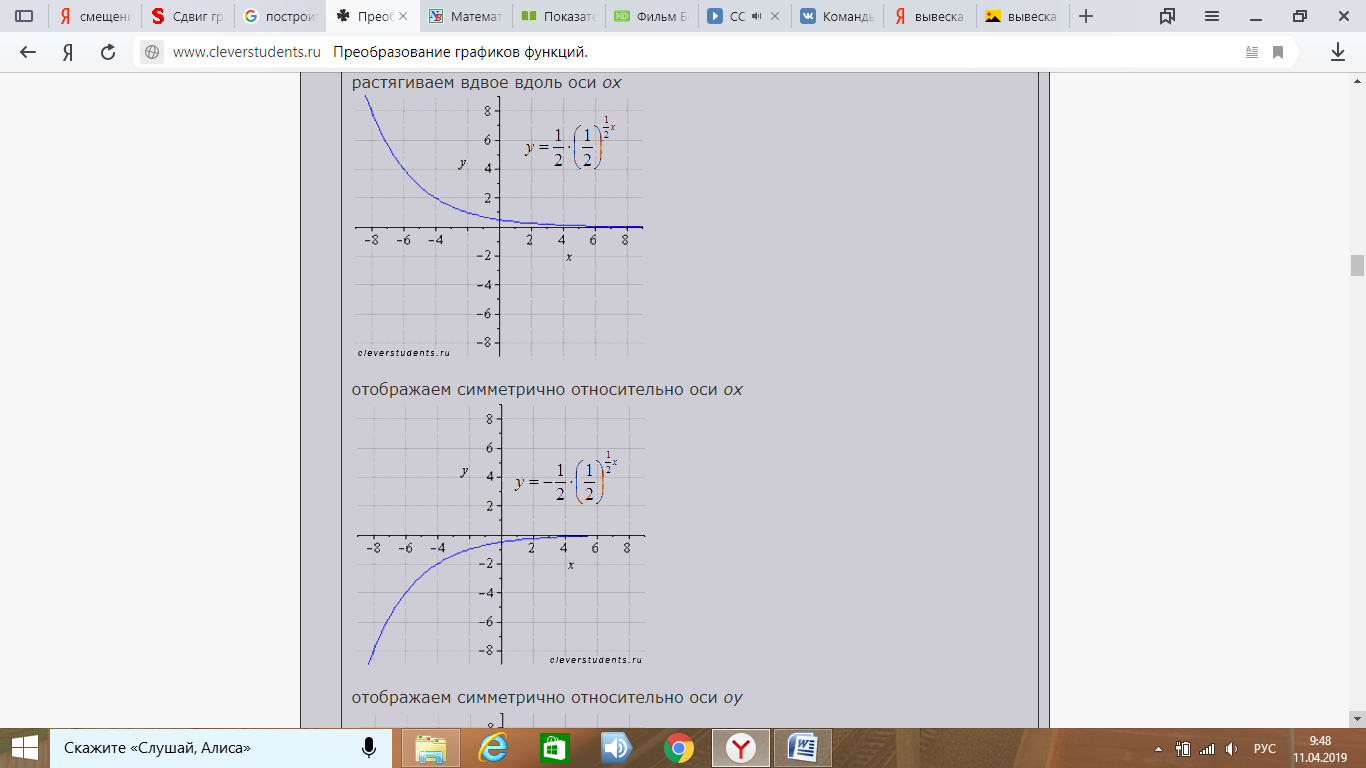
Отображаем от оси Ох: 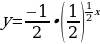 
Отображаем от оси Оу: 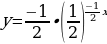 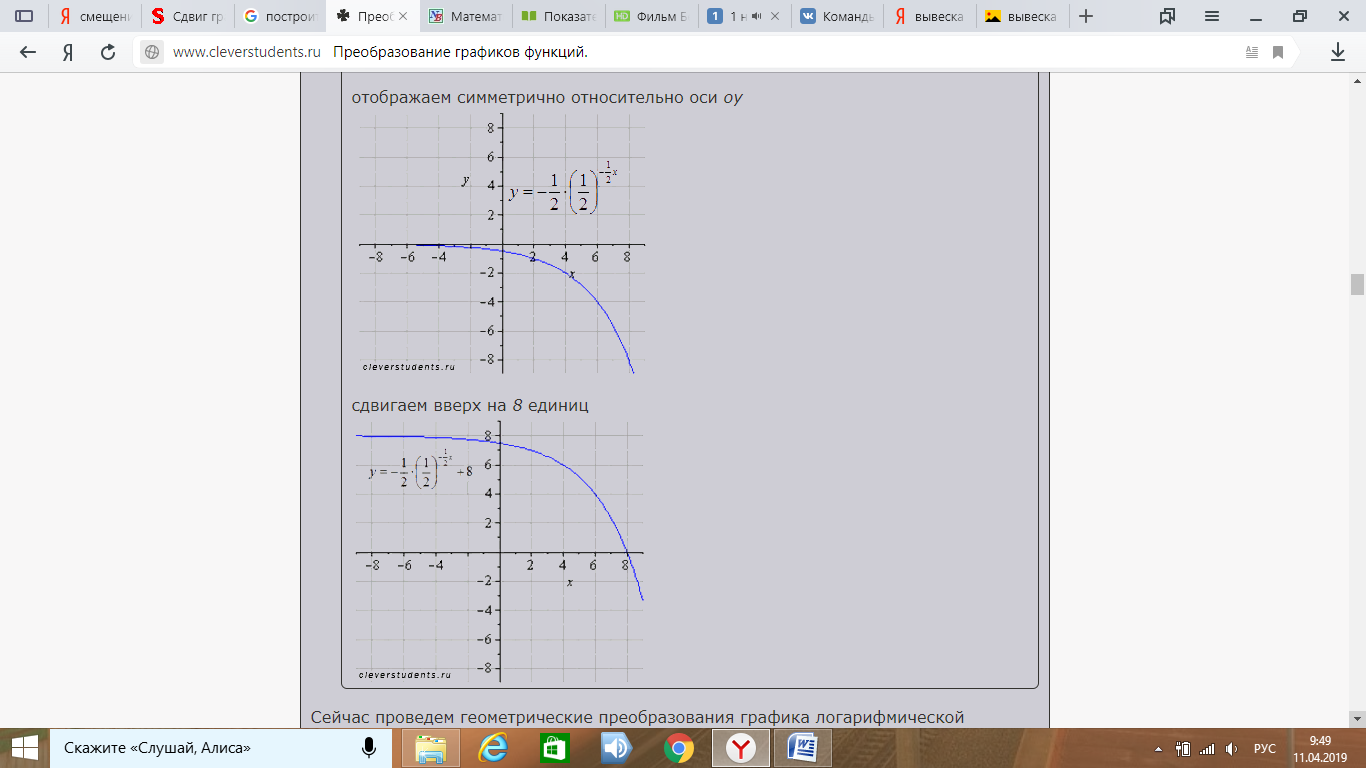
Сдвигаем вдоль оси Оу на 8 единиц вверх: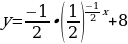 
1) 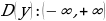 2) 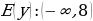 3) Убывает на 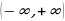 4) Непрерывна Б) Исходная показательная функция: 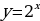 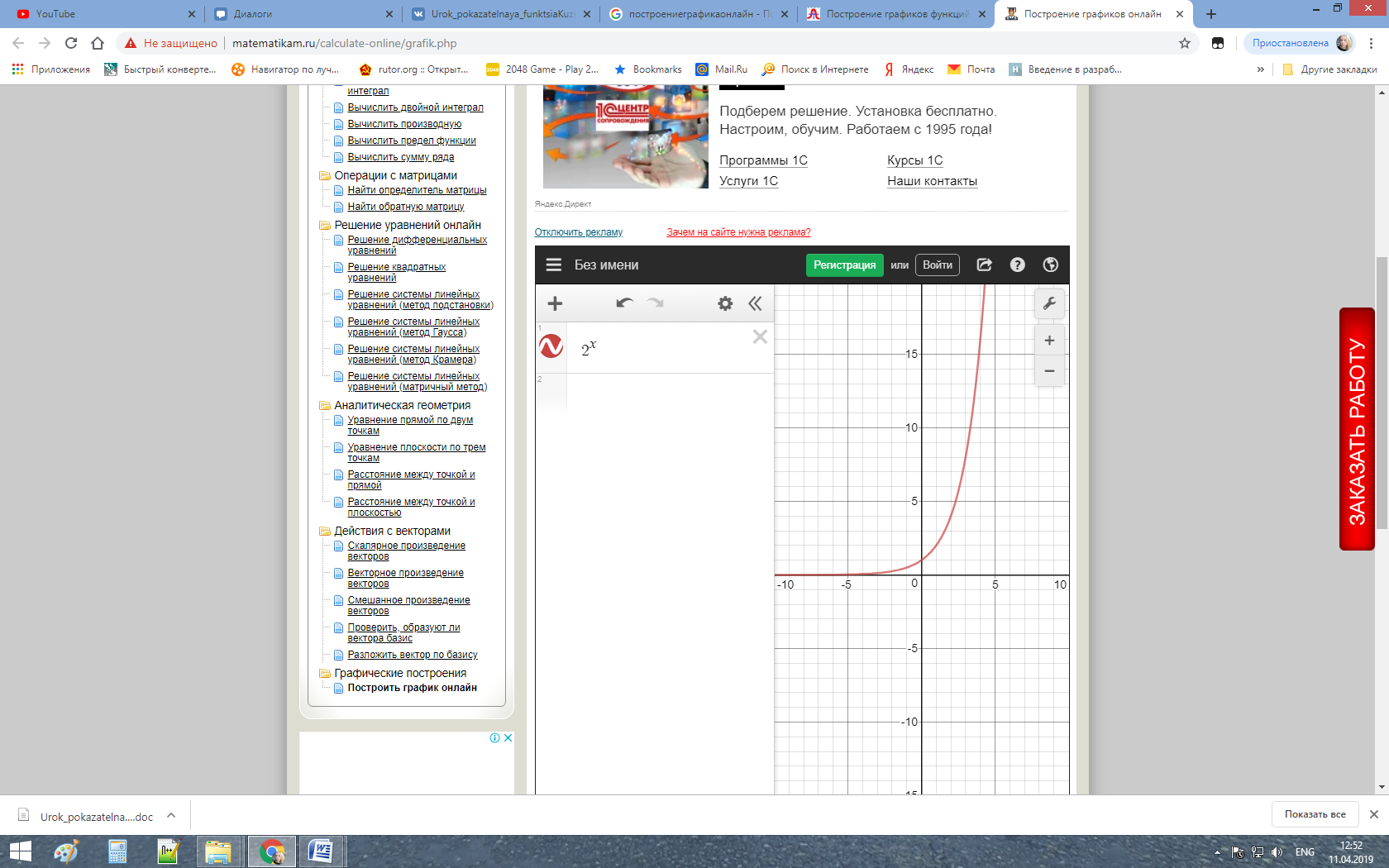
Оставляем часть графика 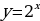 при при 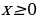 и отображаем от оси Оy: и отображаем от оси Оy: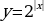 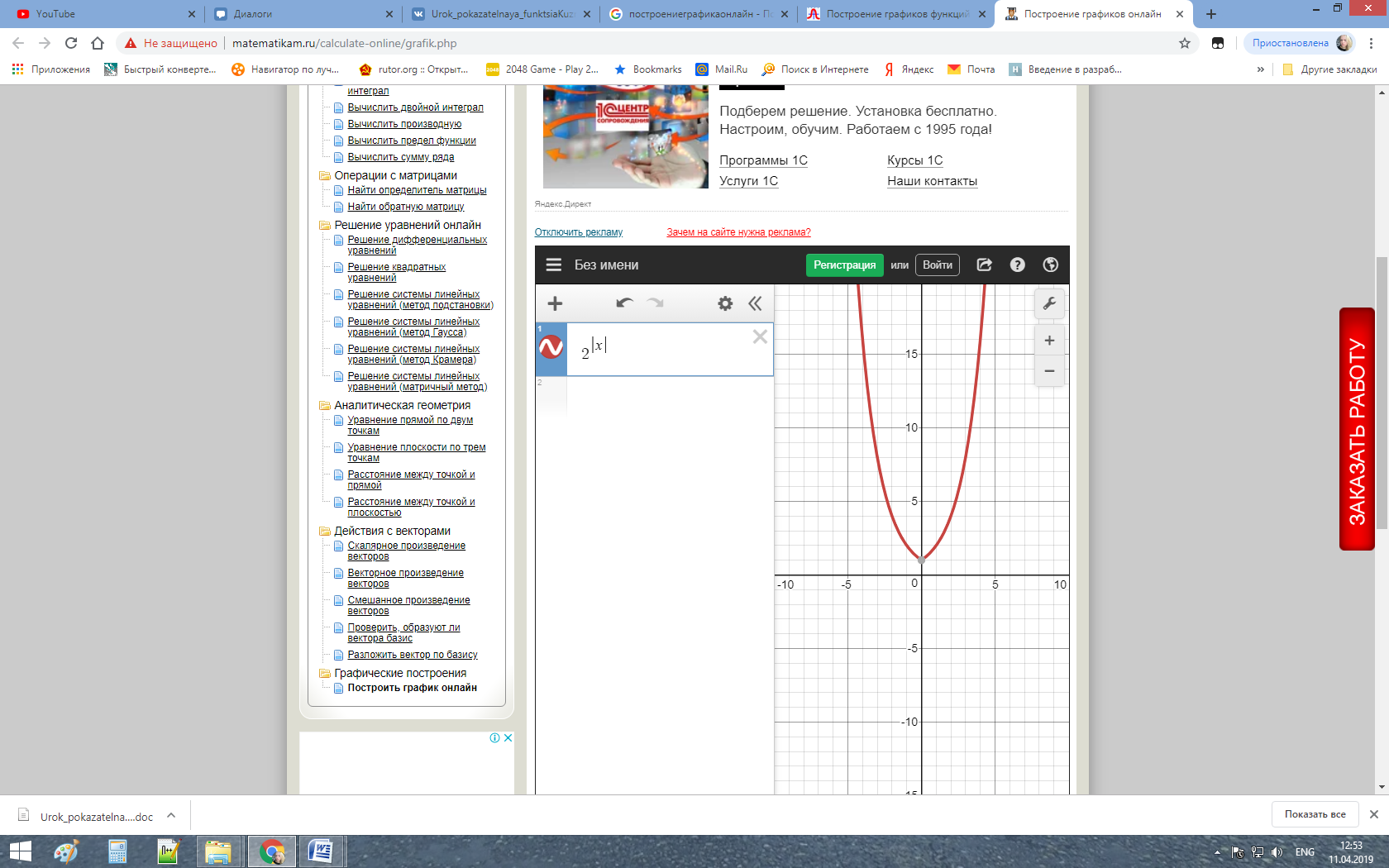
Сдвигаем вдоль оси Оу на 3 единицы вниз: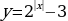 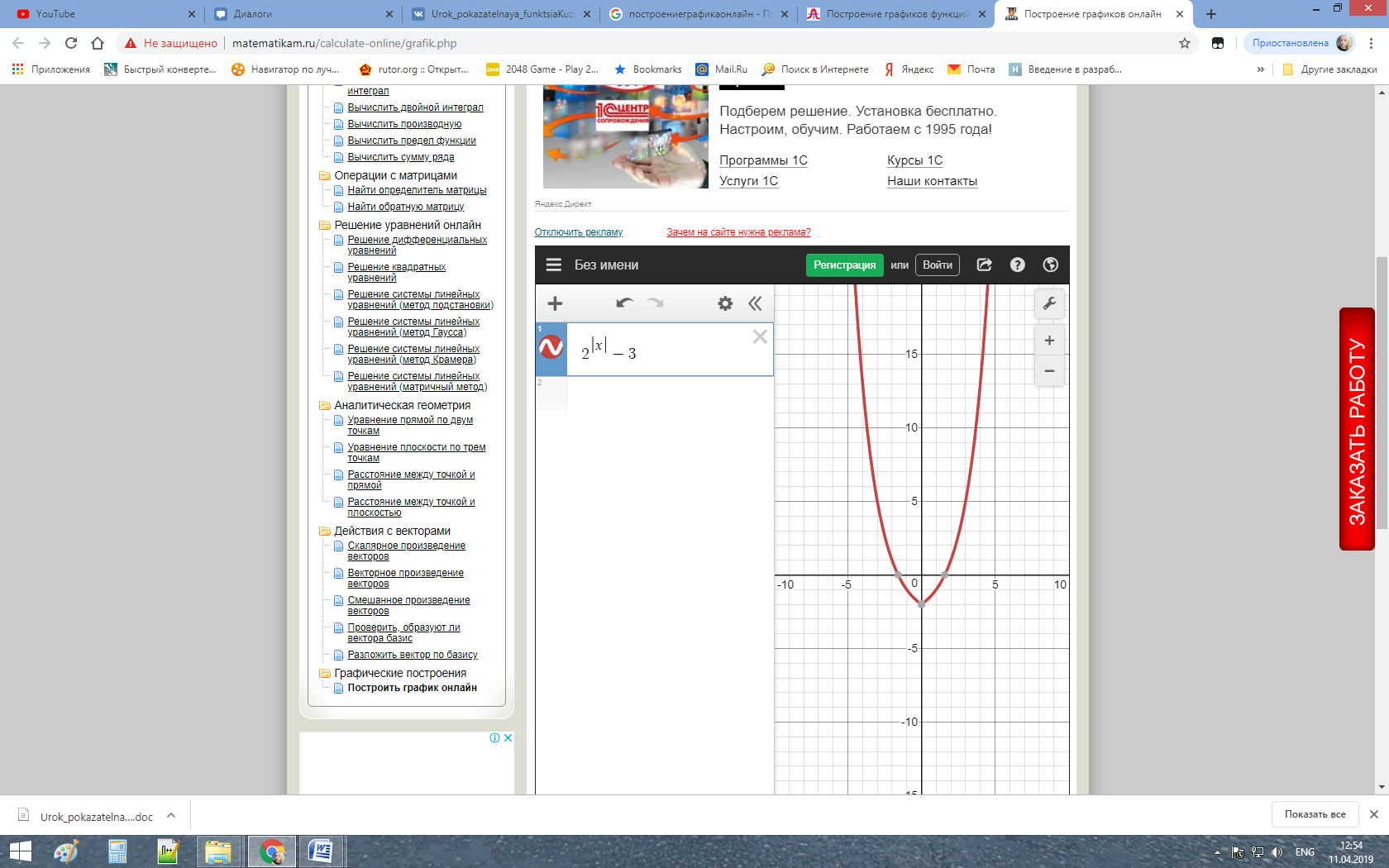
1) 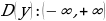 2) 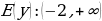 3) Убывает на 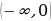 возрастает возрастает 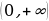 4) Непрерывна Решение: А) 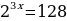 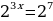
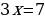
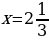
Б) 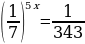 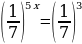
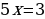
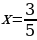
В) 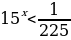 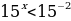
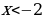
Г) 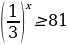 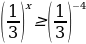
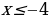
|
-
Рефлексивно-оценочный этап -
Подведение итогов. |
| -Какова была цель урока?
-Достигнута ли она? -Как мы её достигли? Какие задачи решали?
| - Отработать решение основных задач по теме «Показательная функция, её свойства и график» - Да - Решали задачи на сравнение чисел, нахождение области определения функции, области значений функции, находили наименьшее и наибольшее значение функции на промежутке, строили и исследовали график показательной функции, решали показательные уравнения и неравенства |
-
Постановка домашнего задания. |
| Домашнее задание: №11.36 а, б. Найдите наибольшее и наименьшее значения указанной функции на заданном промежутке.
№11.43 б, г. Найдите область определения функции.
№11.50 а, б. Построить графики функций. | 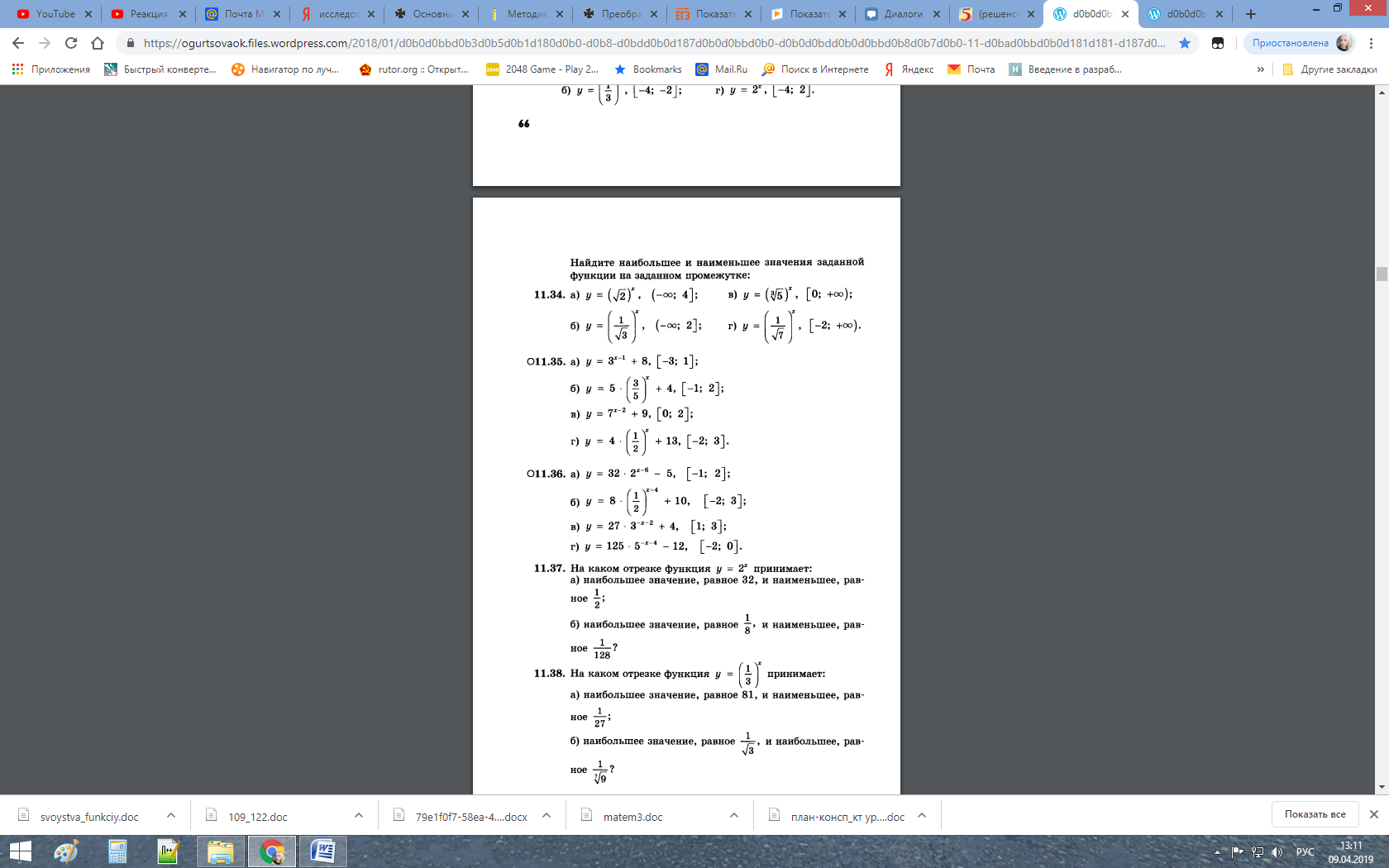 А) Т.к. 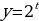 возрастает (a1) и возрастает (a1) и 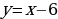 - возрастает, то функция - возрастает, то функция 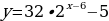 - возрастает. Значит: - возрастает. Значит: 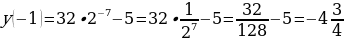 – наименьшее значение функции на – наименьшее значение функции на 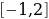 . .
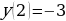 – наибольшее значение функции на – наибольшее значение функции на 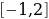 . .
Б) Т.к. 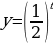 – убывает (0a – убывает (0a 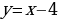 - возрастает, то функция - возрастает, то функция 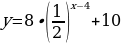 - убывает. Значит: - убывает. Значит: 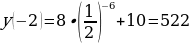 – наибольшее значение функции на – наибольшее значение функции на 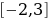 . .
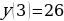 - наименьшее значение функции на - наименьшее значение функции на 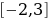 . .
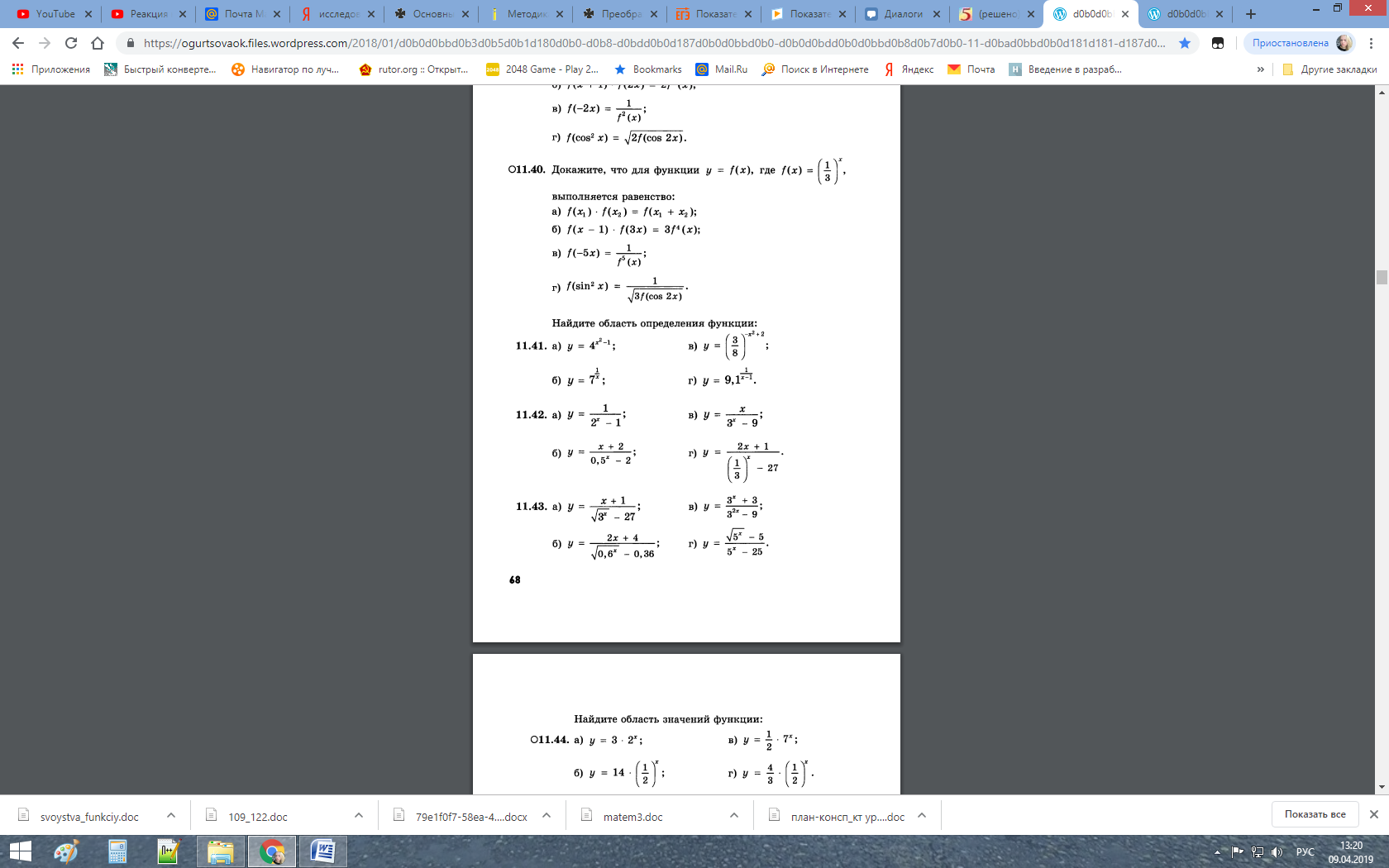
Б) 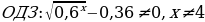 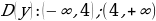
Г) 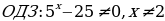 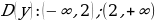
А) Исходная показательная функция: 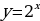 
Сдвигаем вдоль оси Ох на 1 единицу вправо: 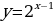 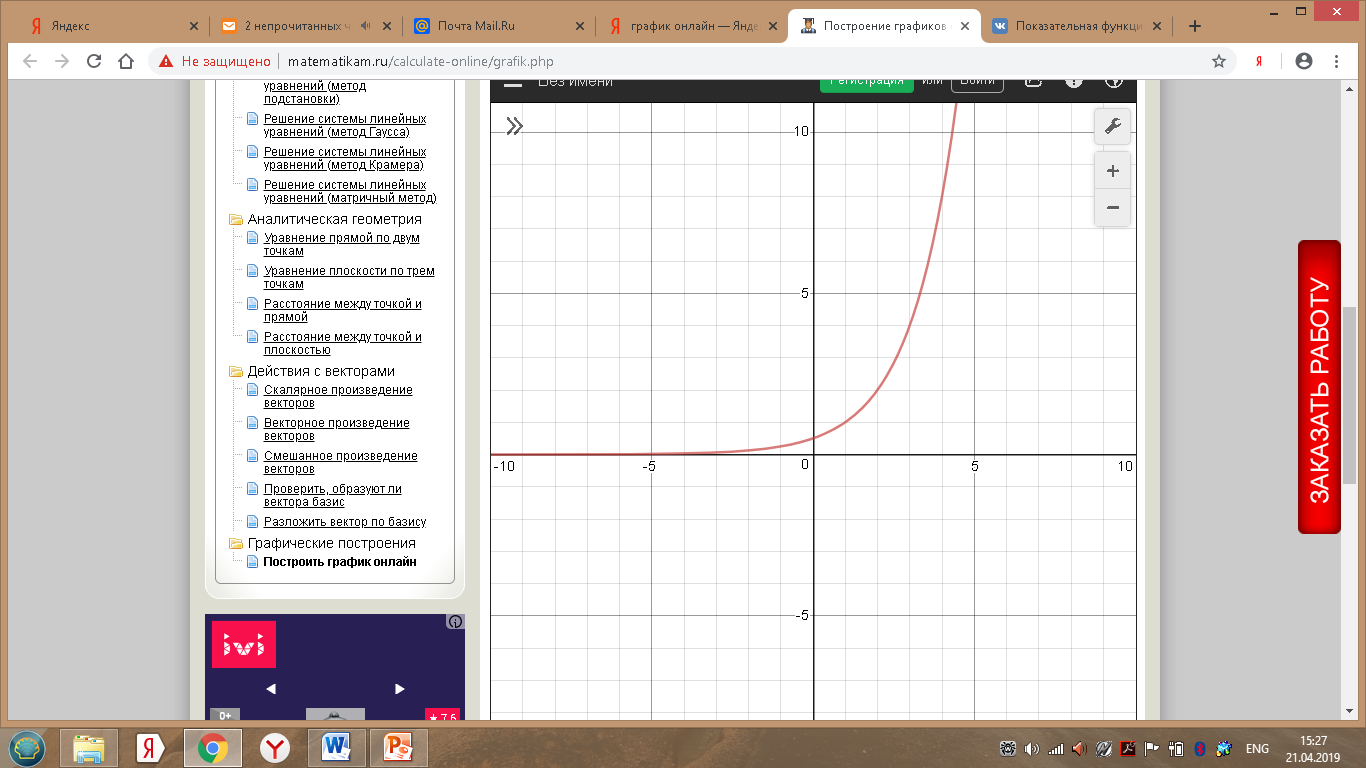
Сдвигаем вдоль оси Оу на 3 единицы вверх: 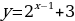 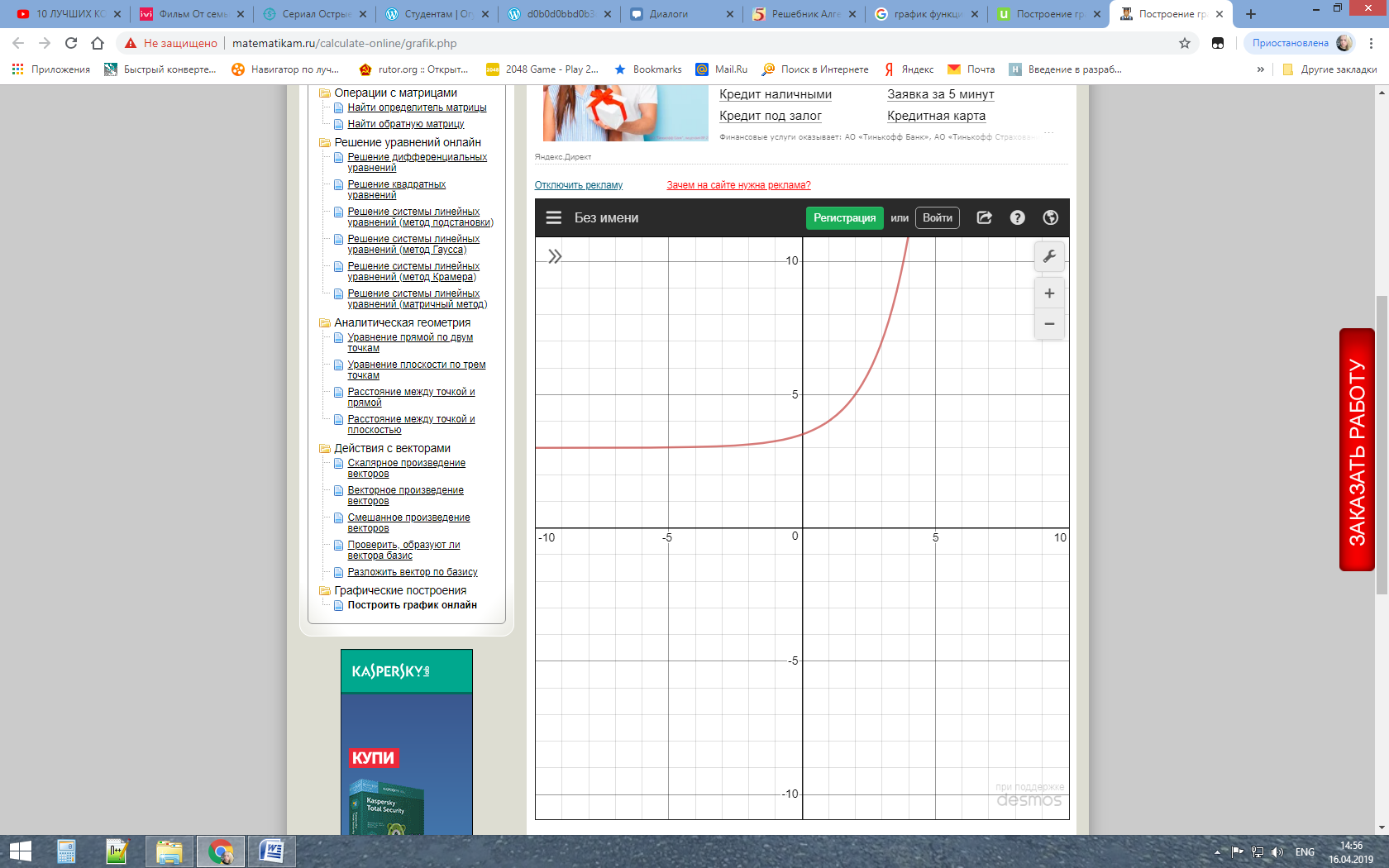
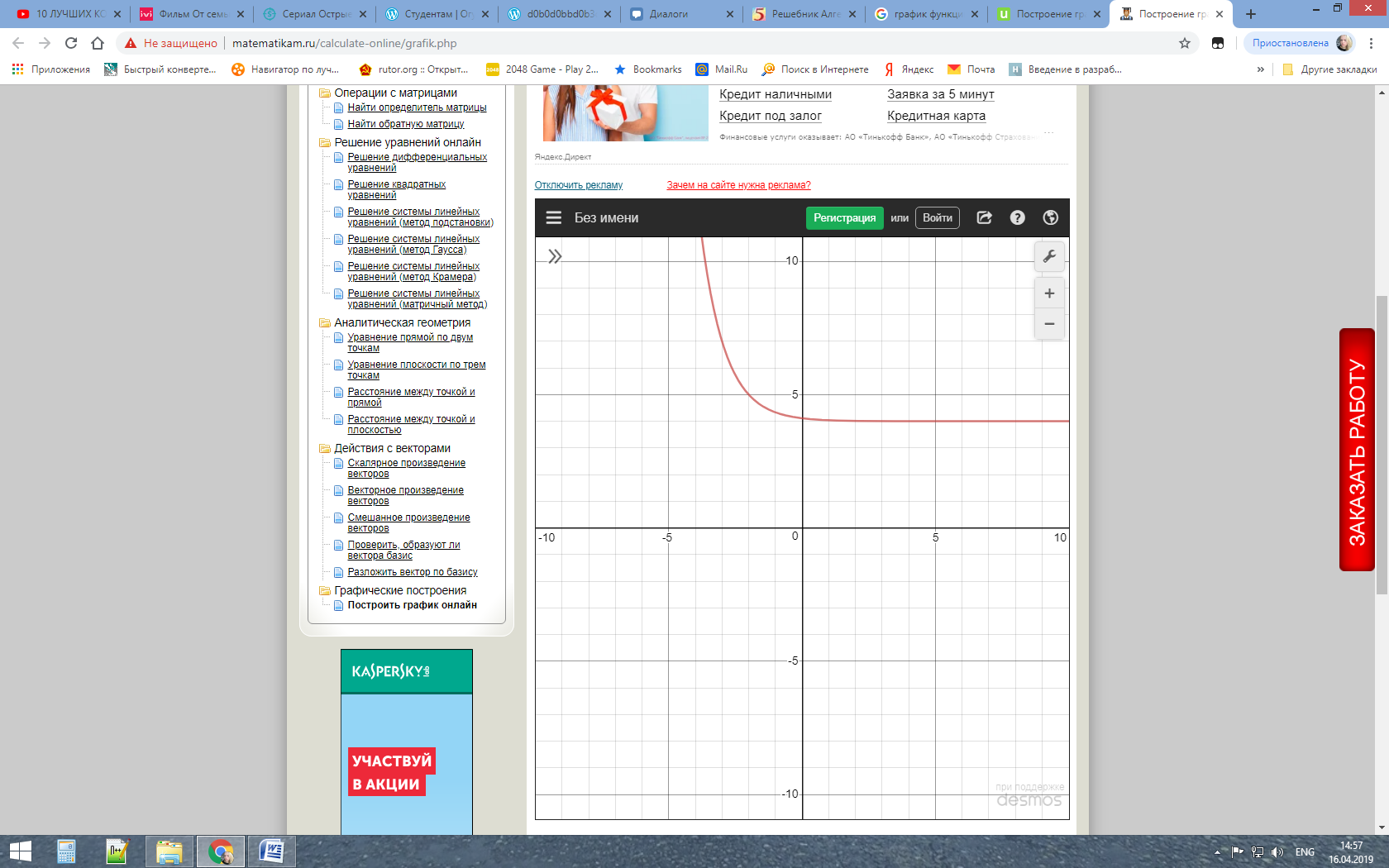
Б) Исходная показательная функция: 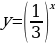 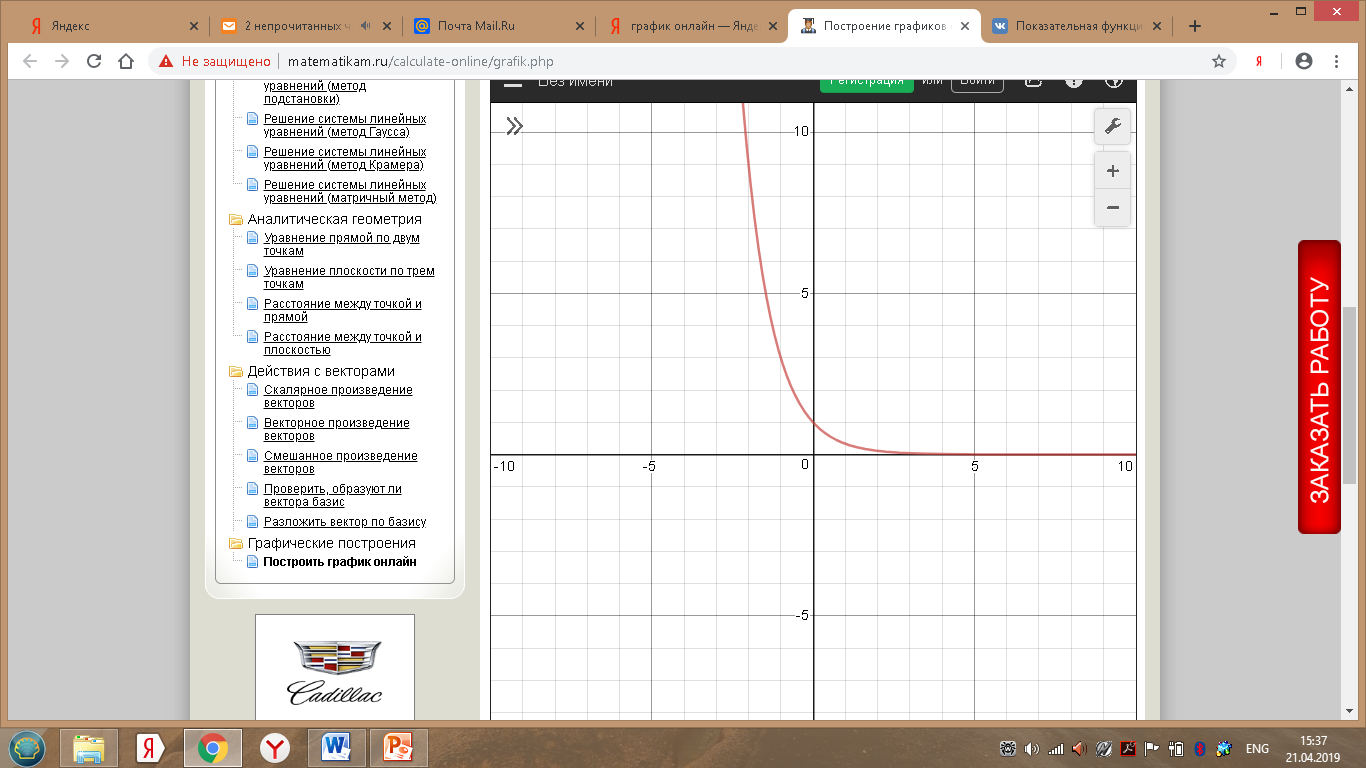
Сдвигаем вдоль оси Ох на 2 единицы влево: 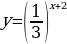 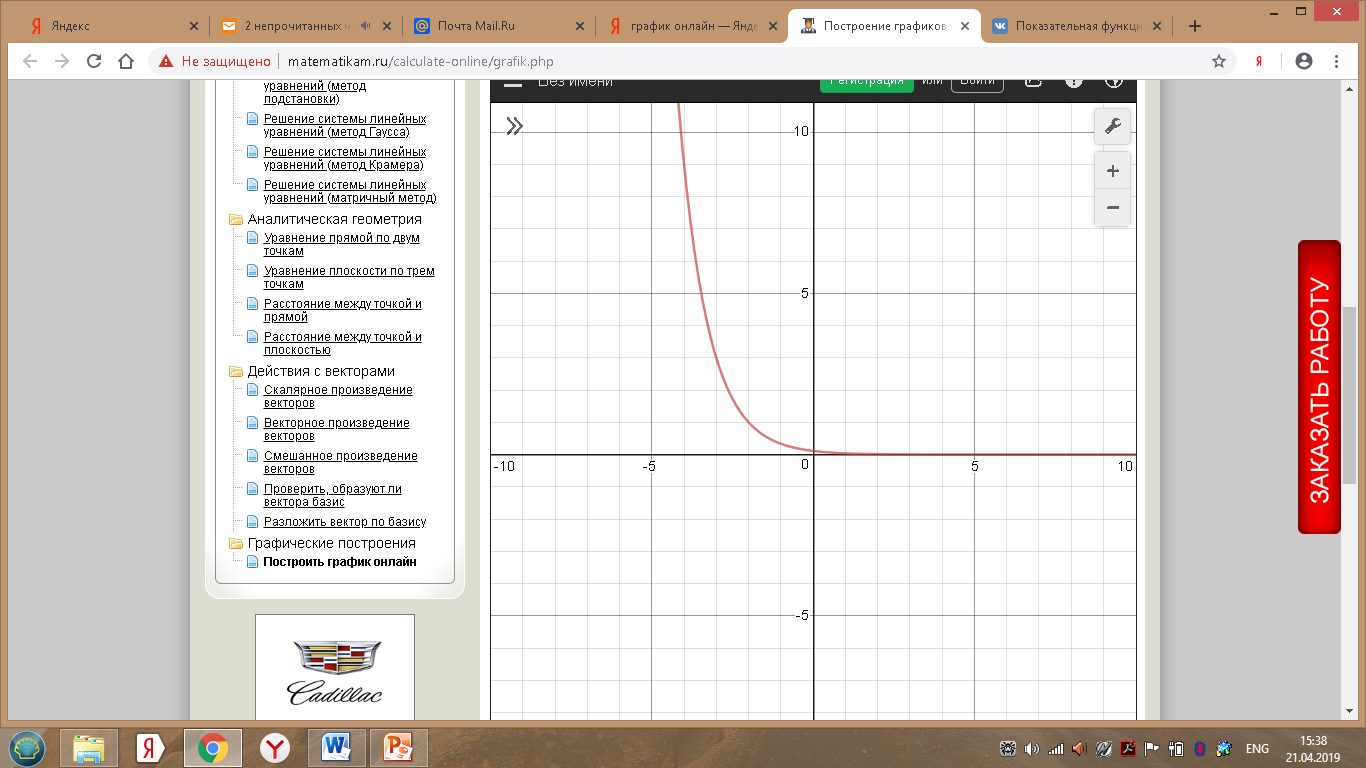
Сдвигаем вдоль оси Оу на 4 единицы вверх: 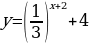
|







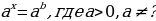 , и неравенств вида
, и неравенств вида 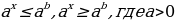 ,
, 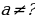 .
.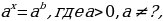 и неравенства вида
и неравенства вида 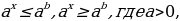
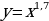
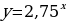
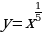
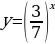
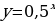
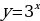
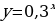
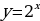 .
.



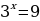
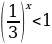
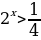
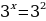
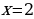
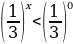
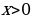
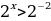
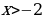
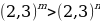
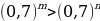
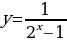
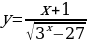
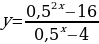
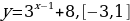
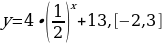
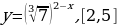
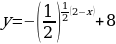
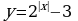
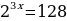
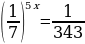
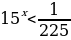
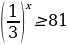
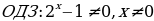
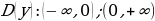
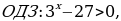
 ,
,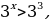
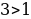 , то
, то 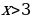
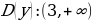
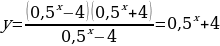 , при
, при 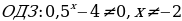
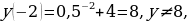
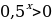 , то
, то 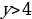
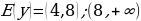
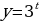 возрастает (a1),
возрастает (a1), 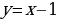 – возрастает, то функция
– возрастает, то функция 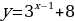 – возрастает. Значит:
– возрастает. Значит: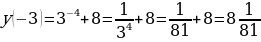 – наименьшее значение функции на
– наименьшее значение функции на 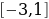 .
.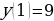 – наибольшее значение функции на
– наибольшее значение функции на 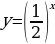 убывает (0a
убывает (0a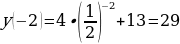 – наибольшее значение функции на
– наибольшее значение функции на 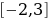 .
.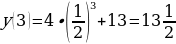 - наименьшее значение функции на
- наименьшее значение функции на 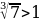 , то
, то 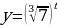 возрастает, но
возрастает, но 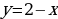 – убывает, то функция
– убывает, то функция 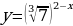 - убывает. Значит:
- убывает. Значит: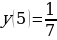 - наименьшее значение функции на
- наименьшее значение функции на 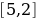 .
.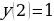 - наибольшее значение функции на
- наибольшее значение функции на 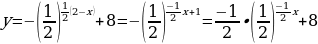

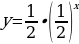
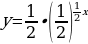

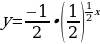
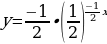

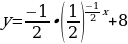
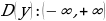
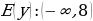
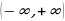

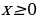 и отображаем от оси Оy:
и отображаем от оси Оy: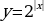

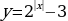

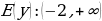
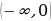 возрастает
возрастает 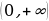
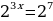
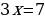
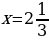
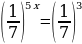
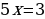
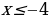

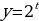 возрастает (a1) и
возрастает (a1) и 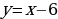 - возрастает, то функция
- возрастает, то функция 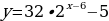 - возрастает. Значит:
- возрастает. Значит: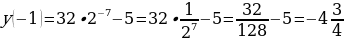 – наименьшее значение функции на
– наименьшее значение функции на 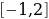 .
.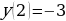 – наибольшее значение функции на
– наибольшее значение функции на 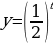 – убывает (0a
– убывает (0a 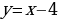 - возрастает, то функция
- возрастает, то функция 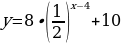 - убывает. Значит:
- убывает. Значит: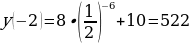 – наибольшее значение функции на
– наибольшее значение функции на 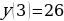 - наименьшее значение функции на
- наименьшее значение функции на