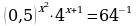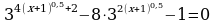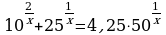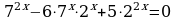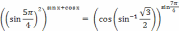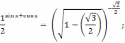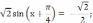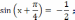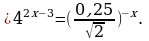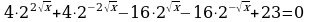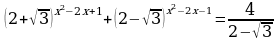Показательные уравнения и методы их решения с применением компьютерных технологий
Определение.
Показательным уравнением называется уравнение, содержащее переменную в
показателе степени.
Показательные уравнения относятся к классу трансцендентных уравнений. Это труднопроизносимое название говорит о том, что такие уравнения, вообще говоря, не решаются в виде формул.
Их можно решать только приближенно численными методами на компьютерах. А какже быть с экзаменационными задачами? Вся хитрость состоит в том, что экзаменатор так составляет задачу, что она как раз допускает аналитическое решение. Иными словами, Вы можете (и должны!) проделать такие тождественные преобразования, которые сводят данное показательное уравнение к самому простому показательному уравнению. Это самое простое уравнение так и называется: простейшее показательное уравнение. Оно решается логарифмированием.
Для успешного решения показательных уравнений необходимо:
Не только активно знать все показательные тождества, но и находить множества значений переменной, на которых эти тождества определены, чтобы при использовании этих тождеств не приобретать лишних корней, а тем более, - не терять решений уравнения.
Активно знать все показательные тождества.
Четко, подробно и без ошибок проделывать математические преобразования уравнений (переносить слагаемые из одной части уравнения в другую, не забыв про смену знака, приводить к общему знаменателю дроби и тому подобное). Это называется математической культурой. При этом сами выкладки должны делаться автоматически руками, а голова должна думать об общей путеводной нити решения. Делать преобразования надо как можно тщательней и подробней. Только это даст гарантию верного безошибочного решения. И помнить: небольшая арифметическая ошибка может просто создать трансцендентное уравнение, которое в принципе не решается аналитически. Выходит, Вы сбились с пути.
4. Знать методы решения задач. Для правильного ориентирования на каждом этапе Вам придется (сознательно или интуитивно!):
Этап обобщения и систематизации изученного материала.
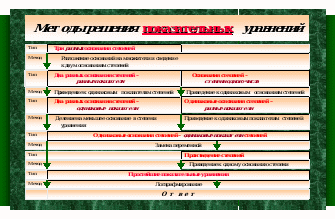
Рис.1. На рисунке представлена общая схема всех типов показательных уравнений.
Как видно из этой схемы стратегия решения показательных уравнений состоит в том, чтобы привести данное показательное уравнение к уравнению, прежде всего, с одинаковыми основаниями степеней, а затем - и с одинаковыми показателями степеней.
Получив уравнение с одинаковыми основаниями и показателями степеней, Вы заменяете эту степень на новую переменную и получаете простое алгебраическое уравнение (обычно, дробно-рациональное или квадратное) относительно этой новой переменной.
Решив это уравнение и сделав обратную замену, Вы в результате приходите к совокупности простейших показательных уравнений, которые решаются в общем виде с помощью логарифмирования.
Особняком стоят уравнения, в которых встречаются лишь произведения (частные) степеней. Воспользовавшись показательными тождествами, удается эти уравнения привести сразу к одному основанию, в частности, - к простейшему показательному уравнению.
Рассмотрим, как решается показательное уравнение с тремя разными основаниями степеней.
(Если у учителя есть обучающая компьютерная программа Л.Я. Боревского "Курс математики - 2000", то естественно работаем с диском, если нет -можно на каждую парту сделать распечатку такого типа уравнения из нее, представленную ниже.)
Приложение 1

Рис.2. План решения уравнения.

Рис.3 Начало решения уравнения

Рис.4 Окончание решения уравнения.
Выполнение практической работы.
Приложение 2 (раздаточный материал в Word для практической работы).
Задание: из списка уравнений выбрать уравнения указанного типа (№ ответа занести в таблицу) и решить их (ответ занести в таблицу):
Три разных основания степеней
Два разных основания - разные показатели степени
Основания степеней - степени одного числа
Одинаковые основания - разные показатели степеней
Одинаковые основания степеней - одинаковые
показатели степеней
Произведение степеней
Два разных основания степеней - одинаковые показатели
Простейшие показательные уравнения
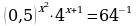
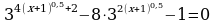
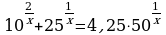
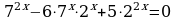
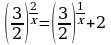
(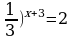
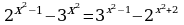
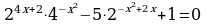
| Фамилия |
|
| № шага | A | B | C | D | E | F | G | H |
| № соотв.типа уравнения |
|
|
|
|
|
|
|
|
| ответ |
|
|
|
|
|
|
|
|
Выполняется попарная взаимопроверка с выставлением оценок.
Нормы оценок:
"5" - 100%
"4" - 1 ош. - 88%
2 ош. - 75%
"3" - 3 ош. - 63%
"2" - 4 ош. - 50%.
Решение нестандартного показательного уравнения.
А теперь решим с вами одно из нестандартных показательных уравнений, которые необходимо научиться решать при подготовке кЕГЭ (задание уровня С).
№218* (См. А.В. Столин. Комплексные упражнения по математике с решениями, 7-11 классы. Харьков, ИМП «Рубикон», 1995)
Решить уравнение:
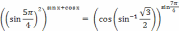
Решение:
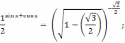
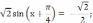
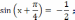
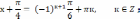
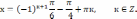
Ответ: ��

Этап информации о домашнем задании
Домашнее задание.
Определить тип уравнения и решить его.
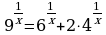

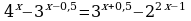
0,125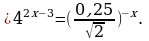
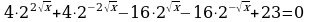

5. 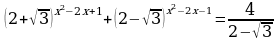
6.