10 класс
Тема: Показательные уравнения, сводящиеся к простейшим заменой
Цель: Закрепить понятие «показательное уравнение»; формирование умений и навыков решения показательных уравнений; научить решать однородные показательные уравнения.
Развивать вычислительные навыки и умения, логическое мышление учащихся.
Воспитывать навыки сотрудничества и ответственное отношение к обучению.
Оборудование: доска, карточки.
Форма урока: классно-урочная
Вид урока: практическое занятие с элементами лекции.
Тип урока: комбинированный.
План урока
Организационный момент
Проверка домашнего задания. Актуализация опорных знаний
Изучение нового материала
Закрепление изученного материала
Самостоятельная работа.
Подведение итогов
Задание на дом
Ход урока.
Организационный момент:
- Здравствуйте, я учитель математики Кулик И. А. сегодня проведу урок по теме «Показательные уравнения, сводящиеся к простейшим заменой»
Проверка домашнего задания:
Вставить пропущенные символы…
Актуализация опорных знаний
Цель: подготовить учащихся к восприятию нового материала
Устный счет: 2¹, 2 ², 3 °, 3⁻², 10 ⁻²,7 ⁻², (1/4) °, (3/2)°, (3/2) ⁻¹, (3/7)²,
Фронтальный опрос:
Какие уравнения называются показательными? Показательными уравнениями называют уравнения вида 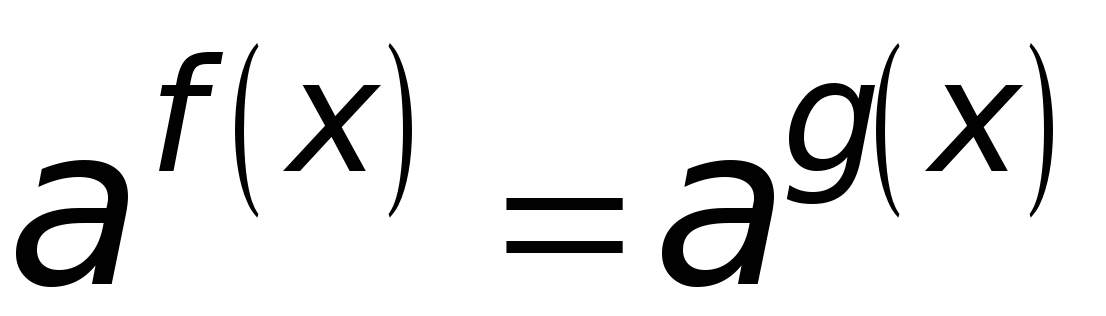 , где
, где  — положительное число, отличное от 1, и уравнения, сводящиеся к этому виду.
— положительное число, отличное от 1, и уравнения, сводящиеся к этому виду.
Какой основной метод решения показательных уравнений? Сведение к одинаковому основанию. Теорема: Показательное уравнение 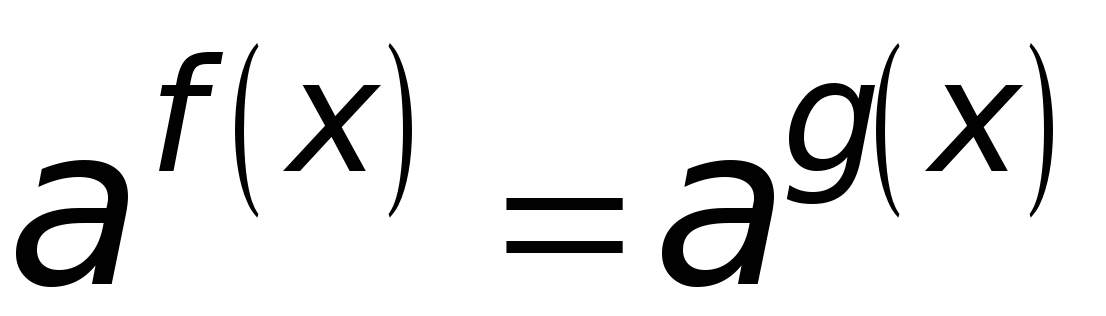 (где
(где 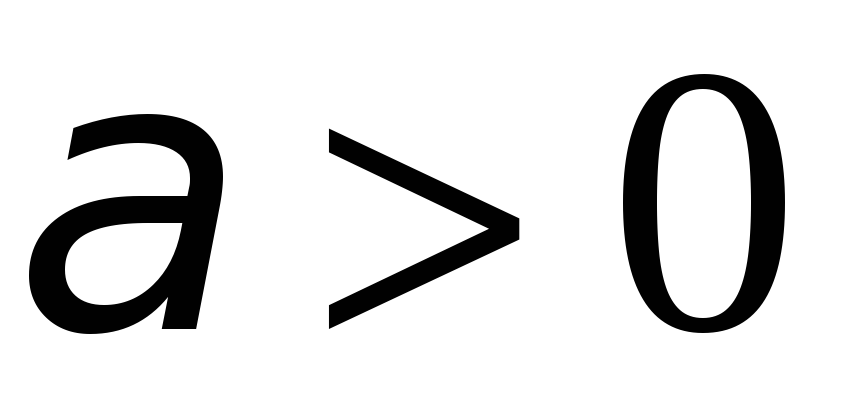 ,
, 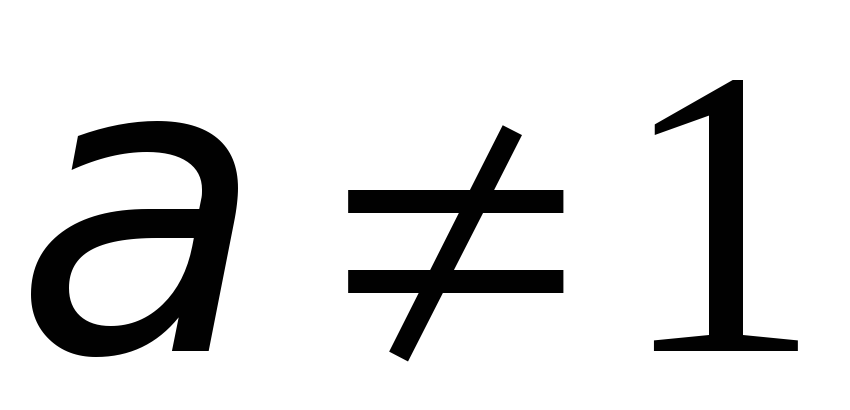 ) равносильно уравнению
) равносильно уравнению 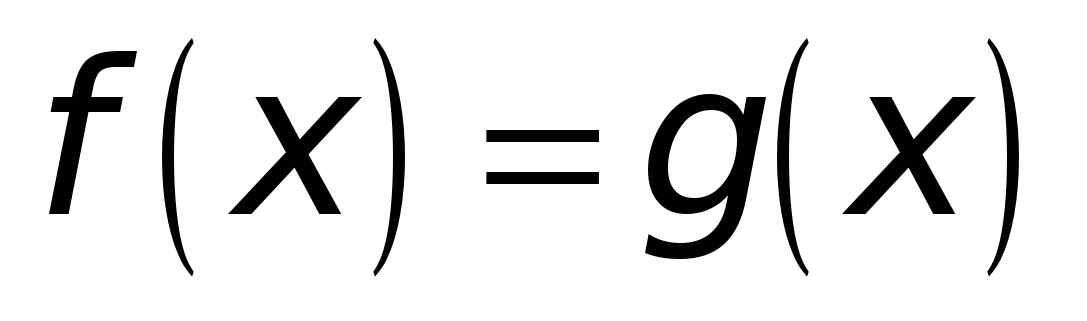 .
.
Какие способы решения показательных уравнений вы знаете еще?
Вынесение общего множителя за скобки, замена.
Давайте назовем методы решения предложенных уравнений: учебник с. 378-379
№ 132 – сведение к одинаковому показателю
№ 134 – вынесение общего множителя за скобки
№ 139 – заменой (Этим методом вы решали показательные уравнения на прошлом занятии).
№ 146 -?
Изучение нового материала
Цель: сформулировать понятие «однородное показательное уравнение», показать методы решения.
Метод: объяснение учителя
Решим уравнение
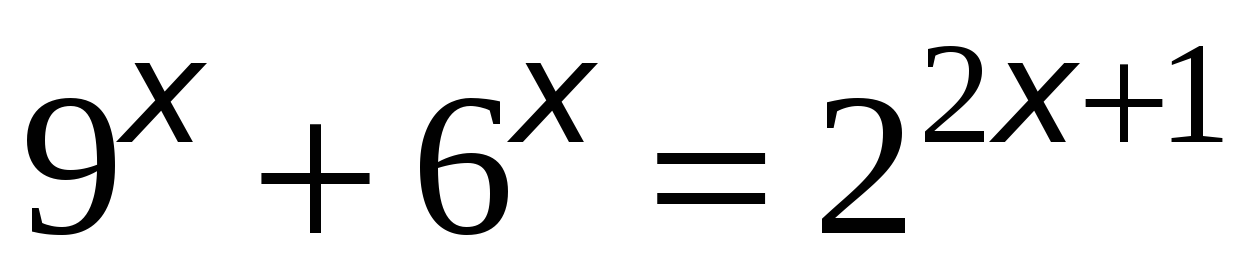 . Перепишем данное уравнение с учетом, что:
. Перепишем данное уравнение с учетом, что: 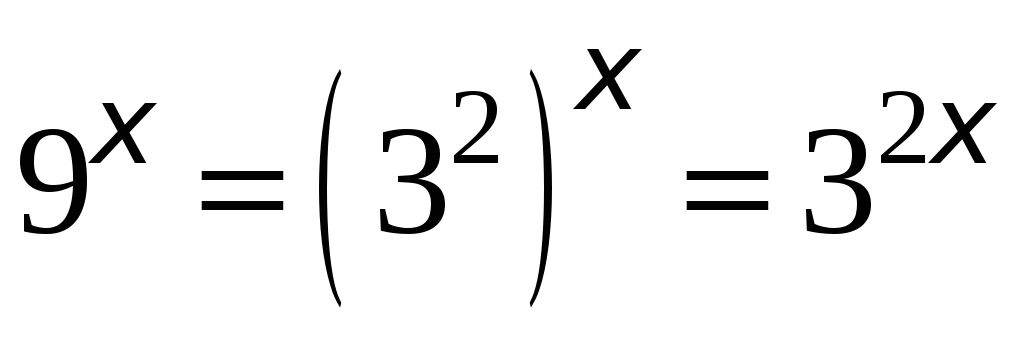 ,
,  ,
, 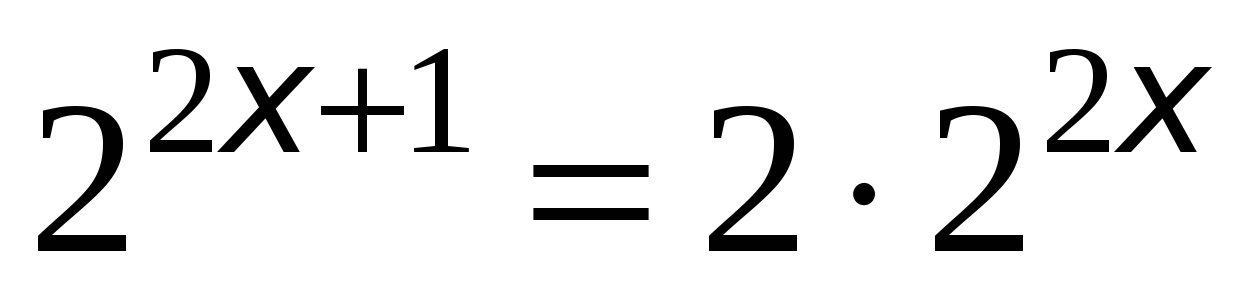 . Получаем уравнение -
. Получаем уравнение - 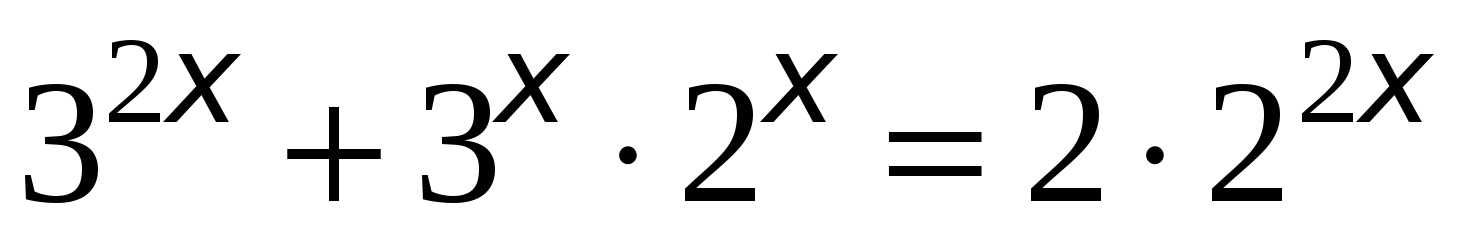 . Перенесём правую часть уравнения в левую:
. Перенесём правую часть уравнения в левую: 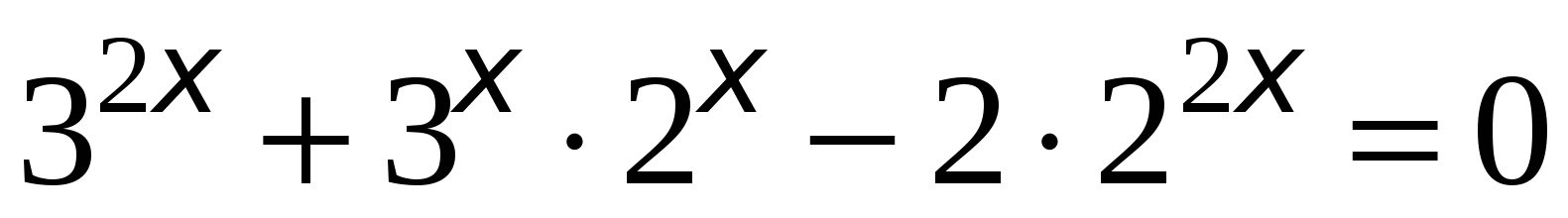 . Разделим обе части уравнения на
. Разделим обе части уравнения на 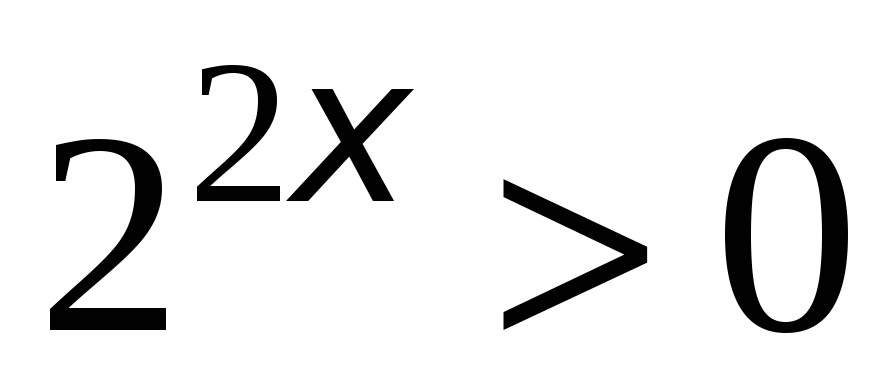 , получим
, получим
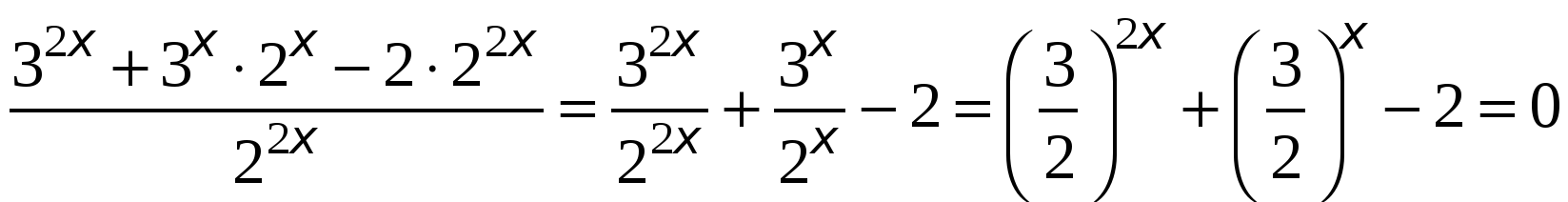 Данное уравнение решается методом введения новой переменной:
Данное уравнение решается методом введения новой переменной: 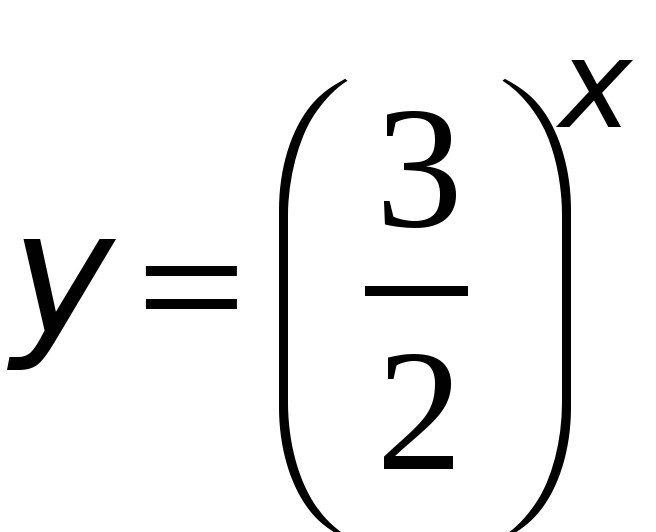 , тогда уравнение примет вид
, тогда уравнение примет вид 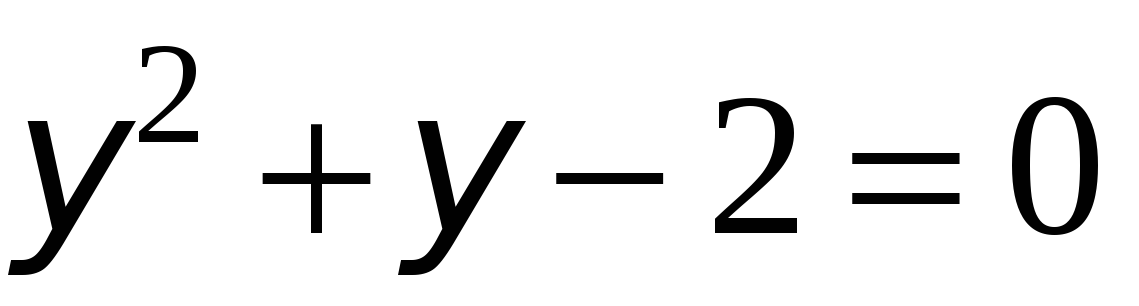 . Решив квадратное уравнение относительно
. Решив квадратное уравнение относительно 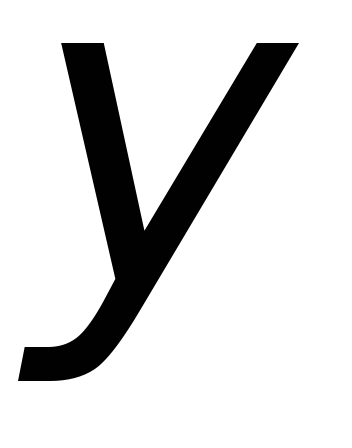 , находим:
, находим: 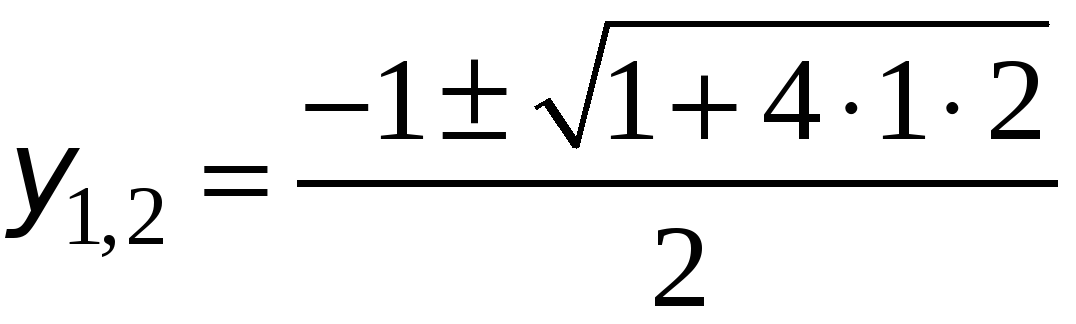 , т.е.
, т.е. 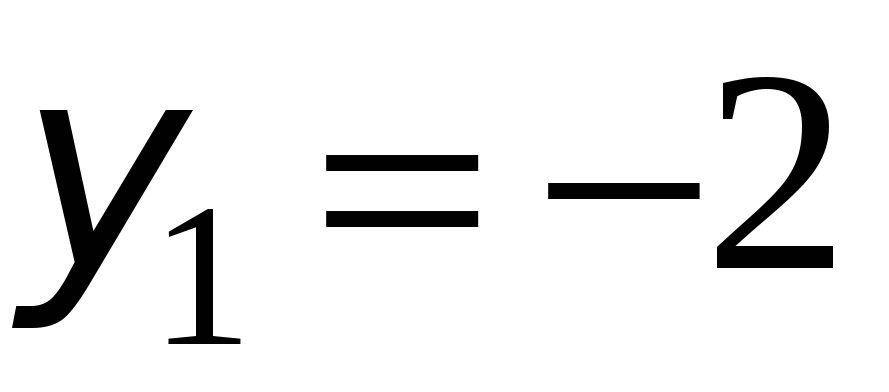 и
и 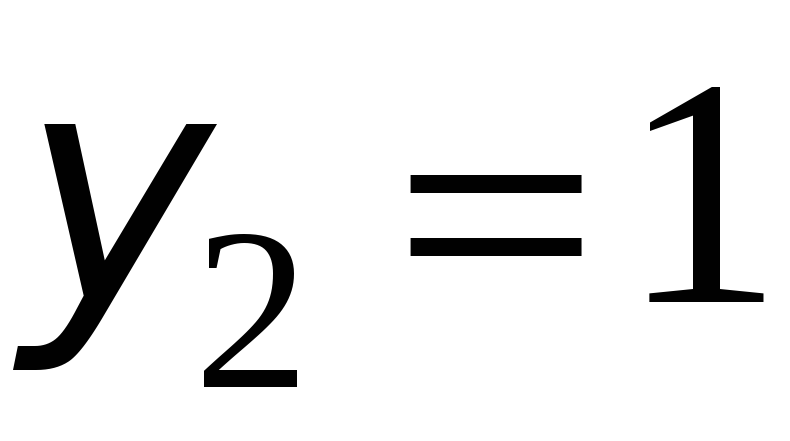 . Но
. Но 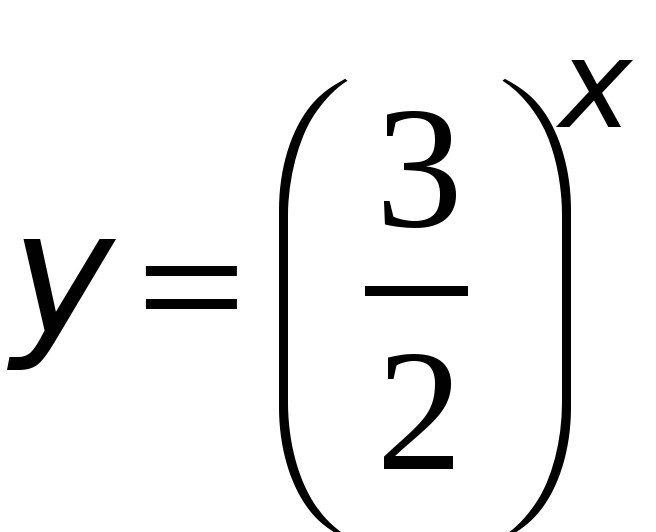 , значит, нам остается решить два уравнения:
, значит, нам остается решить два уравнения: 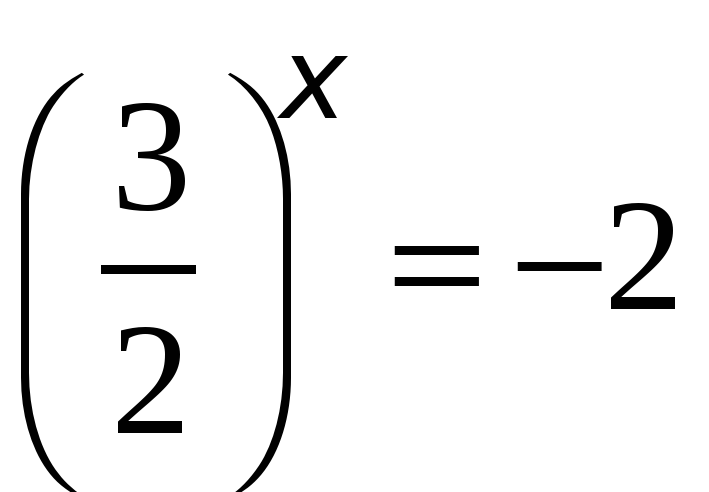 и
и 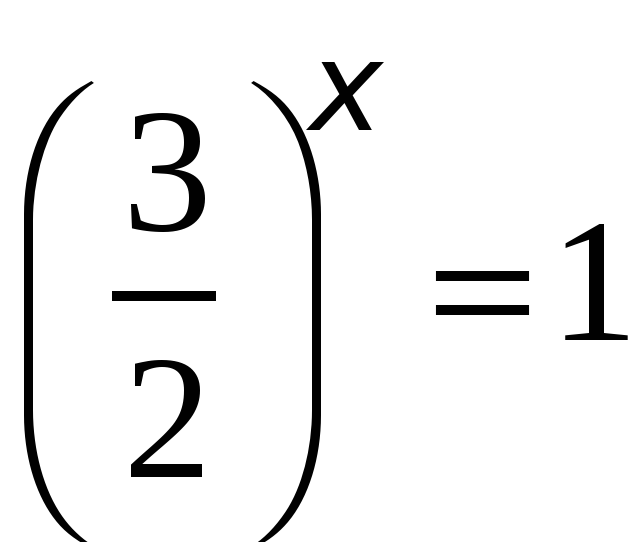 (что то же
(что то же 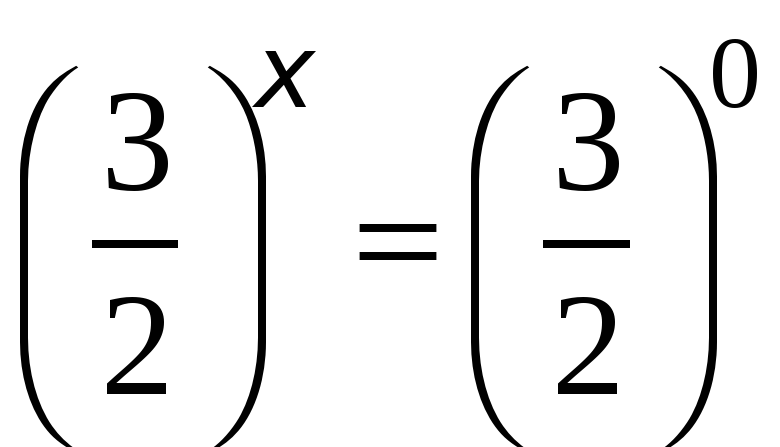 ). Первое уравнение не имеет решения, так как
). Первое уравнение не имеет решения, так как 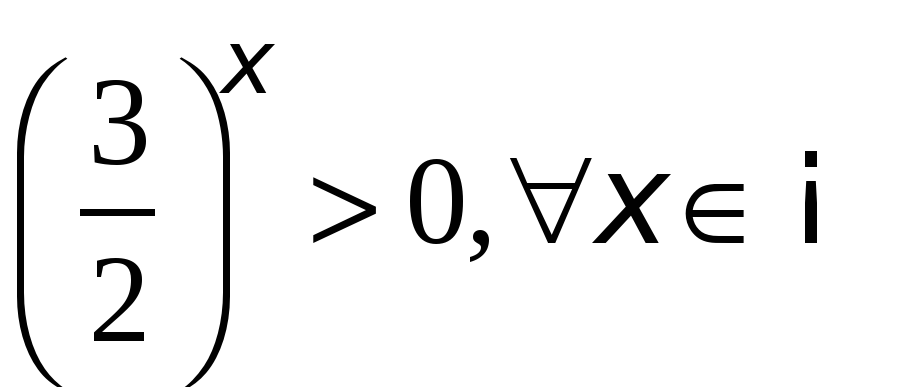 , второе показательное уравнение решаем методом уравнивания коэффициентов, и получаем ответ: .
, второе показательное уравнение решаем методом уравнивания коэффициентов, и получаем ответ: .
- Рассмотренное нами только что уравнение носит название «однородное уравнение» и решается делением на одну из показательных функций.
Закрепление изученного материала № 146(а)
7 ͯ ⁻ ² +38*3 ͯ =7 ͯ ⁺ ¹ разделим на 7 ͯ
7⁻² +38*(3/7) ͯ =7
38*(3/7) ͯ =7 -1/49
(3/7) ͯ =342/49: 38
(3/7) ͯ = 9/49
х=2
Ответ: 2
Самостоятельная работа
|
| 1 вариант | 2 вариант |
| Вычислить
|
10 ⁻² |
(¼)° |
| Заполнить таблицу соответствий методов решений уравнений 1)сведение к одинаковому основанию 2)вынесение общего множителя за скобки 3) замена 4) однородное
| А) 10 ͯ =0,01 Б) 3 ² ͯ + 8*3 ͯ -9=0 В) 9 ͯ +6 ͯ =2 ² ͯ ⁺ ¹ Г) 3 ͯ ⁺ ¹ - 3 ͯ =6
| А) 2 ² ͯ - 6*2 ͯ +8=0 Б) 2 ͯ ⁺ ¹ +2 ͯ = 6 В) (0,1) ͯ =1000 Г) 7 ͯ ⁻ ² +38*3 ͯ =7 ͯ ⁺ ¹ |
| Найти корень уравнения
|
2 ͯ =4 |
3 ͯ = 27
|
| Решить уравнение № 142
| А) 2 ² ͯ - 6*2 ͯ +8=0 | Б) 3 ² ͯ + 8*3 ͯ -9=0 |
Подведение итогов
Цель: сформулировать итоги урока
Задание на дом
Цель: закрепление знаний, полученных на занятие, выработка способности их применения.
По учебнику: № 146 (б-г) с.379







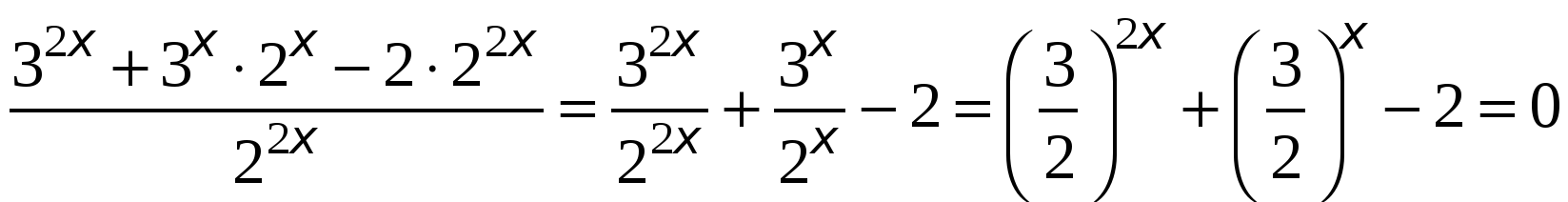 Данное уравнение решается методом введения новой переменной:
Данное уравнение решается методом введения новой переменной: 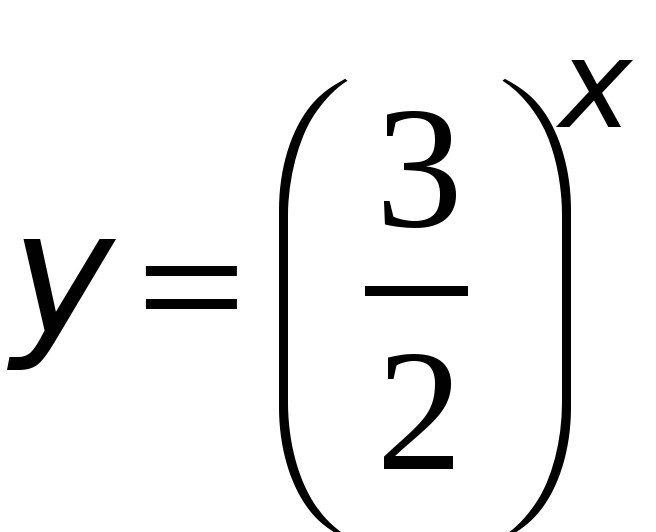 , тогда уравнение примет вид
, тогда уравнение примет вид 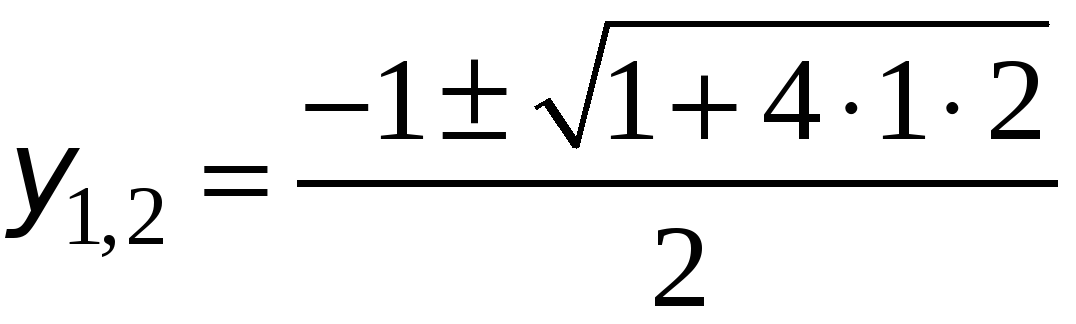 , т.е.
, т.е. 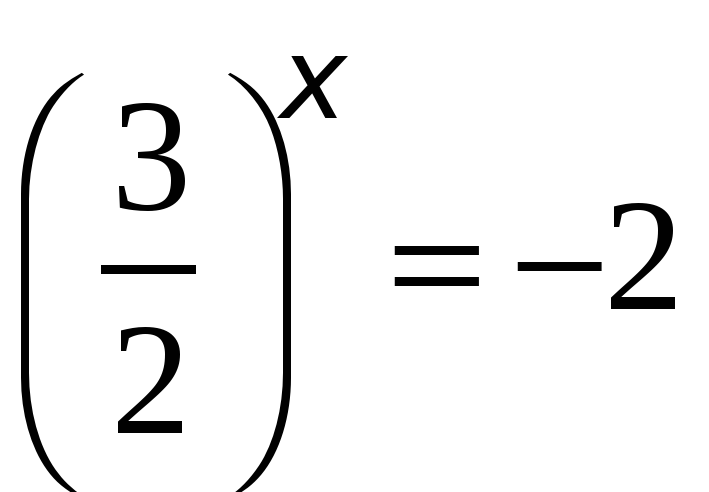 и
и 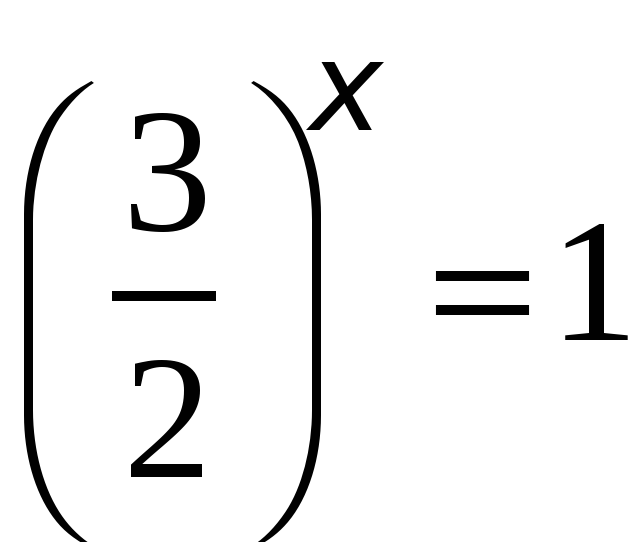 (что то же
(что то же 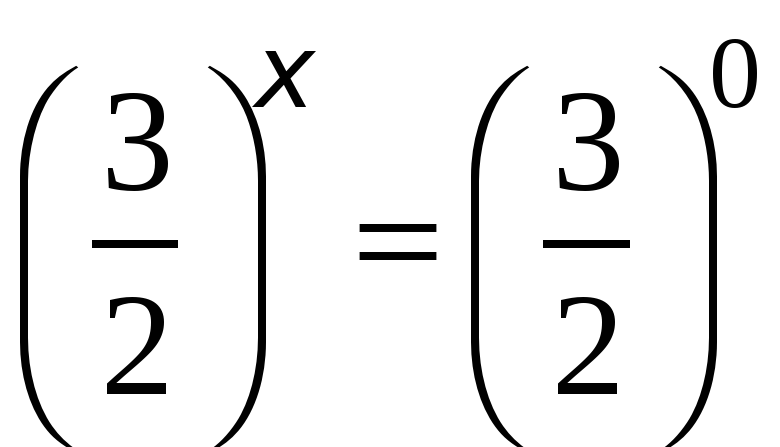 ). Первое уравнение не имеет решения, так как
). Первое уравнение не имеет решения, так как 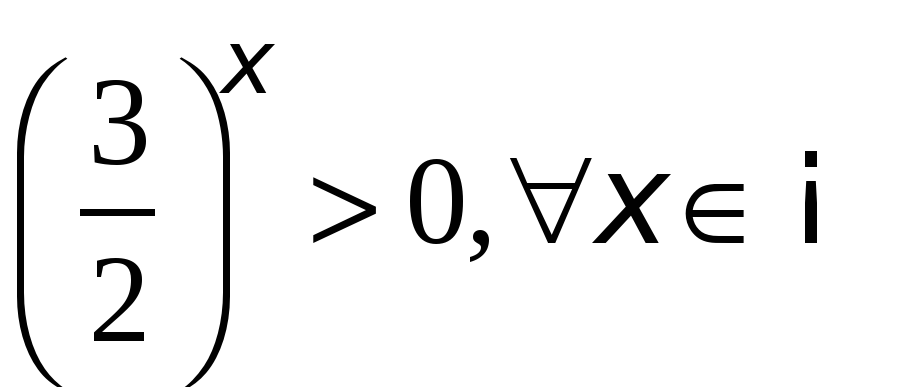 , второе показательное уравнение решаем методом уравнивания коэффициентов, и получаем ответ: .
, второе показательное уравнение решаем методом уравнивания коэффициентов, и получаем ответ: .









