МУНИЦИПАЛЬНОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ
«ПОПОВСКАЯ СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА»
Выступление на МО:
«Понятие и виды функциональной грамотности, понятие «математической» грамотности, определяемой в ходе исследования PISA, основные подходы к оценке математической грамотности, примеры открытых заданий по математике».
Выполнила:
Семенченко Любовь Юрьевна,
учитель математики
сл. Поповка
2022 г.
«Цель обучения ребенка состоит в том,
чтобы делать его способным развиваться дальше,
без помощи учителя».
Элберт Хаббарт
Введение
Цель среднего образования: заключается в обеспечении развития у обучающихся способностей к познанию, творческому использованию полученных знаний в любой учебной и жизненной ситуации, готовности к саморазвитию и самоуправлению посредством развития ключевых и предметных компетенций.
Современная школа обеспечивает учащихся необходимым багажом, но не всегда формирует умения выходить за пределы привычных учебных ситуаций. Педагоги школы дают сильные предметные знания, но не учат применять их в реальных, жизненных ситуациях. Это обусловлено как стремительным развитием науки и техники, так и быстрым моральным устареванием учебной литературы, слабо связанной с проблемами повседневной практики человека.
Хранение и передача знаний, навыков, норм и идеалов, образцов деятельности и поведения, социальных ценностей и ориентаций в системе образования осуществляется через учителя, поэтому к педагогической культуре учителя предъявляют высокие требования, одним из которых является функциональная грамотность.
Понятие функциональной грамотности сравнительно молодо: появилось в конце 60-х годов прошлого века в документах ЮНЕСКО и позднее вошло в обиход исследователей. Примерно до середины 70-х годов концепция и стратегия исследования связывалась с профессиональной деятельностью людей: компенсацией недостающих знаний и умений в этой сфере.
В дальнейшем этот подход был признан односторонним. Функциональная грамотность стала рассматриваться в более широком смысле: включая компьютерную грамотность, политическую, экономическую и т.д.
В таком контексте функциональная грамотность выступает как способ социальной ориентации личности, интегрирующей связь образования (в первую очередь общего) с многоплановой человеческой деятельностью.
Мониторинговым исследованием качества общего образования, призванным ответить на вопрос: «Обладают ли учащиеся 15-летнего возраста, получившие обязательное общее образование, знаниями и умениями, необходимыми им для полноценного функционирования в современном обществе, т.е. для решения широкого диапазона задач в различных сферах человеческой деятельности, общения и социальных отношений», - является PISA(Programme for International Student Assessment). И функциональная грамотность понимается - PISA как знания и умения, необходимые для полноценного функционирования человека в современном обществе. PISA в своих мониторингах оценивает 3 вида грамотности: читательскую, математическую, естественнонаучную.
Проблема развития функциональной грамотности обучающихся в России актуализировалась в 2018 году благодаря Указу Президента РФ от 7 мая 2018 г. № 204 «О национальных целях и стратегических задачах развития Российской Федерации на период до 2024 года». Национальный проект «Образование», который включает следующие цели:
Обеспечение глобальной конкурентоспособности российского образования, вхождение РФ в число 10 стран мира по качеству общего образования.
Воспитание гармонично развитой и социально ответственной личности на основе духовно-нравственных ценностей народов РФ, исторических и национально-культурных традиций.
И планируется реализовать данные направления в срок с 01.01.2019 до 31.12.2024 года.
Поскольку функциональная грамотность понимается как совокупность знаний и умений, обеспечивающих полноценное функционирование человека в современном обществе, ее развитие у школьников необходимо не только для повышения результатов мониторинга PISA, как факта доказательства выполнения Правительством РФ поставленных перед ним Президентом задач, но и для развития российского общества в целом.
В Федеральном государственном образовательном стандарте среднего общего образования (10-11 е классы) (утвержденном приказом Минобрнауки России от 17 апреля № 413) указывается, что в рамках обучения математике (базовый уровень) необходимо добиться у учащихся сформированности представлений о роли и месте математики в современной научной картине мира; понимания математической сущности; понимания роли математики в формировании кругозора и функциональной грамотности для решения практических задач.
Низкий уровень функциональной грамотности подрастающего поколения затрудняет их адаптацию и социализацию в социуме. Современному российскому обществу нужны эффективные граждане, способные максимально реализовать свои потенциальные возможности в трудовой и профессиональной деятельности, и тем самым принести пользу обществу, способствовать развитию страны. Этим объясняется актуальность проблемы развития функциональной грамотности у школьников на уровне общества.
Любой школьник хочет быть социально успешным, его родители также надеются на высокий уровень благополучия своего ребенка во взрослой жизни. Поэтому актуальность развития функциональной грамотности обоснована еще и тем, что субъекты образовательного процесса заинтересованы в высоких академических и социальных достижениях обучающихся, чему способствует их функциональная грамотность.
Достижения российских школьников в обследовании PISA по математике, оценивающем способность применять полученные знания на практике, остаются скромными: в 2021 году 24-е место.
Все вышесказанное позволяет обосновать выбор темы сегодняшнего выступления « Понятие и виды функциональной грамотности, понятие «математической» грамотности, определяемой в ходе исследования PISA, основные подходы к оценке математической грамотности, примеры открытых заданий по математике».
Проблема исследования: как сформировать функциональную грамотность обучающихся на уроках математики.
Цель исследования: выявить и научно обосновать комплекс педагогических условий формирования функциональной математической грамотности.
Задачи:
- раскрыть сущность понятия «функциональная грамотность обучающихся» и «математическая грамотность обучающихся»
- показать необходимость развития функциональной математической грамотности;
- предложить опыт внедрения программы по развития функциональной грамотности
- выявить пути формирования функциональной математической грамотности;
Гипотеза исследования основана на предположении о том, что эффективность развития профессиональной компетентности учителя по формированию функциональной грамотности учащихся основной школы обеспечивается и достигается, если: рассматривать функциональную грамотность учащихся как базовый уровень образованности учащихся, характеризующий степень овладения способами работы с информацией и позволяющий решать реальные жизненные проблемы, адаптироваться к внешнему миру.
Новизна и самостоятельность: активизация мыслительной деятельности учащихся при решении задач практического характера усиливается, а подготовка к международному исследованию PISA выходит на новый уровень за счет использования в школьной практике заданий на функциональную грамотность. Поэтому данная работа направлена на изучение вопроса о введении заданий на развитие функциональной грамотности школьников в школьный курс математики.
Предмет исследования: содержание, технология и организационно-педагогические условия развития по формированию функциональной грамотности учащихся основной школы.
II. Основная часть
В настоящее время в Российской Федерации сформирована единая система оценки качества образования (ЕСОКО), которая позволяет вести мониторинг знаний учащихся на разных ступенях обучения в школе, оперативно выявлять и решать проблемы системы образования в разрез е предметов, школ и регионов.
Данная система дает возможность получить полное представление о качестве образования в стране, анализировать и учитывать влияние различных факторов на результаты работы школ. Она позволяет школам вести самодиагностику и выявлять имеющиеся проблемы, а родителям получать информацию о качестве знаний своих детей. Система оценки качества школьного образования в России в настоящее время является многоуровневой, состоящей из нескольких процедур.
Первая важная процедура этой системы — единый государственный экзамен (ЕГЭ), который является обязательным для всех выпускников школ с 2009 года.
Вторая важная процедура системы оценки качества образования — государственная итоговая аттестация 9-х классов (ГИА-9), ключевой формой которой является основной государственный экзамен (ОГЭ). По результатам ГИА-9 школьник может продолжить обучение в старшей школе и в учреждениях среднего профессионального образования.
Промежуточные срезы знаний обучающихся проводятся по разным предметам и в разных классах при помощи национальных исследований качества образования (НИКО) и всероссийских проверочных работ (ВПР).
Кроме того, Россия принимает участие в международных исследованиях оценки качества образования. Эти исследования позволяют понять, насколько конкурентоспособной является российская школа сегодня, выявить и сравнить изменения, происходящие в системе образования разных стран, проанализировать факторы, позволившие странам-лидерам добиться успеха. Оценку знаний учащихся школ дополняют исследования профессиональных компетенций учителей.
При этом на протяжении нескольких лет по исследованию PISA Россия занимала недостаточно высокое место в рейтинге стран. Однако данные последнего исследования PISA, проведенного в 2021 году, показали динамику роста результатов российских школьников.
2.1. Понятие «функциональная грамотность» н «математической грамотности»
Одним из основных отличительных особенностей реализации стандарта является практическая направленность знаний, накопление и использование жизненного опыта ученика, т.е. не «знания для знаний», а «знания для жизни». Этот общественный заказ уже успешно реализовывает телевидение: образовательные программы, мультфильмы учат действовать в различных жизненных ситуациях.
Углубимся в понятие «функциональная грамотность»
Функциональная грамотность — «способность человека решать стандартные жизненные задачи в различных сферах жизни и деятельности на основе прикладных знаний».
Функционально грамотная личность — это человек, ориентирующийся в мире и действующий в соответствии с общественными ценностями, ожиданиями и интересами.
Основные признаки функционально грамотной личности: это человек самостоятельный, познающий и умеющий жить среди людей, обладающий определёнными качествами, ключевыми компетенциями.
Математическая грамотность - это способность человека мыслить математически, формулировать, применять и интерпретировать математику для решения задач в разнообразных практических контекстах. Она включает в себя понятия, процедуры и факты, а также инструменты для описания, объяснения и предсказания явлений. Она помогает людям понять роль математики в мире, высказывать хорошо обоснованные суждения и принимать решения, которые должны принимать конструктивные, активные и размышляющие граждане в 21 веке.
В определении математической грамотности особое внимание уделяется использованию математики для решения практических задач в различных контекстах.
Математическая грамотность включает также способность выделить в различных ситуациях математическую проблему и решить ее, а также наклонность выполнять такую деятельность, что достаточно часто связано с такими чертами характера, как уверенностью в себе и любознательностью.
Три направления, выделяемые в математической грамотности
Для проведения проверки математической грамотности были выделены три направления: виды деятельности, содержание, ситуации.
Виды деятельности
Задания, используемые в исследовании, группируются вокруг трех уровней компетентности.
Первый - воспроизведение включает проверку определений или простых вычислений, характерных для обычной проверки математической подготовки учащихся.
Второй - установление связей требует интеграции математических фактов и методов для решения явно сформулированных и до некоторой степени знакомых математических задач.
Третий - размышления включает проверку математического мышления, умения обобщать, глубоко понимать, использовать интуицию, анализировать предложенную ситуацию для выделения в ней проблемы, которая решается средствами математики, и формулирования этой проблемы.
Содержание
Содержание проверки в данном исследовании группируется вокруг некоторых общих явлений или типов проблем, которые возникают при рассмотрении этих явлений. В качестве таких явлений предлагаются следующие: количество, пространство и форма, изменение и зависимости, неопределенность.
Ситуации
Один из важных аспектов математической грамотности — это применение математики в различных ситуациях, которые связаны с личной и школьной жизнью, местным обществом, общественной жизнью, работой и отдыхом.
В концепцию по математике было добавлено 8 навыков 21 века*
Критическое мышление
Креативность
Исследование и изучение
Саморегуляция, инициативность, настойчивость
Использование информации
Системное мышление
Коммуникация
Рефлексия
Основа организации исследования математической грамотности включает три структурных компонента:
Контекст, в котором представлена проблема
Содержание математического образования, которое используется в заданиях;
Мыслительная деятельность, необходимая для того, чтобы связать контекст, в котором представлена проблем а, с математическим содержанием, необходимым для её решения.
Математическая грамотность - это способность индивидуума применять математику для решения проблем в разнообразных контекстах реального мира. Она помогает людям понять роль математики в мире.
• формулировать ситуацию математически
• применять математические понятия, факты, процедуры
• интерпретировать, использовать и оценивать математические результаты
• рассуждать (над формулированием, над решением, над результатом)
2.2. Система работы на уроках математики по формированию функциональной грамотности
Функциональная грамотность - явление метапредметное, и поэтому она формируется при изучении всех школьных дисциплин и поэтому имеет разнообразные формы проявления.
Рассмотрим применение этого метода к решению проблемы подготовки школьников к изучению систематических курсов алгебры и геометрии. Для этого необходимо выявить признаки, указывающие на ее существование; определить, в чем состоит ее основное противоречие; найти пути его разрешения; определить необходимое содержание и требования к организации образовательного процесса; спланировать последовательность достижения результатов и определить, каким образом они будут фиксироваться.
Основное противоречие учебной деятельности обучающихся средних классов. Результаты наблюдений, проведенные за последние четыре года в школах России, позволяют сделать вывод о том, что затруднения в начале изучения систематических курсов алгебры и геометрии в большой степени обусловлены дефицитами учебной деятельности учащихся, накопленными в предыдущие годы обучения.
Задача формирования естественнонаучной грамотности и достижения образовательных результатов ФГОС предъявляет определённые требования к содержанию учебной деятельности на уроке и необходимым компетенциям учителя. Развитие профессиональной компетентности учителя, обеспечивающей реализацию педагогического процесса, инициирующего и формирующего функциональную грамотность учащегося, является на современном этапе развития образования одной из главных задач.
Формирования функциональной грамотности учащихся основной школы обеспечивается и достигается, если:
рассматривать функциональную грамотность учащихся как базовый уровень образованности учащихся, характеризующий степень овладения способами работы с информацией и позволяющий решать реальные жизненные проблемы, адаптироваться к внешнему миру;
реализовать содержание профессиональной компетентности учителя по формированию функциональной грамотности учащихся в процессе повышения квалификации в условиях внутришкольной методической работы;
разработать, обосновать и апробировать интерактивную технологию развития профессиональной компетентности учителя по формированию функциональной грамотности учащихся;
выявить совокупность организационно-педагогических условий, обеспечивающих развитие профессиональной компетентности учителя по формированию функциональной грамотности учащихся.
Из того, что надо знать и уметь, мы понимаем, что решением практико-ориентированных задач учитель должен работать уже с начальной школы.
Задачи устного счёта.
Для достижения правильности и беглости устных вычислений в течение всех лет обучения на каждом уроке математики необходимо выделять от 5 — 10 минут для проведения тренировочных упражнений в устных вычислениях. Устный счет стараюсь проводить на каждом уроке. Устный счет я провожу по -разному: по карточкам - продолжите вычисления, закончите фразу, под диктовку учителя и т.д.
Пример (5 класс).
1. Магазин открывается в 10 часов утра, а закрывается в 10 часов вечера. Обеденный перерыв длится с 15 до 16 часов. Сколько часов в день открыт магазин?
Здесь ученик должен прочитать грамотно, внимательно, понять, что ему дано и что надо найти, ответить на поставленный вопрос. Так, напр., с 10 утра до 10 вечера — это 12 часов.
2. Вдоль дороги (по прямой) через каждые 2 метра высажено дерево, всего посадили 120 деревьев, найдите длину зеленого ограждения.
Большинство учащихся мгновенно дает ответ 240 метров. Однако, это неправильный ответ.
Решение: Построим простую геометрическую модель.
Обратим внимание: точек — три, а отрезков — два. Построим аналогичные геометрические модели из трех, четырех точек Замечаем, что количество точек на одну больше, чем отрезков, соединяющих соседние точки По условию деревьев —120 иип, отрезков между соседними деревьями -119. Длина зеленой изгороди 2*119=238 м.
Ответ: 238 м длина зеленой изгороди
Зайцы пилят бревно. Они сделали 10 распилов. Сколько получилось чурбачков? Ответ: 11 чурбачков.
Пример (6 класс).
Спидометр на велосипеде у Саши показывает 250, однако не уточняет единицу измерения. В чем измеряется скорость на спидометре Сашиного велосипеда?
Выберите подходящий момент и обоснуйте.
1) м/с 2) км/ч 3) м мин 4) км мин
Перевод 10 м/с в ... км/ч и наоборот Пример (7 класс-ВПР задания №5)
При закреплении темы "Обозначение десятичных дробей" ученикам предлагается таблица:
| 19,2 | 4,5 | 2,5 | 2,2 | 3,3 | 3,9 |
| 00,35 | 00,23 | 00,44 | 00,3 | 00,46 | 00,27 |
| 26,4 | 4,7 | 3,4 | 41,7 | 20,9 | 32,1 |
| 00,031 | 00,402 | 00,37 | 00,45 | 4,89 | 4,3 |
| 2,1 | 3,8 | 2,8 | 2,4 | 3,6 | 2,09 |
Даются задания:
Назови и покажи числа в возрастающем порядке.
Назови и покажи числа в убывающем порядке.
Увеличь на 0,1 числа первой строчки (назови последующее).
Уменьши на 0,1 числа второй строчки (назови предыдущее).
Покажи числа, в которых сумма цифр в разряде десятых и единиц равна
Найди числа, в которых 7 (5, 8, 9) сотых.
Найди числа, в которых 4 (2, 3) десятых
Найди числа, в которых количество единиц на 2 (на 3, на 4) больше количества десятых.
Найди числа, в которых количество единиц равно количеству десятых.
Найди числа, в которых количество единиц десятых меньше количества сотых и т.д.
Работу можно проводить в виде соревнования: "Кто быстрее?", "Какой ряд сделает меньше ошибок?"
Эту же таблицу можно использовать и на последующих уроках с заданиями:
Увеличь числа второй строчки на 3.
Прибавь 2 к числам третьей строчки.
Увеличь числа четвертой строчки на 1 десяток.
Вычти 1 из чисел пятой строчки.
Прибавь 0,2 к числам первого столбика.
Вычти 0,2 из чисел второго столбика
Сложи числа первой и второй строчки, запиши ответы.
Из чисел третьей строчки вычти числа пятой строчки.
Дополни числа четвертой строчки до ближайшего круглого числа.
В практике распространены таблицы с использованием математических терминов
| слагаемое | 2,3 | 4,4 | 8,1 | | 3,6 | 7,2 |
|
| |
| слагаемое | | 0,6 | | 7 | 4 | |
|
| 5,2 |
| сумма | 3 | | 9,7 | 7,5 | | 8,3 |
|
| 6 |
| уменьшаемое | 5,7 | 8,9 | | 7,6 | 2,9 | | 4,8 |
| вычитаемое | 4,2 | | 5 | 3 | | 7 | |
| разность | | 8,2 | 3,2 | | 2,4 | 6,1 | 4,3 |
Такие таблицы помогают детям лучше понимать математическую речь, лучше ориентироваться в терминах. Работа с такими таблицами готовит учеников к решению уравнений. Работа с таблицами нравится ученикам, поэтому она также нашла свое место на моих уроках математики.
При повторении изученного материала по теме «Признаки делимости», предлагаю таблицу
| 1,2 | 3,2 | 4,2 | 5,5 | 72 |
| 1,8 | 2,8 | 5,6 | 0,40 | 2,7 |
| 2,45 | 1,62 | 6,4 | 0,6 | 0,54 |
| 3,10 | 0,2 | 4,05 | 1,02 | 8,1 |
| 0,36 | 2,1 | 2,25 | 4 | 0,18 |
| 4,8 | 8,3 | 5,05 | 1,4 | 6,3 |
Предлагаются задания:
Выберите из таблицы числа, которые делятся на 2 (3,5 и т.д.)
Разделите числа из первого столбика на 5 (2, 3)
Уменьшите числа последнего столбика в 9 раз.
Найдите «лишнее» число во втором столбике.
Найдите числа, которые не использовали
А теперь перейду непосредственно к практико-ориентированным задачам.
Следующую задачу можно предложить поработать по материалам ОГЭ в разных классах. По изучению соответствующих тем составлять вопросы.
Пример (5-9 классы).
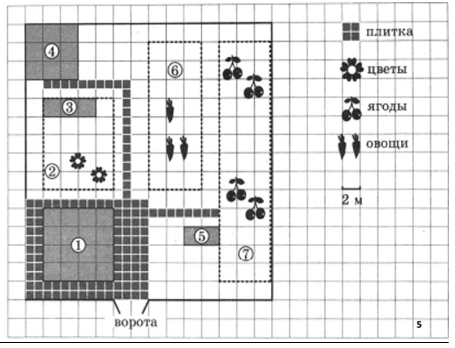
На плане изображен данный участок по адресу: СНГ Рассвет, ул. Морская, 7 (сторона каждой клетки на плане равна 2 м). Участок имеет прямоугольную форму. Въезд и выезд осуществляется через единственные ворота. Площадь, занятая жилым домом, равна 64 кв. м. Помимо жилого дома, на участке есть баня, к которой ведет дорожка, выложенная специальным садовым покрытием. Между жилым домом и баней находится цветник с теплицей. Теплица отмечена на плане цифрой 3.
Напротив жилого дома находится бак с водой для полива растений, за ним плодово-ягодные кустарники. В глубине участка есть огород для выращивания овощей, отмеченный цифрой б. Все дорожки внутри участка имеют ширину 1 ми застелены садовым покрытием, состоящим из плит размером 1м х 1м. Площадка вокруг дома выложена плитами такого же размера, но другой фактуры и цвета. К дачному участку проведено электричество. Имеется магистральное газоснабжение.
Вопросы для устной работы:
Какими цифрами на плане обозначены: жилой дом, цветник, бак с водой, баня. Назовите получившееся число.
Найдите площади этих объектов.
На сколько площадь занятая под ягоды, больше площади занятой под овощи?
 Рассмотрим приемы решения практико-ориентированных задач
Рассмотрим приемы решения практико-ориентированных задач
| Контекст | Математическое содержание | Виды деятельности |
|
|
| Личная жизнь | Количество | Формулировать Применять |
Ширина 40 см
На 10 см 18 петель
18 ∙ 4 = 72(петли)
Ответ. 72 петли.
III. Заключение.
Целенаправленное формирование умений решать задачи вообще, математические в частности, является, безусловно, одним из важнейших путей усовершенствования образования. А это, в свою очередь, связано с формированием навыков анализа условия задачи, поиска путей ее решения, осмысления результатов решения.
Формирование определенной системы математических знаний всегда было в центре внимания в математическом образовании. Объем этой системы является слишком большим с общеобразовательных позиций, а качество владения ими — недостаточно высоким. А главное, формирование этой системы знаний и умений не связана органически с формированием умений применять математику и стратегией решения задач.
Успешное выполнение контекстных заданий может быть обеспечено только при ориентации учебного процесса на решение подобных задач.
Чтобы повысить математическую грамотность учащихся, можно предложить учащимся самим составить задачи и уравнения, ребусы, кроссоворды, разноуровневые задания.
В связи с этим давайте все запомним одну математическую формулу, которая позволит сформировать у учащихся в процессе изучения математики и других дисциплин качества мышления, необходимые для полноценного функционирования человека в современном обществе.
«ОВЛАДЕНИЕ = УСВОЕНИЕ + ПРИМЕНЕНИЕ ЗНАНИЙ НА ПРАКТИКЕ»
Концепция обновления современной школы определила новые приоритеты общего образования, которые предполагают, что формирование модели учебного процесса должно осуществляться на основе развития взаимоотношений сотрудничества учителя и ученика, гармоничного сочетания различных методов обучения, обеспечивающих использование разнообразных видов учебной деятельности. Эти приоритеты составляют основу развития и современного школьного образования. В соответствии с ним уточнены учебно-воспитательные цели обучения на каждой ступени школы, принципы отбора структурирования содержания, а также методы оценки качества подготовки школьников.








 Рассмотрим приемы решения практико-ориентированных задач
Рассмотрим приемы решения практико-ориентированных задач









