Понятие о равных треугольниках и первичные представления о равных фигурах

Понятие о равных треугольниках и первичные представления о равных фигурах

Организационный момент. Девиз урока: “Никогда не беритесь за последующее, не усвоив предыдущее”.

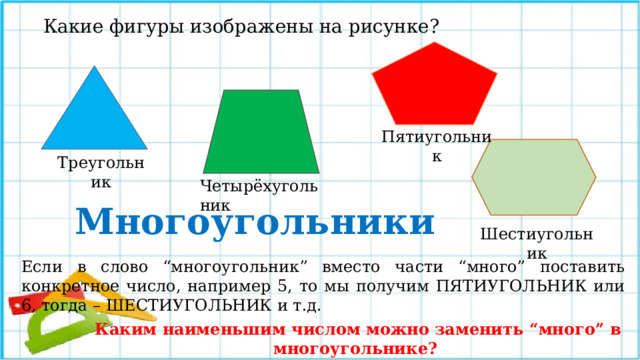
Какие фигуры изображены на рисунке?

Пятиугольник

Треугольник

Четырёхугольник

Многоугольники

Шестиугольник

Все данные фигуры можно назвать одним словом – МНОГОУГОЛЬНИКИ. Слово “многоугольник” указывает на то, что у всех фигур этого семейства “много углов”. Заметьте, сколько углов, столько и сторон.

Если в слово “многоугольник” вместо части “много” поставить конкретное число, например 5, то мы получим ПЯТИУГОЛЬНИК или 6, тогда – ШЕСТИУГОЛЬНИК и т.д.

Каким наименьшим числом можно заменить “много” в многоугольнике?

Что же такое треугольник?

Давайте составим определение треугольника. (Заслушиваются ответы учащихся и составляется определение)

Треугольник

Треугольник   – это геометрическая фигура, которая состоит из трех точек, не лежащих на одной прямой, и трех отрезков, попарно соединяющих эти точки.

В

С

Точки, с которых начиналось построение, называются  вершинами треугольника .

Отрезки, соединяющие вершины треугольника, называются  сторонами треугольника .

А, В, С  – вершины треугольника  АВС.

АВ, ВС, СА  – стороны треугольника  АВС.

∠ А,∠В,∠С –  углы треугольника АВС.

Обозначение: ∆АВС

А

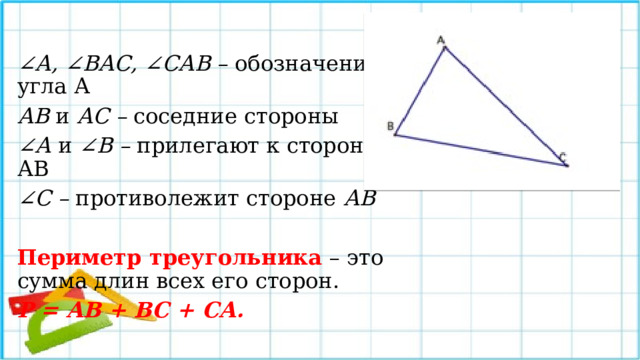
∠ А, ∠ВАС, ∠САВ – обозначение угла А

АВ и АС – соседние стороны

∠ А и ∠В – прилегают к стороне АВ

∠ С – противолежит стороне АВ

Периметр треугольника  – это сумма длин всех его сторон.

Р = АВ + ВС + СА.

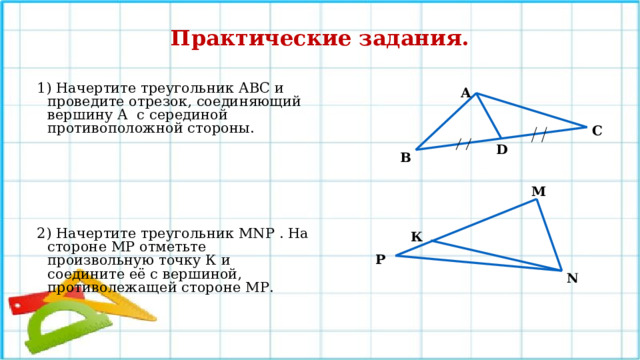
Практические задания.

1) Начертите треугольник АВС и проведите отрезок, соединяющий вершину А с серединой противоположной стороны.

2) Начертите треугольник MNР . На стороне МР отметьте произвольную точку К и соедините её с вершиной, противолежащей стороне МР.

А

С

D

В

М

К

Р

N

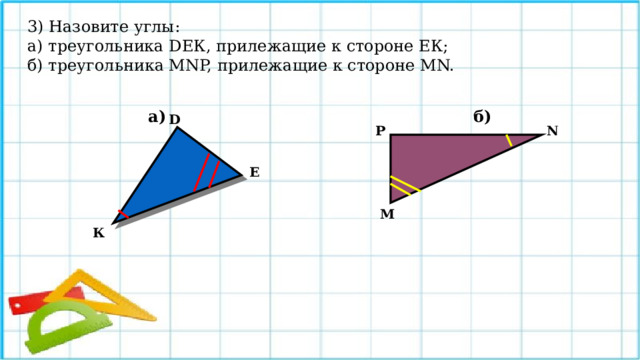
3) Назовите углы:

а) треугольника DЕК, прилежащие к стороне ЕК;

б) треугольника МNP, прилежащие к стороне MN.

а) б)

D

Р

N

Е

М

К

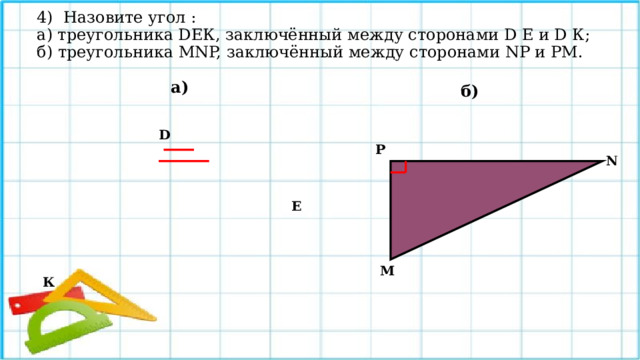
4) Назовите угол : а) треугольника DЕК, заключённый между сторонами D Е и D К; б) треугольника МNP, заключённый между сторонами NP и РМ.

а)

б)

D

Р

N

Е

М

К

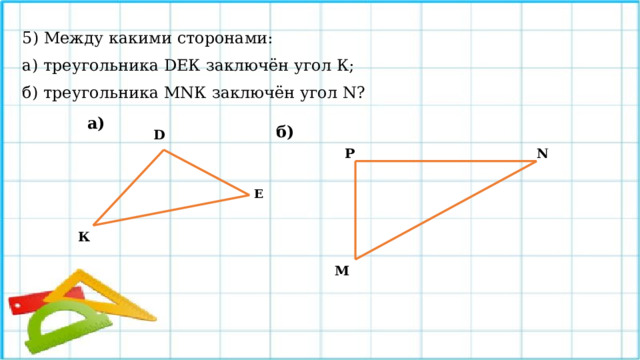
5) Между какими сторонами:

а) треугольника DЕК заключён угол К;

б) треугольника МNК заключён угол N?

а)

б)

D

Р

N

Е

К

М

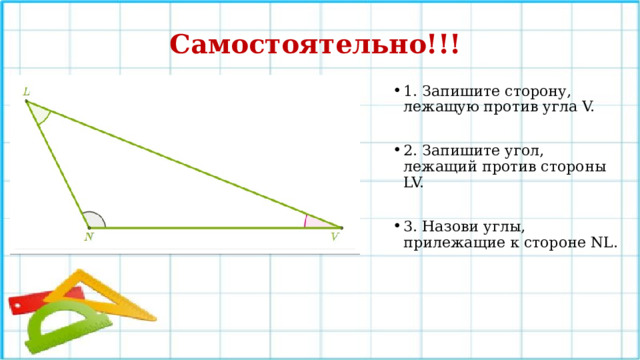
Самостоятельно!!!

• 1. Запишите сторону, лежащую против угла V.

• 2. Запишите угол, лежащий против стороны LV.

• 3. Назови углы, прилежащие к стороне NL.

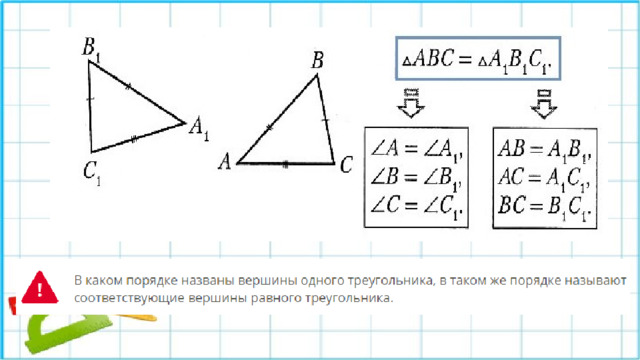
Равные треугольники

В

Два треугольника называют равными, если их можно совместить наложением.

А

Те стороны и те углы, которые совмещаются при наложении треугольников, называют

соответственными сторонами и соответственными углами.

С

На рисунках равные стороны отмечают одинаковым количеством чёрточек, а равные углы — одинаковым количеством дуг ( Заметим, что в равных треугольниках против соответственных углов лежат соответственные стороны, и наоборот: против соответственных сторон лежат соответственные углы).

18

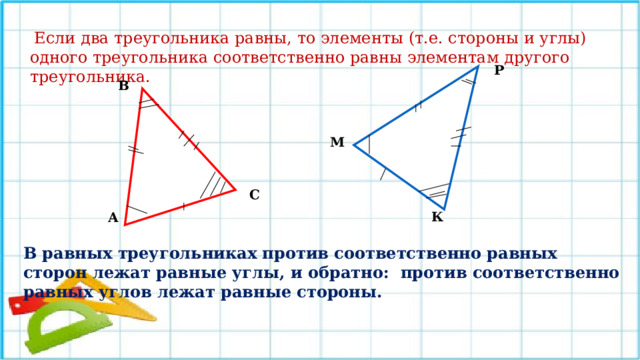
Если два треугольника равны, то элементы (т.е. стороны и углы) одного треугольника соответственно равны элементам другого треугольника.

Р

В

М

С

К

А

В равных треугольниках против соответственно равных сторон лежат равные углы, и обратно: против соответственно равных углов лежат равные стороны.

S

T

Q

F

R

V

D

O

L

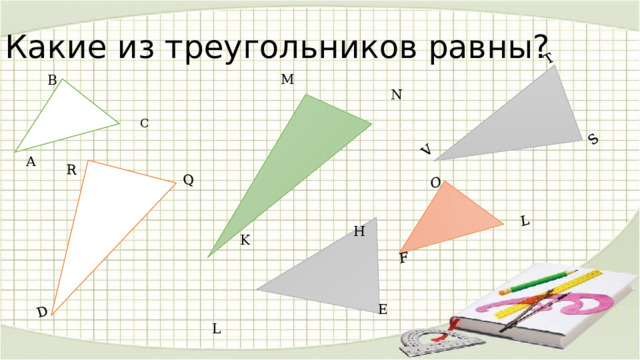
Какие из треугольников равны?

M

В

N

С

А

H

K

E

L

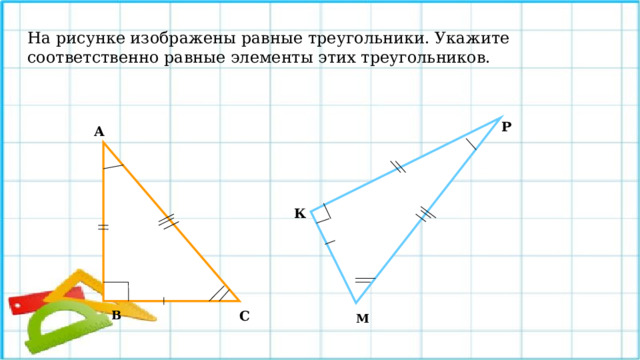
На рисунке изображены равные треугольники. Укажите соответственно равные элементы этих треугольников.

Р

А

К

С

В

М

Как хорошо ты усвоил урок?

Ответь на вопросы:

1. Как называют и обозначают треугольник?

по его вершинам

2. Что называют периметром треугольника?

сумму длин всех его сторон

4. Какие два треугольника называют равными?

которые можно совместить наложением

5. Сколько у каждого треугольника вершин, сторон и углов?

3

Домашнее задание:

§ 1, п.14. стр.28-29-читать, учить.

№ 87, 88

Успешного выполнения домашнего задания!

Успешного выполнения домашнего задания!