

Происхождение науки геометрии.
Для чего нужно было измерять площади?
Людям часто приходилось делить землю по берегам Нила на участки. Подсчитывать площадь трудно, берега извилисты, границы участка неровные. И люди постепенно научились измерять такие площади, разбивая их на прямоугольные и треугольные участки (1 7 век до н. э.)

Понятие площади
- В жизни часто приходится вычислять площади геометрических фигур.
- Например, приходится определять площадь поля, огорода, спортивной площадки или определять площадь пола в здании, площадь стен или окон в комнате.
- При всяком измерении необходимо заранее иметь меру, с которой сравнивается измеряемая величина. При взвешивании употребляются меры веса: килограмм, грамм, тонна, центнер. Время измеряется часами, минутами, секундами.
- При измерении длины отрезка МN сравниваем его с метром, сантиметром или с какой-нибудь другой мерой длины. При измерении углов пользуемся угловыми градусами, минутами.
- Точно так же при измерении площадей геометрических фигур пользуются особыми мерами, с которыми сравниваются эти фигуры.


ПЛОЩАДЬ – это…
некая величина, характеризующая геометрическую фигуру, расположенную на плоскости или на иной поверхности.
Обычно площадь обозначается буквой S .

Измерение площади фигуры
- выбрать единицу площади, т.е. указать единичный квадрат, т.е. квадрат, сторона которого служит единицей длины.
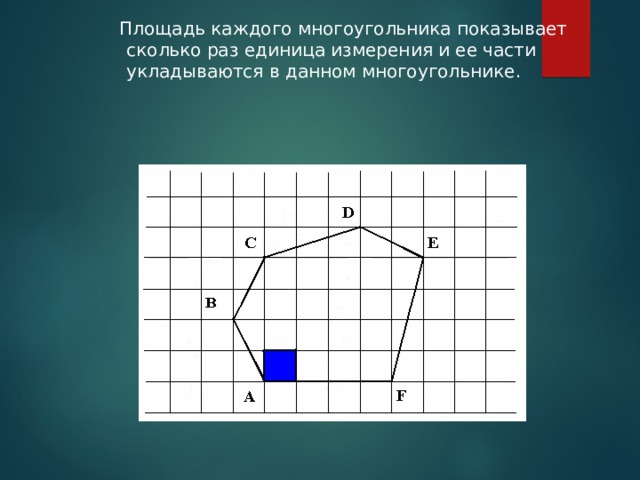
Площадь каждого многоугольника показывает сколько раз единица измерения и ее части укладываются в данном многоугольнике.

Единицы измерения площадей
1 мм 2
1 см 2
1 дм 2
1 м 2
1 км 2
1 а
1 га
100 мм 2
100 см 2 = 10000 мм 2
100 дм 2 = 10000 см 2
1000000 м 2
100 м 2
100 а = 10000 м 2

Старинные меры площадей на Руси
- В 11 – 13 веках употреблялась мера « плуг » - это мера земли , с
которой платили дань. Есть основание считать , что «плуг» -
8 – 9 гектаров.
- В 16 – 18 веках мерою полей служит « десятина »( равная 1,1 га)
и « четверть »( равная половине десятины- поле, на котором высевали
четверть хлеба). Десятина, которая в быту местами имела и другие
размеры, делилась на 2 « четверти », четверть, в свою очередь, на
2 « осьмины », осьмина – на 2 « полуосьмины » ит.д.
- Налоговой единицей земли была « соха », в Новгороде « обжа », которая имела различные размеры, в зависимости от качества земли социального положения владельца.
- Позже землю измеряли « акрами » (4047 м 2 )

Свойства площадей
М
Равные фигуры
имеют равные площади .
F
Если F = М, то S F = S M
F

Определение :
- Многоугольники, имеющие равные площади, называются равновеликими .

Свойства площадей
С
K
М
В
Е
А
Если фигура составлена из нескольких фигур,
то её площадь равна сумме площадей этих фигур .
S ACME = S ABE + S BCKE + S EKM

Свойства площадей
B
C
Площадь квадрата равна
квадрату его стороны .
S ABCD = a 2
A
D
a

Решить задачу по готовым чертежам:
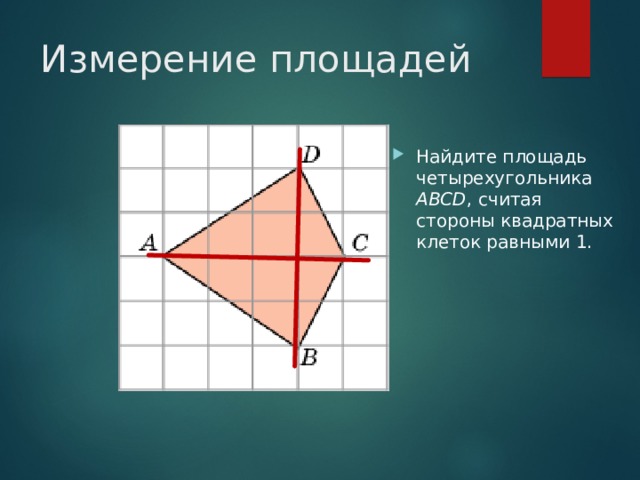
Измерение площадей
- Найдите площадь четырехугольника ABCD , считая стороны квадратных клеток равными 1.
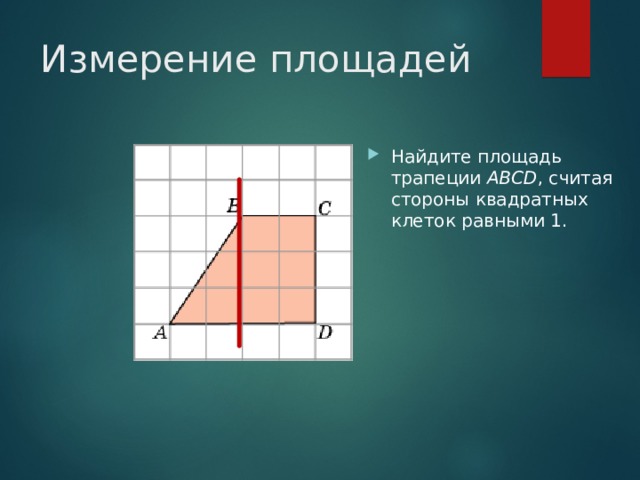
Измерение площадей
- Найдите площадь трапеции ABCD , считая стороны квадратных клеток равными 1.

Измерение площадей (формула Пика)
S – площадь многоугольника;
Г – количество узлов сетки, лежащих на границах многоугольника,
В – количество узлов сетки, лежащих внутри многоугольника
Г=8, В=7,
S=7+4 -1 = 10
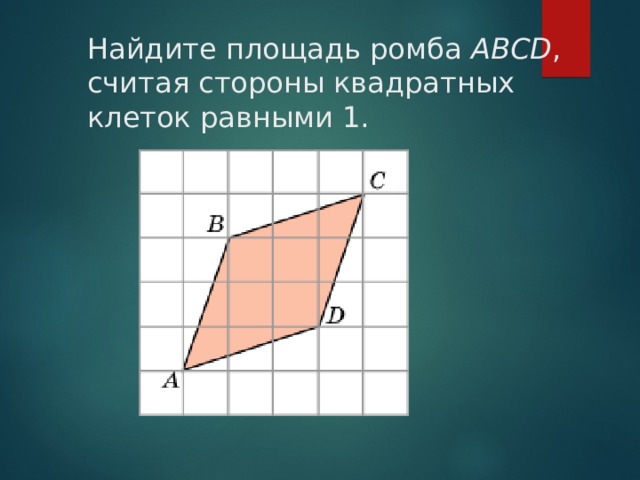
Найдите площадь ромба ABCD , считая стороны квадратных клеток равными 1.

Начертить квадрат, принять его за единицу измерения площадей .
а) квадрат, площадь которого выражена числом 4;
б) прямоугольник, площадь которого выражена числом 4;
в) треугольник, площадь которого выражена числом 2.
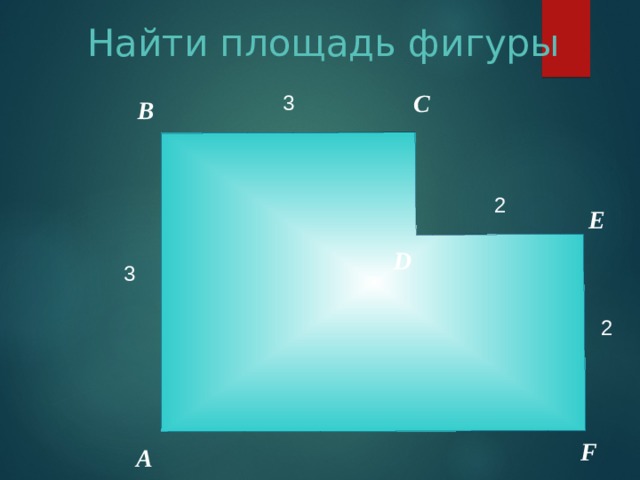
Найти площадь фигуры
С
3
В
2
Е
D
3
2
F
А

Палетка.
В тех случаях, когда измерение площади какой-нибудь фигуры не требует большой точности, а также, когда фигура, площадь которой требуется измерить, ограничена криволинейным контуром , для измерения площади употребляется особый прибор, называемый палеткой.
Палетка представляет собой прозрачную пластинку, на которую наносится масштабная квадратная сетка, например, со стороной квадрата, равной 1 см.
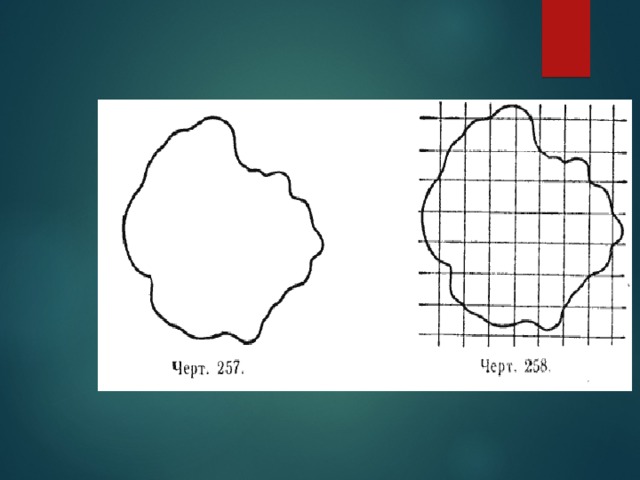

Эта пластинка накладывается на фигуру, площадь которой требуется измерить
Сначала подсчитывается число квадратов, полностью укладывающихся в данной фигуре; на чертеже их 26. Затем подсчитывается число квадратов, пересекаемых контуром фигуры; на чертеже их 21.
Каждый из неполных квадратов принимается за половину квадрата, таким образом, их общая площадь приближённо составит 21 : 2 = 10,5 квадрата.
Общее число квадратов, заключающихся в измеряемой фигуре, таким образом, составит 26 + 10,5 = 36,5 квадрата. Если, например, каждый квадрат в действительности соответствует 1 кв. м, то измеряемая площадь составит 36,5 кв. м.

« Математику уже затем учить следует, что она ум в порядок приводит»
М. В. Ломоносов









































