Понятие правильного многогранника

Понятие правильного многогранника

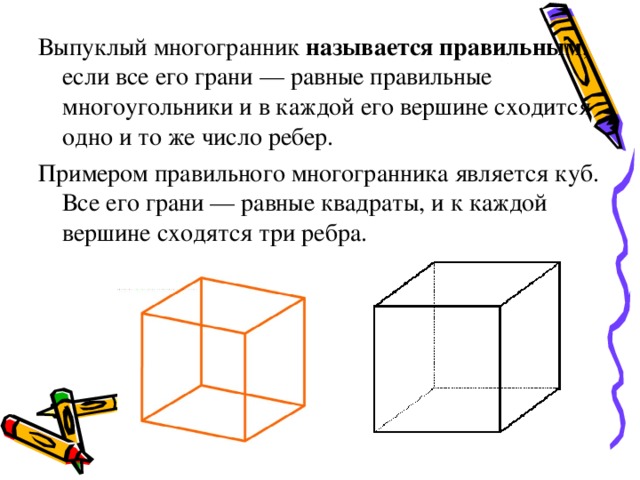
Выпуклый многогранник называется правильным , если все его грани — равные правильные многоугольники и в каждой его вершине сходится одно и то же число ребер.

Примером правильного многогранника является куб. Все его грани — равные квадраты, и к каждой вершине сходятся три ребра.

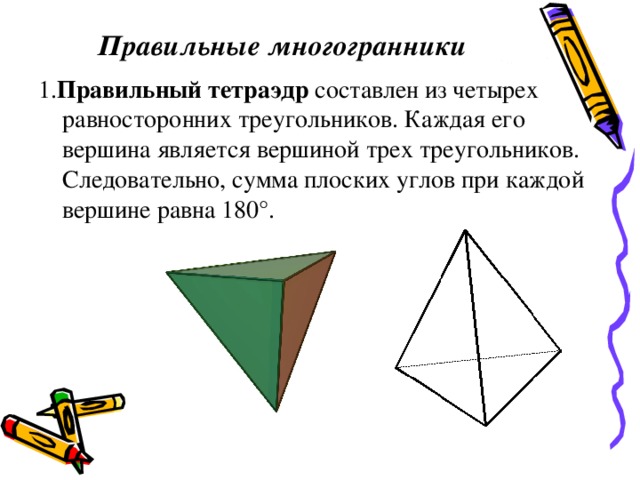
Правильные многогранники

1. Правильный тетраэдр составлен из четырех равносторонних треугольников. Каждая его вершина является вершиной трех треугольников. Следовательно, сумма плоских углов при каждой вершине равна 180°.

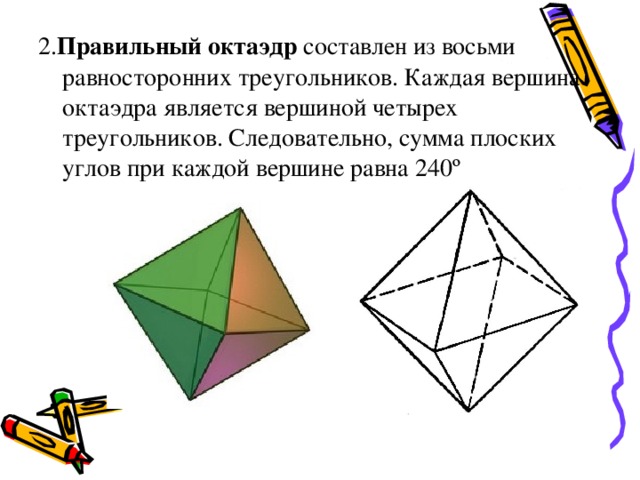
2. Правильный октаэдр составлен из восьми равносторонних треугольников. Каждая вершина октаэдра является вершиной четырех треугольников. Следовательно, сумма плоских углов при каждой вершине равна 240º

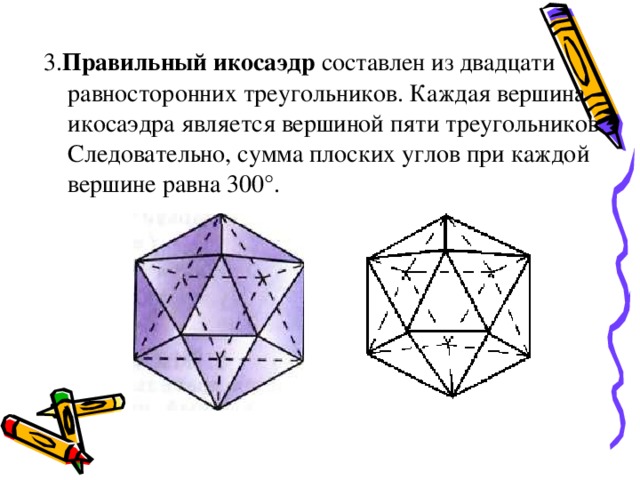
3. Правильный икосаэдр составлен из двадцати равносторонних треугольников. Каждая вершина икосаэдра является вершиной пяти треугольников. Следовательно, сумма плоских углов при каждой вершине равна 300°.

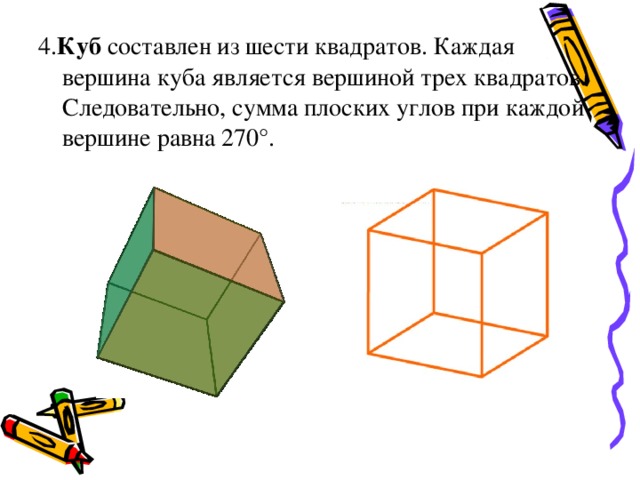
4. Куб составлен из шести квадратов. Каждая вершина куба является вершиной трех квадратов. Следовательно, сумма плоских углов при каждой вершине равна 270°.

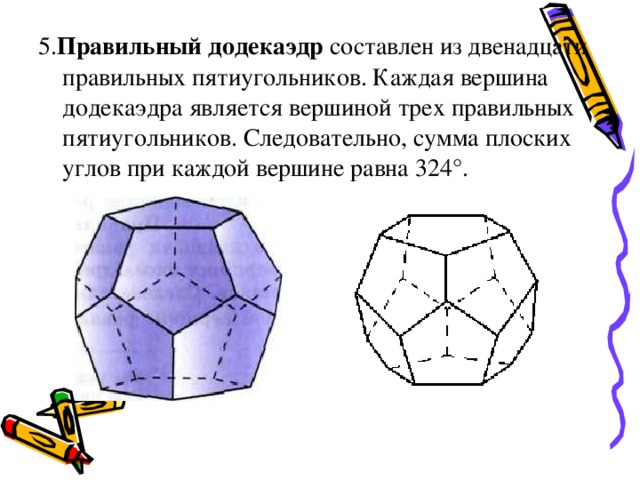
5. Правильный додекаэдр составлен из двенадцати правильных пятиугольников. Каждая вершина додекаэдра является вершиной трех правильных пятиугольников. Следовательно, сумма плоских углов при каждой вершине равна 324°.

Элементы симметрии правильных многогранников

Правильный тетраэдр не имеет центра симметрии . Прямая, проходящая через середины двух противоположных ребер, является его осью симметрии. Плоскость , проходящая через ребро АВ перпендикулярно к противоположному ребру CD правильного тетраэдра ABCD , является плоскостью симметрии. Правильный тетраэдр имеет три оси симметрии и шесть плоскостей симметрии .

Куб имеет один центр симметрии — точку пересечения его диагоналей .

Прямые а и b , проходящие соответственно через центры противоположных граней и середины двух противоположных ребер, не принадлежащих одной грани, являются его осями симметрии.

Куб имеет девять осей симметрии .

Все оси симметрии проходят через центр симметрии. Плоскостью симметрии куба является плоскость, проходящая через любые две оси симметрии.

Куб имеет девять плоскостей симметрии.

Правильный октаэдр, правильный икосаэдр и правильный додекаэдр имеют центр симметрии и несколько осей и плоскостей симметрии.

Задания

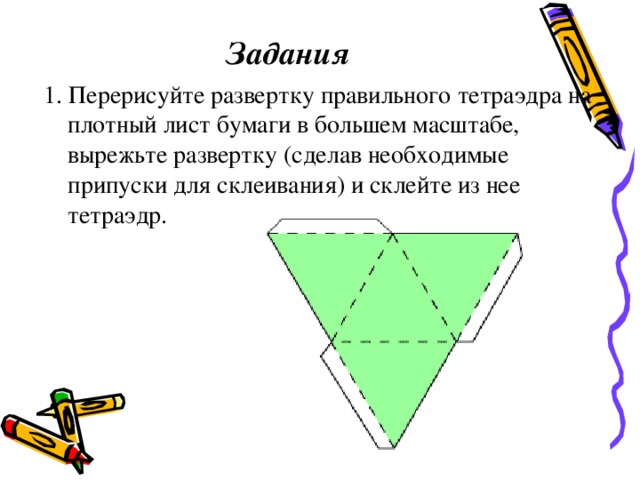
1. Перерисуйте развертку правильного тетраэдра на плотный лист бумаги в большем масштабе, вырежьте развертку (сделав необходимые припуски для склеивания) и склейте из нее тетраэдр.

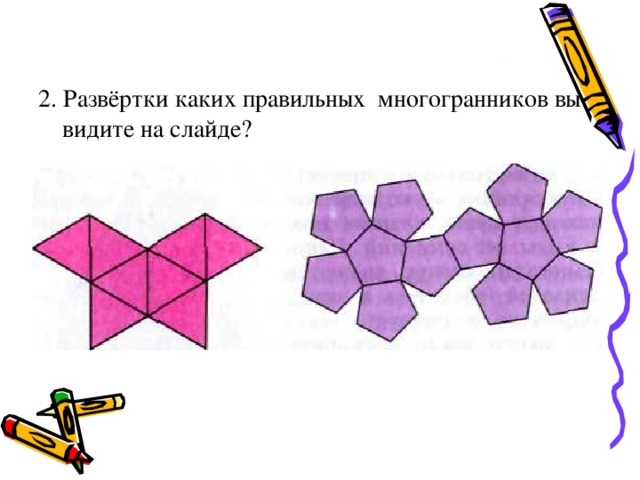
2. Развёртки каких правильных многогранников вы видите на слайде?

Домашнее задание

Перерисуйте развертку куба на плотный лист бумаги в большем масштабе, вырежьте развертку и склейте из нее куб.