Дата 06.03.2025
Класс 9 класс
Предмет Алгебра
Тема Последовательности
Номер урока 71
Тип урока: урок изучения новой темы
Цель урока: познакомить учащихся с понятием последовательности, способами задания последовательности. Выработать умения использовать индексные обозначения и находить n-й член последовательности по заданной формуле.
Задачи урока:
Личностные результаты:
формирование умения сотрудничать со сверстниками в разных социальных ситуациях, умение не создавать конфликтов и находить выходы из спорных ситуаций.
Метапредметные результаты:
регулятивные: планировать свои действия в соответствии с поставленной задачей и условиями ее реализации;
познавательные: формирование умений по использованию математических знаний для решения различных математических задач и оценки полученных результатов, по использованию доказательной математической речи при работе с информацией;
коммуникативные: формирование умений совместно с другими обучающимися находить решение задачи и оценивать полученные результаты.
Предметные результаты:
понимание сути понятий «числовая последовательность», «члены последовательности», «n-й член последовательности», умение определять n-й член последовательности, понимать и различать виды последовательностей и способы их задания, умение точно и грамотно выражать свои мысли, применяя математическую терминологию, развитие способностей обосновывать рассуждения.
Образовательные: формирование представления о последовательности, знаний о способах задания числовых последовательностей, умений находить члены последовательности по предложенной формуле, а также умений находить саму формулу, задающую последовательность.
Развивающие: развитие умений сравнивать и анализировать, обобщать информацию, делать выводы.
Воспитательные: воспитывать навыки самоконтроля, культуру общения, умение работать в коллективе; воспитывать такие качества характера, как настойчивость в достижении цели, умение не растеряться в проблемной ситуации.
Ход урока:
Организационный момент.
1.Актуализация знаний (слайд 1)
Устная работа
Найдите значение выражения 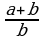 при а= - 2,5 и b=3.
при а= - 2,5 и b=3.
Найдите значение выражения 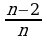 при =1; 3;10. При каких n имеет смысл это выражение?
при =1; 3;10. При каких n имеет смысл это выражение?
Напишите формулу четных чисел; кратных 5; кратных 2 и 5.
Определение темы и цели урока
- Выполним задание и определим закономерности (Слайд 2 )
1,4,7,10,13...
2,6,18,54, 162...
10,19,37,73,145...
1,2,3,4,5,6,7,8.9
33, 31, 32, ...
4, -4, 4,- 4,...
- Да, это числа, записанные в определенном порядке.
Вопрос. Можно ли поставить другое число вместо числа 16 в случае 1? вместо числа 4 в случае 2?
Вопрос. Как вы понимаете слово «закономерность»?
Как стоят эти числа в рядах? (последовательно) Значит, они называются последовательностями. И так, тема нашего урока? (Последовательности) Запишем тему (слайд 4). Какую цель вы поставите себе на данном уроке? (изучить свойства числовых последовательностей и научиться применять их в ходе выполнения упражнений)
- В жизни какие события происходят последовательно? (Дни недели, названия месяцев, нумерация домов, и т.д.) (Слайд 5)
III. Изучение нового материала.
1.Слово учителя.
Числа, записанные в определённом порядке- числовая последовательность (слайд6)
(слайд 7 )
Числа образующие последовательность , называются членами последовательности и нумеруются.
а1; а₂; а₃; а₄;…аn; ... («а первое», «а второе», «а n-ое», …)
Последовательность а₁; а₂; а₃; а₄;…аn; ... обозначают обычно (аn)
- В последовательности 1;4; 7;10;13;… укажите а₁; а₃; а5. (слайд 8)
- Переходим к следующему этапу исследования нужно изучить свойства последовательностей.
Последовательности бывают конечные и бесконечные, возрастающие и убывающие (слайд 9 )
Для того чтобы узнать любой член последовательности, необходимо знать, как задаются последовательности.
- Какими способами можно задать последовательности?
- Последовательности можно задать различными способами.
А) Описательный
Например, на четных местах 0, на нечетных – единица.
Б) Формулой n – ого члена последовательности
аn =2 n, n – натуральное число. При n=1, а₁=2·1=2, при n=2, а₁=2·2=4, и т.д.
В) Название следующего способа задания последовательности – рекурретный – произошло от слова «recurro» - возвращаться. Рекуррентной называется формула, выражающая любой член последовательности, начиная с некоторого, через предыдущие.
Для некоторых последовательностей рассмотренных в начале урока, запишем рекуррентные формулы:
1,4,7,10,13... а₁=1, аn+1= аn+3
2,6,18,54, 162... а₁=2, аn+1= аn ·3
10,19,37,73,145... а₁=10, аn+1= аn ·2 – 1
Физкультминутка
Закрепление нового материала.
-Давайте, теперь определим как наши открытия помогут выполнить задания №560, №564, №565 (а) №569 (а), 567. В оценочных листах оцените себя, если есть затруднения, то пишите вопросы. (После каждого задания ответы проверяются по слайдам (19-22)
1) №560 (работа в парах)
Выпишите первые несколько членов последовательности натуральных чисел, кратных 3, взятых в порядке возрастания. Укажите ее первый, пятый, десятый, сотый и n-й члены.
Решение: 3; 6; 9; 12; … а1 = 3, а5 = 15, а10 = 30, а100 = 300, аn = 3n
2) №564 взаимопроверка
Перечислите члены последовательности (хn), которые расположены между: а) х31 и х35, г ) хn-2 и xn+2.
Решение: а) х32, х33, х34; б) xn-1, xn, xn+1.
3) №565 (а) (индивидуальная)
Найдите первые шесть членов последовательности, заданной формулой n- го члена: хn = 2n – 1.
Решение: х1 = 1, х2 = 3, х3 = 5, х4 = 7, х5 = 9, х6 = 11.
4) №569 (а)
Выпишите первые пять членов последовательности (аn), если а1 = 1, аn+1 = аn+1.
Решение: 1, 2, 3, 4, 5.
№567 (для сильных учащихся)
Последовательность аn задана формулой аn=n2-n-20. Определите номера отрицательных членов и вычислите их.
Решение: а1=-20, а2=-18, а3=-18, а4=-8
IV. Рефлексия
- Что узнали нового? (последовательности)
- Как можно задать числовые последовательности? (словесно, формулой n- го члена, рекуррентным способом)
- Какие бывают последовательности? (конечные, бесконечные, возрастающие, убывающие)
- Где может пригодиться умение работать с последовательностями? (при дальнейшем изучении математики, при сдаче ОГЭ и в жизни)
- Какие трудности у вас возникли при решении задач?
- Проанализируйте свою работу на уроке.
Домашнее задание(Слайд). п. 24, № 562, 565 (в, д), 573(а). Для желающих
Решите задачу: В январе вам подарили пару новорожденных кроликов. Через два месяца у них рождается новая пара кроликов, в следующем месяце – еще одна пара и т.д. ежемесячно. С каждой новой парой кроликов происходит то же самое. Сколько пар кроликов будет у вас в декабре, если ни одна пара не погибнет?
Резерв.
Тестовая проверочная работа
1.Последовательность задана формулой an=5n+2 . Чему равен её третий член?
а) 3 б)17
в) 12 г) 22
2 . Выпишите 5 первых членов последовательности, заданной формулой an=n-3
а) -3,-2,-1,0,1 б) -2,-1,0,1,2
в) 0,-2,-4,-16,-50 г) 1,2,3,4,5
3. Найдите сумму 6-ти первых членов числовой последовательности: 2,4,6,8,
а) 66 б) 36
в) 32 г) 42
4. Какие из перечисленных последовательностей являются бесконечно убывающими:
а) 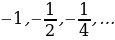 б) 2,4,6,8,…
б) 2,4,6,8,…
в) 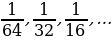 г)
г) 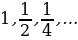
- Сегодня мы познакомимся со знаменитой последовательностью:
1, 1, 2, 3, 5, 8, 13, 21, …, Каждое число, начиная с третьего, равно сумме двух предшествующих. Этому ряду натуральных чисел, имеющему своё историческое название – ряд Фибоначчи, присуща своя логика и красота. Леонардо Фибоначчи (1180-1240). Крупный итальянский математик, автор «Книги абака». Эта книга несколько веков оставалась основным хранилищем сведений по арифметике и алгебре. Именно по трудам Л. Фибоначчи вся Европа осваивала арабские цифры, систему счета, а также практическую геометрию. Они оставались настольными учебниками, чуть ли не до эпохи Декарта (а это уже 17 век!).
Посмотрите фильм о том, как встречаются числа Фибоначчи в явлениях природы.
Приложение 1

Оценочный лист
ФИО ____________________________________________
| Задания | Балл | Вопросы |
| №560 |
|
|
| №564 |
|
|
| №565 (а) |
|
|
| №569 (а) |
|
|
| №567 |
|
|
| ТЕСТ |
|
|
5 б. – все понял и могу объяснить другому;
4 б. – сам понял, но объяснить не берусь;
3 б. – для полного понимания надо повторить;
2 б. – я ничего не понял.
Тестовая проверочная работа
1.Последовательность задана формулой an=5n+2 . Чему равен её третий член?
а) 3 б)17
в) 12 г) 22
2 . Выпишите 5 первых членов последовательности, заданной формулой an=n-3
а) -3,-2,-1,0,1 б) -2,-1,0,1,2
в) 0,-2,-4,-16,-50 г) 1,2,3,4,5
3. Найдите сумму 6-ти первых членов числовой последовательности: 2,4,6,8,
а) 66 б) 36
в) 32 г) 42
4. Какие из перечисленных последовательностей являются бесконечно убывающими:
а) 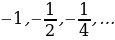 б) 2,4,6,8,…
б) 2,4,6,8,…
в) 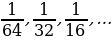 г)
г) 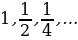
Тестовая проверочная работа
1.Последовательность задана формулой an=5n+2 . Чему равен её третий член?
а) 3 б)17
в) 12 г) 22
2 . Выпишите 5 первых членов последовательности, заданной формулой an=n-3
а) -3,-2,-1,0,1 б) -2,-1,0,1,2
в) 0,-2,-4,-16,-50 г) 1,2,3,4,5
3. Найдите сумму 6-ти первых членов числовой последовательности: 2,4,6,8,
а) 66 б) 36
в) 32 г) 42
4. Какие из перечисленных последовательностей являются бесконечно убывающими:
а) 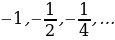 б) 2,4,6,8,…
б) 2,4,6,8,…
в) 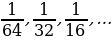 г)
г) 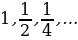






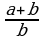 при а= - 2,5 и b=3.
при а= - 2,5 и b=3.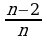 при =1; 3;10. При каких n имеет смысл это выражение?
при =1; 3;10. При каких n имеет смысл это выражение?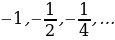 б) 2,4,6,8,…
б) 2,4,6,8,…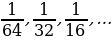 г)
г)