ГОСУДАРСТВЕННОЕ АВТОНОМНОЕ ПРОФЕССИОНАЛЬНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ НОВОСИБИРСКОЙ ОБЛАСТИ «КУПИНСКИЙ МЕДИЦИНСКИЙ ТЕХНИКУМ»
МЕТОДИЧЕСКОЕ ПОСОБИЕ
Для самостоятельной работы студентов
По учебному предмету: МАТЕМАТИКА
Тема: «Решение показательныхх уравнений»
Специальность: 34.02.01 Сестринское дело Курс: 1
(базовой подготовки)
Купино
2021
Рассмотрено на заседании предметной цикловой
Методической комиссии по общеобразовательным предметов,
общему гуманитарному и социально-экономическому, математическому и
естественно-научному циклу
Протокол № _____ от «_____» _________20____г.
Автор – составитель: преподаватель математики высшей категории Тюменцева О.Н.
Купино
2021 г
Пояснительная записка к методическому пособию
Методическое пособие предназначено для повторения теоретических и практических знаний по теме.
Цель пособия – повторить понятия показательной функции и ее свойств, показательного уравнения, методов решения показательных уравнений и подготовиться к занятию по теме «Решение рациональных, показательных, логарифмических уравнений».
Данное пособие рекомендовано для студентов первого курса специальности 34.02.01 Сестринское дело. Пособие содержит определения и формулы по теме: Показательные уравнения, тест для самоконтроля и критерии оценки теста.
Пособие направлено на формирование навыков самостоятельной работы с учебным материалом, формирование навыков решения задач, формирование и развитие творческого потенциала, повышение интереса к предмету.
Решение показательных уравнений
Показательным называется уравнение, содержащее переменную только в показателе степени. Рассмотрим несколько типов показательных уравнений, решаемых методами элементарной математики. Показательные уравнения рассматриваются в множестве действительных чисел. Уравнение вида �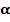 �х = b называется простейшим показательным.
�х = b называется простейшим показательным.
Решение простейших показательных уравнений.
Решение показательных уравнений основано на свойстве степеней: две степени с одним и тем же положительным и отличным от единицы основанием равны тогда и только тогда, когда равны их показатели. Используя это свойство, уравнение �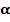 �х = b, где �
�х = b, где �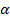 � ˃ 0 , �
� ˃ 0 , �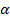 � �
� �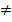 � 1 и b �
� 1 и b � � 0, следует решать следующим образом:
� 0, следует решать следующим образом:
�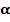 �х = b �
�х = b �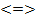 � �
� �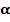 �х = �
�х = �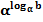 � �
� � � x = �
� x = � � .
� .
Пример 1. Решить уравнение �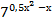 � = �
� = �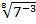 �.
�.
Решение. Поскольку �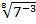 � = �
� = � �; 0,5х2 – х = – �
�; 0,5х2 – х = – � �; 4х2 – 8х +3 = 0.
�; 4х2 – 8х +3 = 0.
D = 16 – 12 = 4; х1,2 = � � ; х1 = 0,5, х2 = 1,5. Ответ: 0,5; 1,5.
� ; х1 = 0,5, х2 = 1,5. Ответ: 0,5; 1,5.
Пример 2. Решить уравнение �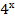 � = �
� = �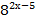 �.
�.
Решение. Поскольку �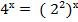 � = �
� = �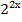 �, �
�, �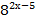 �= �
�= �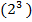 �2х-5 = �
�2х-5 = �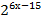 �,
�,
� � �
� �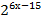 � �
� �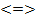 � 2х = 6х – 15 �
� 2х = 6х – 15 �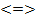 � х = �
� х = � �. Ответ: �
�. Ответ: � �
�
Пример 4. Найти корни уравнения � � = �
� = � �.
�.
Решение. Используя определение логарифма, запишем � � = �
� = � � = �
� = � �
�
Тогда данное уравнение примет вид � � = �
� = � �. Следовательно, можно записать
�. Следовательно, можно записать
� � = х �
� = х �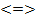 � х2 = �
� х2 = � �, а так как �
�, а так как � � 0 , то х = �
� 0 , то х = � �. Ответ. �
�. Ответ. � �
�
Решение показательных уравнений введением новой переменной.
Пример 1. Решить уравнение � � – �
� – � � + 12 = 12.
� + 12 = 12.
Решение. Поскольку � � = �
� = � �, �
�, � � = 8·�
� = 8·� �, введем новую переменную р = �
�, введем новую переменную р = � �.
�.
Получим уравнение � � – 8р + 12 = 0, из которого находим р1 = 2, р2 = 6. Поэтому исходное уравнение равносильно совокупности простейших показательных уравнений �
� – 8р + 12 = 0, из которого находим р1 = 2, р2 = 6. Поэтому исходное уравнение равносильно совокупности простейших показательных уравнений � � = 2, �
� = 2, � � = 6. Корнем первого уравнения является х = �
� = 6. Корнем первого уравнения является х = � �, а второго – х = �
�, а второго – х = � �.
�.
Ответ: � �; �
�; � �.
�.
Пример 2. Решить уравнение (� � + �
� + � � = 14.
� = 14.
Решение. Используя равенство � � = �
� = � � , введем новую переменную
� , введем новую переменную
р = � �. В этом случае получим уравнение р + �
�. В этом случае получим уравнение р + � � = 14, решая которое, находим его корни, �
� = 14, решая которое, находим его корни, � � -14р + 1 = 0, р = 7 �
� -14р + 1 = 0, р = 7 � � �
� � � = 7 �
� = 7 � � �
� � � .
� .
Исходное уравнение равносильно совокупности уравнений
(� � = 7 �
� = 7 � � �
� � �; (�
�; (� � = 7 �
� = 7 � � �
� � �.
�.
Корень первого уравнения х = 2, второго – х = -2. Ответ: -2; 2.
Пример 3. Решить уравнение � � – 13·�
� – 13·� � – �
� – � � = 0.
� = 0.
Решение. Запишем уравнение в виде � � 13·�
� 13·� � – �
� – � � �
� � � = 0.
� = 0.
Оно является однородным третьей степени относительно степеней � �.
�.
Разделим все члены уравнения на � � �
� �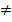 � 0 и получим �
� 0 и получим � � 13·�
� 13·� �– �
�– � �+ 13= 0.
�+ 13= 0.
Введем новую переменную р = � �, уравнение примет вид кубического уравнения
�, уравнение примет вид кубического уравнения
� � – 13�
� – 13� � – р +13 = 0. Разложим методом группировки левую часть уравнения на множители и найдем его корни:�
� – р +13 = 0. Разложим методом группировки левую часть уравнения на множители и найдем его корни:� � – р – 13�
� – р – 13� � – 1) = 0, р(р2 -1) – 13(р2 – 1) = 0, (р2 -1)(р – 13) = 0, р1 = -1, р2 = 1, р3 = 13. Исходное уравнение равносильно совокупности трех простейших показательных уравнений �
� – 1) = 0, р(р2 -1) – 13(р2 – 1) = 0, (р2 -1)(р – 13) = 0, р1 = -1, р2 = 1, р3 = 13. Исходное уравнение равносильно совокупности трех простейших показательных уравнений � � = –1, �
� = –1, � � = 1, �
� = 1, � � = 13. Первое уравнение корней не имеет, корень второго – х = 0, третьего уравнения х = �
� = 13. Первое уравнение корней не имеет, корень второго – х = 0, третьего уравнения х = � �
�
Ответ: 0, � �
�
Аналогично уравнениям, которые были рассмотрены в примерах 1, 2, 3, введением новой переменной р = � �х решение уравнения вида f(�
�х решение уравнения вида f(� �х) = 0 сводится к нахождению всех положительных корней рk уравнения f(р) = 0 и решению простейших показательных уравнений �
�х) = 0 сводится к нахождению всех положительных корней рk уравнения f(р) = 0 и решению простейших показательных уравнений � �х = рk.
�х = рk.
Пример 4. Решить уравнение � � – 5 · �
� – 5 · � � + 1 = 0.
� + 1 = 0.
Решение. Так как � �= �
�= � � = 4·�
� = 4·� � то уравнение можно записать так: 4·�
� то уравнение можно записать так: 4·� � – 5 ·�
� – 5 ·� � + 1 = 0. Введем новую переменную р = �
� + 1 = 0. Введем новую переменную р = � �. Получим квадратное уравнение 4р2 – 5р +1 = 0, которое имеет корни р1 = 1, р2 = �
�. Получим квадратное уравнение 4р2 – 5р +1 = 0, которое имеет корни р1 = 1, р2 = � �. Исходное уравнение равносильно совокупности двух показательных уравнений �
�. Исходное уравнение равносильно совокупности двух показательных уравнений � � = 1, �
� = 1, � � = �
� = � �. Решая первое уравнение, получаем 2х – х2 = 0, х = 0, х = 2. Решая второе уравнение, находим ещё два корня: 2х – х2 = – 2, х = �
�. Решая первое уравнение, получаем 2х – х2 = 0, х = 0, х = 2. Решая второе уравнение, находим ещё два корня: 2х – х2 = – 2, х = � �. Ответ: �
�. Ответ: � �; 0; 2; �
�; 0; 2; � �.
�.
Пример 6. Решить уравнение � � + �
� + � � = 3.
� = 3.
Решение. Так как 2� � = 1 + �
� = 1 + � �, то данное уравнение перепишем в следующем виде �
�, то данное уравнение перепишем в следующем виде � � + �
� + � � = 3. Сделаем замену у = �
� = 3. Сделаем замену у = � �, тогда получим квадратное уравнение у2 + 2у -3 = 0, из которого найдем корни у1 = –3, у2 = 1. Значение у1 = –3, очевидно, постороннее. Поэтому исходное уравнение равносильно уравнению �
�, тогда получим квадратное уравнение у2 + 2у -3 = 0, из которого найдем корни у1 = –3, у2 = 1. Значение у1 = –3, очевидно, постороннее. Поэтому исходное уравнение равносильно уравнению � � = 1, откуда �
� = 1, откуда � � = 0, х = �
� = 0, х = � � + �
� + � � , n�
� , n� �. Ответ: �
�. Ответ: � � + �
� + � � , n�
� , n� �.
�.
Метод вынесения общего множителя за скобки.
Пример 1. Решить уравнение � � + 4 · �
� + 4 · � � + 2 · �
� + 2 · � � = 19 · �
� = 19 · � � – 4 · �
� – 4 · � �.
�.
Решение. Преобразуем данное уравнение, перенеся члены с одинаковыми основаниями в одну и ту же уравнения и вынося за скобки степень с наименьшим показателем, к виду:
� � + 4 · �
� + 4 · � � + 4 · �
� + 4 · � �= 19 · �
�= 19 · � � – 2 · �
� – 2 · � � �
� � � �
� � �(9 + 4 · 3 + 4) = �
�(9 + 4 · 3 + 4) = � �19 – 2 · 5) �
�19 – 2 · 5) � � �
� � � �
� � � 25 = �
� 25 = � � 9. Запишем последнее равенство в виде пропорции и получим:
� 9. Запишем последнее равенство в виде пропорции и получим:
� � = �
� = � � �
� �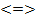 � �
� � �= �
�= � �. Это уравнение равносильно уравнению х – 2 = 2, откуда х = 4. Ответ: 4.
�. Это уравнение равносильно уравнению х – 2 = 2, откуда х = 4. Ответ: 4.
Пример 2. Решить уравнение �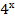 � – �
� – � � = �
� = � � – �
� – � �.
�.
Решение. Сгруппируем члены, содержащие степени с одинаковыми основаниями с разных сторон равенства: �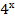 � + �
� + � � �
� � � = �
� = � � + �
� + � � . Выносим общие множители за скобки:
� . Выносим общие множители за скобки:
�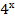 �(1 + �
�(1 + � �) = �
�) = � �(1 + 3). Разделим это уравнение на выражение, стоящее в правой части, получим �
�(1 + 3). Разделим это уравнение на выражение, стоящее в правой части, получим � � = 1. Таким образом, находим �
� = 1. Таким образом, находим � � = 0; следовательно, �
� = 0; следовательно, � � – единственный корень исходного уравнения. Ответ: �
� – единственный корень исходного уравнения. Ответ: � �.
�.
Метод использования монотонности показательной функции.
Пример 1. Решить уравнение � � + �
� + � � + �
� + �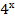 � = 9.
� = 9.
Решение. Можно заметить, что х = 1 – корень данного уравнения. Покажем, что других корней уравнение не имеет. Рассмотрим функцию f(x) = � � + �
� + � � + �
� + �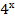 �. Она монотонно возрастает на всем множестве действительных чисел и f(1) = 9. Свойством монотонной функции является то, что она принимает каждое свое значение только один раз. Поэтому, х = 1 – единственный корень данного уравнения. Ответ: 1.
�. Она монотонно возрастает на всем множестве действительных чисел и f(1) = 9. Свойством монотонной функции является то, что она принимает каждое свое значение только один раз. Поэтому, х = 1 – единственный корень данного уравнения. Ответ: 1.
Пример 2. Решить уравнение � � + �
� + � � = 34.
� = 34.
Решение. Заметим, что корнем уравнения является число х = 2 (32 + 52 = 34). Докажем, что других корней уравнение не имеет. Каждая из функций � � и �
� и � � является возрастающей, следовательно, их сумма – тоже возрастающая функция. При х = 2 левая часть равна 34, при х 2 – больше 34. Итак, уравнение имеет единственный корень. Ответ: 2.
� является возрастающей, следовательно, их сумма – тоже возрастающая функция. При х = 2 левая часть равна 34, при х 2 – больше 34. Итак, уравнение имеет единственный корень. Ответ: 2.
Пример 3. Решить уравнение � � + �
� + � � = �
� = � �
�
Решение. Убеждаемся, что х = 1 – корень уравнения. Можно доказать, что других корней уравнение не имеет. Для этого оценим его левую и правую части уравнения. Если х 1, то вследствие убывания функции у = � � имеем �
� имеем � � + �
� + � � �
� � �+ �
�+ � � = 2, а вследствие возрастания функции у = �
� = 2, а вследствие возрастания функции у = � � имеем �
� имеем � � Поэтому, при х 1 левая часть уравнения строго меньше 2, а правая строго больше 2. Следовательно, при х 1 уравнение корней не имеет. Аналогично, при х
� Поэтому, при х 1 левая часть уравнения строго меньше 2, а правая строго больше 2. Следовательно, при х 1 уравнение корней не имеет. Аналогично, при х
Метод логарифмирования для решения показательных уравнений.
В основе этого метода лежит следующее утверждение: если выражения f(x) и h(x) положительны на множестве D, то уравнение f(x) = h(x) равносильно уравнению � �= �
�= � �на множестве D, где �
�на множестве D, где �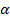 �0 и �
�0 и � � 1.
� 1.
Пример1. Решите уравнение � � = �
� = � �.
�.
Решение. Область допустимых значений уравнения х� �. Так как обе части уравнения положительные, то, прологарифмировав уравнение, например, по основанию 2, получим равносильное ему уравнение: 3х – 2 = (3 – х) · �
�. Так как обе части уравнения положительные, то, прологарифмировав уравнение, например, по основанию 2, получим равносильное ему уравнение: 3х – 2 = (3 – х) · � �.
�.
Решая это уравнение с помощью равносильных переходов, имеем:
3х – 2 = 3� � �
� �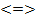 � 3х + �
� 3х + � �3�
�3� � +2 �
� +2 �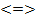 � х(3 + �
� х(3 + � � = 3�
� = 3� � + 2 �
� + 2 �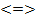 � х = �
� х = � �. Ответ: �
�. Ответ: � �.
�.
Пример 2. Решить уравнение � � · �
� · � � = 500.
� = 500.
Решение. Прологарифмируем это уравнение по основанию 5 или 2. (Можно логарифмировать по любому основанию, но не совсем удачный выбор основания может привести к громоздким преобразованиям). Тогда имеем следующее уравнение х + 3 · � � �
� � � = 3 + 2�
� = 3 + 2� � х2 + х(�
� х2 + х(� � – 3) – 3�
� – 3) – 3� � = 0. Дискриминант
� = 0. Дискриминант
D = (� � – 3)2 + 12�
� – 3)2 + 12� � = (�
� = (� � + 3)2, следовательно, корни уравнения будут
� + 3)2, следовательно, корни уравнения будут
х1,2 = � � отсюда х1 = 3, х2 = – �
� отсюда х1 = 3, х2 = – � � Ответ: – �
� Ответ: – � �
�
Пример 3. Решить уравнение � � (�
� (� �х-1 = �
�х-1 = � �.
�.
Решение. Обе части данного уравнения положительны. Прологарифмируем обе части этого уравнения по основанию 5: (х – 1)� � + �
� + � � �
� � � = �
� = � � – �
� – � �, т.е. уравнение
�, т.е. уравнение
х(� � – 1) – �
� – 1) – � �+ 1 – �
�+ 1 – � � + �
� + � � = �
� = � � х – 1 – �
� х – 1 – � � , равносильное исходному уравнению. Отсюда получаем х�
� , равносильное исходному уравнению. Отсюда получаем х� � = �
� = � � , т.е. х = �
� , т.е. х = � �. Ответ: �
�. Ответ: � �.
�.
Пример 4. Решить уравнение � � = 9.
� = 9.
Решение. Область допустимых значений уравнения: х 0.
Поскольку обе части уравнений положительны, то прологарифмируем по основанию 3:
� �)�
�)� � = 2, (�
� = 2, (� � + �
� + � � = �
� = � �, �
�, � � = 1 и �
� = 1 и � � = 2, следовательно,
� = 2, следовательно,
(1 + � � = 2, �
� = 2, � � + �
� + � � – 2 = 0. Сделаем замену �
� – 2 = 0. Сделаем замену � � = у, тогда у2 + у – 2 = 0, корнями которого являются числа у1 = – 2 и у2 = 1. Возвращаемся к нашей замене и получаем: �
� = у, тогда у2 + у – 2 = 0, корнями которого являются числа у1 = – 2 и у2 = 1. Возвращаемся к нашей замене и получаем: � � = – 2 или �
� = – 2 или � � = 1. Тогда х1 = �
� = 1. Тогда х1 = � � и х2 = 3. Ответ: �
� и х2 = 3. Ответ: � �; 3.
�; 3.
Пример 5. Решить уравнение |� � = 1.
� = 1.
Решение. Понятно, что х �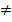 � 3,следовательно, |х – 3| �
� 3,следовательно, |х – 3| � � 0. Прологарифмируем обе части уравнения по основанию 10, тогда (3х2 – 10х + 3)�
� 0. Прологарифмируем обе части уравнения по основанию 10, тогда (3х2 – 10х + 3)� � = 0, откуда
� = 0, откуда
3х2 – 10х + 3 = 0 или � � = 0. Корнями квадратного уравнения 3х2 – 10х + 3 = 0 будут
� = 0. Корнями квадратного уравнения 3х2 – 10х + 3 = 0 будут
х1 = � � и х2 = 3. Из уравнения �
� и х2 = 3. Из уравнения � � = 0 находим |х – 3| =1 �
� = 0 находим |х – 3| =1 � � х – 3 = – 1 или х – 3 = 1.
� х – 3 = – 1 или х – 3 = 1.
Поэтому х3 = 2, х4 = 4; х2 = 3 не подходит по ОДЗ логарифма. Ответ: � �; 2; 4.
�; 2; 4.
Нестандартные методы решений показательных уравнений.
Пример 1. Решите уравнение 3 � � + (3х – 10)�
� + (3х – 10)� � + 3 – х = 0.
� + 3 – х = 0.
Решение. Данное уравнение кроме показательных функций содержит линейные функции у = 3х – 10 и у = 3 – х. Можно заметить, что относительно р = � � оно является квадратным:
� оно является квадратным:
3р2 + (3х – 10)р + 3 – х = 0 и поэтому р = � � = �
� = � � = �
� = � � = �
� = � � = �
� = � �, откуда р = �
�, откуда р = � �, р = 3 – х. Таким образом, исходное уравнение равносильно совокупности уравнений: �
�, р = 3 – х. Таким образом, исходное уравнение равносильно совокупности уравнений: � � = �
� = � � , �
� , � � = 3 – х. Корень первого уравнения х = �
� = 3 – х. Корень первого уравнения х = � �. Второе уравнение имеет корень х = 1, а других корней не имеет, т. к. его левая часть – всюду возрастающая функция, а правая – всюду убывающая. Ответ: 1; �
�. Второе уравнение имеет корень х = 1, а других корней не имеет, т. к. его левая часть – всюду возрастающая функция, а правая – всюду убывающая. Ответ: 1; � �.
�.
Пример 2. Решить уравнение � � + х = 2.
� + х = 2.
Решение. Применив формулу основного логарифмического тождества, получим уравнение х2 – 2х – 1 + х = 2(*), корни которого х1 = � � и х2 = �
� и х2 = � �. Теперь достаточно проверить, какое из полученных чисел удовлетворяет неравенству: х2 – 2х – 1 �
�. Теперь достаточно проверить, какое из полученных чисел удовлетворяет неравенству: х2 – 2х – 1 � � 0 (**). Это можно сделать проще (не подставляя в неравенство полученные числа). Перепишем уравнение (*) в виде х2 – 2х – 1 = 2 – х, тогда видим, что выражение х2 – 2х – 1 положительно тогда и только тогда, когда х �
� 0 (**). Это можно сделать проще (не подставляя в неравенство полученные числа). Перепишем уравнение (*) в виде х2 – 2х – 1 = 2 – х, тогда видим, что выражение х2 – 2х – 1 положительно тогда и только тогда, когда х � � 2. Таким образом, вместо Дубова Мария Игоревна 273 – 784 - 574
� 2. Таким образом, вместо Дубова Мария Игоревна 273 – 784 - 574
проверки неравенства (**) можно проверить условие х � � 2. Теперь видно, что только х = �
� 2. Теперь видно, что только х = � � является корнем данного уравнения. Ответ: �
� является корнем данного уравнения. Ответ: � �.
�.
Пример 3. Решить уравнение � � = �
� = � �.
�.
Решение. В данном уравнении удобно применить следующий прием: разделив числители и знаменатели в обеих частях уравнения на � � �
� � � 0, получим равносильное исходному уравнение: �
� 0, получим равносильное исходному уравнение: � � =�
� =� �.�
�.� �Далее сделаем замену �
�Далее сделаем замену � � = у, у�
� = у, у� �0 и получаем �
�0 и получаем � � =�
� =� �. (*)
�. (*)
Можно заметить, что у �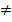 � 1, у �
� 1, у �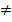 � �
� � �. Таким образом, получаем равносильное (*) уравнение
�. Таким образом, получаем равносильное (*) уравнение
(5 + 5у)(2 – 3у) = 4 – 4у; 10 – 5у – 15у2 – 4 + 4у = 0; 15у2 + у – 6 = 0; D = 1 + 360 = 361;
у1= � � у2= �
� у2= � �; у1 = �
�; у1 = � � , у2 �
� , у2 � �0. Вернемся к нашей замене, получим уравнение �
�0. Вернемся к нашей замене, получим уравнение � � = �
� = � �, откуда х = 1. Ответ: 1.
�, откуда х = 1. Ответ: 1.
Пример 4. Решить уравнение � � + �
� + � �= �
�= � � + 1.
� + 1.
Решение. Перепишем данное уравнение в виде:
� � + �
� + � � = �
� = � � + 1.
� + 1.
Сделаем замену � � = �
� = �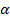 �; �
�; � �= b, тогда �
�= b, тогда � � + �
� + � �-1 – �
�-1 – � �2 – 1 = 0;
�2 – 1 = 0;
� �2b + b – �
�2b + b – � �3 – �
�3 – � � = 0; �
� = 0; � �2(b – �
�2(b – � �) + (b – �
�) + (b – � �) = 0; (b – �
�) = 0; (b – � �)(�
�)(� �2 + 1) = 0, откуда b = �
�2 + 1) = 0, откуда b = � � поскольку уравнение �
� поскольку уравнение � �2 + 1 = 0 корней не имеет. Таким образом, �
�2 + 1 = 0 корней не имеет. Таким образом, � �= �
�= � � и
� и
х2 + 1 = 2х. Очевидно, что х = 1. Ответ: 1.
Пример 5. Решить уравнение 6 · � � + 8 · �
� + 8 · � �= 48.
�= 48.
Решение. Разделим обе части уравнения на 24, получим уравнение
� �+ �
�+ � � = 2. Применяя неравенство |�
� = 2. Применяя неравенство |� �|�
�|� �|�
�|� � + |b| (его легко доказать возведением обеих частей в квадрат), получим |х – 2| + |х – 4| �
� + |b| (его легко доказать возведением обеих частей в квадрат), получим |х – 2| + |х – 4| � � |х – 2 – (х – 4)| = 2 и |х – 1| + |х – 3| = |х – 1 – (х – 3)| = 2, поэтому �
� |х – 2 – (х – 4)| = 2 и |х – 1| + |х – 3| = |х – 1 – (х – 3)| = 2, поэтому � � 1 и �
� 1 и � � 1.
� 1.
Знак равенства возможен, если имеет решение система уравнений:
� � �
� �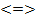 � �
� � � �
� �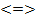 � �
� � �. Ответ: �
�. Ответ: � � Пример 5. Решить уравнение х2 – 2х + 2 = 2 · �
� Пример 5. Решить уравнение х2 – 2х + 2 = 2 · � � – �
� – � �Решение. Представим уравнение в виде (�
�Решение. Представим уравнение в виде (� � – 1)2 + (х – 1)2 = 0. Это уравнение равносильно системе: �
� – 1)2 + (х – 1)2 = 0. Это уравнение равносильно системе: � � откуда х = 1. Ответ: 1.
� откуда х = 1. Ответ: 1.
Тест по теме: Решение показательных уравнений
Эталоны ответов теста по теме: Решение показательных уравнений
Критерии оценивания тестовых заданий
10 вопросов 5 (отлично) (10-9 ответов)
10 вопросов 4 (хорошо) (8-7 ответов)
10 вопросов 3 (удов) (6 ответов)
Литература
-
Алимов Ш.А. и др. Алгебра и начала математического анализа. 10 (11) кл. – М.: 2018
-
Башмаков М.И. Сборник задач: учеб. пособие (базовый уровень). 11 кл. – М.: 2012
Интернет-ресурсы
-
http://school-collection.edu.ru – Электронный учебник «Математика в
школе, XXI век».
-
http://fcior.edu.ru - информационные, тренировочные и контрольные материалы.
-
www.school-collection.edu.ru – Единая коллекции Цифровых образовательных ресурсов
























