Россия,
СДЕЛАЙТЕ СВОИ УРОКИ ЕЩЁ ЭФФЕКТИВНЕЕ, А ЖИЗНЬ СВОБОДНЕЕ
Благодаря готовым учебным материалам для работы в классе и дистанционно
Скидки до 50 % на комплекты
только до 07.06.2025
Готовые ключевые этапы урока всегда будут у вас под рукой
Организационный момент
Проверка знаний
Объяснение материала
Закрепление изученного
Итоги урока
Была в сети 04.12.2024 13:18
Писарева Ксения Сергеевна
Преподаватель
33 года
2 590
23 229 
Местоположение
Специализация
Построение дерева игры по заданному алгоритму.
Категория:
Информатика
27.01.2022 11:12
Просмотр содержимого документа
«Построение дерева игры по заданному алгоритму.»
Практическая работа №11
Тема: Построение дерева игры по заданному алгоритму.
Цель: Формировать навыки решения задач методами перебора возможных вариантов и построения деревьев
Ход работы
1 Ознакомьтесь с теоретической частью
2 Выполните задания практической части
3 Оформите отчет, ответьте на вопросы
-
Какие методы поиска выигрышной стратегии вы знаете?
-
В чем суть этих методов?
-
Что такое выигрышная позиция?
-
Какую позицию называют проигрышной?
-
Какая игра называется стратегически правильной?
-
Как определить: кто выиграет при стратегически правильной игре?
Теоретическая часть
Выигрышная стратегия
-
для того чтобы найти выигрышную стратегию в несложных играх, достаточно использовать метод перебора всех возможных вариантов ходов игроков;
-
для решения задач 19 задания чаще всего для этого применяется метод построения деревьев;
-
если от каждого узла дерева отходят две ветви, т.е. возможные варианты хода, то такое дерево называется двоичным (если из каждой позиции есть три варианта продолжения, дерево будет троичным).
Выигрышные и проигрышные позиции
-
все позиции в простых играх делятся на выигрышные и проигрышные;
-
выигрышная позиция – это такая позиция, в которой игрок, делающий первый ход, обязательно выиграет при любых действиях соперника, если не допустит ошибки; при этом говорят, что у данного игрока есть выигрышная стратегия – алгоритм выбора очередного хода, позволяющий ему выиграть;
-
если игрок, делающий первый ход, находится в проигрышной позиции, то он обязательно проиграет, если ошибку не сделает его оппонент; в этом случае говорят, что у данного игрока нет выигрышной стратегии; таким образом, общая стратегия игры состоит в том, чтобы своим ходом создать проигрышную позицию для оппонента;
-
выигрышные и проигрышные позиции характеризуются так:
-
позиция, из которой все возможные ходы ведут в выигрышные позиции – проигрышная;
-
позиция, из которой хотя бы один из последующих возможных ходов ведет в проигрышную позицию — выигрышная, при этом стратегия игрока состоит в том, чтобы перевести игру в эту проигрышную(для оппонента) позицию.
Кто выиграет при стратегически правильной игре?
-
для того чтобы определить, какой из игроков выиграет при стратегически правильной игре, необходимо ответить на вопросы:
-
Может ли какой-либо из игроков выиграть, независимо от ходов других игроков?
-
Что должен сделать игрок с выигрышной стратегией первым ходом, чтобы он смог выиграть, независимо от действий ходов игроков?
Рассмотрим пример:
Игра: в кучке лежит 5 спичек; играют два игрока, которые по очереди убирают спички из кучки; условие: за один ход можно убрать 1 или 2 спички; выигрывает тот, кто оставит в кучке 1 спичку
Решение:
-
Будем использовать метод построения дерева. Первый играющий может убрать одну спичку (в этом случае их останется 4) или сразу 2 (останется 3), эти два варианта отобразим при помощи дерева:
-
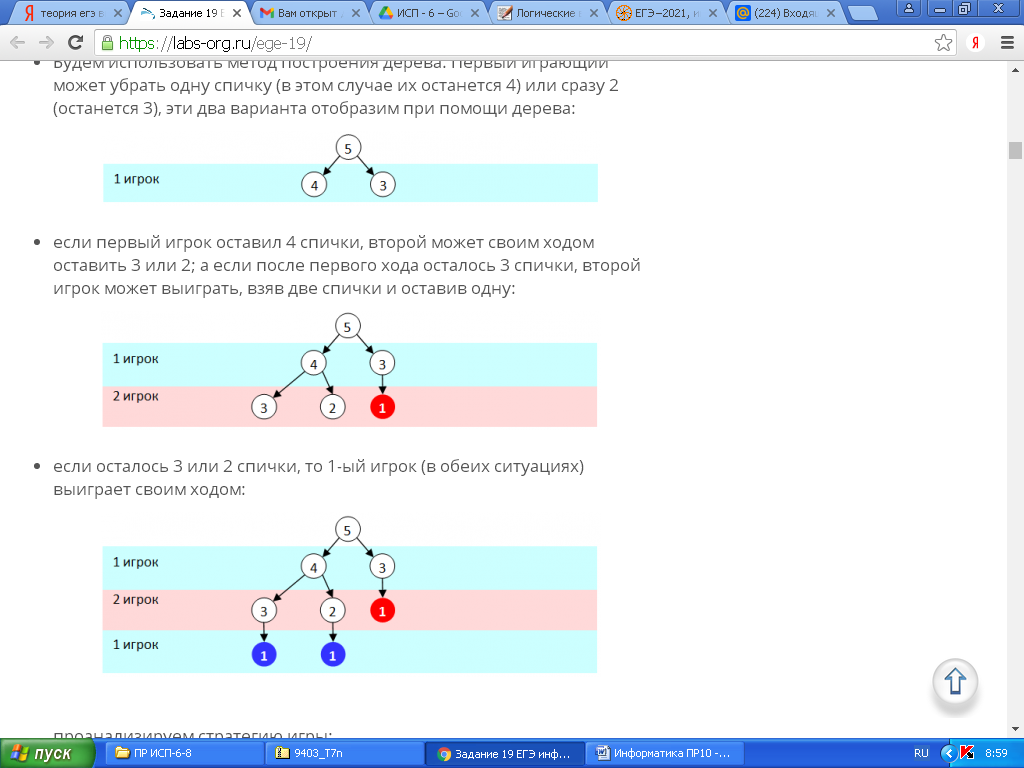
если первый игрок оставил 4 спички, второй может своим ходом оставить 3 или 2; а если после первого хода осталось 3 спички, второй игрок может выиграть, взяв две спички и оставив одну:
-
если осталось 3 или 2 спички, то 1-ый игрок (в обеих ситуациях) выиграет своим ходом:
проанализируем стратегию игры:
-
если первый игрок своим первым ходом взял две спички, то второй сразу выигрывает; если же он взял одну спичку, то своим вторым ходом он может выиграть, независимо от хода второго игрока;
-
итак, убрав всего одну спичку первым ходом, 1-ый игрок всегда может выиграть на следующем ходу;
-
тогда как второй игрок не может выиграть, независимо от действий первого: потому что, если первый игрок сначала убрал одну спичку, второй всегда проиграет.
Ответ: при правильной игре (стратегии игры) выиграет первый игрок; для этого ему достаточно своим первым ходом убрать одну спичку.
Практическая часть
Задача 1) Два игрока, Петя и Ваня, играют в следующую игру. Перед игроками лежит куча камней. Игроки ходят по очереди, первый ход делает Петя. За один ход игрок может
а) добавить в одну из куч (по своему выбору) один камень или
б) увеличить количество камней в куче в два раза.
Игра завершается в тот момент, когда количество камней в куче становится не менее 24. Если при этом в куче оказалось не более 38 камней, то победителем считается игрок, сделавший последний ход. В противном случае победителем становится его противник. Например, если в куче был 21 камень и Петя удвоит количество камней в куче, то игра закончится и победителем будет Ваня. В начальный момент в куче было S камней, 1
Задание 1. а) При каких значениях числа S Петя может выиграть в один ход? Укажите все такие значения и соответствующие ходы Пети.
б) У кого из игроков есть выигрышная стратегия при S = 22, 21, 20? Опишите выигрышные стратегии для этих случаев.
Задание 2. У кого из игроков есть выигрышная стратегия при S = 11, 10? Опишите соответствующие выигрышные стратегии.
Задание 3. У кого из игроков есть выигрышная стратегия при S = 9? Постройте дерево всех партий, возможных при этой выигрышной стратегии (в виде рисунка или таблицы). На рёбрах дерева указывайте, кто делает ход; в узлах – количество камней в позиции.
Решение:
1) Задание 1а. Сложность состоит в том, что Петя проиграет, если в результате его хода количество камней станет больше, чем 38. Он может сделать ход «+1» или «*2». Ходом «+1» он сможет получить 24 камня в куче (и таким образом выиграет!) из позиции S = 23.
Теперь проверим ход «*2». Для выигрыша Пети количество камней в результате этого хода должно стать от 24 до 38, поэтому Петя выиграет этим ходом при S от 12 до 19.
2) Задание 1б. При S = 22 возможные ходы дают кучи в 23 и 44 камня. В первом случае (S = 23) противник оказывается в выигрышной позиции (см. предыдущий пункт), во втором случае тот, кто ходит, проигрывает, потому что 44 38. Поэтому позиция S = 22 – проигрышная, Петя проиграет, у Вани есть выигрышная стратегия: в случае S = 23 сделать ход «+1» .
При S = 21 Петя может перевести игру в позицию S = 22, она, как мы только что показали, проигрышная для Вани. Поэтому у Пети есть выигрышная стратегия.
При S = 20 ходом «+1» Петя переведет игру в выигрышную (для Вани) позицию, а при ходе «*3» он сразу проиграет, получив 40 38 камней. Поэтому выигрышная стратегия есть у Вани.
Задание 2. У кого из игроков есть выигрышная стратегия при S = 11, 10? Опишите соответствующие выигрышные стратегии.
Задание 3. У кого из игроков есть выигрышная стратегия при S = 9? Постройте дерево всех партий, возможных при этой выигрышной стратегии (в виде рисунка или таблицы). На рёбрах дерева указывайте, кто делает ход; в узлах – количество камней в позиции.
3) Задание 2. При S = 11 или S = 10 Петя может ходом «*2» перевести игру в позиции S = 22 и S = 20, обе они, как мы показали в предыдущем пункте, проигрышные. Поэтому выигрышную стратегию имеет Петя.
4) Задание 3. При S = 9 возможно 2 хода: ход «+1» приводит к позиции S = 10, она выигрышная (см. предыдущий пункт); ход «*2» приводит к позиции S = 18, она тоже выигрышная (см. первый пункт). Таким образом, все возможные ходы ведут в выигрышные для соперника позиции, и позиция S = 9 – проигрышная (для Пети). Выигрышную стратегию имеет Ваня. При построении дерева для проигрывающего (Пети) указываем все возможные ходы, а для выигрывающего (Вани) – только один выигрышный ход. Дерево можно нарисовать так:
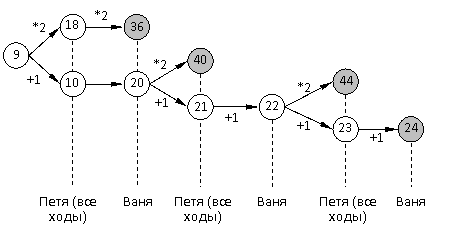
или записать в виде таблицы
|
| Петя | Ваня | Петя | Ваня Петя Ваня |
| 9 | 9*2=18 | 18*2=36 |
|
|
| 9+1=10 | 10*2=20 | 20*2=40 |
|
|
| 20+1=21 | 21+1=22 | 22+1=23 | 23+1=24 |
|
| 22*2=44 |
|
|
|
|
© 2022, Писарева Ксения Сергеевна 2545 94
Рекомендуем курсы ПК и ППК для учителей
Похожие файлы
Вебинар для учителей
Свидетельство об участии БЕСПЛАТНО!
Полезное для учителя
Реализация образовательных программ осуществляется с применением исключительно электронного обучения и ДОТ
