Просмотр содержимого документа
«Построение графиков функций, содержащих модуль»

Графики функций, содержащих модуль.
Методическое пособие для элективного курса «Модуль»
(8 – 9 класса)

Графики функций и

Два способа построения графиков
1)На основании определения модуля.
2) С помощью геометрических преобразований графиков.

Построение графика функции
1 способ.
если х ≥ 0
если х
График функции состоит из двух графиков, лежащих в правой и левой полуплоскостях

Построение графика
2 способ.
Используем свойство чётности этой функции.
Строим график функции для всех
х ≥ 0 и отразим полученную часть симметрично оси ординат.

Пример
1 способ
у
00
0
х
-2

2 способ
- Строим график у=2 х -2 для х ≥ 0.
2. Достраиваем его левую часть для х симметричной относительно оси ординат.
у
0
х
-2

Пример
1 способ
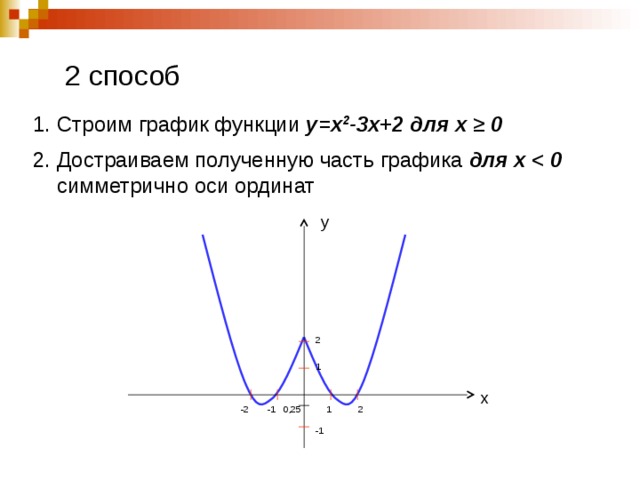
2 способ
- Строим график функции у=х 2 -3х+2 для х ≥ 0
- Достраиваем полученную часть графика для х симметрично оси ординат
у
2
1
х
0,25
-2
-1
2
1
-1

Построение графика функции
1 способ.
График состоит из двух графиков, расположенных в верхней полуплоскости

2 способ.
- Строим график функции у = f (x) .
- Часть графика у = f (x), лежащую над осью абсцисс сохраняем.
- Часть графила, лежащую под осью абсцисс отображаем симметрично относительно оси абсцисс.
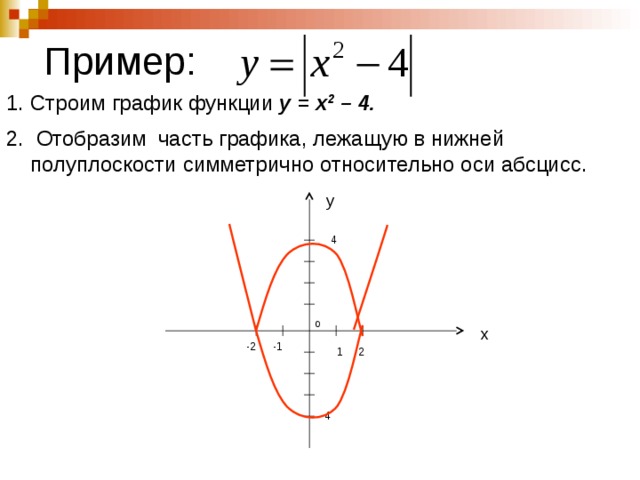
Пример:
- Строим график функции у = х 2 – 4.
- Отобразим часть графика, лежащую в нижней полуплоскости симметрично относительно оси абсцисс.
у
4
0
х
-1
-2
1
2
-4

График функции

Алгоритм построения
1. Строим график функции
для х ≥ 0
2. Отображаем полученную часть графика симметрично относительно оси ординат.
3. Отображаем симметрично относительно оси абсцисс часть графика расположенную в нижней полуплоскости
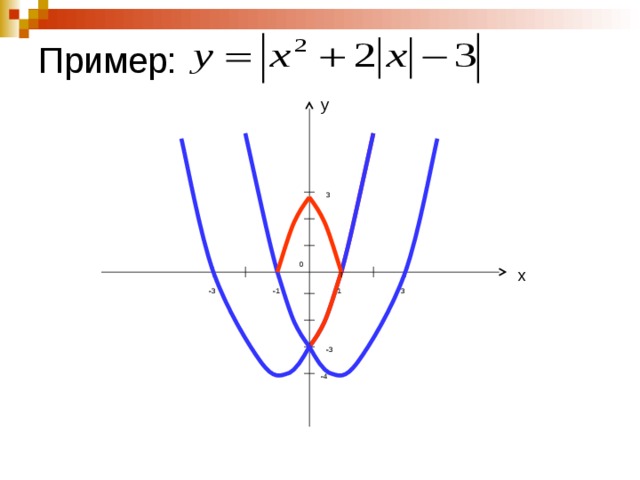
Пример:
у
3
0
х
-3
3
-1
1
-3
-4

Графики кусочно-линейных функций
 3 y=x-1+x-3=2x-4 " width="640"
3 y=x-1+x-3=2x-4 " width="640"
График функции
Графиком непрерывной кусочно-линейной функцией является ломаная линия с двумя бесконечными крайними звеньями.
1-ый способ: на основании определения модуля.
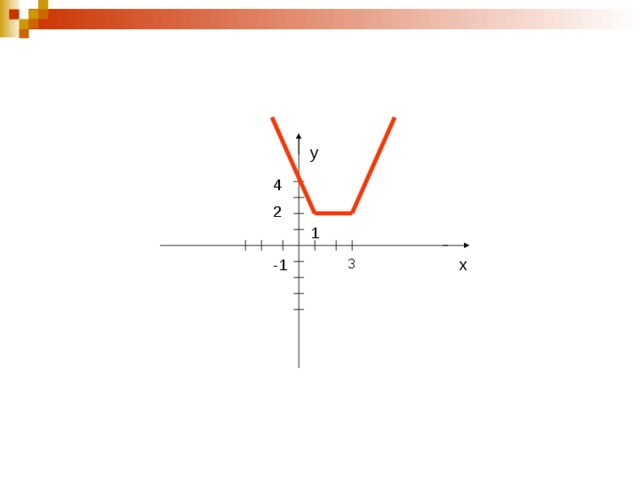
Пример: Точки x=1 и x=3 разбивают числовую ось на 3 промежутка.
- x ≤ 1 y=1-x+3-x=4-2x
- 1≤x ≤3 y=x-1+3-x=2
- x3 y=x-1+x-3=2x-4
y
4
2
1
-1
3
x

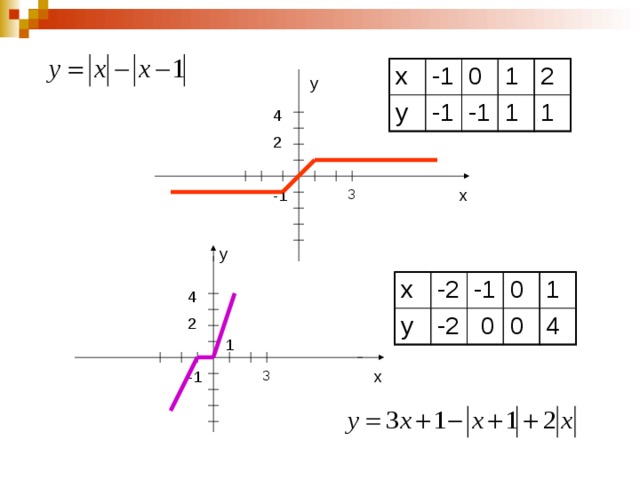
2 способ. Метод вершин
Алгоритм:
1.находим нули подмодульных выражений.
2.Составим таблицу, в которой кроме этих нулей записывается по одному целому значению х слева и справа от них.
3.Наносим эти точки на координатной плоскости и соединяем последовательно, точки перелома и есть вершины ломаной.
х
у
-1
0
-1
-1
1
2
1
1
y
4
2
x
3
-1
у
х
у
-2
-2
-1
0
0
0
1
4
4
2
1
-1
3
x
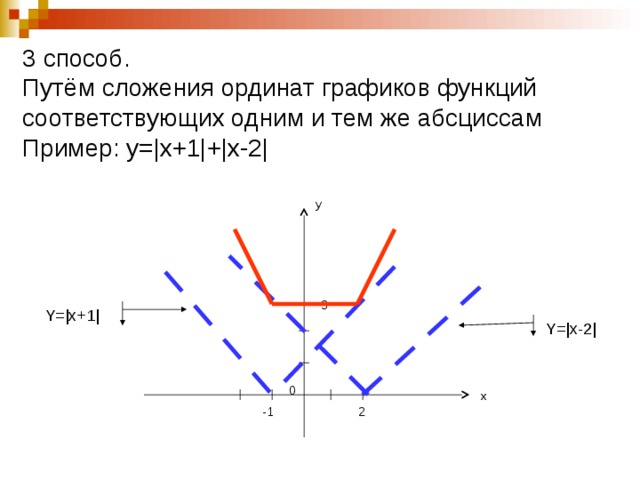
3 способ. Путём сложения ординат графиков функций соответствующих одним и тем же абсциссам Пример: y=|x+1|+|x-2|
у
3
Y=|x+1|
Y=|x-2|
0
х
-1
2

График зависимостей

График зависимости |y|=f(x)
Y= ± f(x), где f(x) ≥ 0
Алгоритм построения графиков зависимости.
1. Строим график функции у = f(х) для тех х из области определения, при которых f(х) ≥ 0.
2. Отобразим полученную часть графика симметрично оси абсцисс.
График данной зависимости состоит из графиков двух функций: у=f(x) и у=-f(x), где f(x) ≥ 0
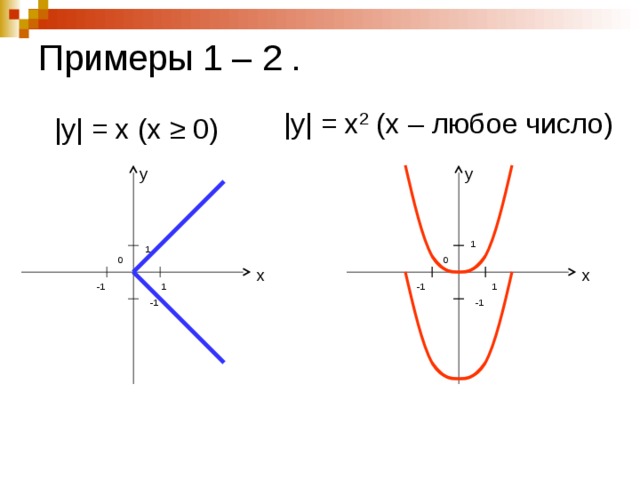
Примеры 1 – 2 .
|y| = x 2 (х – любое число )
|y| = x (х ≥ 0)
у
у
1
1
0
0
х
х
1
-1
1
-1
-1
-1
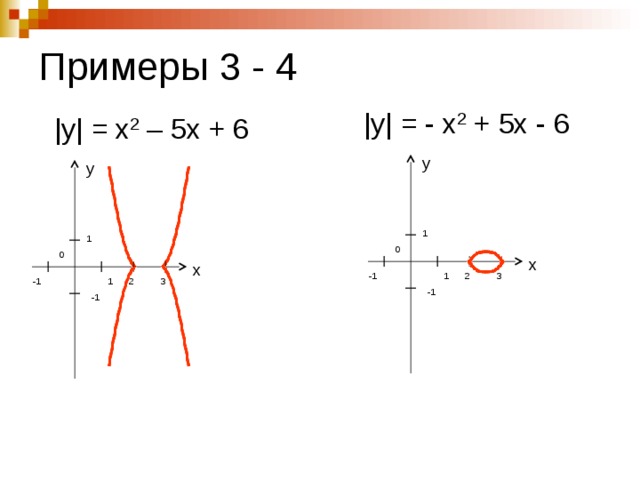
Примеры 3 - 4
|y| = - x 2 + 5х - 6
|y| = x 2 – 5х + 6
у
у
1
1
0
0
х
х
1
-1
2
3
2
-1
1
3
-1
-1























 3 y=x-1+x-3=2x-4 " width="640"
3 y=x-1+x-3=2x-4 " width="640"


















