муниципальное казенное образовательное учреждение
«Черницынская средняя общеобразовательная школа»
Октябрьского района Курской области
ИТОГОВЫЙ ПРОЕКТ
на тему
«Построение графиков функций, содержащих знак модуля»
по дисциплине
«Математика»
Обучающаяся: Дмитрова Вероника
Класс 9Б
Руководитель проекта С.А. Пятницкова
Апрель 2021г.
с.Черницыно
Содержание
ВВЕДЕНИЕ………………………………………………………………………3
ГЛАВА I. Методы построения графиков функций, содержащих знак модуля……………………………………………………………………………5
1.1. Историческая справка…………………………………………………...5
1.2. Определение модуля числа и его свойства……………………………6
1.3. Геометрическая интерпретация понятия модуля………………………6
1.4. Построение графика с помощью определения модуля «снятие модуля»……………………………………………………………………….6
1.5. Построение графика с использованием метода симметрии…………..7
1.6. Построение графика с помощью метода интервалов…………………9
1.7. Построение графика с помощью метода вершин……………………10
1.8. Сравнение методов построения графиков функции…………………10
ГЛАВА II. Исследование школьных учебников на наличие упражнений по теме «Модуль», задачи ОГЭ 9………………………………………………….12
ЗАКЛЮЧЕНИЕ……………………………………………………………..15
СПИСОК ИНФОРМАЦИОННЫХ ИСТОЧНИКОВ……………………..16
Приложение 1………………………………………………………………17
ВВЕДЕНИЕ
Понятие «модуль» является одним из основных понятий элементарной математики. Термин (module) в буквальном переводе с латинского означает «мера». Это понятие было введено в математику английским учёным Р. Котесом. А немецкий математик К. Вейерштрасс ввёл в обращение знак модуля – символ, которым это понятие обозначается при написании. Слово «модуль» имеет множество значений и применяется не только в математике, физике и технике, но и в других точных науках.
Актуальность исследования
Модуль числа и уравнения с модулем — тема особенная, прямо-таки заколдованная. Она совсем не сложная, просто в школе её редко объясняют нормально. В результате без специальной подготовки почти никто из школьников не может дать правильное определение модуля и тем более решить уравнение с модулем и построить график функции, содержащий модуль. И эту картину я наблюдала в своем классе. На уроке математики в нашем 9 Б классе учитель предложила выполнить задания:
-
вычислить |5,3|, |– 5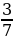 |, |0|;
|, |0|;
-
решить уравнение |2х + 3| = 5;
-
построить график функции у = |4х–3|
Получили следующие результаты:
| Кол-во обучающихся | Задание | Приступили | Выполнили | % выполнения |
| 20 | Вычислить | 20 | 18 | 90 |
| Решить | 20 | 9 | 45 |
| Построить | 20 | 0 | 0 |
Анализ правильных ответов показал, что самым сложным из предложенных заданий оказалось построение графика функции с модулем.
Я выбрала эту тему, потому что в дальнейшем она поможет мне на экзамене, так как я хочу получить высокую оценку.
Все вышесказанное обосновывает актуальность моего проекта.
Меня заинтересовало:
-
Какие существуют методы построения графиков функций, содержащих модули?
-
Какие из методов наиболее рациональные?
-
Какой из методов менее затратный по времени?
Объектом исследования являются графики функций.
Предмет исследования: методы построения графиков функций, содержащих знак модуля.
Цель исследования: исследование методов построения графиков функций, содержащих знак модуля.
Задачи исследования:
-
Проанализировать количество учебных часов, отведенных на изучение темы «Модуль числа».
-
Изучить методы построения графиков функций, содержащих знак модуля.
-
Найти общие подходы к построению графиков с модулями.
-
Разработать систему заданий для подготовки к ОГЭ по математике.
Решение поставленных задач потребовало привлечения следующих методов исследования: изучение и анализ дополнительной литературы по теме исследования, школьных учебников и учебных пособий, интернет-ресурсов.
Гипотеза: Я предполагаю, что существует метод построения графиков функций, содержащих знак модуля, менее затратный по времени и простой для понимания.
Практическая значимость исследования определяется тем, что в нем выявлены особенности решения задач на построение графиков функций, содержащих знак модуля; сформирована система упражнений для учащихся 5-9 классов и подготовки к ОГЭ.
ГЛАВА I. Методы построения графиков функций, содержащих знак модуля
1.1. Историческая справка
В первой половине ХVII века начинает складываться представление о функции как о зависимости одной переменной величины от другой. Так, французские математики Пьер Ферма (1601-1665) и Рене Декарт (1596-1650) представляли себе функцию как зависимость ординаты точки кривой от ее абсциссы. А английский ученый Исаак Ньютон (1643-1727) понимал функцию как изменяющуюся в зависимости от времени координату движущейся точки.
Термин «функция» (от латинского function – исполнение, совершение) впервые ввел немецкий математик Готфрид Лейбниц (1646-1716). У него функция связывалась с геометрическим образом (графиком функции). В дальнейшем швейцарский математик Иоганн Бернулли (1667-1748) и член Петербургской Академии наук знаменитый математик XVIII века Леонард Эйлер (1707-1783) рассматривали функцию как аналитическое выражение. У Эйлера имеется и общее понимание функции как зависимости одной переменной величины от другой.
Слово «модуль» произошло от латинского слова «modulus», что в переводе означает «мера». Это многозначное слово (омоним), которое имеет множество значений и применяется не только в математике, но и в архитектуре, физике, технике, программировании и других точных науках.
В архитектуре – это исходная единица измерения, устанавливаемая для данного архитектурного сооружения и служащая для выражения кратных соотношений его составных элементов.
В технике – это термин, не имеющий универсального значения и служащий для обозначения различных коэффициентов и величин, например, модуль зацепления, модуль упругости.
1.2. Определение модуля числа и его свойства
Абсолютной величиной (модулем) действительного числа а называется само число а, если оно неотрицательное, и число противоположное а, если а отрицательное.
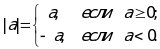
Из определения следует, что для любого действительного числа a
-
|a| ≥ 0
-
| – a| = |a|
-
|a·в| = |a|·|b|
-
|a|2 = a2
-
| , где b ≠ 0.
, где b ≠ 0.
-
|a + b| ≤ |a| + |b|
-
|a – b| ≥ |a| – |b|
-
Для а1, а2, …, ап справедливо |a1 + а2 + … + ап| ≤ |a1| + |а2| + … + |ап|.
1.3. Геометрическая интерпретация понятия модуля
Каждому действительному числу можно поставить в соответствие точку числовой прямой, тогда эта точка будет геометрическим изображением данного числа.
Каждой точке числовой прямой соответствует ее расстояние от начала отсчета или длина отрезка, начало которого в точке начала отсчета, а конец – в данной точке. Это расстояние или длина отрезка рассматривается всегда как величина неотрицательная. Таким образом, геометрической интерпретацией действительного числа служит вектор, выходящий из начала отсчета и имеющий конец в точке, изображающей данное число. Длина этого вектора будет геометрической интерпретацией модуля данного действительного числа (Рис.1).

-а 0 а
Рис.1. Геометрическая интерпретация понятия модуля
1.4. Построение графика с помощью определения модуля - «снятие модуля»
Пример 1. Для того чтобы построить график квадратичной функции у = │х² – 4х + 3│ (Рис. 2) нужно:
а) построить параболу у = х² – 4х + 3, если х² – 4х + 3 ≥0,
б) построить параболу у = – х² +4х – 3, если х² – 4х + 3 ˂0.
Пример 2. Для того, чтобы построить график линейной функции у=│х│+2 (Рис.3) надо:
а) построить график функции у = х +2 для х ≥ 0,
б) график функции у = – х +2, для х

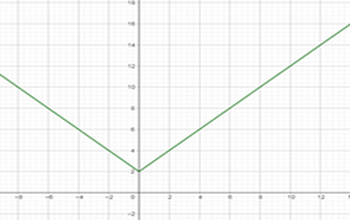
Рис.2. График функции у = │х² - 4х + 3│
Рис. 3. График функции у = │х │ + 2
Рис.2. График функции у = │х² - 4х + 3│
1.5. Построение графика с использованием метода симметрии
Симметрия — это отображение объекта в себя, сохраняющее структуру объекта.
Целесообразно рассматривать построение графиков в следующей последовательности: у=f(∣x∣); у=∣f(x)∣; у=∣f(∣x∣)∣; ∣у∣=f(x); ∣у∣=∣f(x)∣.
График функции у=f(∣x∣) получается из графика функции у = f(x) следующим преобразованием: х≥0 график сохраняется, а при х
График функции у=∣f(x)∣ получается из графика у = f(x) следующим преобразованием: х≥0 график сохраняется, а при х
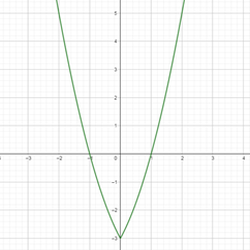

Рис.5. График функции у =| х2+6х –5|
Рис.4. График функции у = х2+2|х| –3
Г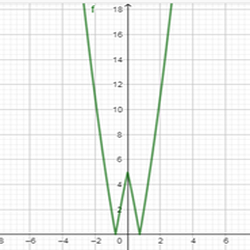
Рис.6. График функции у =| х2+6|х| –5|
рафик функции у=∣f(∣x∣)∣ получается из графика функции у = f(x) следующим преобразованием: строим график функции при х0, а затем при х∣x∣)∣x∣) относительно оси Ох (Рис. 6).
График ׀у ׀ =f(x) строится следующим преобразованием (Рис. 7):
1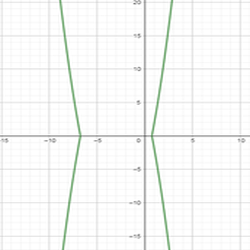 . Построить график функции y = f(x).
. Построить график функции y = f(x).
2. Исключить его часть, расположенную ниже оси абсцисс, поскольку указанное равенство возможно только для положительных значений f(x).
3
Рис.7. График функции |у| = х2+6х –5
. Построить нижнюю часть линии (при отрицательных
y) симметричным отображением относительно оси
Ox.
Г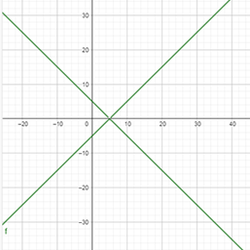 рафик функции вида ∣у∣=∣f(x)∣ строится преобразованием (Рис. 8):
рафик функции вида ∣у∣=∣f(x)∣ строится преобразованием (Рис. 8):
-
Строим график функции у= f(x).
-
Строим график функции у=∣f(x)∣ (часть графика f(x)
-
С
Рис.8. График функции |у| =|х -5|
троим график функции ∣у∣=∣f(x)∣ (полученный график симметрично отображаем относительно оси Ох).
1.6. Построение графика с помощью метода интервалов
Для построение графиков функции вида у=∣f(x)∣+∣f1(x)∣+∣f2(x)∣+...+∣fn(x)∣ можно использовать метод интервалов, при котором координатная прямая разбивается на интервалы и полуинтервалы нулями модулей. Далее, используя определение модуля, для каждой из найденных областей получим уравнение, которое необходимо решить на данном промежутке и получить функцию.
Пример 3: Построить график функции у = │х + 3│ + │2х +1│ - х
1. Находим нули модулей
А) х + 3=0, х = -3
Б) 2х + 1=0, х= - 0,5
2

 . Наносим на координатную прямую эти точки и разбиваем прямую на три части
. Наносим на координатную прямую эти точки и разбиваем прямую на три части
-3 -0,5
3. Находим значение функции на каждом из интервалов
у = - (х+ 3) – (2х + 1) – х= -х – 3 – 2х – 1 – х = -4х – 4, при х ≤ -3
у = (х+ 3) – (2х + 1) – х= х +3 – 2х – 1 – х = -2х + 2, при -3≤ х ≤ -0,5
у = (х+ 3) + (2х + 1) - х = 2х +4, при х ≥ -0,5
4. Строим на каждом интервале полученные функции (Рис.9).
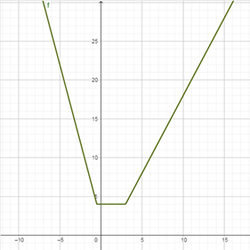
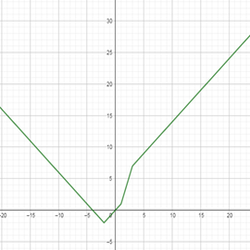
Рис.9. График функции у = │х + 3│ + │2х +1│ - х
Рис.10. График функции у=׀х+2׀ + ׀х-1׀ – ׀х-3׀
1.7. Построение графика с помощью метода вершин
Этот метод называют еще методом расширения области нулей.
Для построения графика функции у=∣f(x)∣ + ∣f1(x)∣ + ∣f2(x)∣+ ...+ ∣fn(x)∣ можно применить метод вершин:
-
Найти нули каждого подмодульного выражения
-
Составить таблицу, в которой кроме нулей записать по одному значению аргумента слева и справа
-
Нанести точки на координатную плоскость и соединить последовательно
П
Рис.4. График функции у = х2+2|х| –3
Рис.4. График функции у = х2+2|х| –3
ример 4. Построить график у=׀х+2׀ + ׀х-1׀ – ׀х-3׀ (Рис.10).
-
Найдем нули подмодульных выражений: -2; 1; 3
-
| х | -3 | -2 | 1 | 3 | 4 |
| у | -1 | -2 | 1 | 7 | 8 |
Составим таблицу:
1.8. Сравнение методов построения графиков функции
Чтобы ответить на вопросы: «Какие из методов наиболее рациональные?» и «Какой из методов менее затратный по времени?» составим следующую таблицу (Таб. 1).
Таблица 1. Сравнение методов построения графиков функции
| Метод | Функция | По рациональности и затраченному времени |
| По определению модуля | Для любой функции, содержащей знак модуля | Менее удобный |
| Метод симметрии | у=f(∣x∣) у=∣f(x)∣ у=∣f(∣x∣)∣ ∣у∣=f(x) ∣у∣=∣f(x)∣ | Более удобный |
| Метод интервалов | у=∣f(x)∣ + ∣f1(x)∣ + ∣f2(x)∣+ ...+ ∣fn(x)∣ | Более удобный |
| Метод вершин | у=∣f(x)∣ + ∣f1(x)∣ + ∣f2(x)∣+ ...+ ∣fn(x)∣ | Более удобный |
Таким образом, для разных видов функций, содержащих знак модуля, лучше применять разные методы построения. Одного метода, который самый мало затратный по времени для всех функций, содержащих знак модуля, нет.
ГЛАВА II. Исследование школьных учебников на наличие заданий по теме «Модуль», задачи ОГЭ 9
Проанализировав мои школьные учебники, я получила следующие результаты (Таб. 2).
Таблица 2. Сравнение школьных учебников на наличие упражнений по теме «Модуль»
| Класс | Автор учебника | Кол-во часов по теме «Модуль» | Кол-во часов всего | Кол-во заданий по теме «Модуль» | Кол-во всех заданий | % от всех заданий |
| 6 | Н.Я. Виленкин и др. | 2 | 170 | 30 | 1595 | 2 |
| 7 | Ю.Н. Макарычев и др. | 0 | 102 | 15 | 1183 | 1,3 |
| 8 | Ю.Н. Макарычев и др. | 2 | 102 | 13 | 1146 | 1,1 |
| 9 | Ю.Н. Макарычев и др. | 2 | 102 | 14 | 1097 | 1,2 |
Из таблицы видно, что количество часов, отводимых на изучение темы «Модуль» решение уравнений, неравенств и построение графиков функций со знаком модуля недостаточно.
Основное внимание в 6 классе уделялось определению абсолютной величины и геометрическому смыслу этого понятия. А в курсе алгебры 7-9 классов «модуль» упоминался эпизодически в пунктах учебника «Для тех, кто хочет знать больше» и в разделе «Задачи повышенной трудности».
Но задачи, связанные с модулем, встречаются и в текстах ОГЭ-9. И оцениваются наибольшим количеством баллов. Приведу примеры решения некоторых задач.
№ 316295. Постройте график функции у=∣х+1∣-∣х-1∣ и найдите все значения k, при которых прямая у = k х имеет с графиком данной функции ровно одну общую точку.
Решение.
Р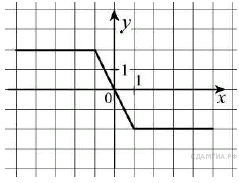 аскрывая модули, получаем, что
аскрывая модули, получаем, что
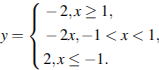
Рис.11. График функции у=∣х+1∣-∣х-1∣
Прямая у = кх имеет с графиком данной функции (Рис. 11) ровно одну общую точку при
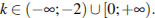
Ответ: 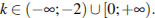
№ 314722. Постройте график функции
314722. Постройте график функции 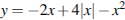 и определите, при каких значениях c прямая y = c имеет с графиком ровно три общие точки.
и определите, при каких значениях c прямая y = c имеет с графиком ровно три общие точки.
Решение.
Раскрывая модуль, получим, что график функции можно представить следующим образом:
Рис.12. График функции 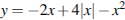
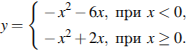
Прямая y = c имеет с графиком функции (Рис. 12) ровно три общие точки при с=0 и с=1
Ответ: 0; 1.
№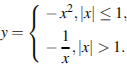 314759. Постройте график функции
314759. Постройте график функции
и определите, при каких значениях с прямая у = с будет иметь с графиком единственную общую точку.
Р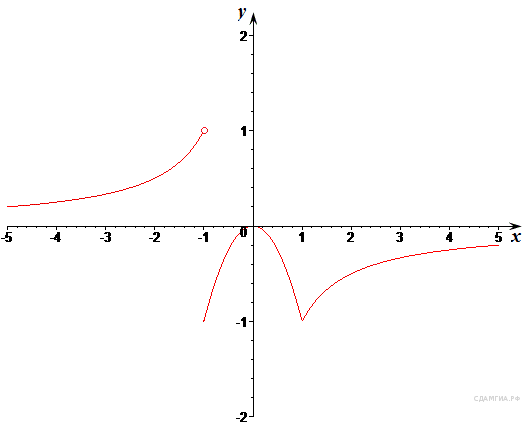 ешение.
ешение.
Построим график функции (Рис. 13). Из графика видно, что прямая у = с будет иметь с графиком функции единственную точку пересечения при с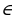 [0; 1).
[0; 1).
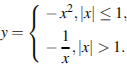 Ответ: [0; 1).
Ответ: [0; 1).
Рис.13. График функции 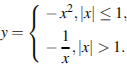
Заключение
В ходе исследовательской работы я рассмотрела теоретический материал по абсолютной величине (модулю) и решила практические задачи. В результате работы над темой я сумела изучить поведения линейных, квадратичных функций. Научилась преобразованию графиков, содержащих переменную под знаком модуля.
Гипотеза, которую я ставила перед изучение темы, в ходе работы не подтвердилась, т.к. для разных видов функций, содержащих переменную под знаком модуля, лучше применять разные методы построения. Т.е. одного метода, который самый мало затратный по времени для всех функций, содержащих переменную под знаком модуля, я не нашла.
Данная исследовательская работа может быть использована учащимися для самоподготовки при подготовке к экзаменам. Применение разработанной мною темы, поможет мне решить задания из второй части ОГЭ и выбрать наиболее удобный способ, который сэкономит мое время на экзамене.
СПИСОК ИНФОРМАЦИОННЫХ ИСТОЧНИКОВ
-
Гельфанд И. М. и др. « Функции и графики » - М. Наука, 1973
-
Садыкина И. « Построение графиков функций и зависимостей, содержащих знак модуля » - Математика №33, 2004
-
Пичурин Л. Ф. « За страницами учебника алгебры » - М. Просвещение, 1999
-
Факультативный курс по математике: Учебное пособие для 7-9 классов средней школы. И. Л. Никольская – М. Просвещение, 1991
-
Виленкин Н.Я. Математика. 6 класс : учеб. для общеобразоват. учреждений / Н.Я. Виленкин, В.И. Жохов, А.С. Чесноков, С.И. Шварцбурд. – 30-е изд., стер. – М.: Мнемозина, 2013. – 288 с.: ил.
-
Макарычев Ю.Н. Алгебра. 7 класс : учеб.дляобщеоразоват. Учреждений / Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова; под ред. С.А. Теляковского. – 18-е изд. – М. : Просвещение, 2009. – 240 с.: ил.
-
Макарычев Ю.Н. Алгебра. 8 класс : учеб.для общеоразоват. учреждений / Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова; под ред. С.А. Теляковского. – 15-е изд. – М.: Просвещение, 2007. – 271 с. : ил.
-
Макарычев Ю.Н. Алгебра. 9 класс : учеб.дляобщеоразоват. Учреждений / Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.Б. Суворова; под ред. С.А. Теляковского. – 18-е изд. – М.: Просвещение, 2000. – 272 с. : ил.
-
http://ppt4web.ru/matematika/postroenie-grafikov-funkcijj-soderzhashhikh-peremennuju-pod-znakom-modulja.html
-
http://www.tutoronline.ru/blog/stroim-grafiki-funkcij,-soderzhawie-modul-chast-1






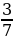 |, |0|;
|, |0|;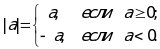
 , где b ≠ 0.
, где b ≠ 0.





 . Построить график функции y = f(x).
. Построить график функции y = f(x). рафик функции вида ∣у∣=∣f(x)∣ строится преобразованием (Рис. 8):
рафик функции вида ∣у∣=∣f(x)∣ строится преобразованием (Рис. 8):

 . Наносим на координатную прямую эти точки и разбиваем прямую на три части
. Наносим на координатную прямую эти точки и разбиваем прямую на три части

 аскрывая модули, получаем, что
аскрывая модули, получаем, что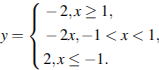
 314722. Постройте график функции
314722. Постройте график функции 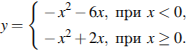
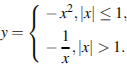 314759. Постройте график функции
314759. Постройте график функции ешение.
ешение.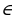 [0; 1).
[0; 1).



















