
Квадратичная функция

График любой квадратичной
функции – парабола.
Квадратичная функция
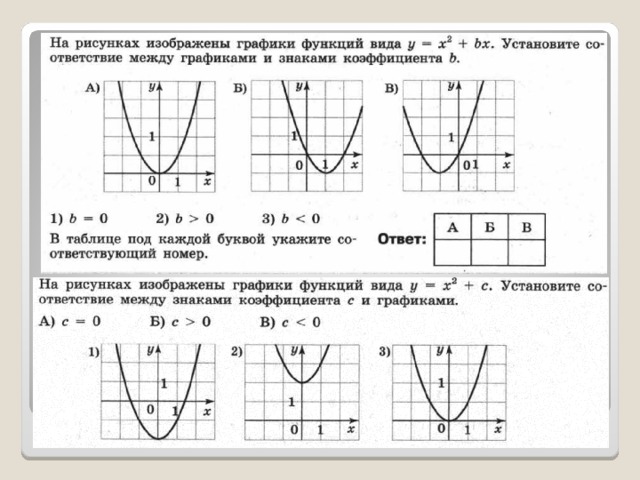
Квадратичной функцией называют функцию, которую можно задать формулой вида y = ax 2 + bx + c , где a , b и с - некоторые числа, причём а ≠ 0 .

 0 D 0 a 0 D 0 a 0 D = 0 x x x y y y x x x a 0 D 0 a 0 D 0 a 0 D = 0 " width="640"
0 D 0 a 0 D 0 a 0 D = 0 x x x y y y x x x a 0 D 0 a 0 D 0 a 0 D = 0 " width="640"
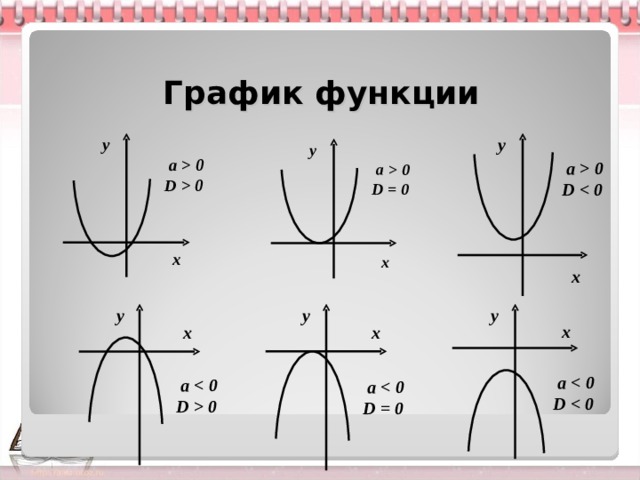
График функции
y
y
y
a 0
D 0
a 0
D 0
a 0
D = 0
x
x
x
y
y
y
x
x
x
a 0
D 0
a 0
D 0
a 0
D = 0
 X 1 , то f (X 2 )f (X 1 )) и убывание функции ( если X 2 X 1 , то f (X 2 )4. Промежутки знакопостоянства : f (x) 0 и f (x)5. Непрерывность функции (разрыв - нельзя провести график не отрываясь). 6. Наибольшее и наименьшее значение. " width="640"
X 1 , то f (X 2 )f (X 1 )) и убывание функции ( если X 2 X 1 , то f (X 2 )4. Промежутки знакопостоянства : f (x) 0 и f (x)5. Непрерывность функции (разрыв - нельзя провести график не отрываясь). 6. Наибольшее и наименьшее значение. " width="640"
Свойства функции
- 1. Нули функции: y= 0 (пересечения с осью Ох)
- 2.Точки пересечения с осью О y
- 3 .Возрастание функции ( если X 2 X 1 , то f (X 2 )f (X 1 )) и убывание функции ( если X 2 X 1 , то f (X 2 )
- 4. Промежутки знакопостоянства :
f (x) 0 и f (x)
- 5. Непрерывность функции (разрыв - нельзя провести график не отрываясь).
- 6. Наибольшее и наименьшее значение.

Схема построения графика квадратичной функции y = a x 2 - b x + c :
- Построить вершину параболы.
- Провести через вершину параболы прямую,
параллельную оси ординат, - ось симметрии
параболы.
- Найти нули функции, если они есть, и построить
на оси абсцисс соответствующие точки параболы.
- Построить дополнительные точки.
- Провести через построенные точки параболу.
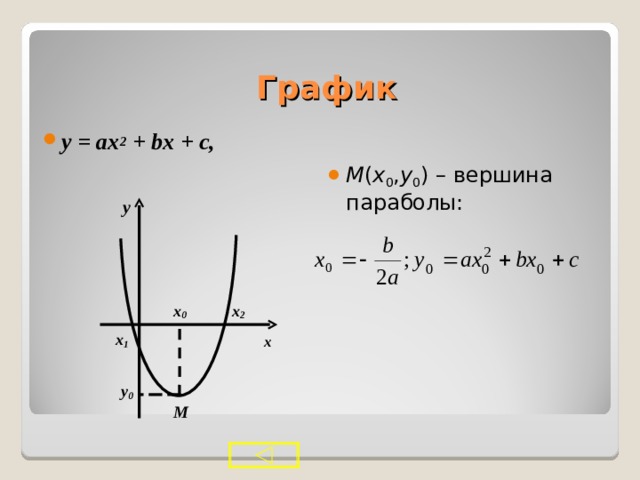
График
- M ( x 0 , y 0 ) – вершина параболы:
y
x 2
x 0
x 1
x
y 0
M
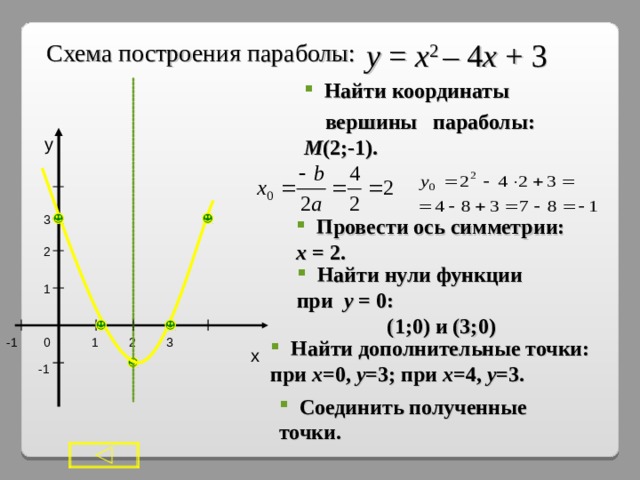
Схема построения параболы:
у = х 2 – 4 х + 3
вершины параболы: М (2;-1).
у
3
- Провести ось симметрии: х = 2.
2
- Найти нули функции при у = 0: (1;0) и (3;0)
1
0
3
-1
2
1
- Найти дополнительные точки: при х =0, у =3; при х =4, у =3.
х
-1
- Соединить полученные точки.
 0. M(x 0 ; y 0 )- вершина параболы x 0 = ; x 0 = -12 : 6 = -2 y 0 = 3(-2) 2 +12(-2)+9 = -3 . M(-2 ; 3) Прямая х = -2 – ось симметрии Нули функции: y=0 3x 2 +12x+9 = 0 x 2 + 4 x+ 3 = 0 x 1 = -1 , x 2 = -3 2 а - b у 9 3 1 -3 -2 -1 1 0 x x y 0 - 1 9 0 -3 " width="640"
0. M(x 0 ; y 0 )- вершина параболы x 0 = ; x 0 = -12 : 6 = -2 y 0 = 3(-2) 2 +12(-2)+9 = -3 . M(-2 ; 3) Прямая х = -2 – ось симметрии Нули функции: y=0 3x 2 +12x+9 = 0 x 2 + 4 x+ 3 = 0 x 1 = -1 , x 2 = -3 2 а - b у 9 3 1 -3 -2 -1 1 0 x x y 0 - 1 9 0 -3 " width="640"
Пример:
y = 3x 2 + 12x + 9
Графиком функции является парабола , ветви параболы
направлены вверх , т.к. а = 3, a 0.
M(x 0 ; y 0 )- вершина параболы
x 0 = ; x 0 = -12 : 6 = -2
y 0 = 3(-2) 2 +12(-2)+9 = -3 . M(-2 ; 3)
Прямая х = -2 – ось симметрии
Нули функции: y=0
3x 2 +12x+9 = 0
x 2 + 4 x+ 3 = 0
x 1 = -1 , x 2 = -3
2 а
- b
у
9
3
1
-3
-2
-1
1
0
x
x
y
0
- 1
9
0
-3

Работа с учебником:

Домашняя работа:











 0 D 0 a 0 D 0 a 0 D = 0 x x x y y y x x x a 0 D 0 a 0 D 0 a 0 D = 0 " width="640"
0 D 0 a 0 D 0 a 0 D = 0 x x x y y y x x x a 0 D 0 a 0 D 0 a 0 D = 0 " width="640"
 X 1 , то f (X 2 )f (X 1 )) и убывание функции ( если X 2 X 1 , то f (X 2 )4. Промежутки знакопостоянства : f (x) 0 и f (x)5. Непрерывность функции (разрыв - нельзя провести график не отрываясь). 6. Наибольшее и наименьшее значение. " width="640"
X 1 , то f (X 2 )f (X 1 )) и убывание функции ( если X 2 X 1 , то f (X 2 )4. Промежутки знакопостоянства : f (x) 0 и f (x)5. Непрерывность функции (разрыв - нельзя провести график не отрываясь). 6. Наибольшее и наименьшее значение. " width="640"




 0. M(x 0 ; y 0 )- вершина параболы x 0 = ; x 0 = -12 : 6 = -2 y 0 = 3(-2) 2 +12(-2)+9 = -3 . M(-2 ; 3) Прямая х = -2 – ось симметрии Нули функции: y=0 3x 2 +12x+9 = 0 x 2 + 4 x+ 3 = 0 x 1 = -1 , x 2 = -3 2 а - b у 9 3 1 -3 -2 -1 1 0 x x y 0 - 1 9 0 -3 " width="640"
0. M(x 0 ; y 0 )- вершина параболы x 0 = ; x 0 = -12 : 6 = -2 y 0 = 3(-2) 2 +12(-2)+9 = -3 . M(-2 ; 3) Прямая х = -2 – ось симметрии Нули функции: y=0 3x 2 +12x+9 = 0 x 2 + 4 x+ 3 = 0 x 1 = -1 , x 2 = -3 2 а - b у 9 3 1 -3 -2 -1 1 0 x x y 0 - 1 9 0 -3 " width="640"





















