Построение сечений многогранников 2 (сложнее).

Вдохновение нужно в геометрии

не меньше, чем в поэзии.

А.С. Пушкин

Содержание

• Введение
• Сечение в разных областях
• Основные определения и понятия
• Базовые задачи
• Примеры
• Методы

При изучении курса стереометрии большое значение имеет изображение пространственных фигур. При построении рисунка, изображающего пространственную фигуру, следует позаботится о том, чтобы

• на чертеже были бы видны основные линии и углы;
• положение изображаемого тела было оптимальным;
• по разному отмечены видимые и невидимые линии;
• правильно построены сечения и проекции на плоскость.

Пространственная задача сводится к одной или нескольким планиметрическим задачам при помощи различных приемов. Обратимся к методу сечений. Этот метод часто помогает найти наиболее эффективный способ решения стереометрической задачи.

• Цель: повторить способы построения сечений многогранников, способствовать развитию пространственных представлений, выработке практических навыков в построении сечений многогранников плоскостью.
• Примечание: работа не содержит сложных случаев построения сечений

К содержанию

Сечения в медицине

Сечения в истории и археологии

Сечения в архитектуре

К содержанию

Золотое сечение пирамиды Хеопса

Основные определения

• Сечением многогранника P плоскостью называется фигура, состоящая из общих точек многогранника P и плоскости β
• Плоскость, по обе стороны от которой имеются точки данного тела, называется секущей плоскостью.
• Фигура, которая образуется при пересечении тела плоскостью (т.е. общая часть тела и секущей плоскости), называется сечением тела .

При построении сечения многогранника, плоскостью α следует иметь в виду, что:

• Построение сечения сводится к построению линий пересечения плоскости α с гранями многогранника.
• Сечение однозначно определяется тремя точками многоугольника.
• Если точки сечения лежат на ребрах многогранника, то они являются вершинами многоугольника, который получится в сечении.
• Если точки сечения лежат на гранях многогранника, то они лежат на сторонах многоугольника, который получится в сечении.
• Если сечение пересекает две параллельные грани, то и отрезки (стороны многоугольника, который получится в сечении) будут параллельны.

Осуществляя контроль за правильностью построения сечений многогранника, следует иметь в виду, что:

• Если многогранник выпуклый, то сечение - выпуклый многоугольник.
• Вершины многоугольника всегда лежат на ребрах многогранника.
• Если точки сечения лежат на ребрах многогранника, то они являются вершинами многоугольника, который получится в сечении.
• Если точки сечения лежат на гранях многогранника, то они лежат на сторонах многоугольника, который получится в сечении.
• Две стороны многоугольника, который получится в сечении, не могут принадлежать одной грани многогранника.
• Если сечение пересекает две параллельные грани, то и отрезки (стороны многоугольника, который получится в сечении) будут параллельны.

К содержанию

Базовые задачи

• Если две плоскости имеют две общие точки, то прямая, проведенная через эти точки, является линией пересечения этих плоскостей.

D 1

C 1

S

A 1

B 1

Q

N

N

P

B

A

M

Q

D

C

C

M

B

A

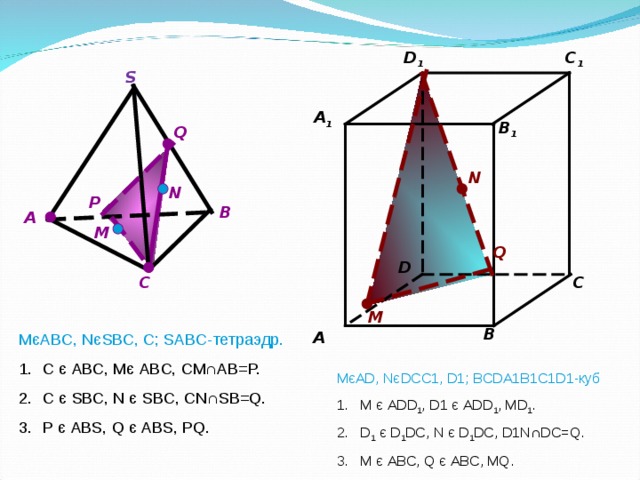
M є ABC, N є SBC, C; SABC- тетраэдр .

• C є ABC, M є ABC, CM ∩ AB=P.
• C є SBC, N є SBC, CN ∩ SB=Q.
• P є ABS, Q є ABS, PQ.

M є AD, N є DCC1, D1 ; BCDA1B1C1D1- куб

• M є ADD 1 , D1 є ADD 1 , MD 1 .
• D 1 є D 1 DC, N є D 1 DC, D1N ∩ DC=Q.
• M є ABC, Q є ABC, MQ.

Базовые задачи

II. Если две параллельные плоскости пересечены третьей, то линии их пересечения параллельны .

C 1

D 1

S

М

A 1

N

B 1

M

B

K

А

D

C

C

K

B

A

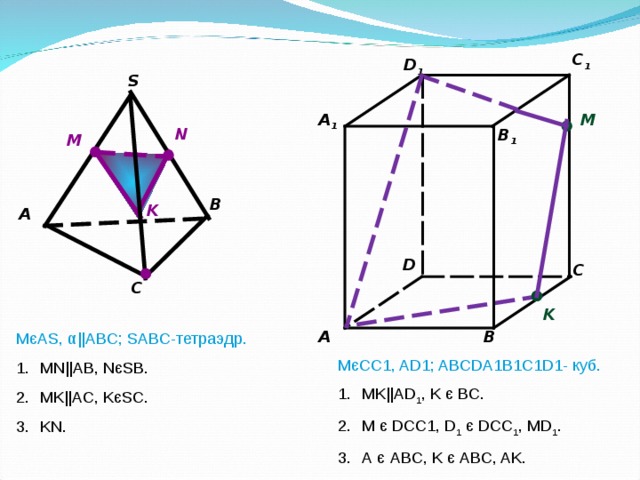
M є AS, α ||ABC; SABC- тетраэдр.

• MN||AB, N є SB.
• MK||AC, K є SC.
• KN.

M є CC1, AD1; ABCDA1B1C1D1- куб.

• MK||AD 1 , K є BC.
• M є DCC1, D 1 є DCC 1 , MD 1 .
• A є ABC, K є ABC, AK.

Базовые задачи

III. Общая точка трех плоскостей (вершина трехгранного угла) является общей точкой линий их парного пересечения (ребер трехгранного угла).

S

F 3

M

Q

C 1

D 1

K

N

B 1

F

B

A 1

А

K

L

P

N

С

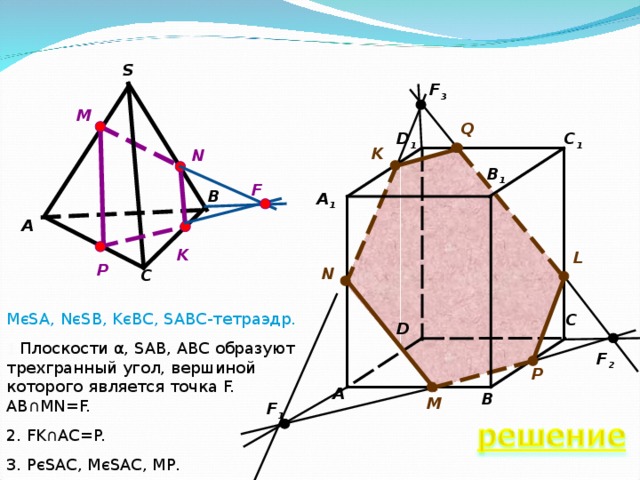
M є SA, N є SB, K є BC, SABC- тетраэдр.

1 Плоскости α , SAB, ABC образуют трехгранный угол, вершиной которого является точка F. AB∩MN=F.

2. FK∩AC=P.

3. P є SAC, M є SAC, MP .

C

D

F 2

P

A

B

M

F 1

M є AB, N є AA 1 , K є A1D 1 ; ABCDA 1 B 1 C 1 D 1 - куб.

• NK∩AD=F 1 - вершина трехгранного угла образованного плоскостями α , ABC, ADD 1 .
• F 1 M∩CD=F 2 - вершина трехгранного угла образованного плоскостями α , ABC, CDD 1 . F 1 M ∩BC=P.
• NK∩DD 1 =F 3 - вершина трехгранного угла образованного плоскостями α , D 1 DC, ADD 1 .
• F 3 F 2 ∩D 1 C 1 =Q, F 3 F 2 ∩CC 1 =L.

1) Сечение параллелепипеда по трем точкам,

лежащим на трех параллельных ребрах (случай 1)

2) Сечение параллелепипеда по трем точкам,

лежащим на трех параллельных ребрах ( случай 2 )

3) Сечение параллелепипеда по трем точкам,

не лежащим на трех параллельных ребрах ( случай 1)

4) сечение параллелепипеда по трем точкам,

лежащим на трех соседних ребрах.

5) Маленькая проверка

К содержанию

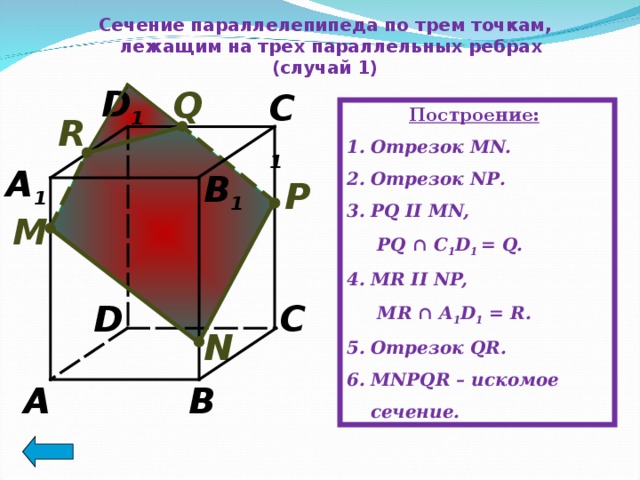
Сечение параллелепипеда по трем точкам,

лежащим на трех параллельных ребрах (случай 1)

D 1

Q

C 1

Построение:

• Отрезок MN.
• Отрезок N Р .
• Р Q II MN,

PQ ∩ C 1 D 1 = Q.

• MR II NP,

MR ∩ A 1 D 1 = R.

• Отрезок QR.
• MN Р QR – искомое сечение.

R

A 1

B 1

P

М

D

C

N

B

A

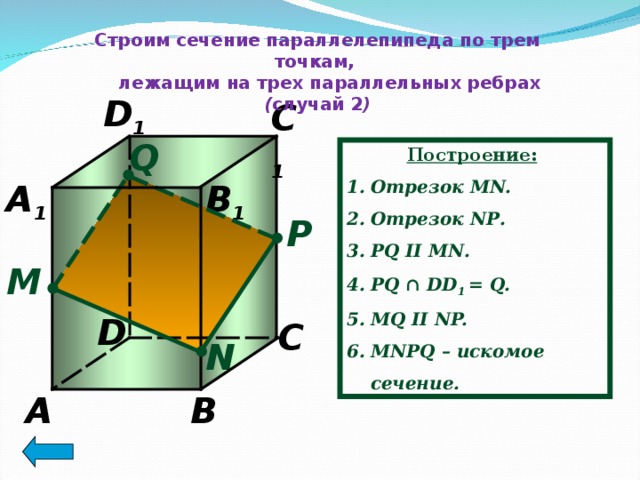
Строим сечение параллелепипеда по трем точкам,

лежащим на трех параллельных ребрах ( случай 2 )

D 1

C 1

Q

Построение:

• Отрезок MN.
• Отрезок N Р .
• Р Q II MN .
• PQ ∩ DD 1 = Q.
• MQ II NP.
• MN Р Q – искомое сечение.

A 1

B 1

P

М

D

C

N

A

B

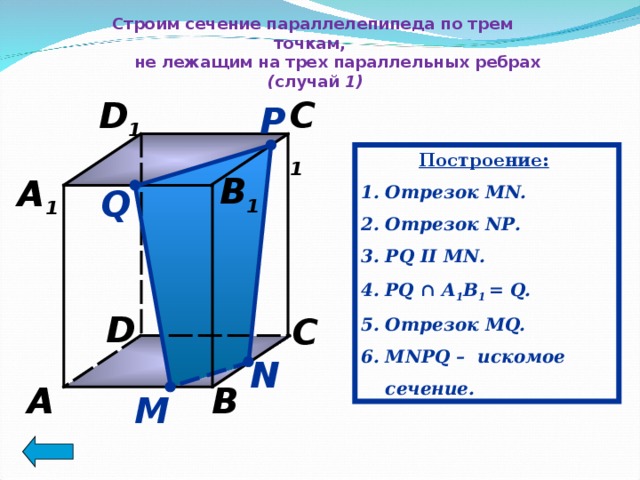
Строим сечение параллелепипеда по трем точкам,

не лежащим на трех параллельных ребрах ( случай 1)

C 1

D 1

P

Построение:

• Отрезок MN.
• Отрезок N Р .
• Р Q II MN .
• PQ ∩ А 1 В 1 = Q.
• Отрезок MQ.
• MN Р Q – искомое сечение.

B 1

A 1

Q

D

C

N

B

A

М

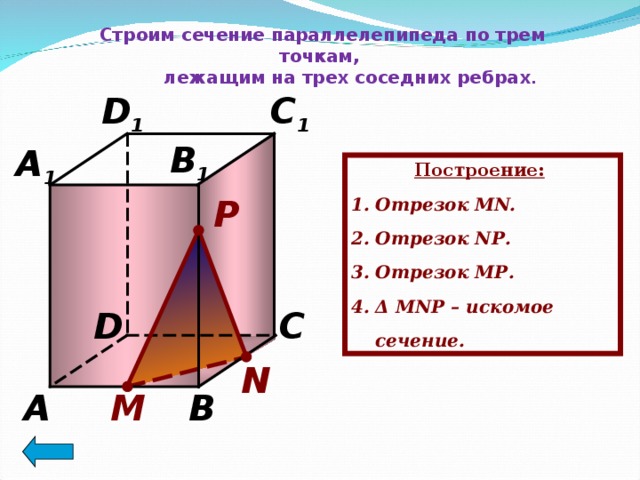
Строим сечение параллелепипеда по трем точкам,

лежащим на трех соседних ребрах .

C 1

D 1

B 1

A 1

Построение:

• Отрезок MN.
• Отрезок N Р .
• Отрезок M Р .
• Δ MN Р – искомое сечение.

P

D

C

N

B

A

М

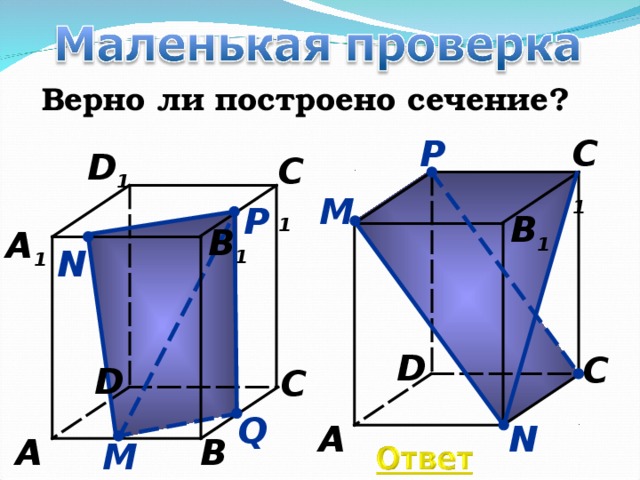
Верно ли построено сечение?

P

C 1

D 1

C 1

М

P

B 1

B 1

A 1

N

D

C

D

C

Q

A

N

B

A

М

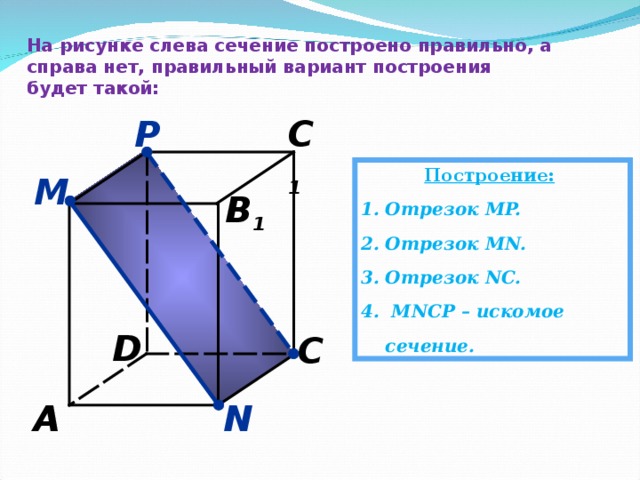
На рисунке слева сечение построено правильно, а справа нет, правильный вариант построения будет такой:

C 1

P

Построение:

• Отрезок MP.
• Отрезок MN.
• Отрезок NC.
• MNC Р – искомое сечение.

М

B 1

D

C

A

N

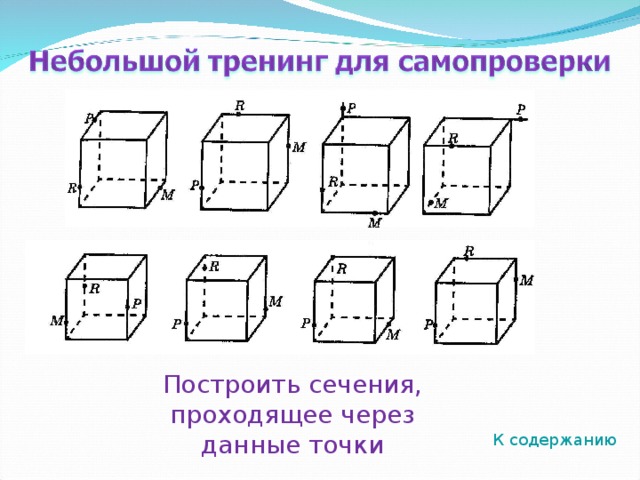
Построить сечения, проходящее через данные точки

К содержанию

Все рассмотренные ранее построения плоских сечений многогранников осуществлялись на основании аксиом стереометрии и теорем о параллельности прямых и плоскостей.

Вместе с тем, существуют определенные методы построения плоских сечений многогранников Наиболее эффективными в школьном курсе геометрии являются следующие три метода :

• метод следов;
• метод внутреннего проектирования;
• комбинированный метод.

Определение : Прямая, по которой секущая плоскость α пересекает плоскость основания многогранника, называется следом плоскости α в плоскости этого основания

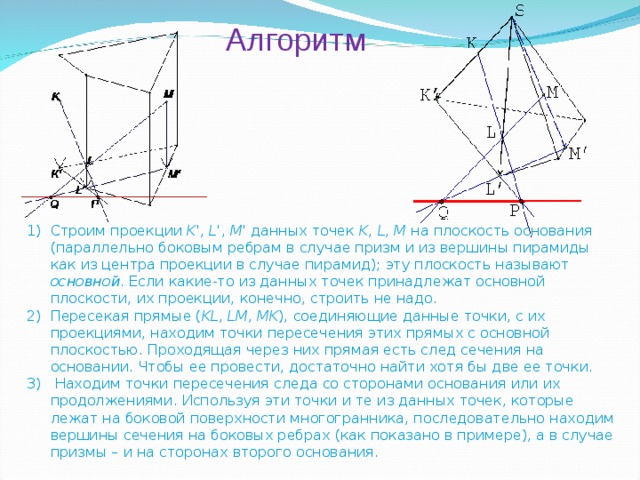
Алгоритм

• Строим проекции K ', L ', M ' данных точек K , L , M на плоскость основания (параллельно боковым ребрам в случае призм и из вершины пирамиды как из центра проекции в случае пирамид); эту плоскость называют основной . Если какие-то из данных точек принадлежат основной плоскости, их проекции, конечно, строить не надо.
• Пересекая прямые ( KL , LM , MK ), соединяющие данные точки, с их проекциями, находим точки пересечения этих прямых с основной плоскостью. Проходящая через них прямая есть след сечения на основании. Чтобы ее провести, достаточно найти хотя бы две ее точки.
• Находим точки пересечения следа со сторонами основания или их продолжениями. Используя эти точки и те из данных точек, которые лежат на боковой поверхности многогранника, последовательно находим вершины сечения на боковых ребрах (как показано в примере), а в случае призмы – и на сторонах второго основания.

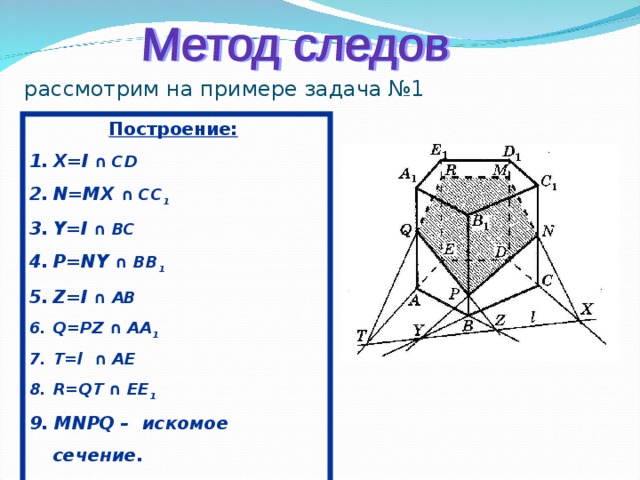
рассмотрим на примере задача №1

Построение:

• Х= l ∩ CD
• N=MX ∩ CC 1
• Y=l ∩ BC
• P=NY ∩ BB 1
• Z=l ∩ AB
• Q=PZ ∩ AA 1
• T=l ∩ AE
• R=QT ∩ EE 1

9. MN Р Q – искомое сечение.

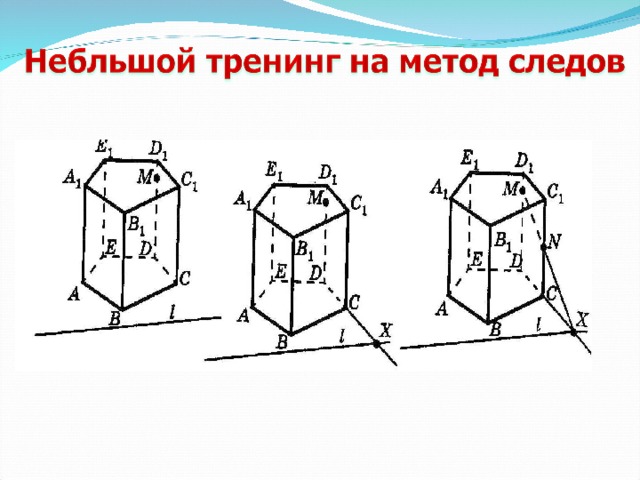
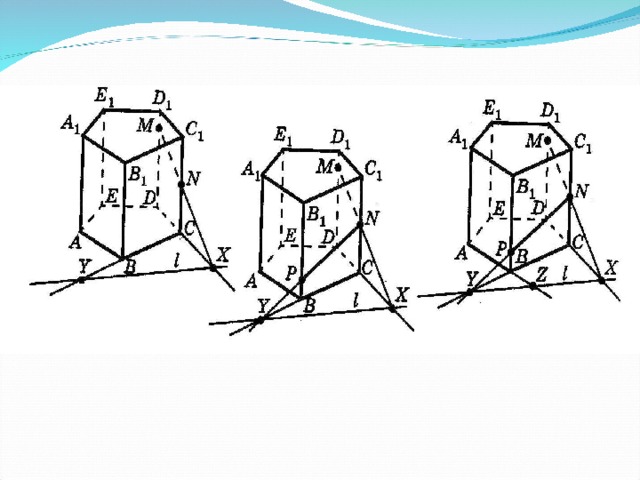
В некоторых учебных пособиях метод построения сечений многогранников, который мы сейчас будем рассматривать, называют методом внутреннего проектирования или методом соответствий, или методом диагональных сечений. Мы примем первое название метода.

Сущность метода внутреннего проектирования рассмотрим на примерах построения сечений призмы и пирамиды.

Алгоритм построения сечения методом внутреннего проектирования.

• Построить вспомогательные сечения и найти линию их пересечения.
• Построить след сечения на ребре многогранника.
• Если точек сечения не хватает для построения самого сечения повторить пп.1-2.

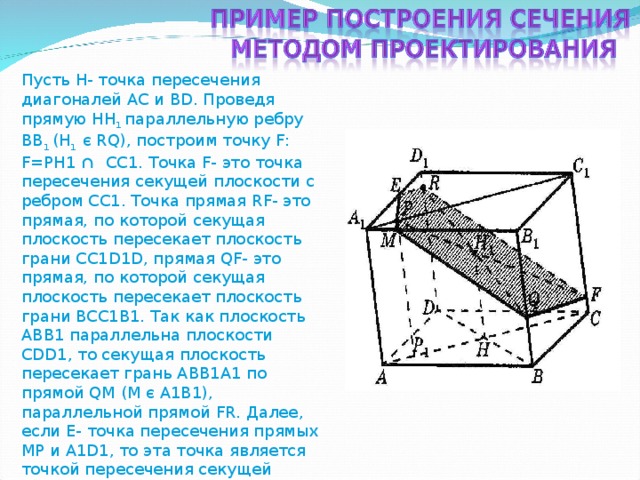
Пусть H- точка пересечения диагоналей AC и BD . Проведя прямую HH 1 параллельную ребру BB 1 (H 1 є RQ) , построим точку F : F=PH1 ∩ CC1. Точка F- это точка пересечения секущей плоскости с ребром CC1. Точка прямая RF- это прямая, по которой секущая плоскость пересекает плоскость грани CC1D1D , прямая QF- это прямая, по которой секущая плоскость пересекает плоскость грани BCC1B1. Так как плоскость ABB1 параллельна плоскости CDD1 , то секущая плоскость пересекает грань ABB1A1 по прямой QM (М є A1B1) , параллельной прямой FR . Далее, если E- точка пересечения прямых MP и A1D1 , то эта точка является точкой пересечения секущей плоскости и ребра A1D1 .

Пятиугольник ERFQM- искомое сечение.

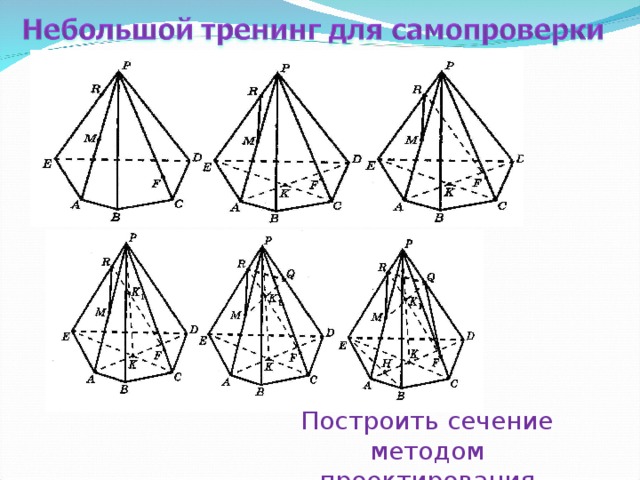
Построить сечение методом проектирования

Сущность комбинированного метода построения сечений многогранников состоит в том, что на некоторых этапах построения сечения применяется или метод следов, или метод внутреннего проектирования, а на других этапах построение этого сечения осуществляется с использованием теорем, изученных в разделе “ Параллельность в пространстве ” и др.

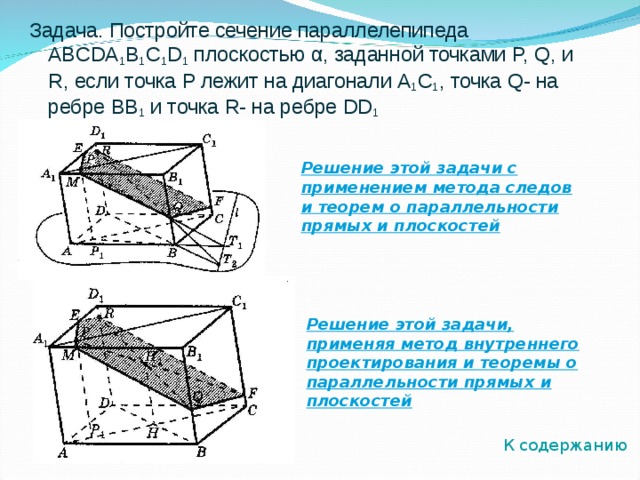
Задача. Постройте сечение параллелепипеда ABCDA 1 B 1 C 1 D 1 плоскостью α , заданной точками P, Q, и R , если точка P лежит на диагонали A 1 C 1 , точка Q- на ребре BB 1 и точка R- на ребре DD 1

Решение этой задачи с применением метода следов и теорем о параллельности прямых и плоскостей

Решение этой задачи, применяя метод внутреннего проектирования и теоремы о параллельности прямых и плоскостей

К содержанию