Департамент образования Ивановской области
ОГБПОУ «Кинешемский педколледж»
Построение таблиц истинности
Методическое пособие
Подготовила: Совина М.В.
преподаватель высшей категории
2015
М.В. Совина
Методическое пособие «Построение таблиц истинности»- Кинешма, 2015
В данном методическом пособии предлагаются материалы для самостоятельного изучения правил построения таблиц истинности в алгебре логики студентами заочного отделения. Пособие включает теоретическую часть, примеры и задания.
Содержание
| Алгебра логики………………………………………………………………... | 4 |
| Логические операции…………………………………………………………. | 5 |
| Этапы построения таблиц истинности……………………………………… | 9 |
| Пример построения таблиц истинности……………………………………. | 10 |
| Задания для самоконтроля…………………………………………………… | 12 |
| Рекомендуемая литература…………………………………………………... | 13 |
Алгебра логики
Логика - это наука о формах и способах мышления. Логика позволяет строить формальные модели окружающего мира.
Первые учения о формах и способах рассуждений возникли
в странах Древнего Востока (Китай, Индия), но в основе
современной логики лежат учения, созданные древнегреческими
мыслителями.
Основными формами мышления являются: понятие, высказывание, умозаключение.
Понятие - это форма мышления, фиксирующая основные, существенные признаки объекта.
Высказывание - это форма мышления, в которой что-либо утверждается или отрицается о свойствах реальных предметов и отношениях между ними. Высказывание может быть либо ИСТИННО либо ЛОЖНО.
Умозаключение - это форма мышления, с помощью которой из одного или нескольких суждений может быть получено новое суждение
Основы формальной логики заложил Аристотель.
Алгебра логики была разработана для того, чтобы можно было
оперировать высказываниями, не вникая в их содержание.
Алгебра логики — это математический аппарат, с помощью которого записывают, вычисляют, упрощают и преобразовывают логические высказывания.
Создателем алгебры логики является живший в ХIХ веке английский математик Джордж Буль, в честь которого эта алгебра названа булевой алгеброй.
Логические операции
Простые высказывания обозначаются латинскими буквами: А, В, С …
Bысказывания, образованные из других высказываний с помощью логических связок, называются составными.
Употребляемые в обычной речи слова и словосочетания "не”, “и”, “или”, “если... , то”, “тогда и только тогда” и другие позволяют из простых высказываний строить новые высказывания. Такие слова и словосочетания называются логическими связками.
Каждая логическая связка рассматривается как операция над логическими высказываниями и имеет свое название и обозначение.
Пусть через А обозначено высказывание “Тимур поедет летом на море”,
а через В — высказывание “Тимур летом отправится в горы”.
А, В — логические переменные, каждое из которых мoжет принимать только два значения — “истина” или “ложь”, обозначаемые, соответственно, “1” или “0”.
Составное высказывание “Тимур летом побывает на море и в горах” можно кратко записать как А и В.
Здесь “и” — логическая связка.
Составное высказывание “Тимур летом побывает на море или в горах” можно кратко записать как А или В.
Здесь “или” — логическая связка.
Истинность или ложность получаемых составных высказываний зависит от истинности или ложности элементарных высказываний.
В алгебре логики в соответствии с логическими связками используют 5 базовых логические операций: конъюнкция, дизъюнкция, инверсия, импликация и эквивалентность. Для каждой из операций составлены таблицы истинности
Таблица истинности логической операции выражает соответствие между всевозможными наборами значений исходных данных, переменными и значениями, получаемыми в результате выполнения операции.


Приоритеты логических операций:
инверсия (отрицание),
конъюнкция (логическое умножение),
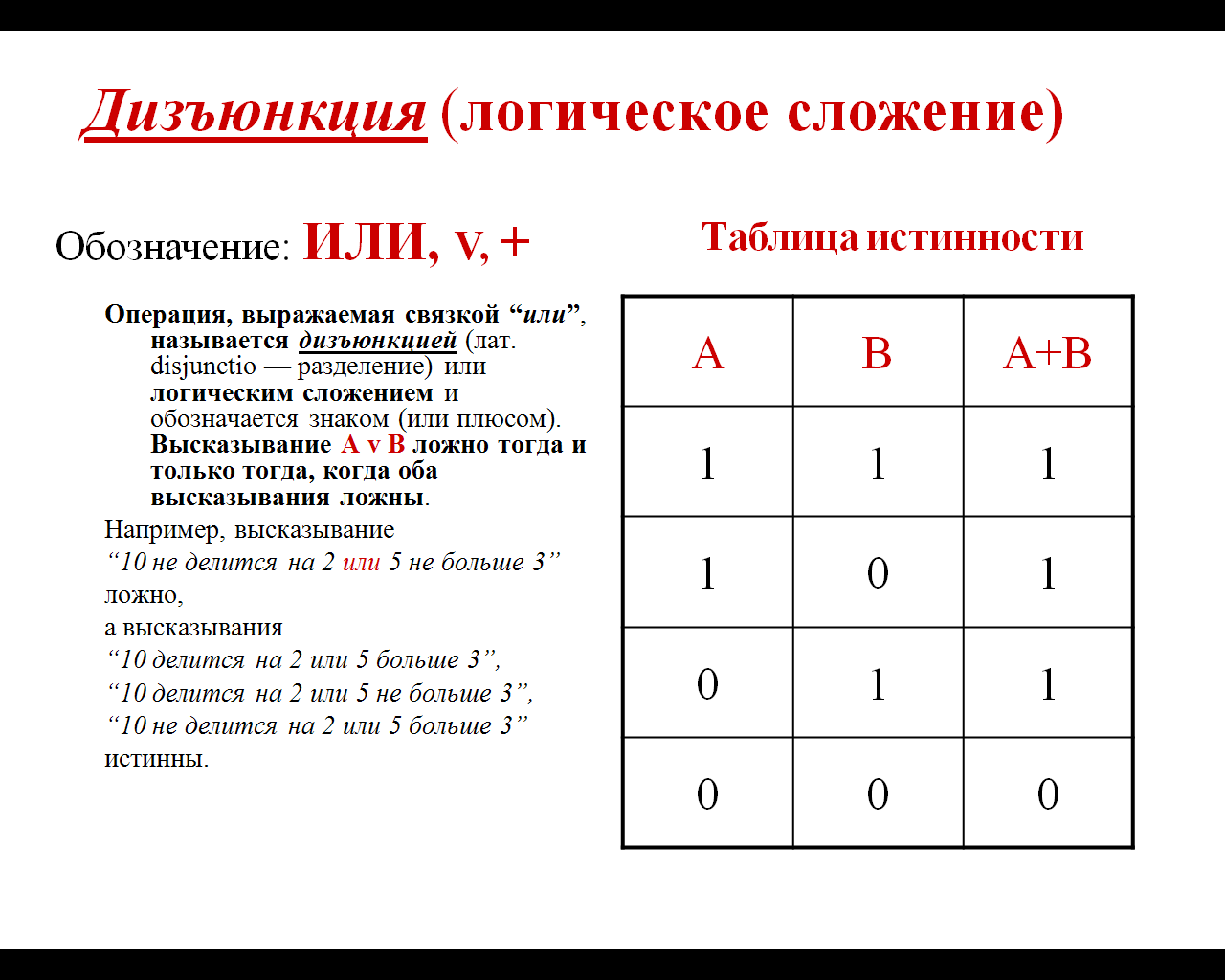
дизъюнкция (логическое сложение),
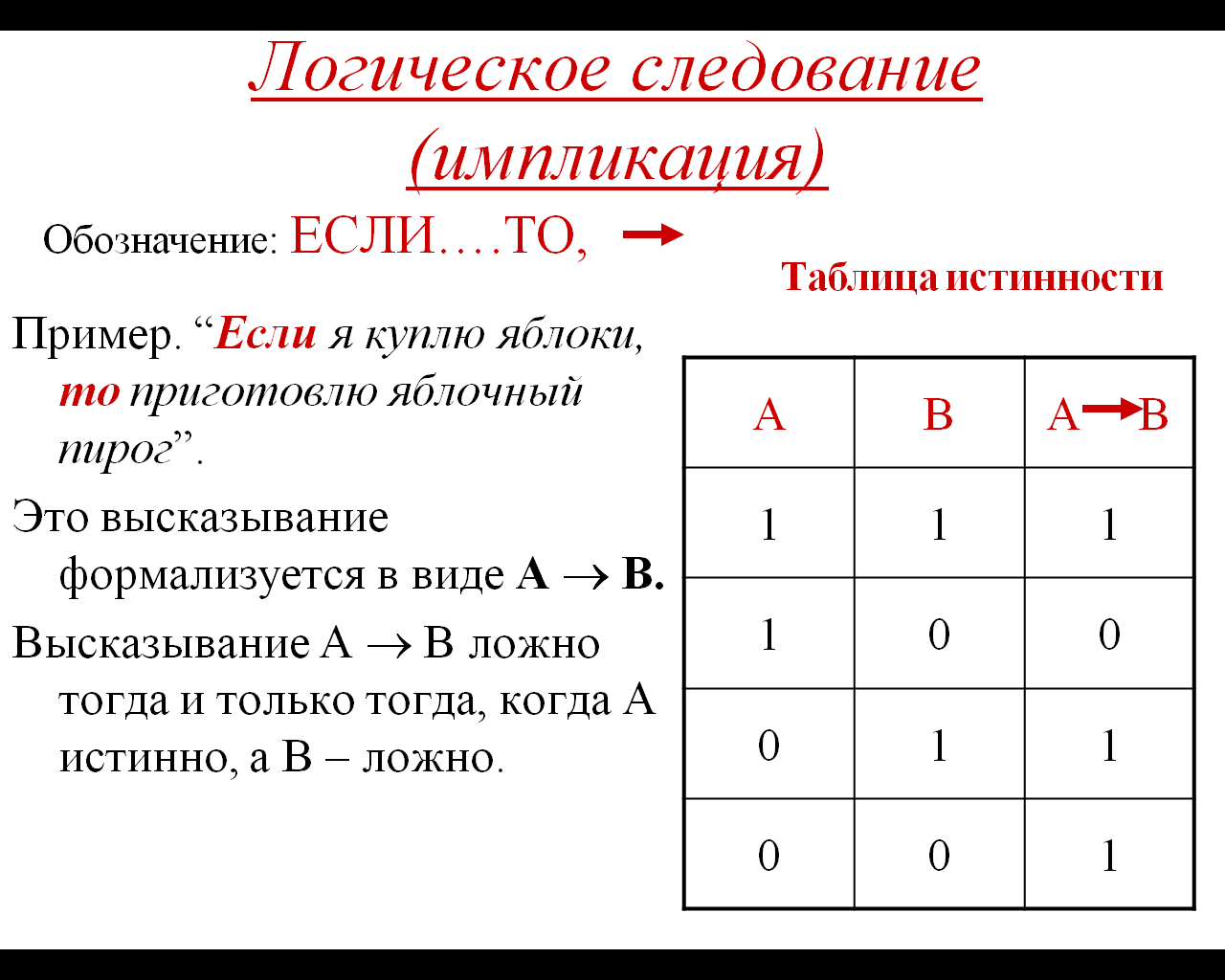
импликация (следование),
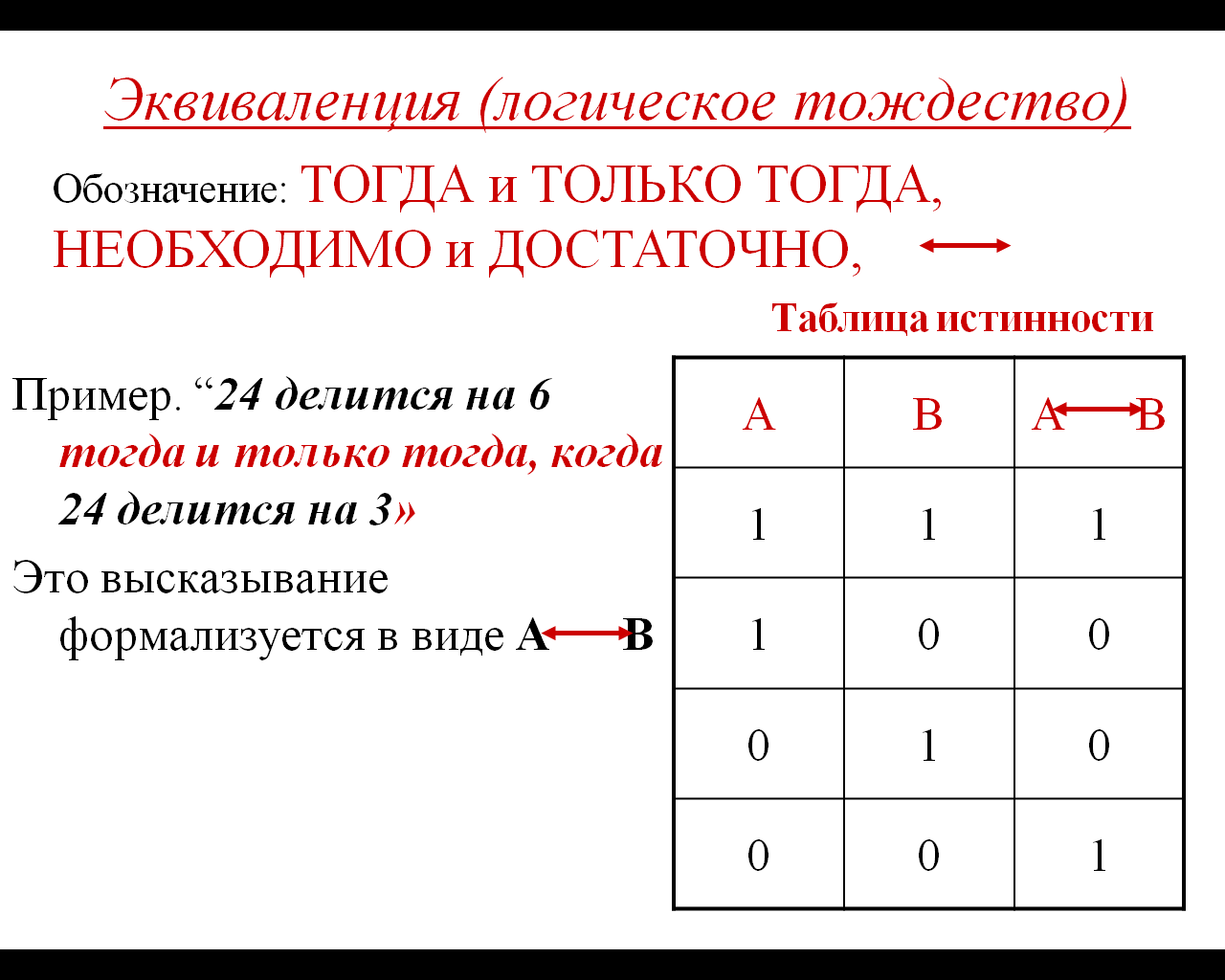
эквивалентность (равносильность).
Изменить последовательность выполнения логических операций можно с помощью скобок.
Этапы построения таблиц истинности
Решение логических выражений принято записывать в виде таблиц истинности – таблиц, в которых по действиям показано, какие значения принимает логическое выражение при всех возможных наборах его переменных.
Для составления таблицы необходимо:
Выяснить количество строк в таблице. Оно равно 2n+1, где n-количество переменных.
Выяснить количество столбцов. Оно равно количество переменных плюс количество логических операций.
Установить последовательность выполнения логических операций с учетом скобок и приоритетов.
Построить таблицу, указывая названия столбцов и возможные наборы значений исходных логических переменных.
Заполнить таблицу истинности по столбцам.
Заполнение столбцов значений переменных таблицы:
1. разделить колонку значений первой переменной пополам и заполнить верхнюю часть «0», а нижнюю «1»;
2. разделить колонку значений второй переменной на четыре части и заполнить каждую четверть чередующимися группами «0» и «1», начиная с группы «0»;
3. продолжать деление колонок значений последующих переменных на 8, 16 и т.д. частей и заполнение их группами «0» или «1» до тех пор, пока группы «0» и «1» не будут состоять из одного символа.
Заполнение столбцов, содержащих логические операции, выполняется в соответствии с таблицами истинности этих логических операций
Примеры построения таблиц истинности
Пример 1. Для формулы A/\ (B \/ ¬B /\¬C) постройте таблицу истинности.
1этап: Количество логических переменных 3, следовательно, количество строк - 23 +1= 9.
2 этап: Количество логических операций в формуле 5, количество логических переменных 3, следовательно количество столбцов - 3 + 5 = 8.
3этап: Последовательность операций:
1) ¬B
2) ¬C
3) ¬B /\¬C
4) B \/ ¬B /\¬C
5) A/\ (B \/ ¬B /\¬C)
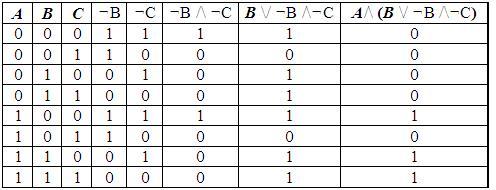
4 этап: Построение таблицы
| A | B | C | ¬B | ¬C | ¬B¬C | B¬B¬C | A(B¬B¬C) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 этап: Заполнение таблицы
Пример 2. Определите истинность логического выражения
F(А, В) = (А\/ В)/\(¬А\/¬В) .
1. В выражении две переменные А и В (n=2).
2. mстрок=2n, m=22=4 строки.
3. В формуле 5 логических операций.
4. Расставляем порядок действий
1) А\/ В; 2) ¬А; 3) ¬В; 4) ¬А\/¬В; 5) (А\/ В)/\(¬А\/¬В).
5. Кстолбцов=n+5=2+5=7 столбцов.
| А | В | А\/ В | ¬А | ¬В | ¬А\/¬В | F |
| 0 | 0 | 0 | 1 | 1 | 1 | 0 |
| 0 | 1 | 1 | 1 | 0 | 1 | 1 |
| 1 | 0 | 1 | 0 | 1 | 1 | 1 |
| 1 | 1 | 1 | 0 | 0 | 0 | 0 |
Вывод: логическое выражение принимает значение истина при наборах F(0,1)=1 и F(1,0)=1.
Задания для самоконтроля
Составьте таблицу истинности логического выражения:
A B (A B)
Определите истинность логического выражения :
F(А,В) =A B C A
Постройте таблицу истинности сложного высказывания
А V (A ^ B) V (B ^ C)
Составить таблицу истинности для формулы
X·Y v X v Y v X
Составить таблицу истинности для формулы
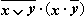
Рекомендуемая литература
Андреева Е.В. Математические основы информатики. Элективный курс: учебное пособие.-М.:БИНОМ. Лаборатория знаний, 2005
Выгодский М.Я. Справочник по элементарной математике. М. «Наука»,1989.
Соколова О.А. Универсальные поурочныеразработки по информатике 10 класс:- М.:ВАКО,2008, -400с.
Угринович Н. Информатика и ИТ 10-11- М.:Лаборатория Базовых Знаний,2001. – 464с.
Щеглов А.И. Элементарное введение в теорию множеств и алгебру логики. Иваново, 1978.
Математическая логика.- Режим доступа: // http://mathlog.h11.ru/index.html
Cистемa федеральных образовательных порталов . -
Режим лоступа:























