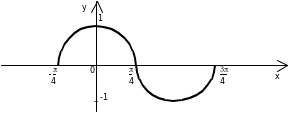Урок 27. Зачет по теме «Тригонометрические функции»
Цели урока: проверить теоретические и практические знания по теме: «Тригонометрические функции».
Ход урока:
I. Организационный момент.
Приветствие, сообщение темы и задач урока.
II. Работа по билетам.
Теоретический вопрос билета каждый учащийся рассказывает у доски. Во время ответа учитель не прерывает учащегося замечаниями, все ошибки допущенные учеником, будут разобраны в конце ответа. Учащиеся, которые слушают ответы своих одноклассников у доски, тоже должны запоминать оговорки и ошибки, чтобы принять участие в обсуждении. На подготовку отводится 10-15 минут.
| Билет №1. Теория. Числовая окружность. Пример. Найдите все числа 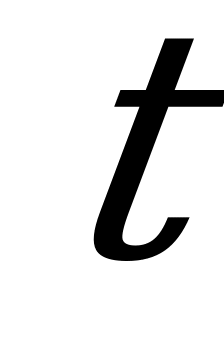 , которым на числовой окружности соответствуют точки, принадлежащие дугам: , которым на числовой окружности соответствуют точки, принадлежащие дугам:  (где (где  , соответственно, середина первой и третьей четверти числовой окружности). , соответственно, середина первой и третьей четверти числовой окружности). |
| Билет №2. Теория. Числовая окружность на координатной плоскости. Пример. Найдите координаты точек 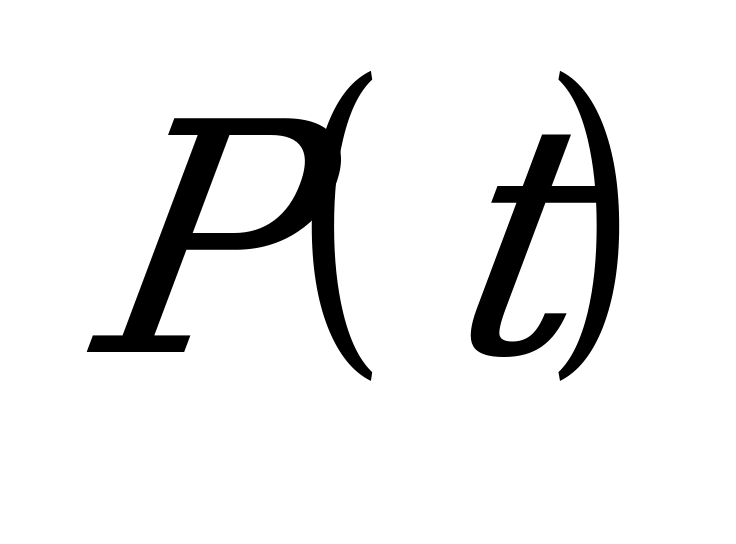 числовой окружности, если числовой окружности, если 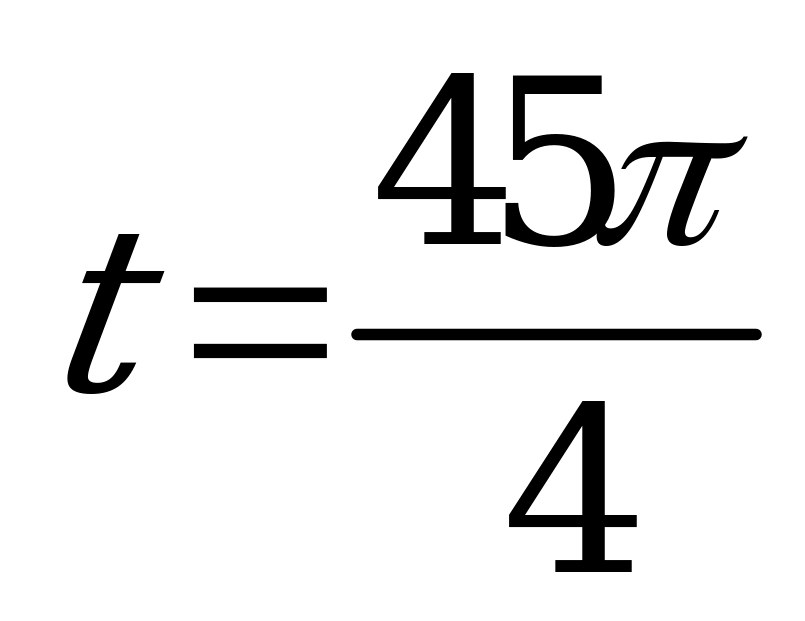 ; ; 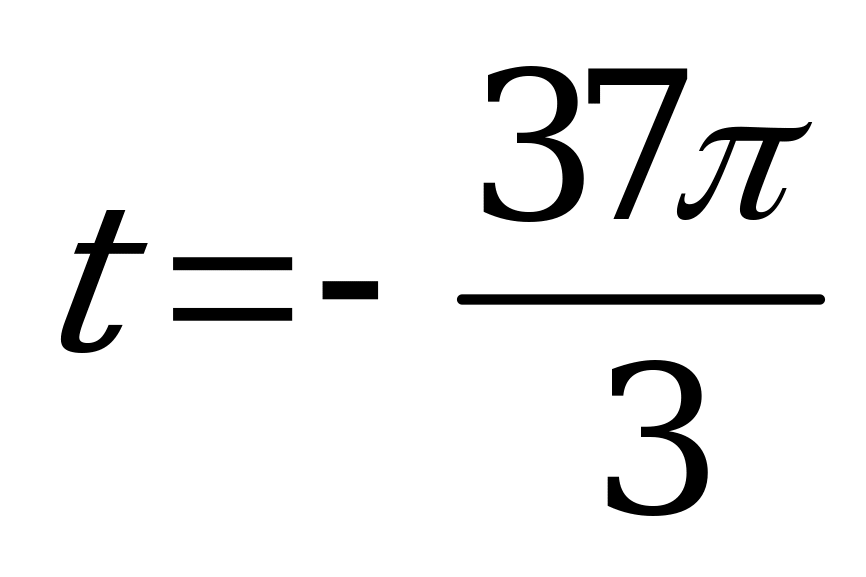 ; ; 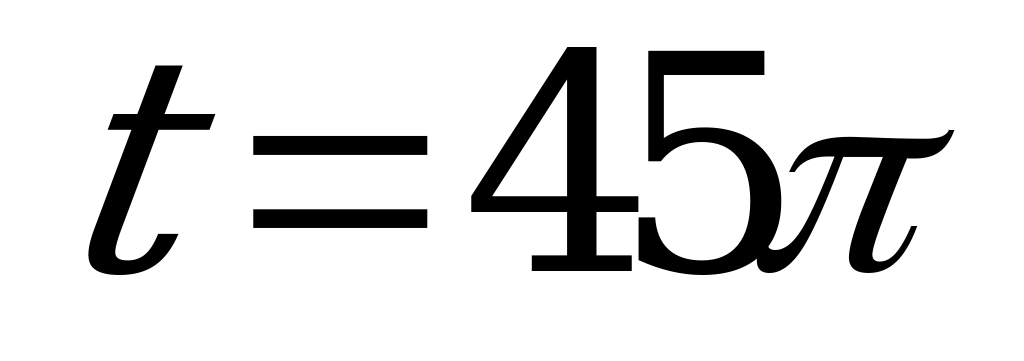 ; ; 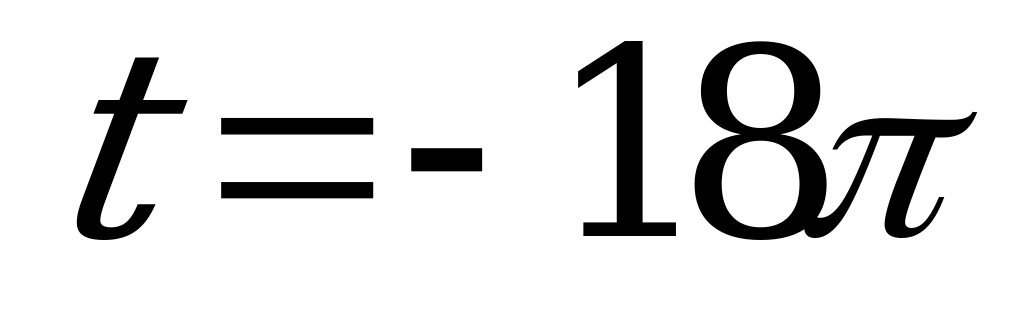 . . |
| Билет №3.. Теория. Синус, косинус, тангенс и котангенс числового аргумента. Пример. Вычислить 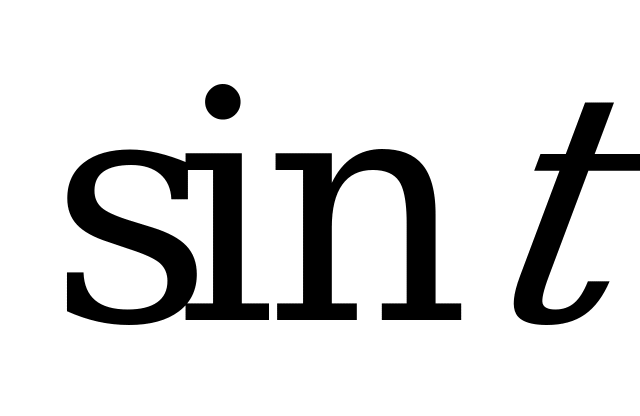 , , , , и и 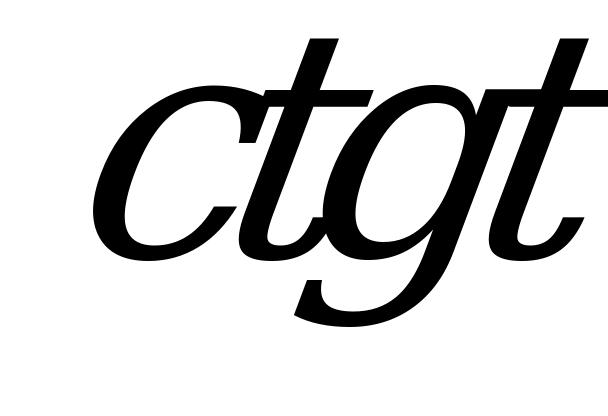 , если , если 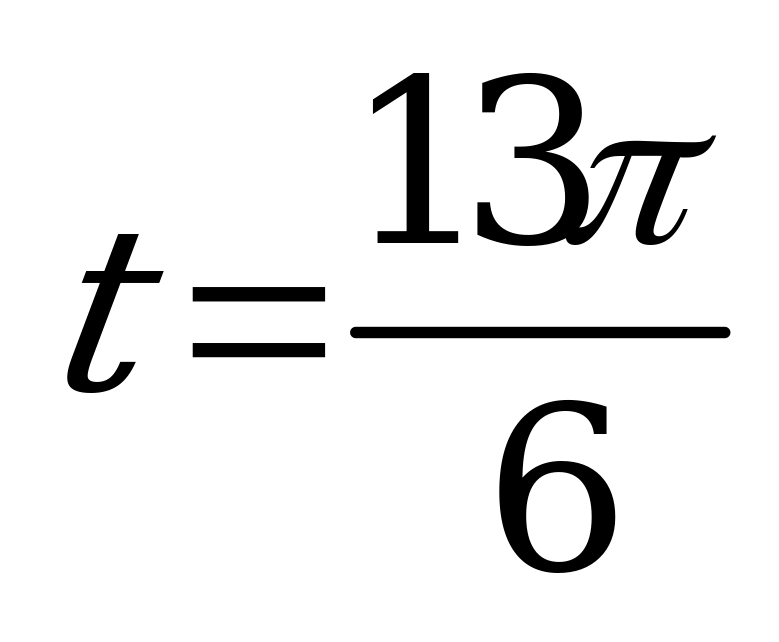 ; ; 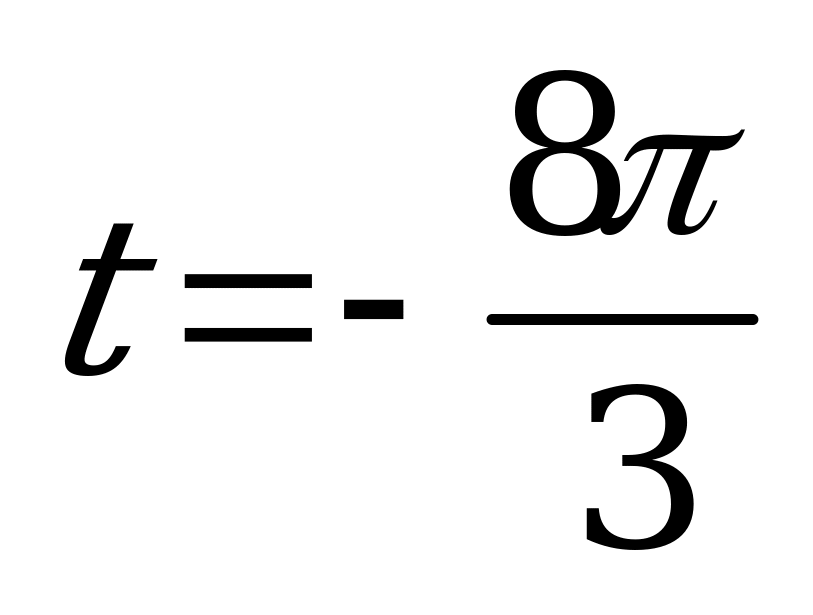 ; ; 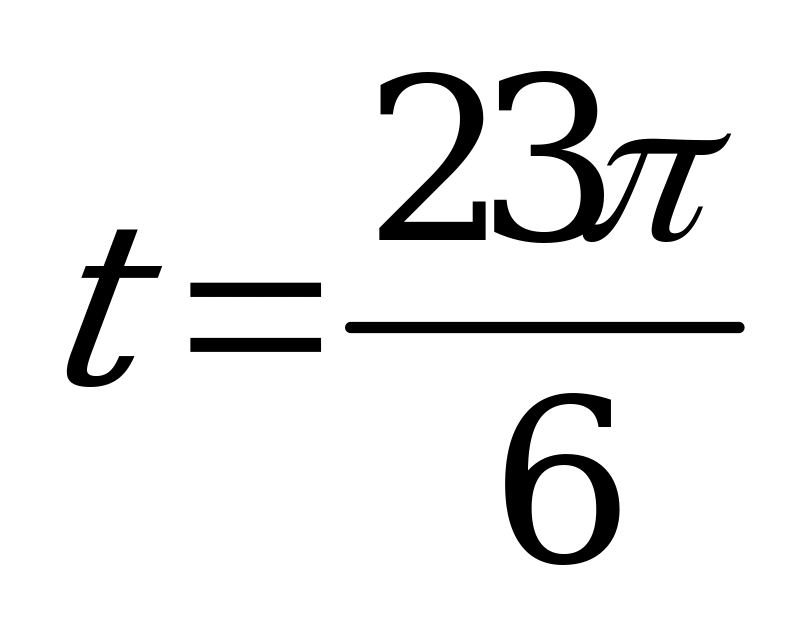 ; ;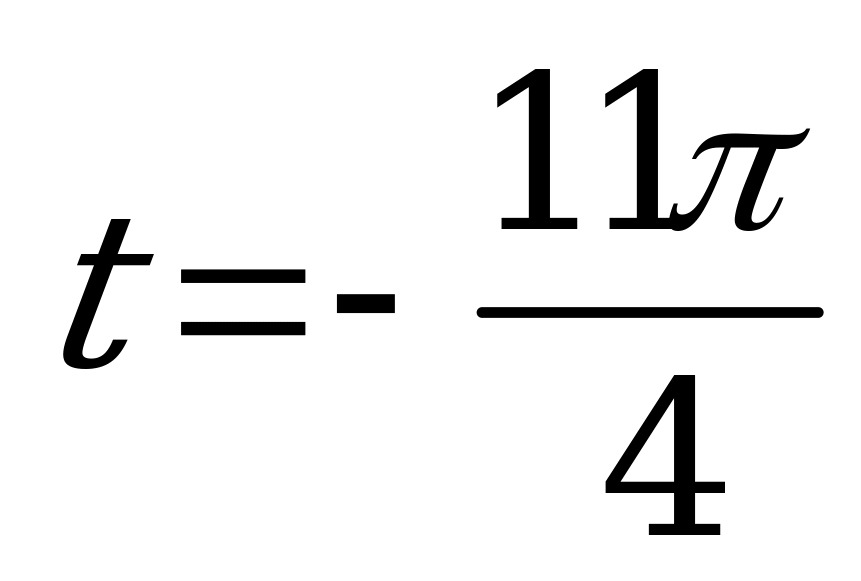 . . |
| Билет №4. Теория. Радиан, радианная мера угла. Тригонометрические функции углового аргумента Пример. 1) Переведите из градусной меры в радианную и расположите в порядке возрастания: 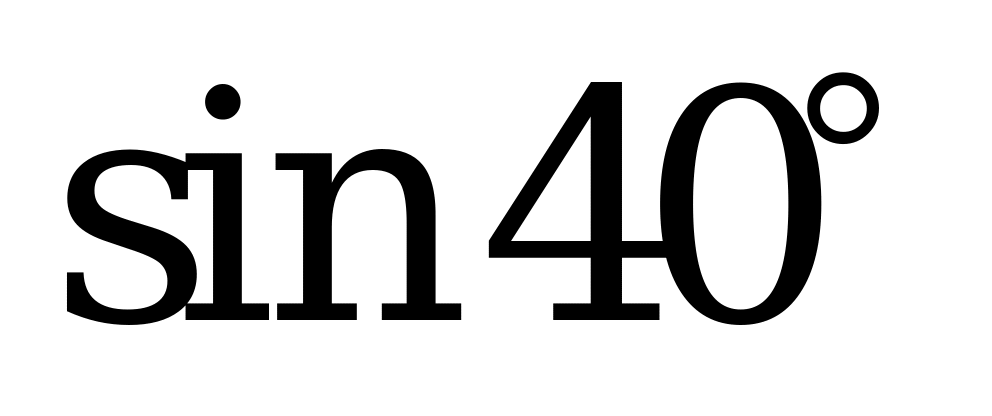 , , 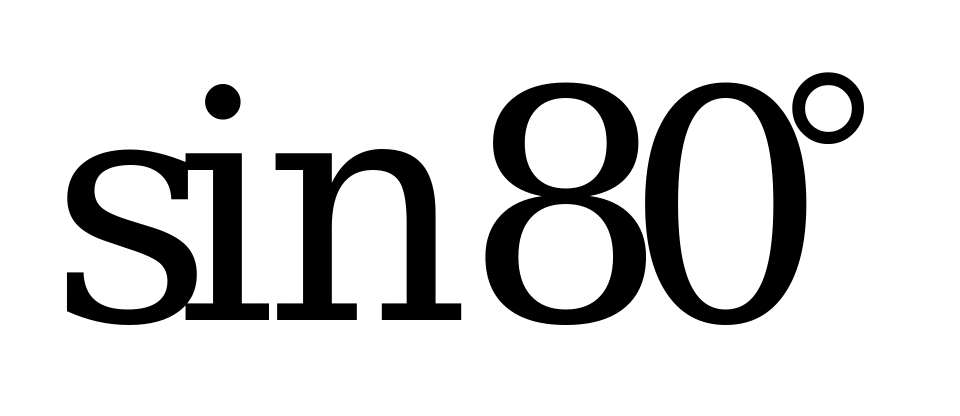 , ,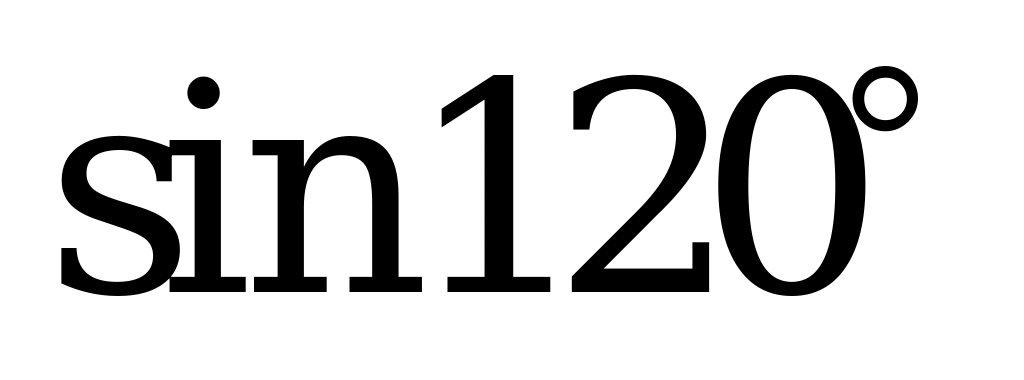 , ,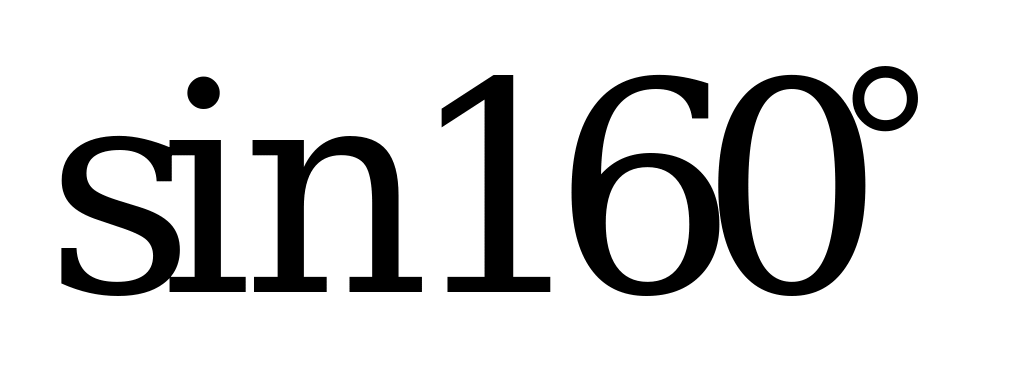 . . 2) Переведите из радианной меры в градусную и расположите в порядке убывания: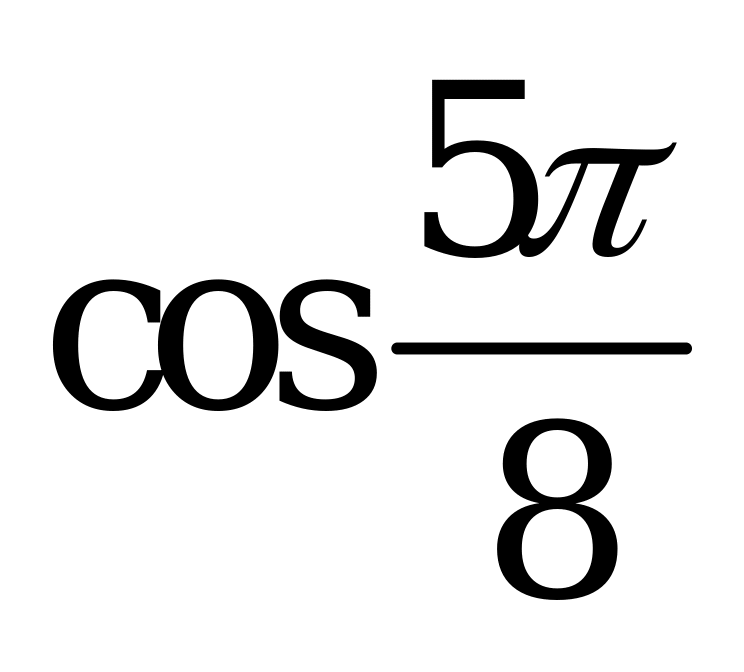 , , 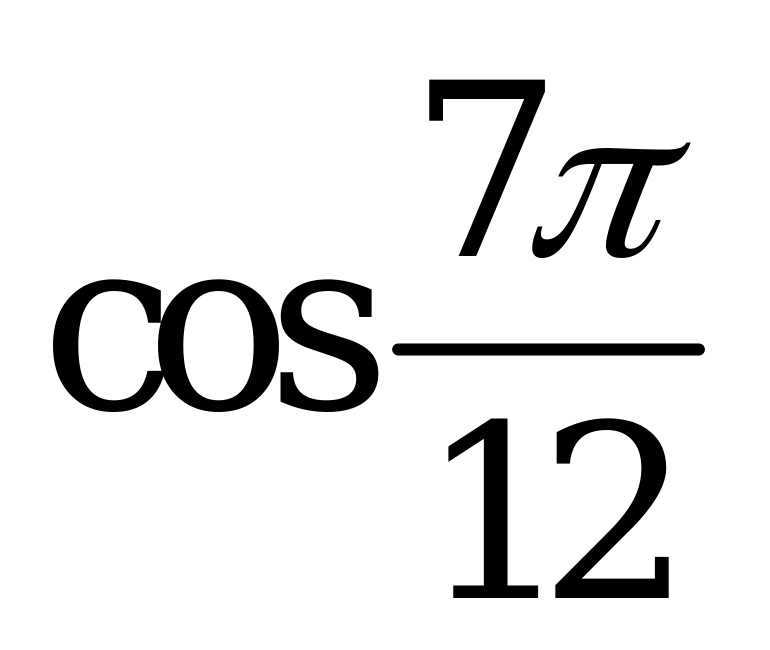 , , 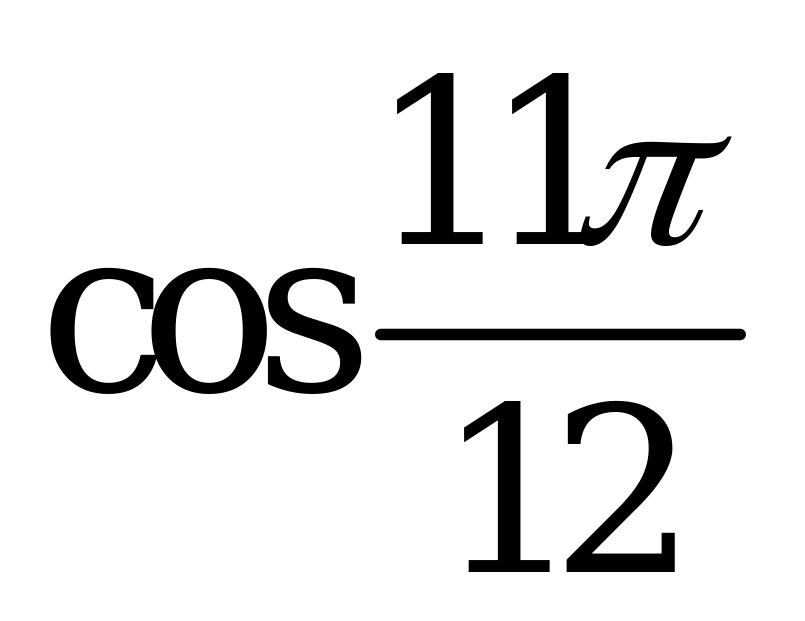 , , 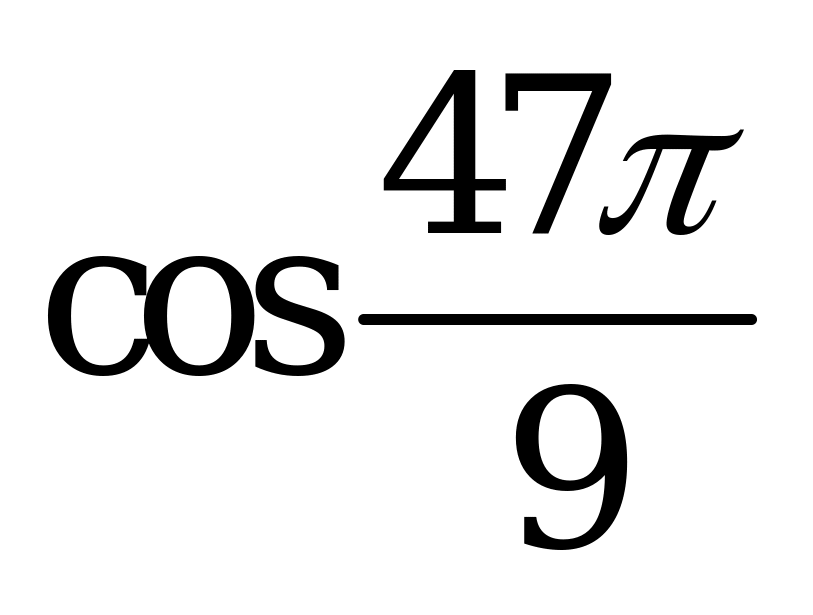 . . |
| Билет №5. Теория. Функция 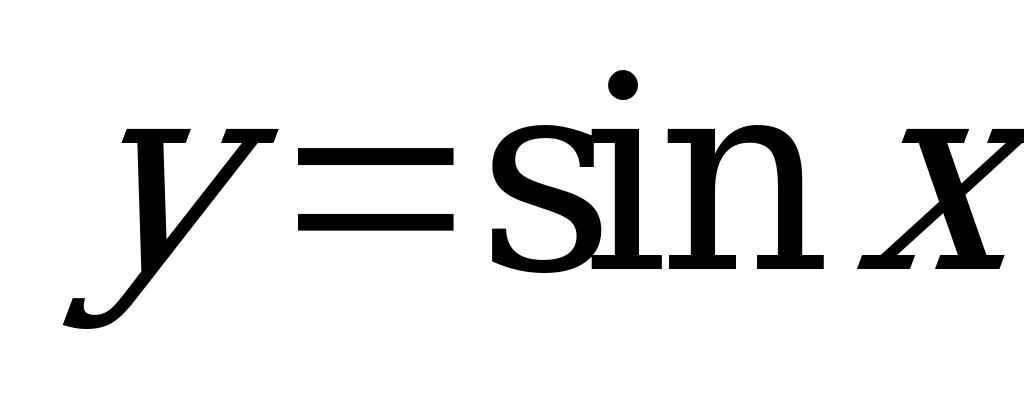 , ее график. , ее график. Пример. Построить график функции 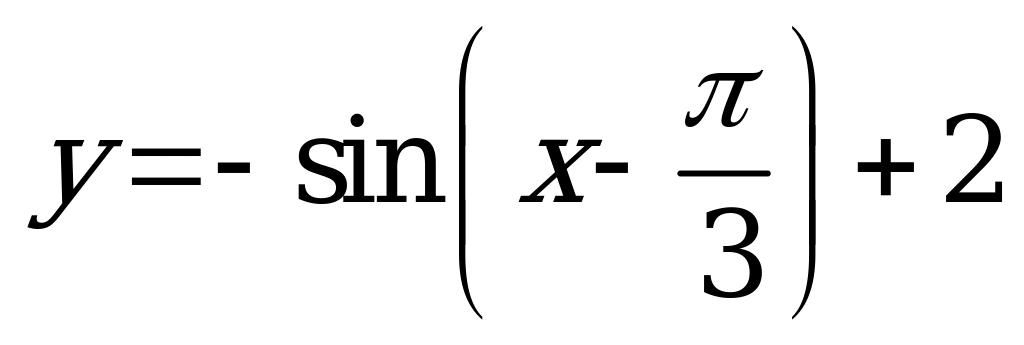 . Решить графически уравнение . Решить графически уравнение 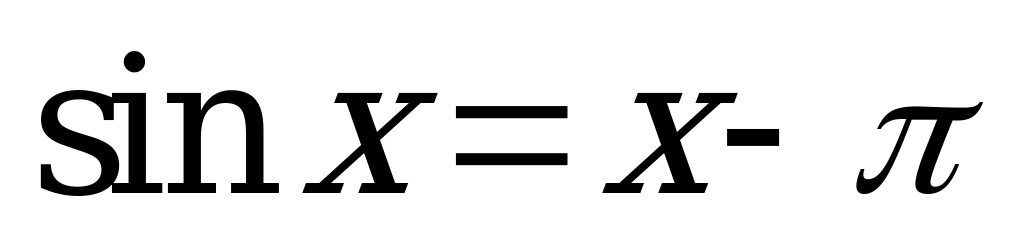 . . |
| Билет №6. Теория. Функция 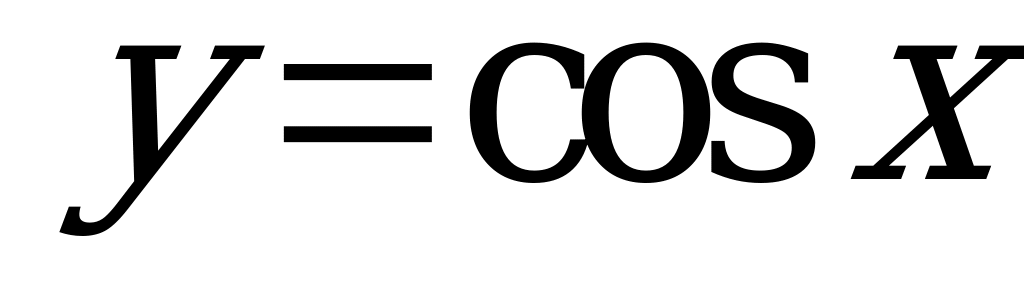 , ее график. , ее график. Пример. Построить график функции 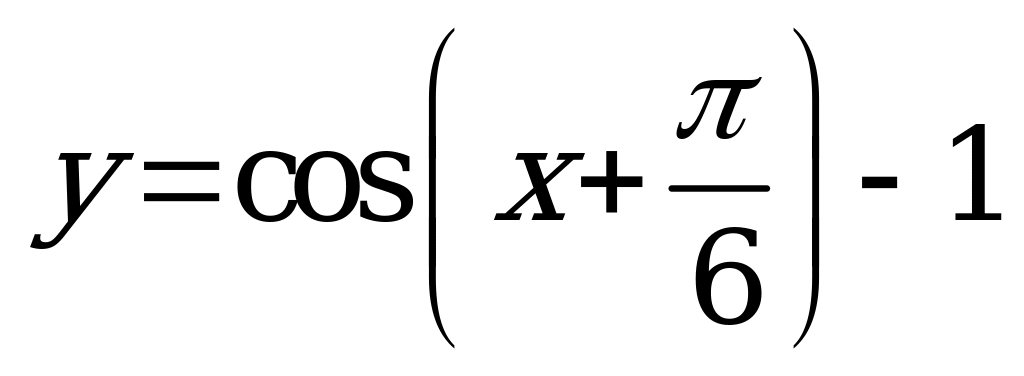 . Решить графически уравнение . Решить графически уравнение 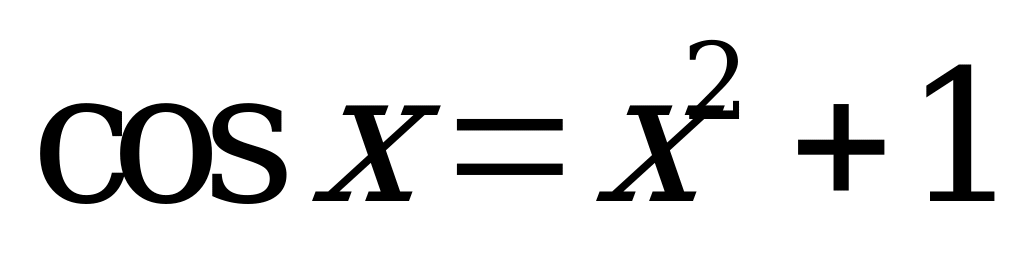 . . |
| Билет №7. Теория. Периодичность функций 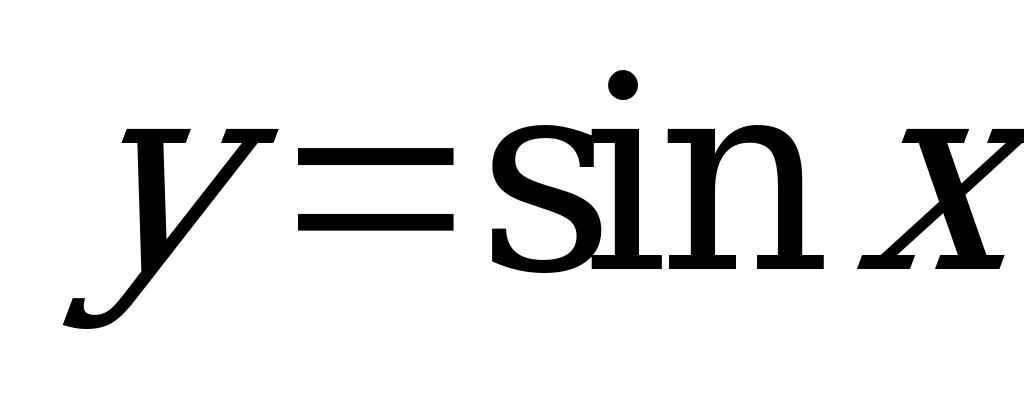 и и 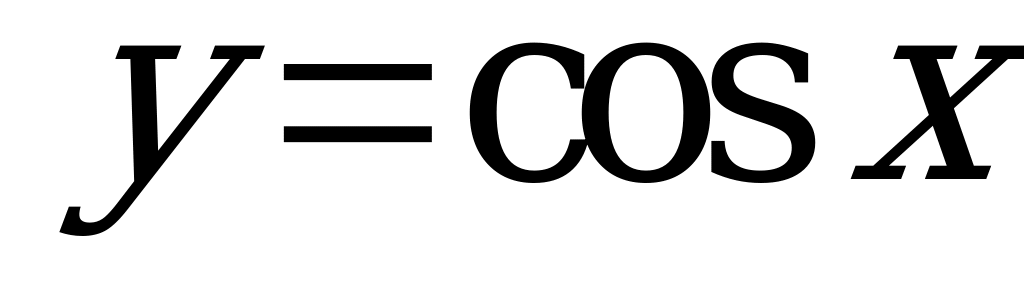 . . Пример. Найдите основной период функций: 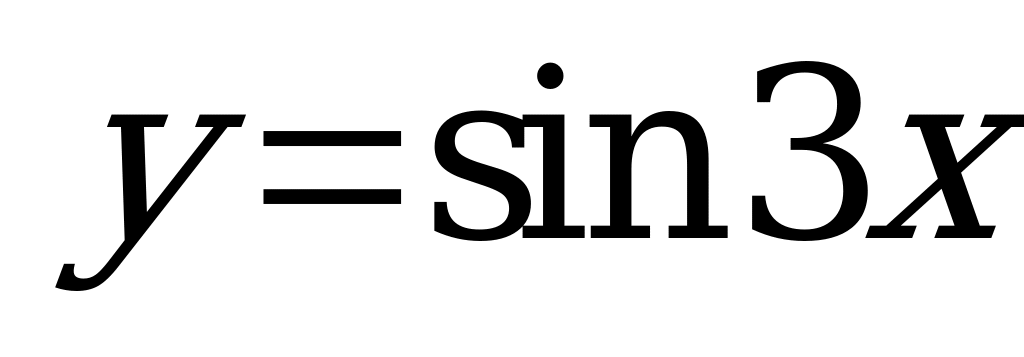 , , 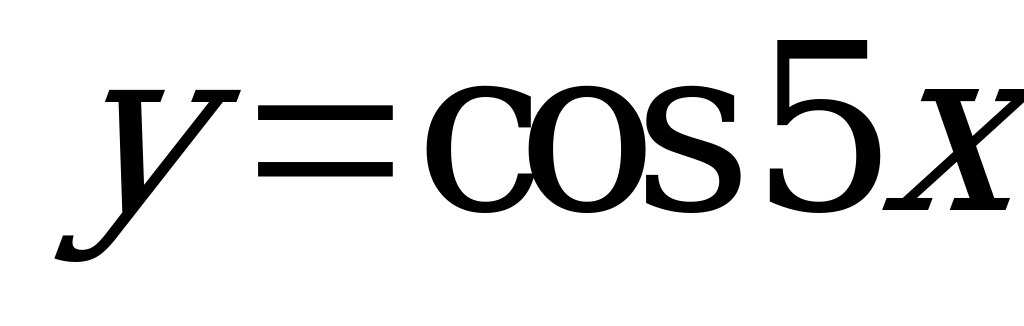 , , 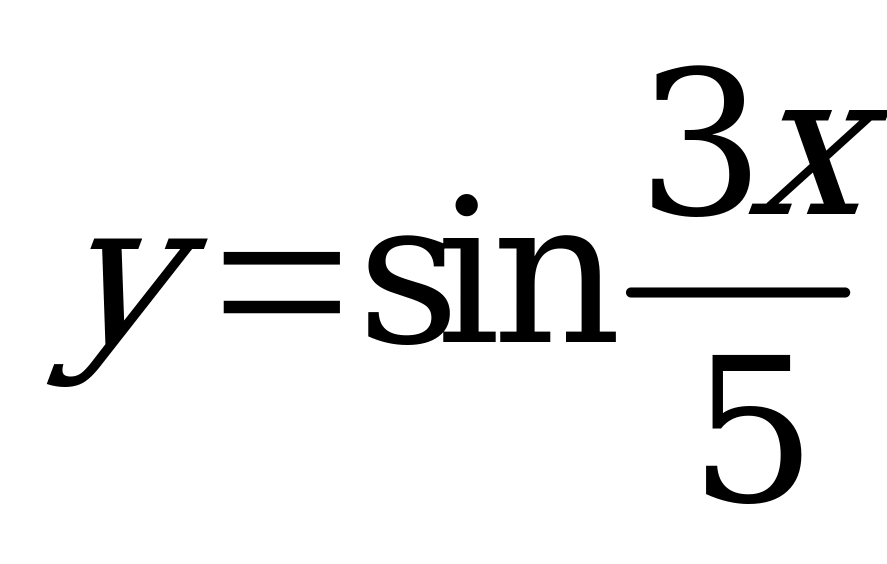 , , 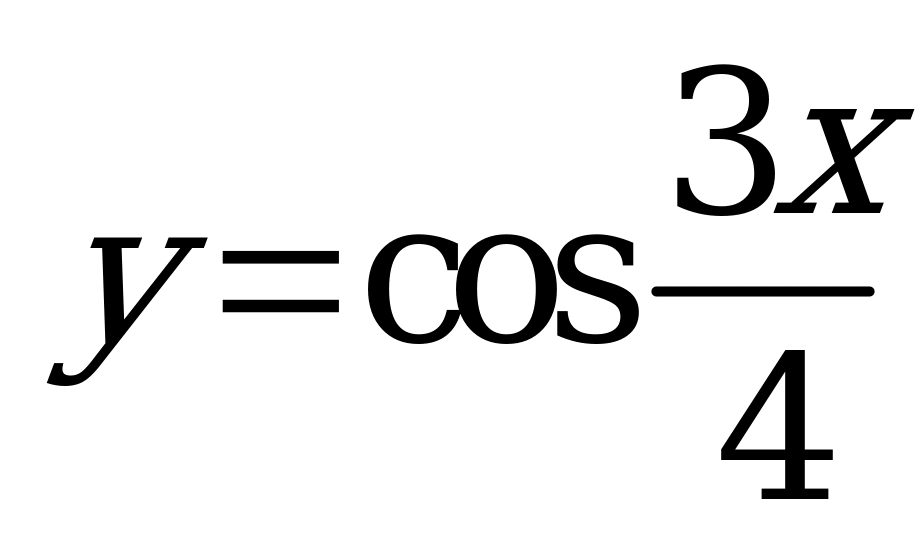 . . |
| Билет №8. Теория. Функции 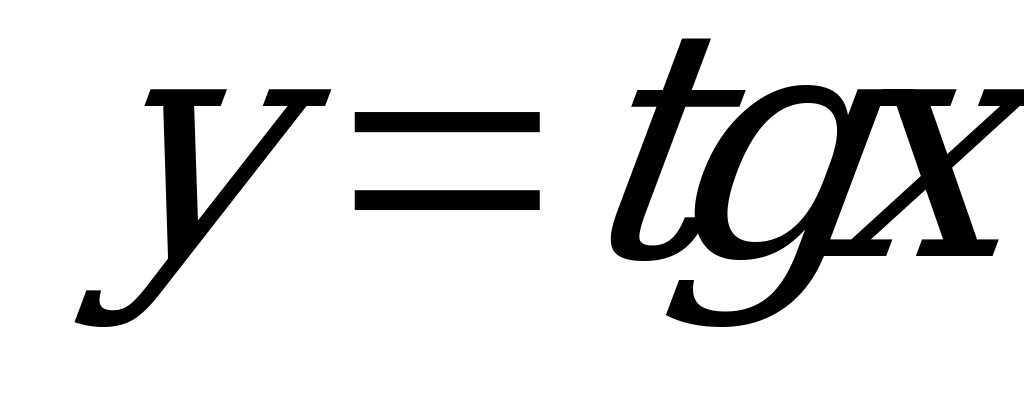 и и 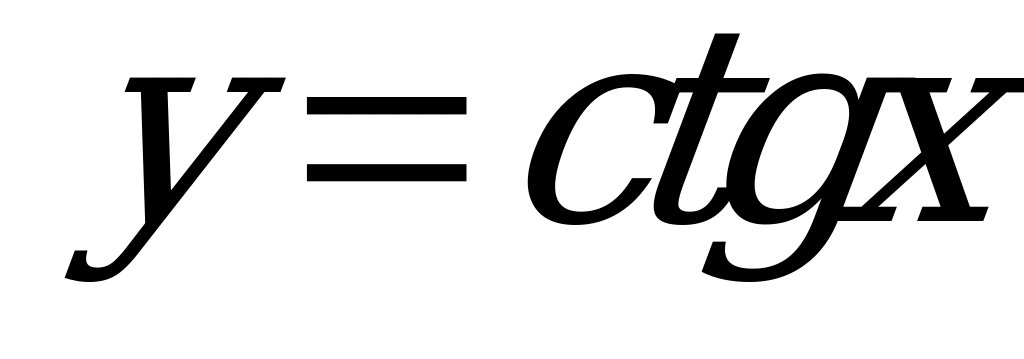 , их графики. , их графики. Пример. Построить график функций 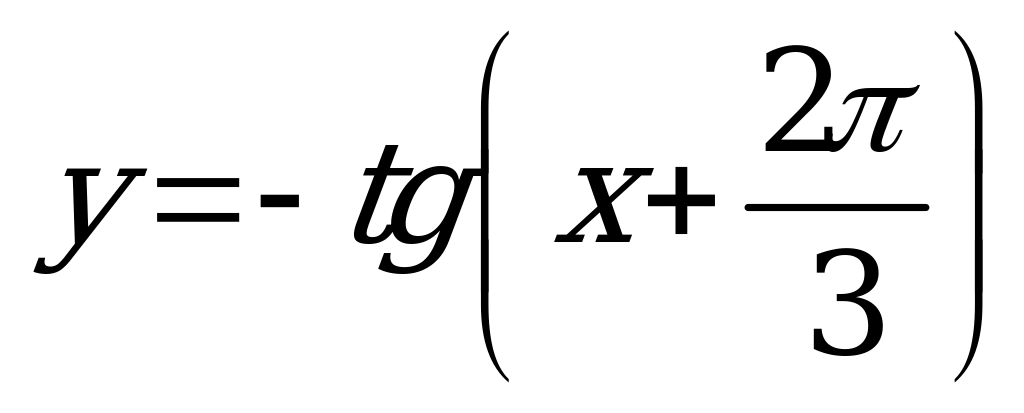 . Решить графически уравнение . Решить графически уравнение 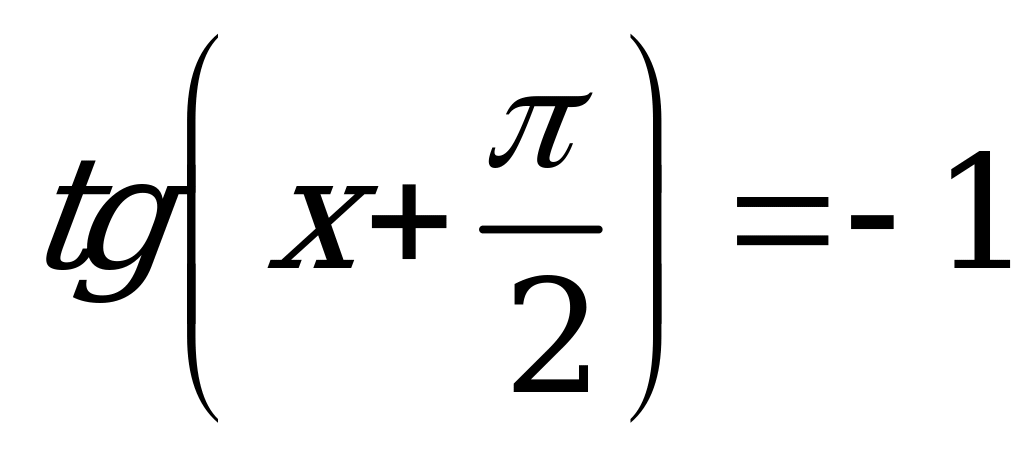 . . |
| Билет №9. Теория. Свойства функции 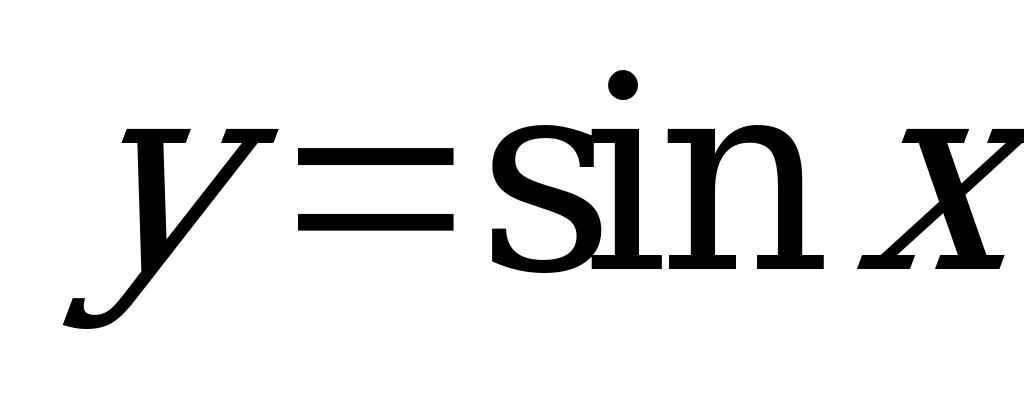 . . Пример. Построить в одной системе координат и прочитать график функций 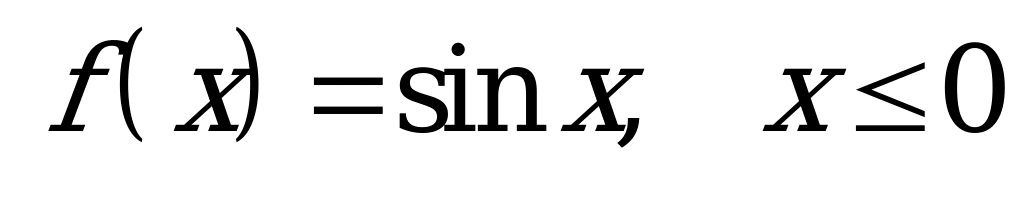 и и 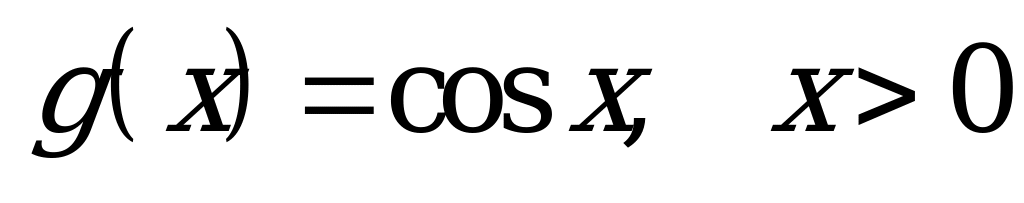 . . |
| Билет №10. Теория. Свойства функции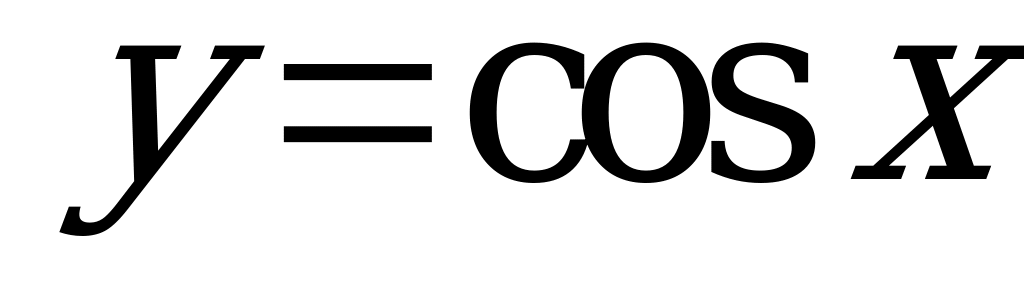 . . Пример. Построить в одной системе координат и прочитать график функций 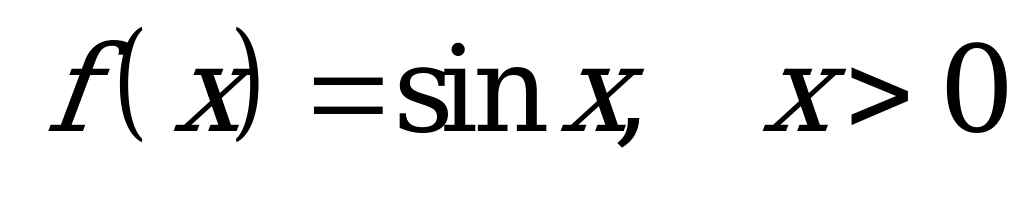 и и 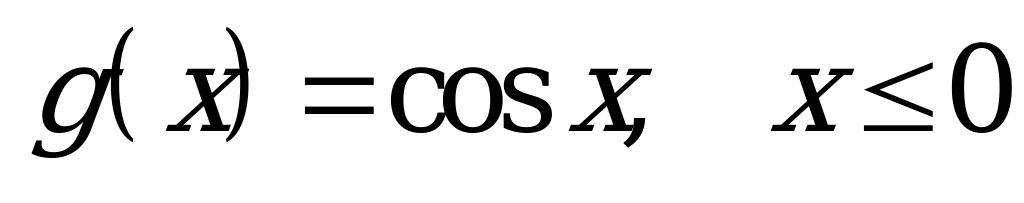 . . |
| Билет №11. Теория. Свойства функций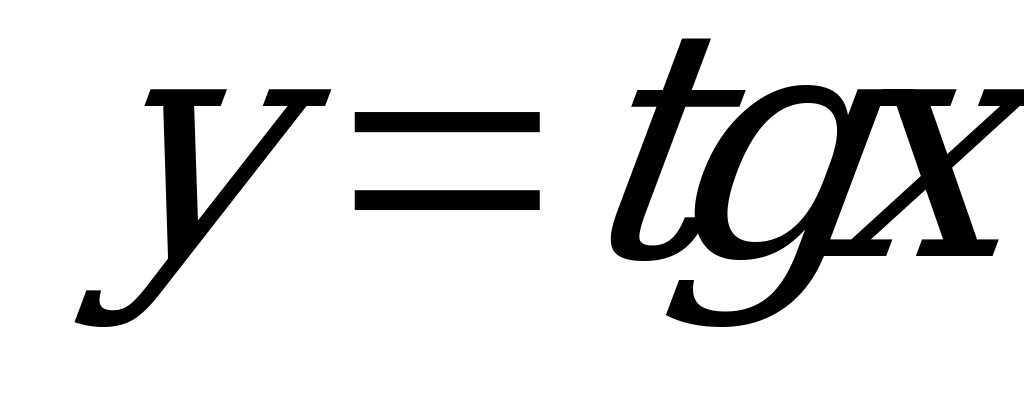 и и 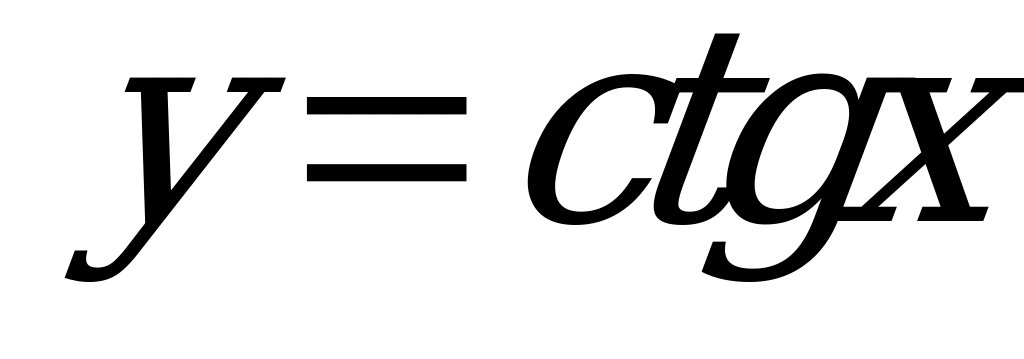 . . Пример. Построить в одной системе координат и прочитать график функции 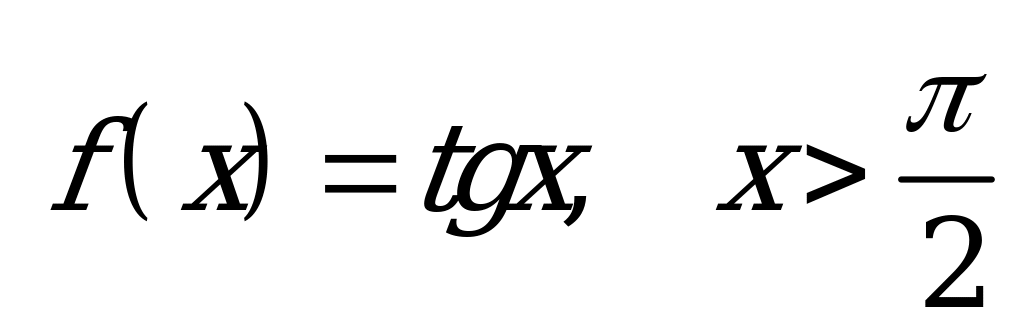 и и 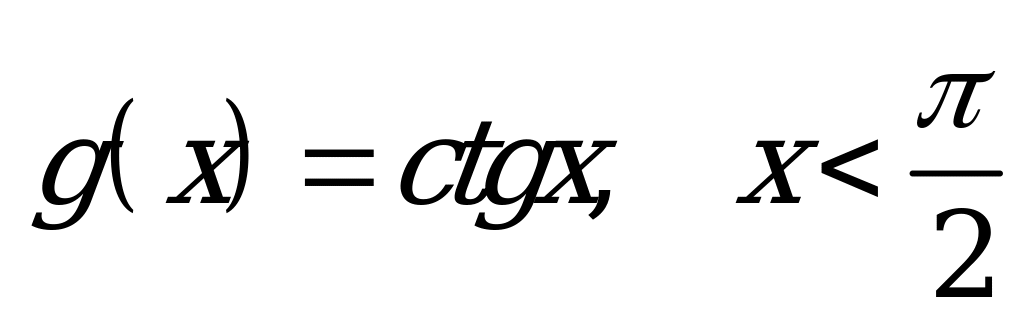 . . |
| Билет №12. Теория. Формулы приведения. Пример. Упростить выражения: 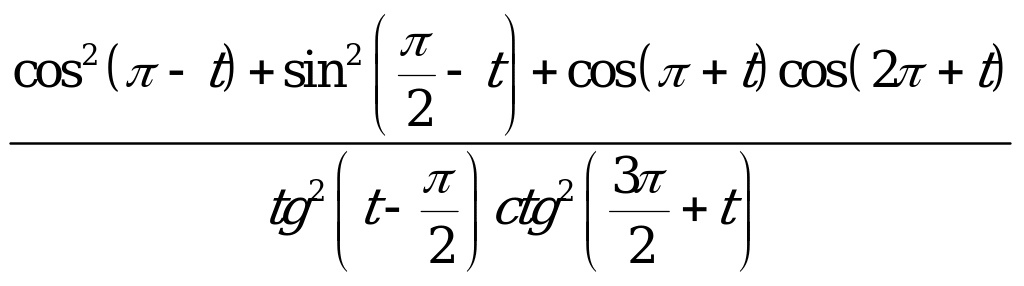 . .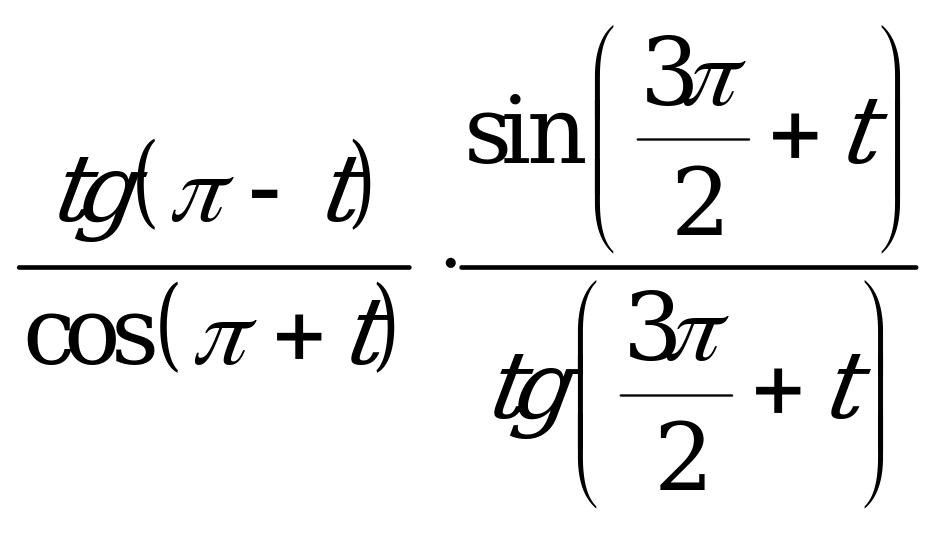
|
| Билет №13. Теория. Тригонометрические функции числового аргумента. Пример. Известно, что 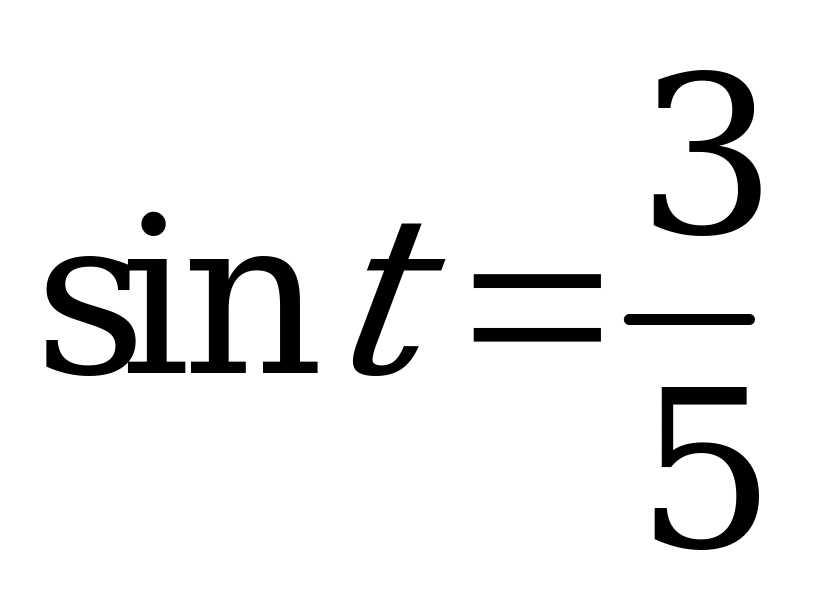 и и 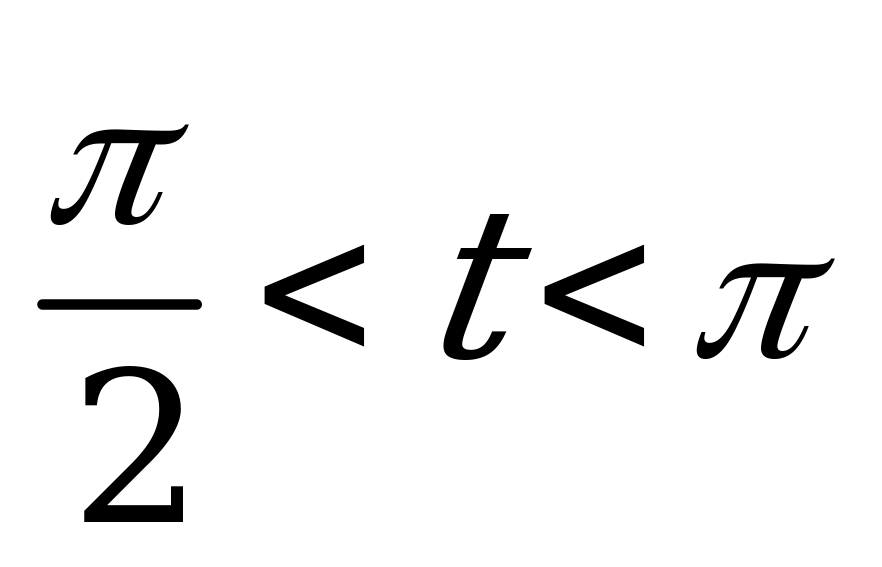 . Найти соответствующие значения . Найти соответствующие значения , , и и 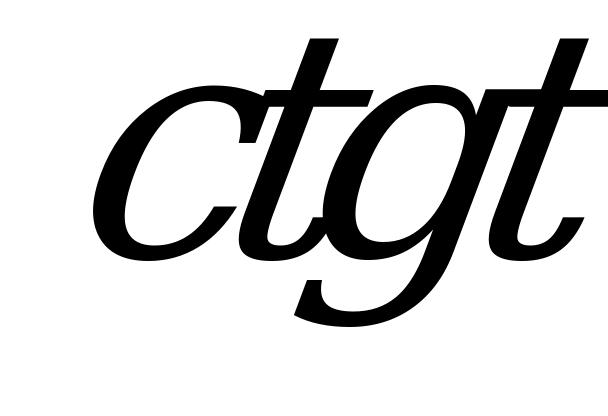 . . |
| Билет №14. Теория. Функция 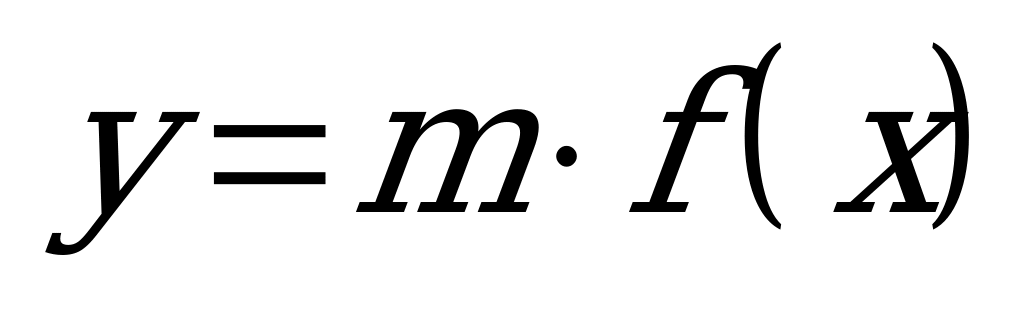 , ее свойства и график. , ее свойства и график. Пример. Постройте график функции 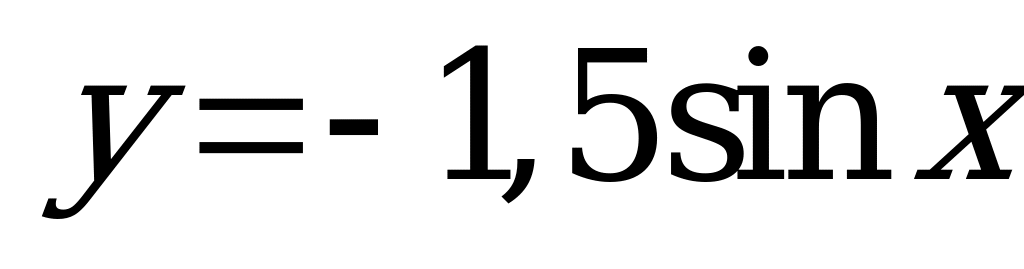 и опишите свойства. и опишите свойства. |
| Билет №15. Теория. Функция 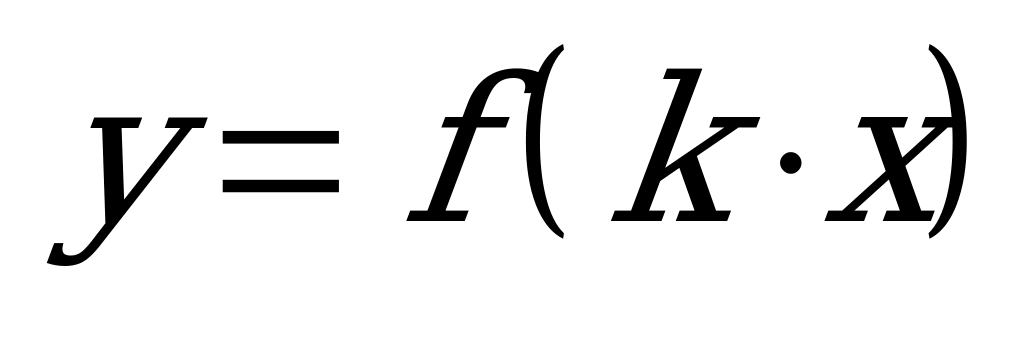 , ее свойства и график. , ее свойства и график. Пример. Постройте график функции 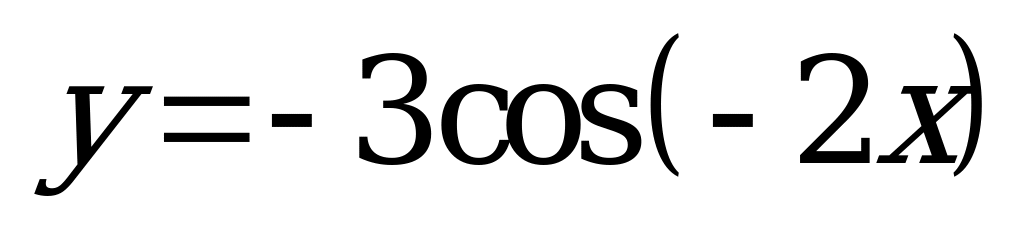 и опишите свойства. и опишите свойства. |
| Билет №16. Теория. Гармоническая функция, ее график. Пример. Постройте график функции 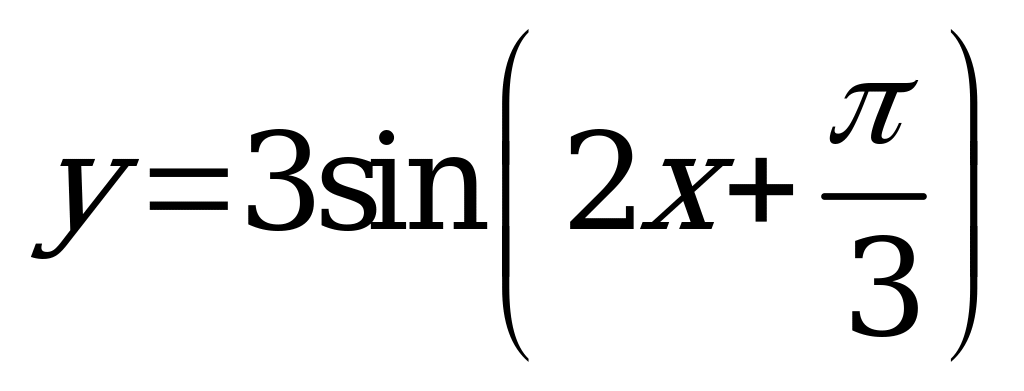 и опишите свойства. и опишите свойства. |
III. Решение заданий у доски.
После обсуждения теоретического вопроса, учащийся решает у доски пример из билета, без объяснений. Учитель проверяет и делает замечания лично ученику, не привлекая весь класс. В этот момент может отвечать на теоретический вопрос другой учащийся. Те учащиеся, которые ответили на свой билет, слушают ответы на теоретические вопросы.
Подведение итогов.
Домашнее задание: теория из учебника стр.8-71.
Урок 28. Зачет по теме «Тригонометрические функции»
Цели урока: проверить теоретические и практические знания по теме: «Тригонометрические функции».
Ход урока:
I. Организационный момент.
Приветствие, сообщение темы и задач урока.
II. Работа по группам.
На уроке, учащиеся объединяются в шесть групп по четыре человека в каждой группе. Учащиеся группы получают карточку с заданиями. Решая задания в нутрии группы, можно помогать друг другу, но оценка будет выставляться каждому учащемуся индивидуально.
| Карточка №1 | №26, 45, 69, 106, 181, 125, 186 |
| Карточка №2 | №27, 46, 70, 121, 185, 126, 210 |
| Карточка №3 | №28, 47, 71, 122, 208, 127, 228 |
| Карточка №4 | №42, 48, 72, 123, 209, 165, 270 |
| Карточка №5 | №43, 49, 83, 161, 225, 166, 271 |
| Карточка №6 | №44, 73, 102, 162, 265, 167, 211 |
III. Решение заданий у доски.
Учитель в процессе урока вызывает к доске учащихся, которые справились с заданием в своей группе, для того, чтобы записать решение на доске. В течение всего урока на доске будут выписаны решения многих задач из разных тем. Записи на доске могут помочь тем учащимся, которые сомневаются в решении.
Подведение итогов.
Домашнее задание: обменявшись карточками по кругу, выполнить задания карточки.
Урок 29. Контрольная работа №1
Цели урока: проверить знания и умение учащихся по теме «Тригонометрические функции».
Ход урока:
I. Организационный момент.
Приветствие, сообщение темы и задач урока.
II. Решение контрольных заданий.
Уровень  :
:
| Вариант №1 | Вариант №2 |
| 1. Вычислите: |
| 1) 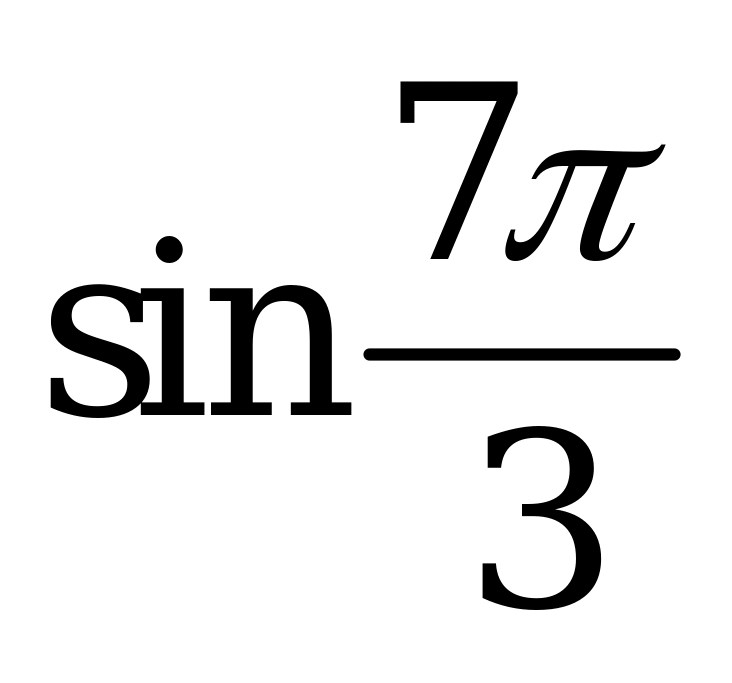 , , 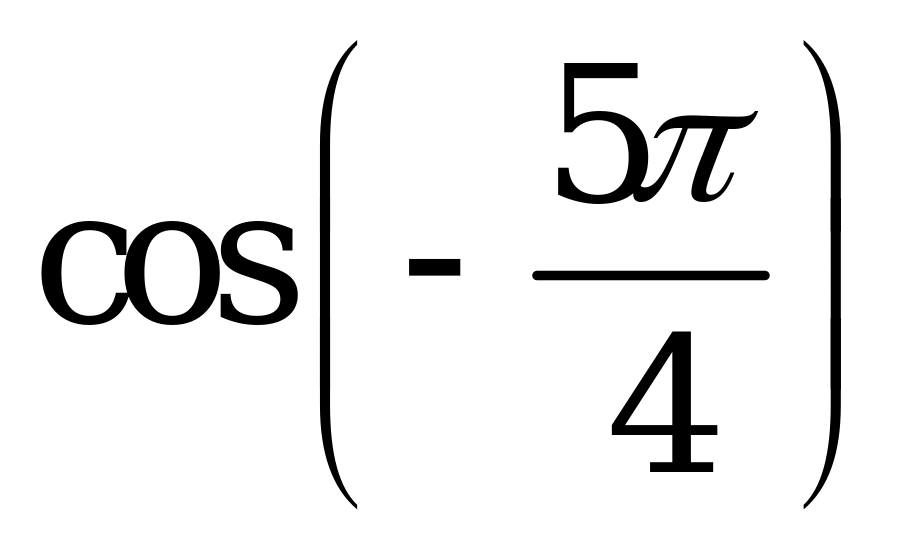 , , 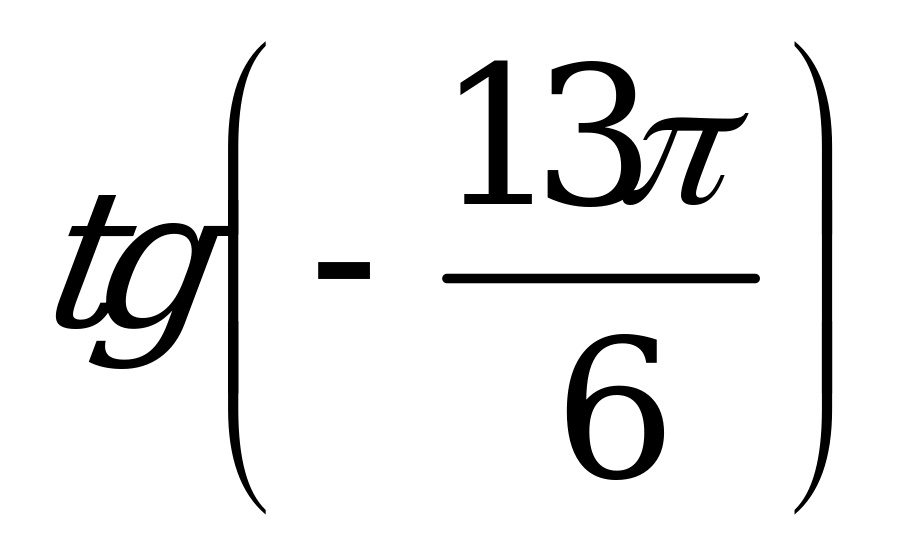 , , 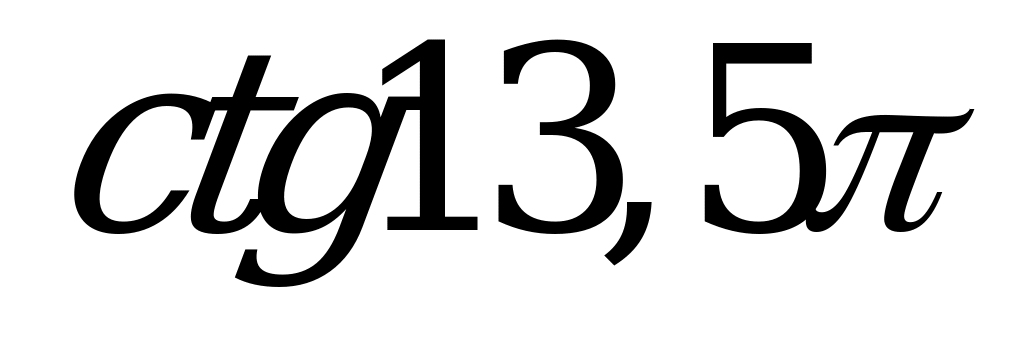 ; ; 2) 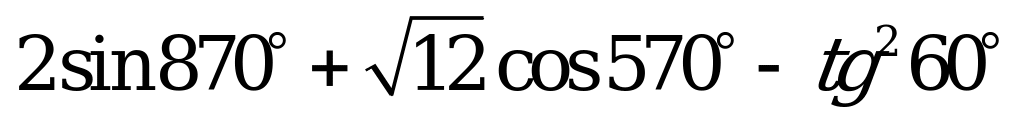 3) | 1) 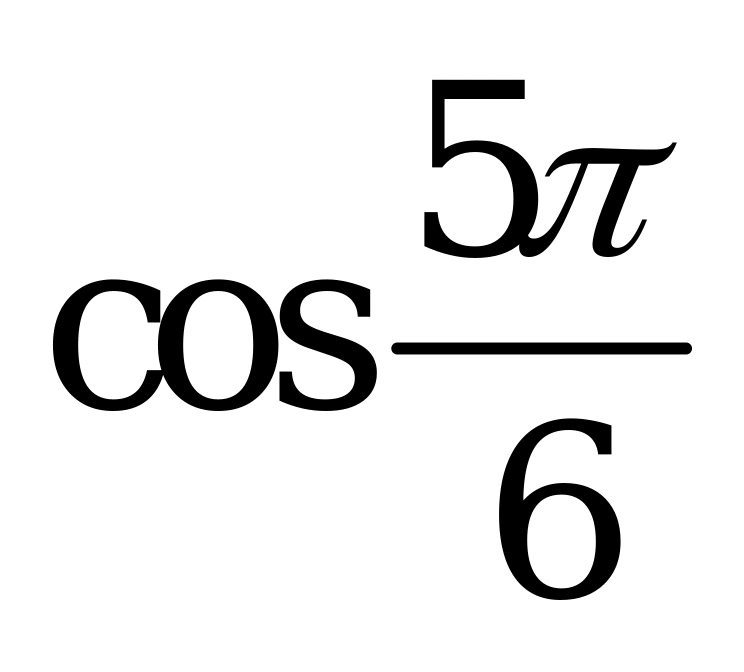 , , 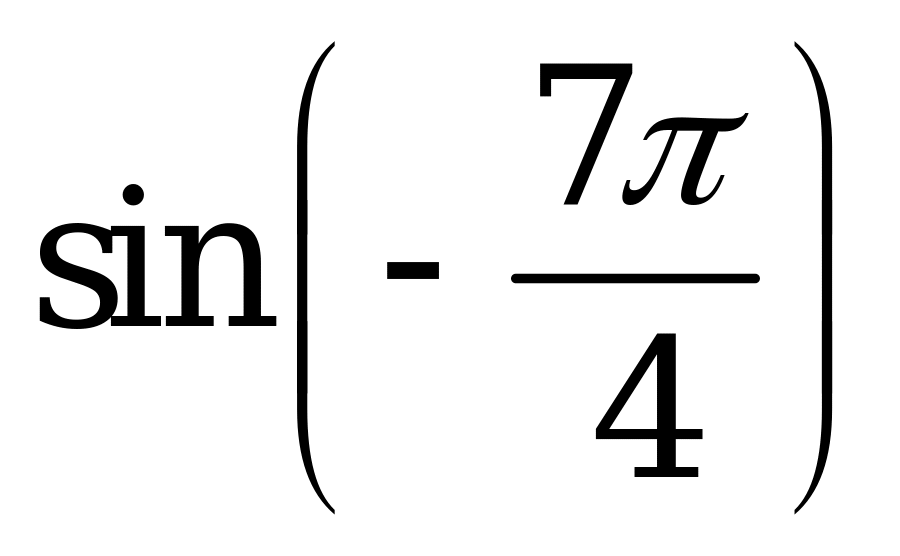 , , 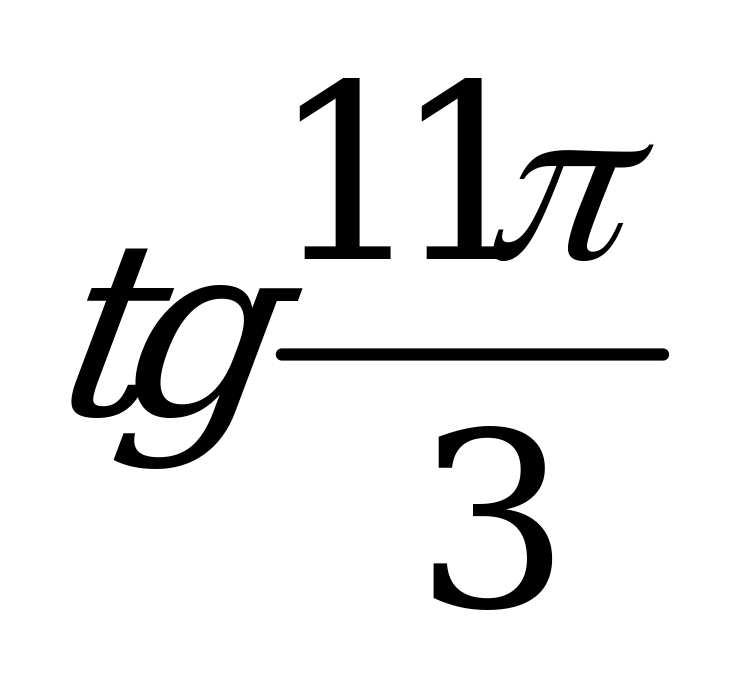 , , 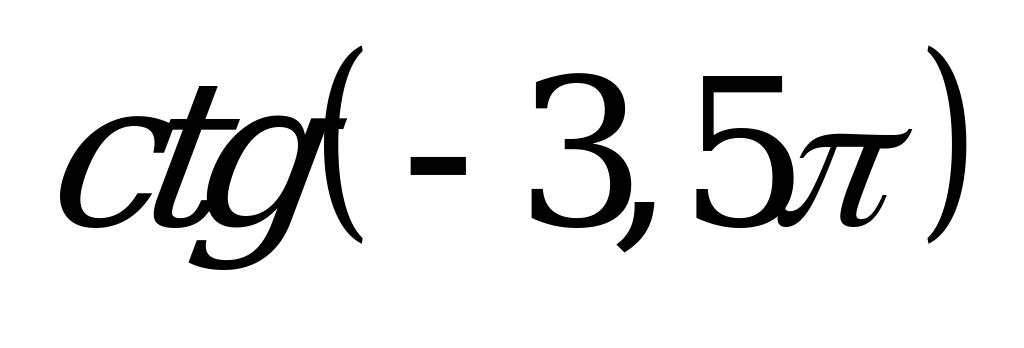 ; ; 2)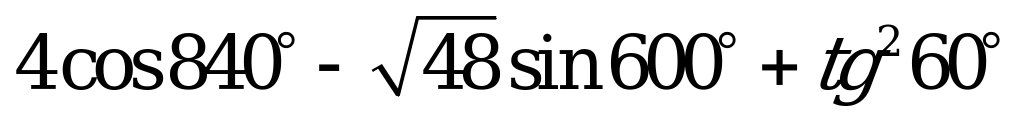 3) 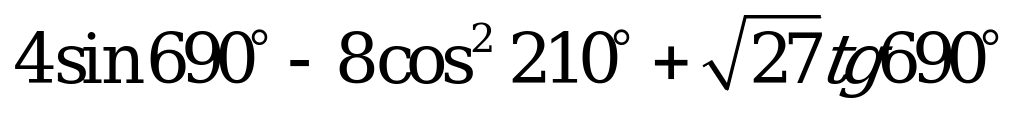 |
| 2. Упростить выражение |
| 1) 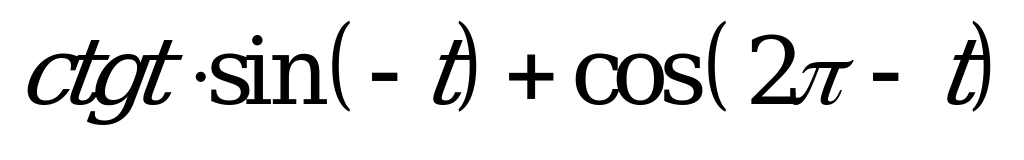 2) 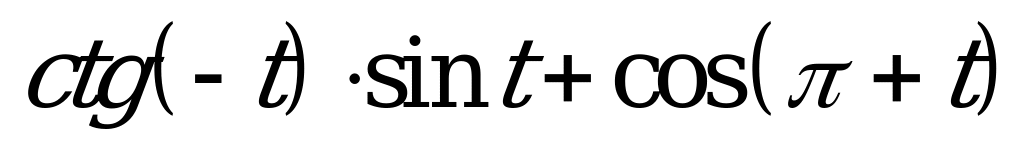 | 1) 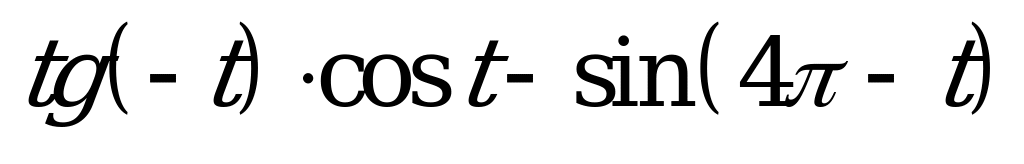 2) 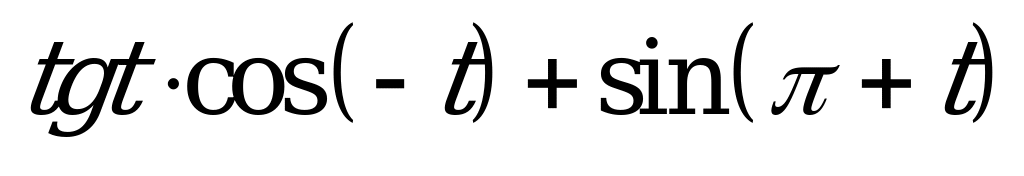 |
| 3. Известно, что 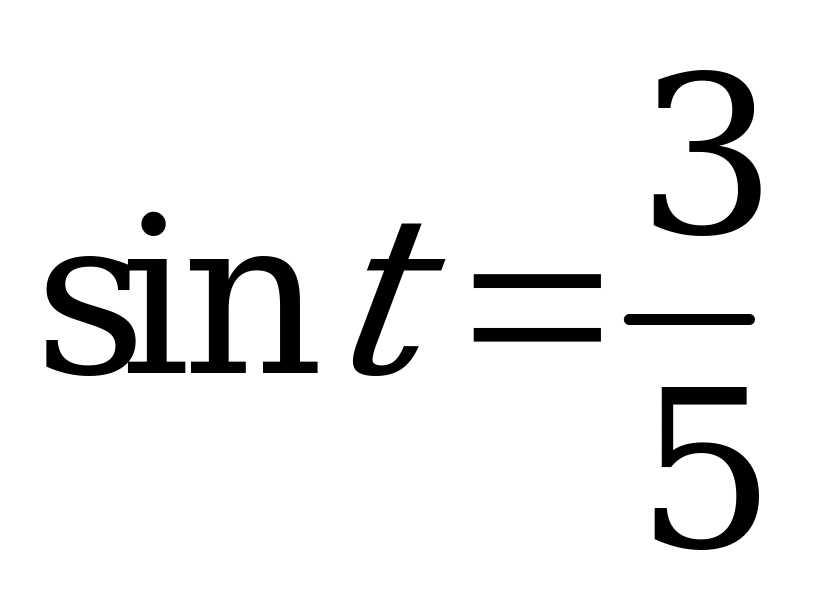 , , 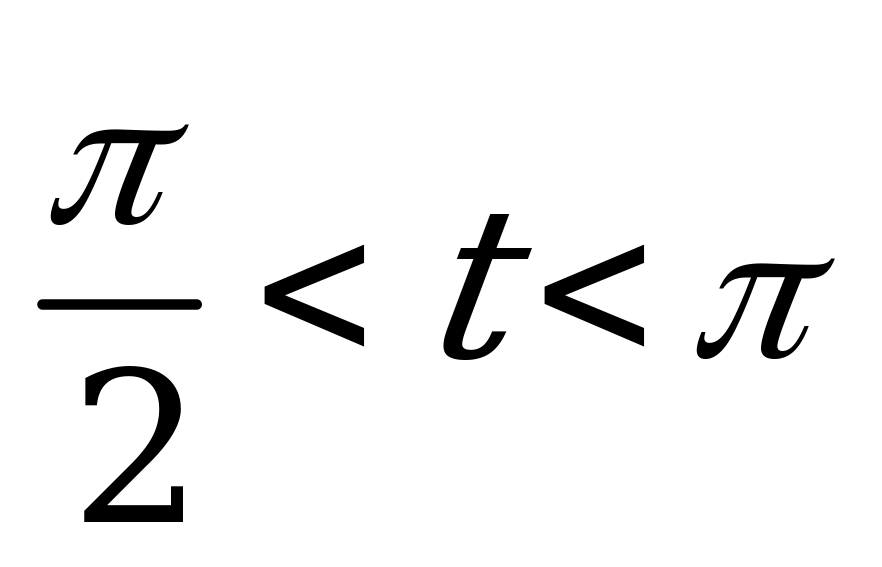 . Вычислите . Вычислите  , ,  , ,  . . | 3. Известно, что 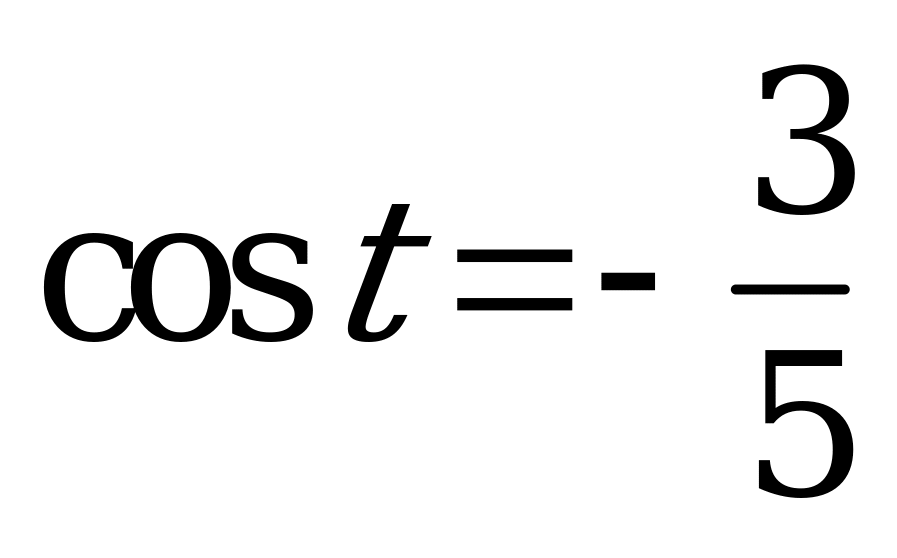 , , 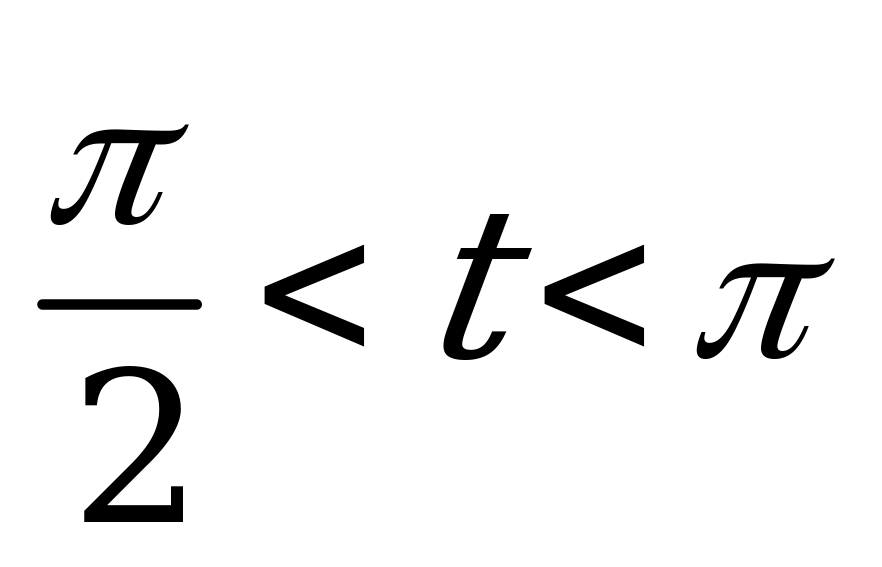 . Вычислите . Вычислите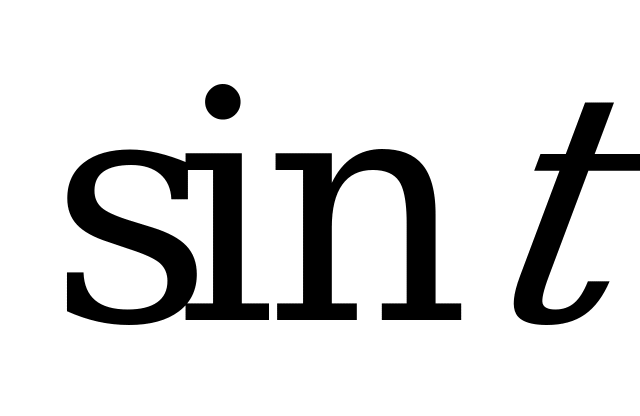 , ,  , , 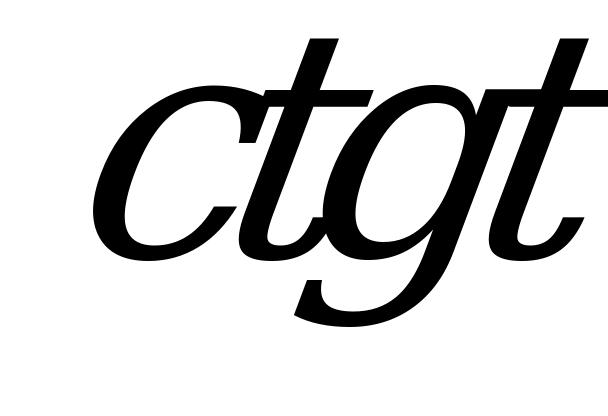 . . |
| 4. Найдите наименьшее и наибольшее значение функции: |
| 1) 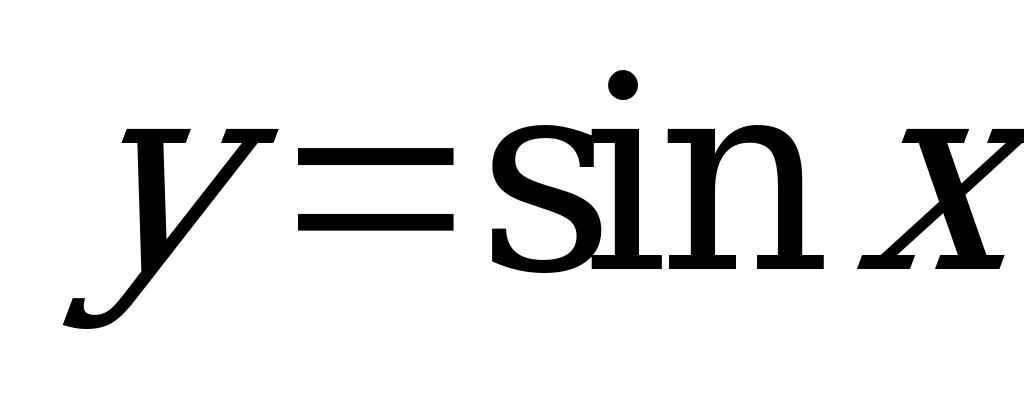 на отрезке на отрезке 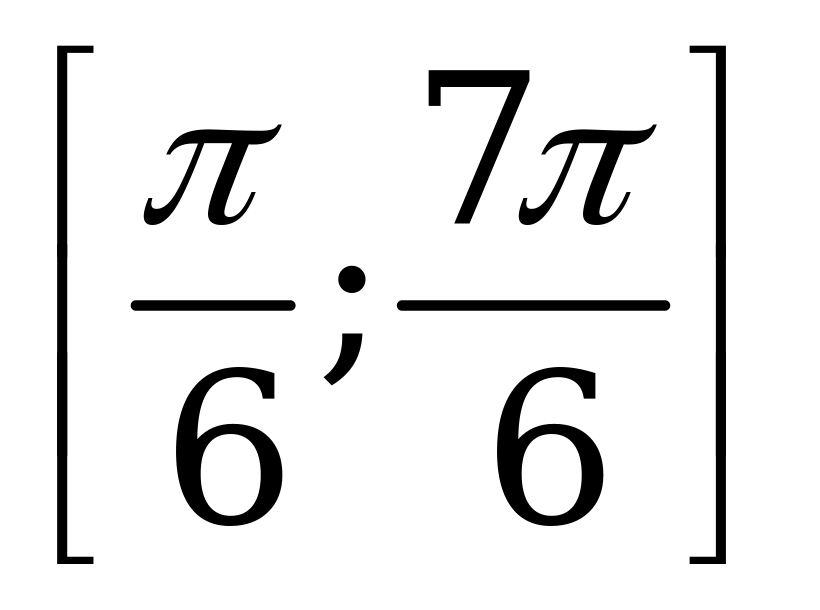 ; ; 2) 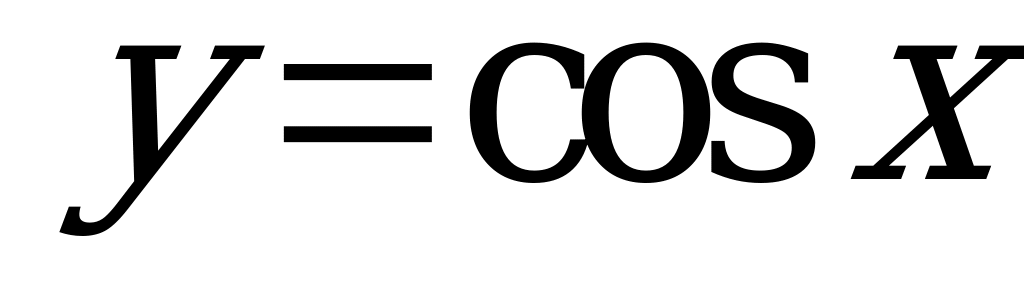 на отрезке на отрезке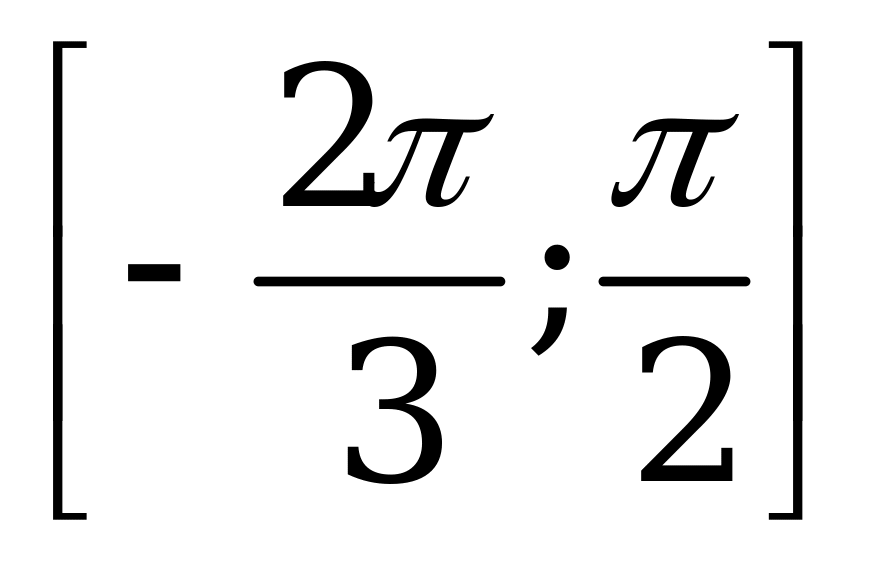 . . | 1) 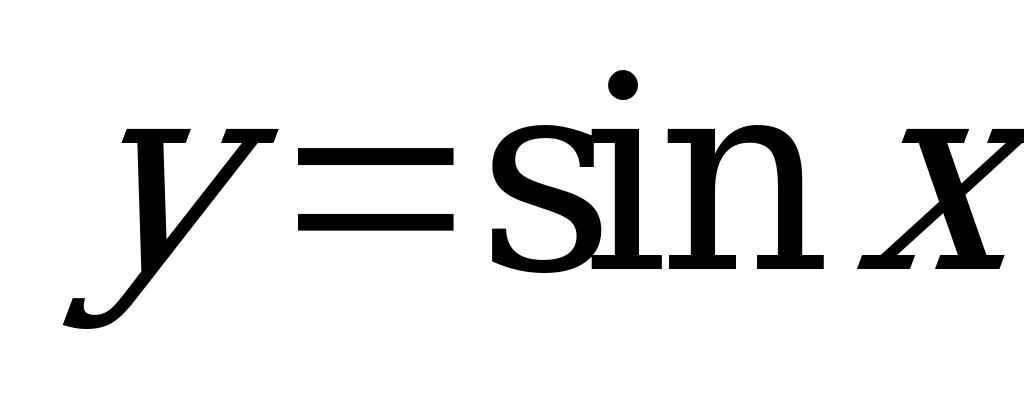 на отрезке на отрезке 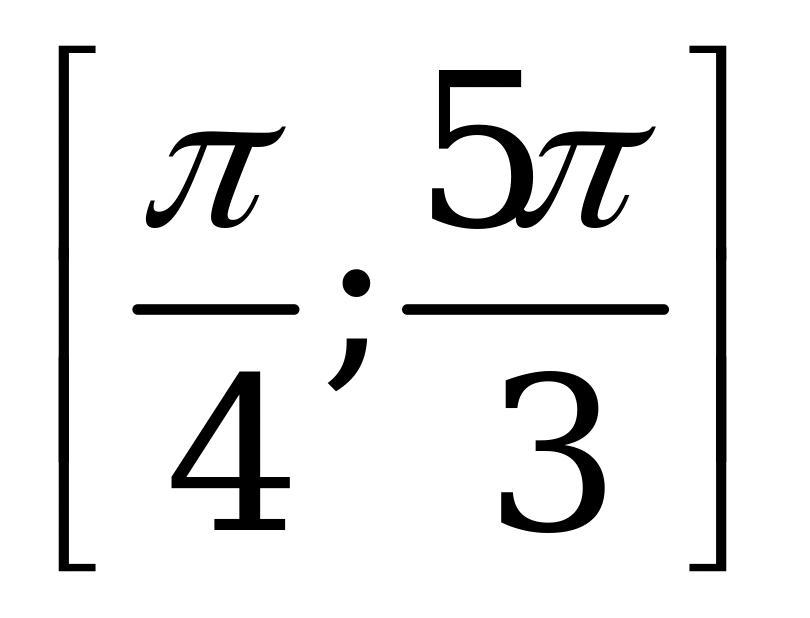 ; ; 2) 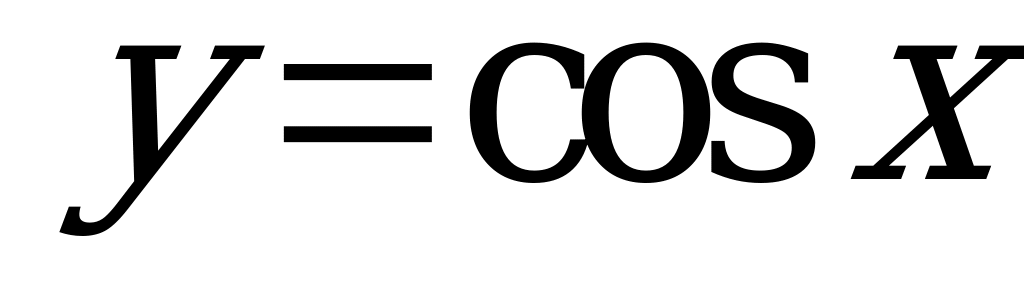 на отрезке на отрезке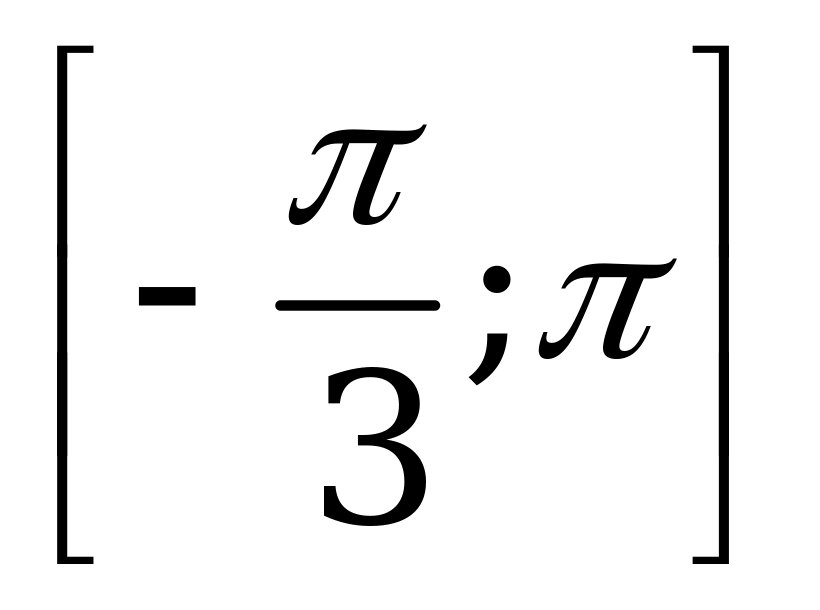 . . |
Уровень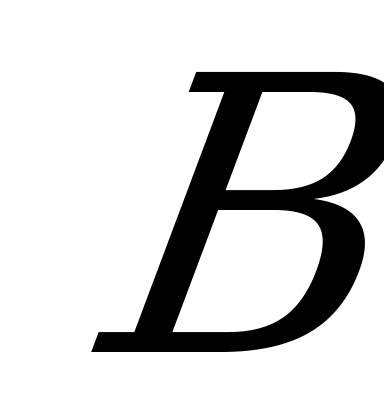 :
:
| Вариант №1 | Вариант №2 |
| 1.Доказать тождество: |
| 1) 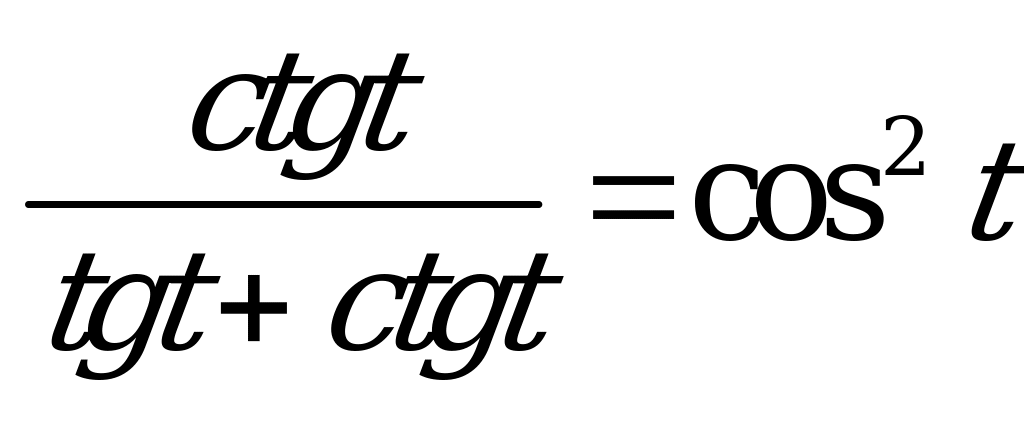 ; ; 2) 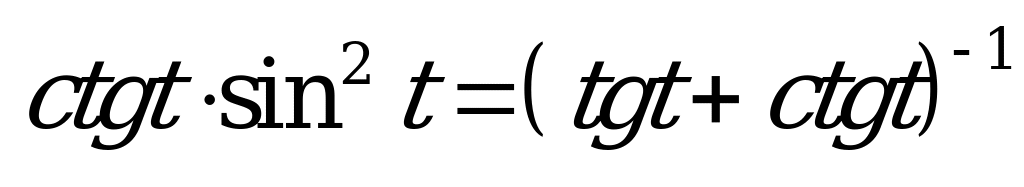 . . | 1) 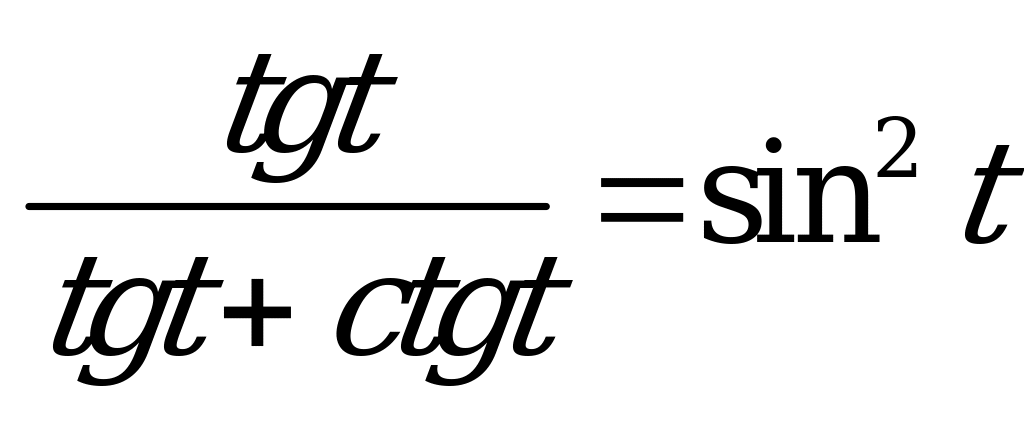 ; ; 2) 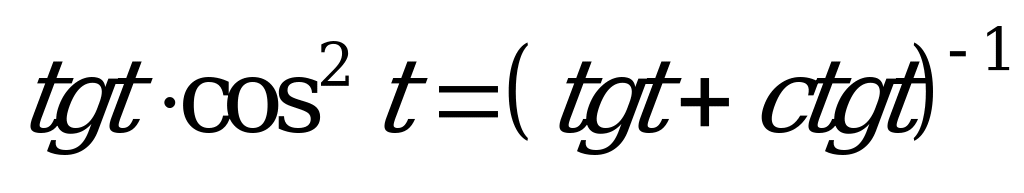 . . |
| 2. Упростить выражение |
| 1) 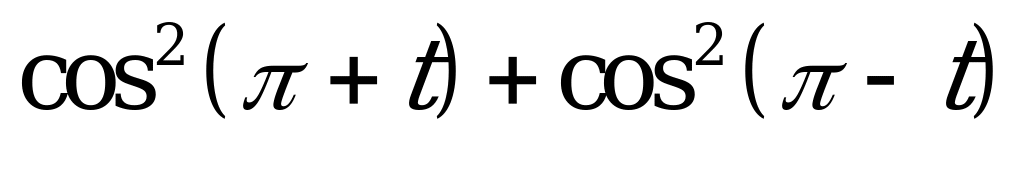 ; ; 2) 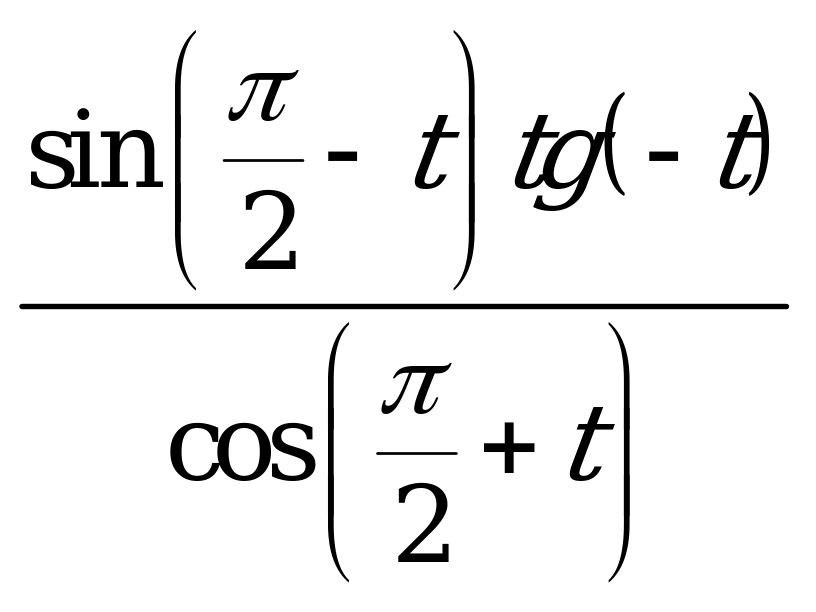 ; ; 3) 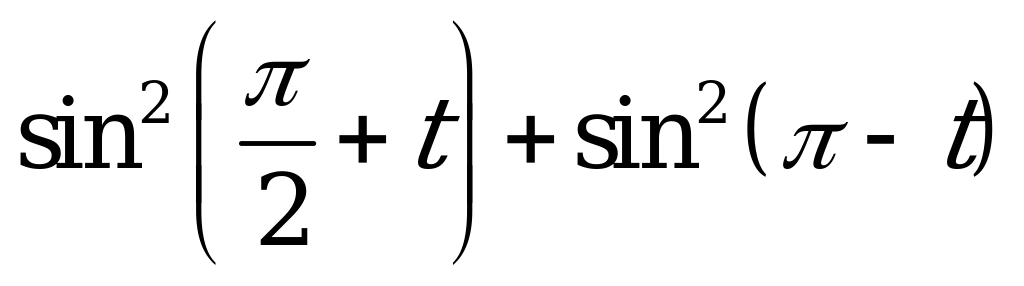 . . | 1) 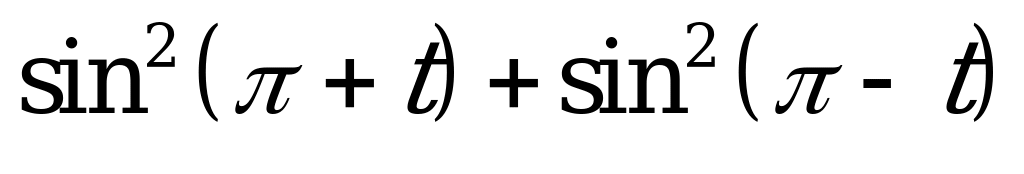 ; ; 2) 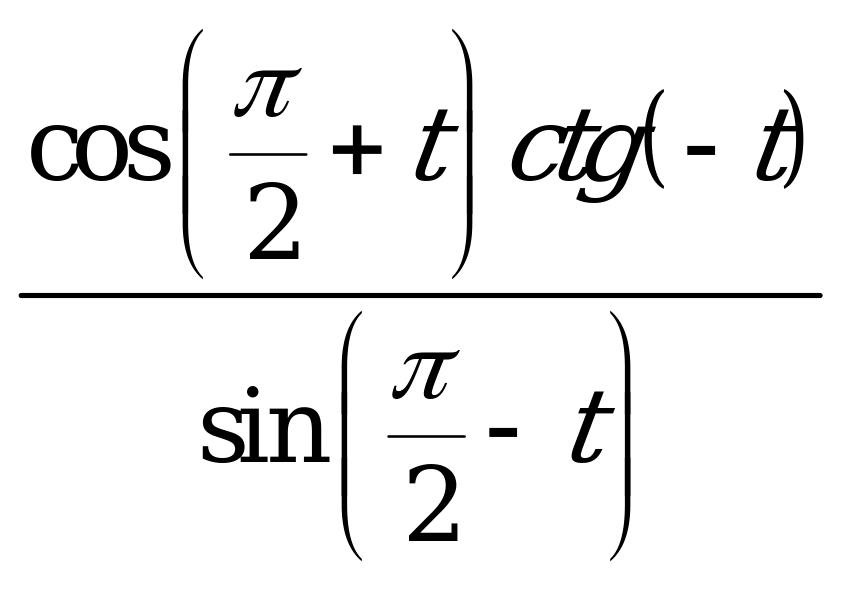 ; ; 3) 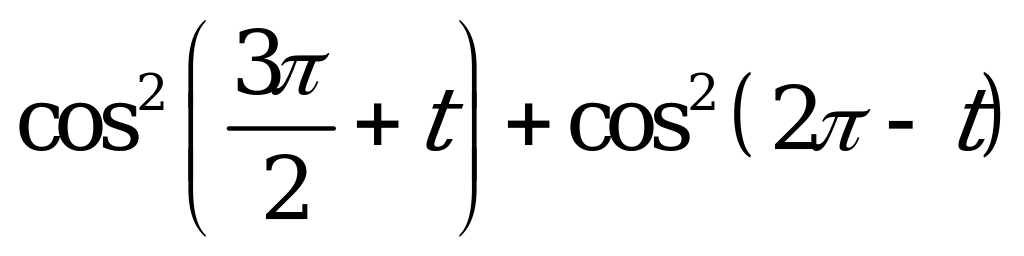 . . |
| 3. Решите уравнение и покажите решение на окружности: |
| 1) 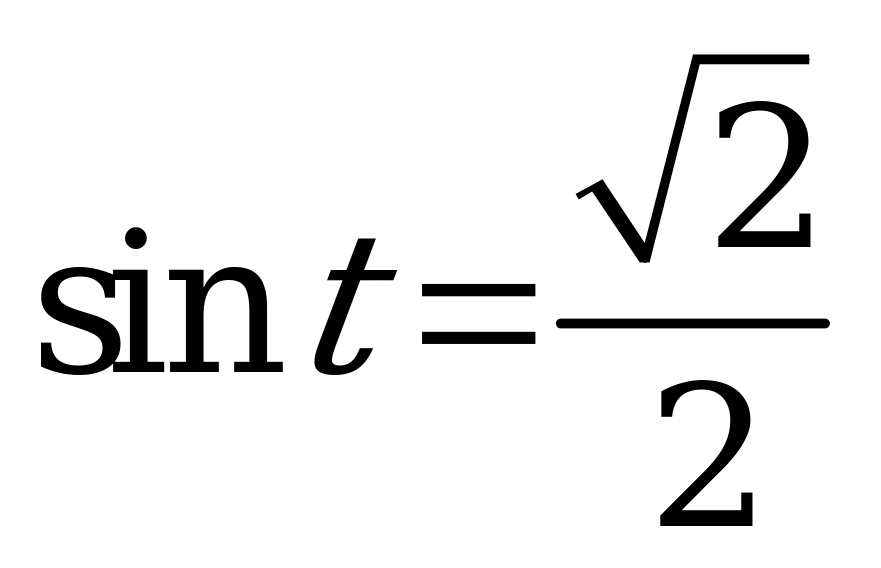 , , 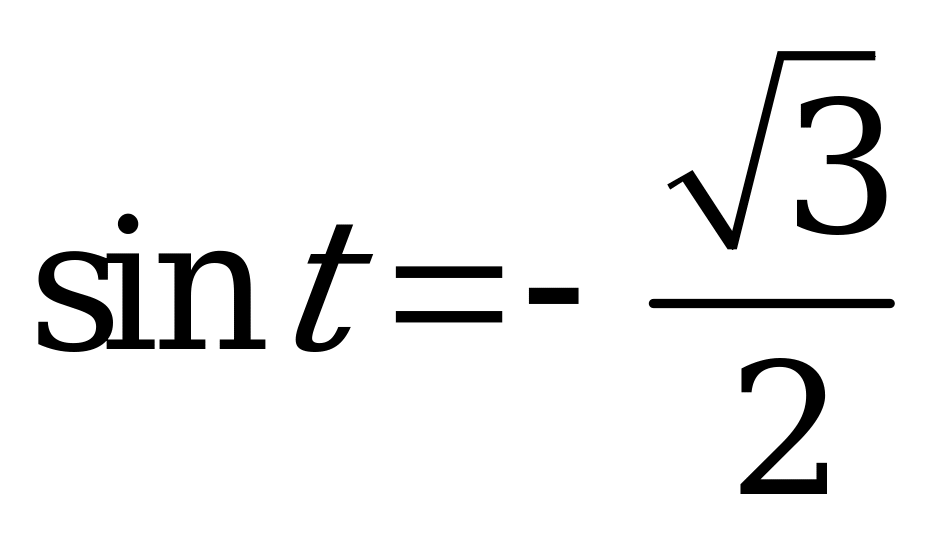 ; ; 2) 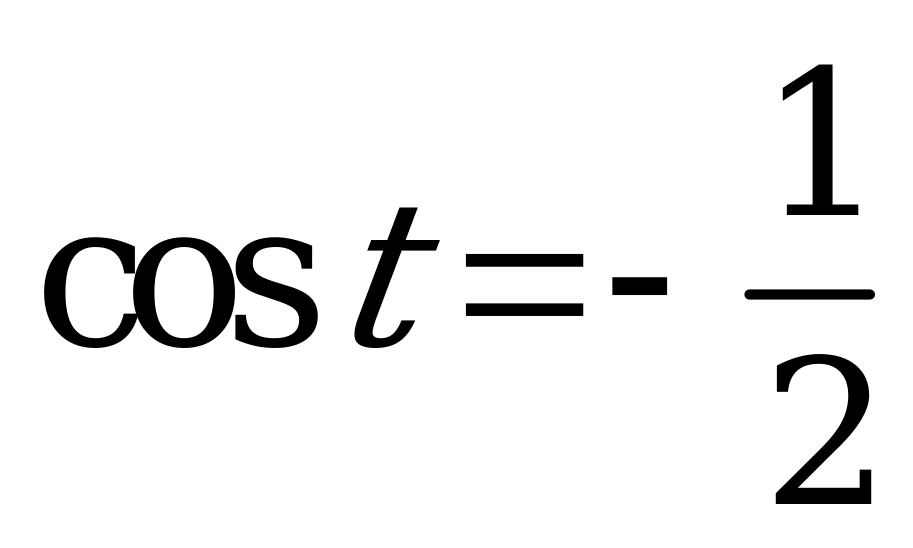 , , 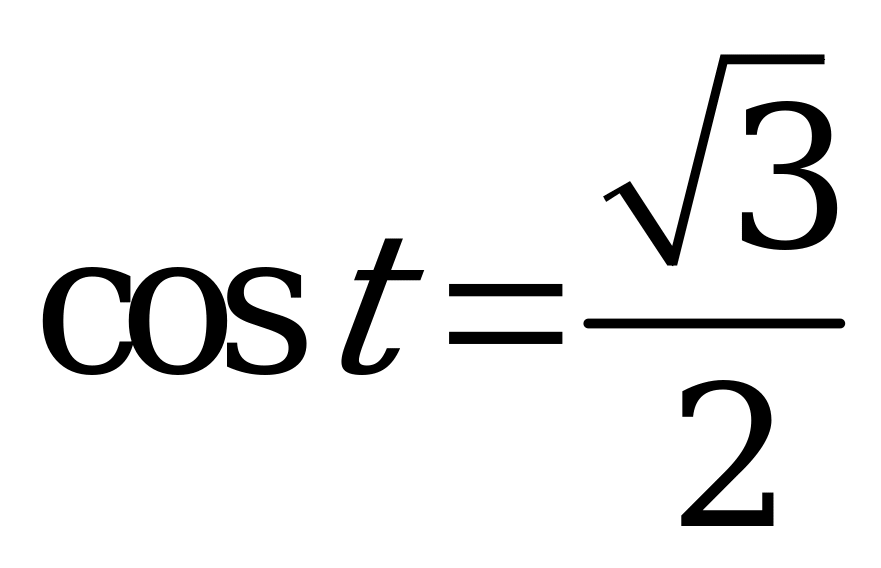 . . | 1) 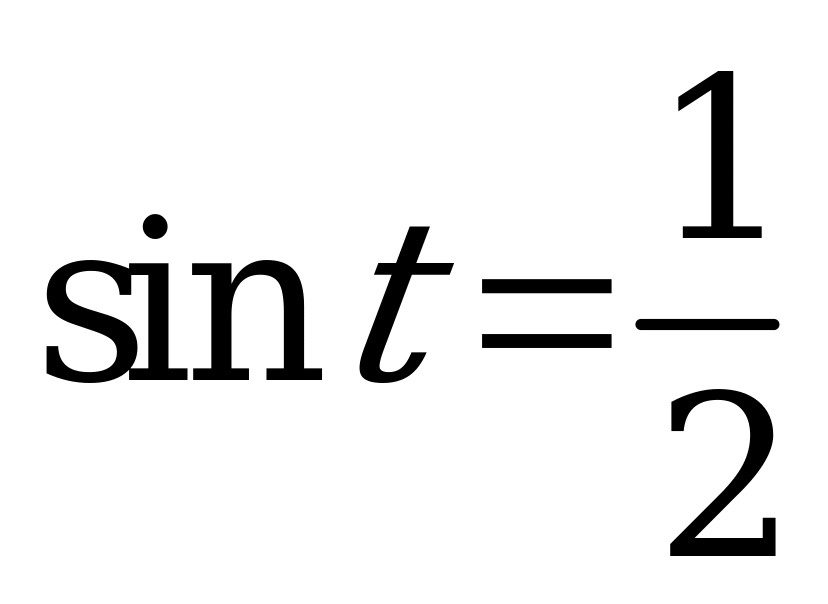 , , 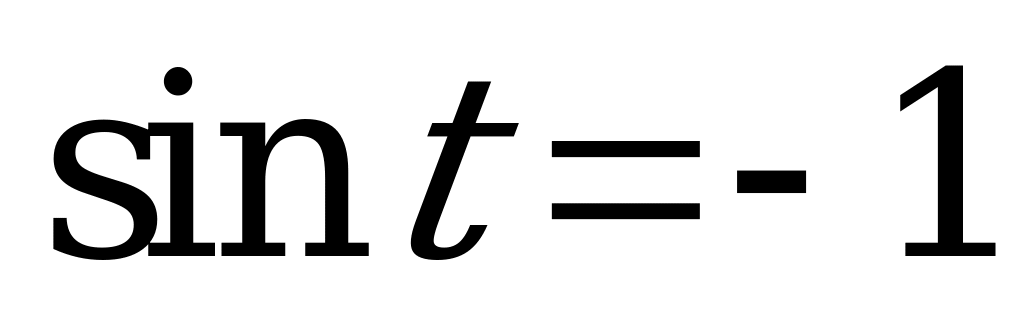 ; ; 2) 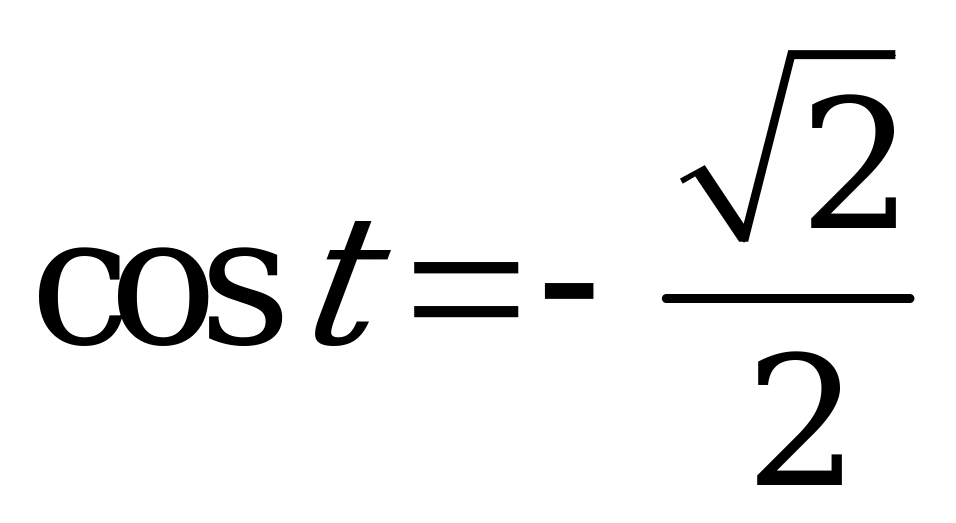 , , 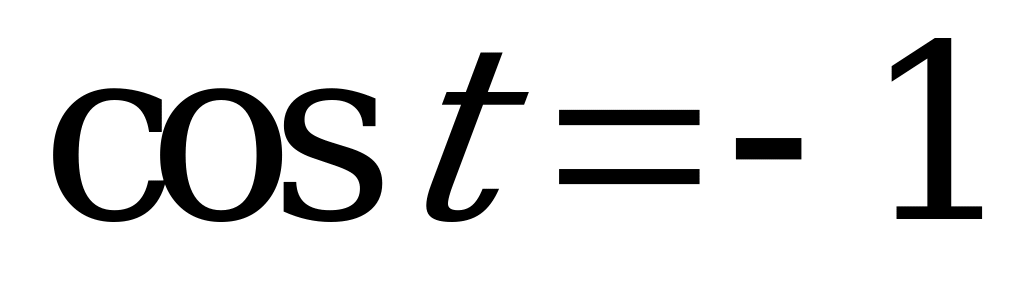 . . |
| 4. Исследуйте функцию на четность-нечетность: |
| 1) 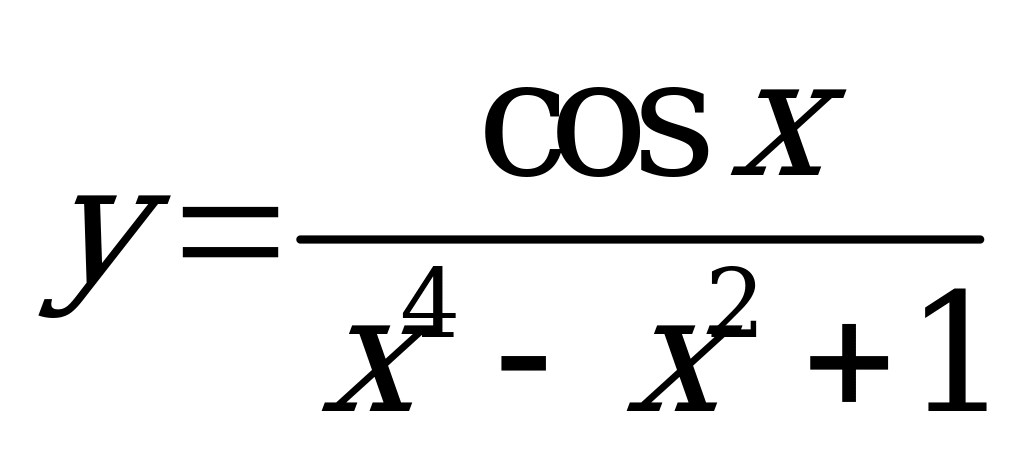 ; 2) ; 2) 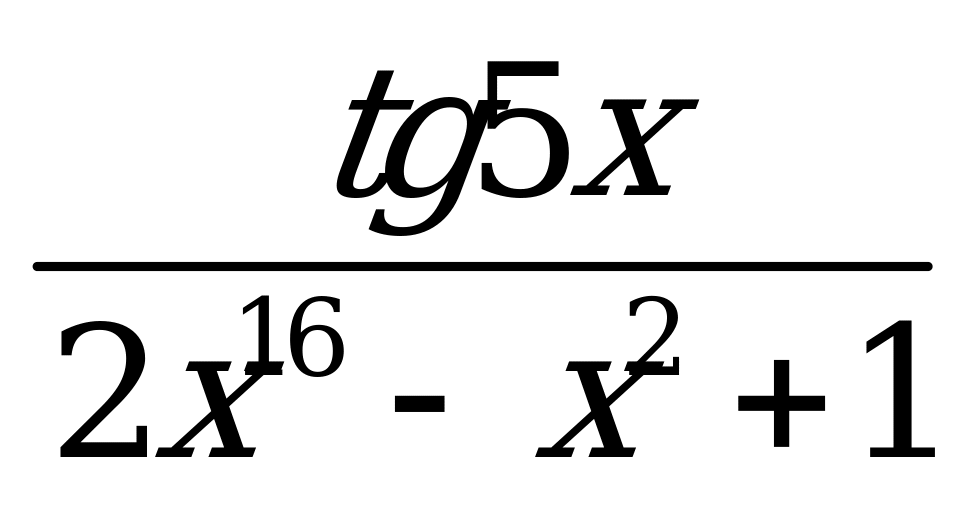 . . | 1) 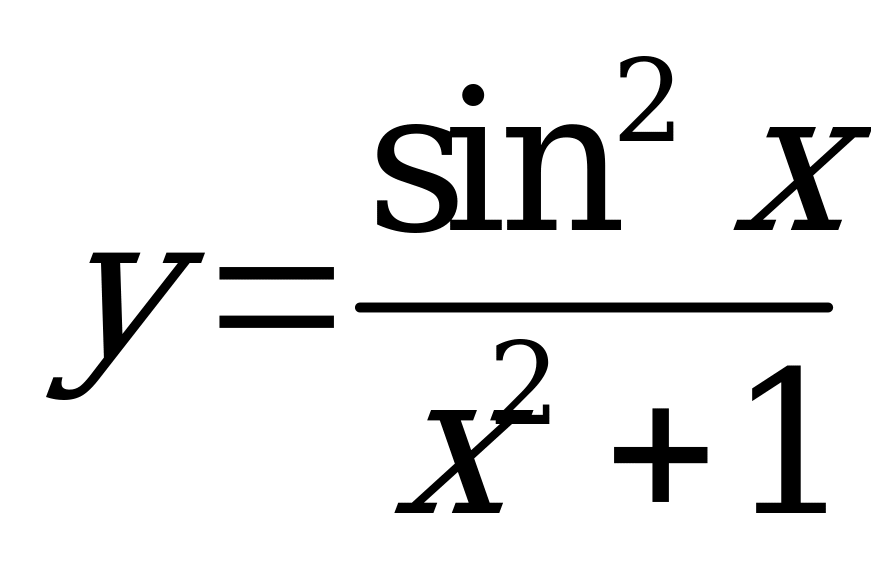 ; 2) ; 2) 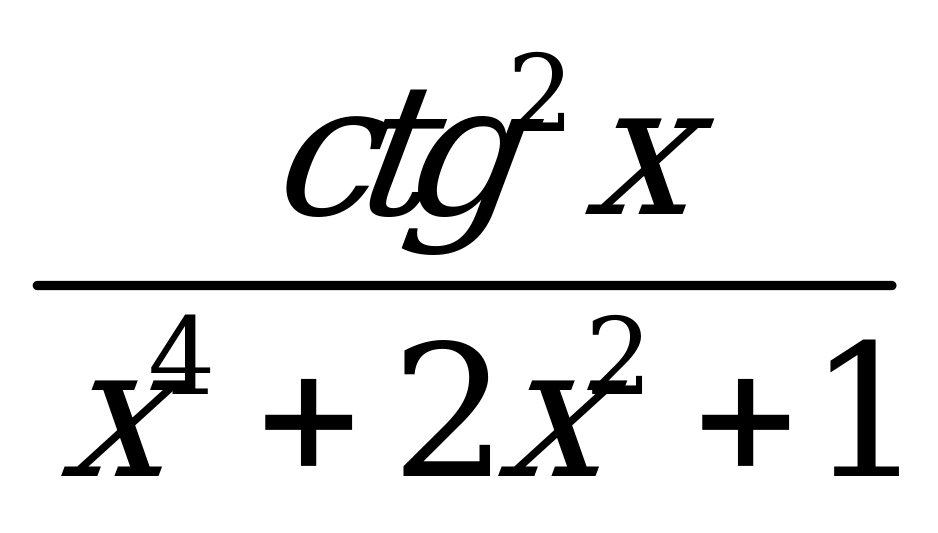 . . |
| 5. Постройте график функции: |
| 1) 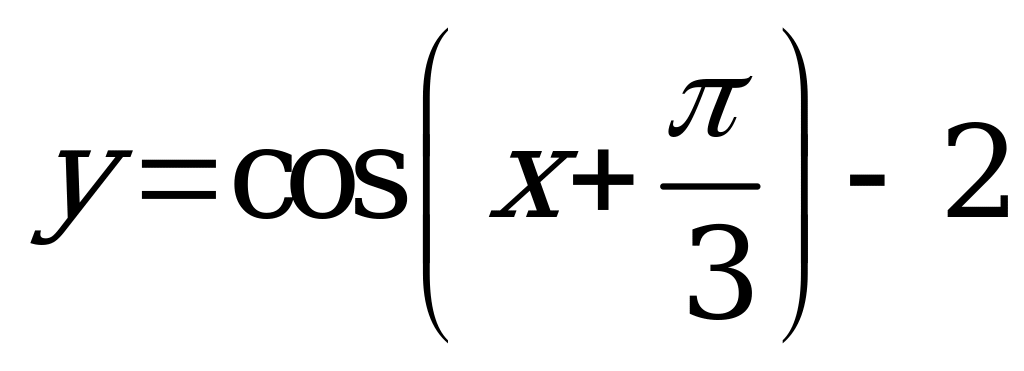 ; ; 2) 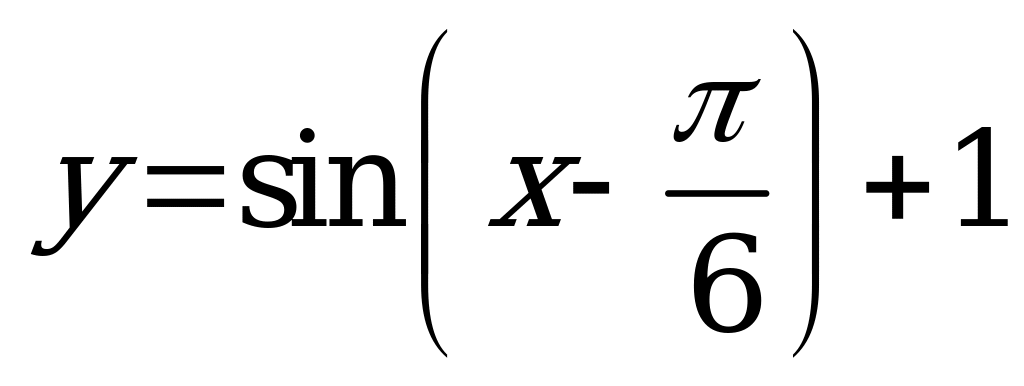 . . | 1) 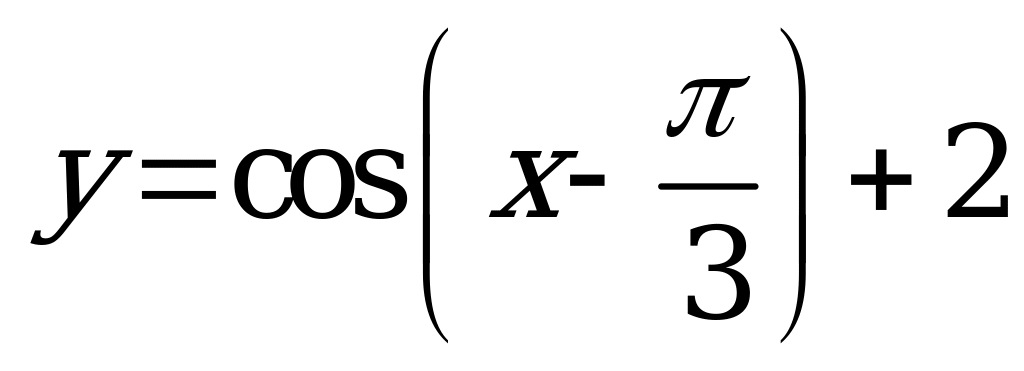 ; ; 2) 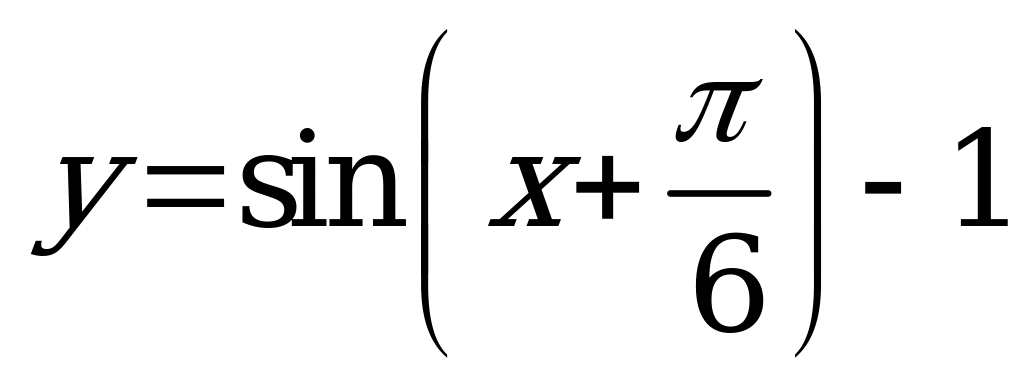 . . |
Уровень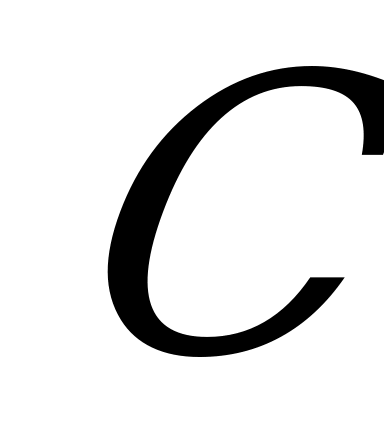 :
:
| Вариант №1 | Вариант №2 |
| 1. Расположить в порядке возрастания: |
| 1; 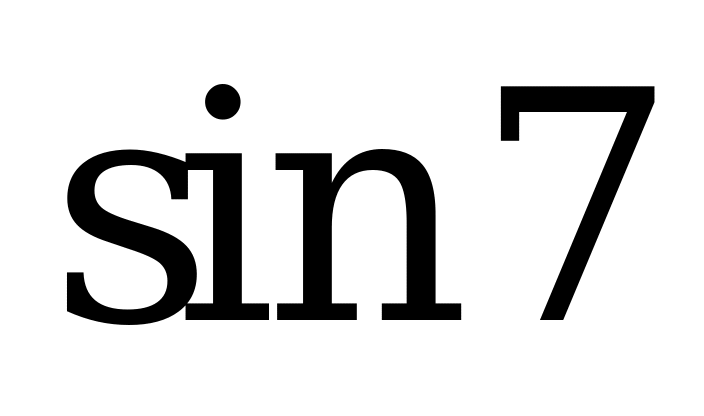 ; ;  ; ; 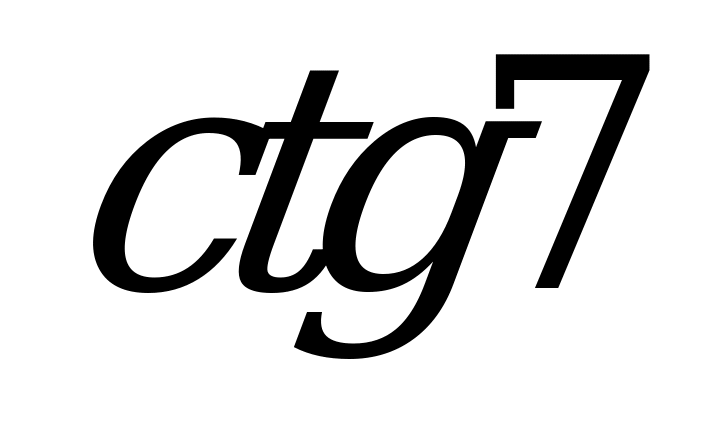 . . |  ; ; 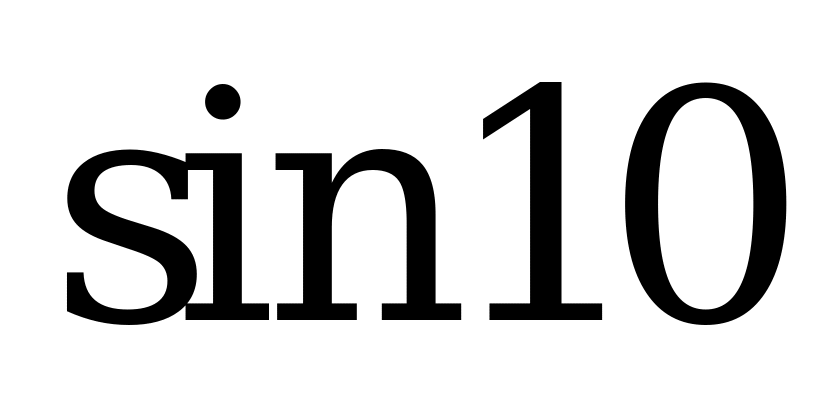 ; ; 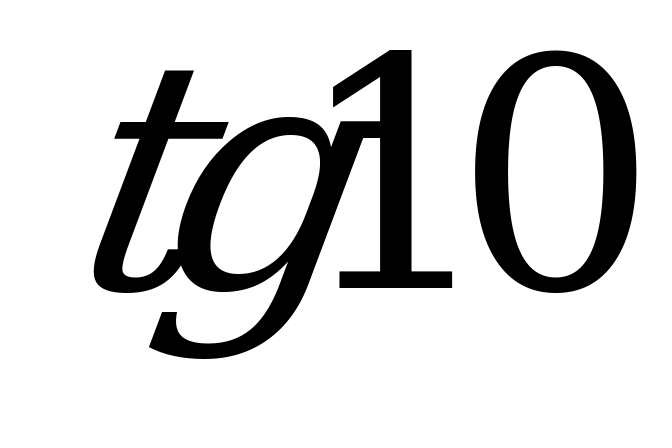 ; ; 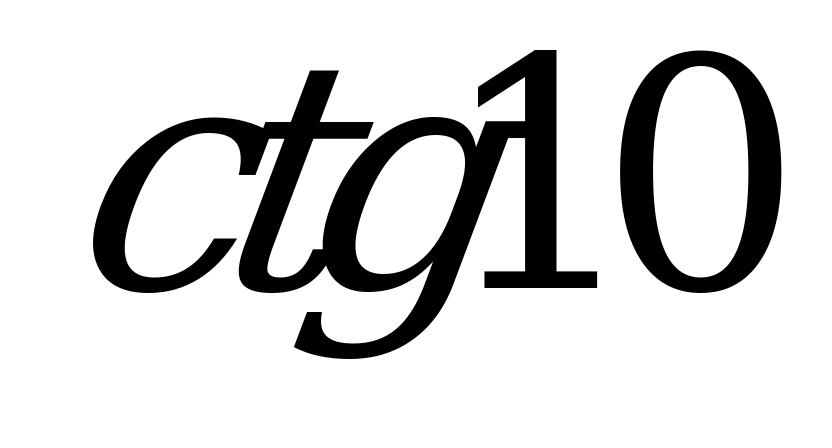 . .
|
| 2. Решите неравенство и покажите решение на окружности: |
| 1) 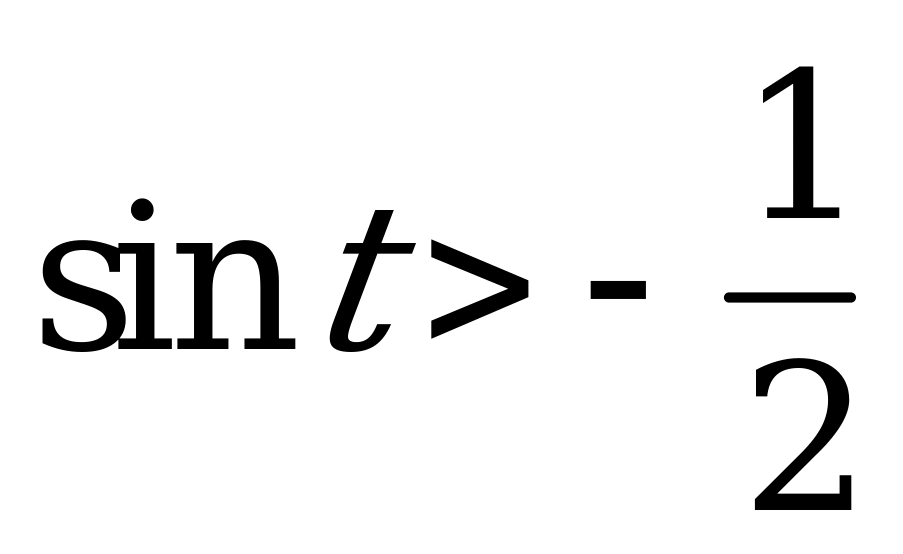 и и 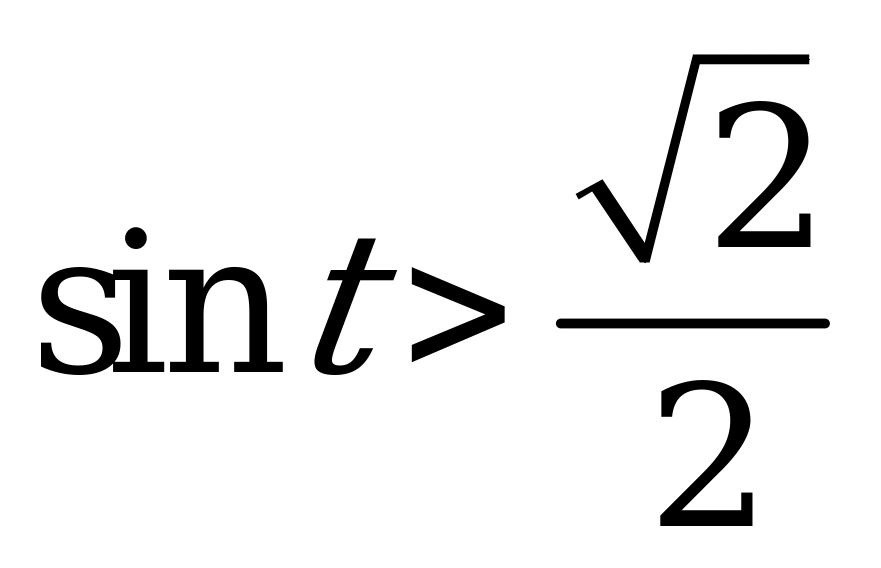 ; ; 2) 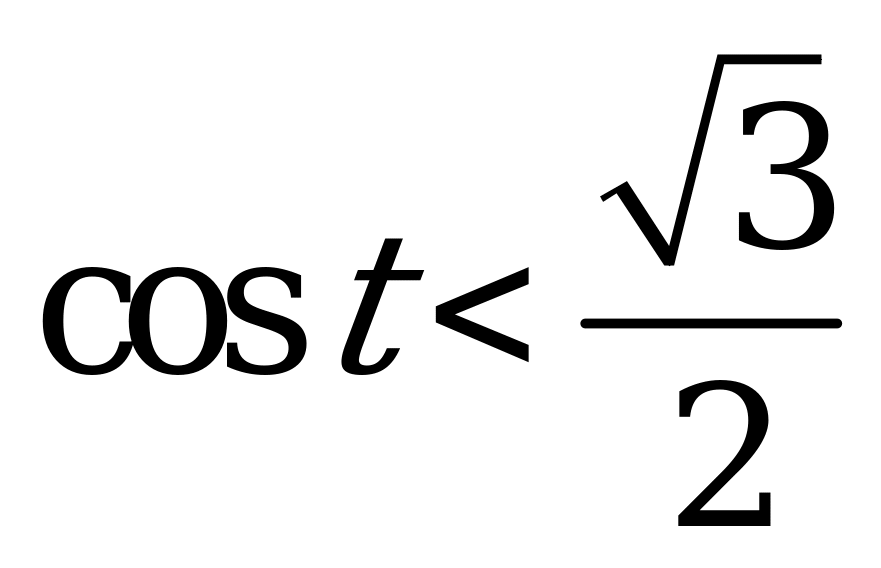 и и 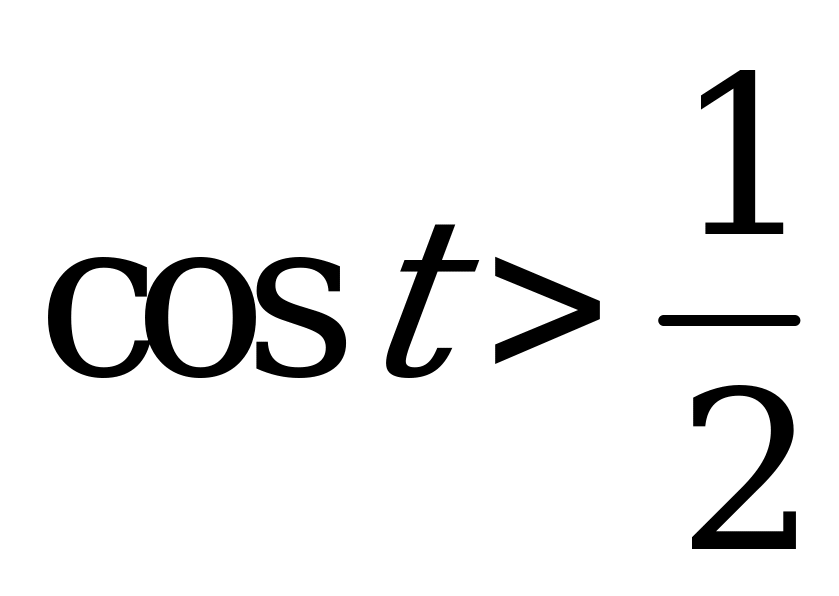 . . | 1) 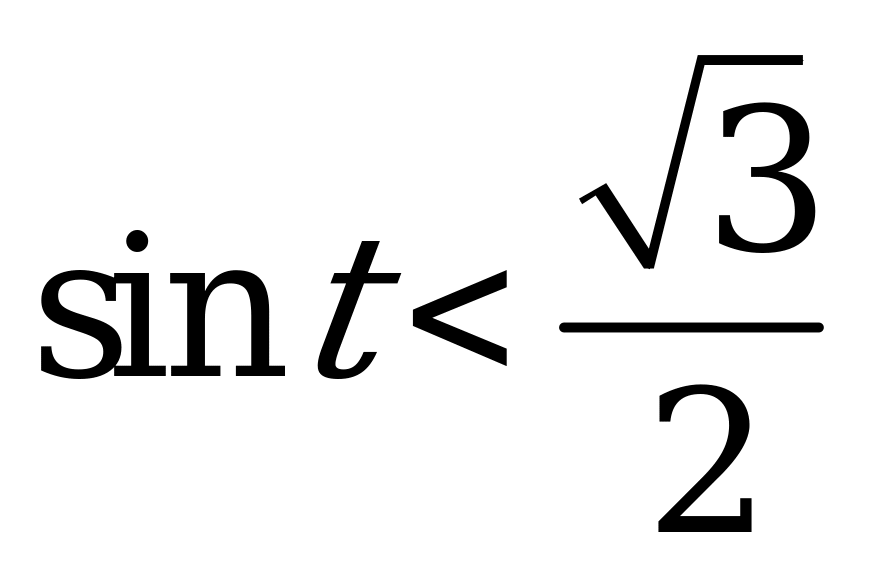 и и 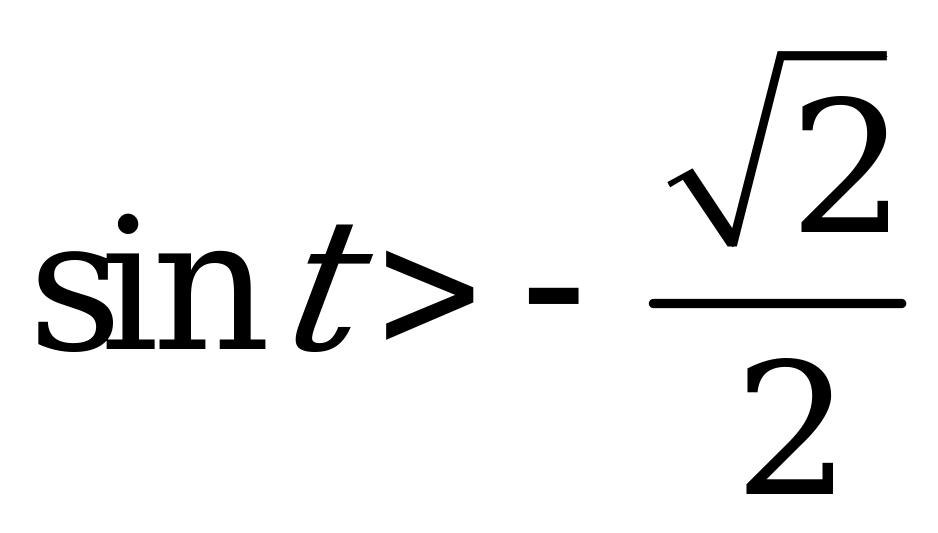 ; ; 2) 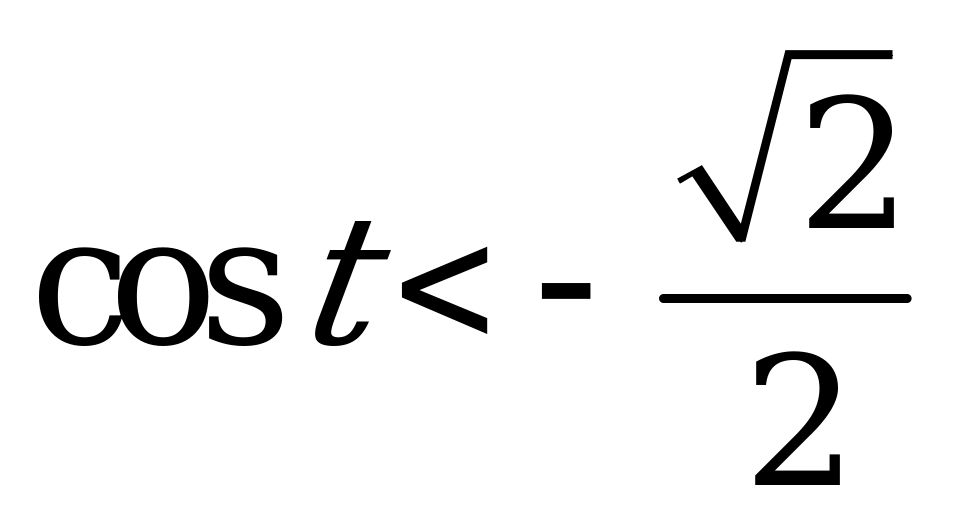 и и 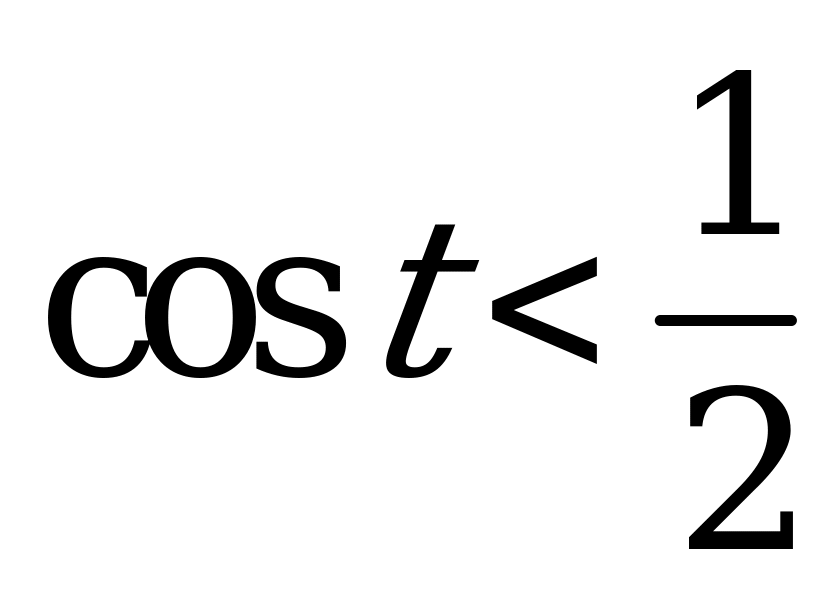 . . |
| 3.Известно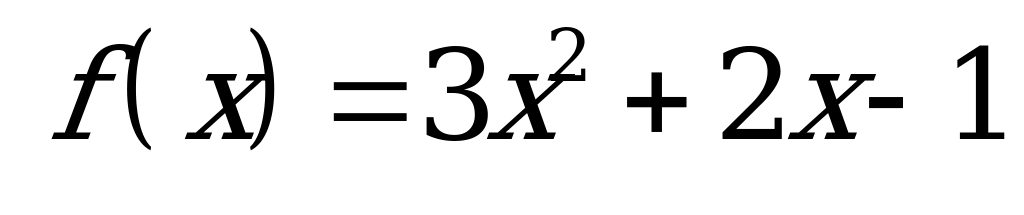 . Докажите, что . Докажите, что 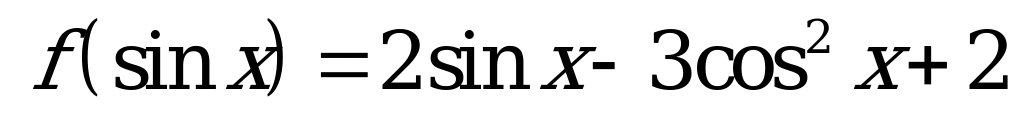 . .
| 3.Известно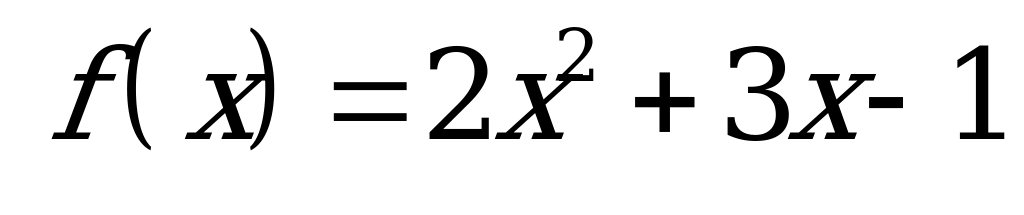 . Докажите, что . Докажите, что 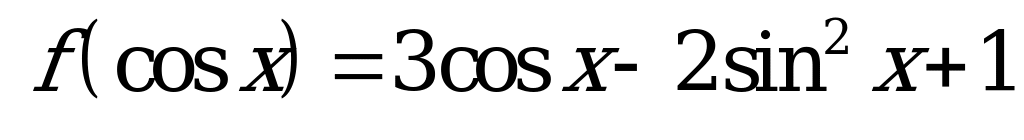 . .
|
| 4. Постройте график функции: |
| 1) 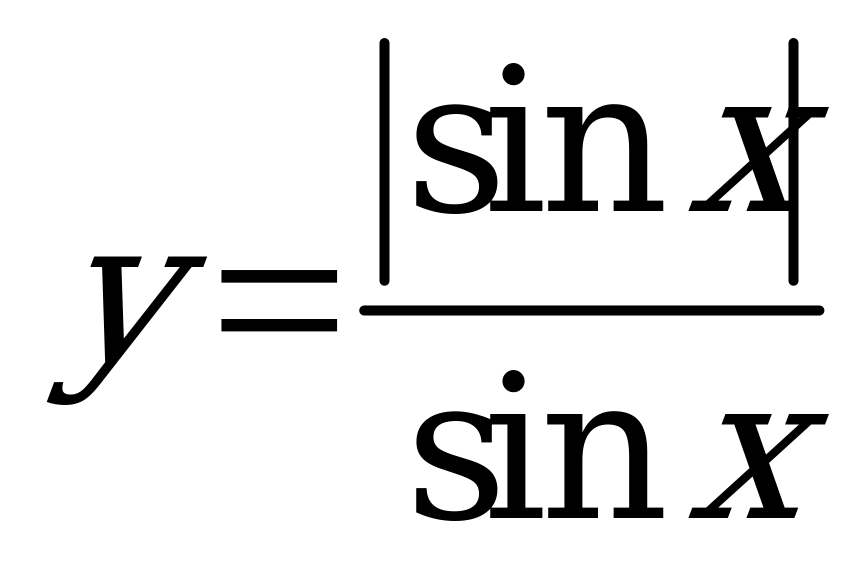 ; 2) ; 2) 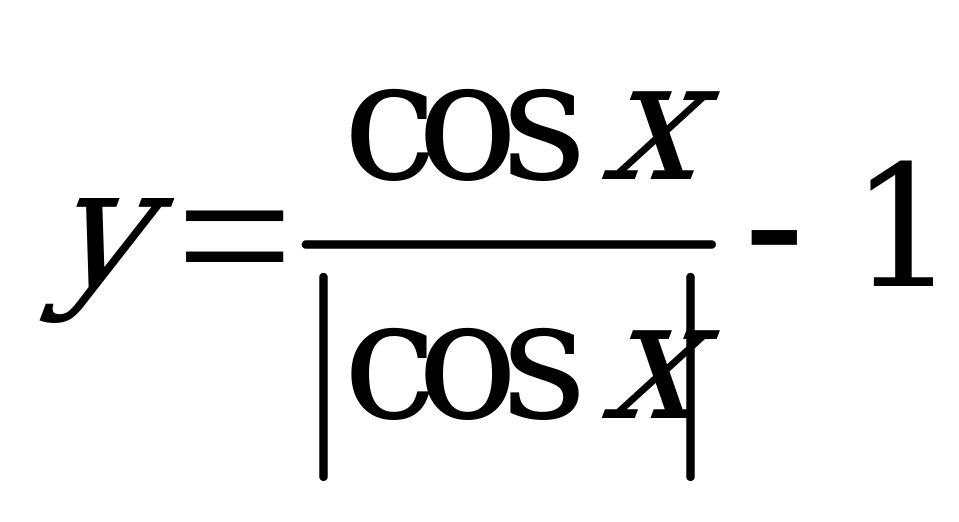 | 1) 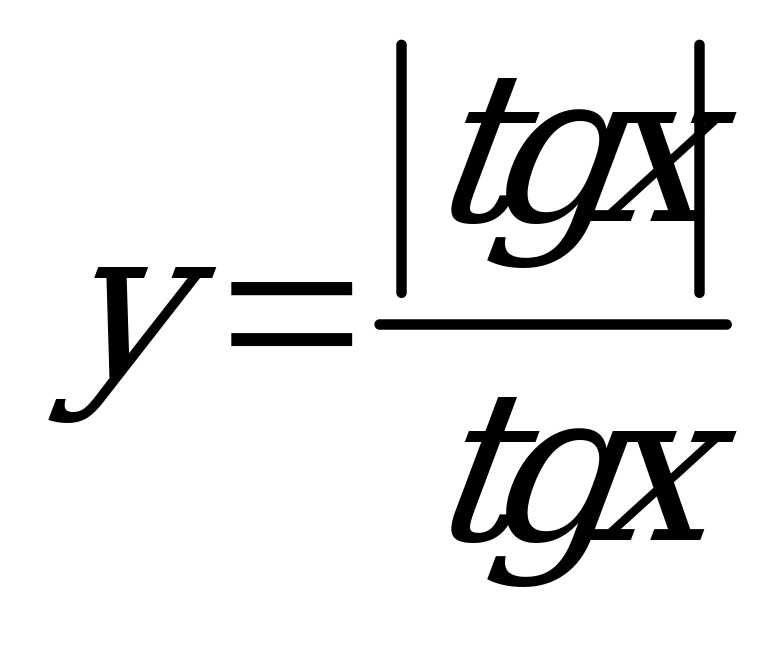 ; 2) ; 2) 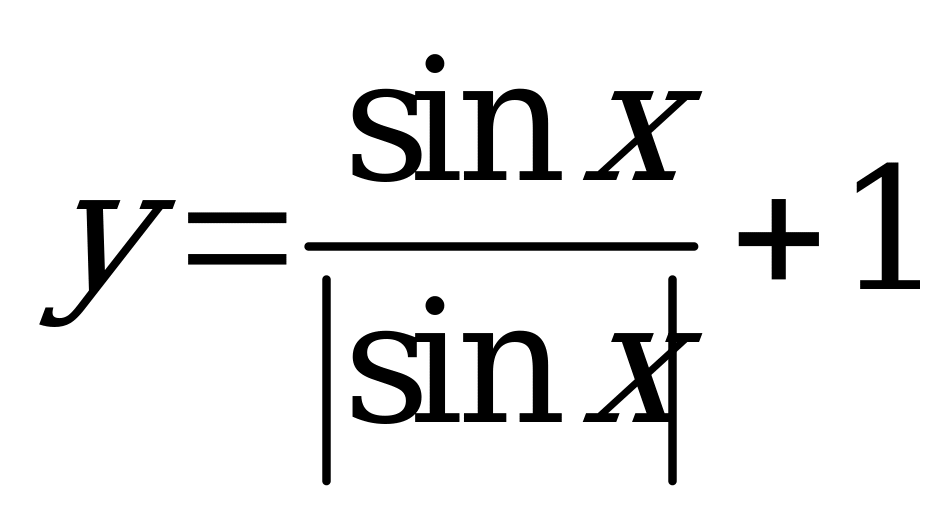 |
Подведение итогов.
Домашнее задание: Сделать краткий конспект теории по теме
«Тригонометрические функции».
Уроки 30 - 33. Учебно-тренировочные тестовые задания ЕГЭ по теме: «Тригонометрические функции»
Цели уроков: решение тестовых заданий базового уровня , более сложного уровня
, более сложного уровня 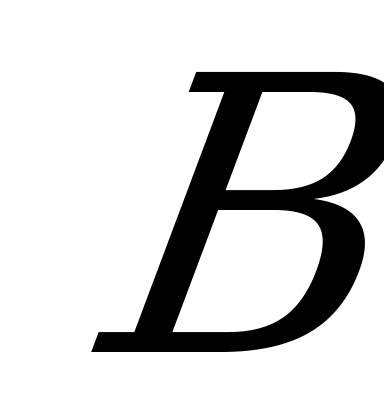 , наиболее сложного уровня
, наиболее сложного уровня 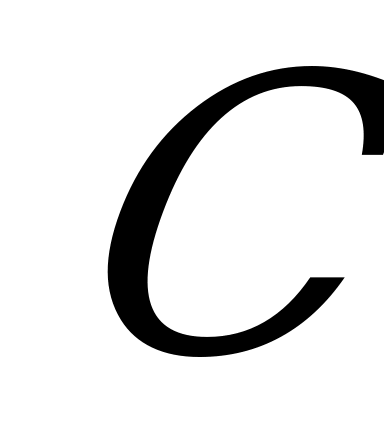 по теме «Тригонометрические функции»
по теме «Тригонометрические функции»
Ход каждого урока:
I. Организационный момент.
Приветствие, сообщение темы и задач урока.
II. Организация решения тестовых заданий.
Учитель распределяет тестовые задания на четыре урока
следующим образом:
Урок 30. Решение тестовых заданий базового уровня .
.
Урок 31. Решение тестовых заданий базового уровня и тестовых заданий более сложного уровня
и тестовых заданий более сложного уровня 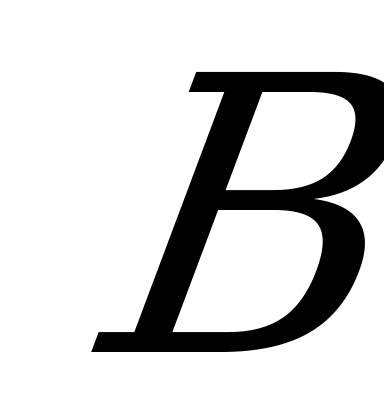 .
.
Урок 32. Решение тестовых заданий более сложного уровня 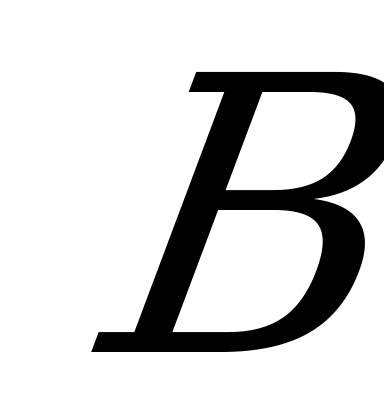 .
.
Урок 33. Решение тестовых заданий наиболее сложного уровня 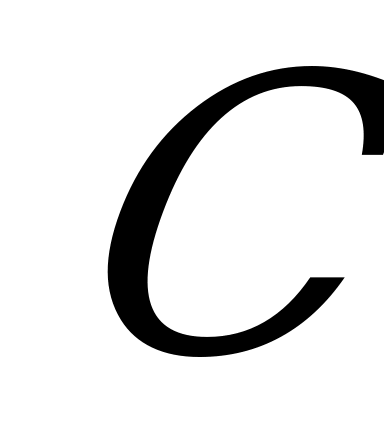 .
.
На каждом уроке рекомендуется проводить проверочные работы, математические диктанты. Домашние задания учитель может приготовить, используя тестовые задания из любых источников.
III. Учебно-тренировочные тестовые задания ЕГЭ
Тестовые задания базового уровня .
.
| А1. Формулы приведения. Стандартные значения. | Ответы |
| А1.1 Вычислите: 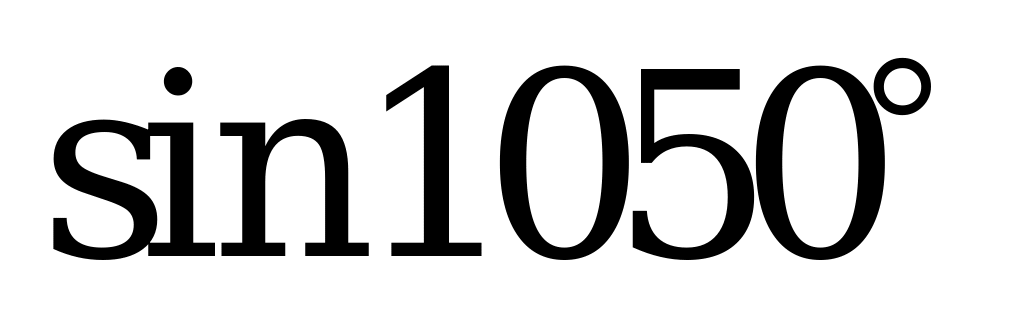 - - 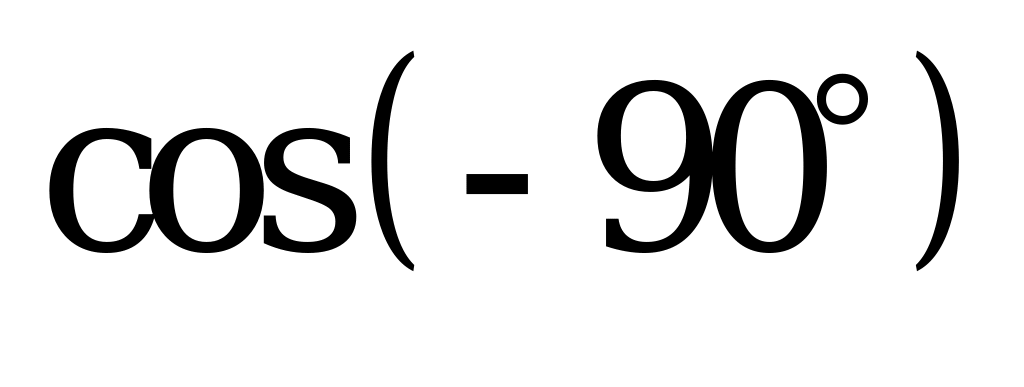 + + 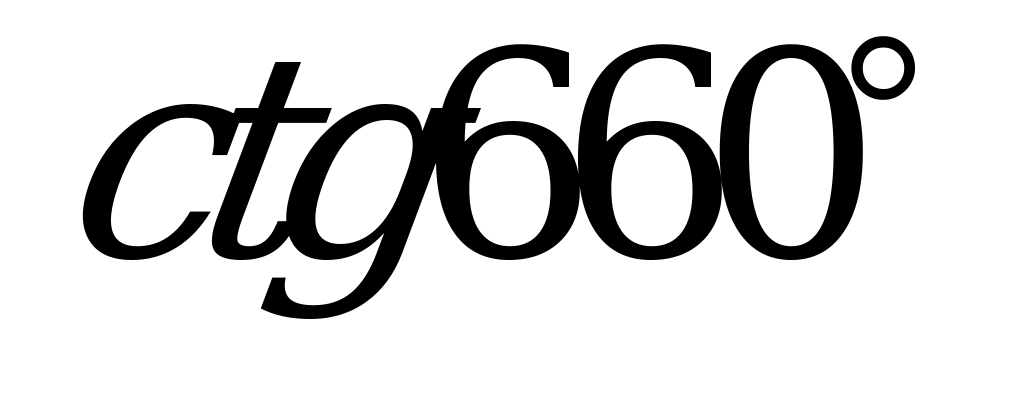 A) 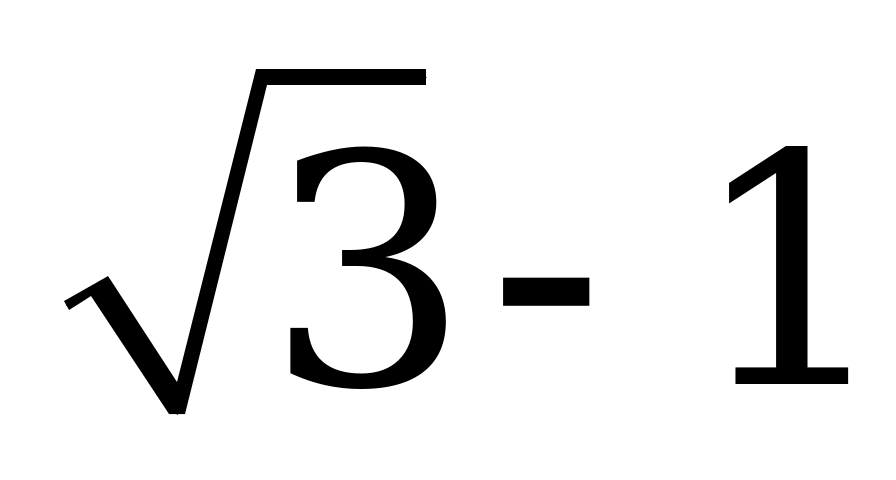 B) - B) -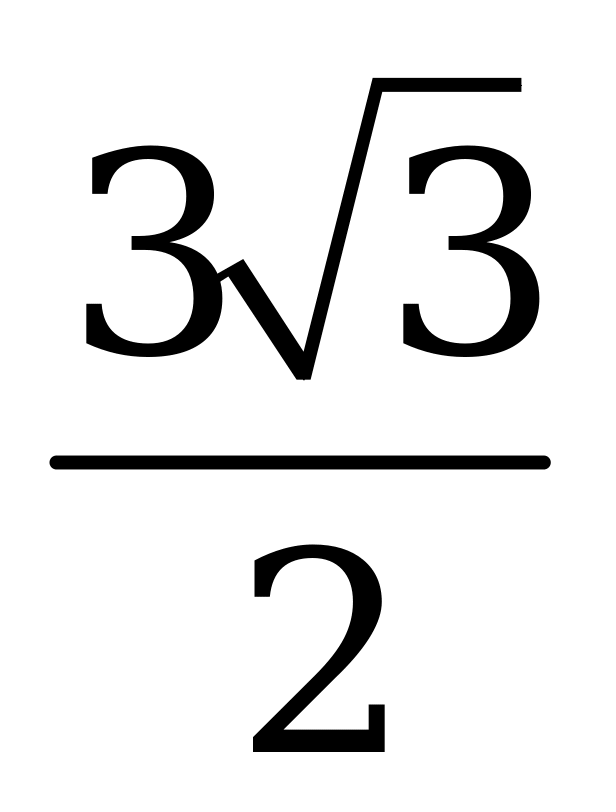 C) - C) -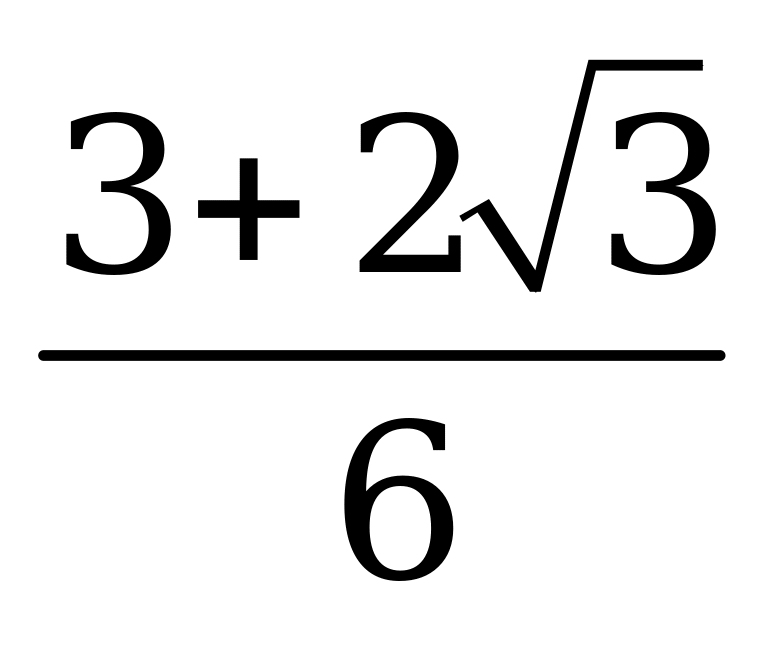 D) 0,5 + D) 0,5 + 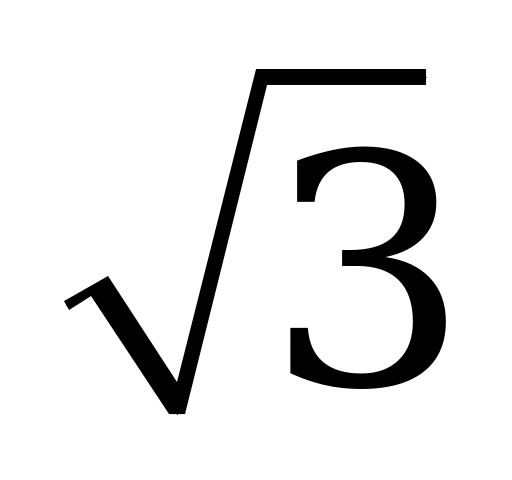 E) 2 E) 2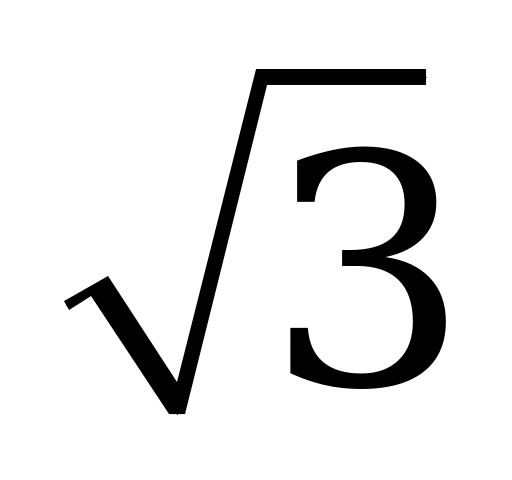 | C |
| А1.2 Вычислите: 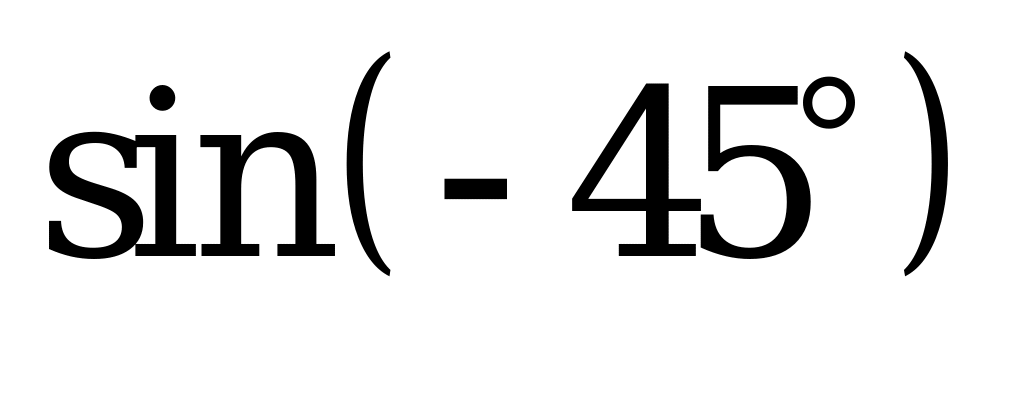 + + 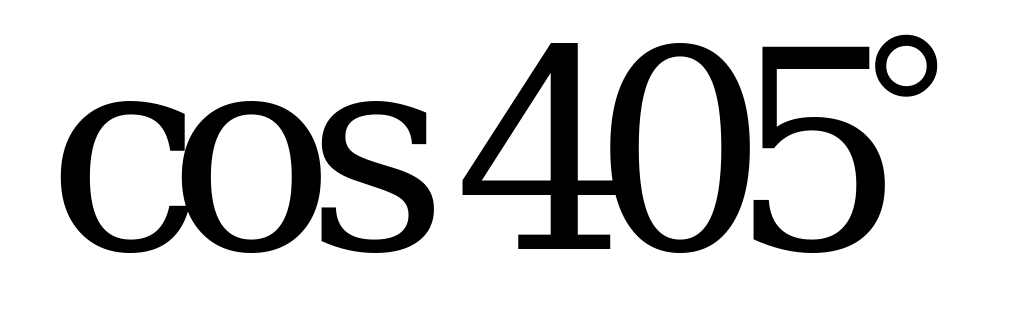 + + 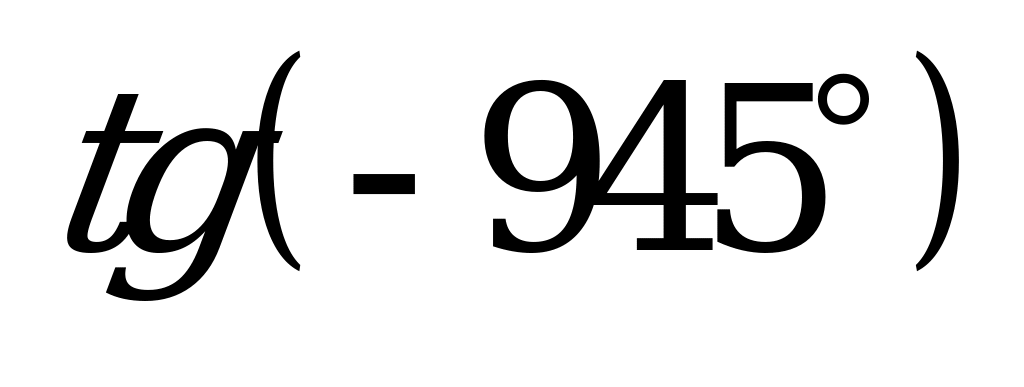 A) 1 B) -1 C) -2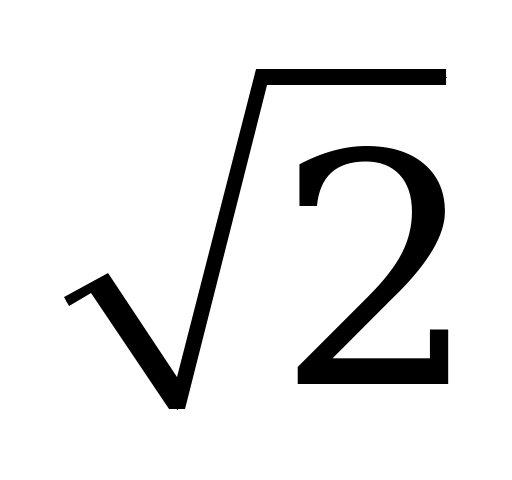 D) D) 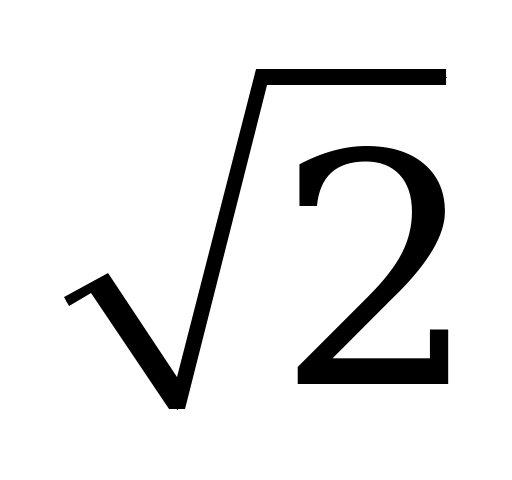 - 1 E) - 1 E) 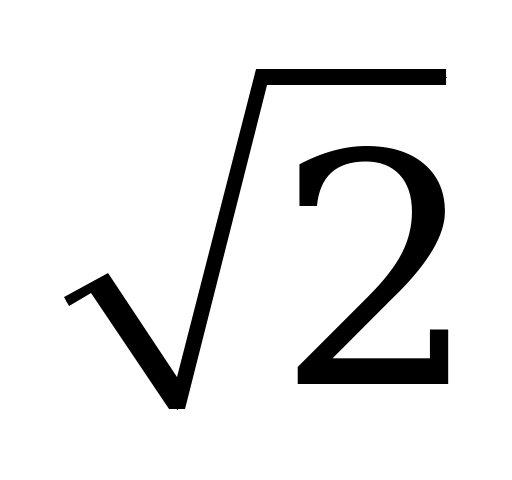 + 1 + 1 | B |
| А1.3 Вычислите: 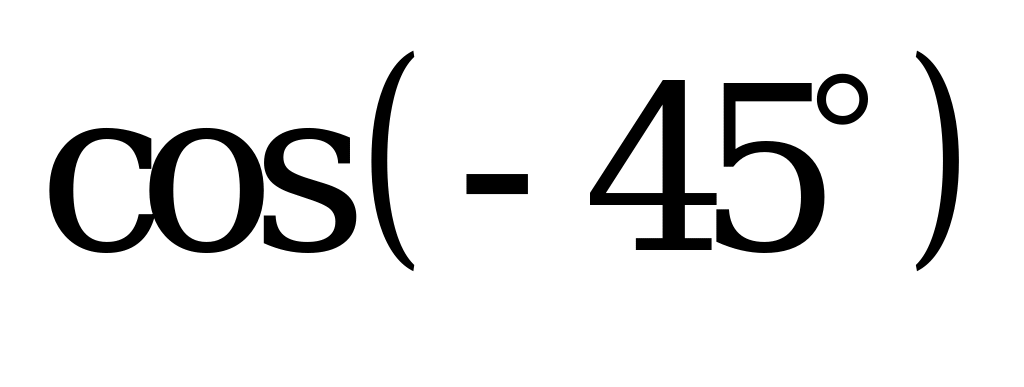 + + 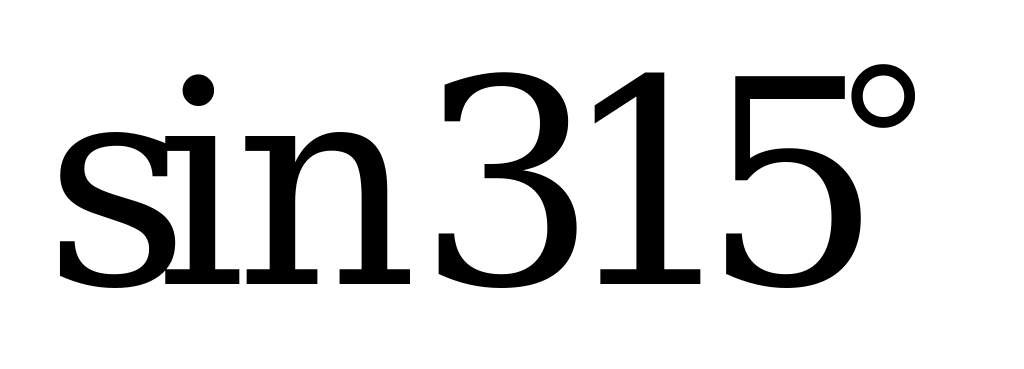 + + 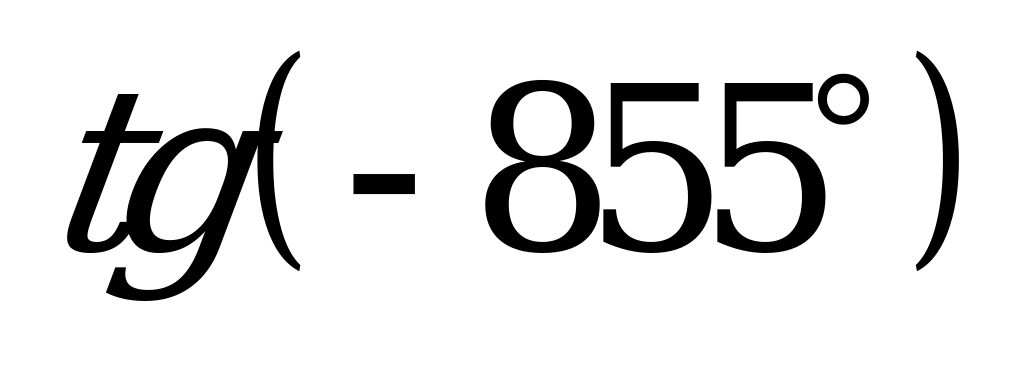 A) 0 B)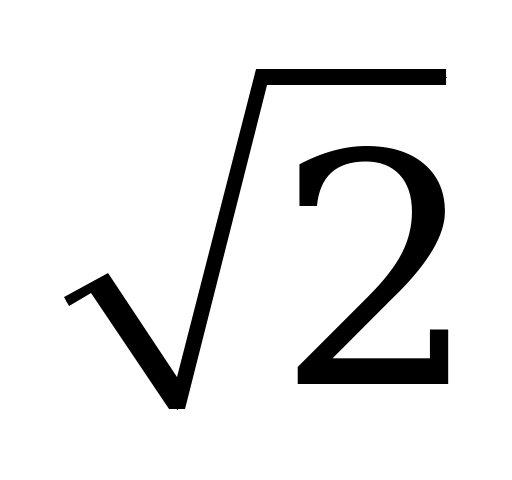 – 1 C) 1 + – 1 C) 1 +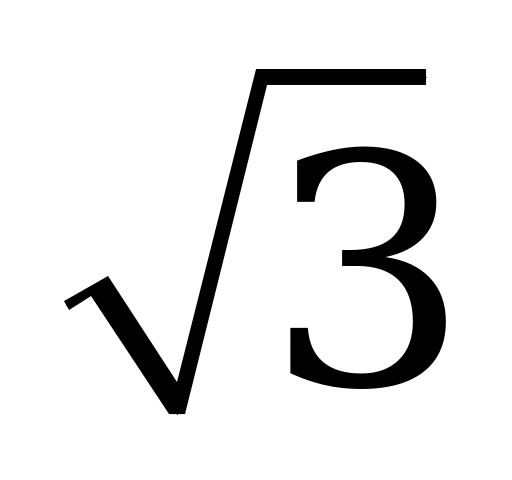 D) -1 E) 1 D) -1 E) 1 | E |
| А1.4 Укажите неверное равенство. A) 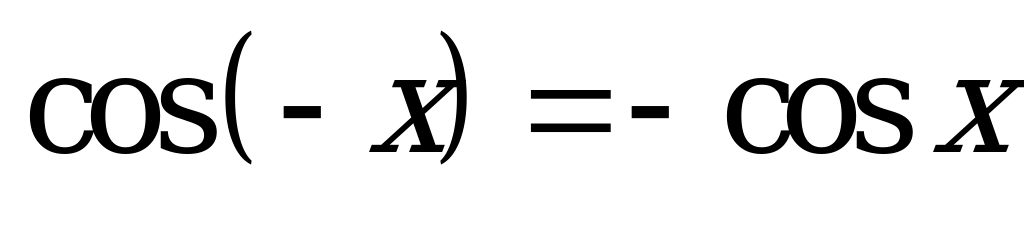 B) B) 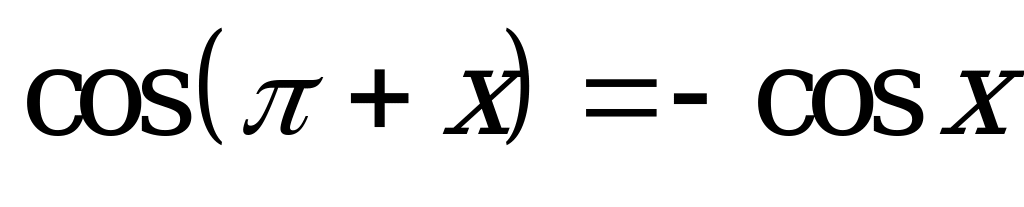 C) 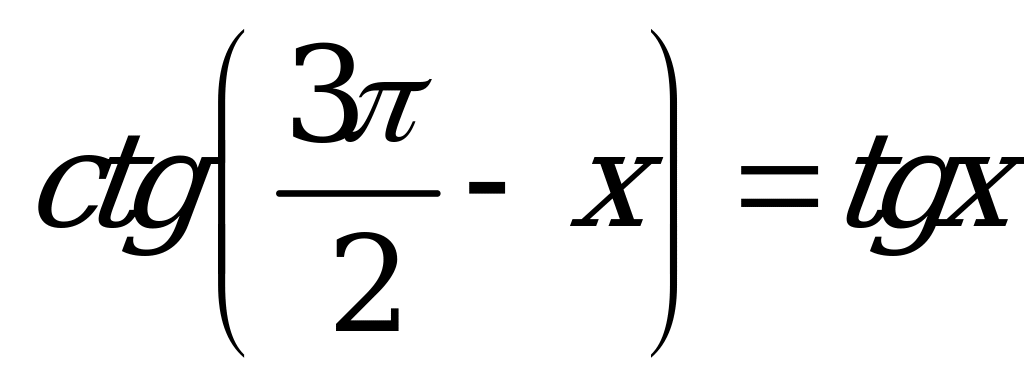 D) D) 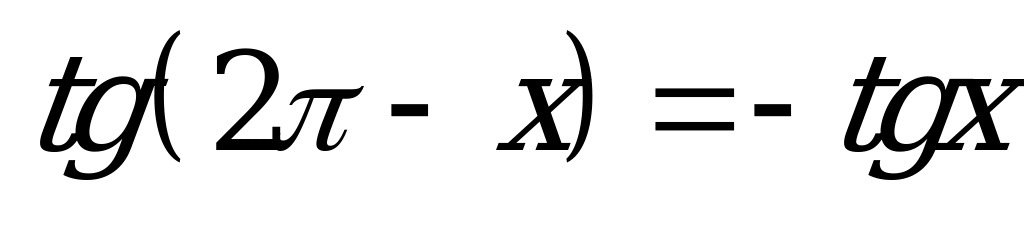 E) 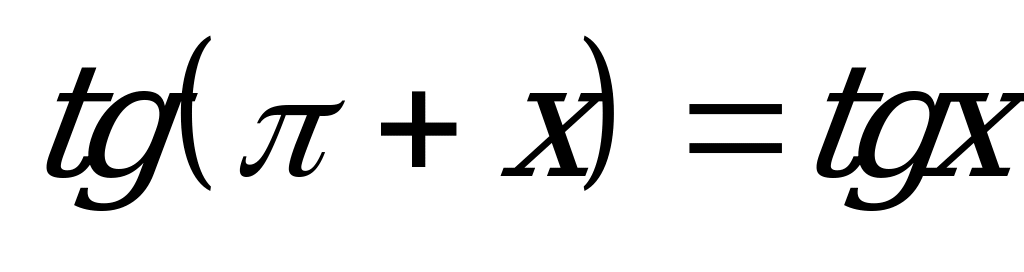 | A |
| А1.5 Упростите выражение 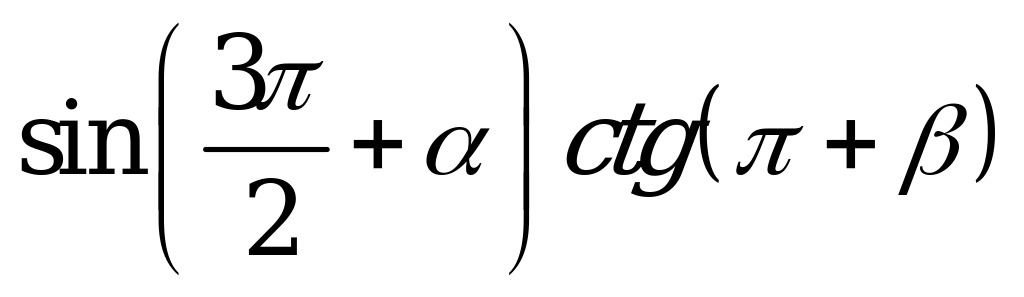 A) 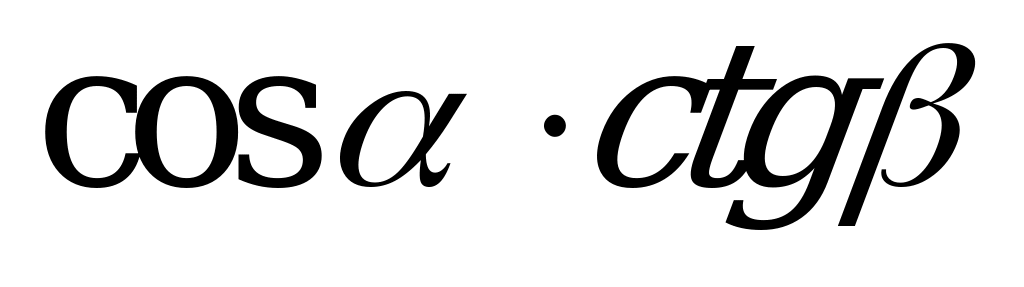 B) B) 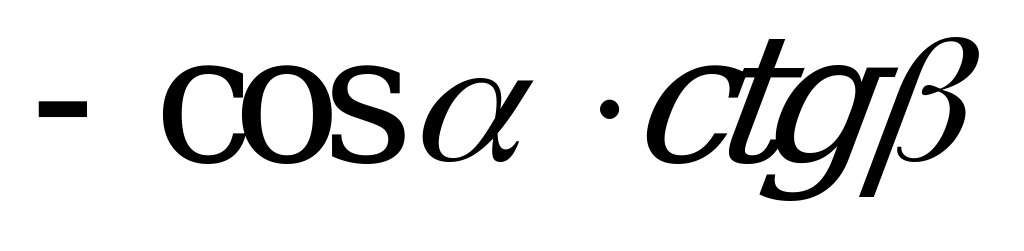 C) C) 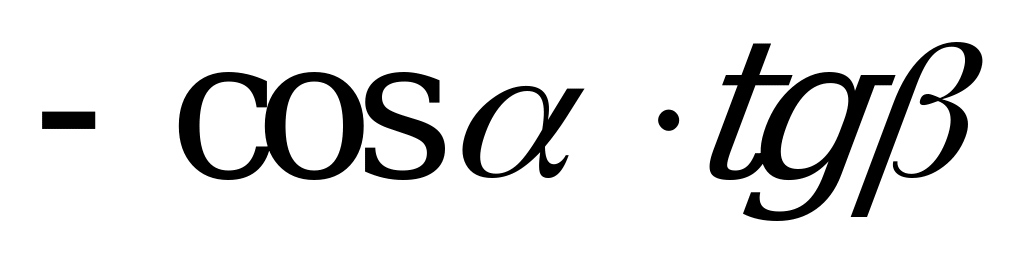 D) 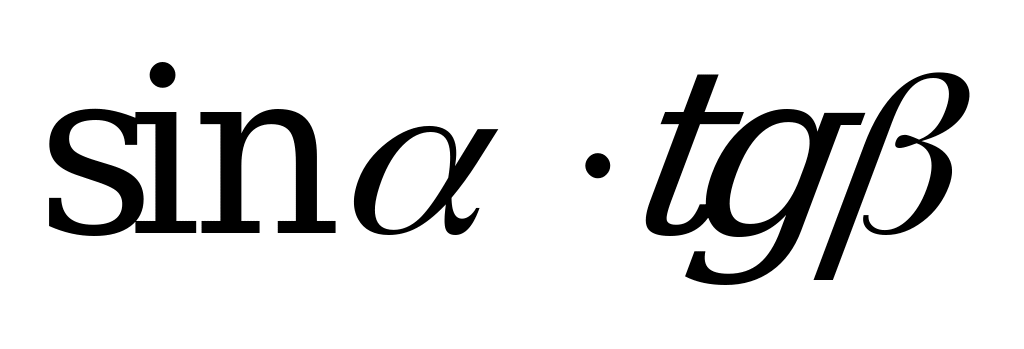 E) E) 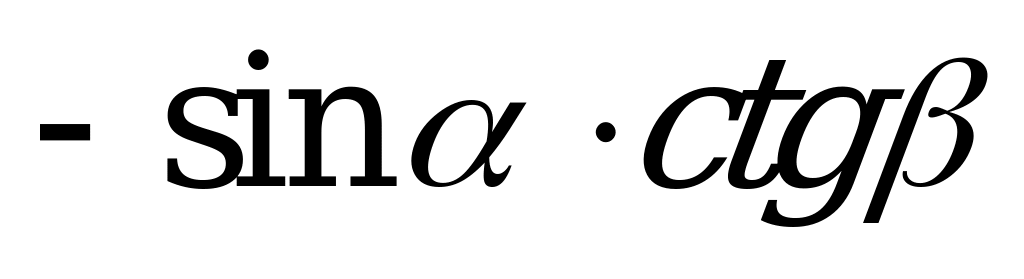 | B |
| А1.6 Упростите выражение: 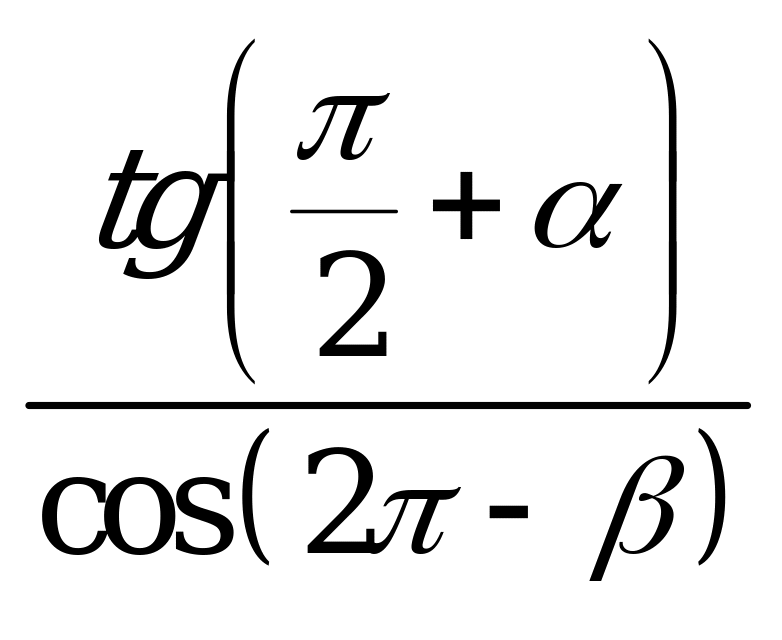 . . A) 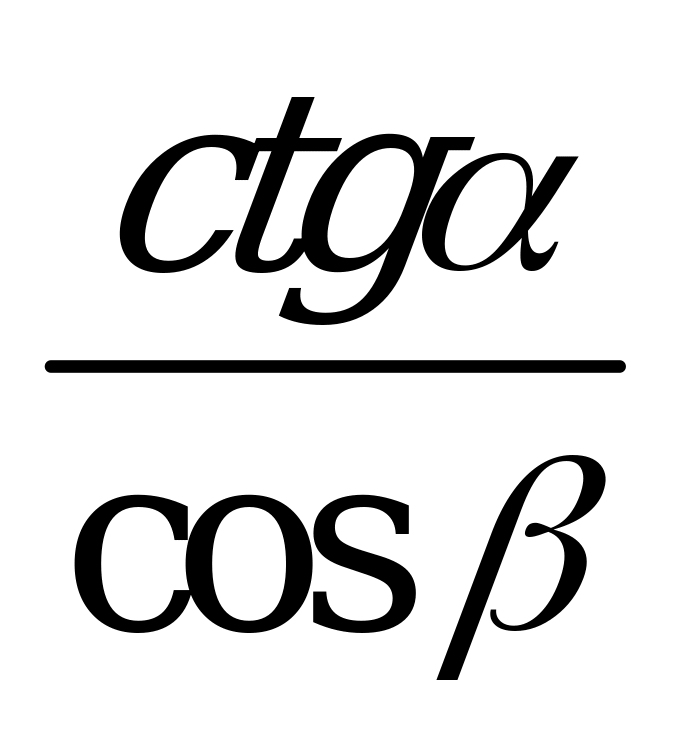 B) - B) -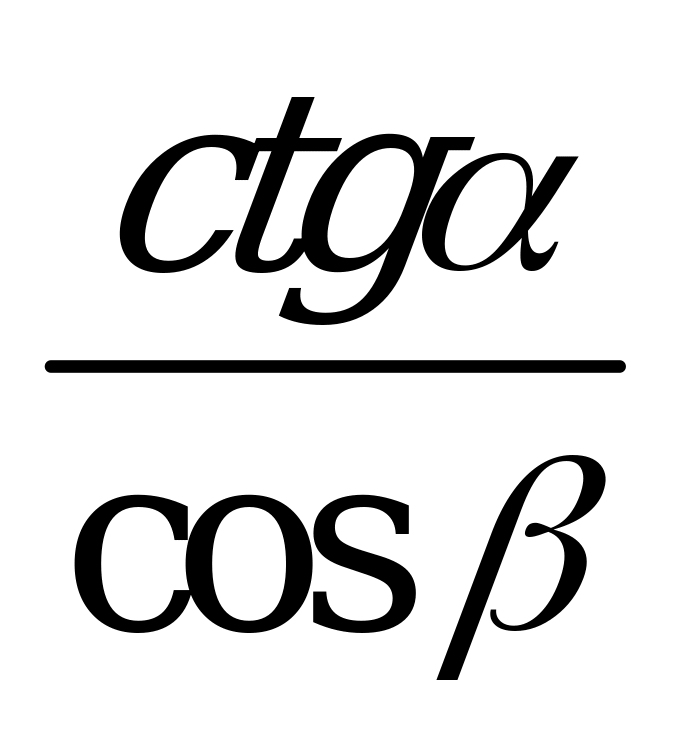 C) - C) -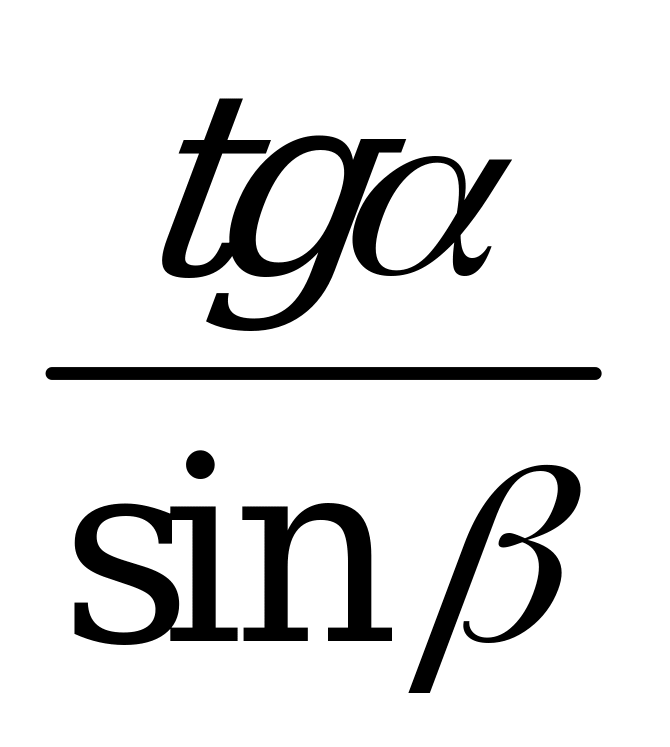 D) D) 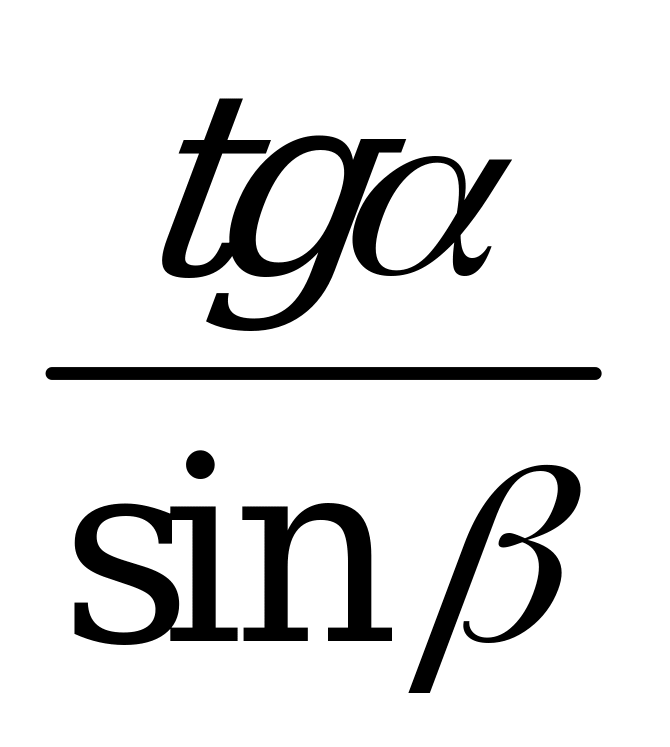 E) - E) - 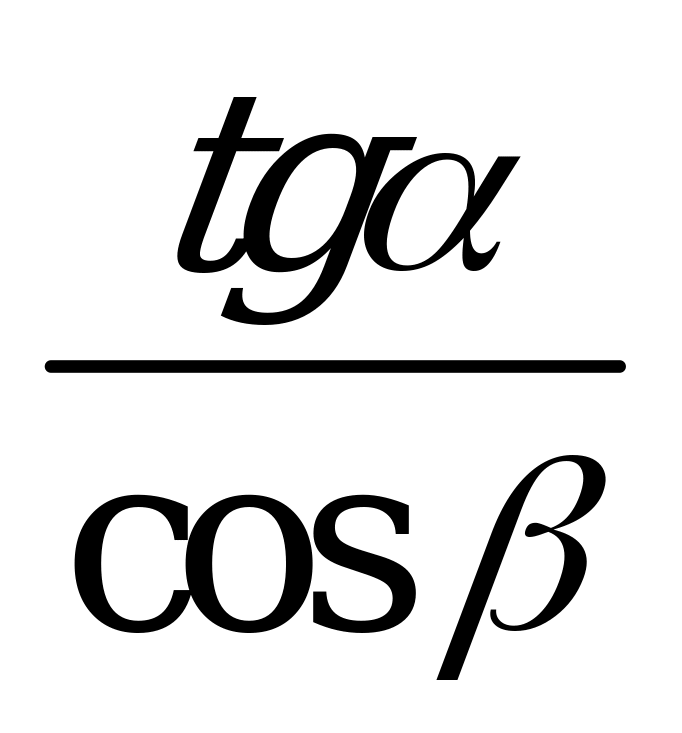 | B |
| А1.7 Упростите выражение: 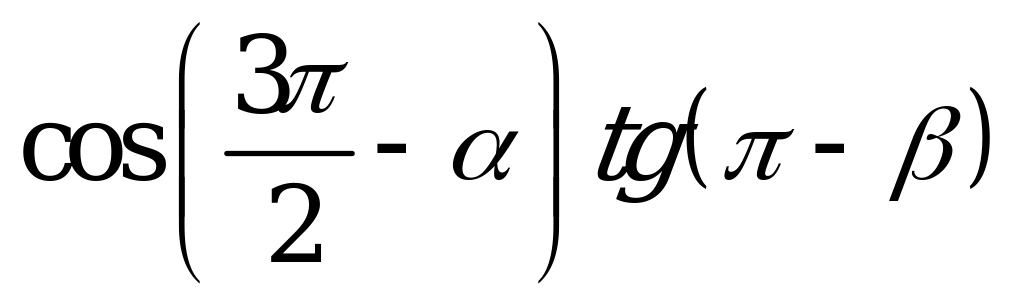 A) -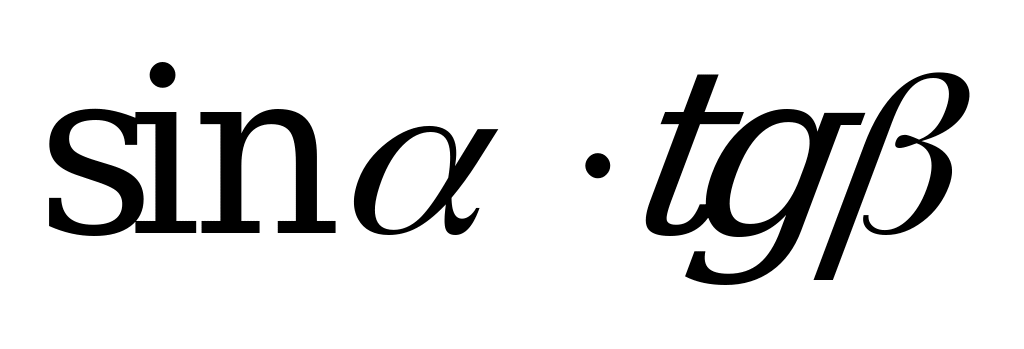 B) B) 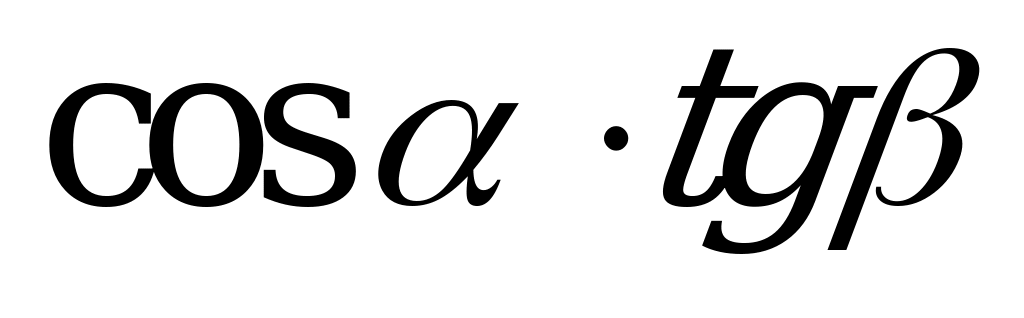 C) C) 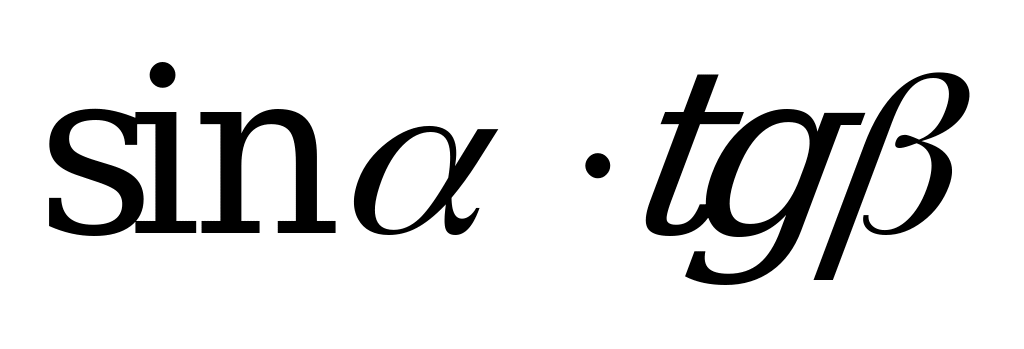 D) -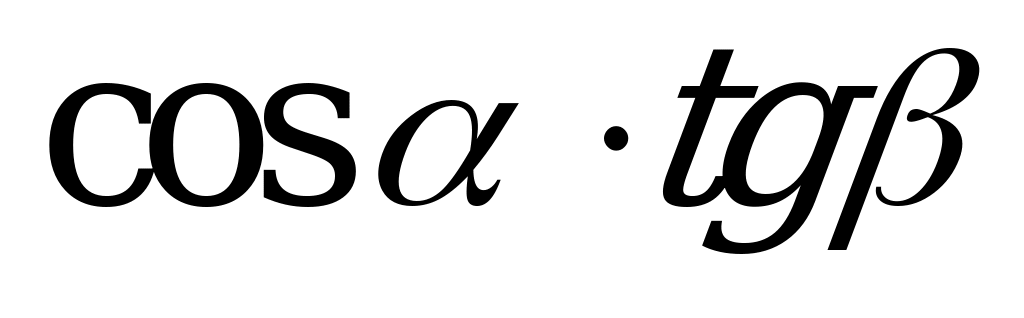 E) E) 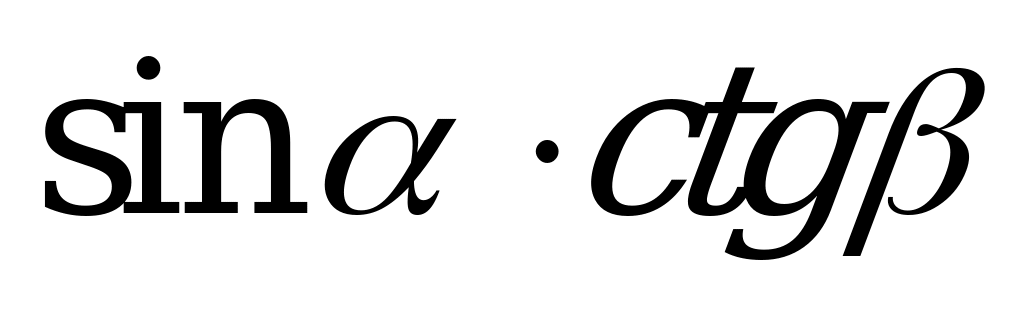 | C |
| А1.8 Упростите: 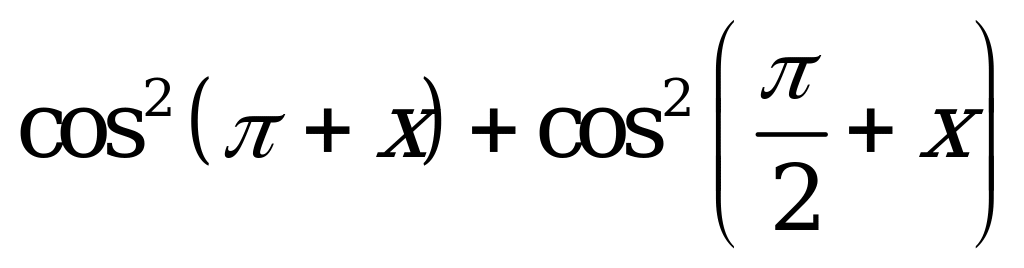 A)  B) B)  C) C) 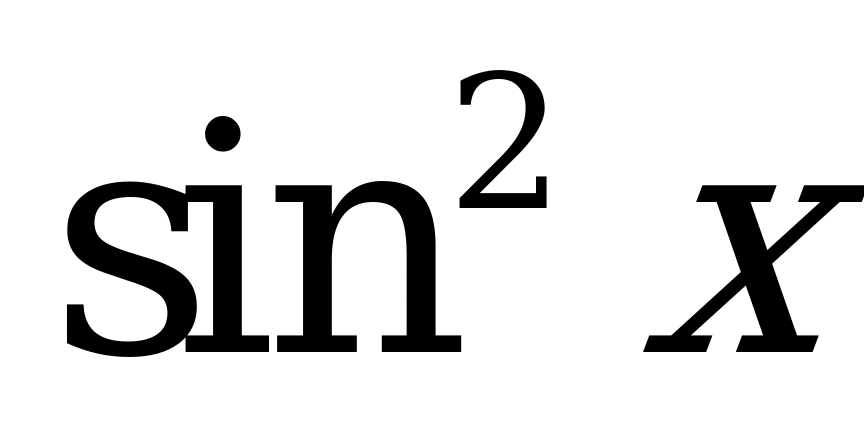 D) 2 E) 1 D) 2 E) 1 | E |
| А1.9 Упростите выражение: 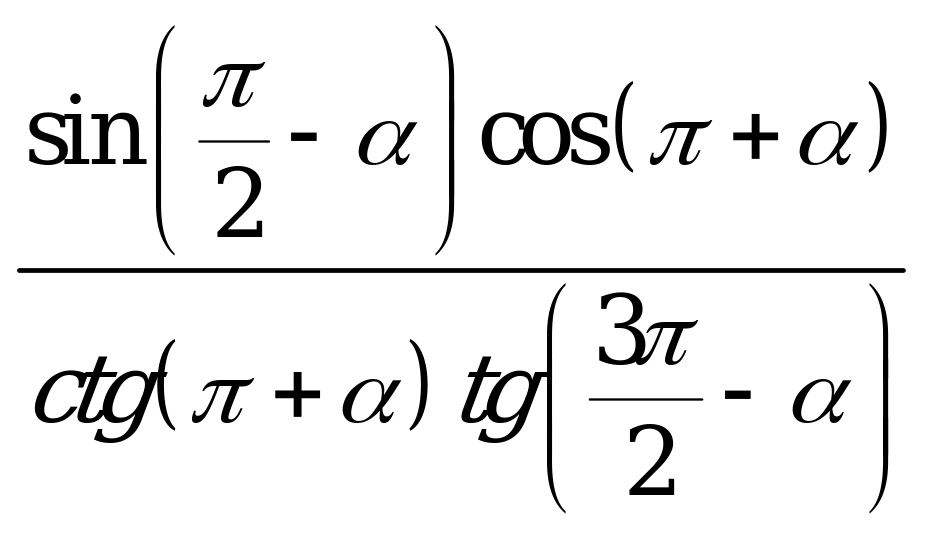 A) 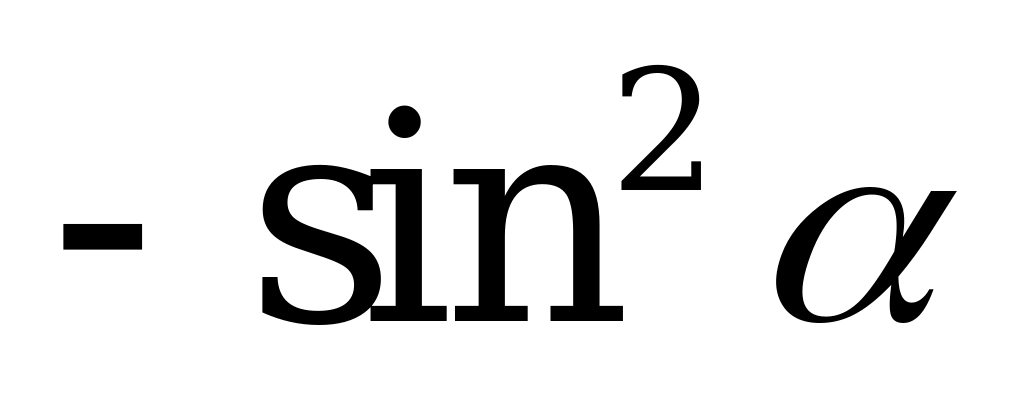 B) B) 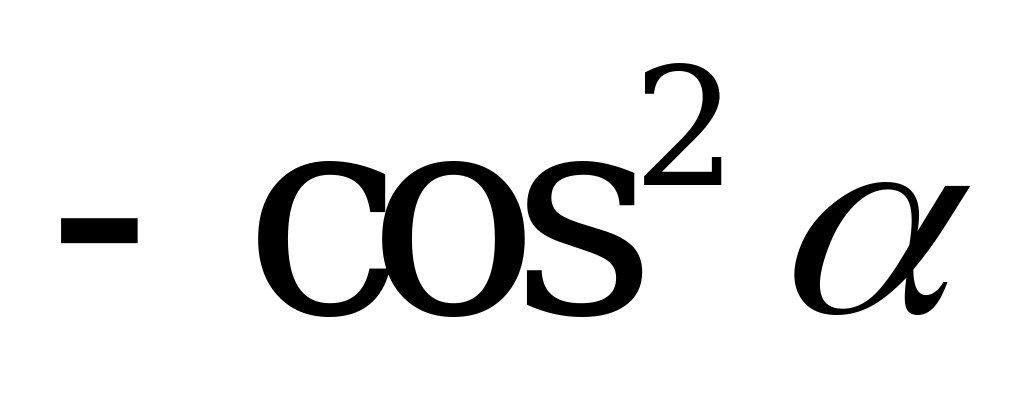 C) C) 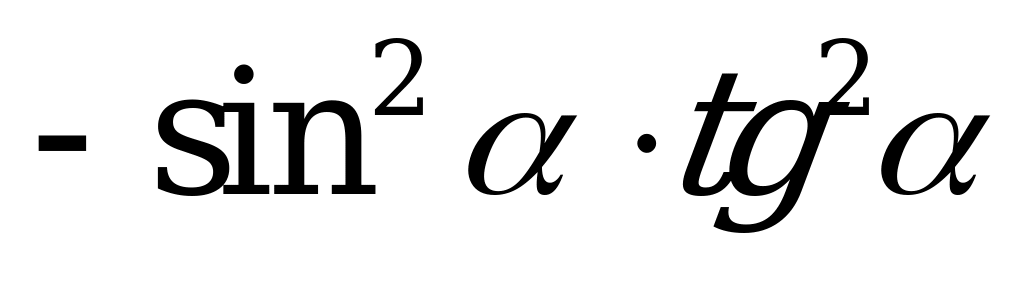 D) 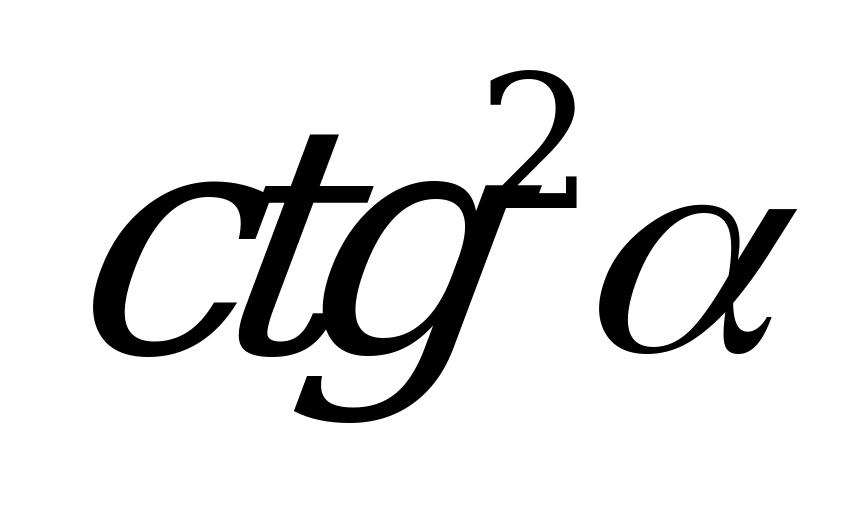 E) E) 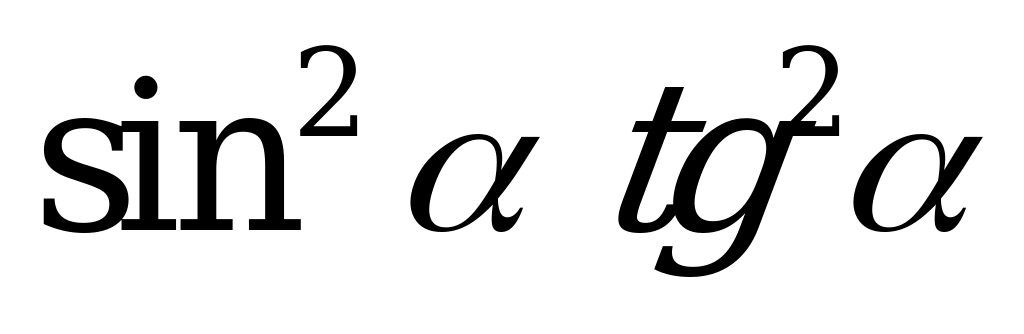 | A |
| А1.10 Упростите: 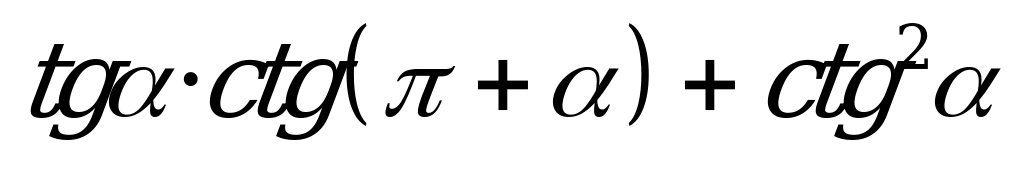 A) 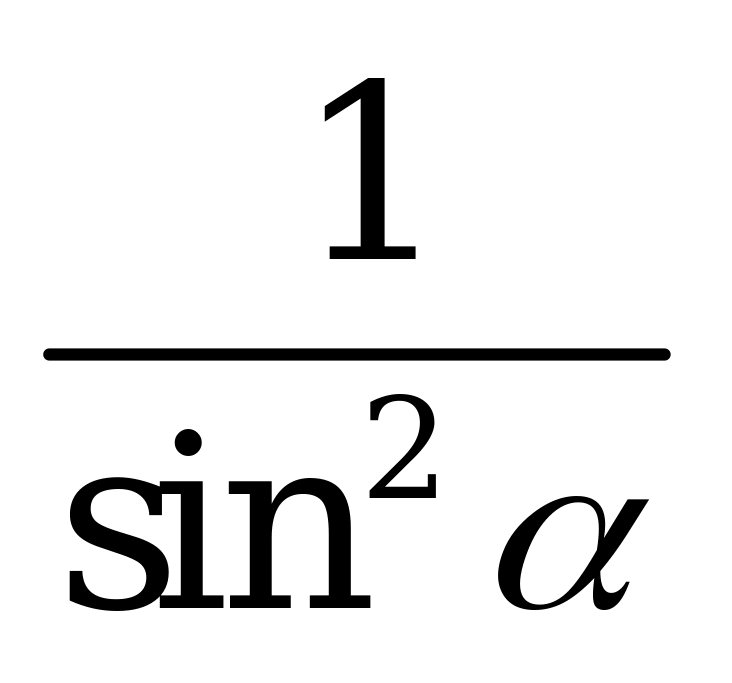 B) B) 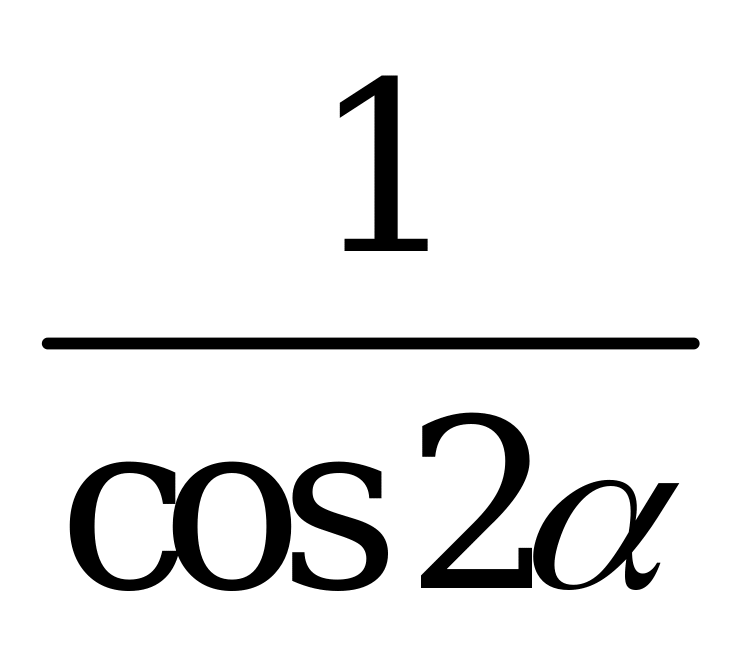 C) C) 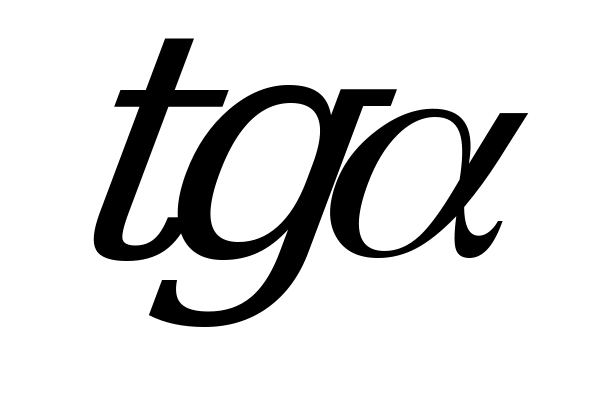 D) D) 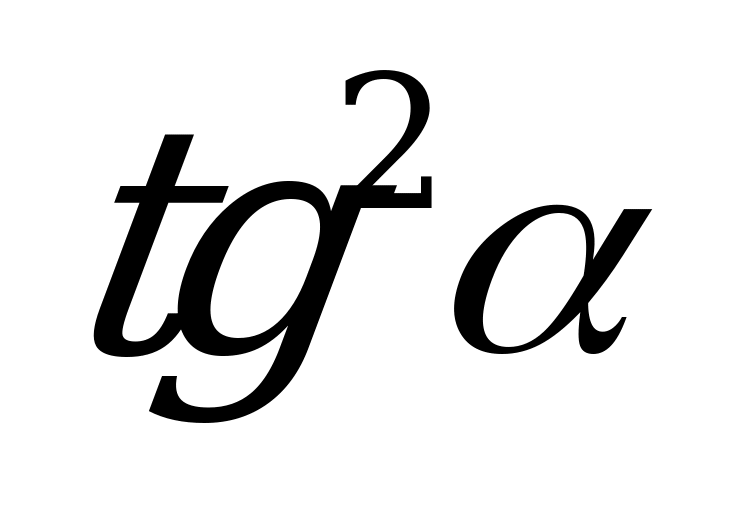 E) 1 E) 1 | A |
| А2. Знак тригонометрической функции. Сравнение значений | Ответы |
| А2.1 Какое из следующих чисел отрицательное? A) 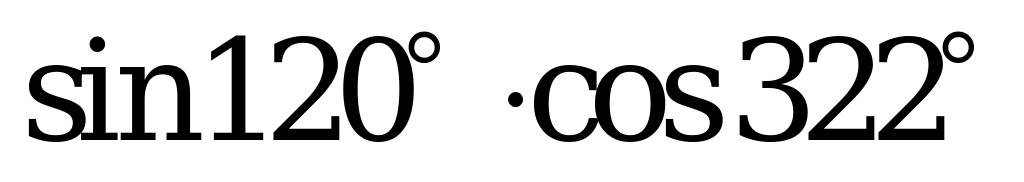 B) B) 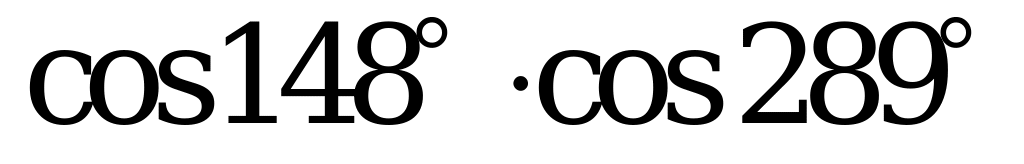 C)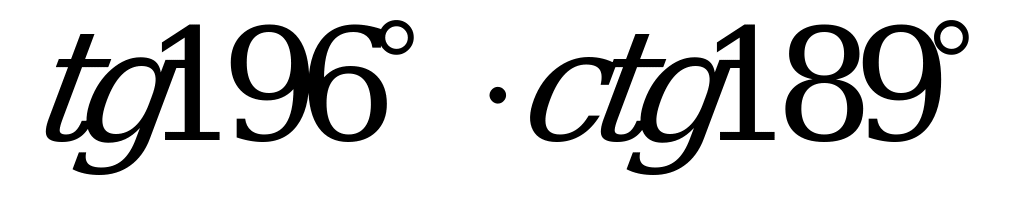 D) D)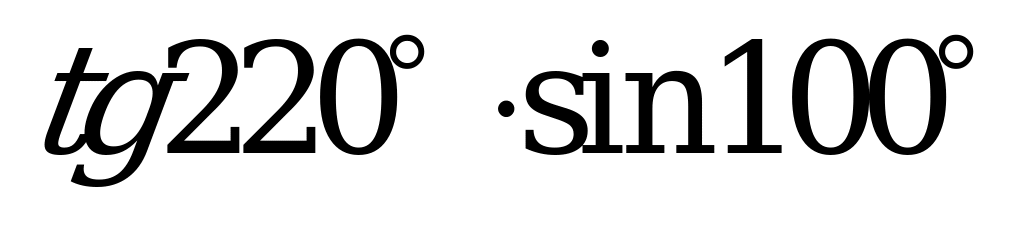 E) E) 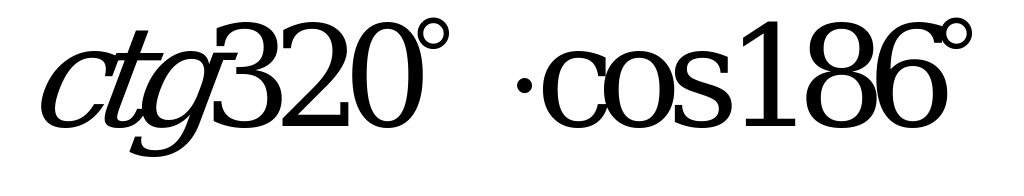 | B |
| А2.2 Какое из нижеследующих чисел отрицательное? A)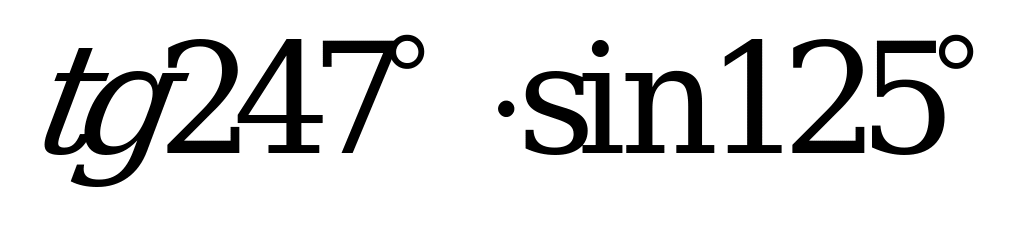 B) B)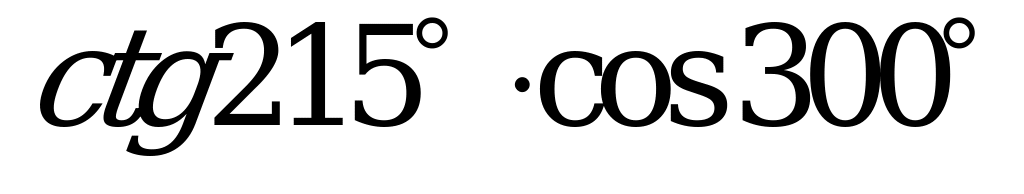 C)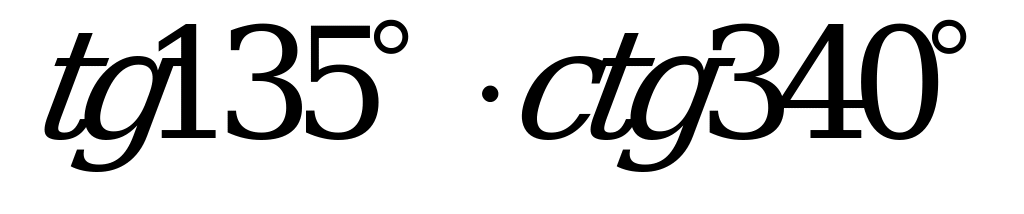 D) D)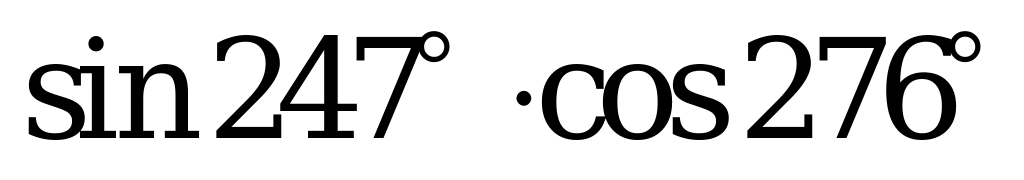 E) E) 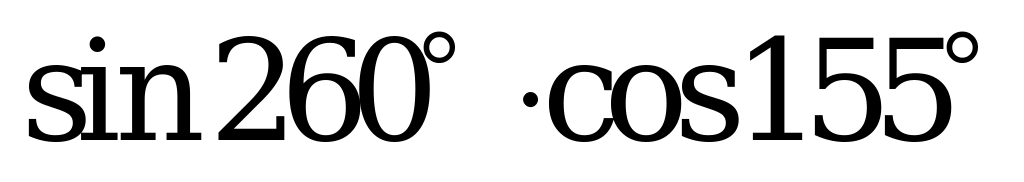 | D |
| А2.3 Какие из следующих чисел 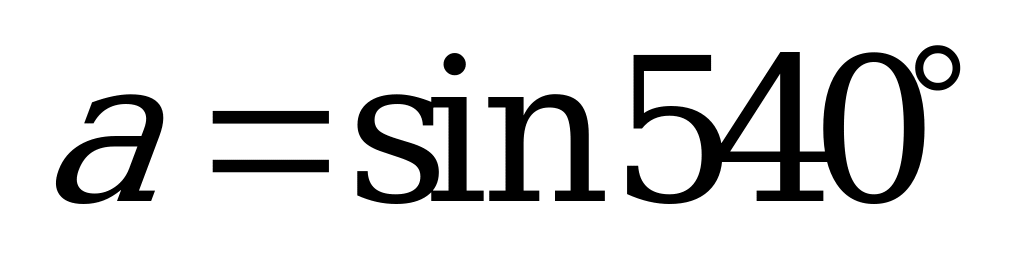 , ,  , , 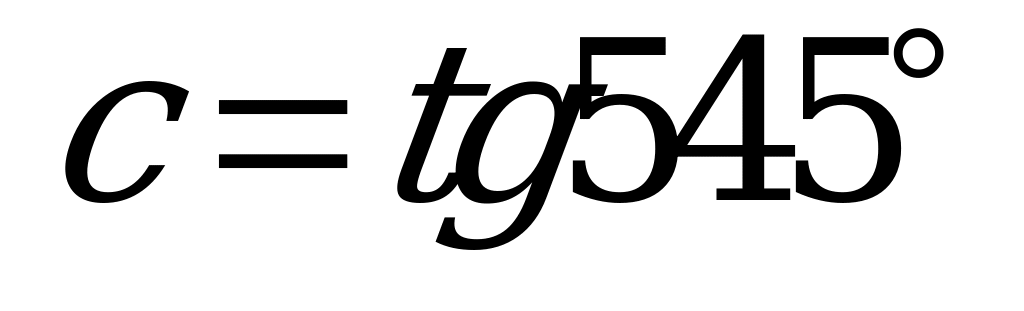 и и  отрицательные? отрицательные? A)  B) B) 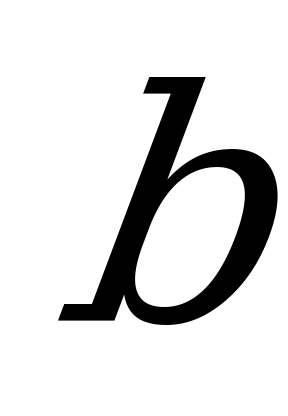 C) C) 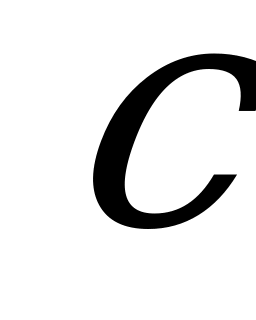 D) D) 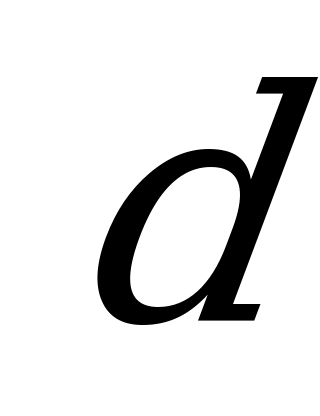 E) таких нет E) таких нет | E |
| А2.4 Расставьте в порядке убывания числа: 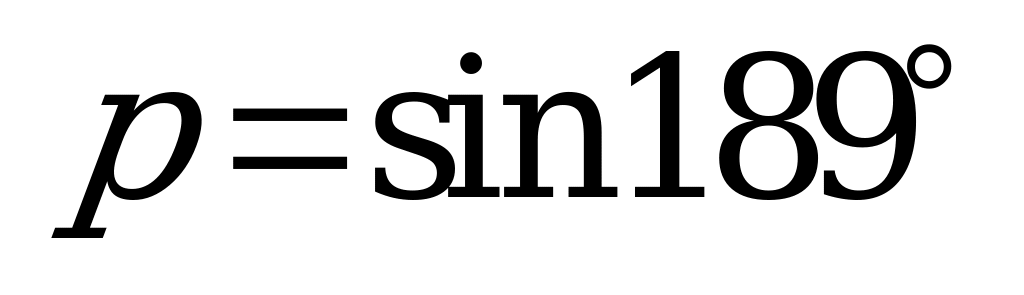 , , 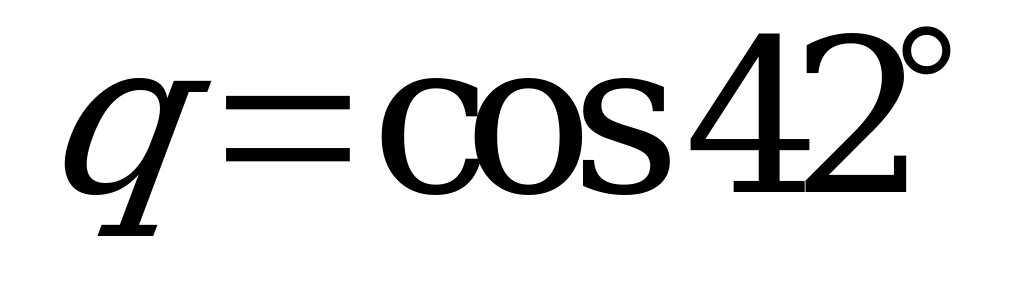 и и 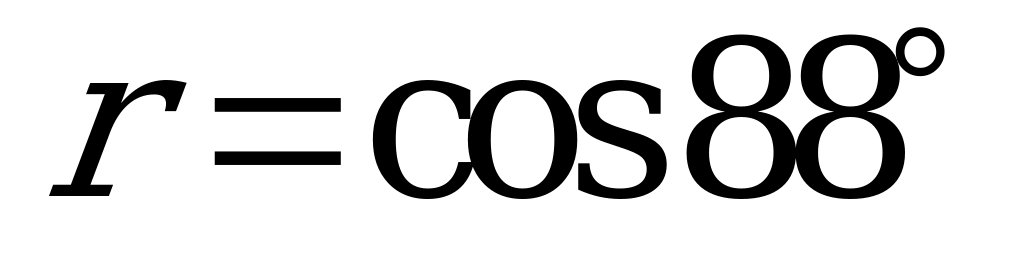 A) q p r B) p q r C) p r q D) r q p E) q r p | E |
| А2.5 Расположите числа в порядке возрастания: 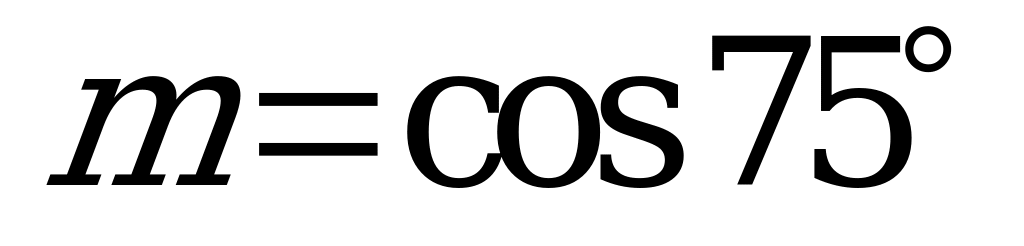 , ,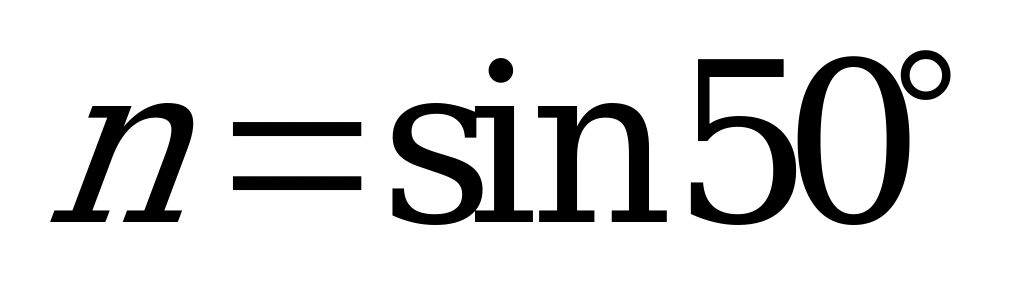 , ,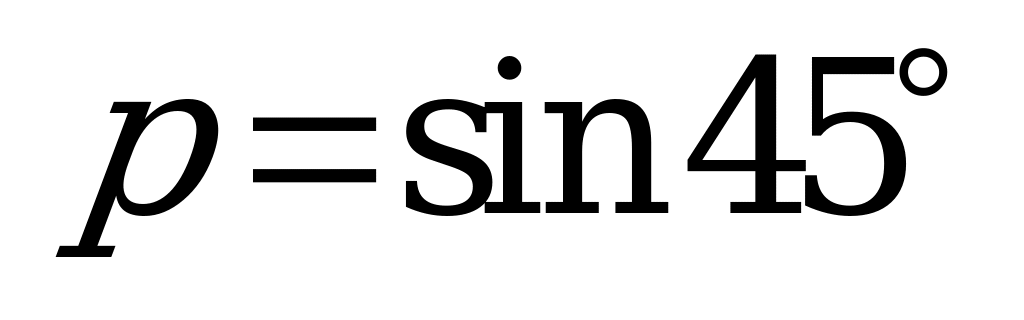 , ,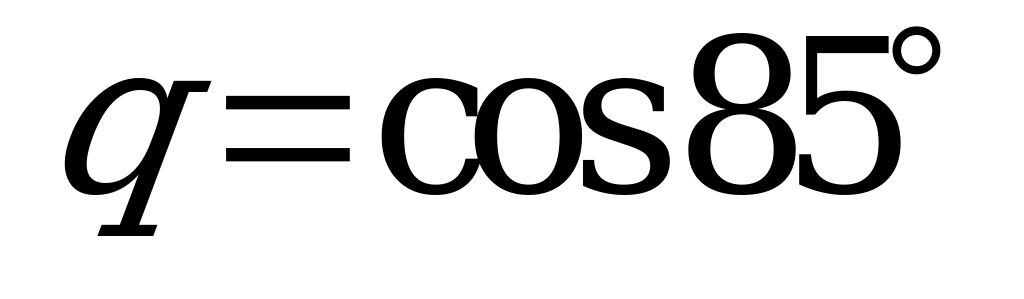 . . A) q D) p m q n E) q m n p | A |
| А2.6 Среди указанных чисел найдите наибольшее. A) 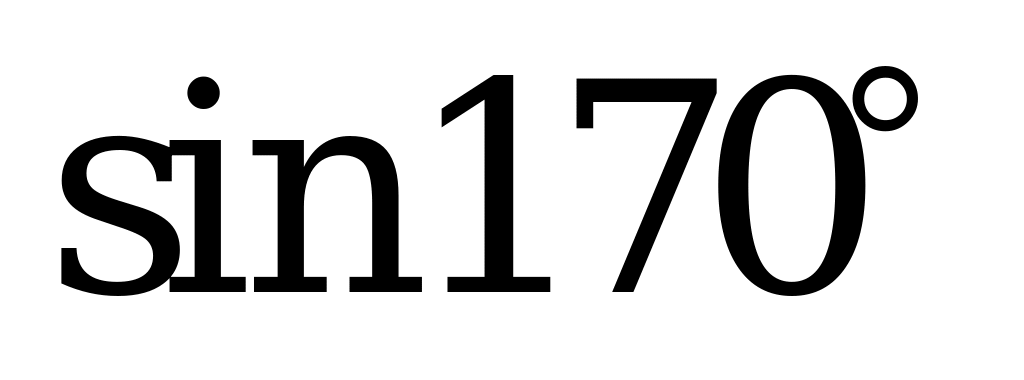 B) B) 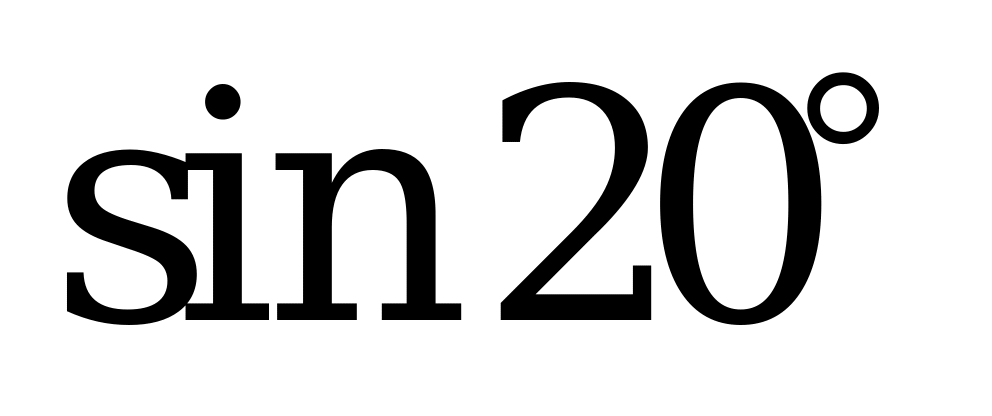 C) C)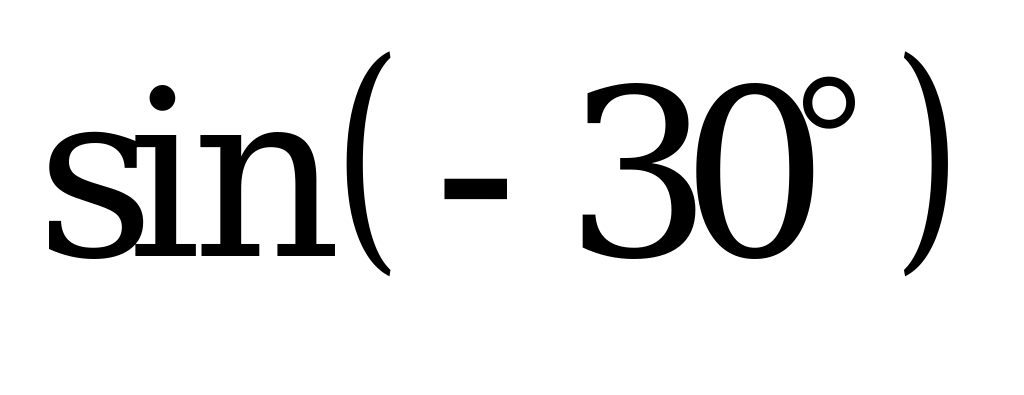 D) 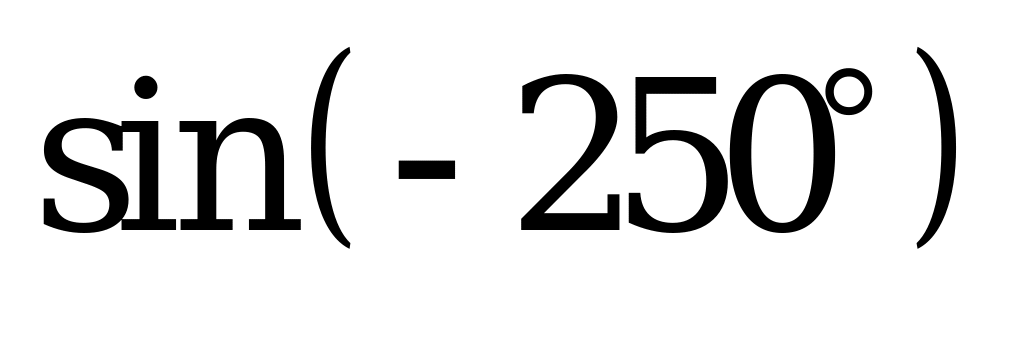 E) E) 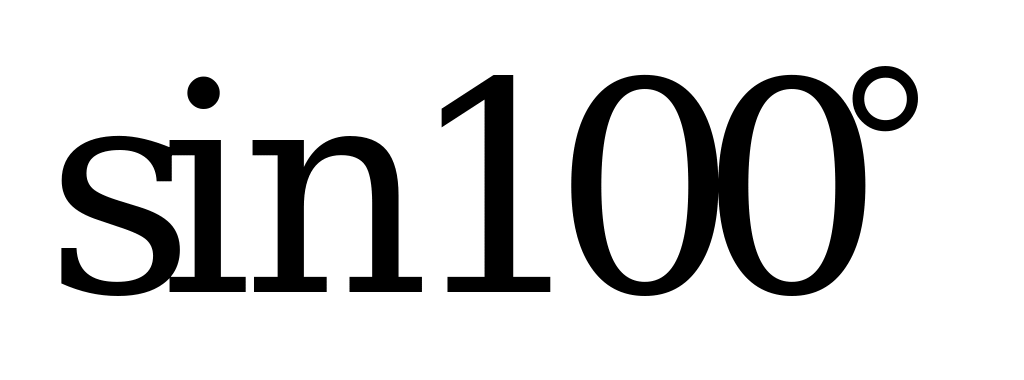 | E |
| А2.7 Расположите числа 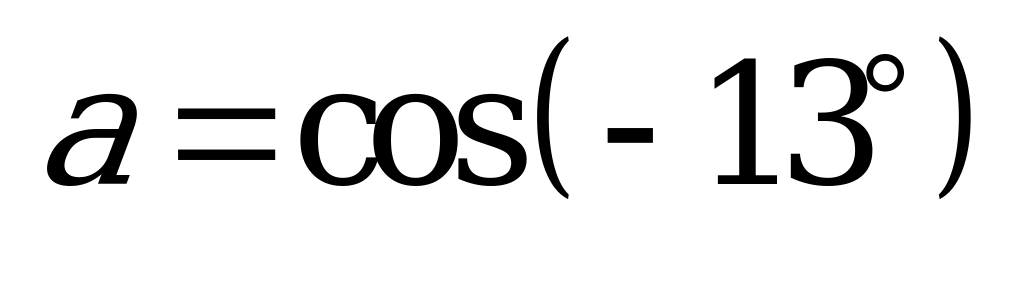 , ,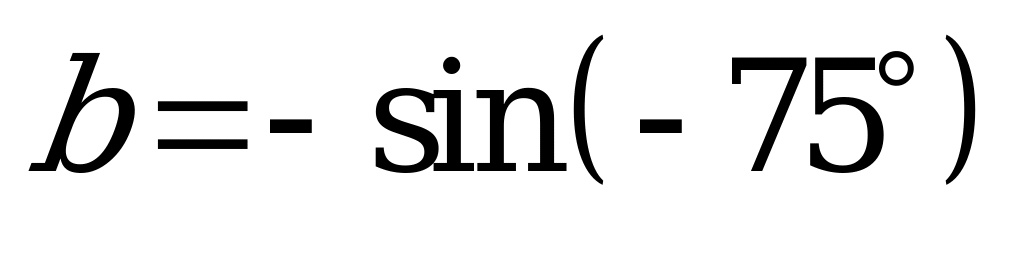 , , 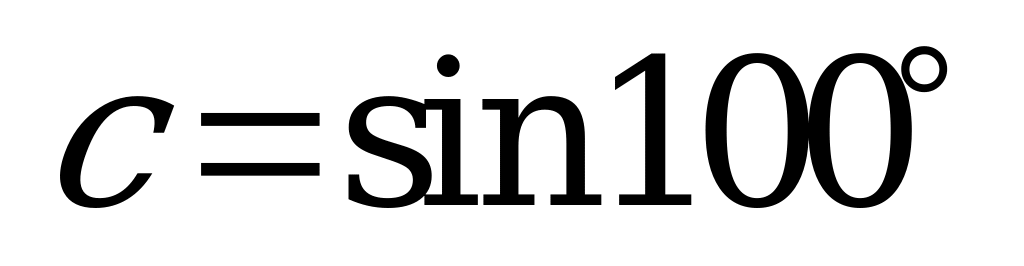 в порядке возрастания. в порядке возрастания. A) b D) b c a E) c b a | A |
| А2.8 Какое из следующих неравенств ложно? A) sin650 cos350 B) tg170 0 C) cos150 cos350 D) cos400 sin800 E)  | D |
| А2.9 Какая разность отрицательна? A) sin1400 - sin1500 B) cos100 - cos500 C) tg870 - tg850 D) ctg450 - ctg400 E)  - sin100 - sin100 | D |
| А2.10 Расставьте в порядке возрастания числа k =  , t = cos320 и q = sin1120. , t = cos320 и q = sin1120. A) q ) t ) t E) k | D |
| А3. Основные тригонометрические формулы. | Ответы |
| А3.1 Упростите выражение 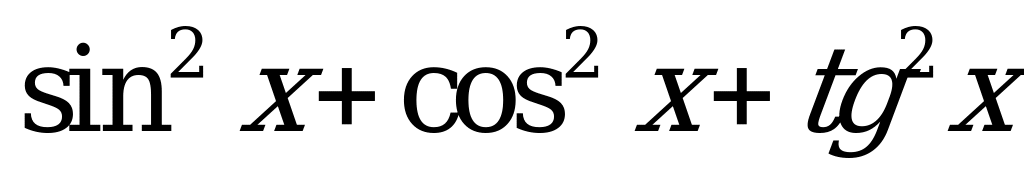 . . A) -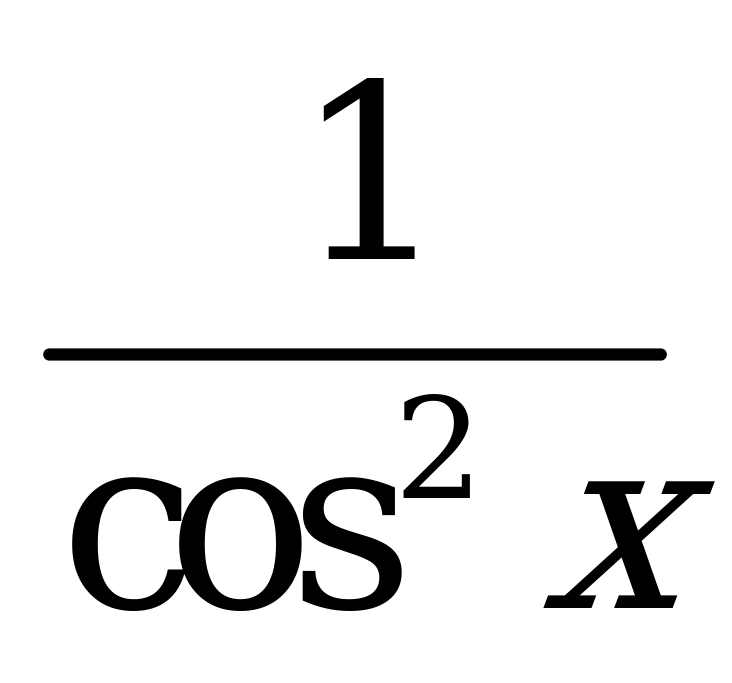 B) - B) -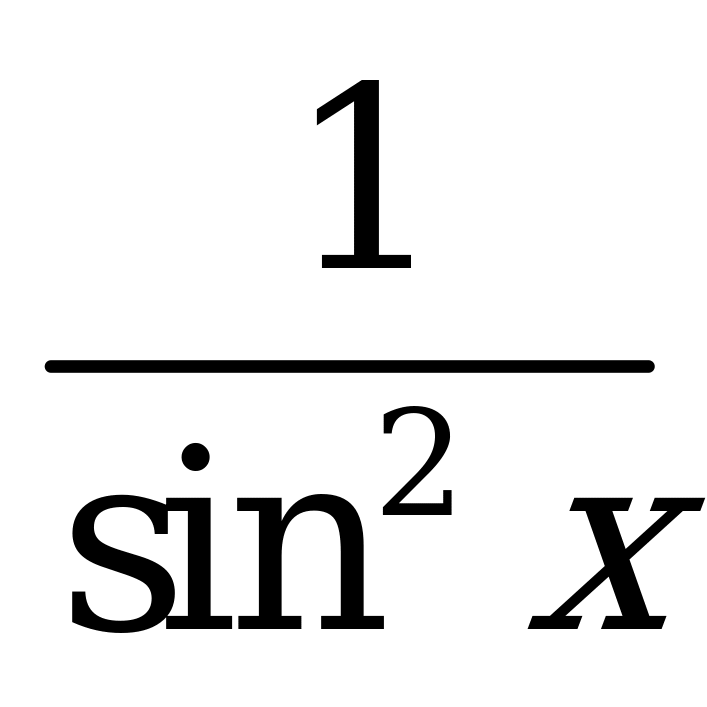 C) C) 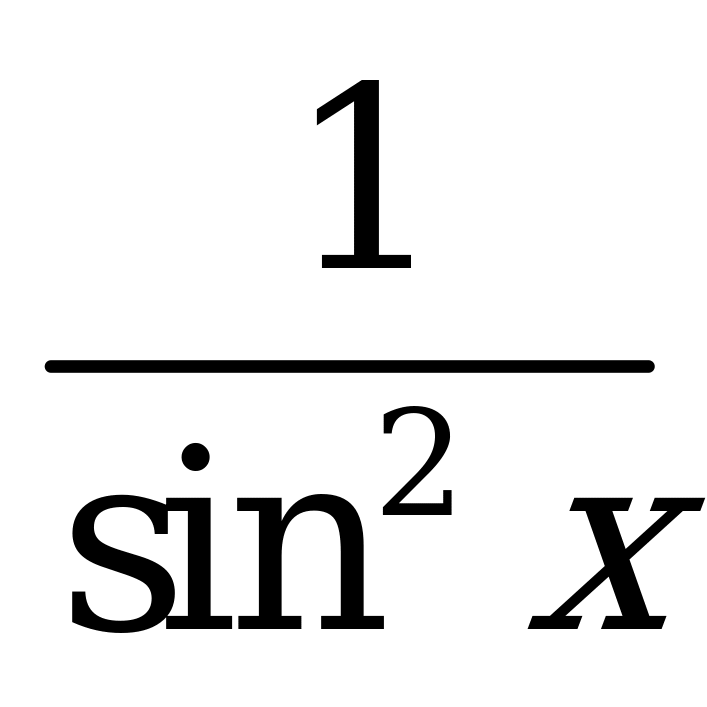 D) D) 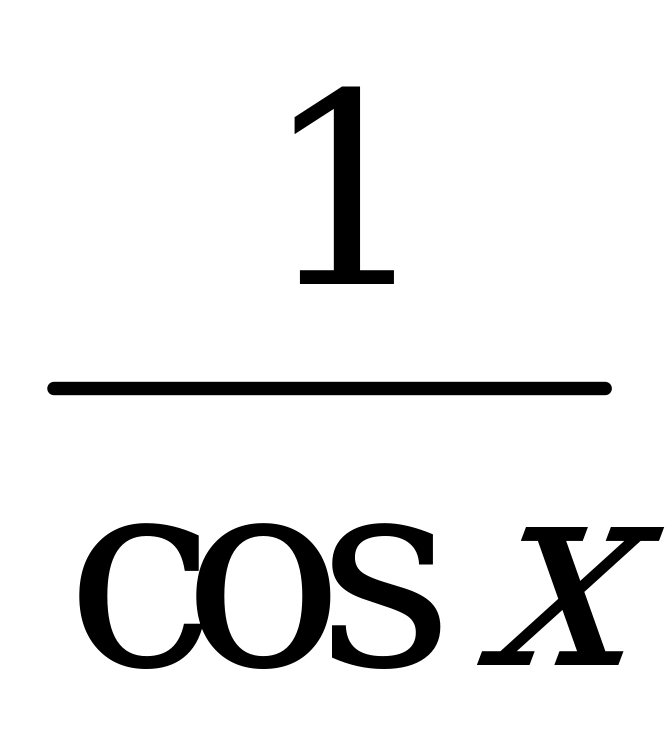 E) E) 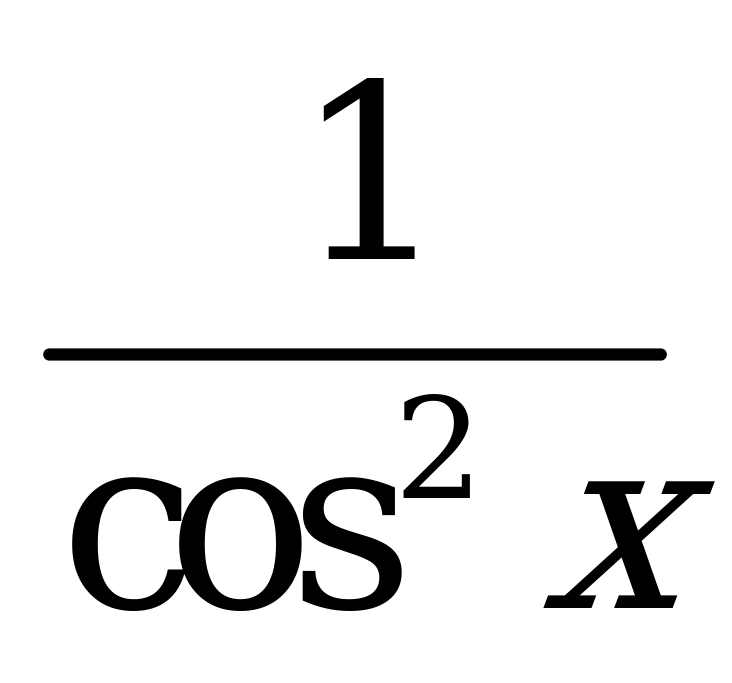 | E |
| А3.2 Упростите выражение: 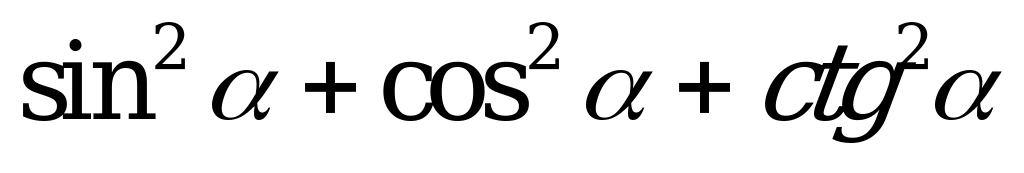 A) 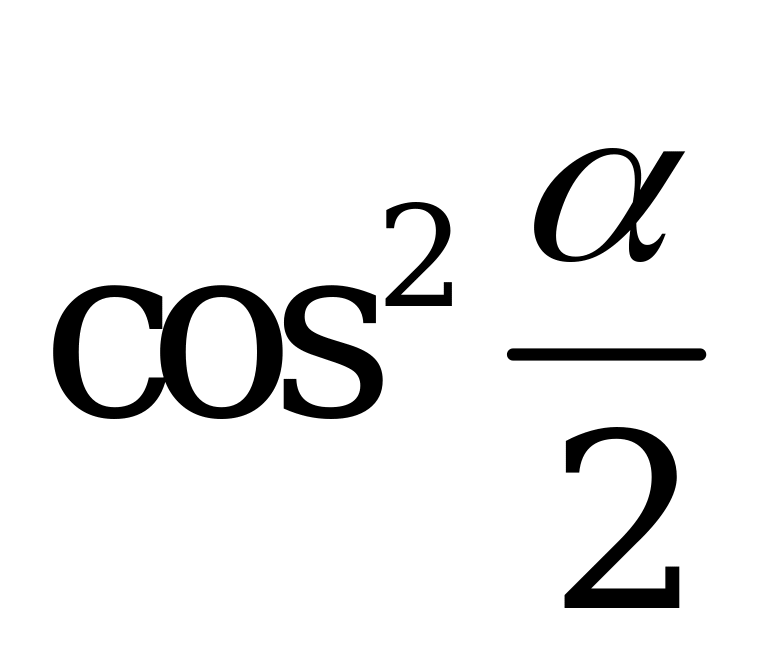 B) B) 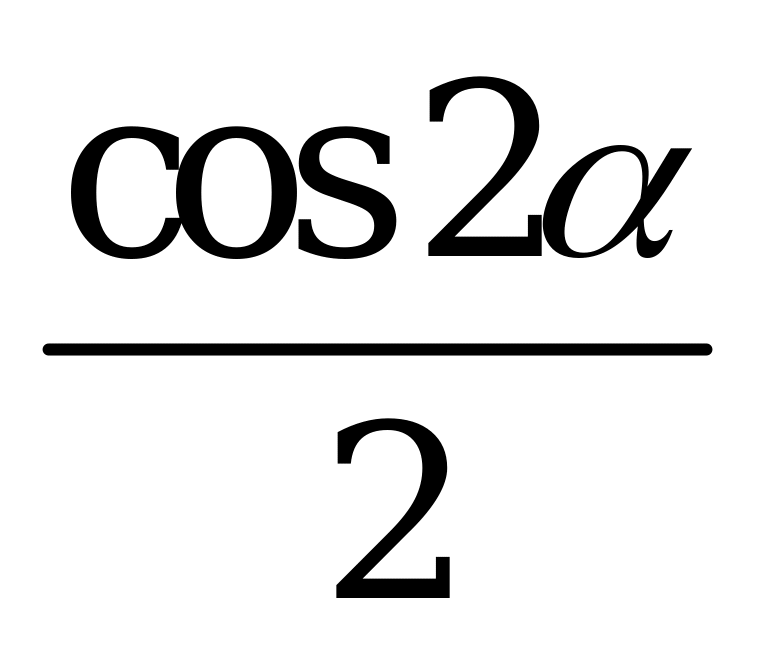 C) C) 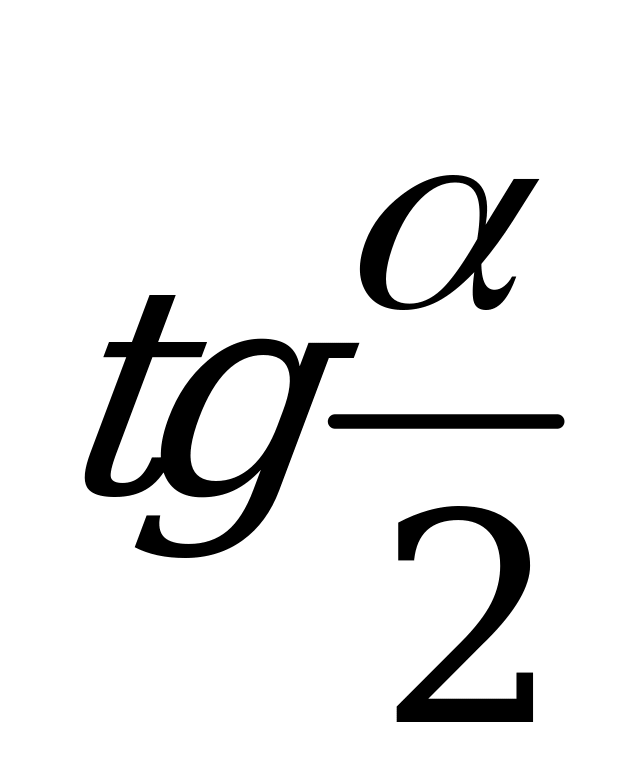 D) D) 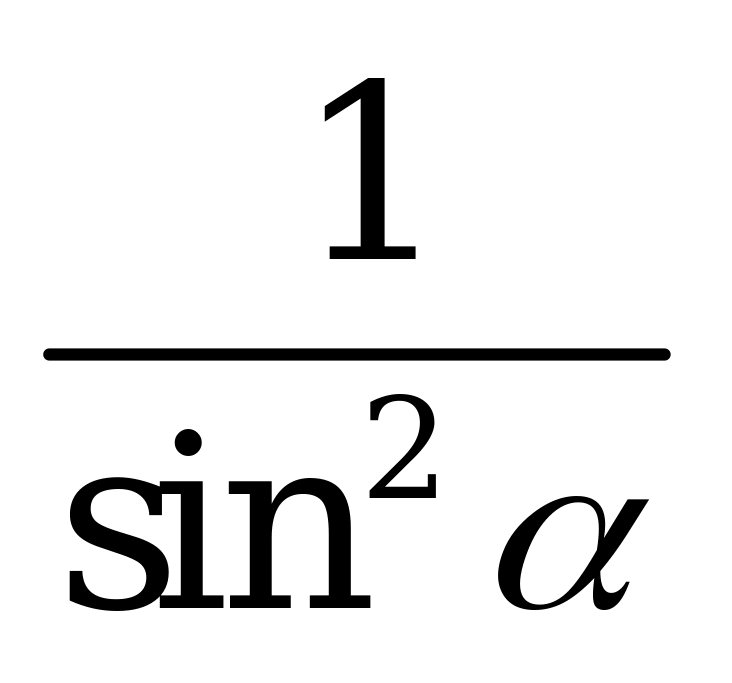 E) E) 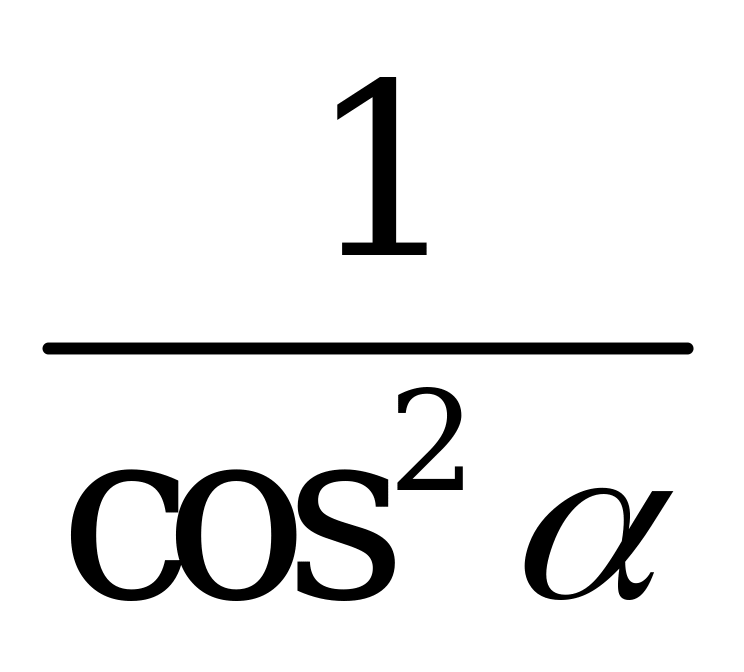 | D |
| А3.3 Упростите: 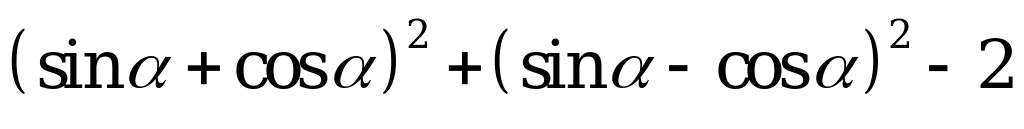 A) 0 B) 4 C) 2sin2 D) 1 E) 1 + 2sin2 D) 1 E) 1 + 2sin2 | A |
| А3.4 Упростите выражение 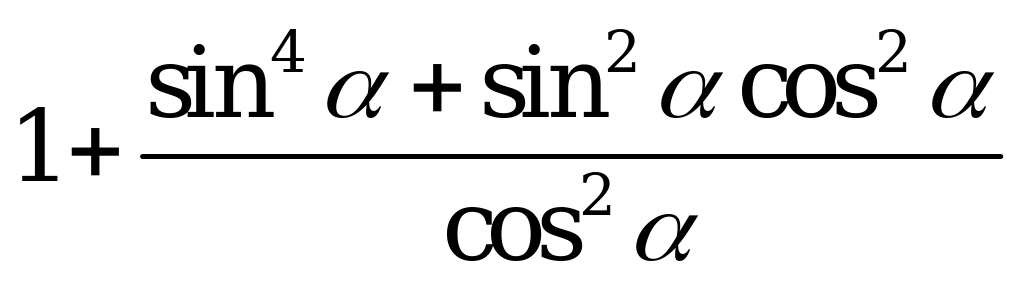 A) 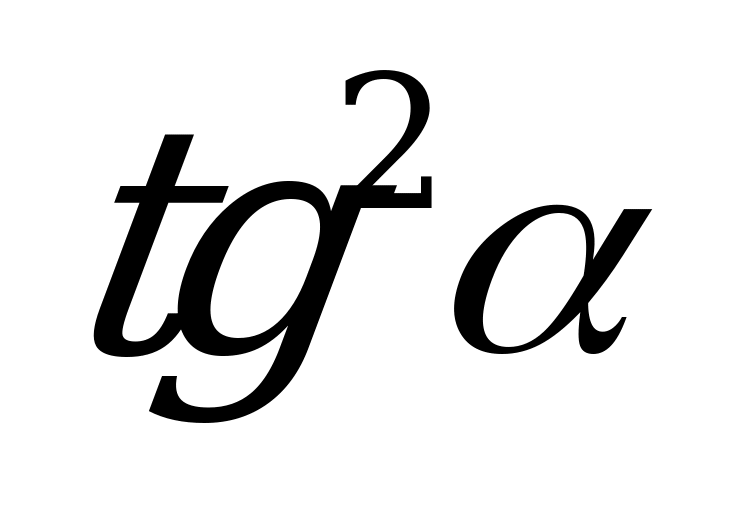 B) 1 + B) 1 +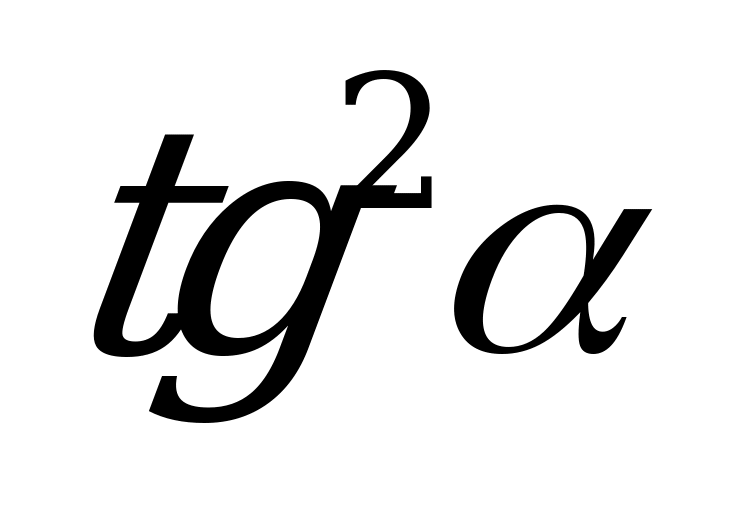 C) C) 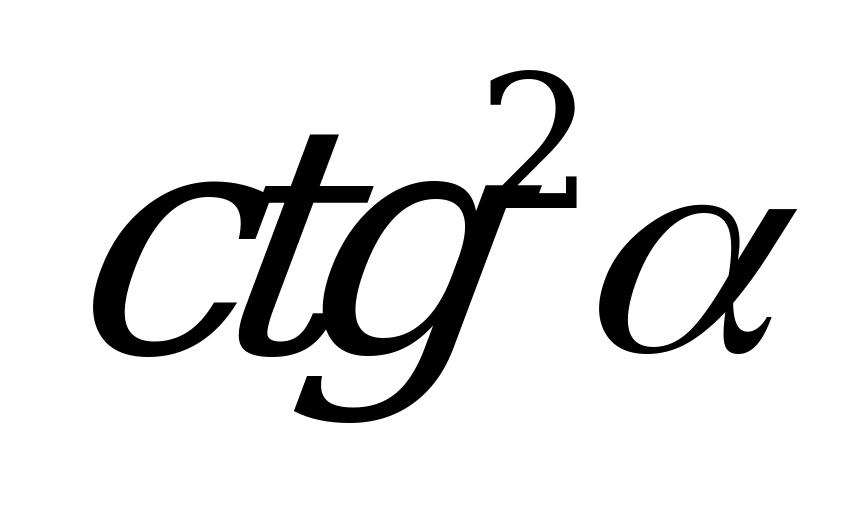 D) 1 + D) 1 +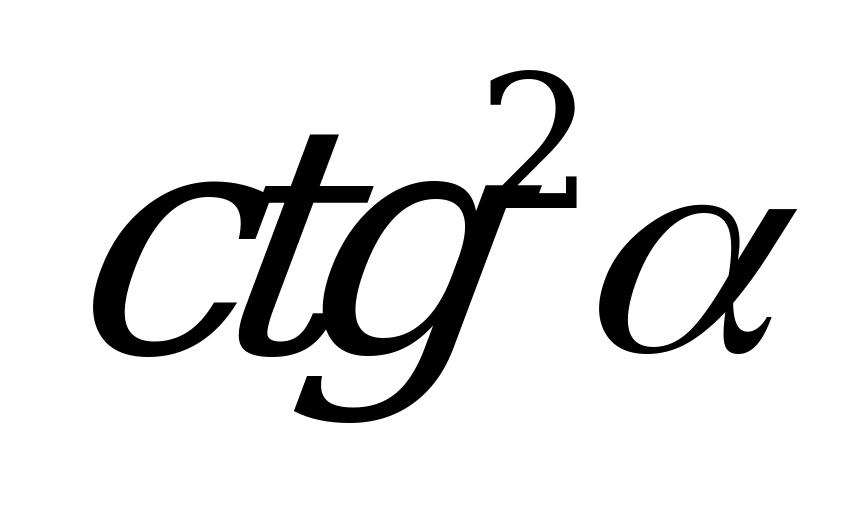 E) 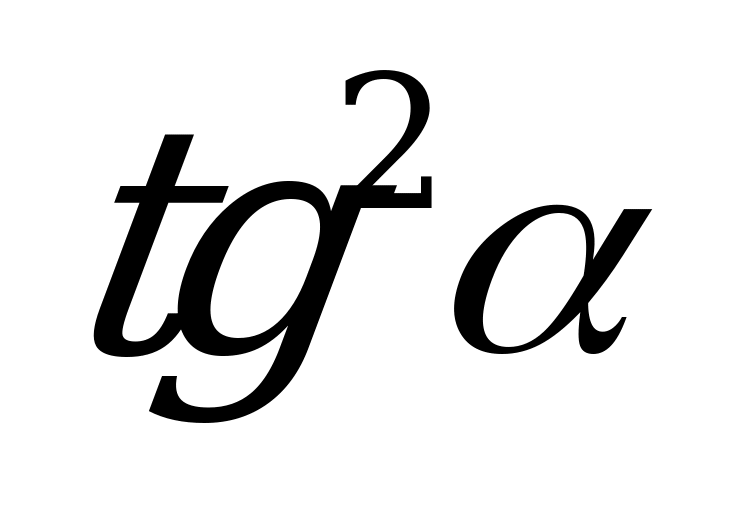 + + 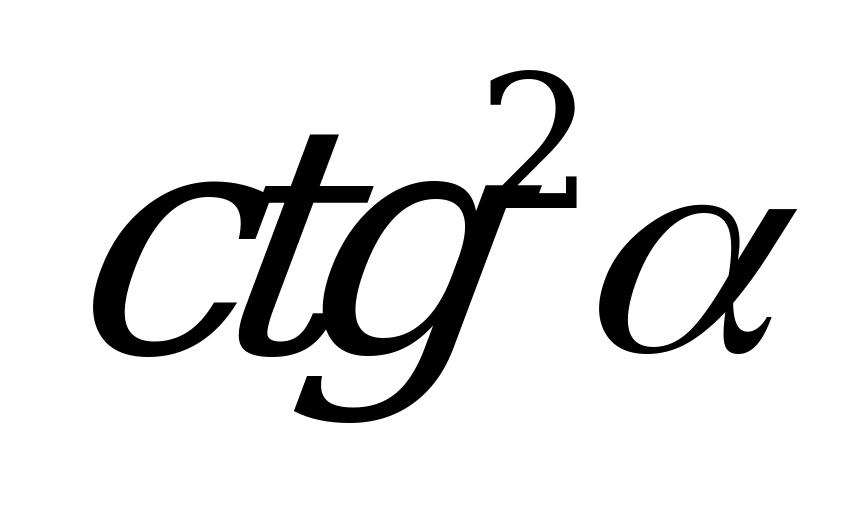 | B |
| А3.5 Вычислите 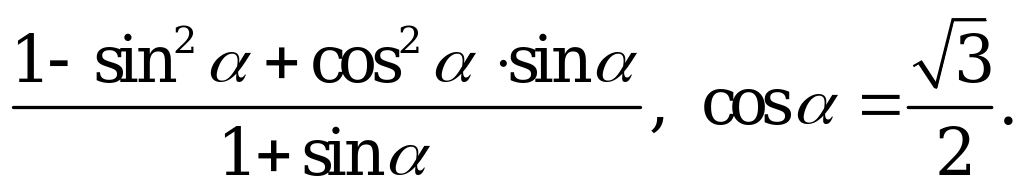 A) 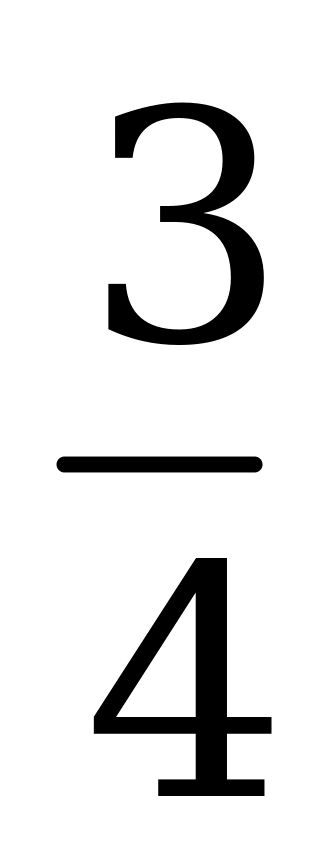 B) 1,5 C) B) 1,5 C) 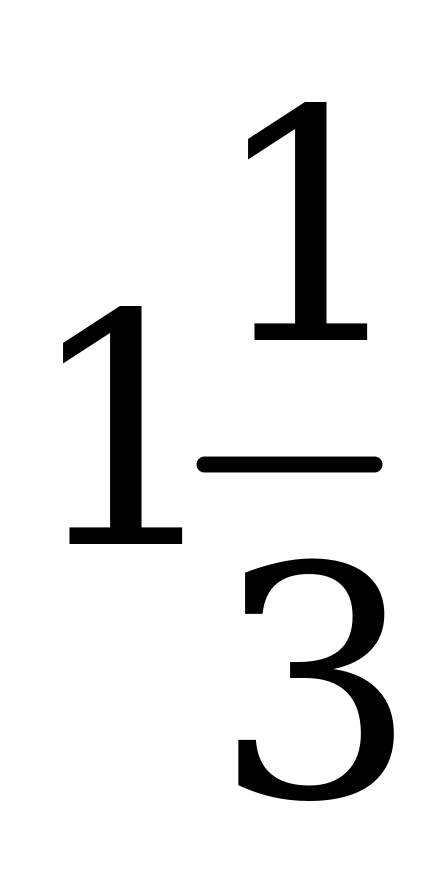 D) 1 E) D) 1 E) 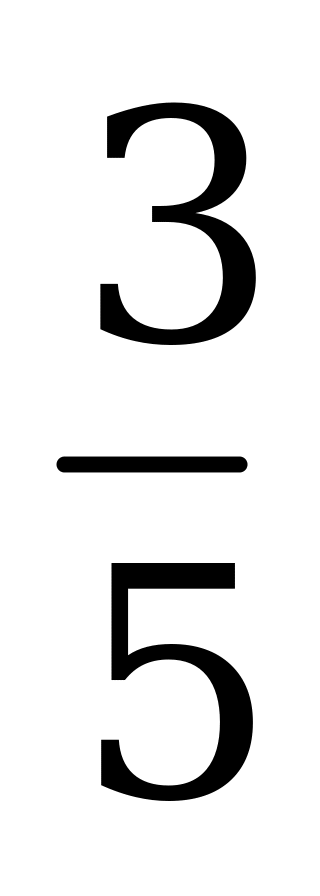 | A |
| А3.6 Упростите: sin6x + cos6x + 3sin2xcos2x A) -1 B) 0 C) 1 D) 2 E) 4 | C |
| А3.7 Упростите: 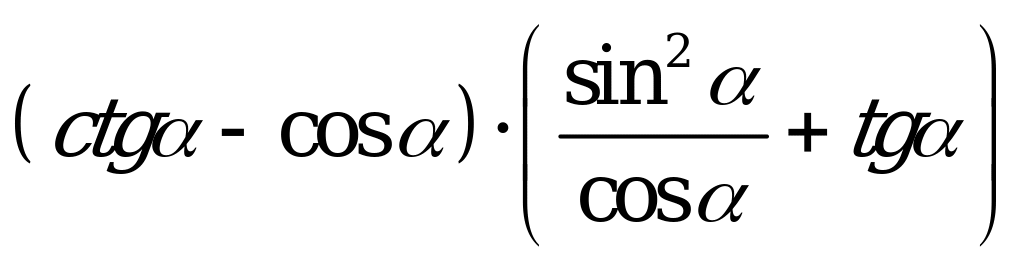 A) 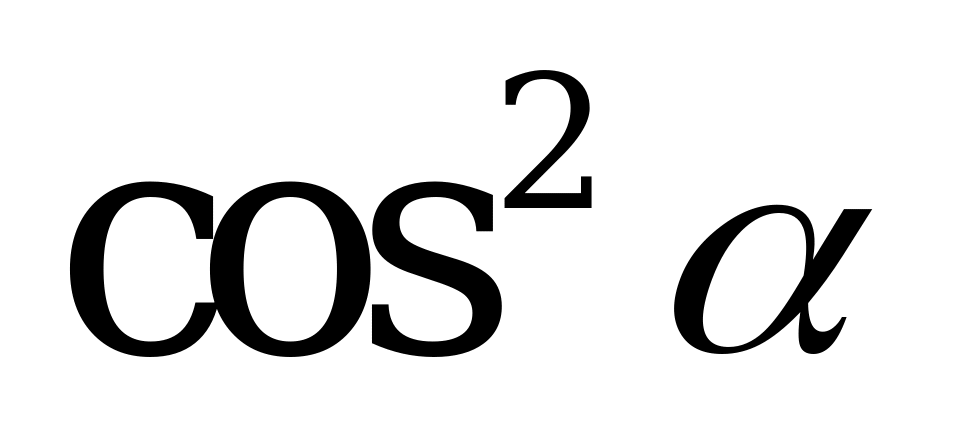 B) B) 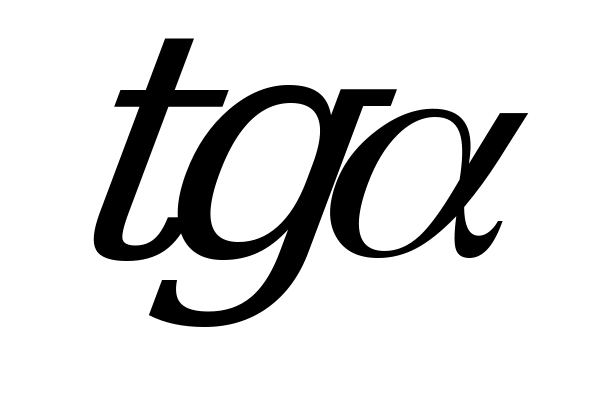 C) C) 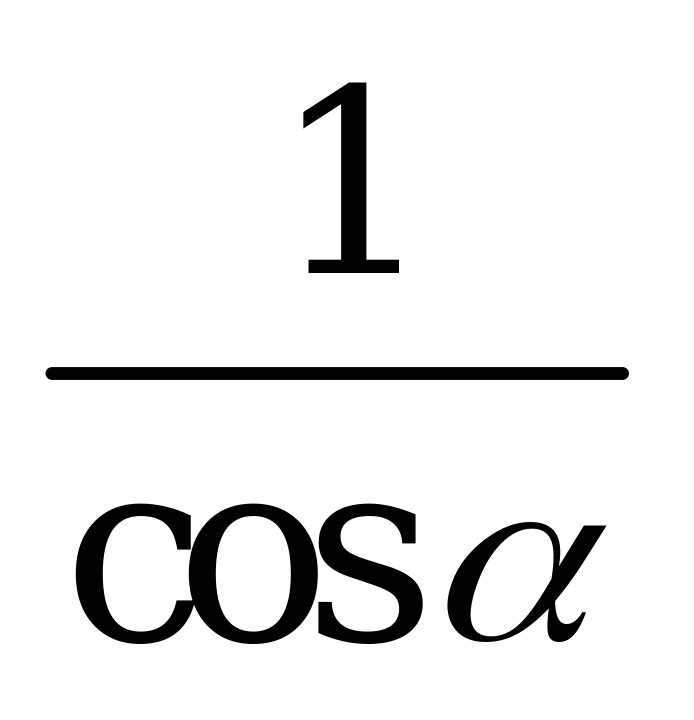 D) D) 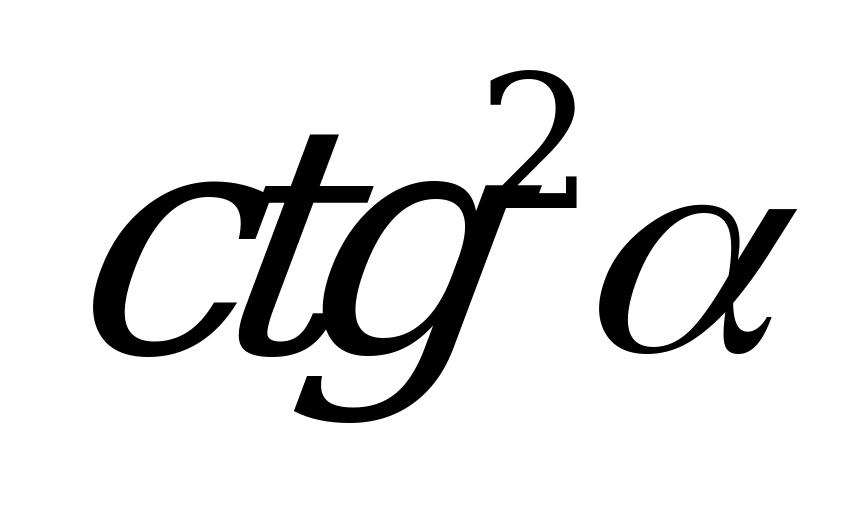 E) E) 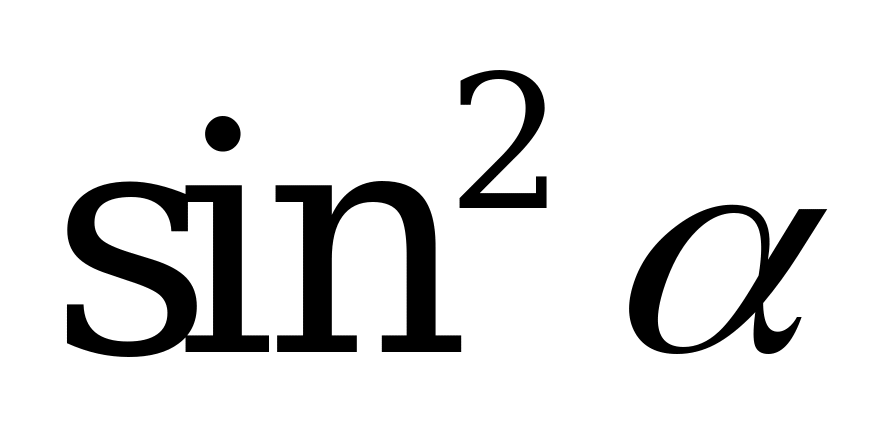 | A |
| А3.8 Упростите выражение: 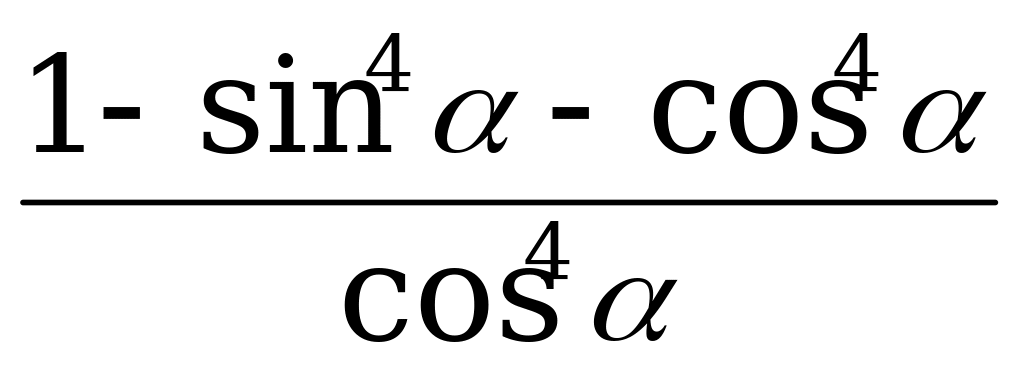 A) 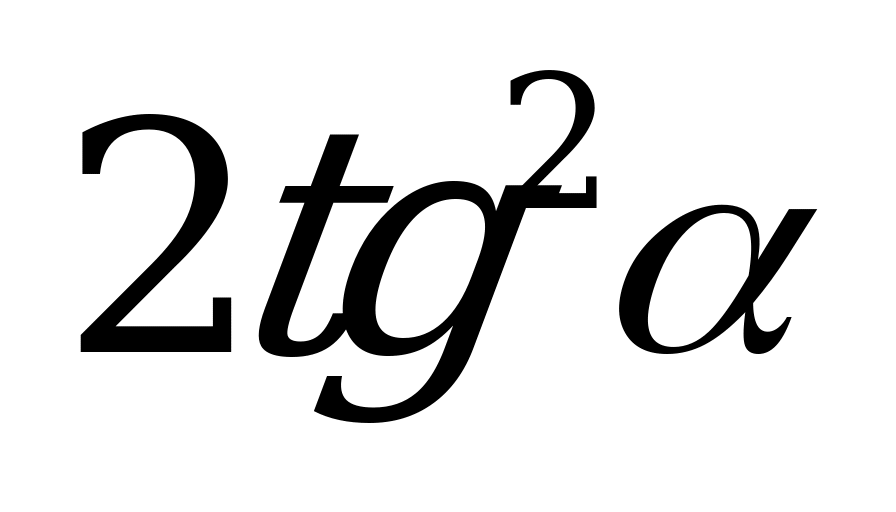 B) B) 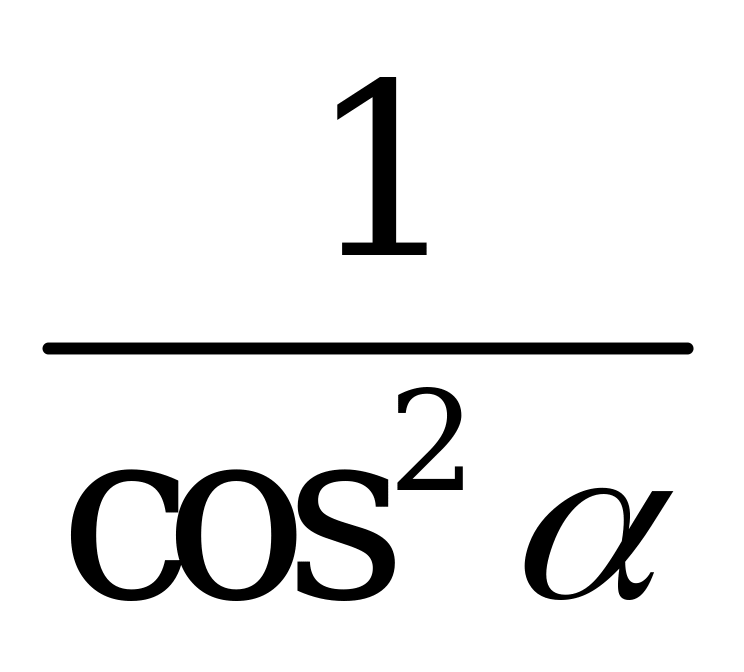 C) 2 D) C) 2 D) 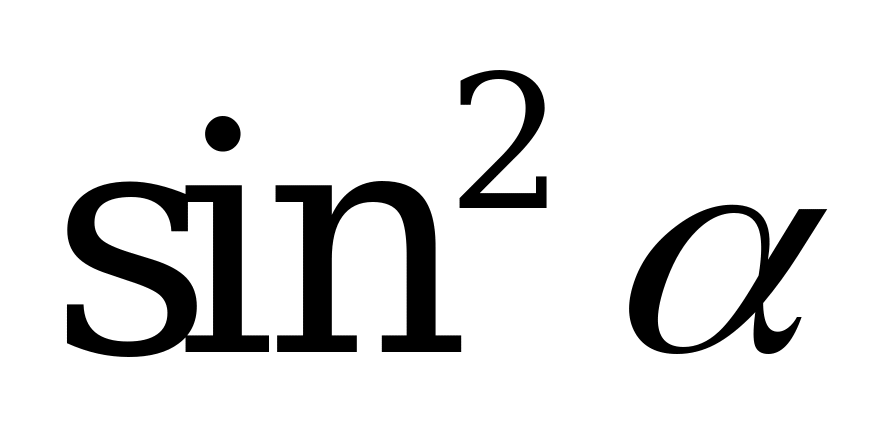 E) E) 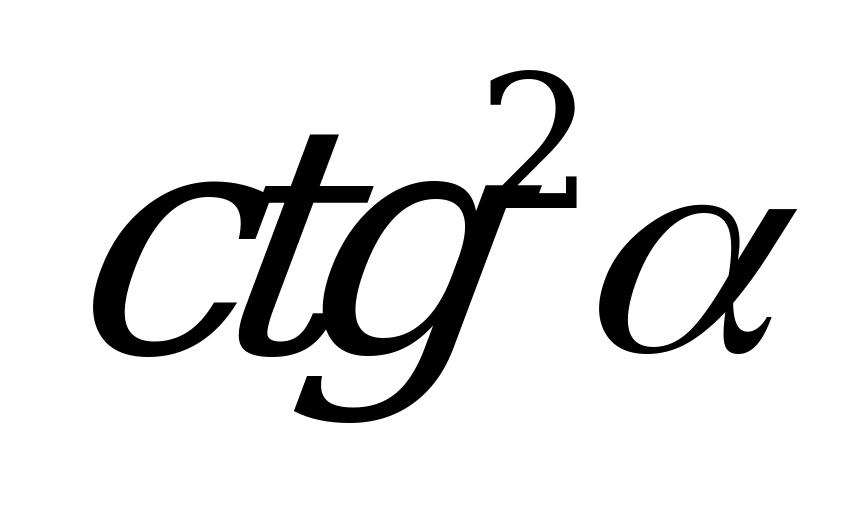 | A |
| А3.9 Упростите выражение: 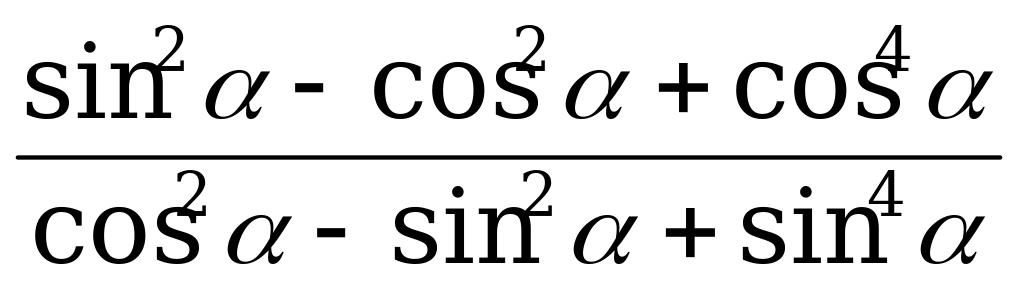 A) 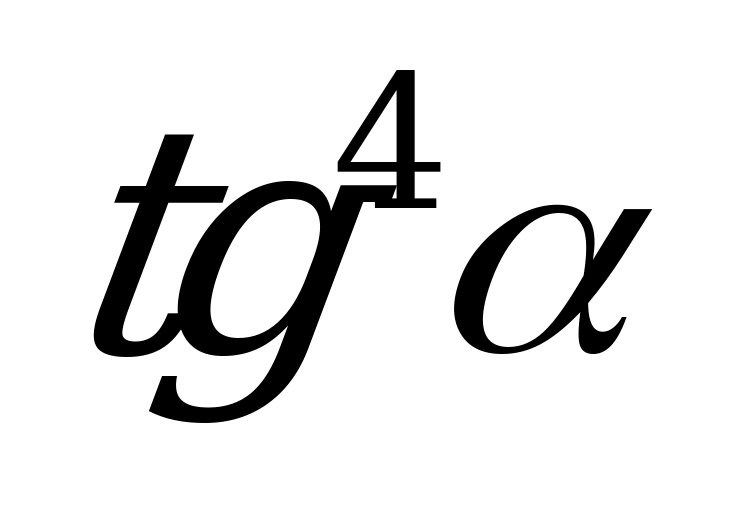 B) B) 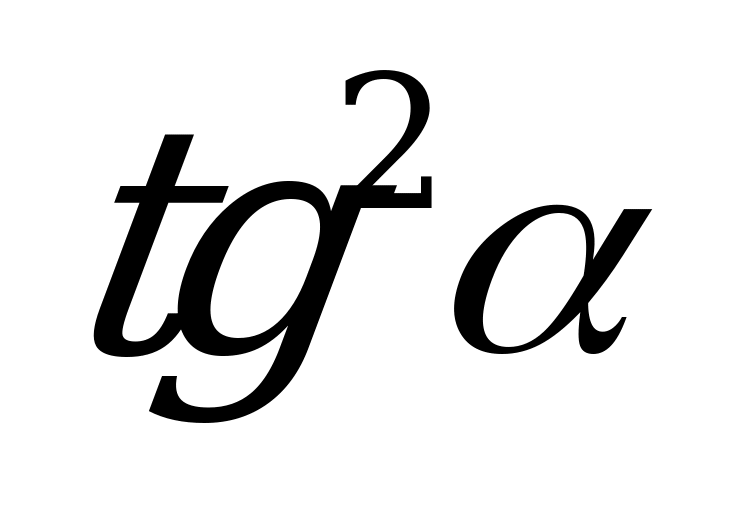 C) C) 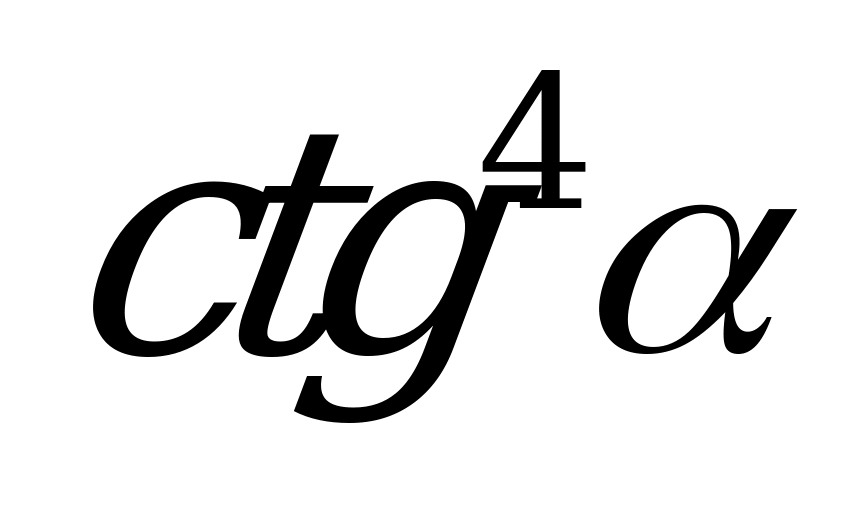 D) D) 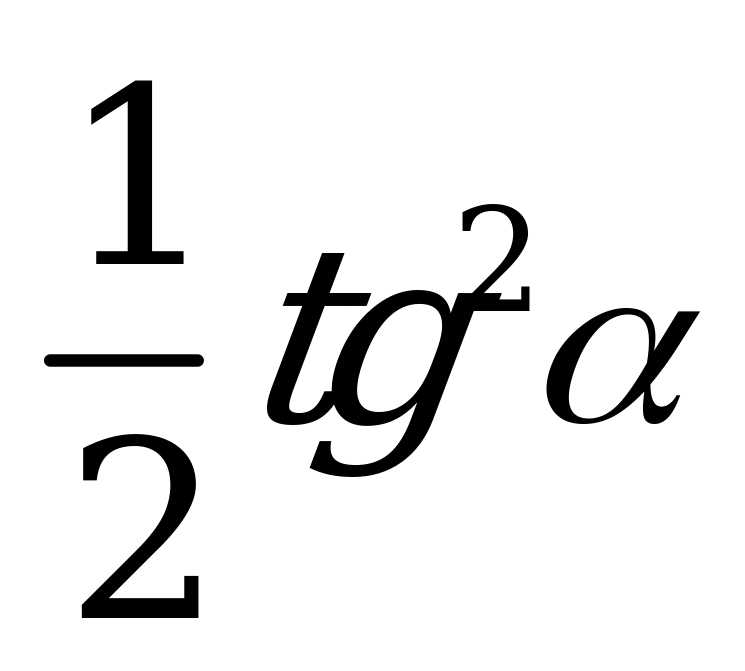 E) E) 
| A |
| А3.10 Упростите 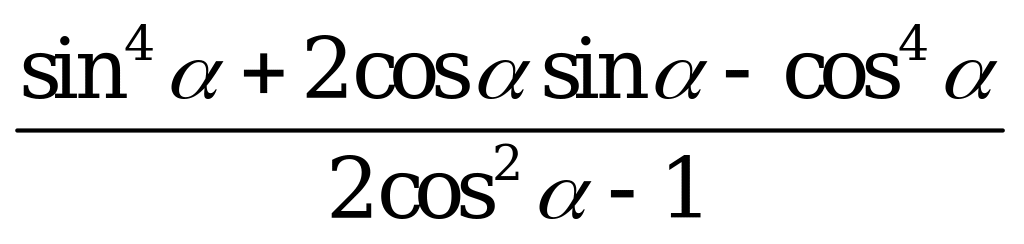 A) 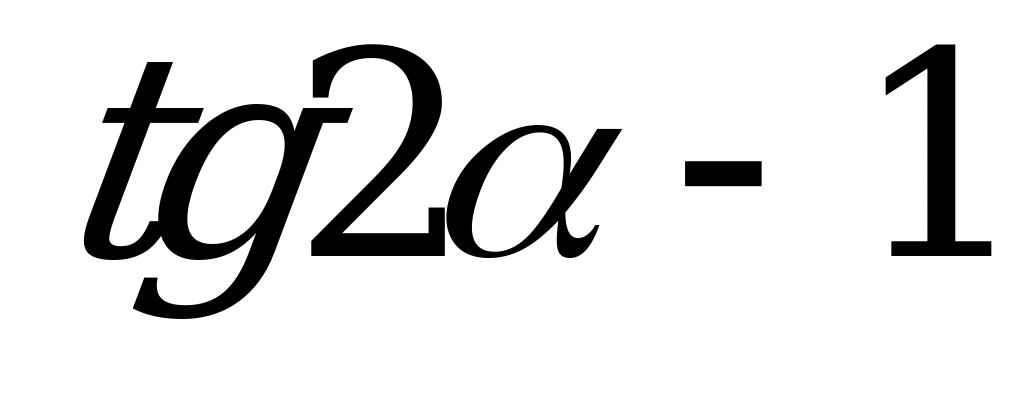 B) B) 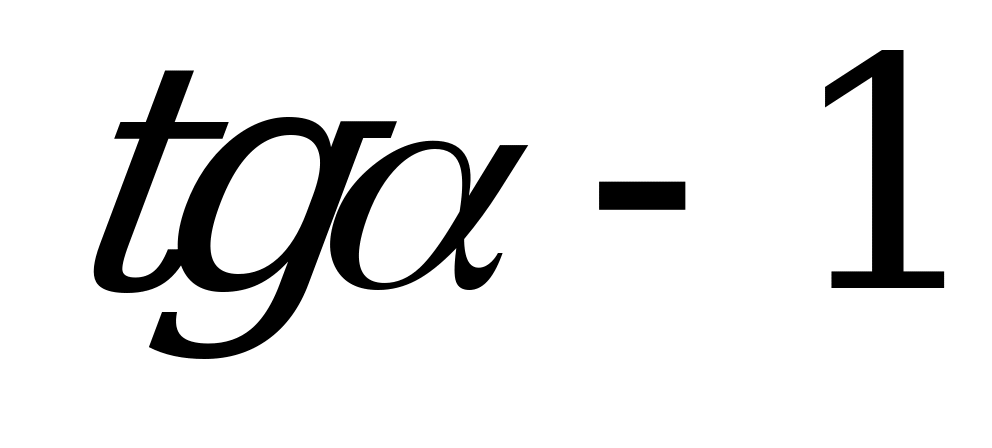 C) C) 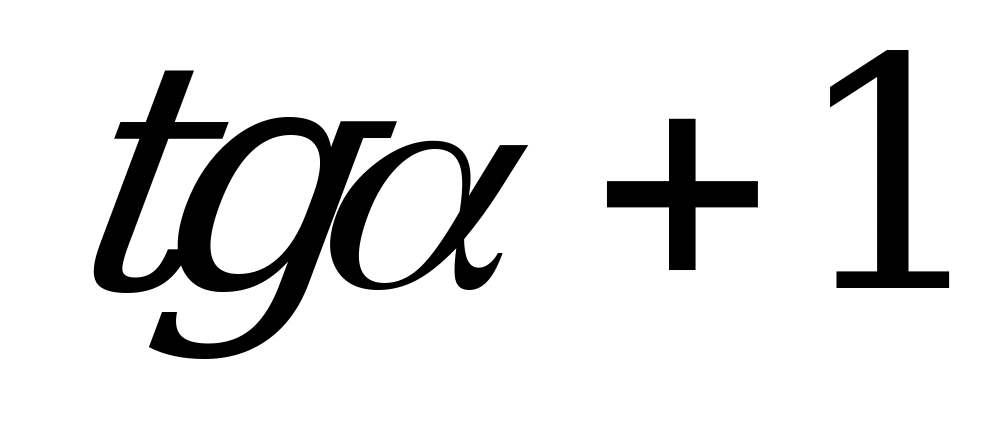 D) D)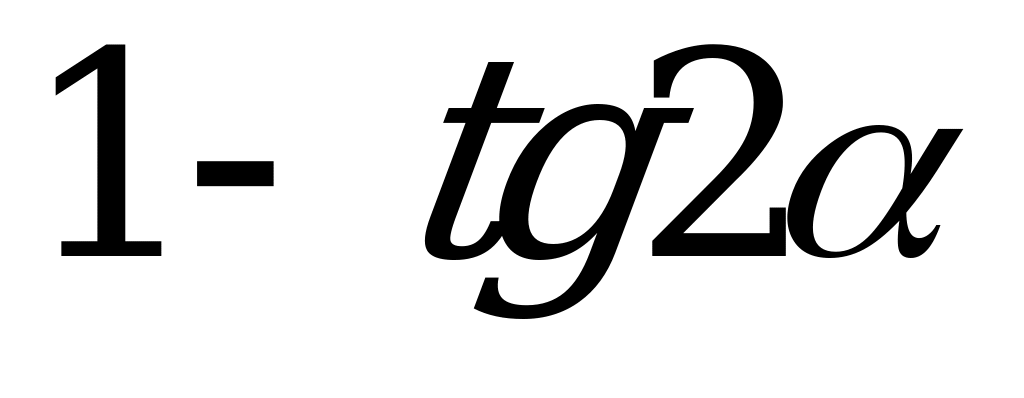 E) E) 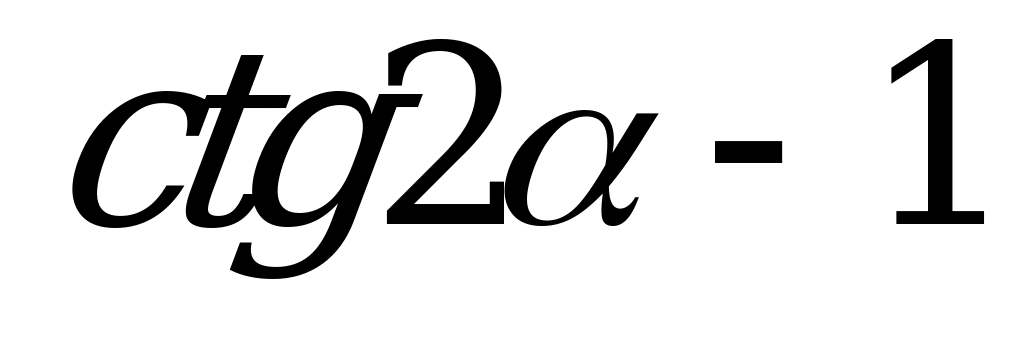 | A |
| А4. Множество значений тригонометрических выражений | Ответы |
| А4.1 Укажите наименьшее значение функции 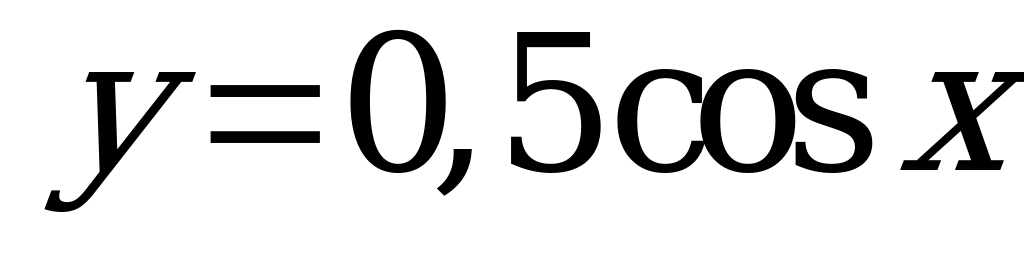 на промежутке на промежутке 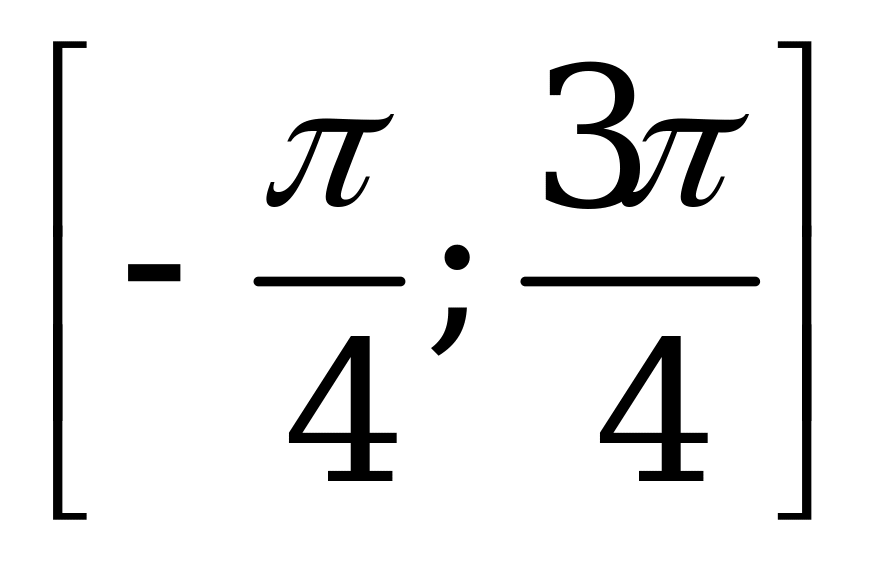 . . A) -1/2 B) -1 C) 0 D) -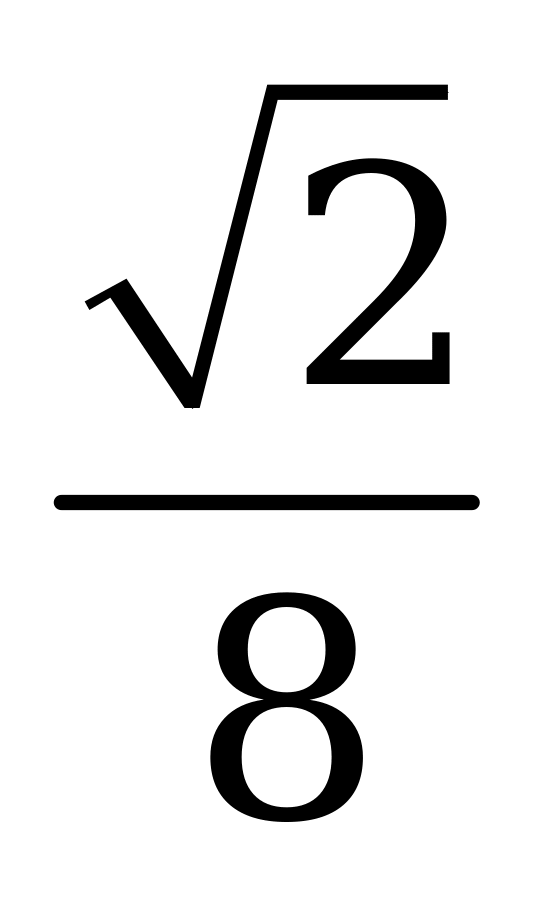 E) - E) -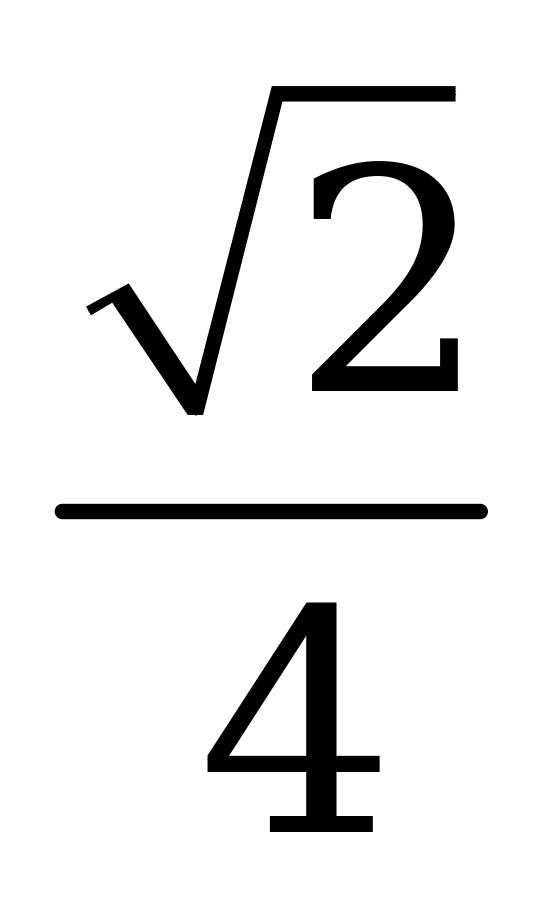 | E |
| А4.2 Найдите наименьшее значение функции 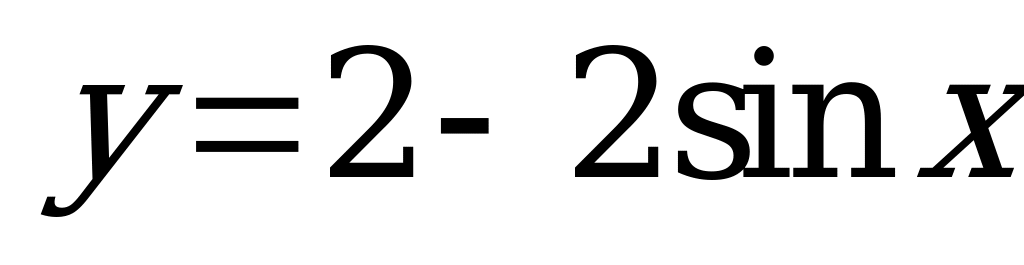 на отрезке [ на отрезке [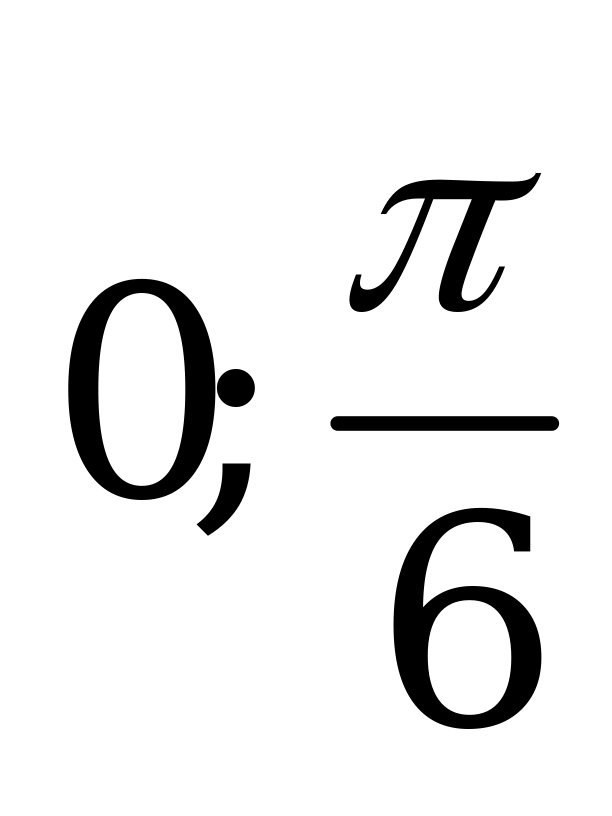 ]. ]. A) 0 B) 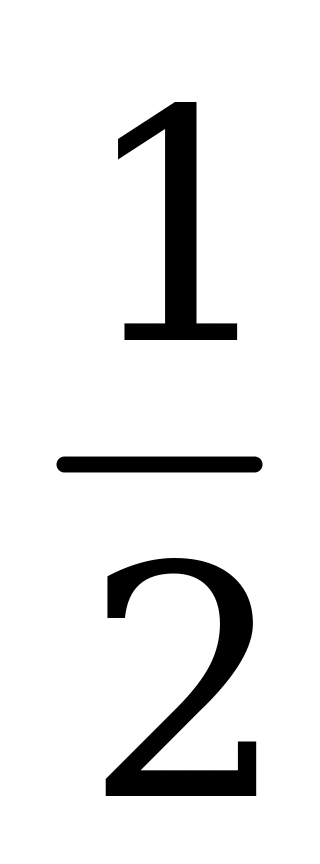 C) 2 - C) 2 -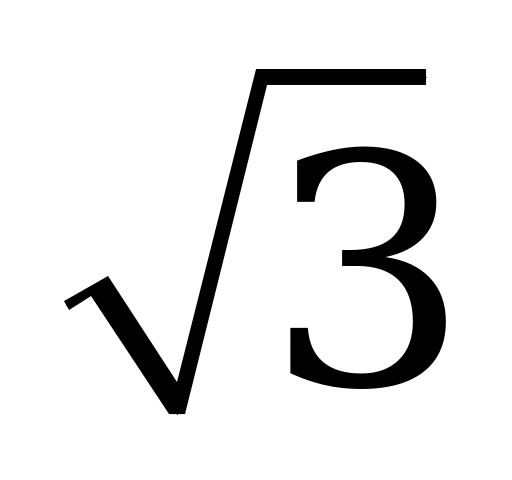 D) 1 E) 2 - D) 1 E) 2 - 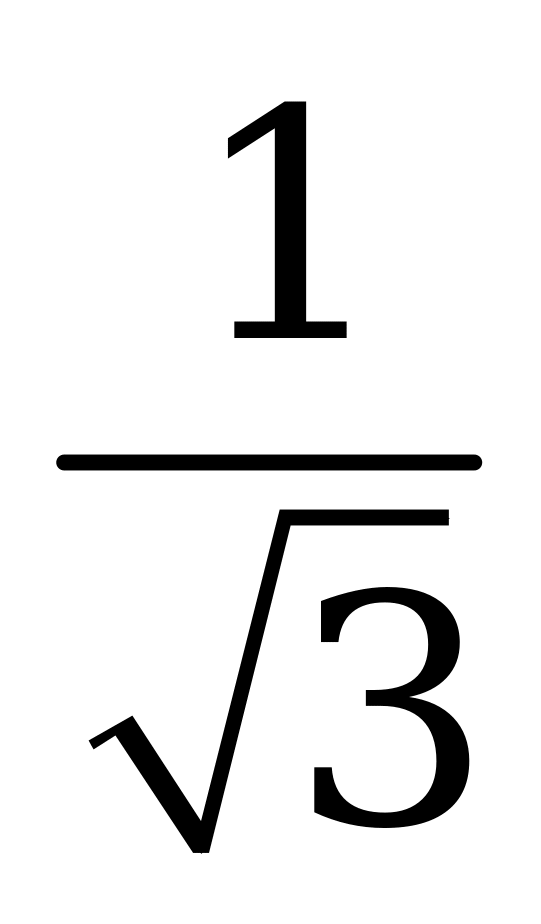 | D |
| А4.3 Найти множество значений функции 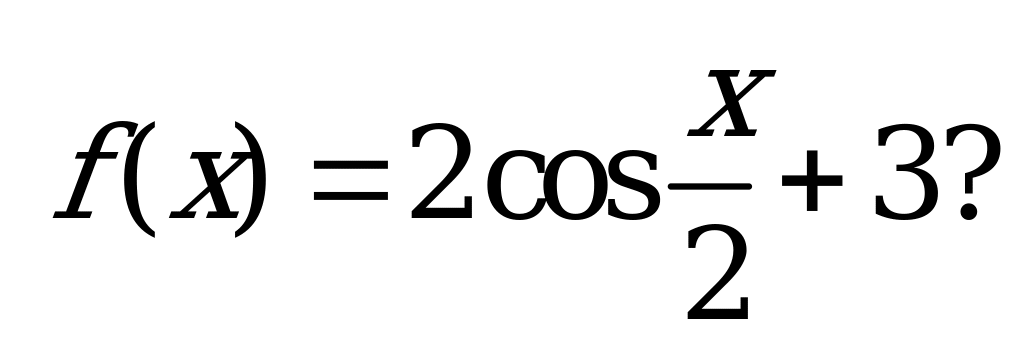 A) [3; 5] B) [4; 5] C) [2; 5] D) [-1; 5] E) [1; 5] | E |
| А4.4 Найдите множество значений функции f(x) = 16 – 6sin2x. A) (0; 22) B) (10; 22) C) [0; 16] D) [10; 22] E) (0; 22] | D |
| А4.5 Найдите область изменения функции 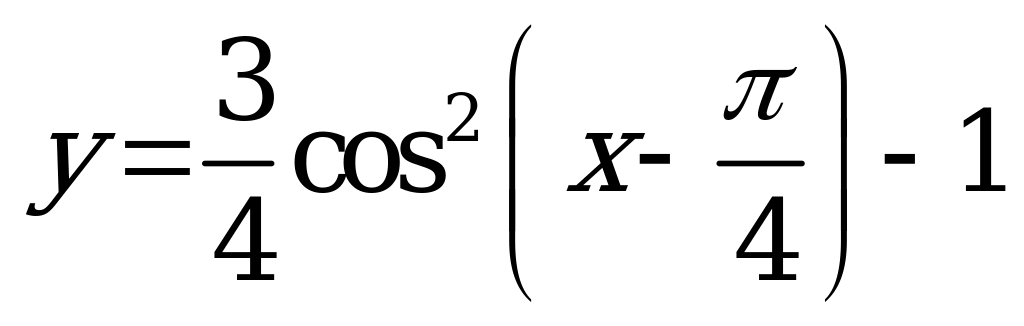 . A) . A) 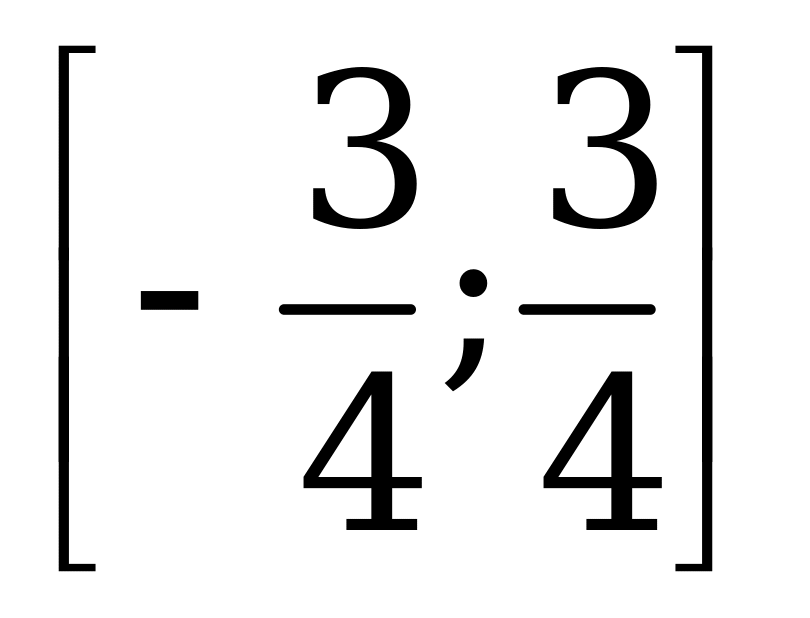 B) [-1; 0] B) [-1; 0] C) [-1; -0,25] D) [-0,25; 0] E) 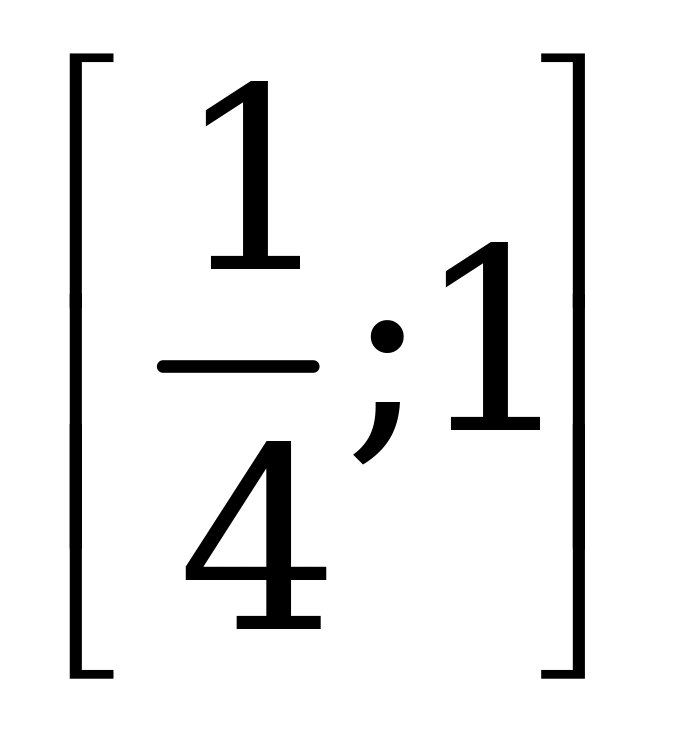 | C |
| А4.6 Найдите наименьшее значение 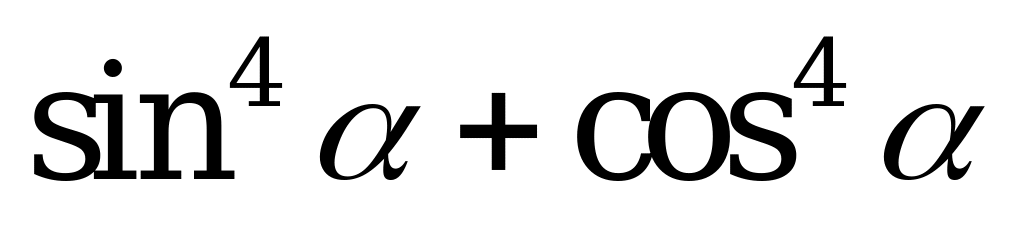 A) 0 B) 1 C) 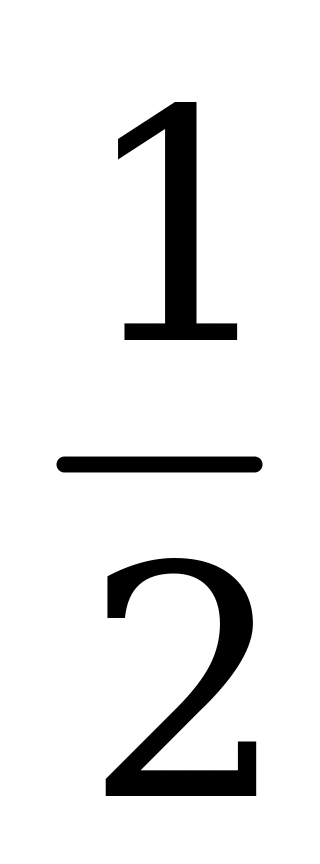 D) D) 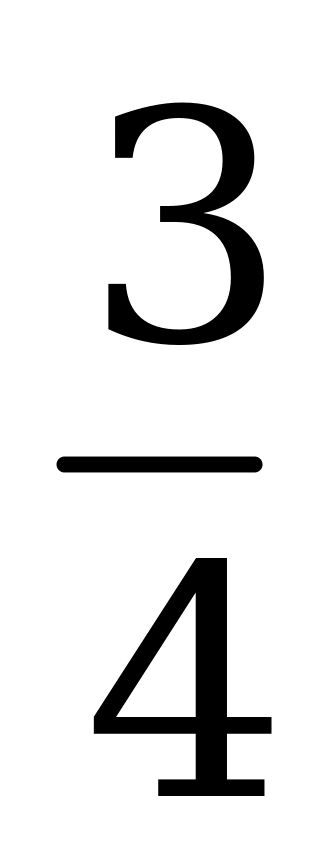 E) E) 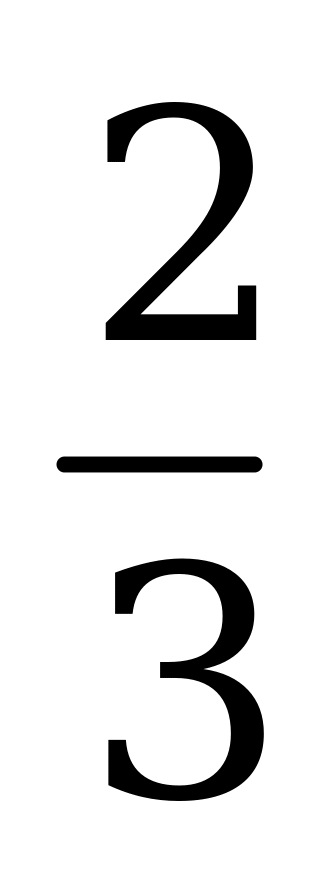 | C |
| А4.7 Какое наименьшее значение может принимать выражение 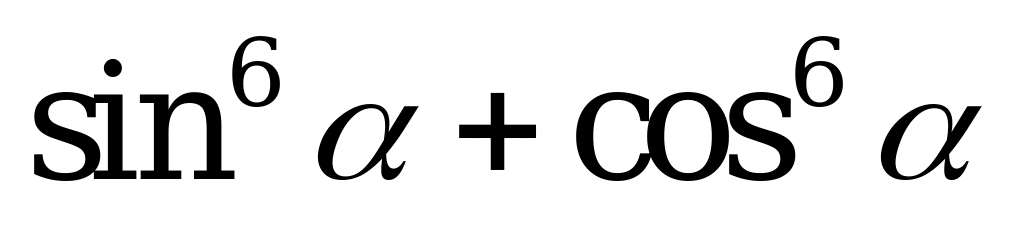 ? ? A) 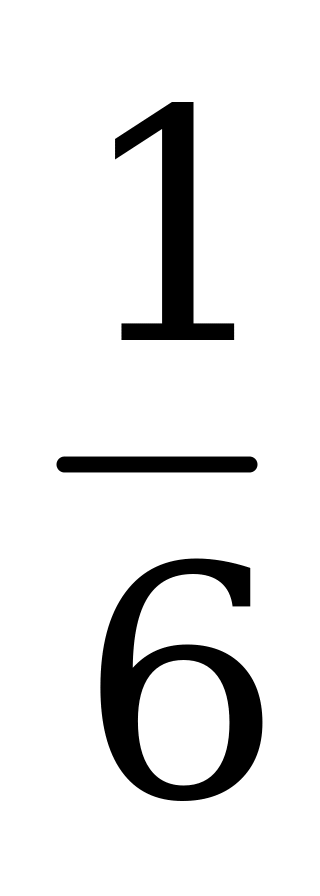 B) B) 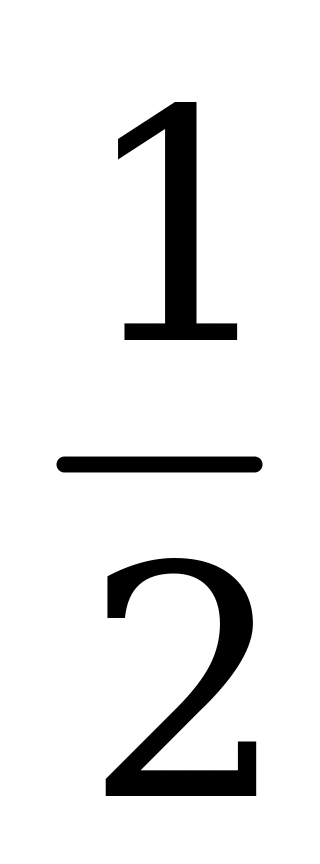 C) C) 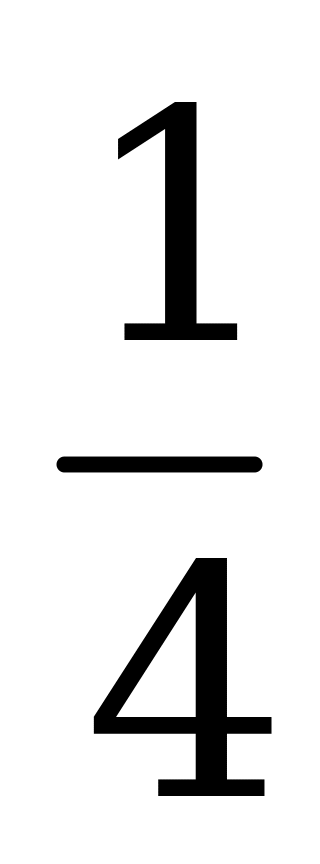 D) D) 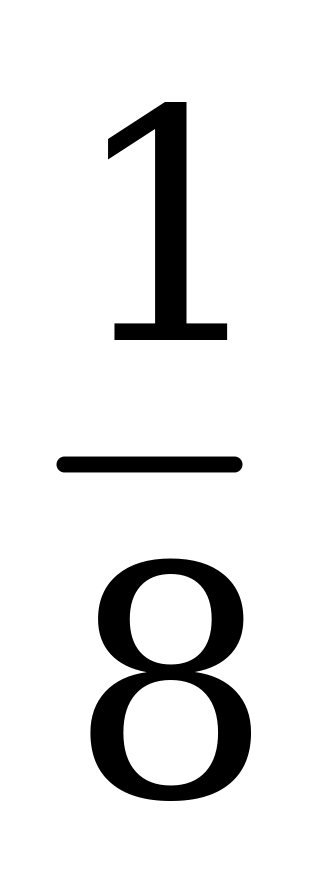 E) E) 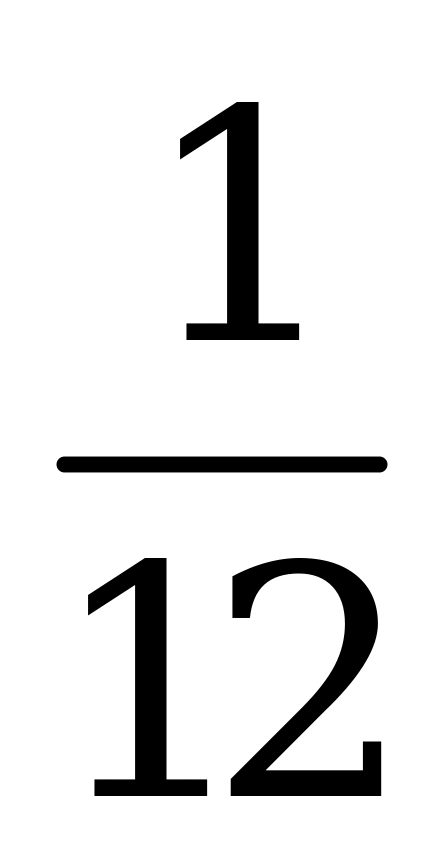 | C |
| А4.8 Каково наибольшее значение функции f(x) = 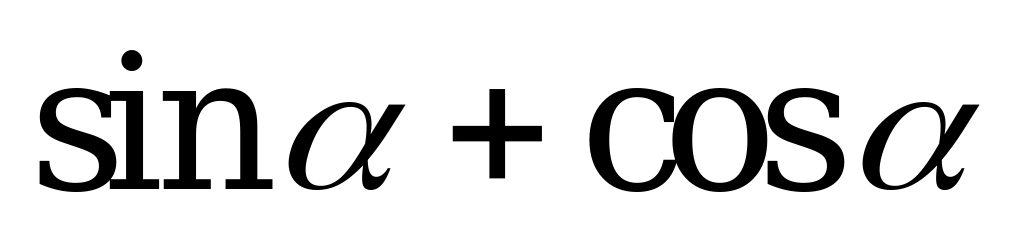 ? ? A) 1,4 B) 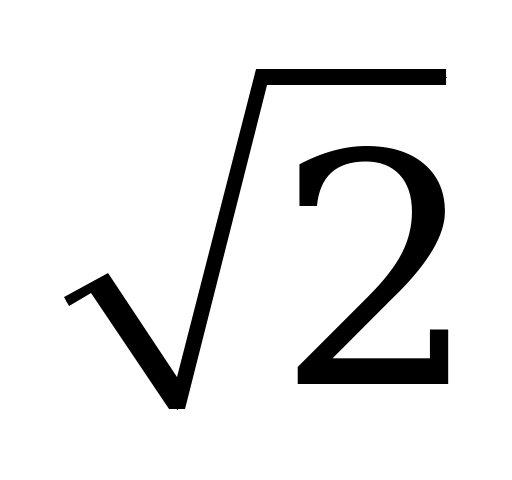 C) C) 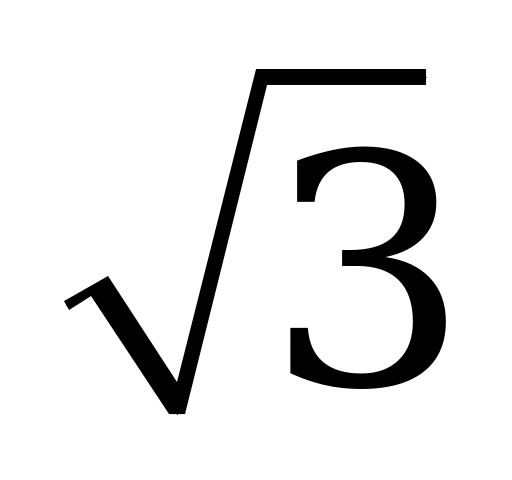 D) 1,6 E) 1 D) 1,6 E) 1 | B |
| А4.9 Найдите наименьшее значение выражения 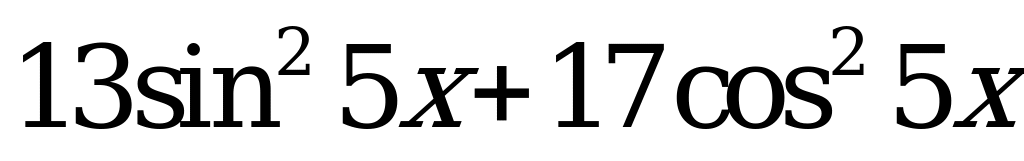 . . A) 12 B) 15 C) 13 D) 17 E) 14 | C |
| А4.10 Найти наибольшее значение 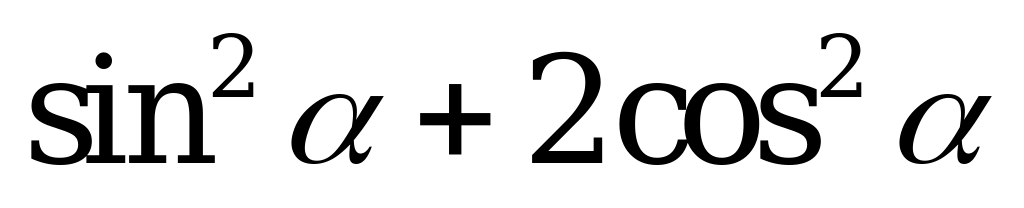 ? ? A) 1,2 B) 1,4 C) 1,6 D) 2 E) 1,8 | D |
| А5. Период тригонометрических .функций | Ответы |
| А5.1 Укажите период функции: 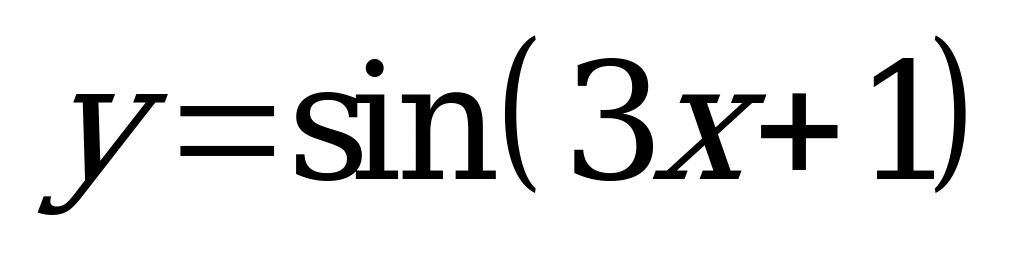 A) 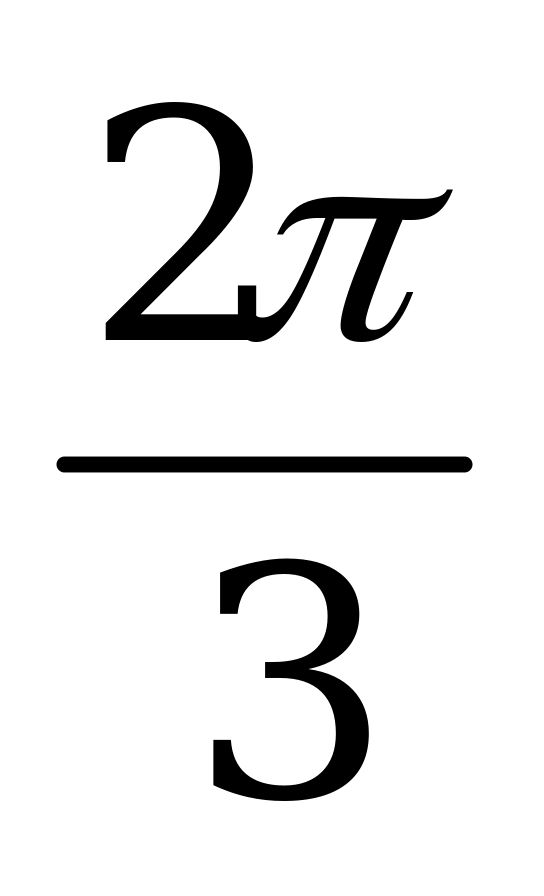 B) B)  C) C) 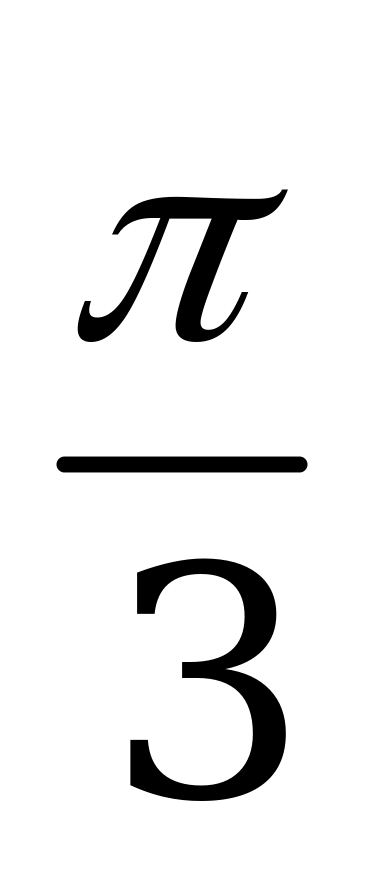 D) D)  E) правильного ответа нет E) правильного ответа нет | A |
| А5.2 Определите наименьший положительный период функции 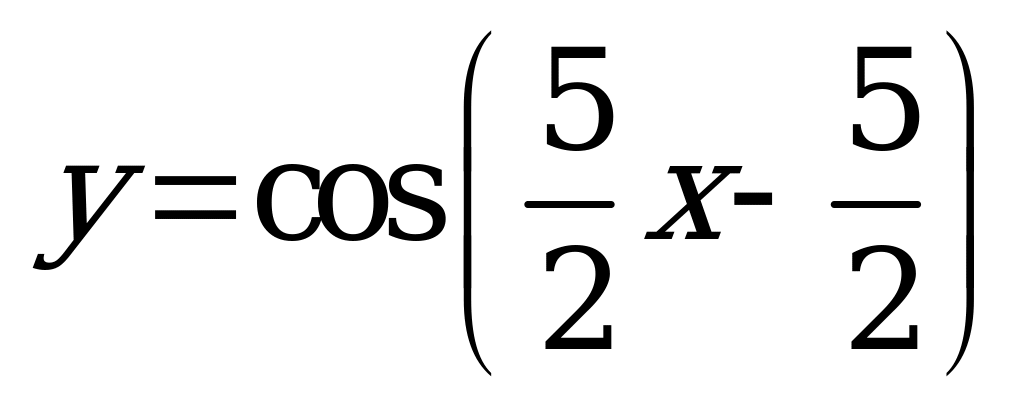 A) 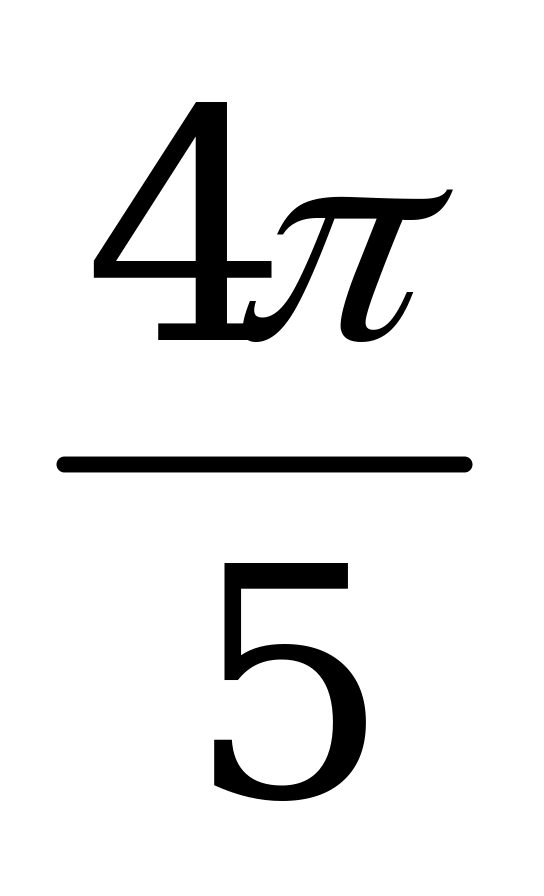 B) B)  C) C)  D) D) 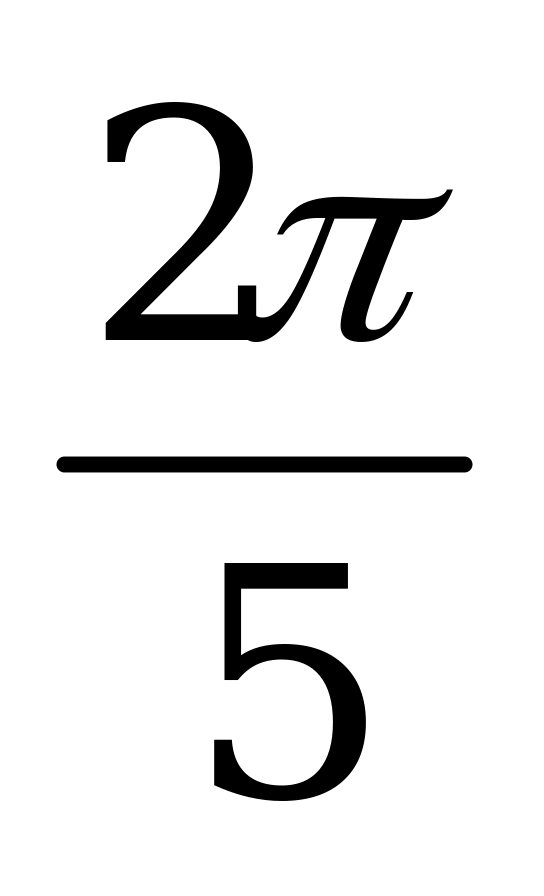 E) E) 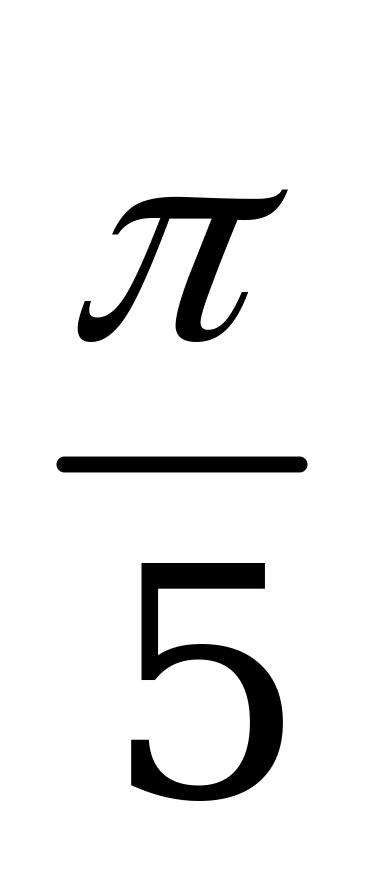 | A |
| А5.3 Найдите наименьший положительный период функции 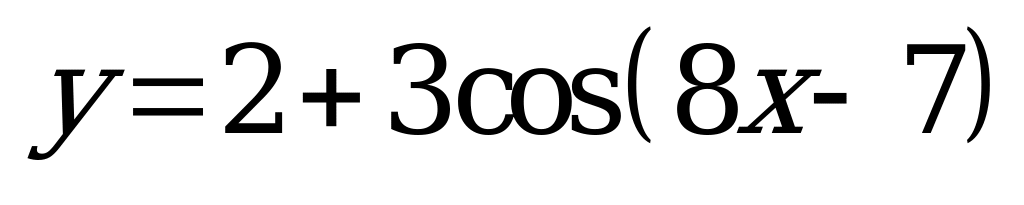 A) 2 B) 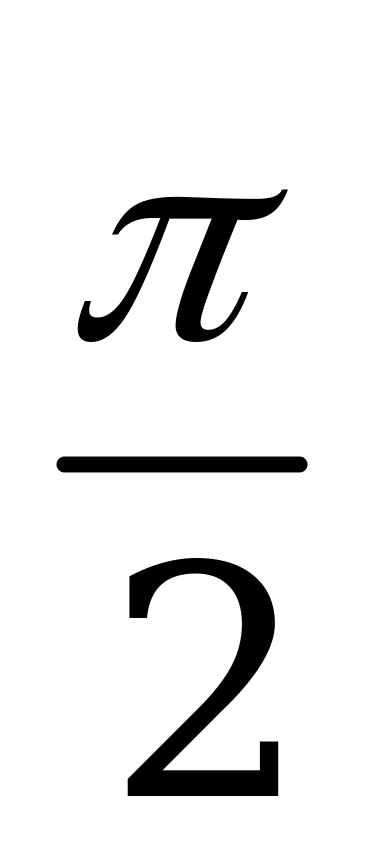 C) C) 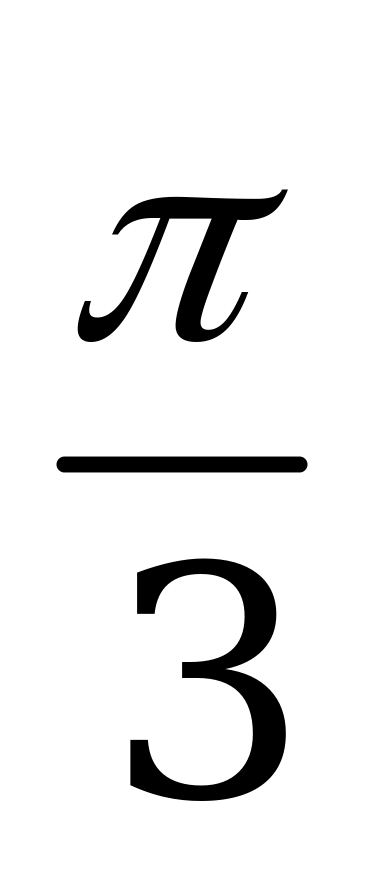 D) D) 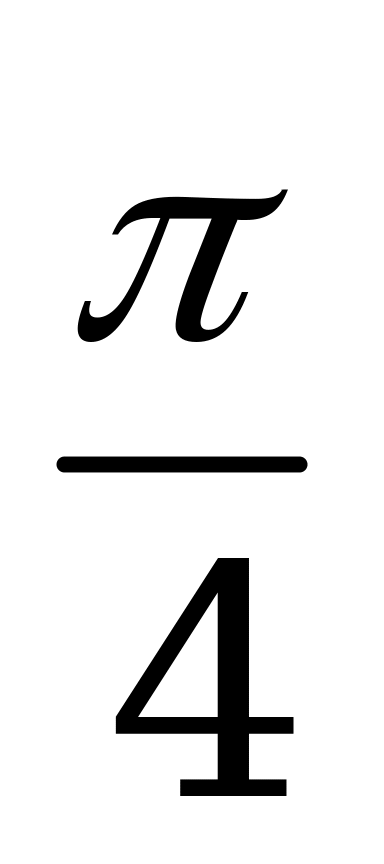 E) E) | D |
| А5.4 Найти отношение наименьших положительных периодов функций 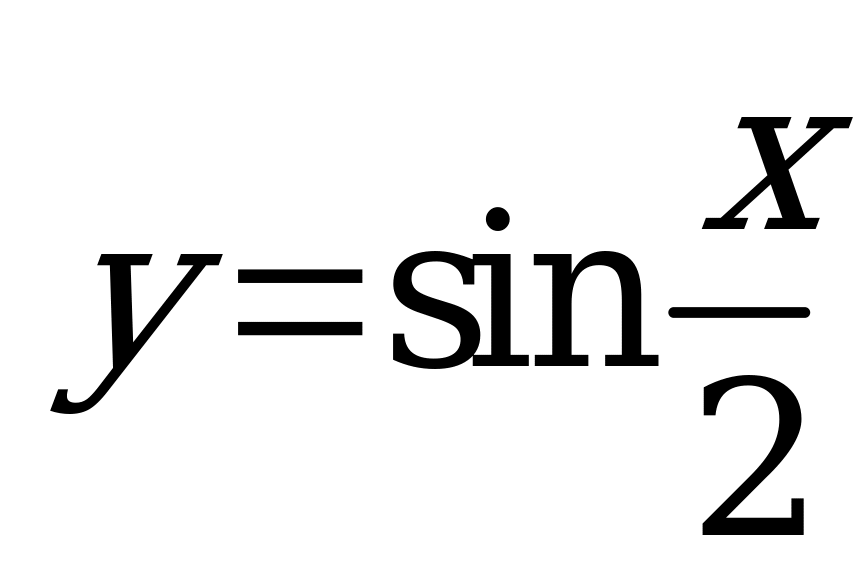 и и 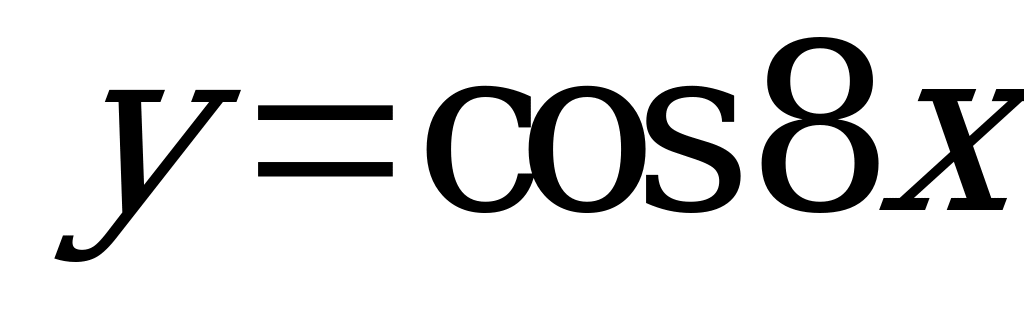 ? ? A) 12 B) 14 C) 10 D) 18 E) 16 | E |
| А5.5 Найдите наименьший положительный период функции 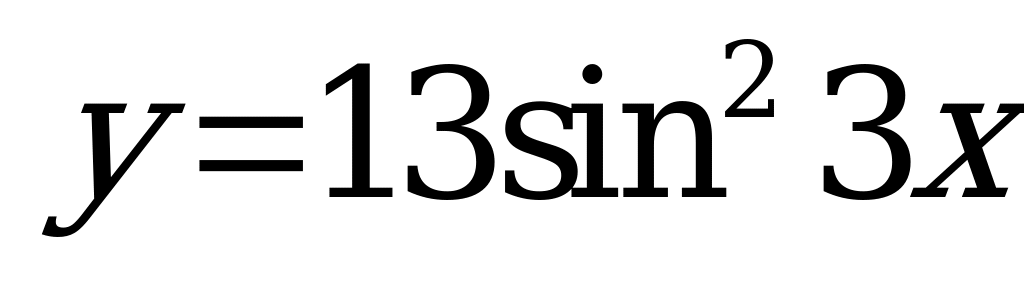 . . A) 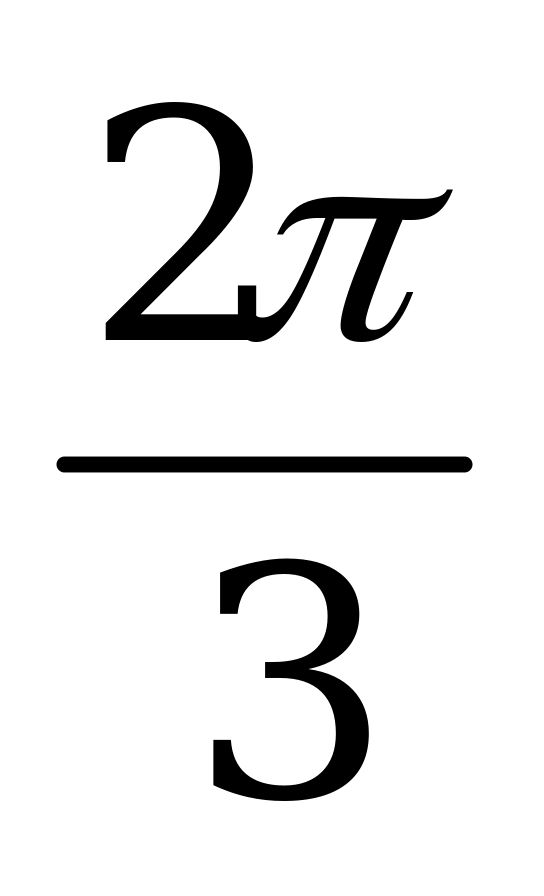 B) B) 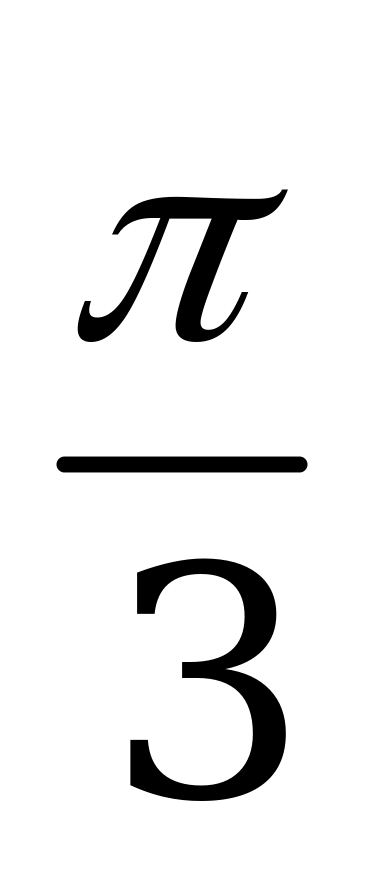 C) C) 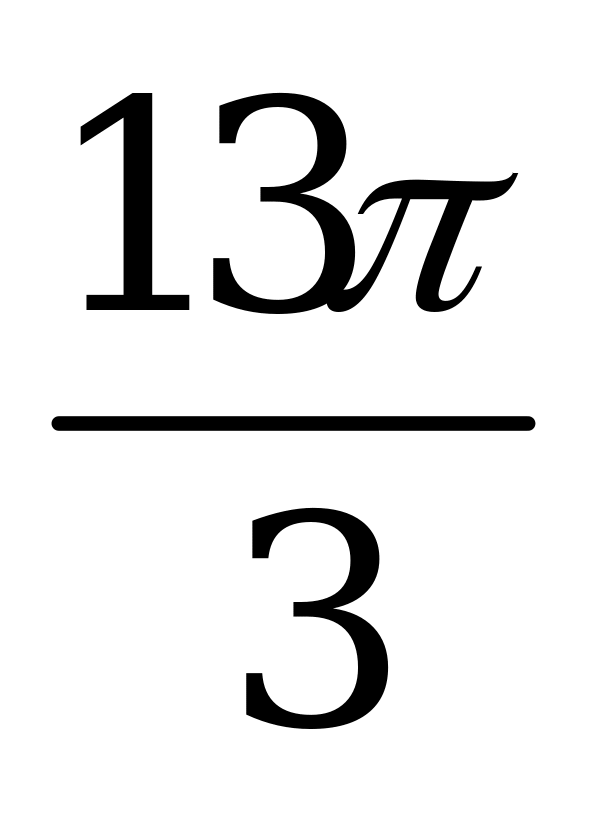 D) D) 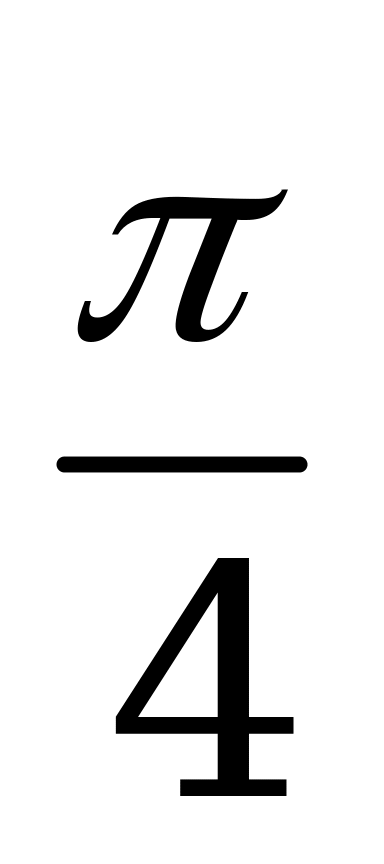 E) E) 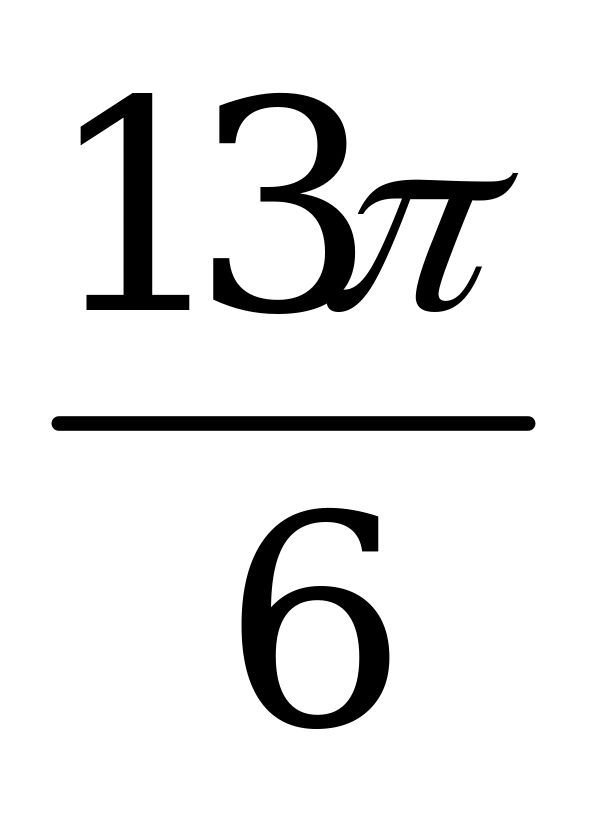 | B |
| А5.6 Укажите наименьший положительный период функции 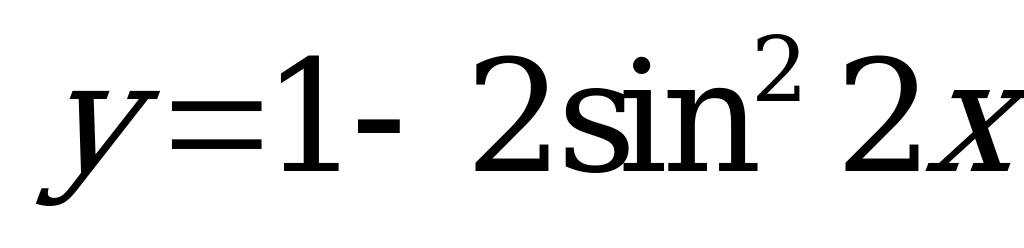 . . A) 2 B) C) 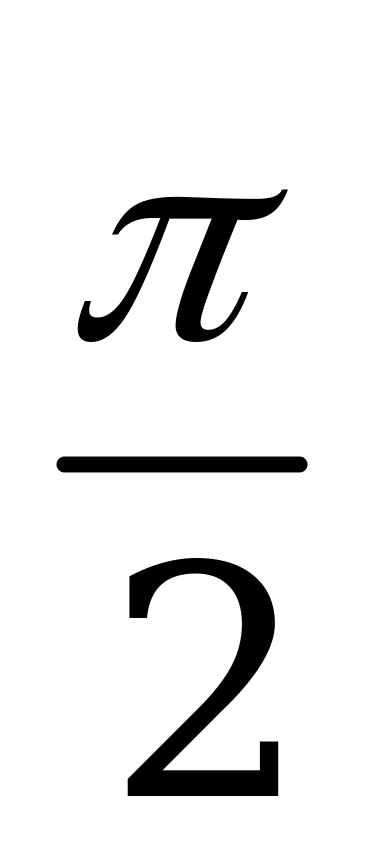 D) D) 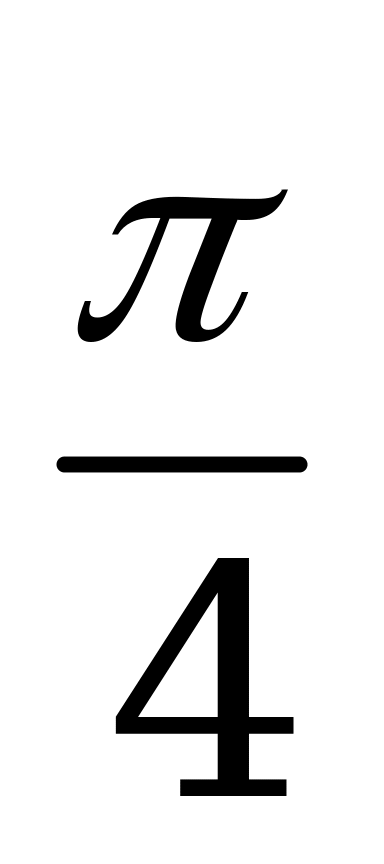 E) нет периода E) нет периода | C |
| А5.7 Найдите наименьший положительный период функции 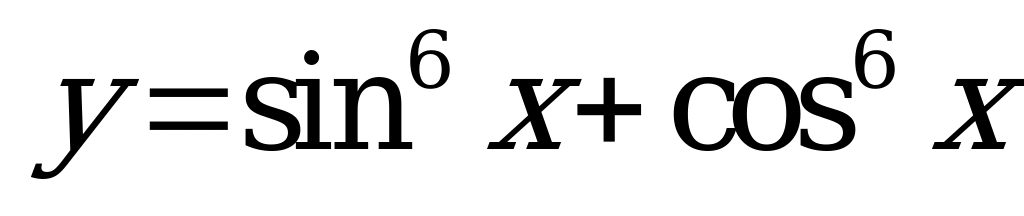 . . A) 2 B) C) 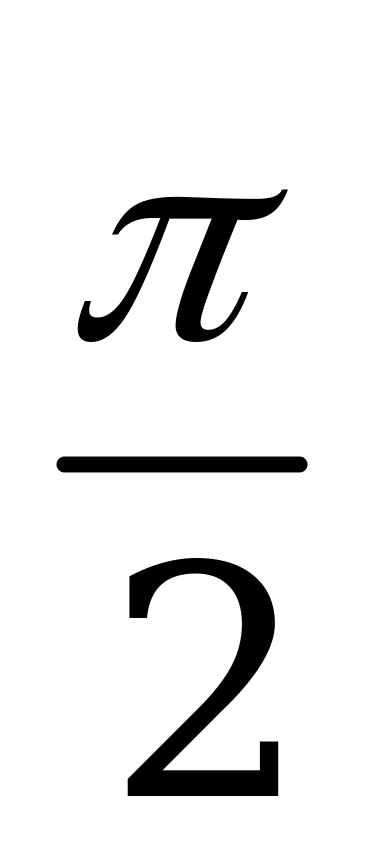 D) D) 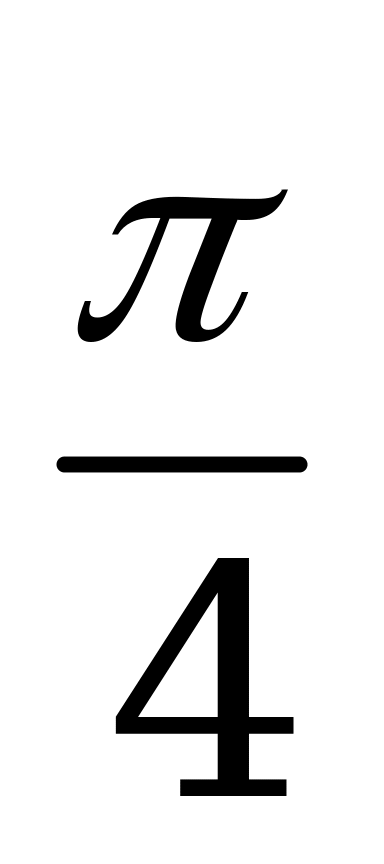 E) E) 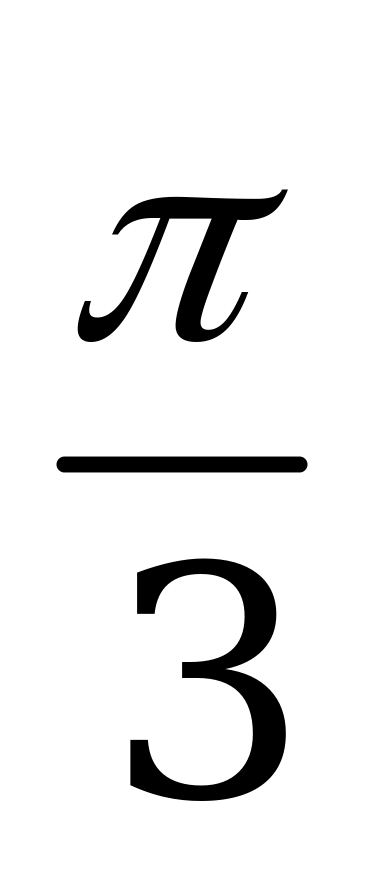 | C |
| А5.8 Найти наименьший общий положительный период для функций 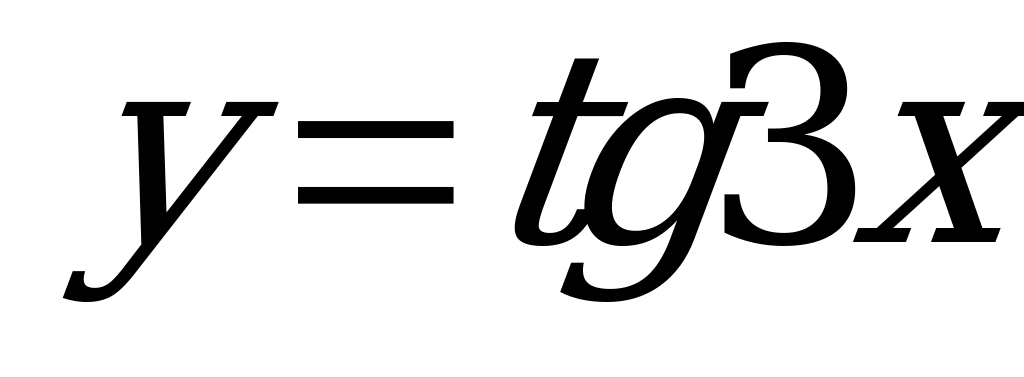 , , 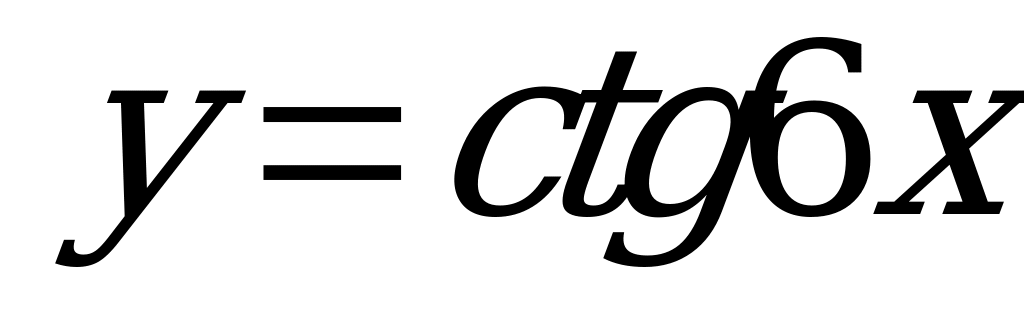 , ,  и и 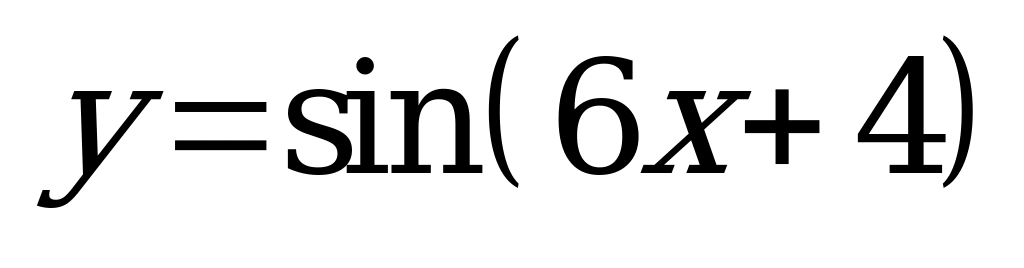 . . A) 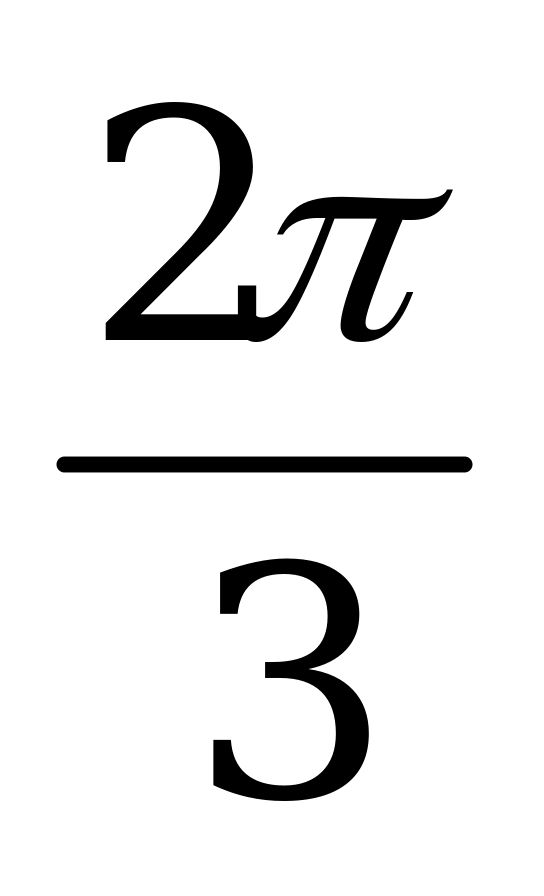 B) B) 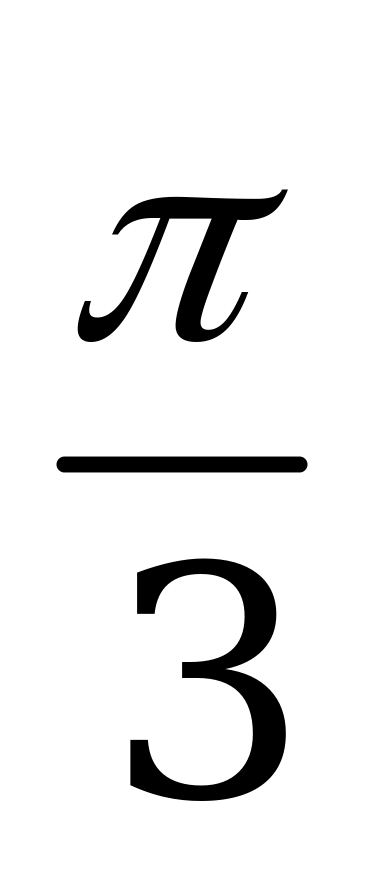 C) C) 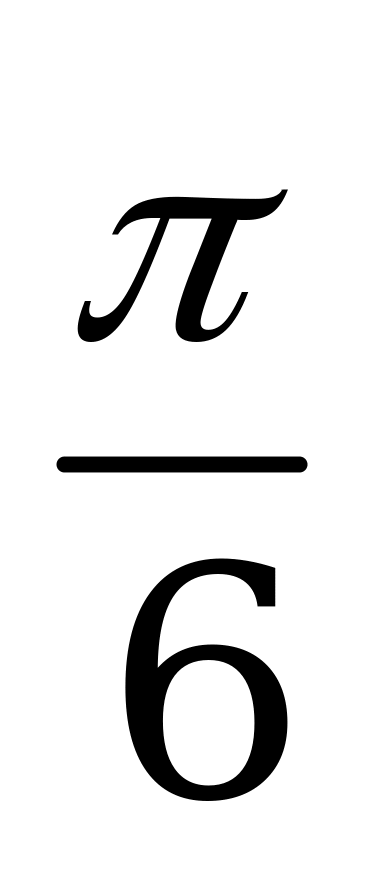 D) D)  E) E)  | A |
| А5.9 Найти наименьший общий положительный период для функций 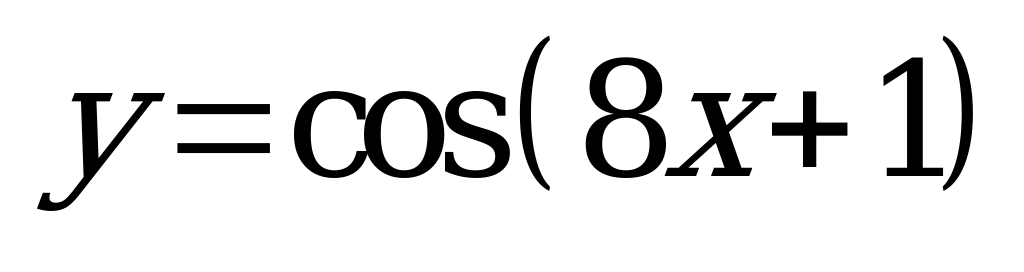 , , 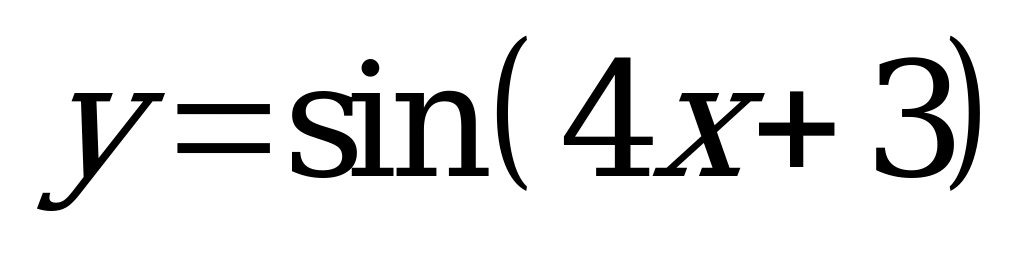 , , 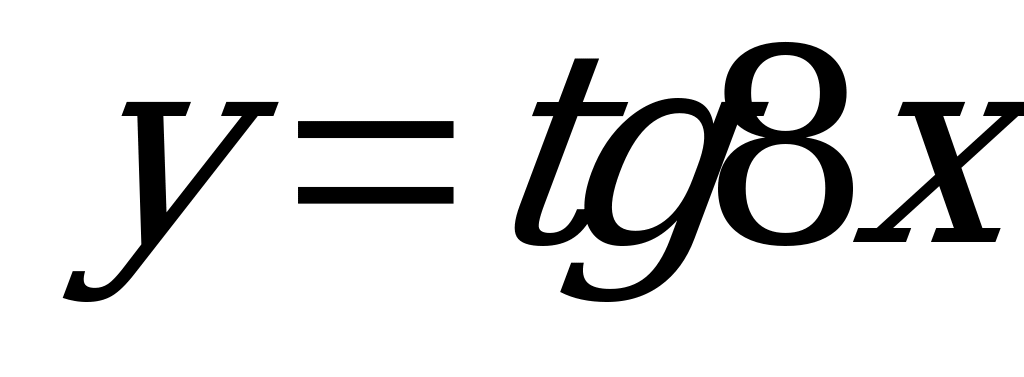 и и 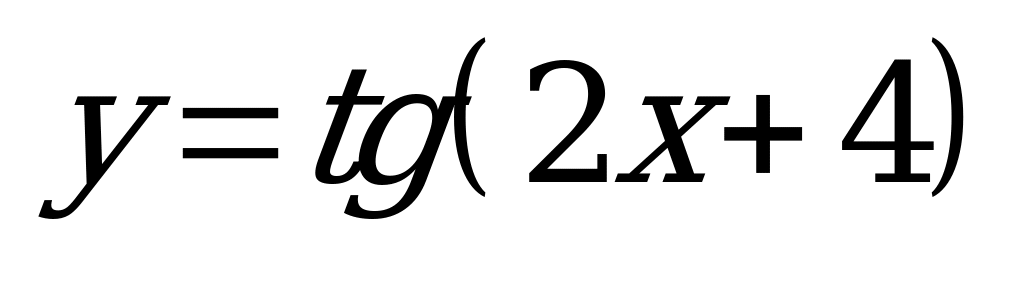 . . A)  B) B)  C) C) 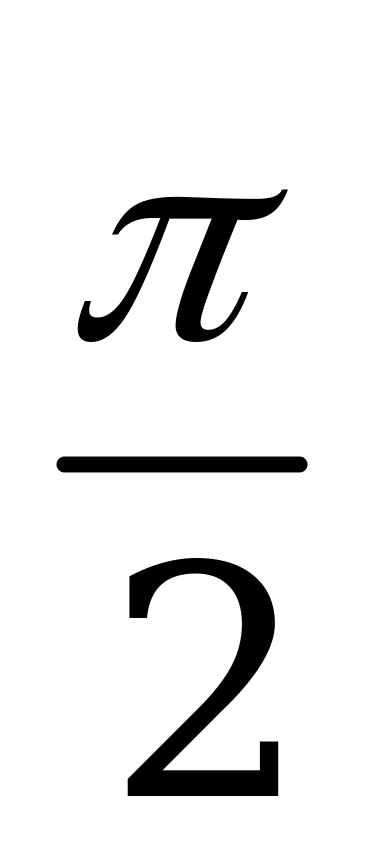 D) D) 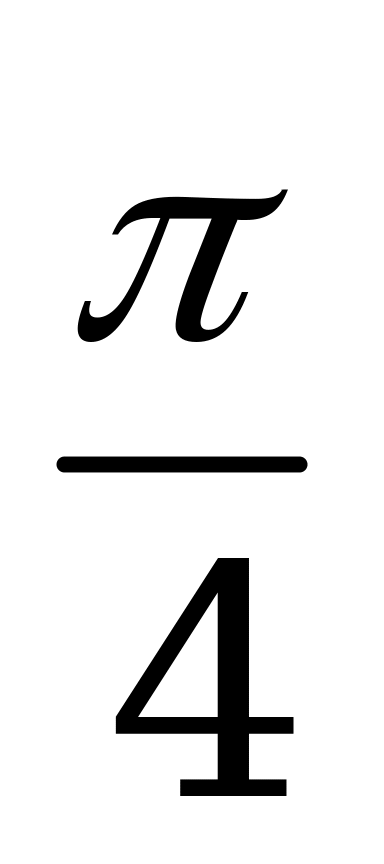 E) E) 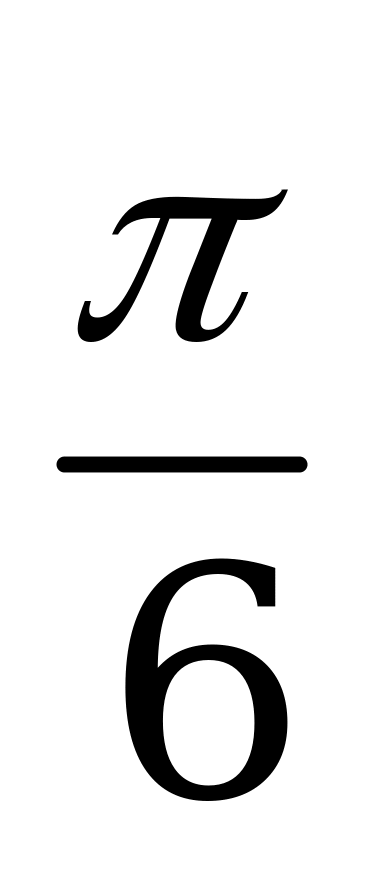 | C |
| А5.10 Найдите наименьший положительный период функции: 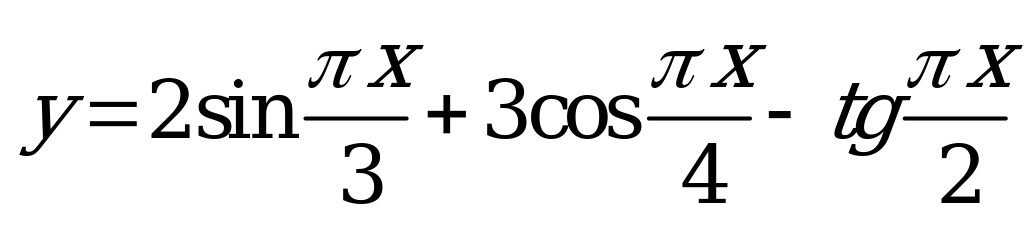 A) 12 B) 12 C) 2 C) 2 D) 24 D) 24 E) 24 E) 24 | E |
Тестовые задания более сложного уровня 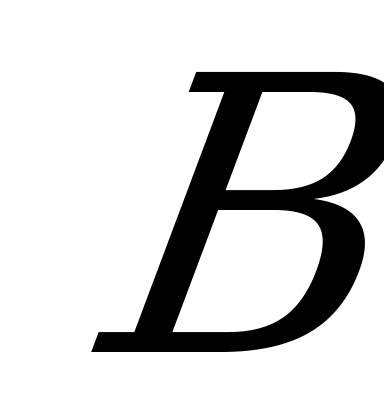 .
.
| В1. Формулы приведения. Стандартные значения. | Ответы |
| В1.1 Решите уравнение 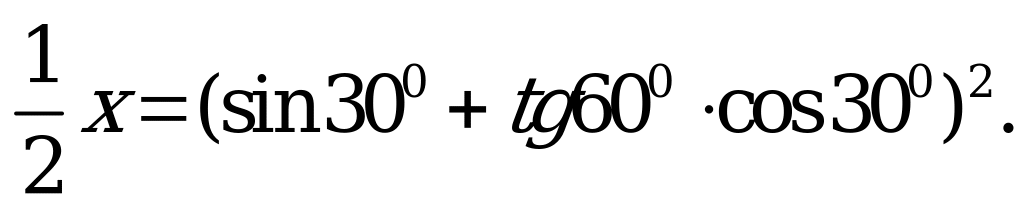 A) 8 B) 4 C) 2 D) 16 E) 1 | A |
| В1.2 Решите уравнение 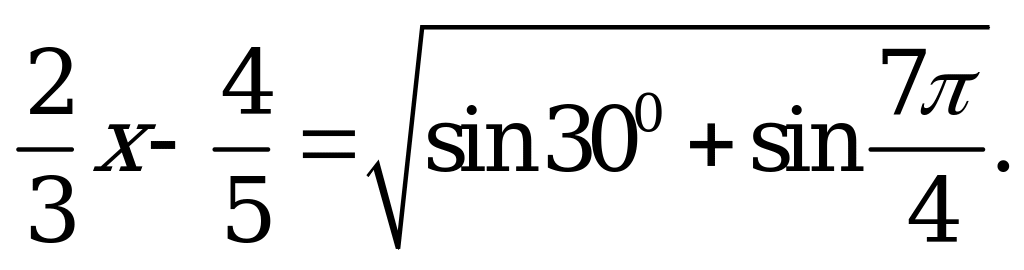 A) 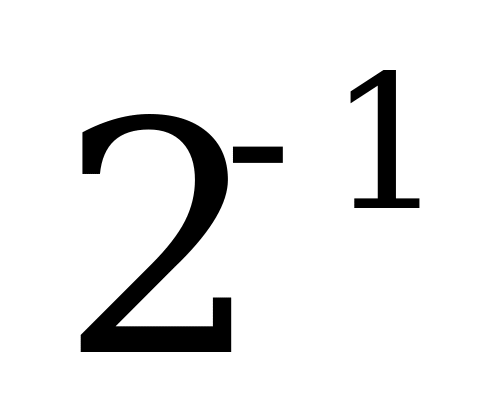 B) C) 2 D) B) C) 2 D) 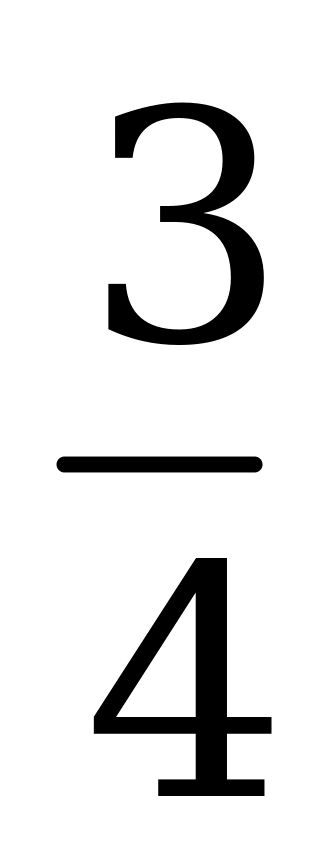 E) E) 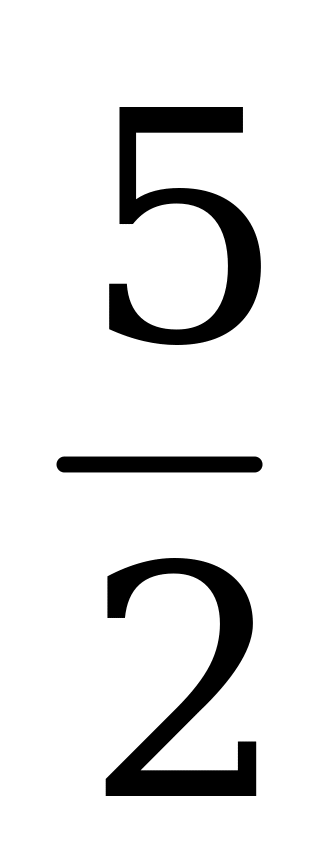 | B |
| В1.3 Решите уравнение 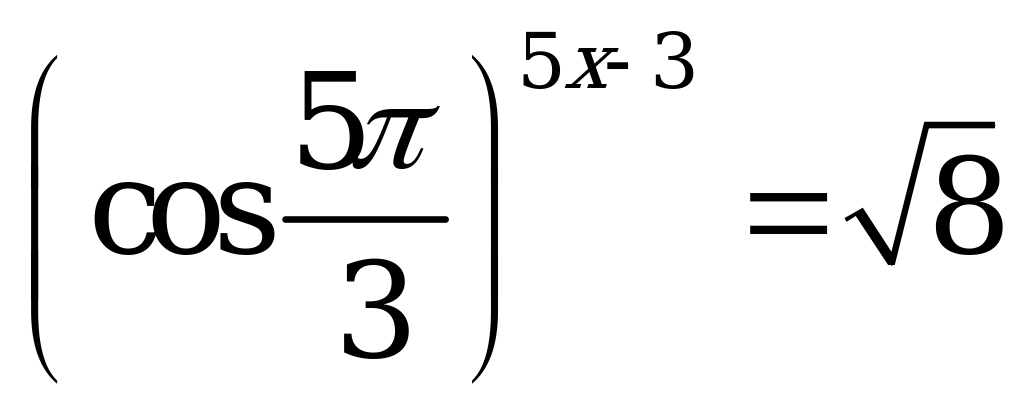 . . A) 0,2 B) 0,3 C) 0,4 D) 0,6 E) 0,8 | B |
| В1.4 Решите неравенство 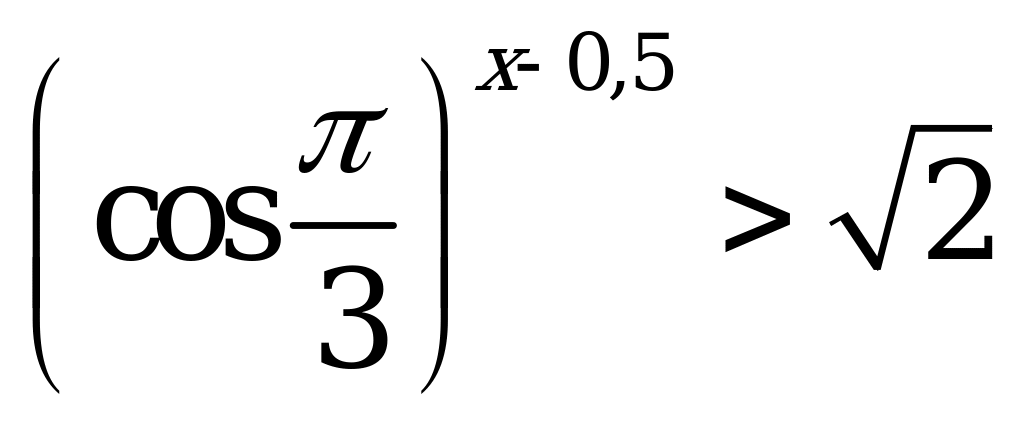 A) (-; 0) B) (0; ) C) (0; 0,5) D) (1; ) E) (0; 1) | A |
| В1.5 Найдите наибольшее целое решение неравенства 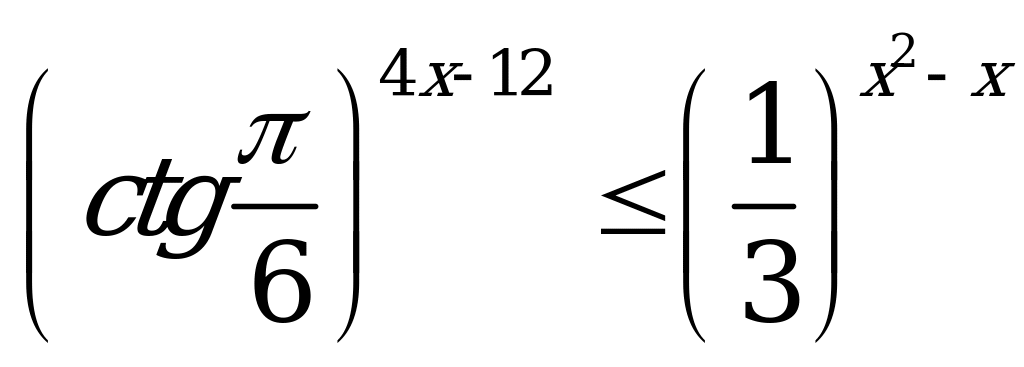 A) 2 B) 5 C) 6 D) 9 E) 1 A) 2 B) 5 C) 6 D) 9 E) 1 | A |
| В1.6 Упростите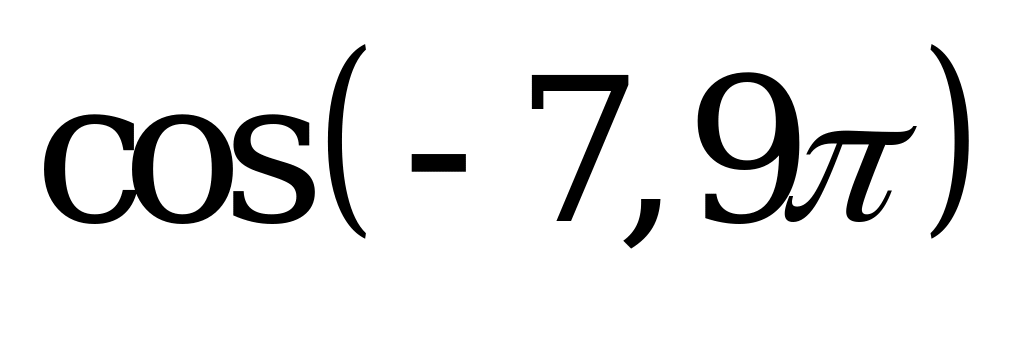 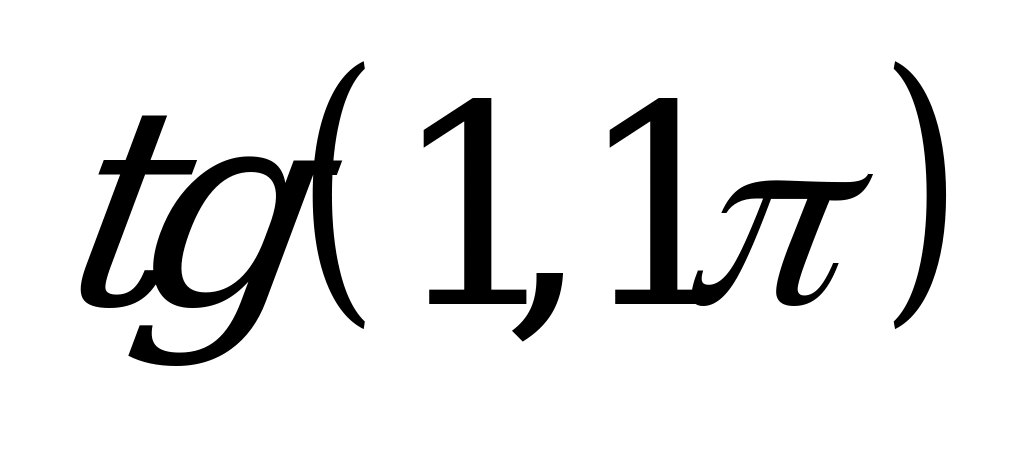 – – 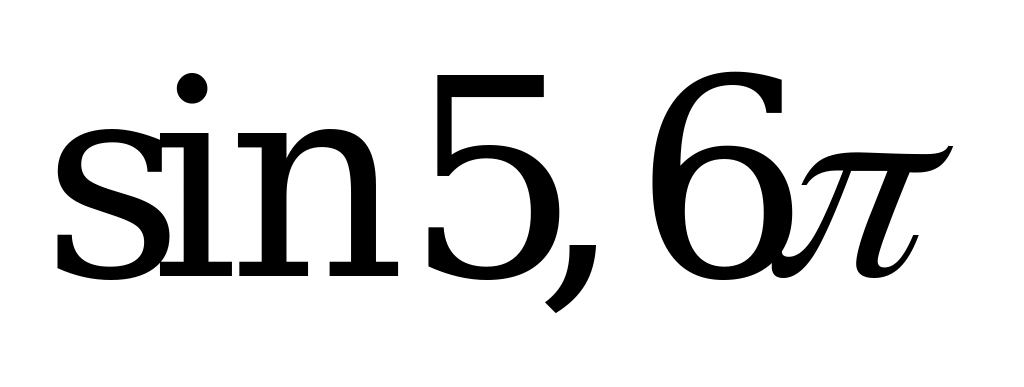 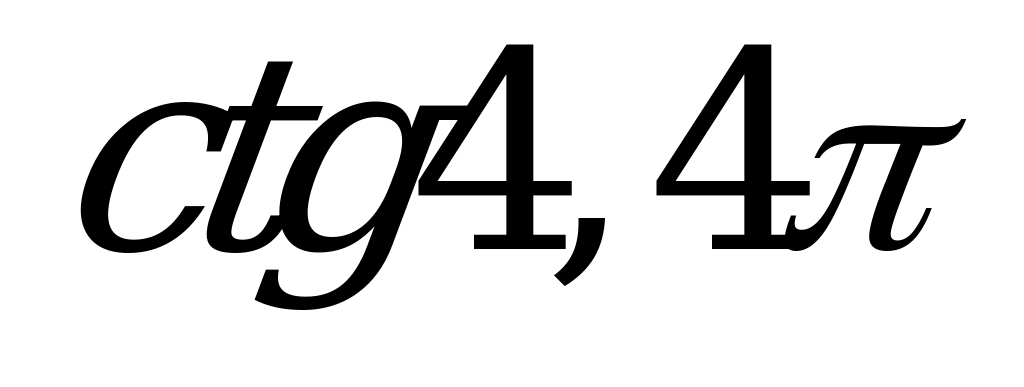 . . A) 0 B) 1 C) -1 D) 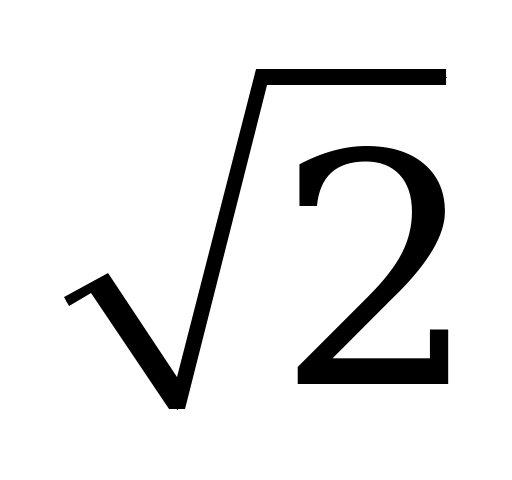 E) - E) -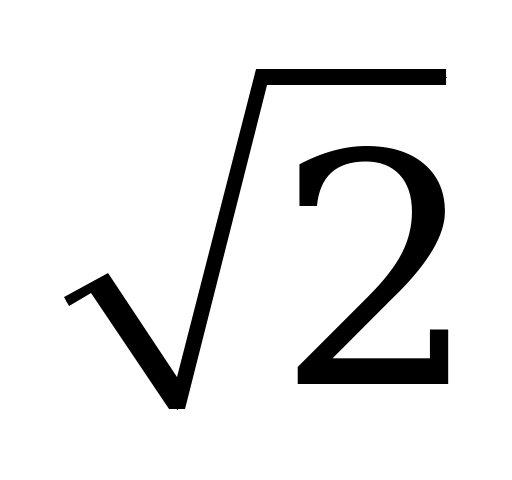 | A |
| В1.7 Найдите значение 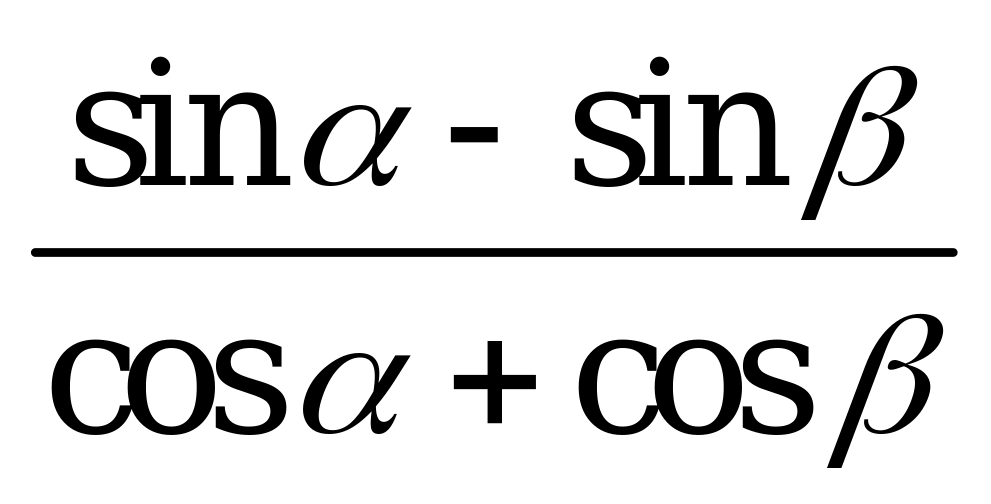 , если - = , если - = 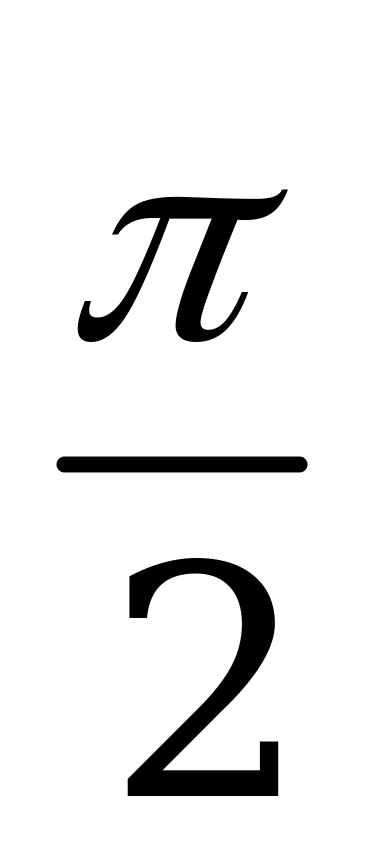 . . A) 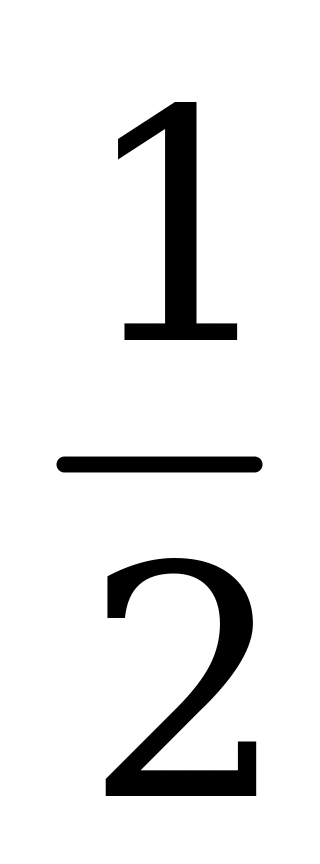 B) B) 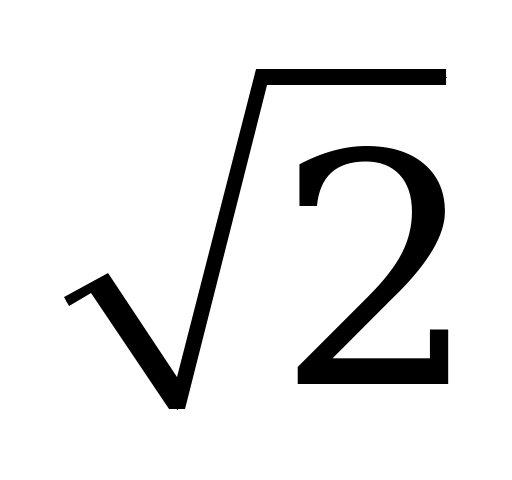 C) C) 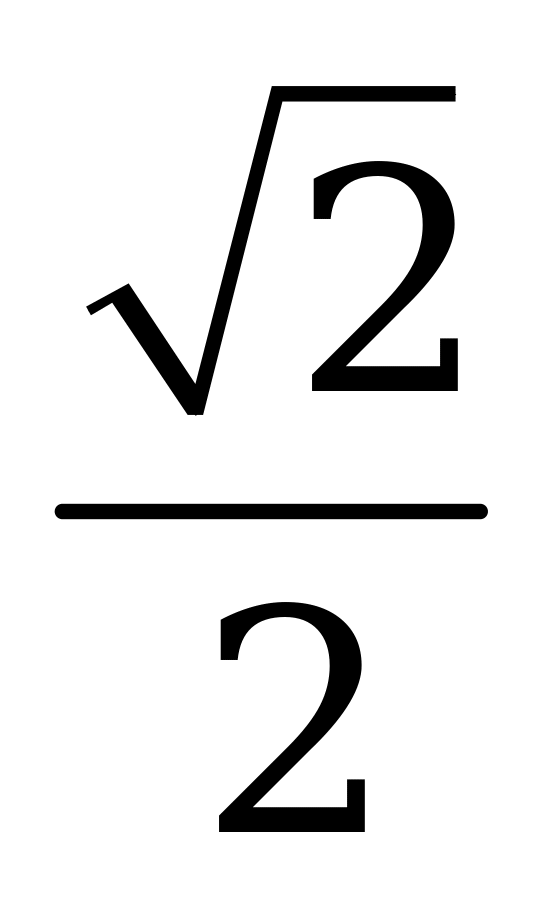 D) 1 E) 2 D) 1 E) 2 | D |
| В1.8 Упростите 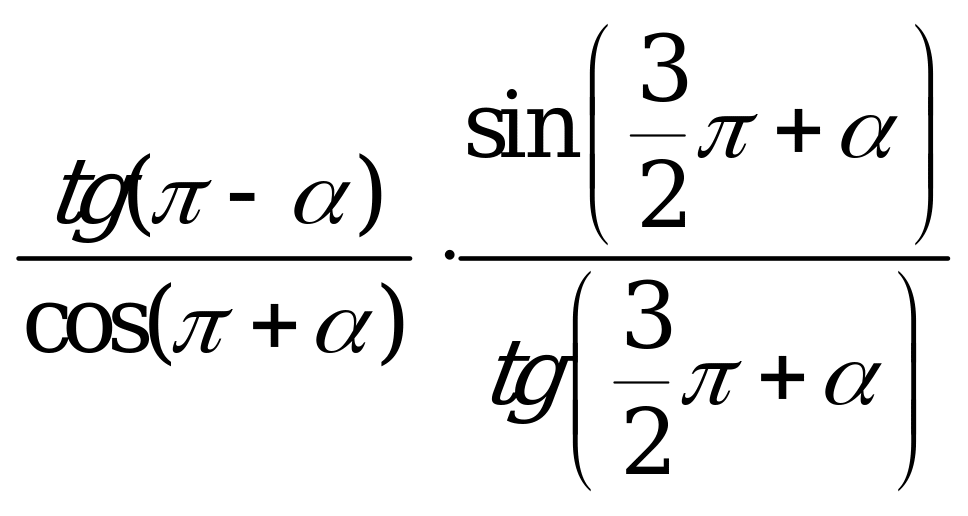 . . A) 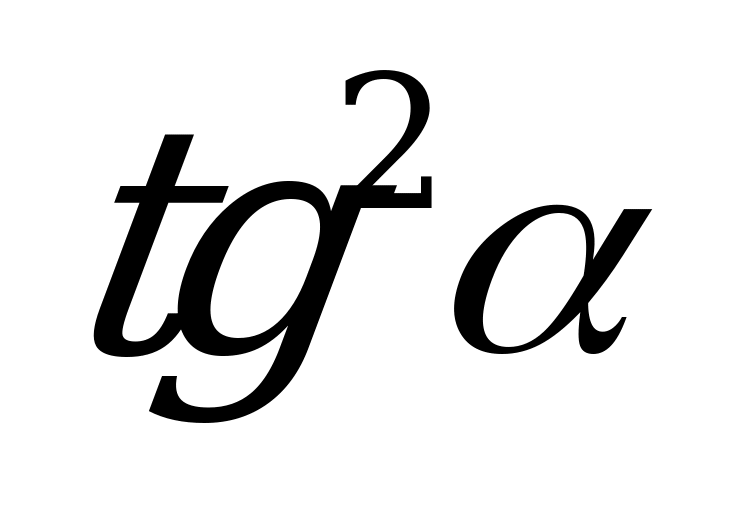 B) B) 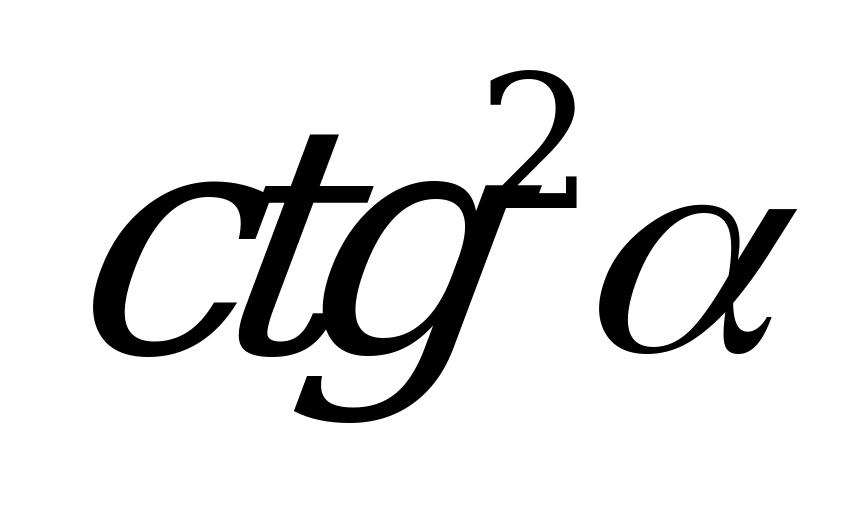 C) - C) -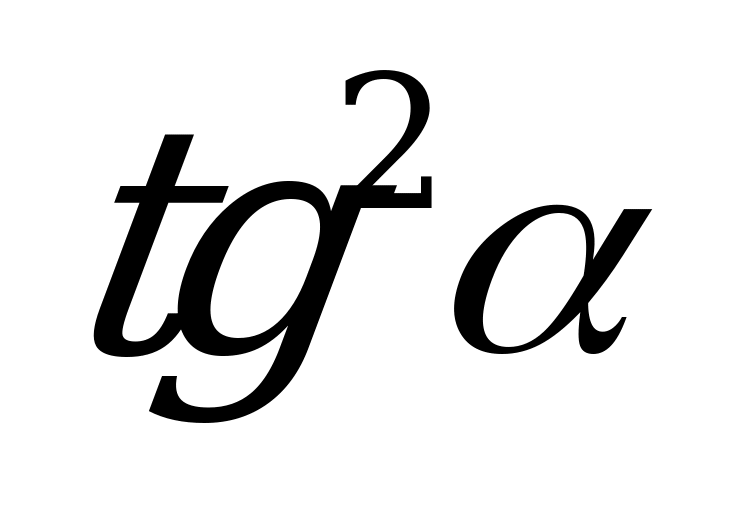 D) D) 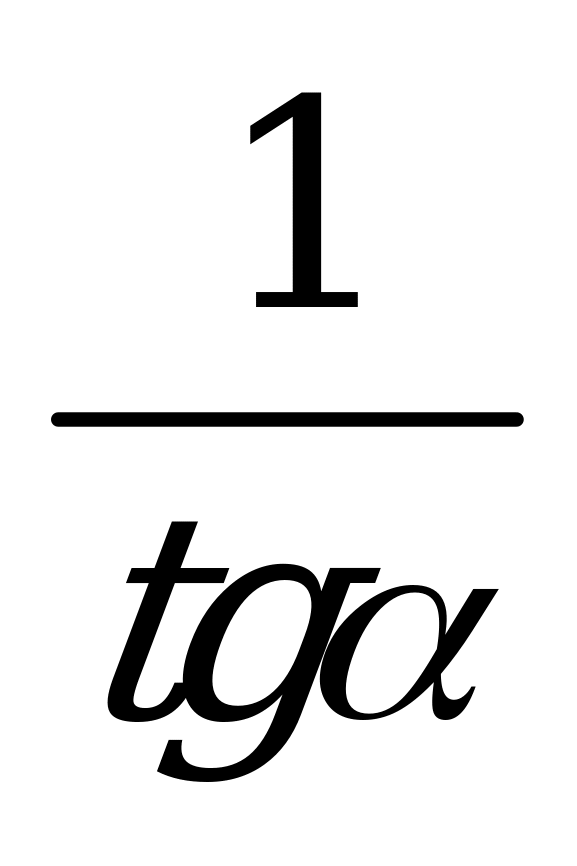 E) E) 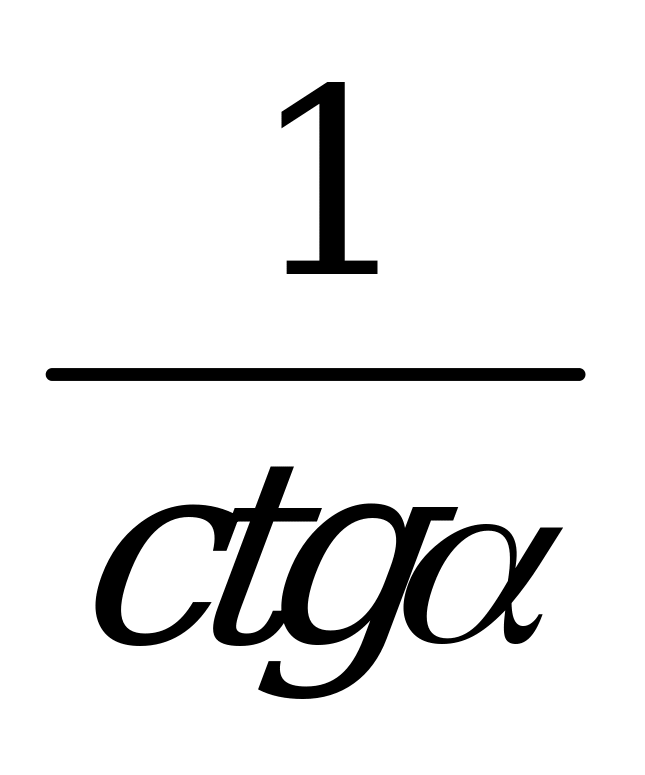 | A |
| В1.9 Упростите 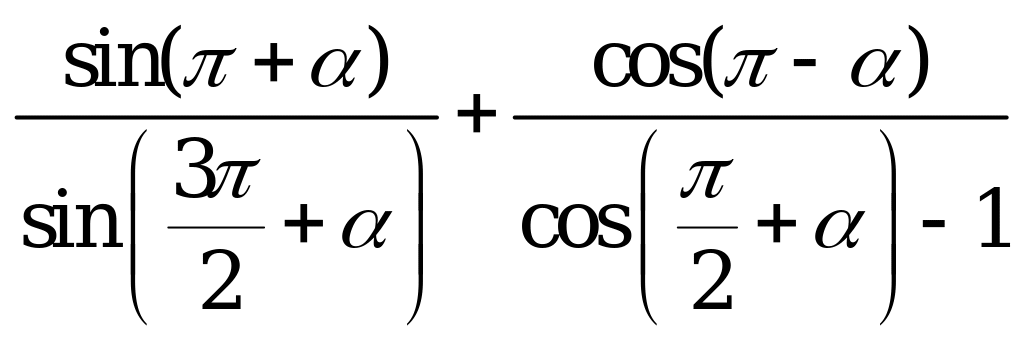 A) 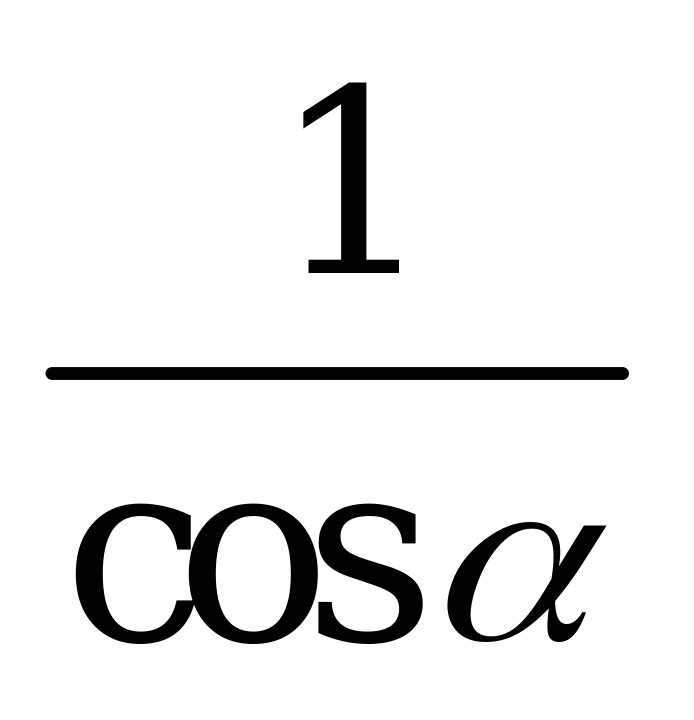 B) B) 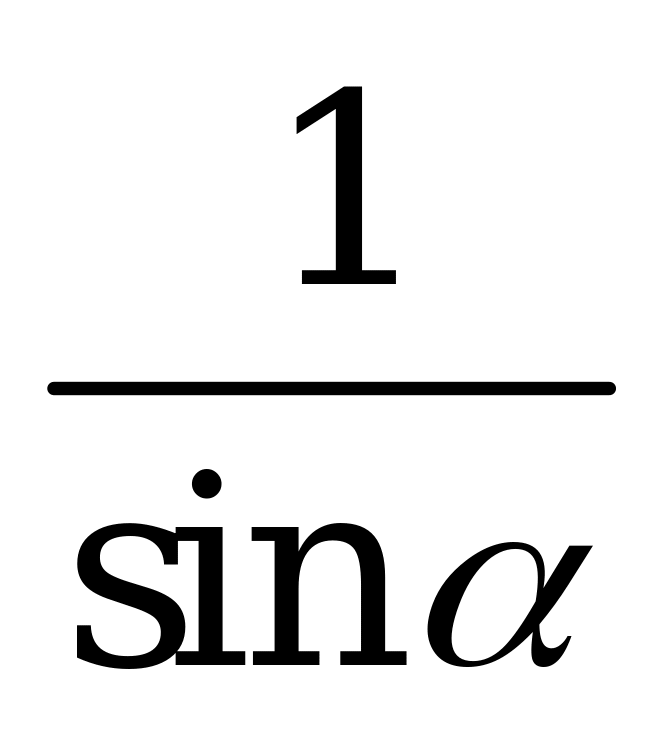 C) C) 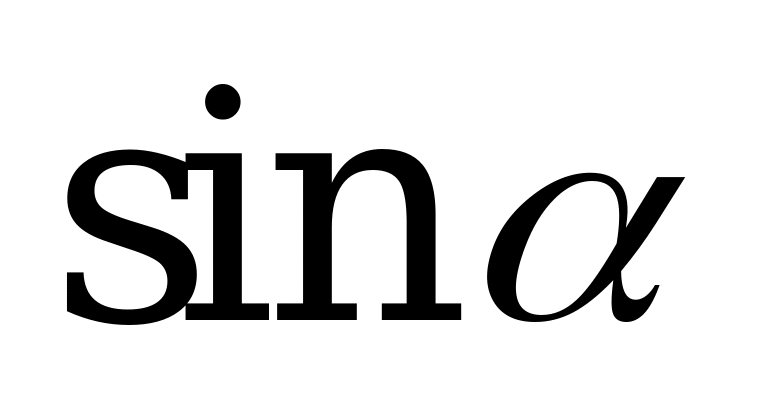 D) D)  E) 1 E) 1 | A |
| В1.10 Вычислите значение выражения: 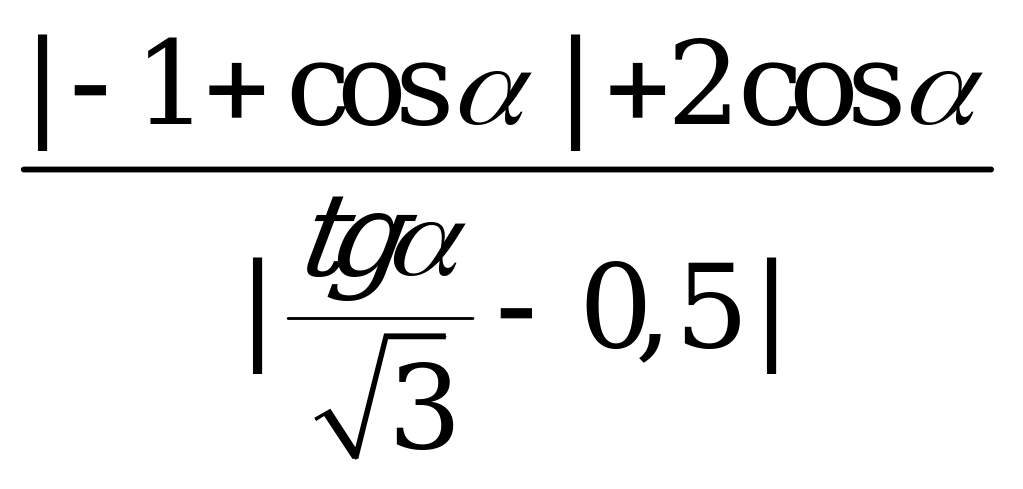 , если , если 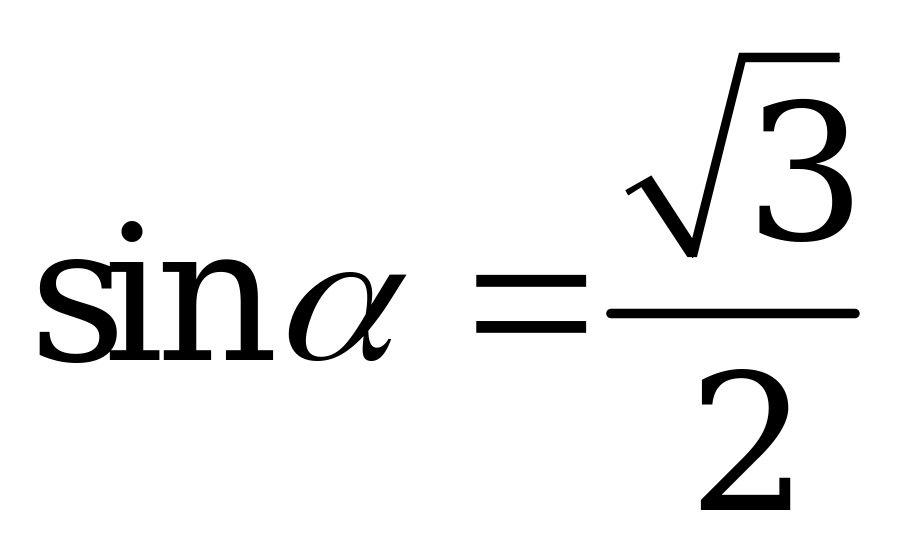 и и 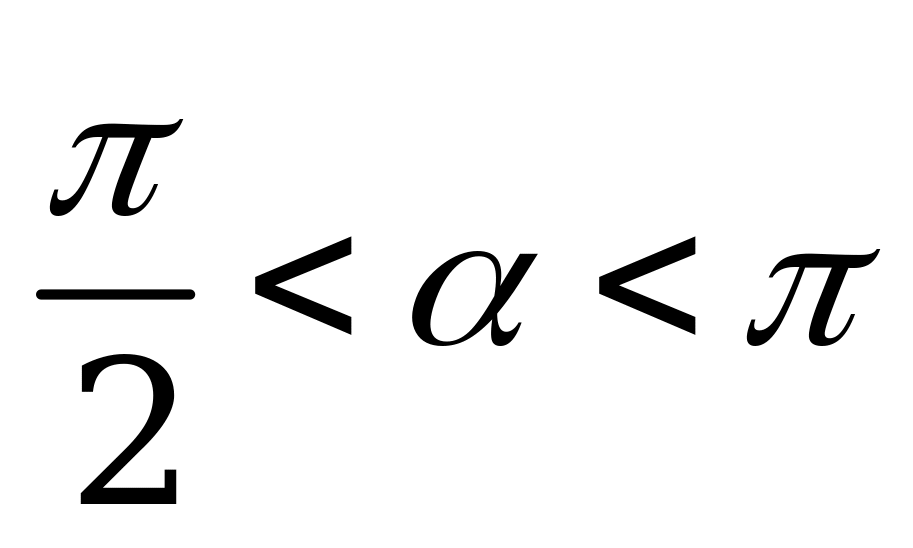 A) 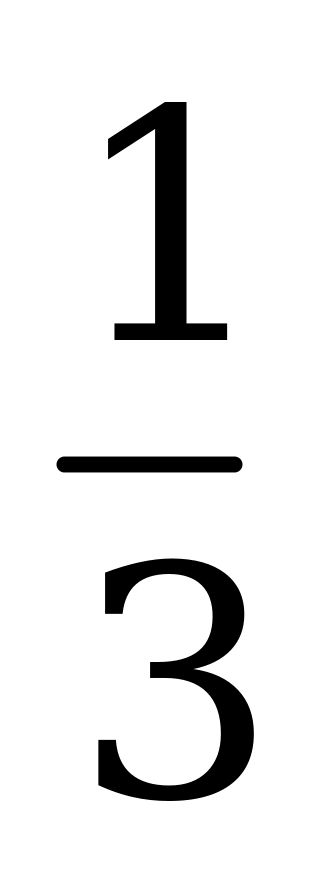 B) 1 C) 3 D) -1 E) -3 B) 1 C) 3 D) -1 E) -3 | A |
| В2. Знак тригонометрической функции. Сравнение значений |
|
| В2.1 Какое выражение (число) положительно? A)  B) B)  C) C) 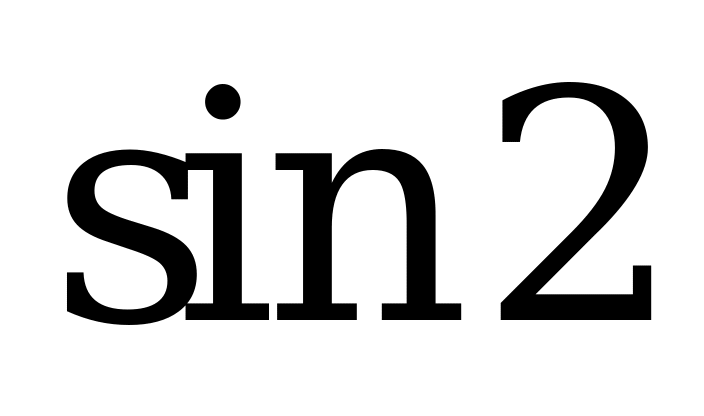 D) D) 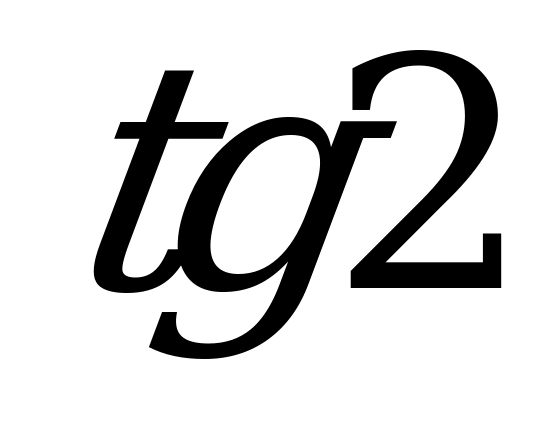 E) E)  | C |
| В2.2 Какое число положительно? A) 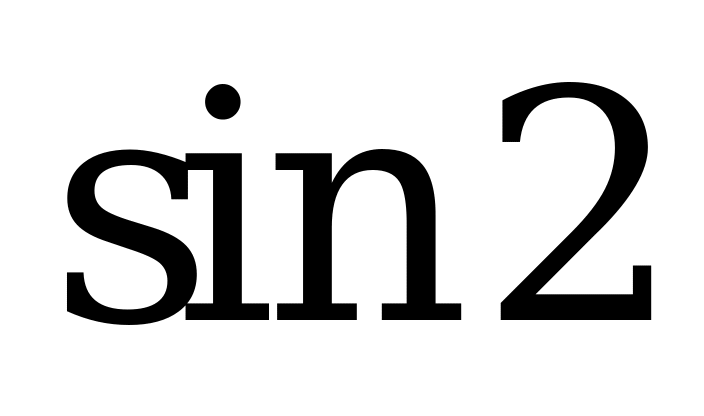 B) B)  C) C) 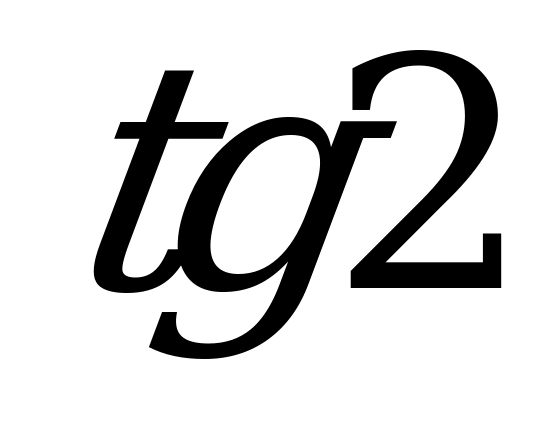 D) D) 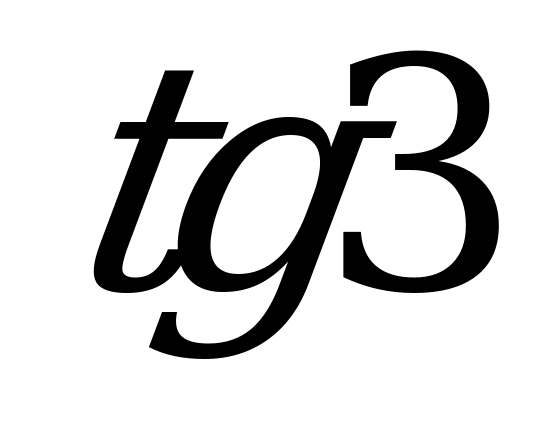 E) E)  | A |
| В2.3 Расположите числа x = sin600, y =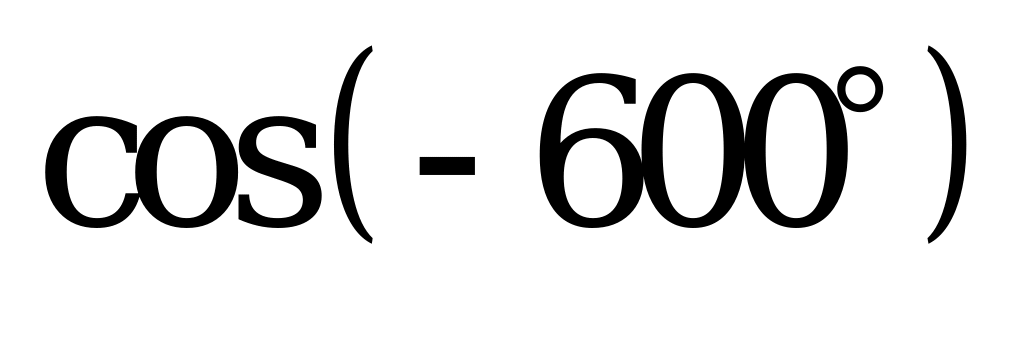 и и z = 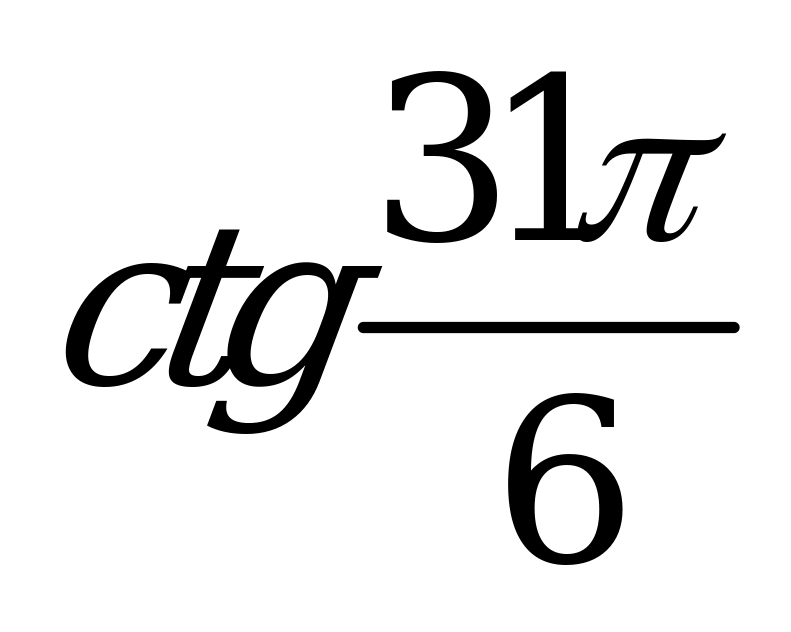 в порядке убывания. в порядке убывания. A) z x y B) x y z C) y z x D) z y x E) y x z | A |
| В2.4 Расставьте в порядке убывания числа: 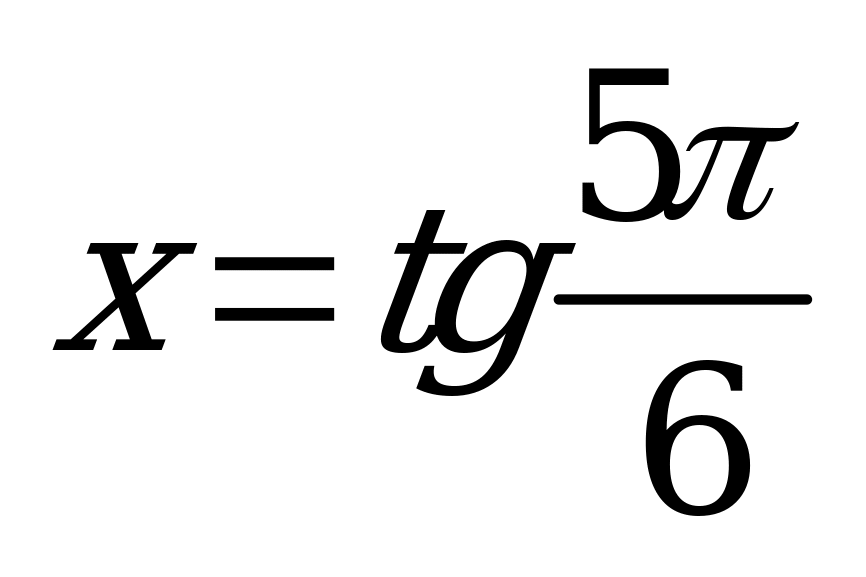 , , 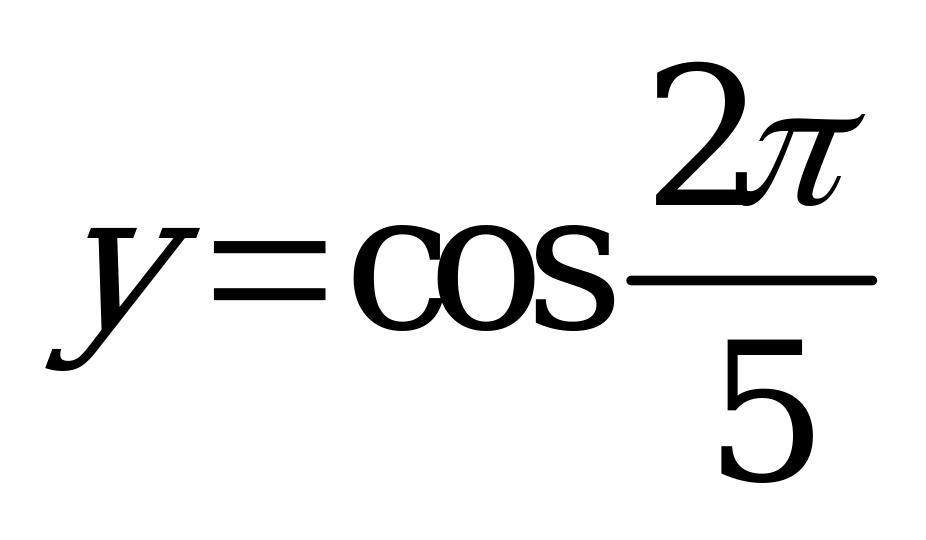 и и 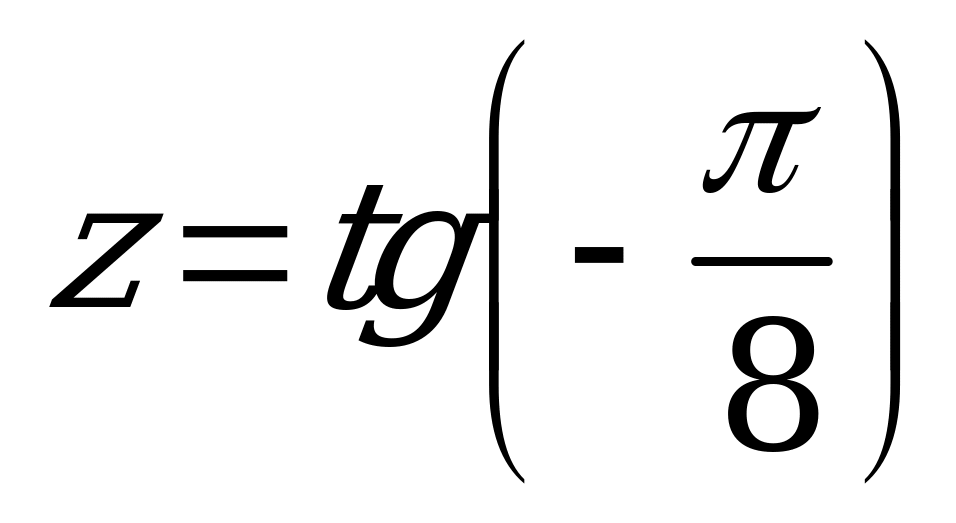 A) x y z B) y x z C) x z y D) y z x E) z y x | D |
| В2.5 Расставьте в порядке убывания числа: 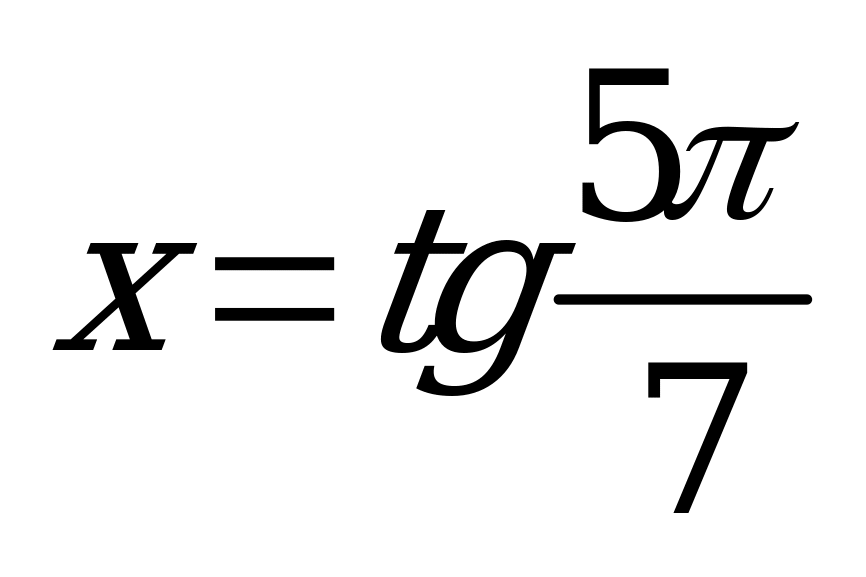 ; ; 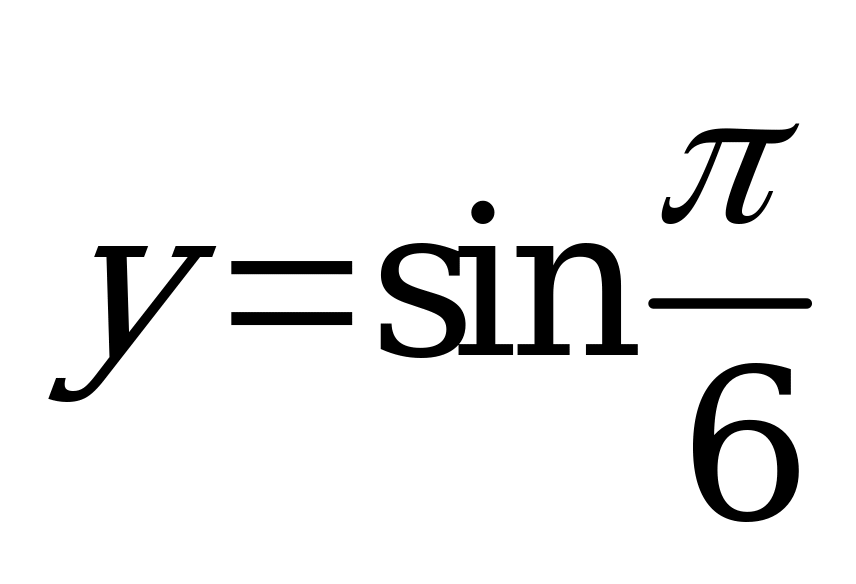 и и 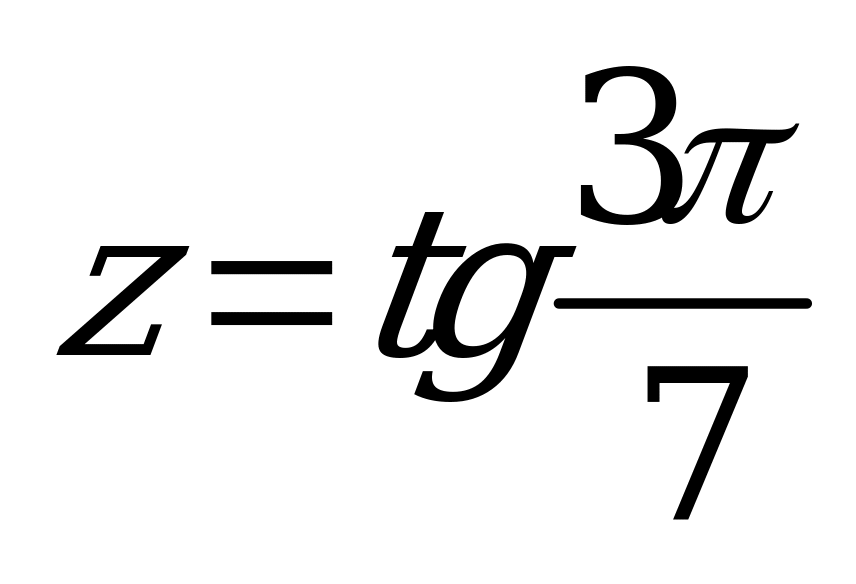 A) z y x B) x z y C) y x z D) x y z E) y z x | A |
| В2.6 Расставьте в порядке возрастания числа: 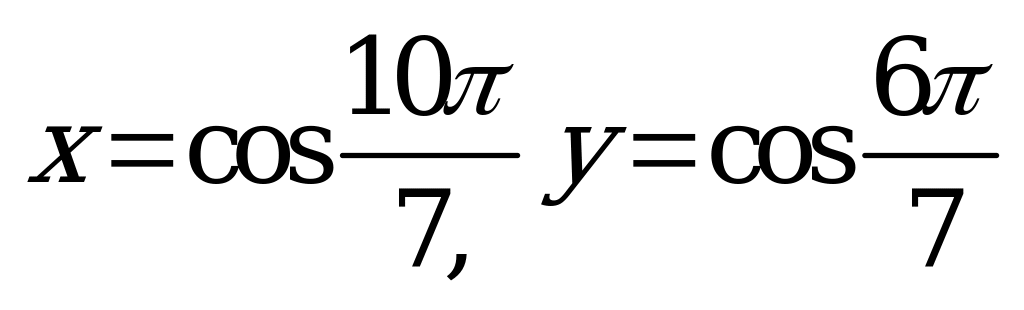 и и 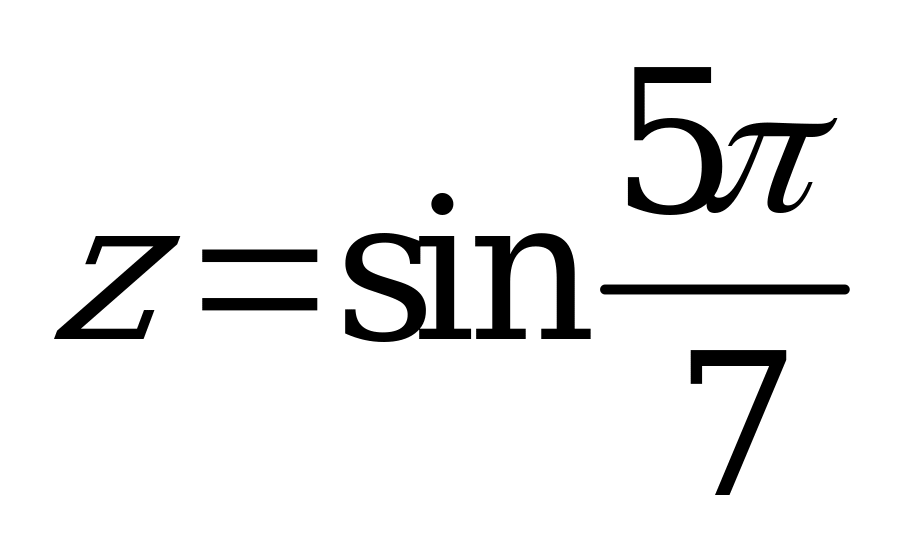 A) x D) y z x E) z y x | B |
| В2.7. Расположите числа 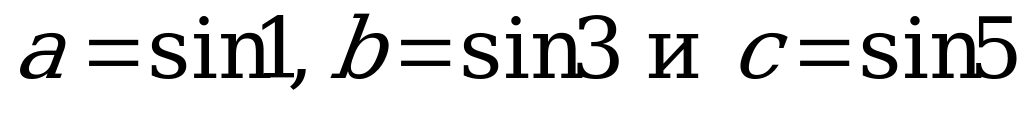 в порядке их убывания. в порядке их убывания. A) a b c B) a c b C) c b a D) c a b E) b c a | A |
| В2.8. Расположите числа a = sin1; b = sin2; c = sin3; d = sin4 и e = sin5 в порядке убывания. A) a b c d e B) e d b c a C) b c a d e D) c b a d e E) b a c d e | E |
| В2.9. Расположите числа в порядке убывания: m = sin750; n = cos750; p = tg750; q = ctg750 A) p m q n B) p m n q C) p n m q D) m p q n E) q p m n | A |
| В2.10 Среди приведенных чисел найдите наибольшее. A) 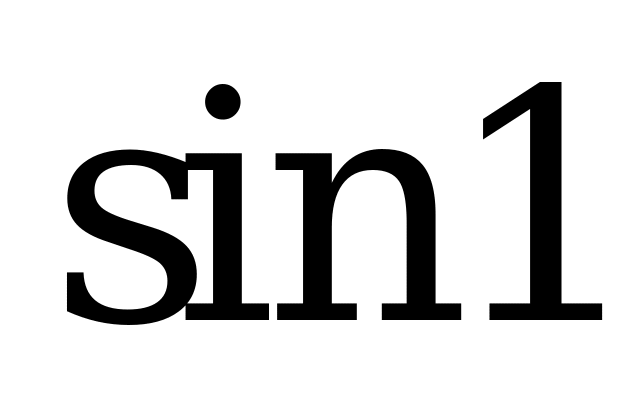 B) B) 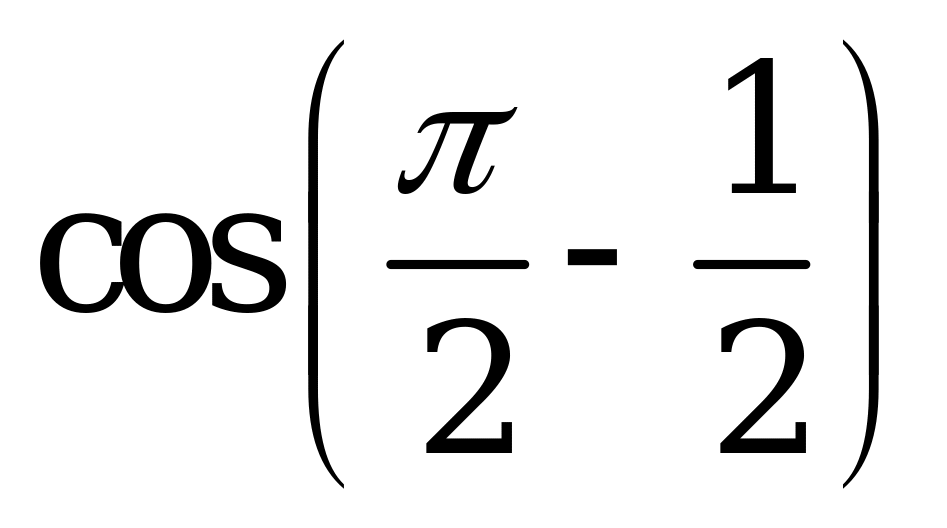 C) C)  D) D)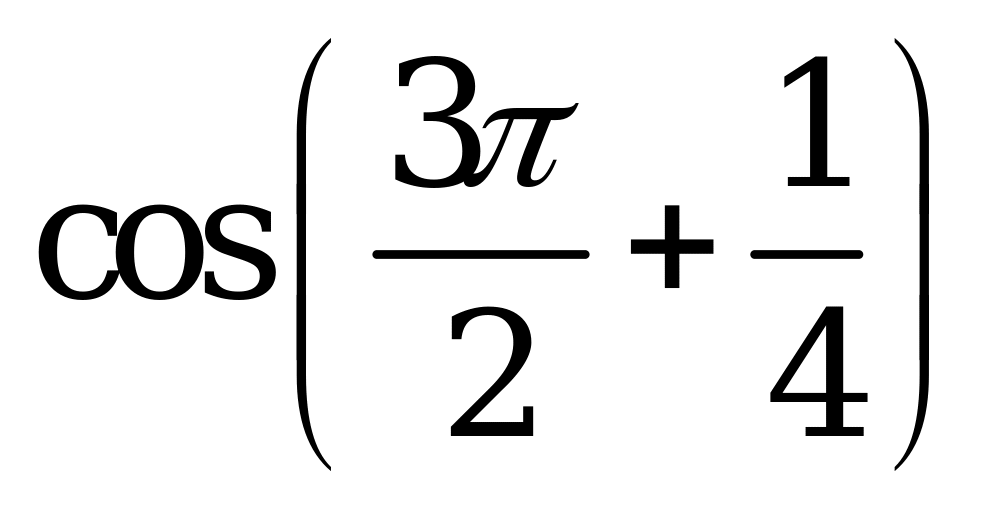 E) E)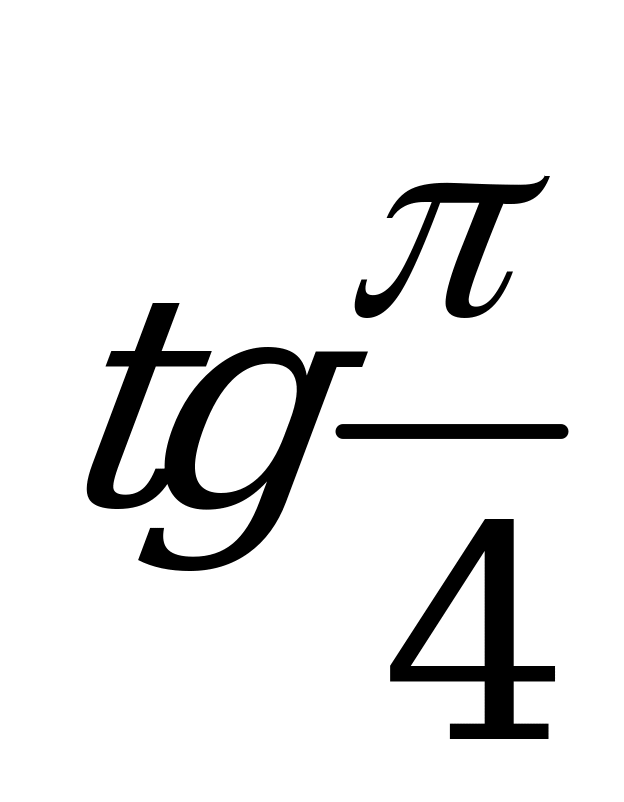 | E |
| В3. Основные тригонометрические формулы. | Ответы |
| В3.1 Упростите выражение: 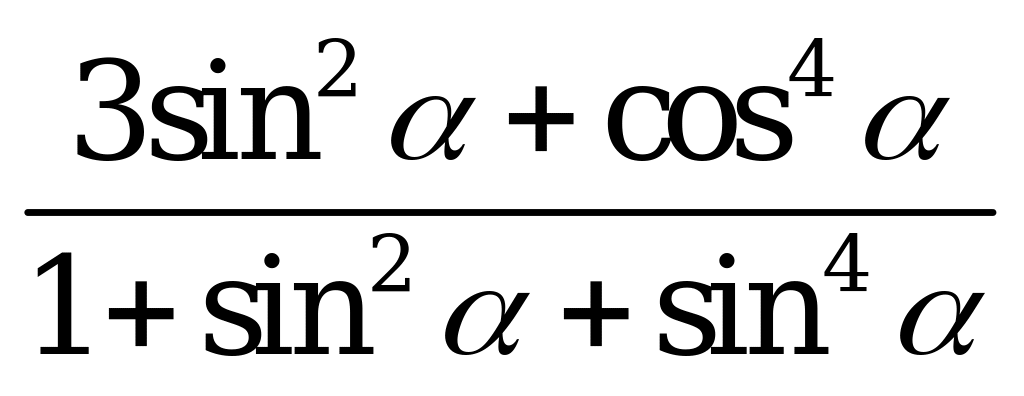 A) 2sin B) 2 C) B) 2 C) 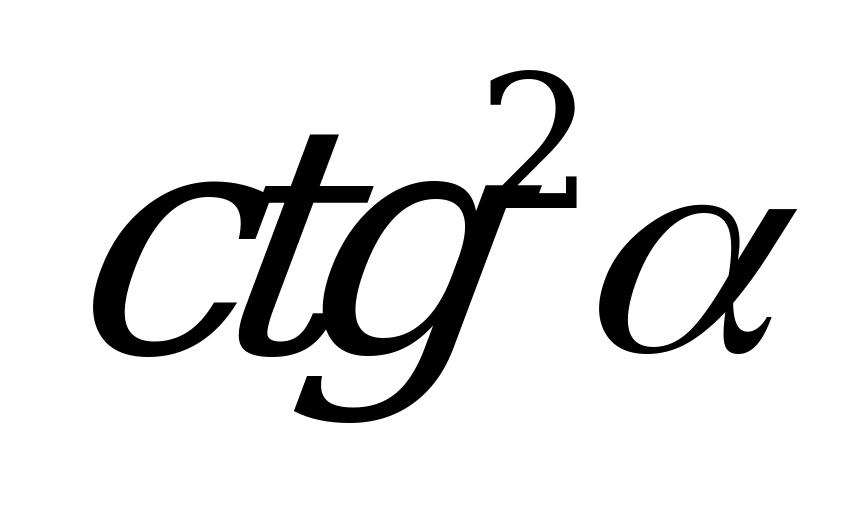 D) 1 E) 3 D) 1 E) 3 | D |
| В3.2 Упростите выражение: 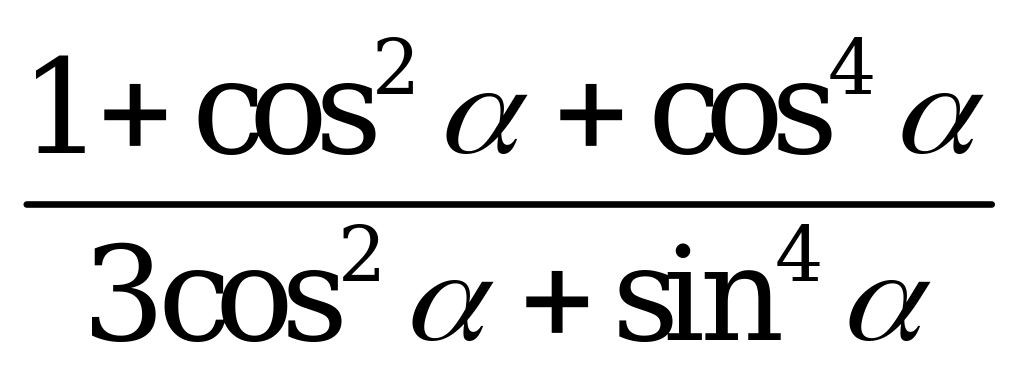 A) 3 B) 2 C) 1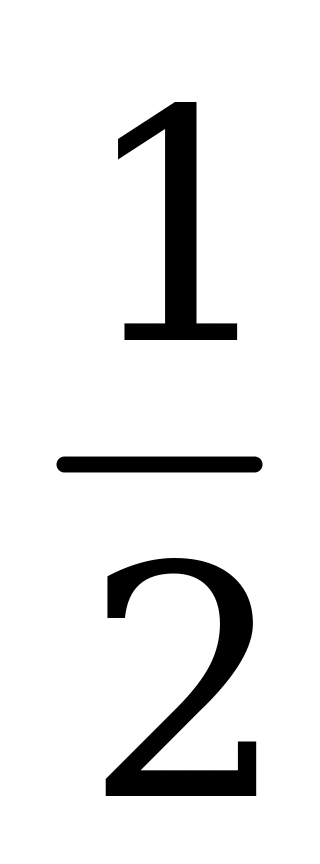 D) D) 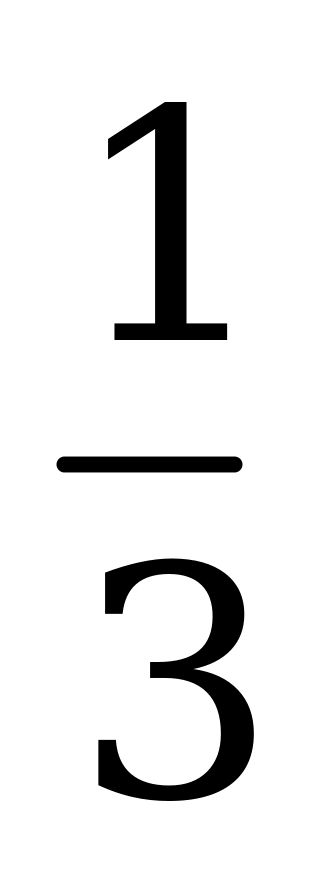 E) 1 E) 1 | E |
| В3.3 Выразите 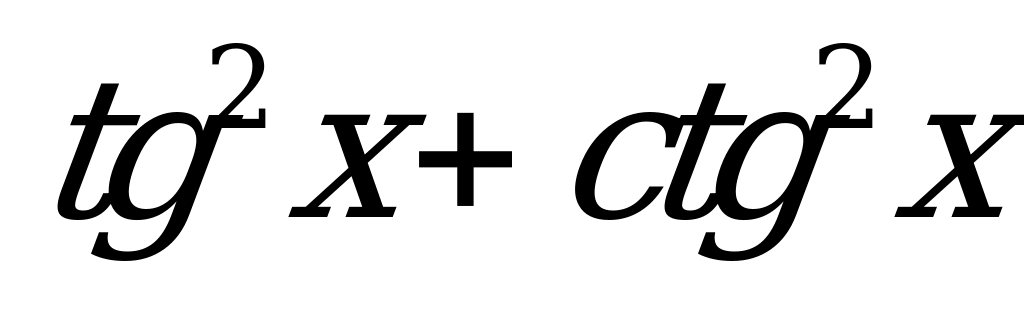 через p, если через p, если 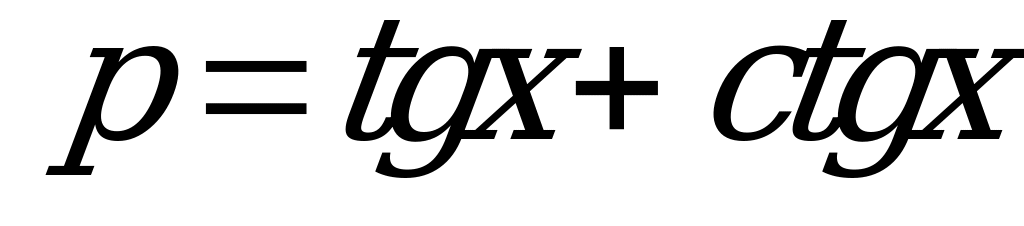 A) p2 - 2 B) -p2 + 2 C) p2 + 2 D) p2 - 1 E) p2 + 1 | A |
| В3.4 Найдите 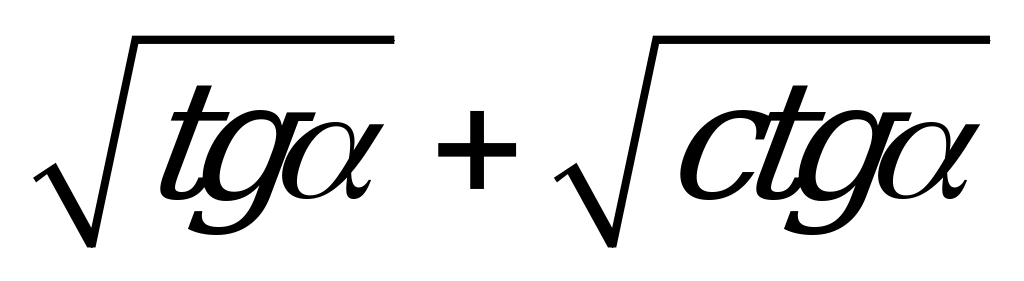 , если , если 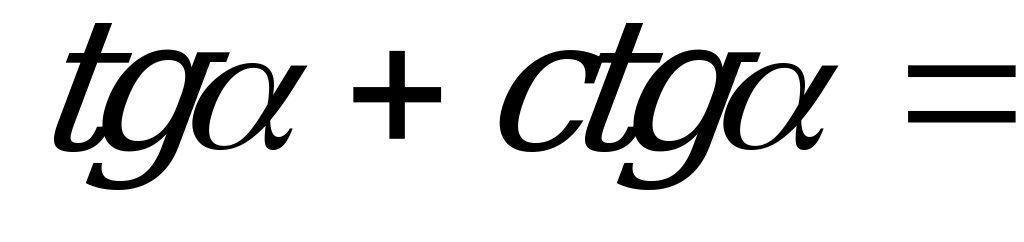 a (a 0) a (a 0) A) 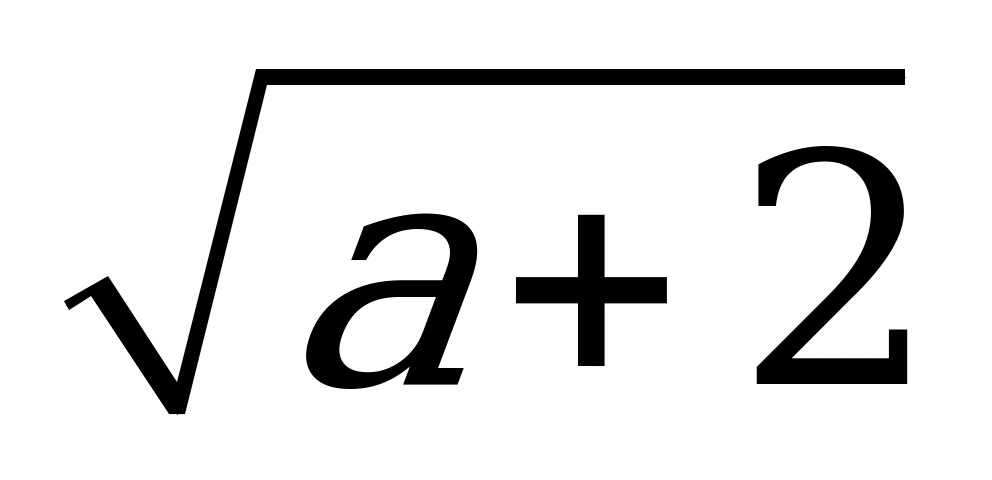 B) a – 2 C) B) a – 2 C) 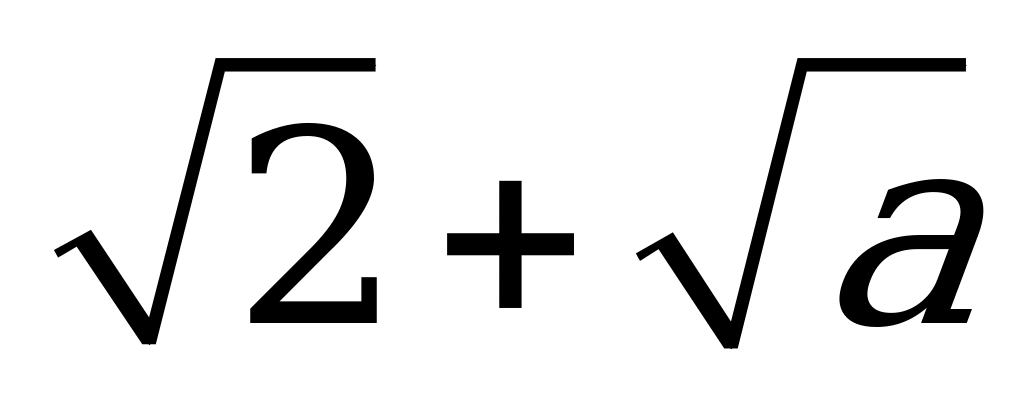 D) a + 2 E) D) a + 2 E) 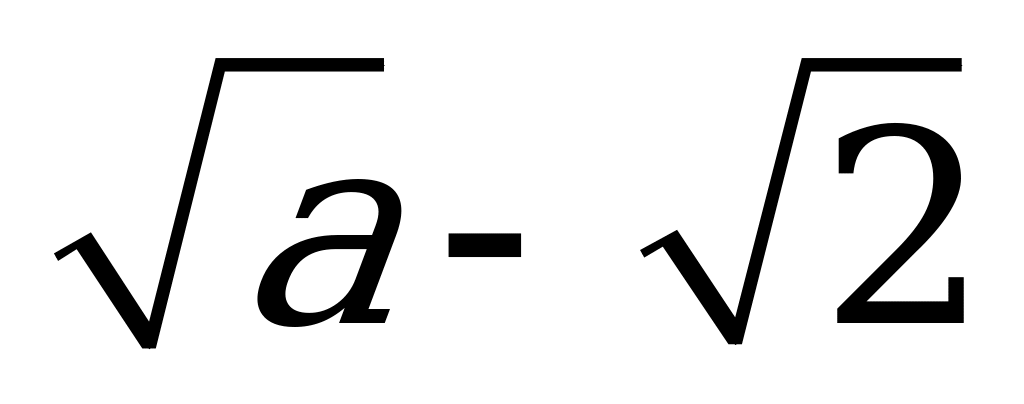 | A |
| В3.5 Выразите 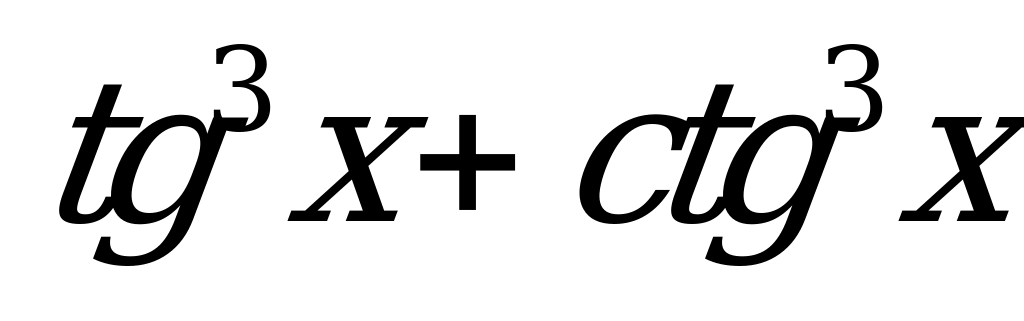 через p, если через p, если 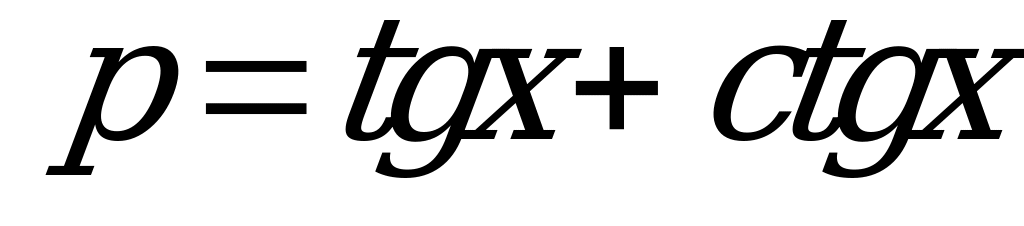 A) -p3 - 3p B) p3 - 3p C) p3 + 3p D) 3p - p3 E) 3p3 - p | B |
| В3.6 Найдите 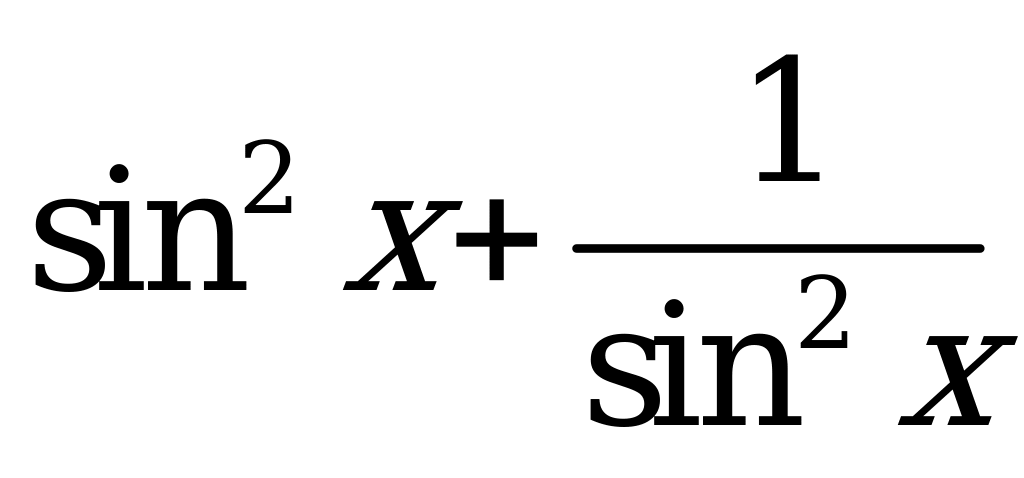 , если , если 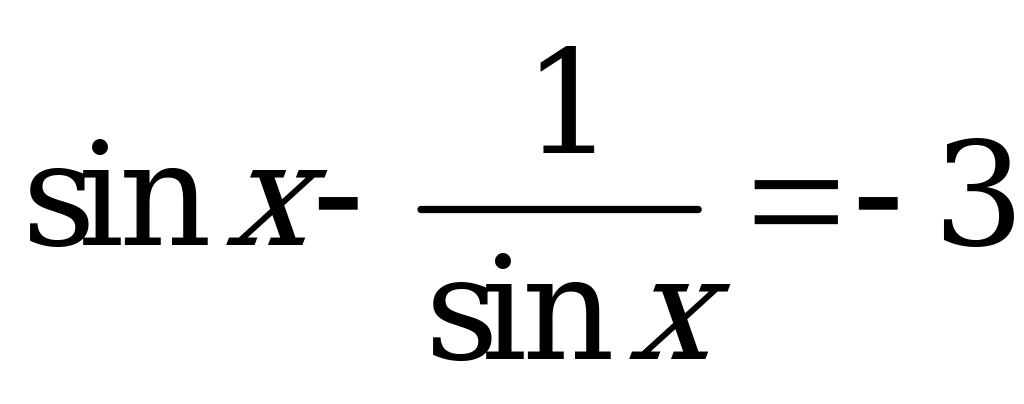 A) 7 B) 8 C) 9 D) 11 E) 6 | D |
| В3.7 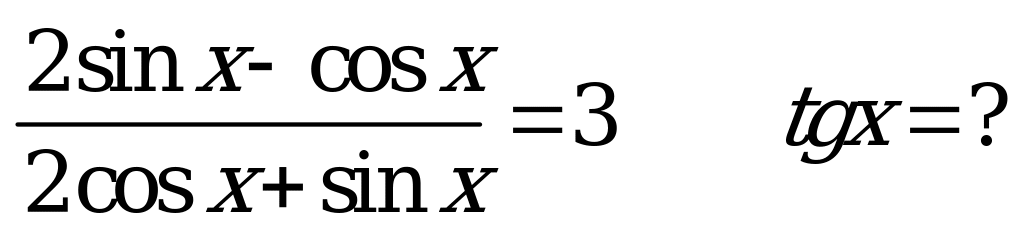 A) 7 B) -3 C) 3 D) -7 E) 2 | D |
| В3.8 Если 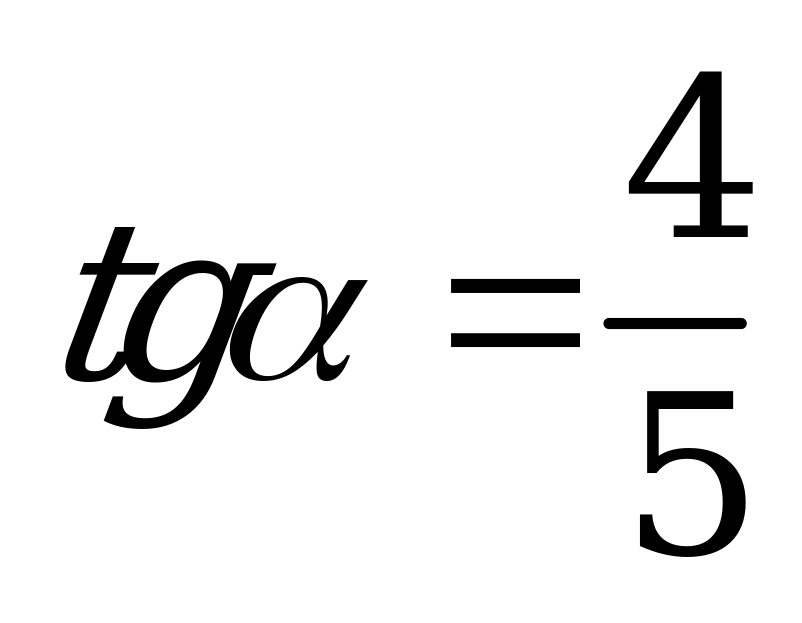 , найти , найти 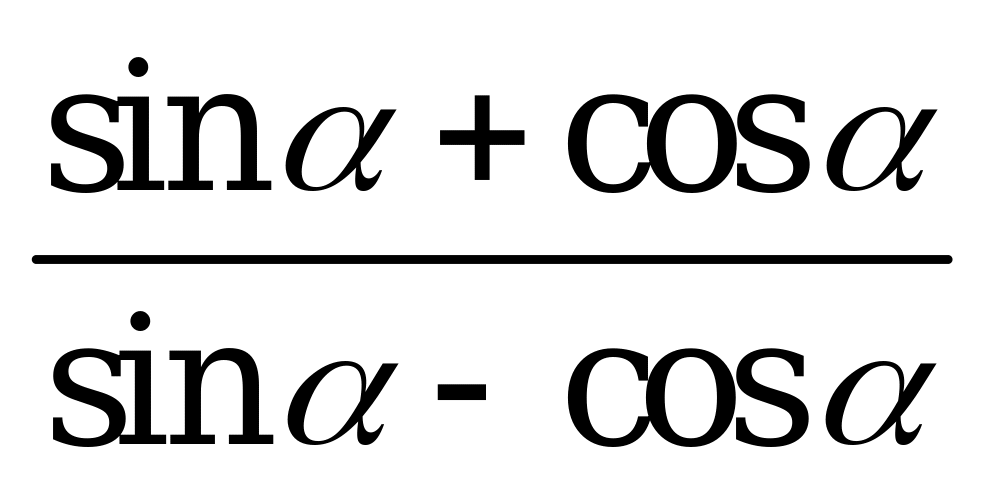 A) -3 B) 3 C) -9 D) 9 E) 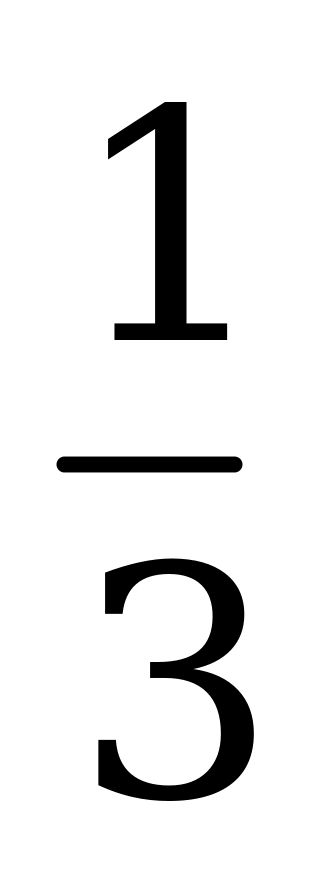 | C |
| В3.9 Найдите 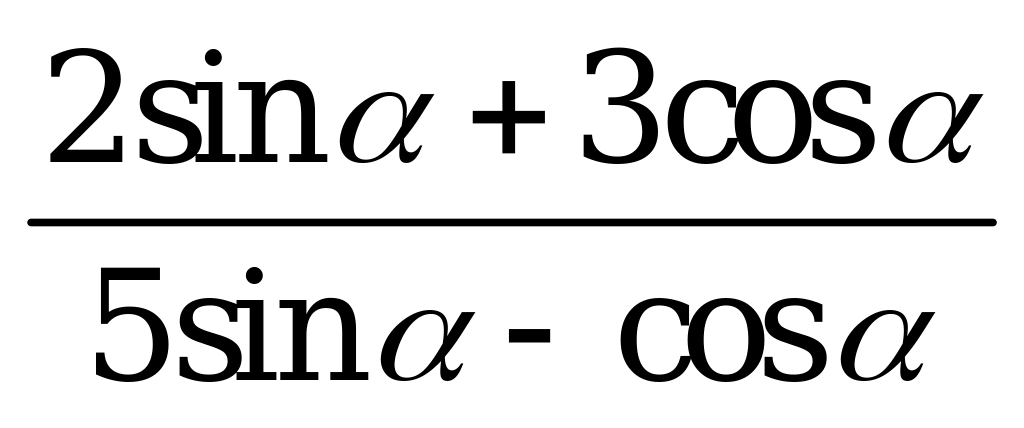 , если , если 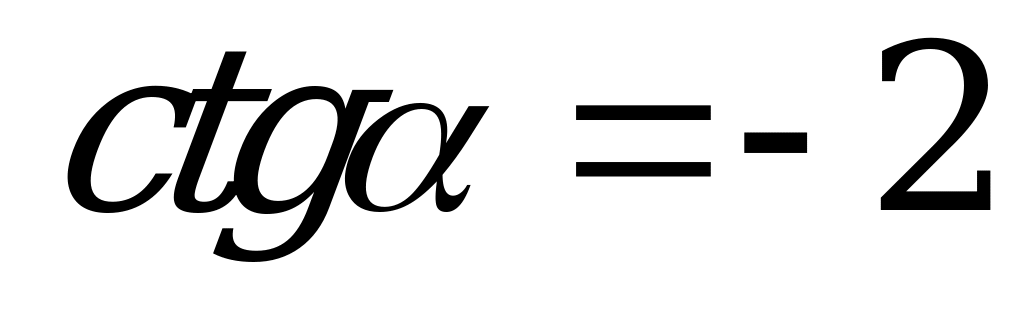 A) 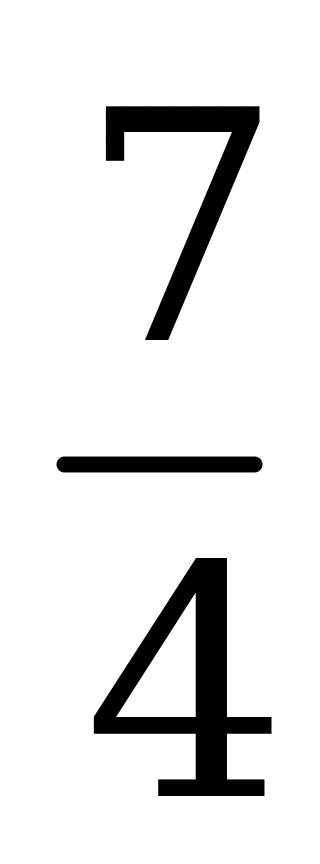 B) - B) -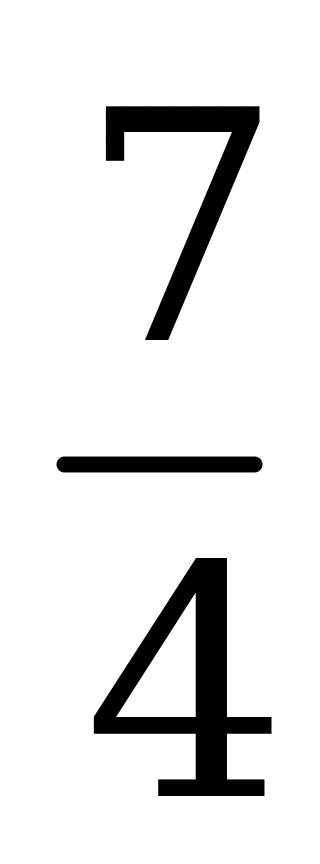 C) C)  D) D)  E) - E) -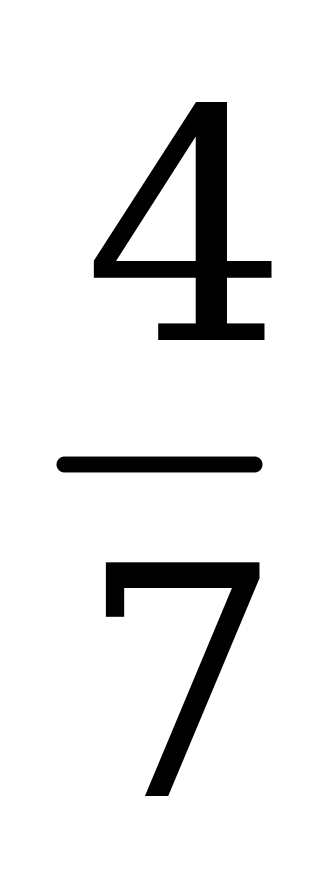 | E |
| В3.10 Вычислите 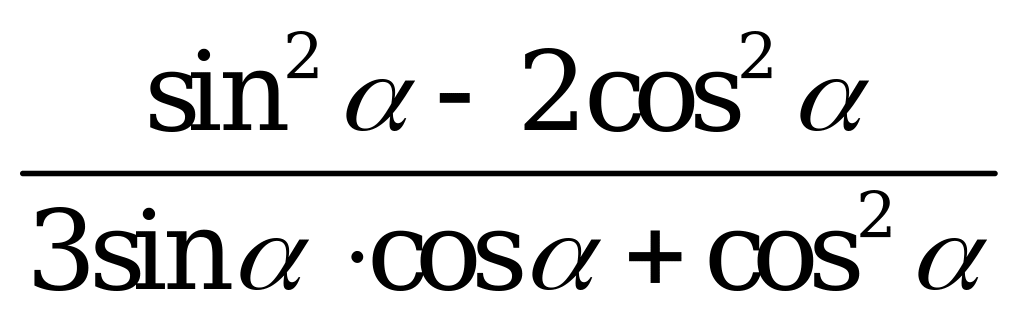 , если , если 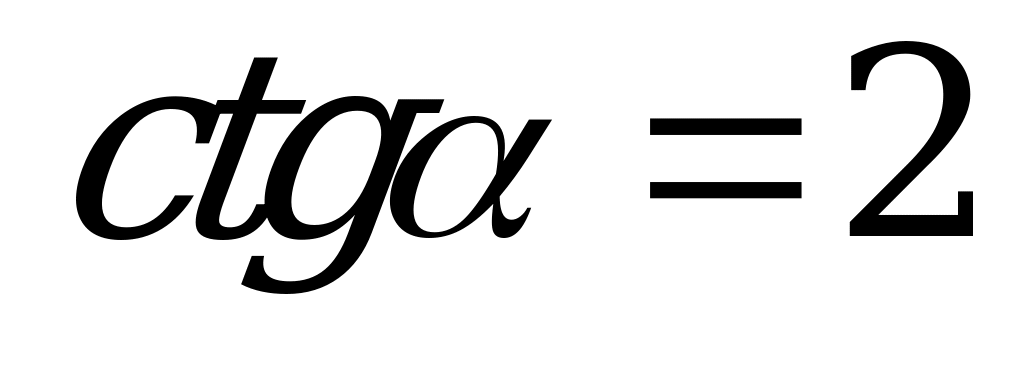 . . A) –0,7 B) -0,5 C) 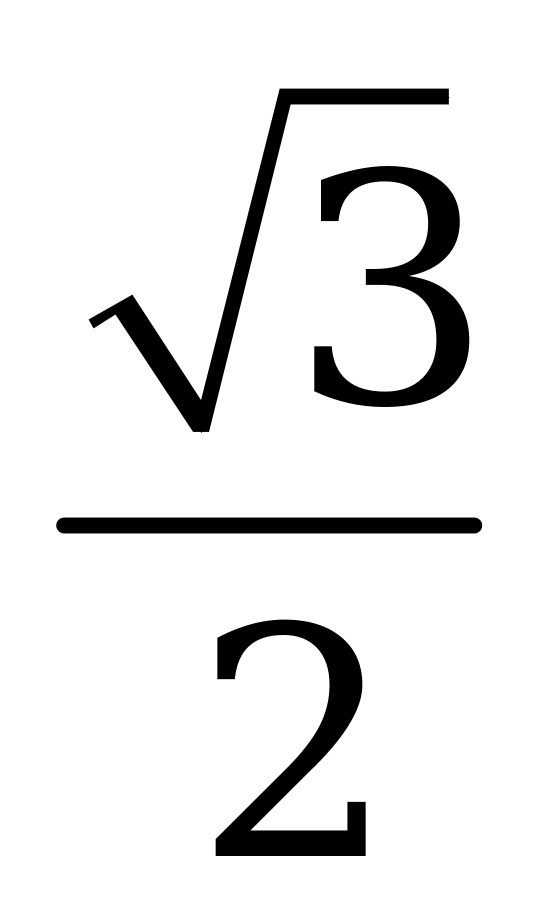 D) - D) -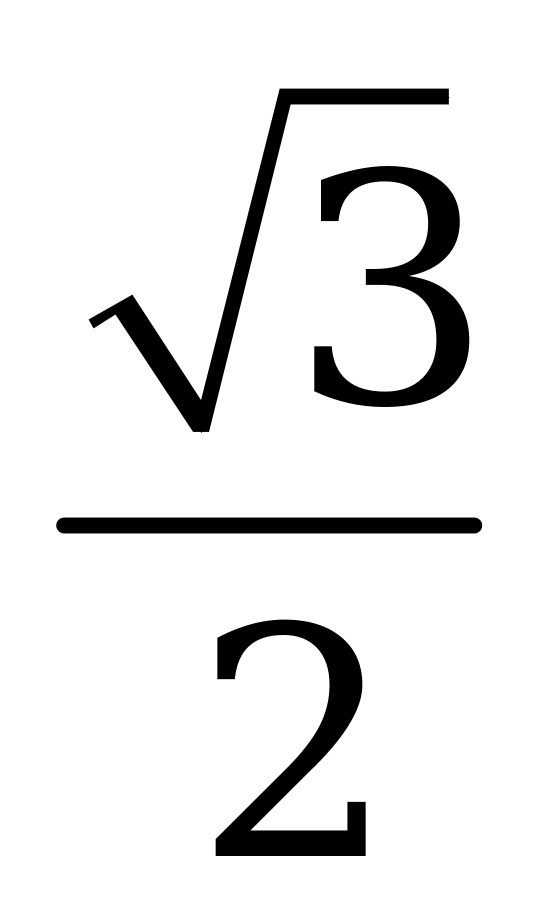 E) - E) -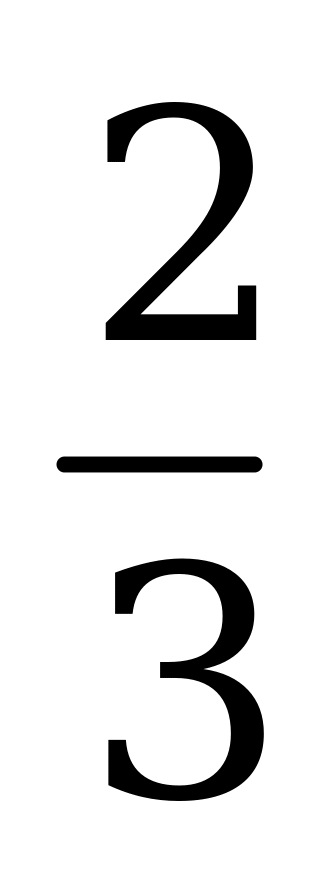 | A |
| В4. Множество значений тригонометрических выражений | Ответы |
| В4.1 Если  - переменная величина, то чему равно наибольшее значение выражения - переменная величина, то чему равно наибольшее значение выражения 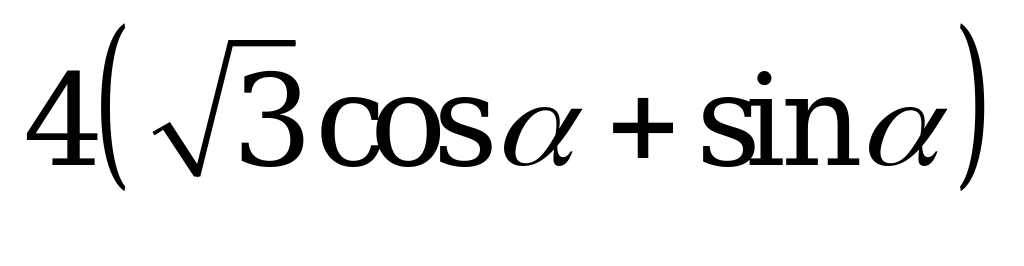 ? ? A) 9,5 B) 7 C) 8 D) 6,5 E) 7,5 | C |
| В4.2 Чему равно наименьшее значение выражения 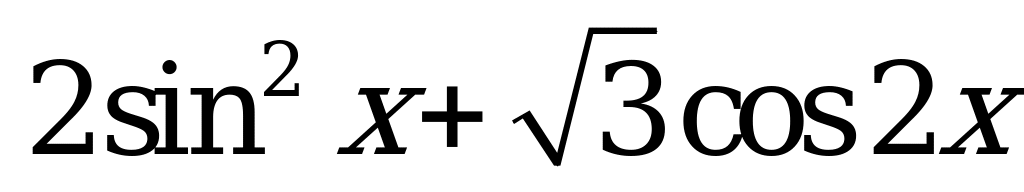 ? ? A) -1 B) 1 C) 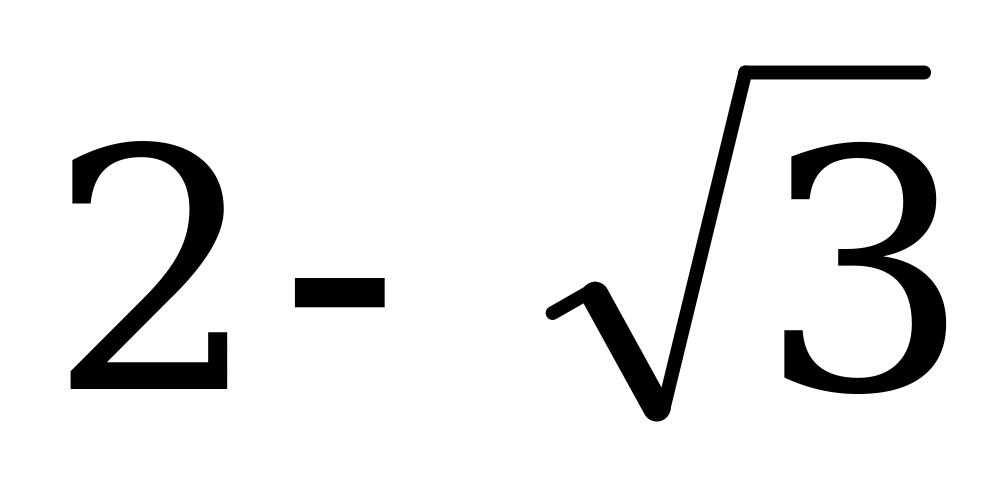 D) D) 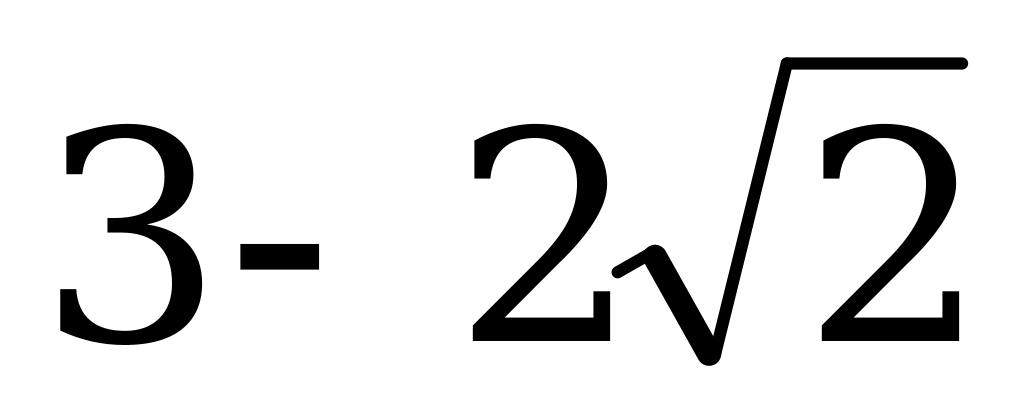 E) E) 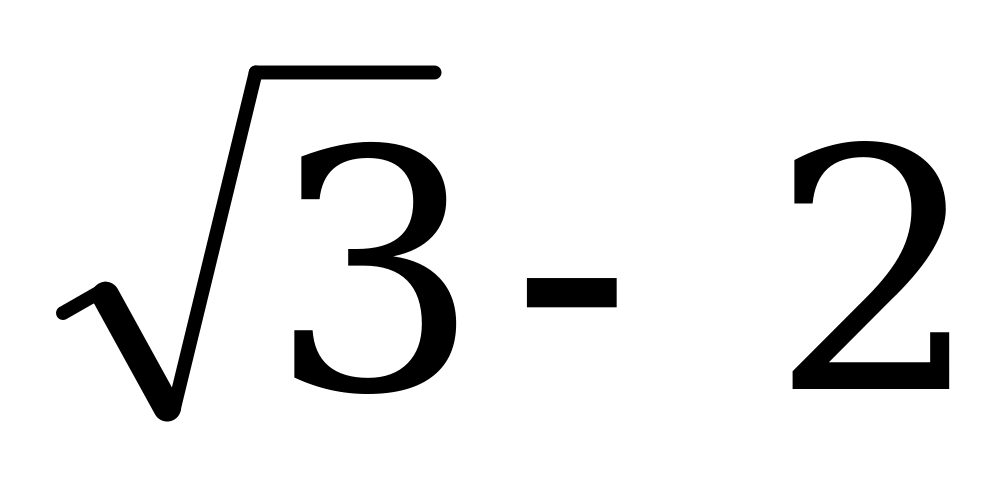 | C |
| В4.3 Найдите наибольшее значение выражения 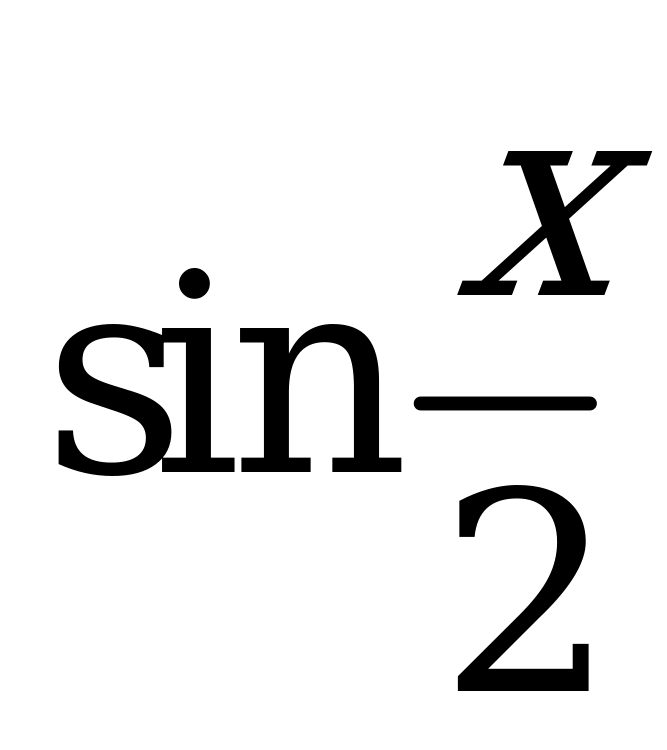 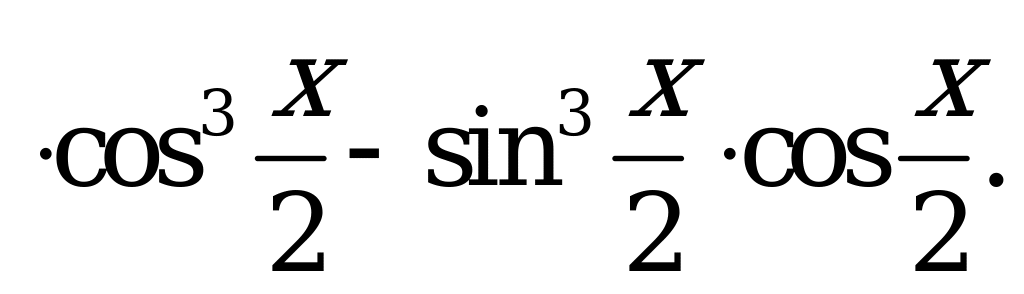 A) 1 B) 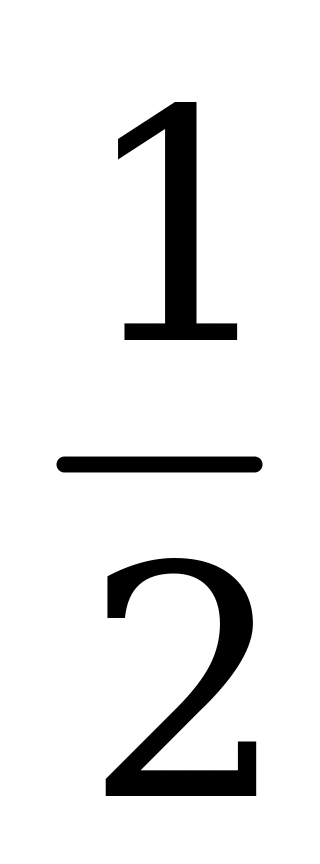 C) 2 D) C) 2 D) 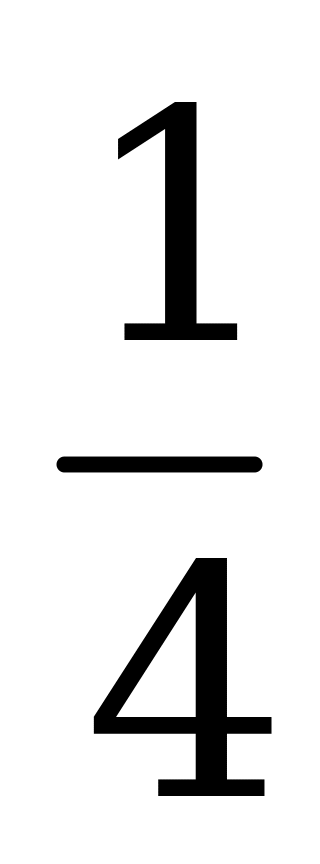 E) E) 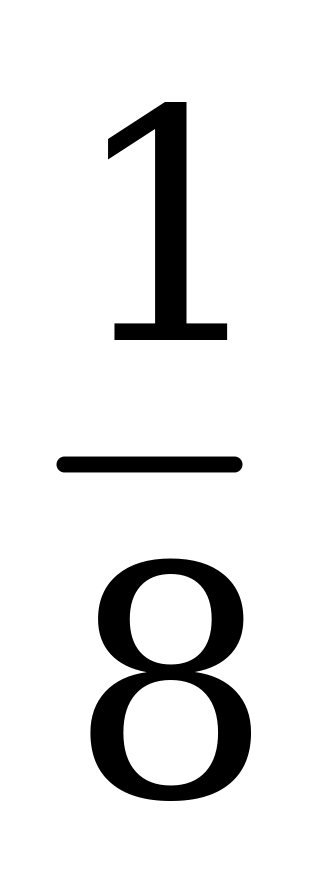 | D |
| В4.4 Сколько простых чисел содержится в области значений функции 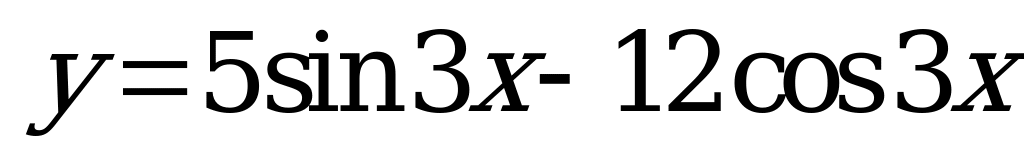 ? ? A) 12 B) 14 C) 6 D) 7 E) 3 | C |
| В4.5 Какое наименьшее значение может принимать выражение 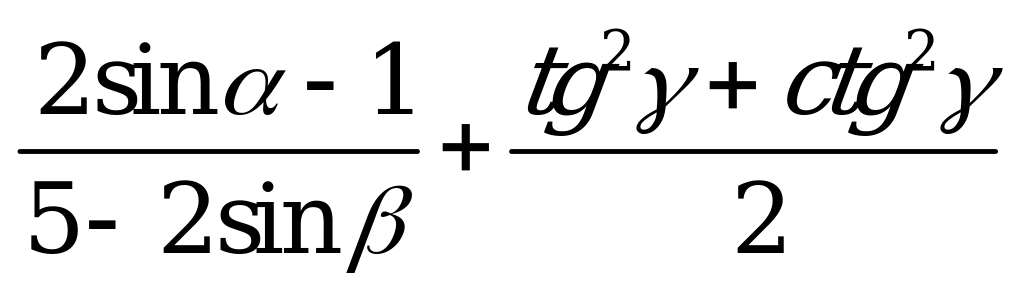 A) 0 B) 1 C) -1 D) 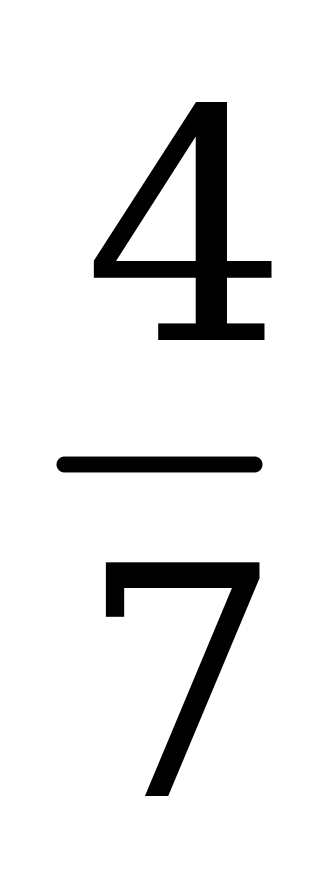 E) невозможно определить E) невозможно определить | A |
| В4.6 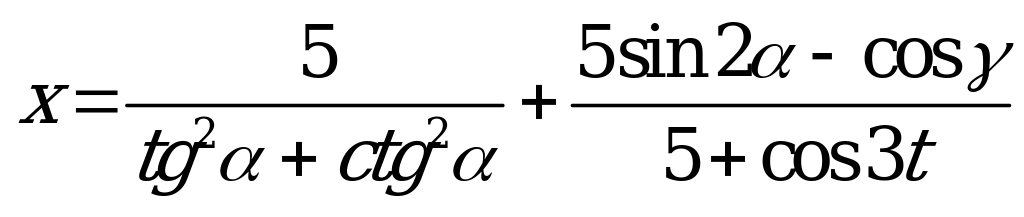 Чему равно наибольшее значение выражения x ? A) 5 B) 2 C) 3 D) 6 E) 4 | E |
| В4.7 Найдите число простых чисел, принадлежащих области значений функции 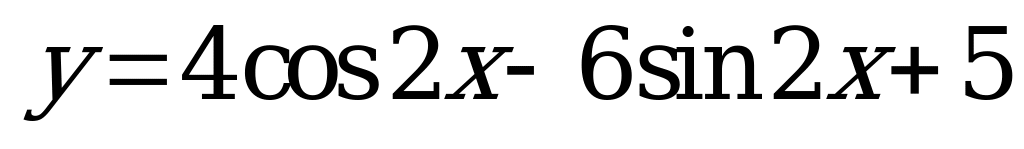 . . A) 2 B) 4 C) 5 D) 6 E) 7 | C |
| В4.8 Найдите область значений функции 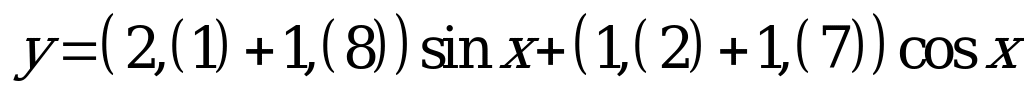 . . A) [-5; 5] B) [-4; 4] C) [-3; 3] D) (-4; 4) E) (-5; 5) | A |
| В4.9 Найдите область значений функции 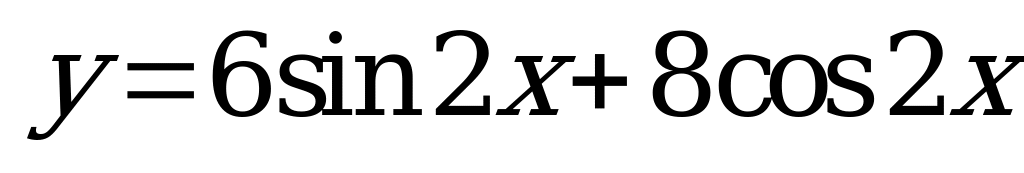 . . A) [-10; 10] B) [-14; 14] C)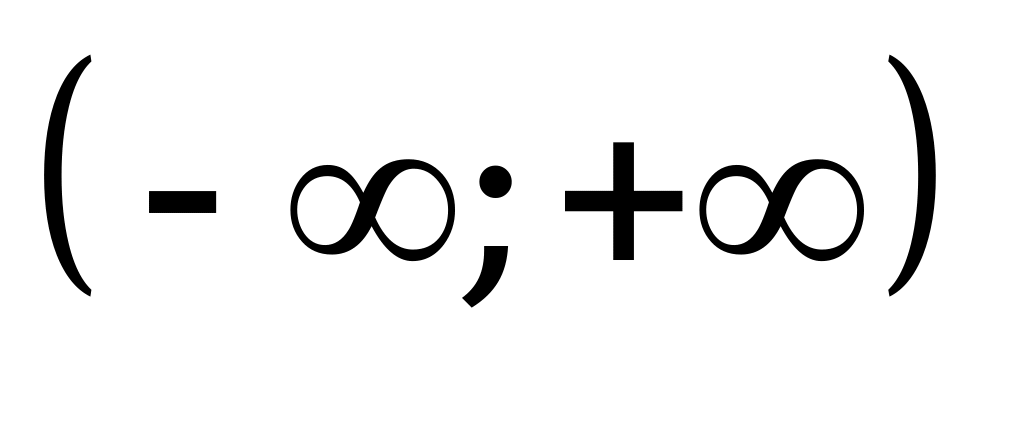 D) [0; 6] E) [0; 8] D) [0; 6] E) [0; 8] | A |
| В4.10 Найдите наименьшее значение функции  . . A) -14 B) -21 C) -64 D) -128 E) -37 | D |
| В5. Период тригонометрических функций | Ответы |
| В5.1 Какая из нижеследующих функций имеет наименьший положительный период? A) 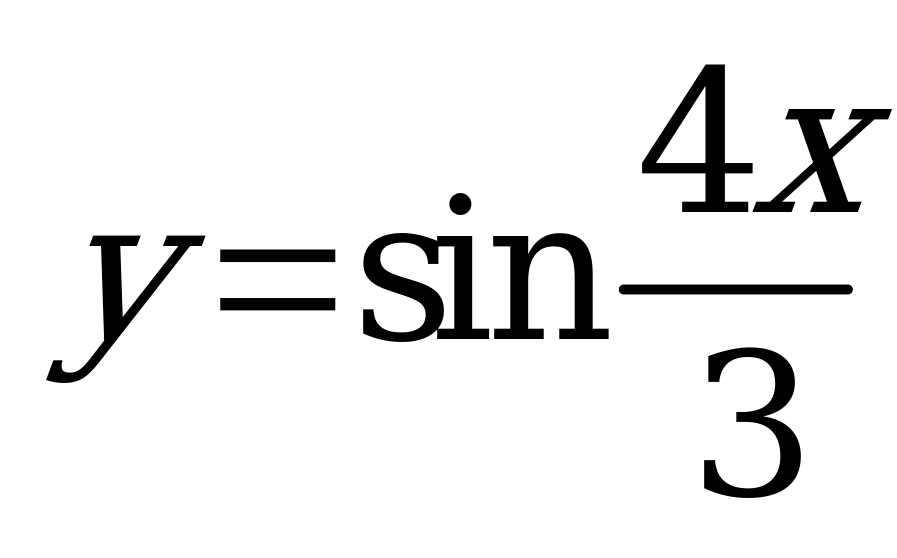 B) B) 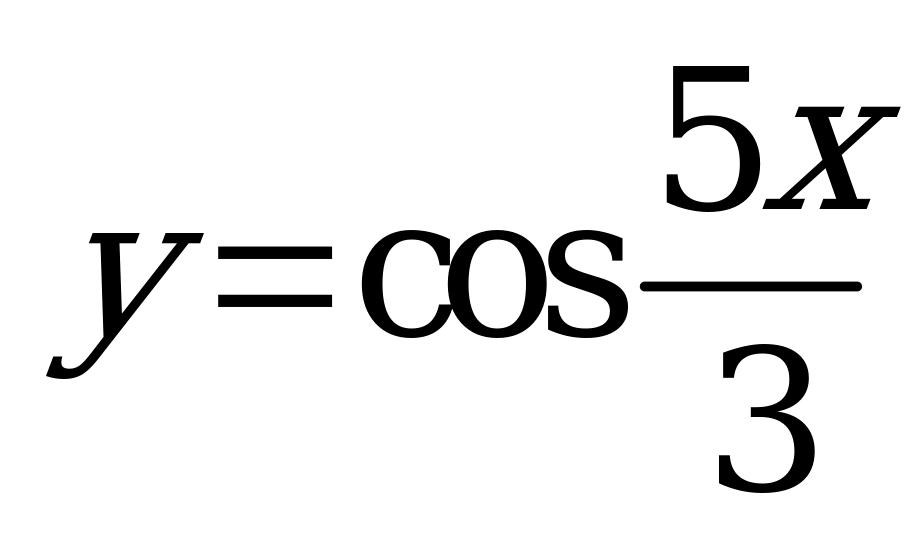 C) C) 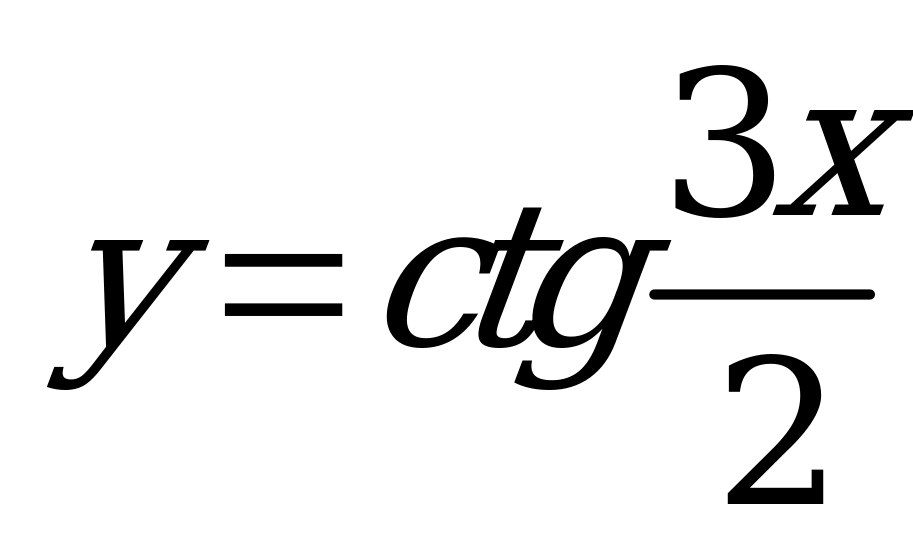 D) 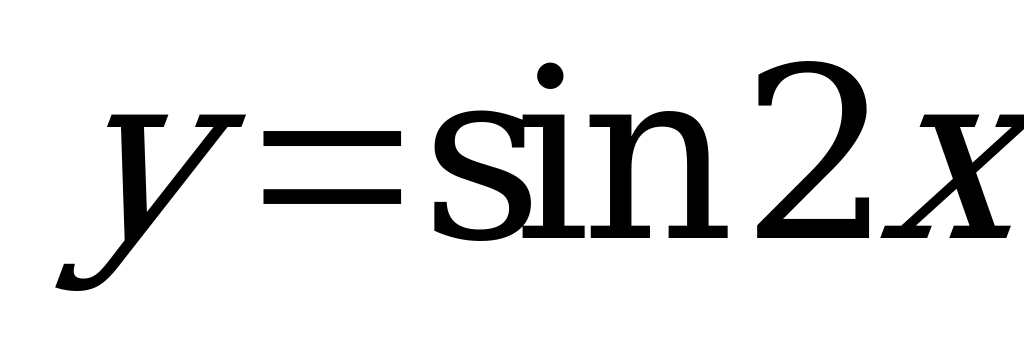 E) E) 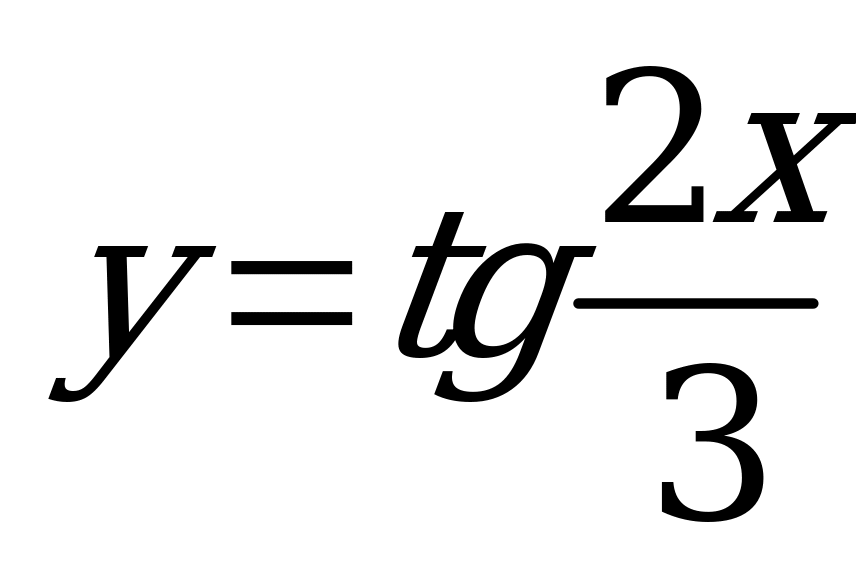 | C |
| В5.2 Найдите наименьший положительный период функции 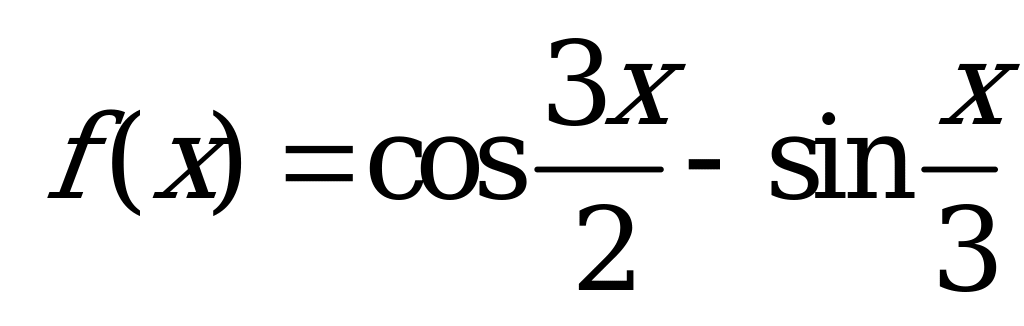 A) 6 B) 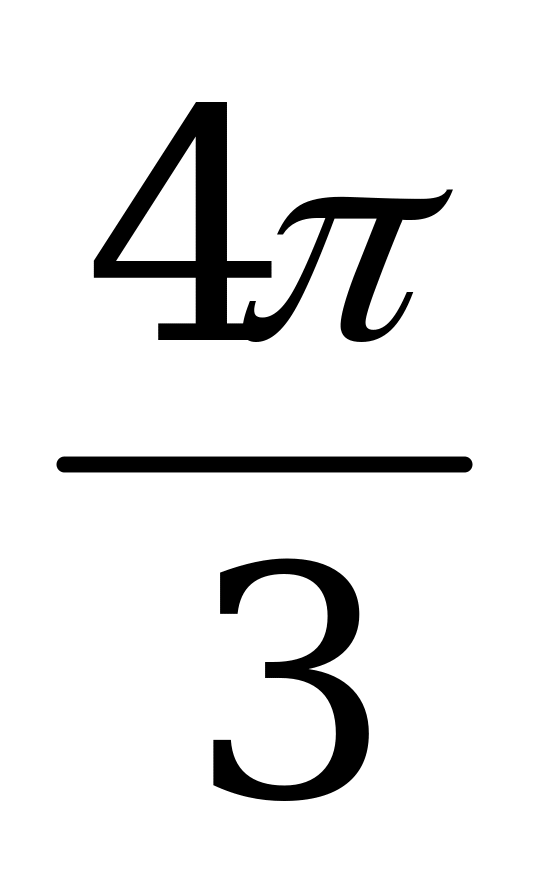 C) 8 D) 10 E) 12 C) 8 D) 10 E) 12 | E |
| В5.3 Чему равен наименьший положительный период функции 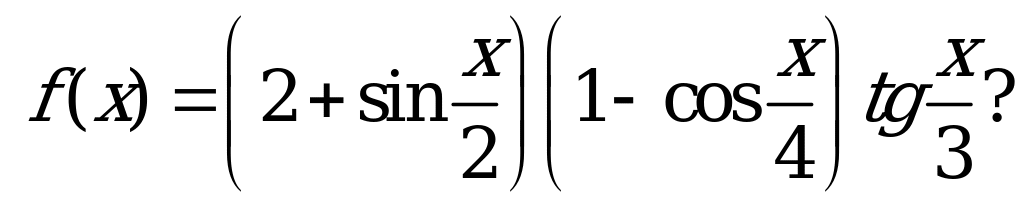 A) 22 B) 28 C) 26 D) 30 E) 24 | E |
| В5.4 Укажите наименьший положительный период функции 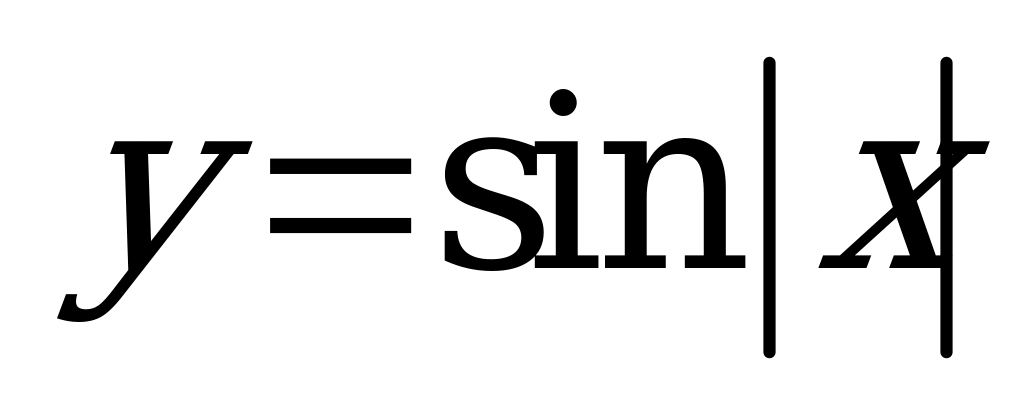 A)  B) B)  C) непериодическая D) C) непериодическая D) 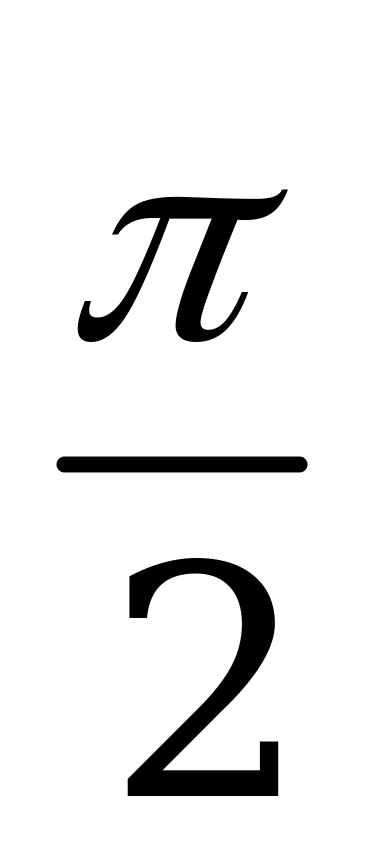 E) 3 E) 3 | C |
| В5.5 Какая функция непериодическая: 1) 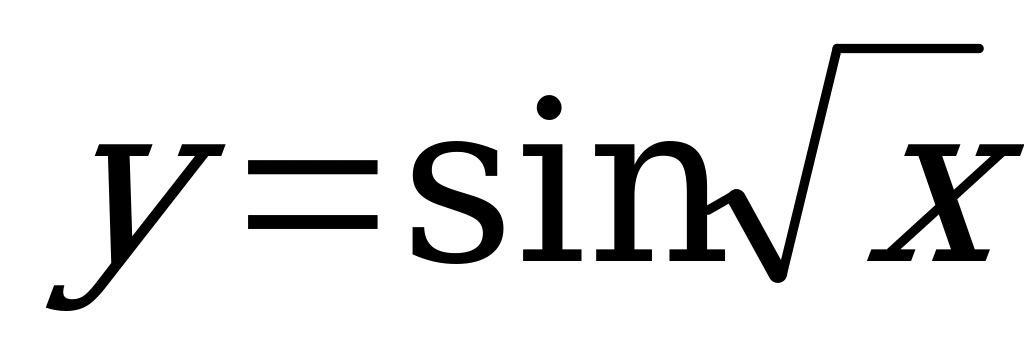 ; 2) ; 2) 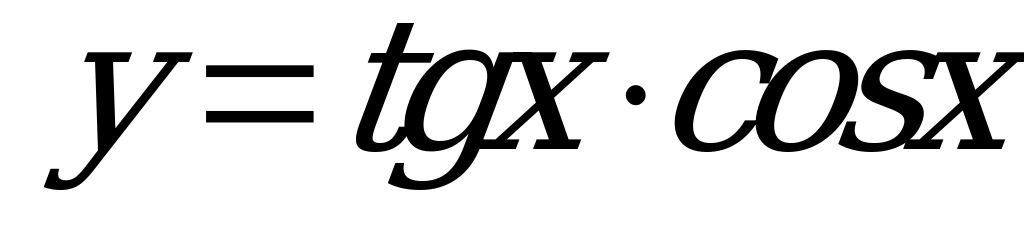 ; 3) ; 3) 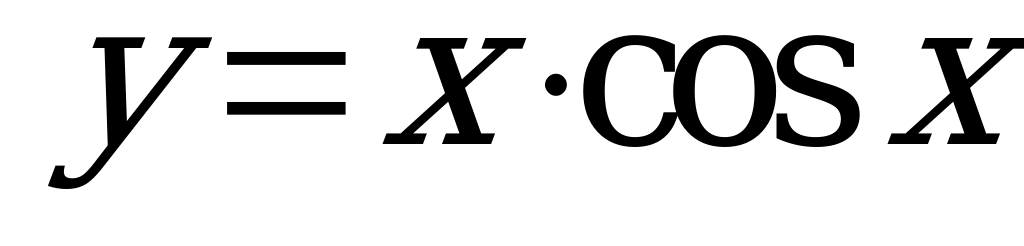 ; 4) y = sin2x + 1? ; 4) y = sin2x + 1? A) 1; 3 B) 1; 2 C) 2; 3 D) 1; 4 E) 3; 4 | A |
| В5.6 Какая функция непериодическая? A) 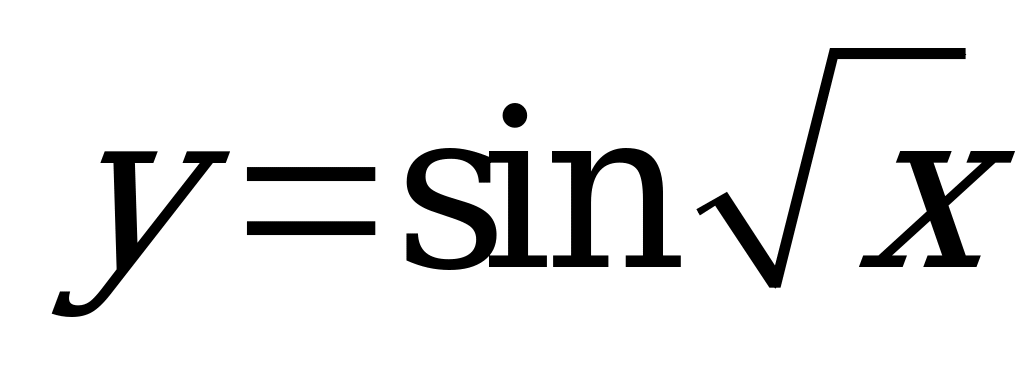 B) B) 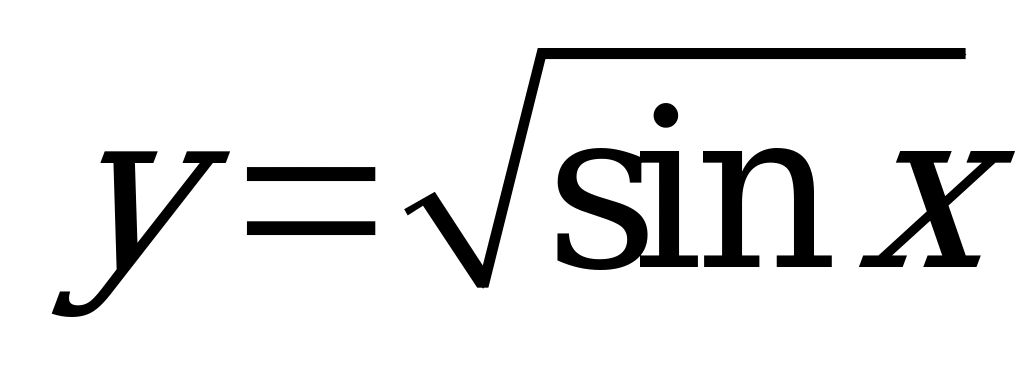 C) C) 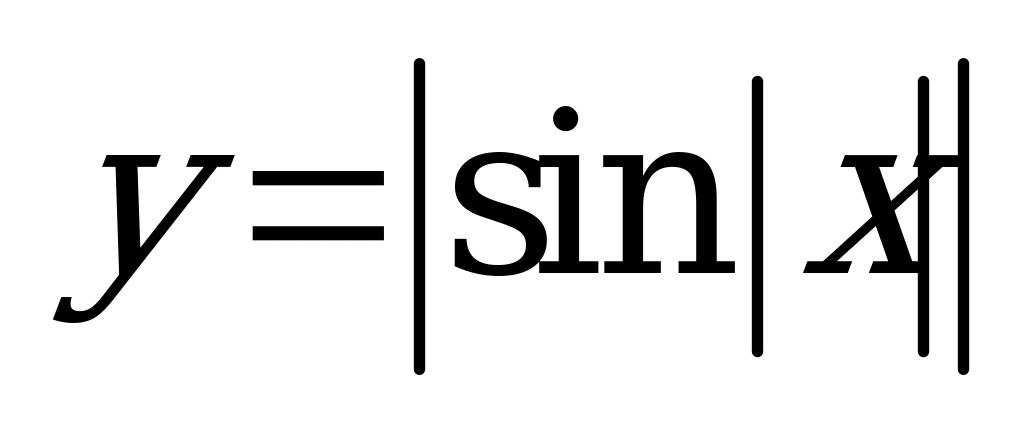 D) 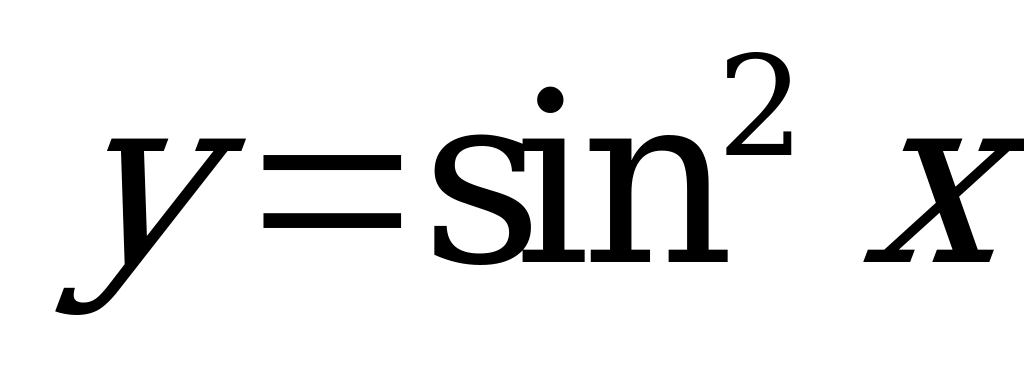 E) E) 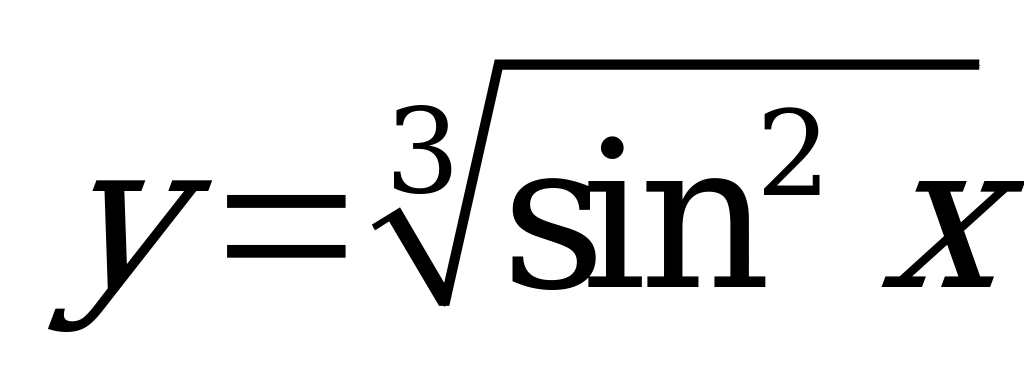 | A |
| В6. Свойства сложных функций | Ответы |
| В6.1 Чему равно наибольшее значение функции 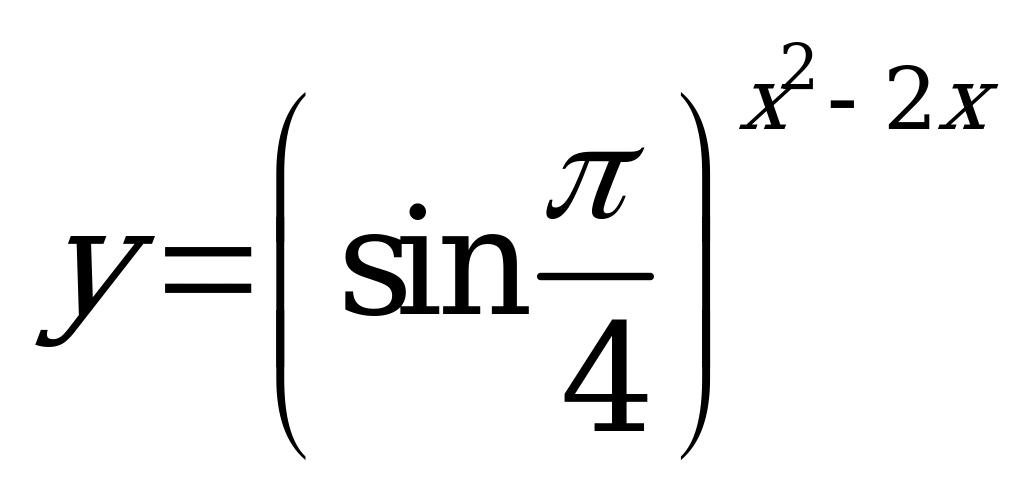 A)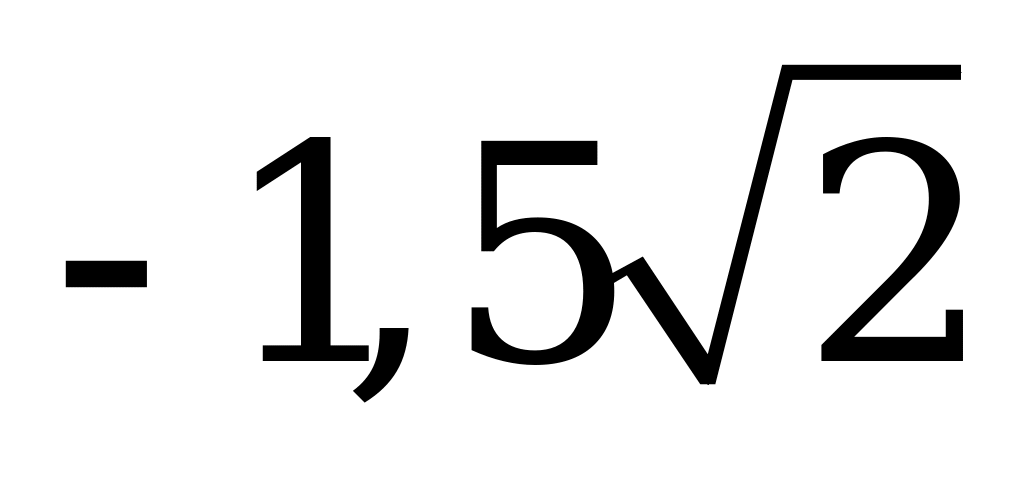 B) B)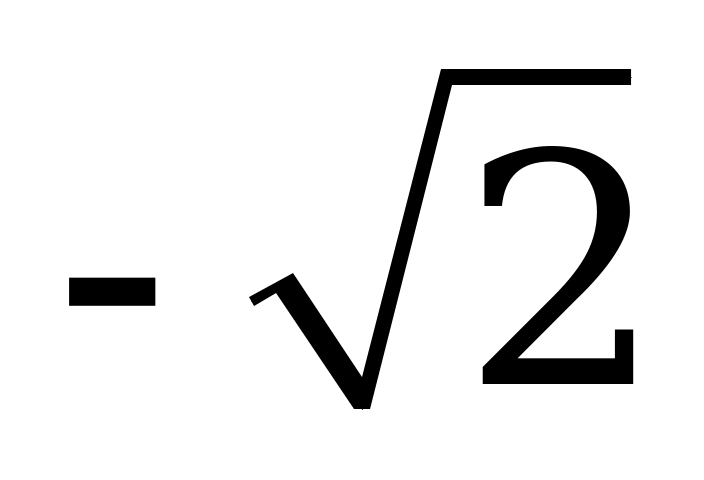 C) C)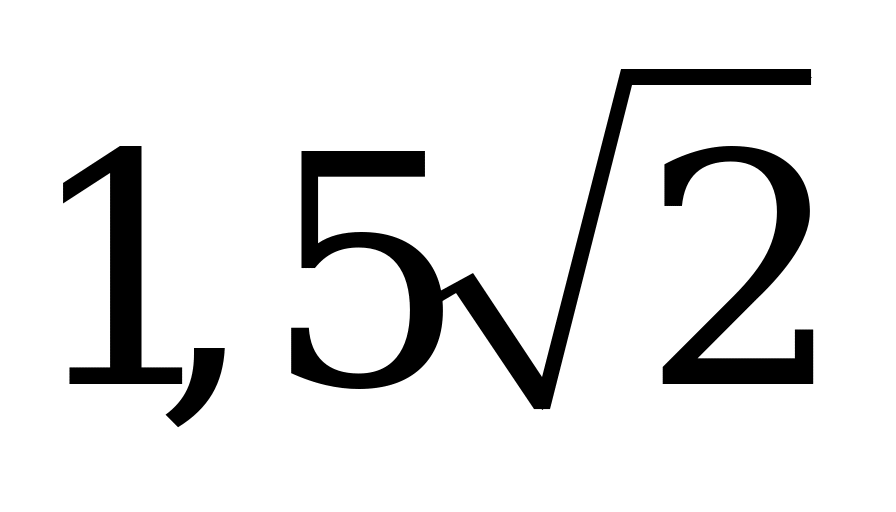 D) D)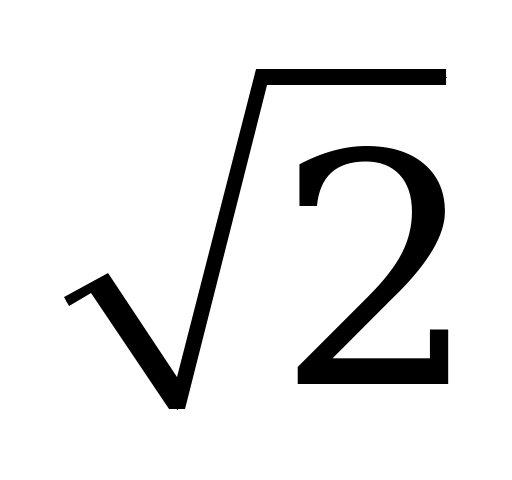 E) E)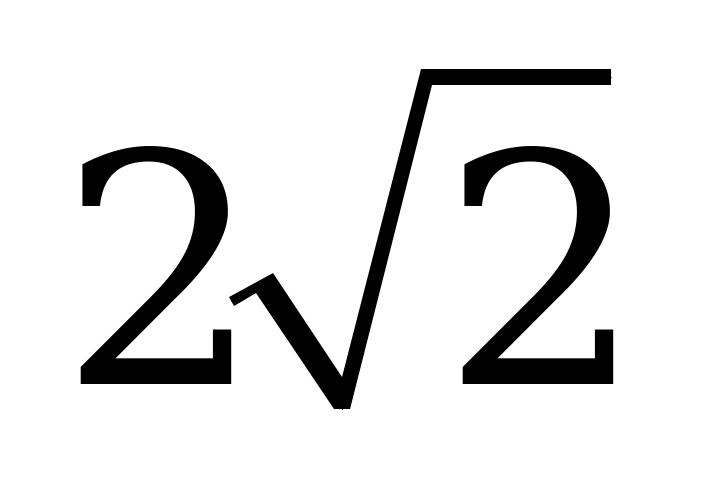 | D |
| В6.2 Найдите область значений функции 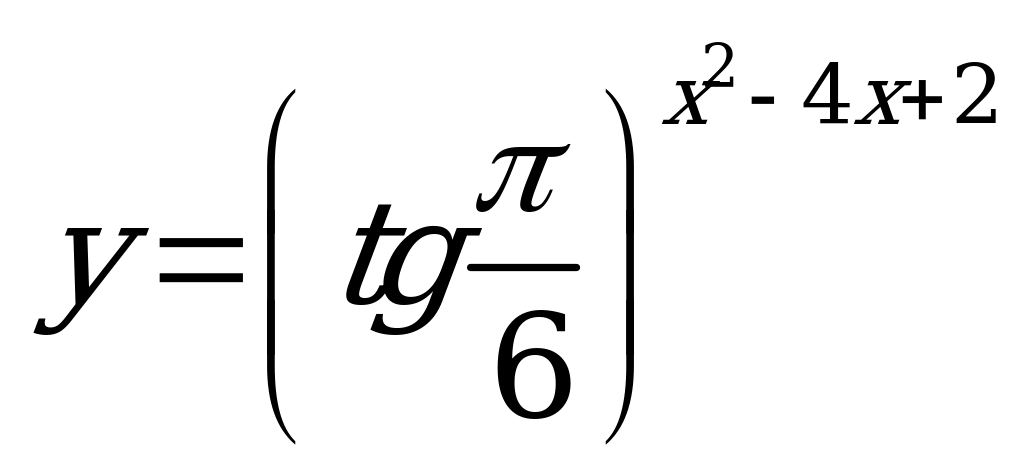 . A) . A)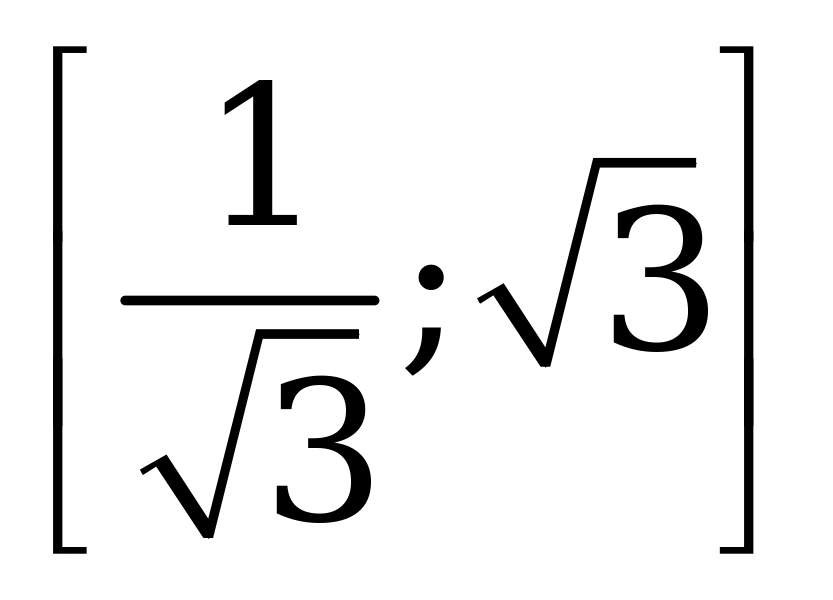 B) (0; B) (0; 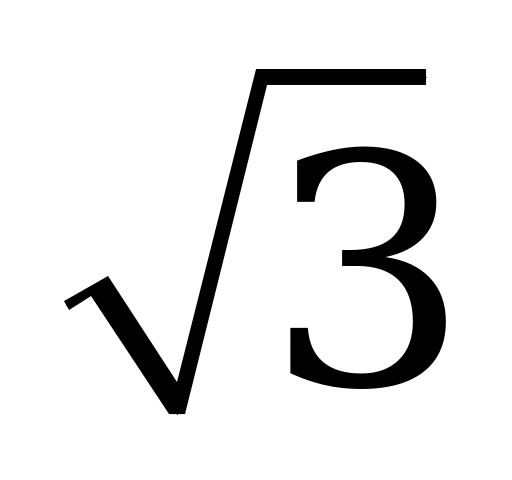 ] ] C) (0; 3] D) (-; 3] E)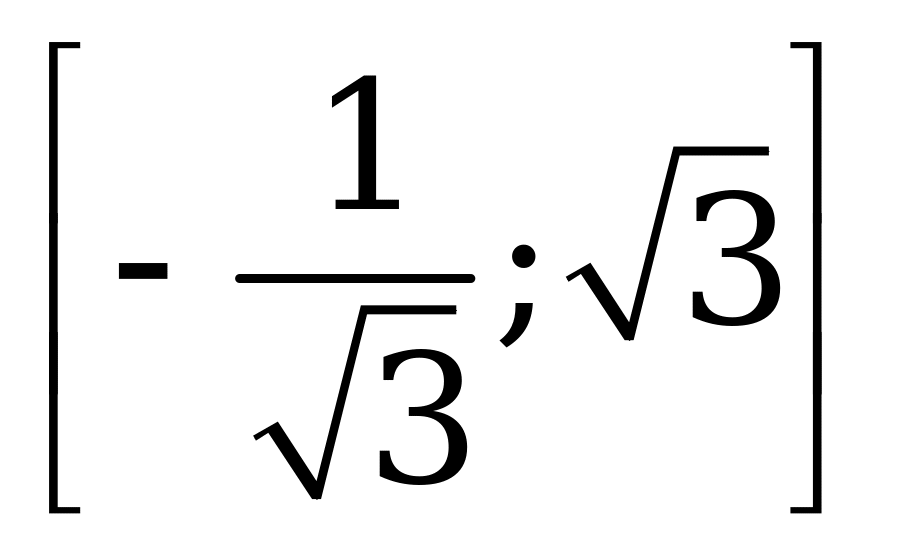 | C |
| В6.3 Найдите наибольшее значение функции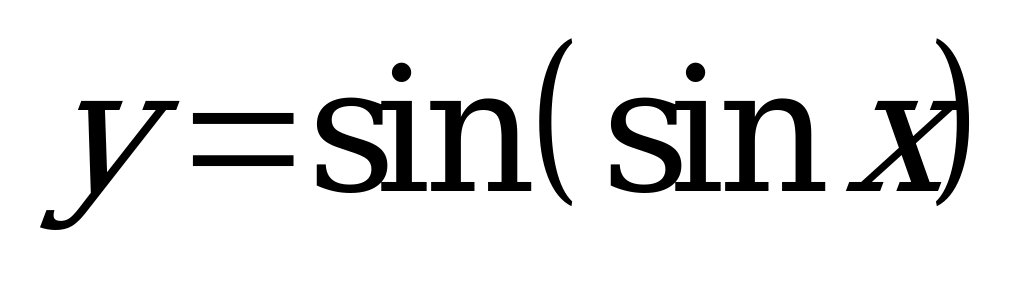 . . A) sin1 B) 1 C) 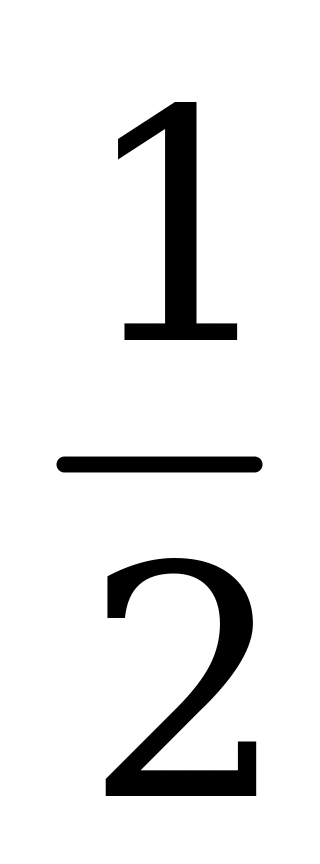 D) 0 E) D) 0 E) 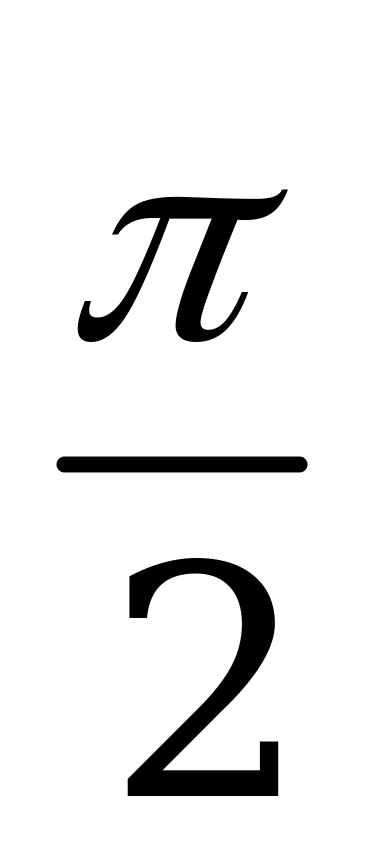 | A |
| В6.4 Какое наибольшее значение может принимать выражение 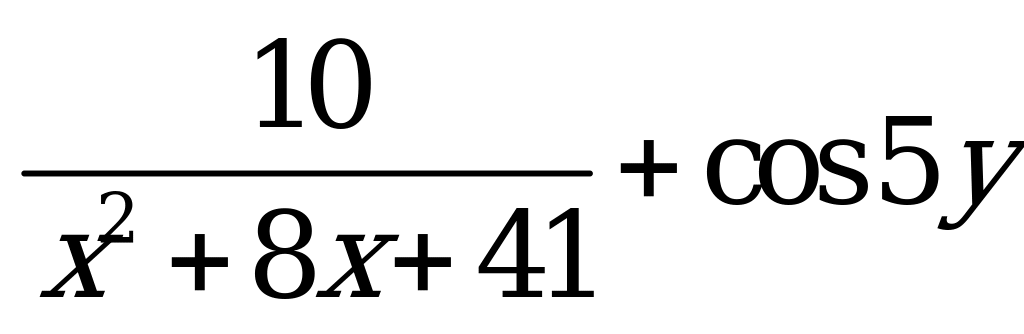 . . A) 1,8 B) 1,5 C) 1,4 D) 2 E) 2,5 | C |
| В6.5 Найдите наибольшее значение 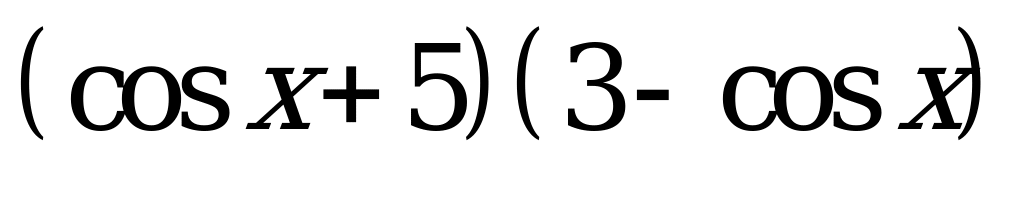 A) 8 B) 12 C) 15 D) 16 E) 24 | D |
| В6.6. Найдите наибольшее значение выражения 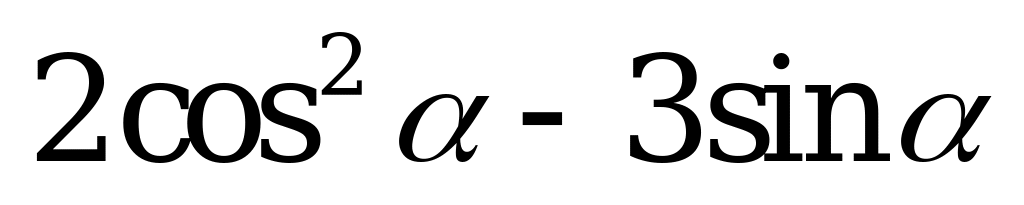 . A) 5 B) 3 C) -3 D) . A) 5 B) 3 C) -3 D) 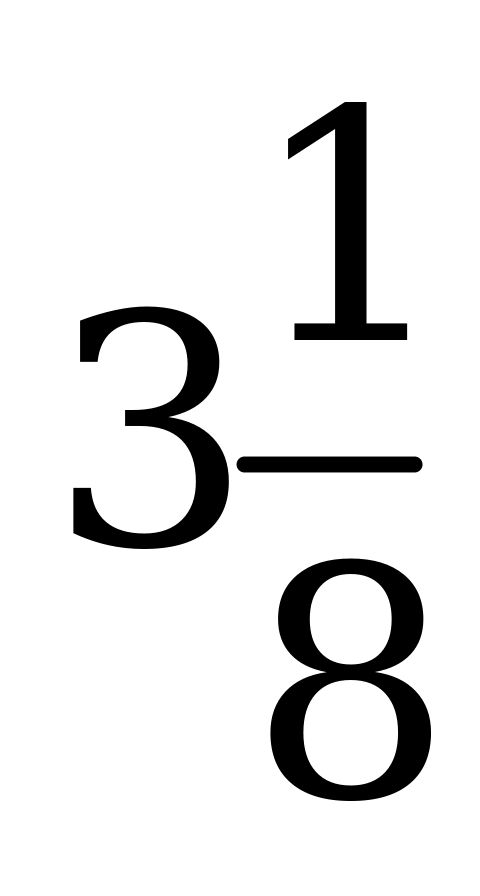 E) 2,5 E) 2,5
| D |
| В6.7 Найдите наименьшее значение функции 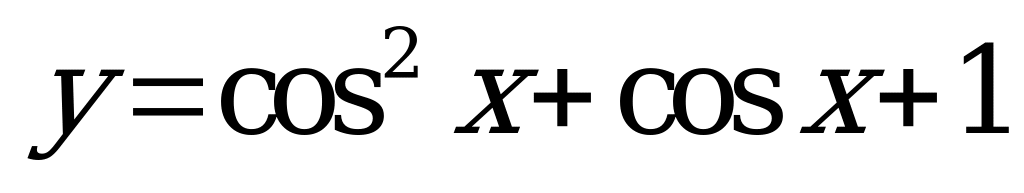 . A) . A) 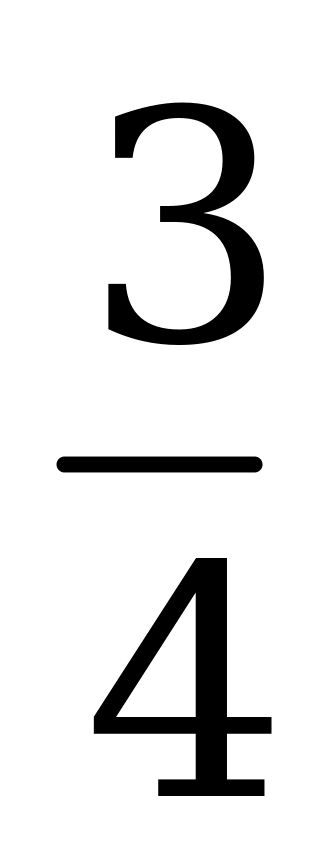 B) B) 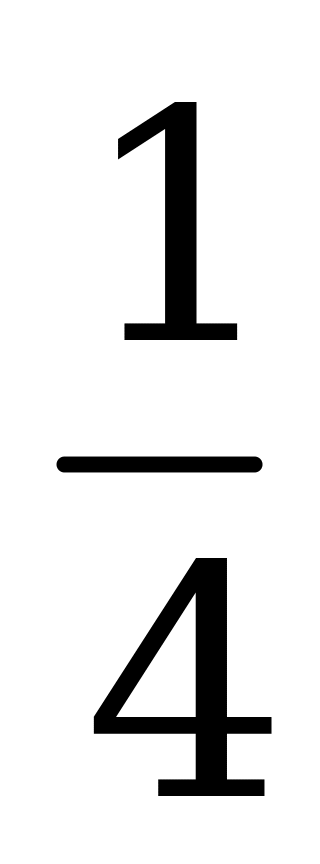 C) C) 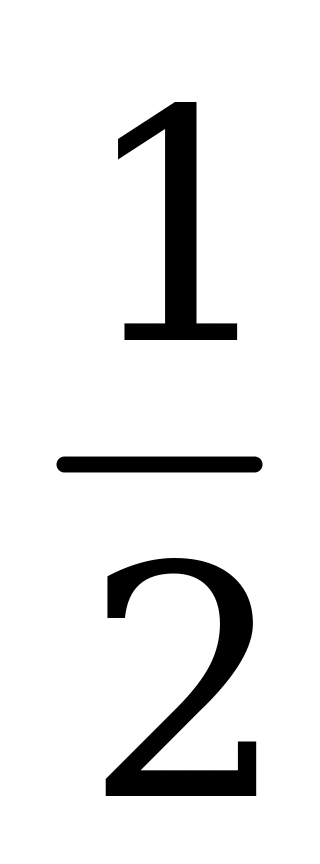 D) D) 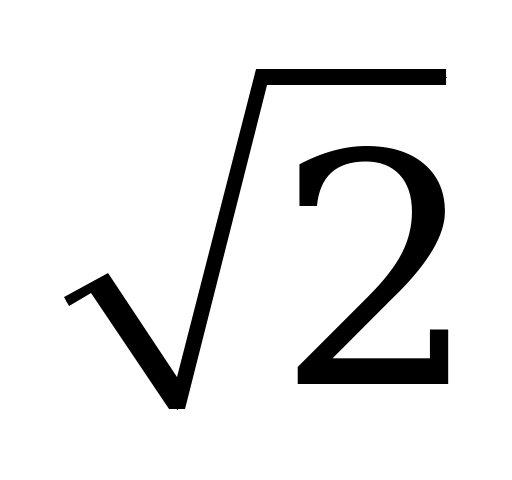 E) E) 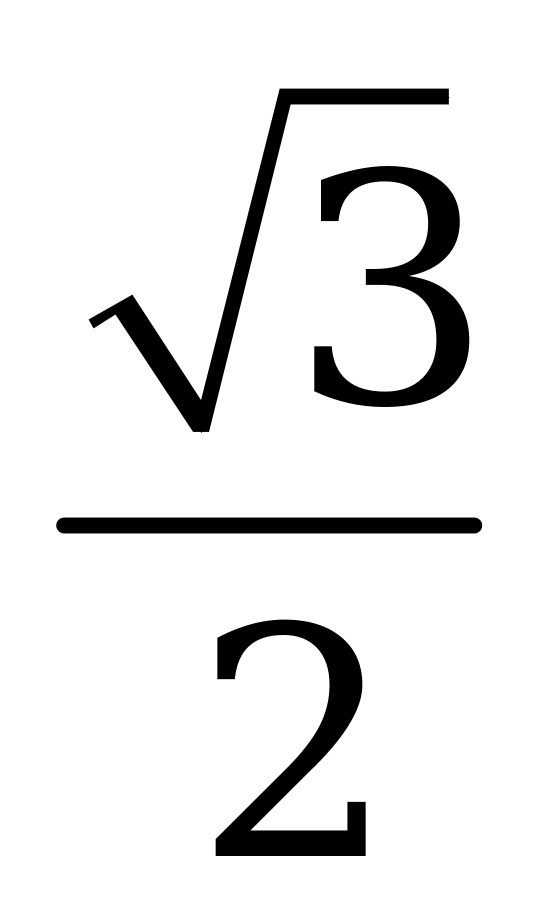 | A |
| В6.8 Найдите наименьшее значение функции 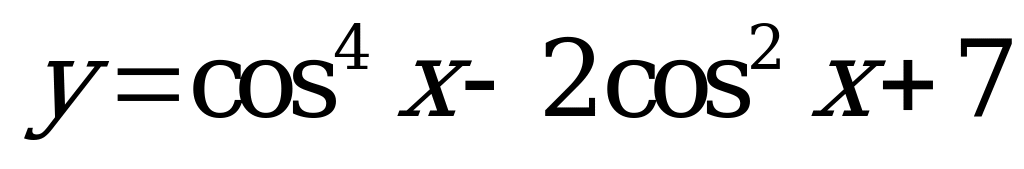 . A) 5 B) 3 C) 2 D 1 E) -5 . A) 5 B) 3 C) 2 D 1 E) -5
| A |
| В6.9 Найдите наименьшее значение функции 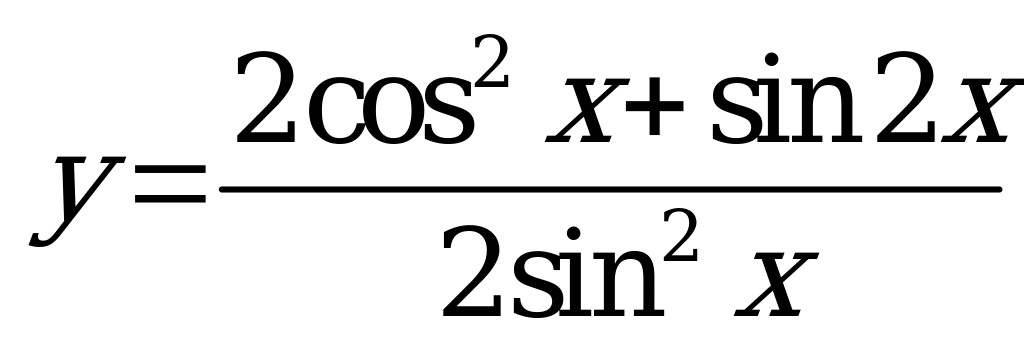 . A) - . A) -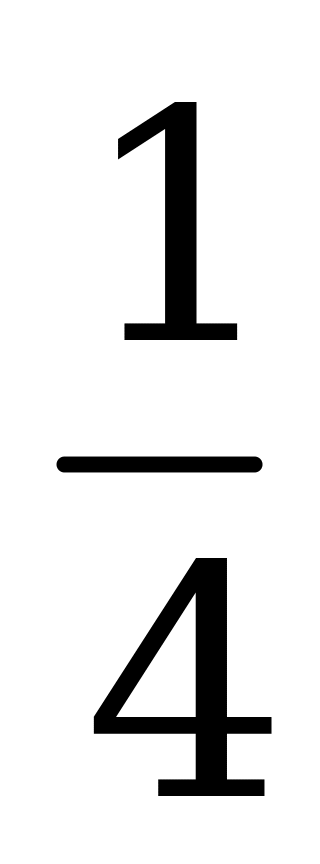 B) B) 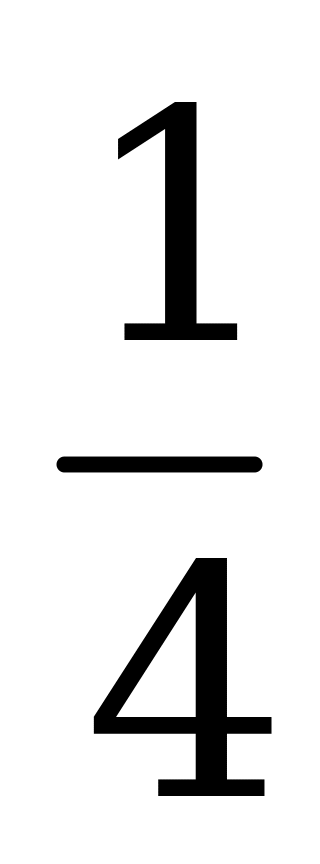 C) C) 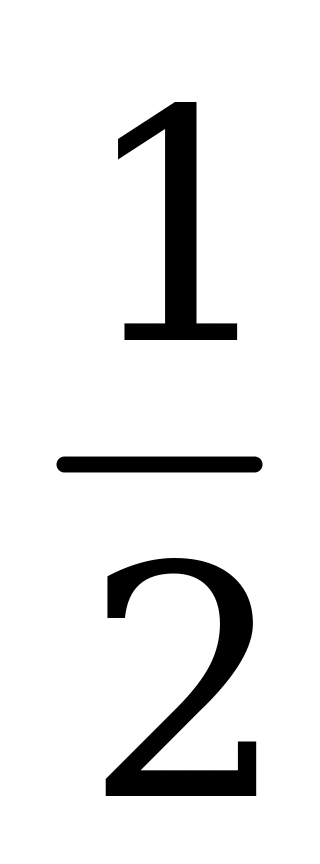 D) - D) -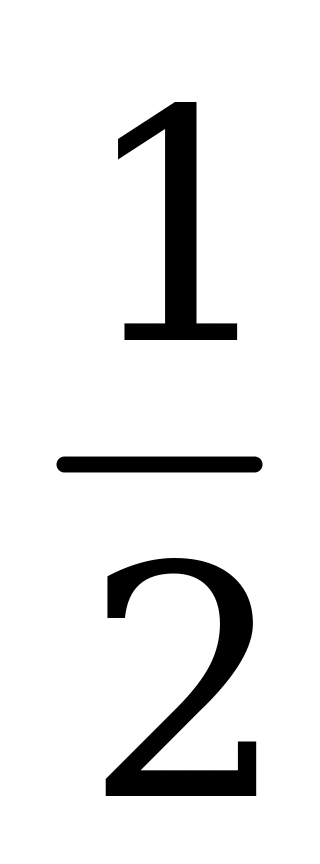 E) 1 E) 1 | A |
| В6.10 Найдите область определения функции 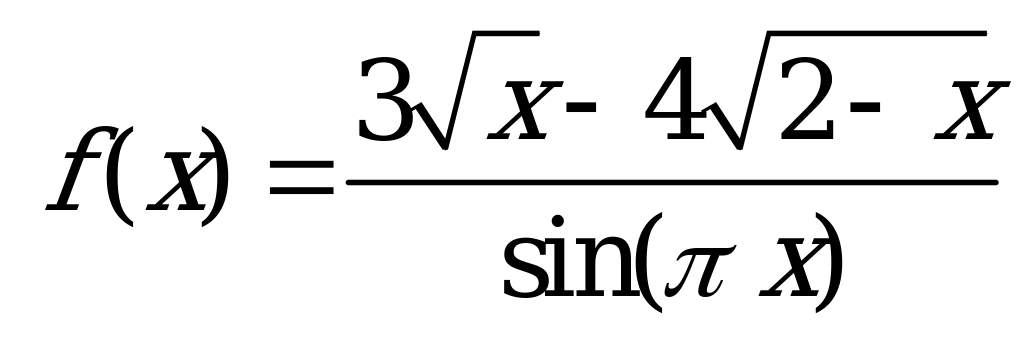 . . A) [0; 2] B) [0; 1) C) (0; 1) (1; 2) D) [0; 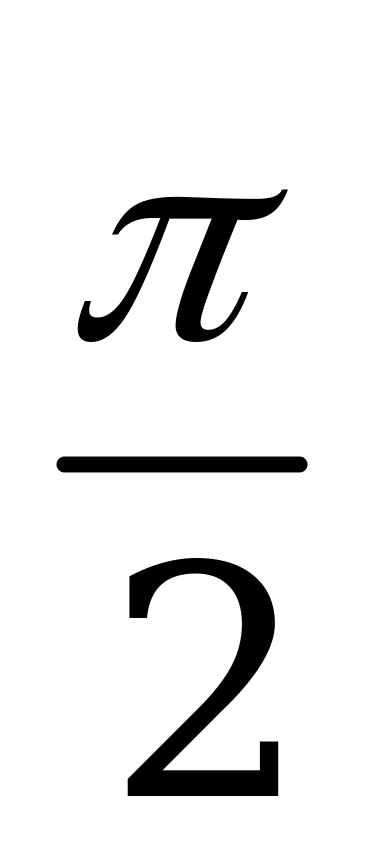 ) ( ) (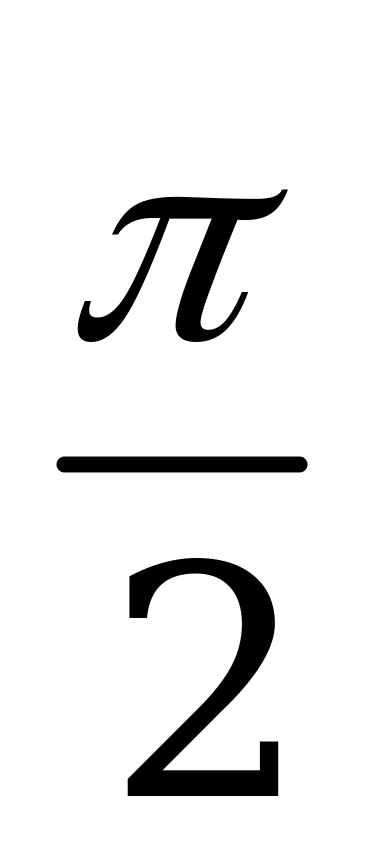 ; 2] E) [0; ; 2] E) [0; 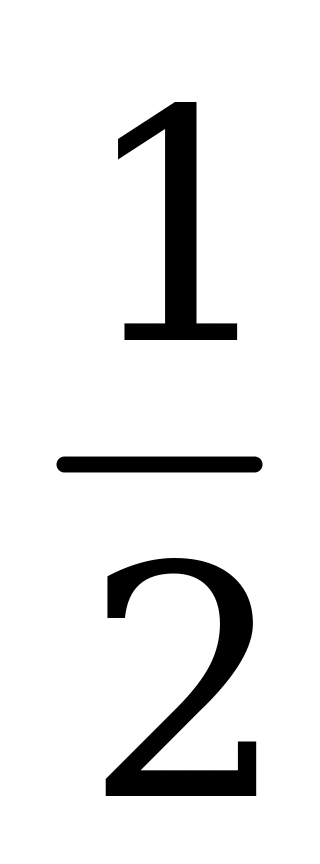 ) ( ) (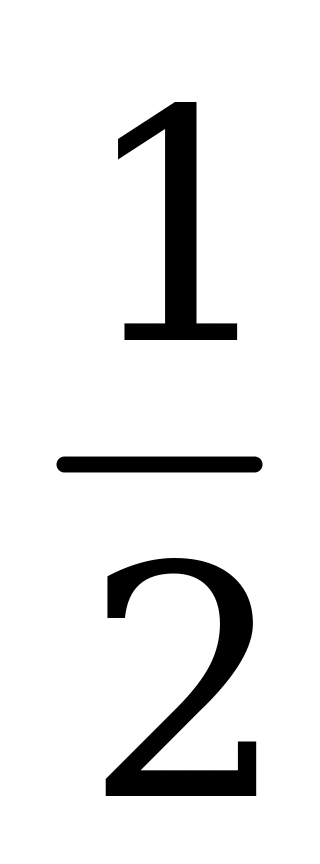 ; 2] ; 2] | C |
| В6.11 Какая из следующих функций четная ? A) 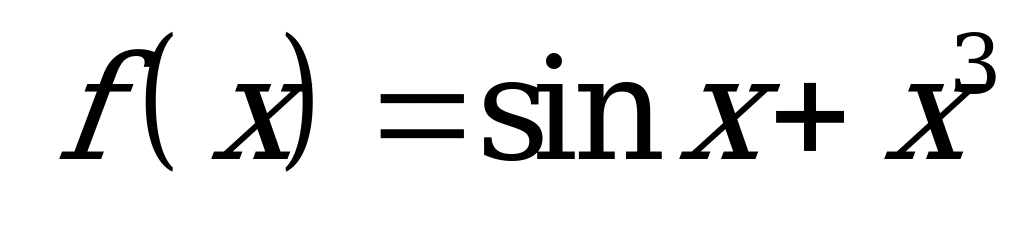 B) B) 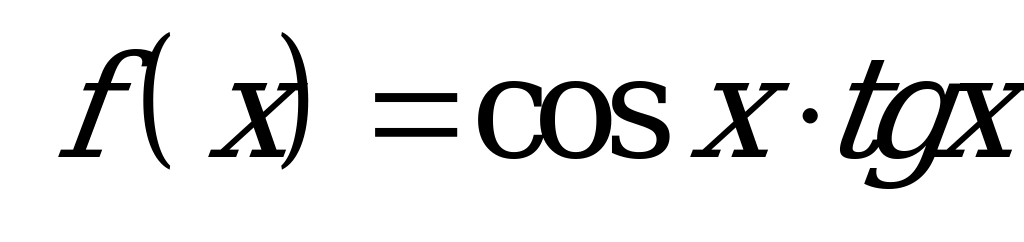 C) f(x) = x2ctgx D) 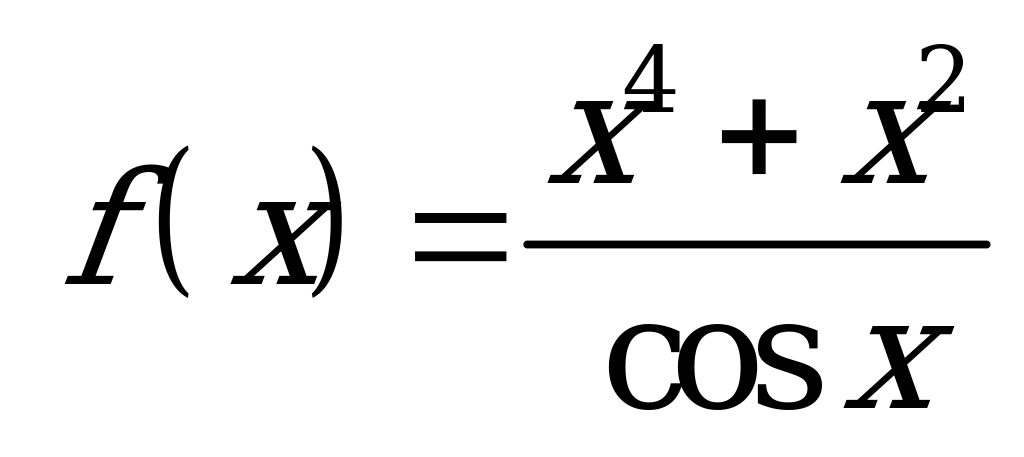 E) E) 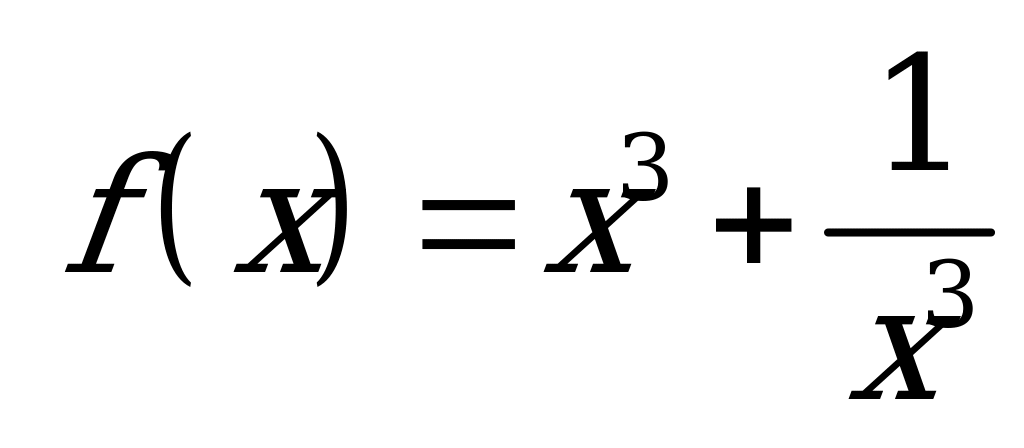 | B |
| В6.12 Какая из следующих функций нечетна ? A) 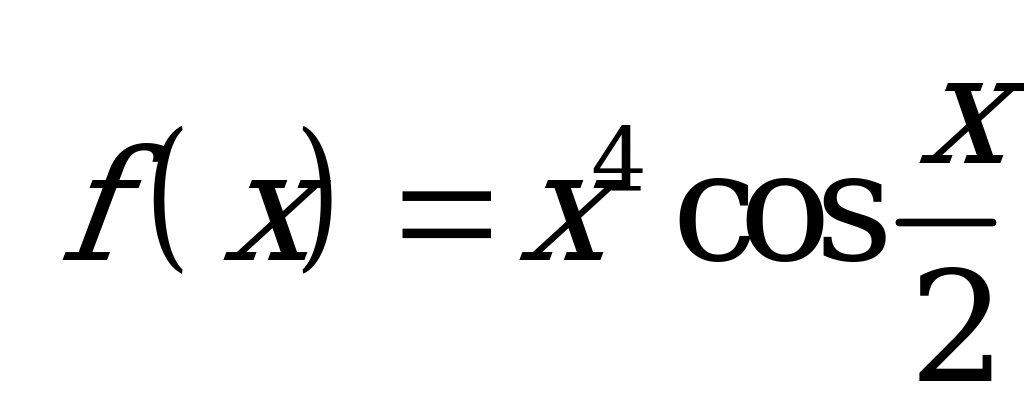 B) B) 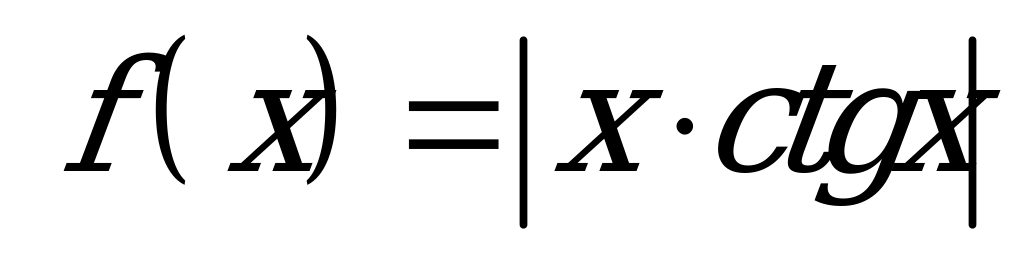 C) 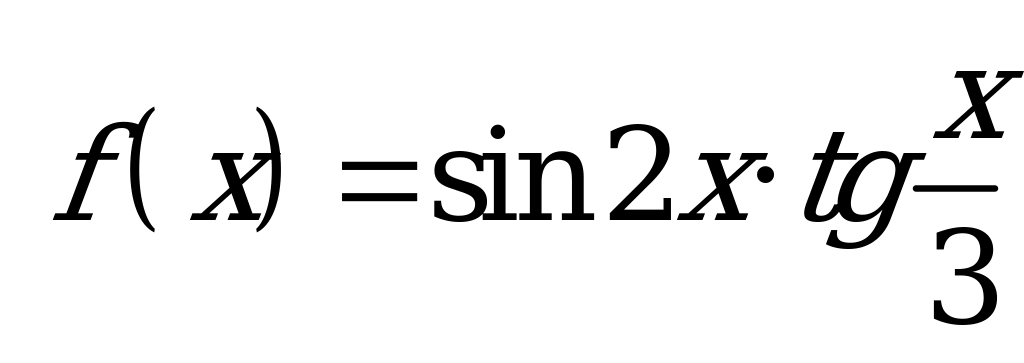 D) f(x) = |x|ctgx E) D) f(x) = |x|ctgx E) 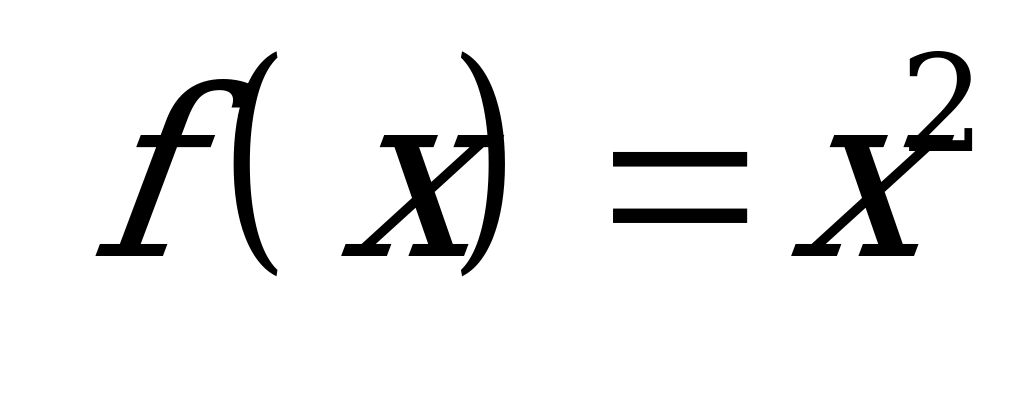 | D |
| В6.13 Какая из следующих функций нечетная ? A) 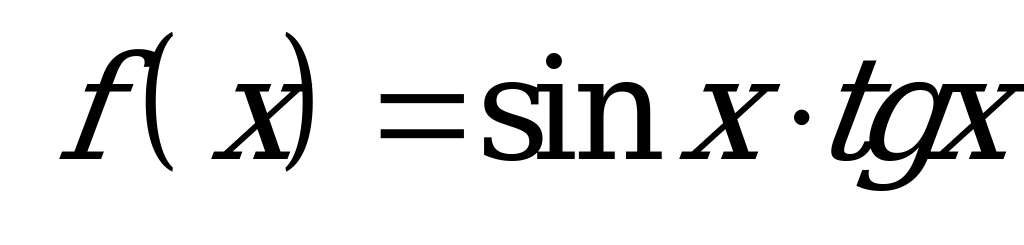 B) B) 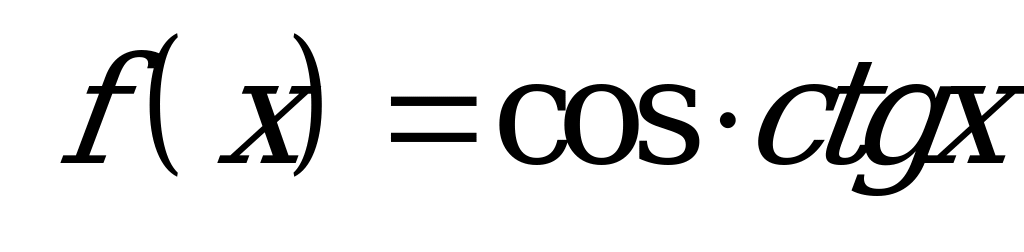 C) 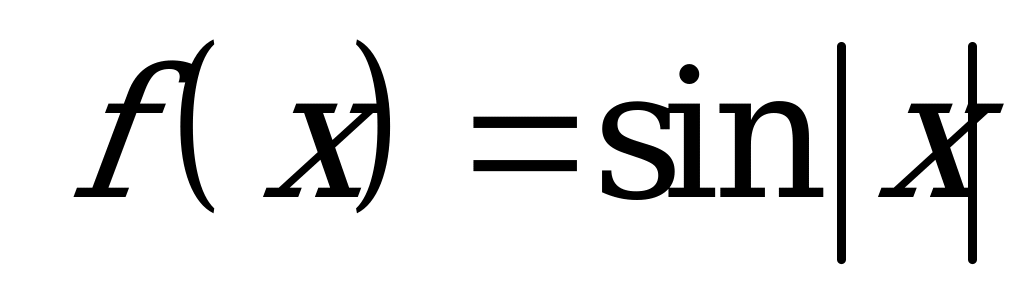 D) D) 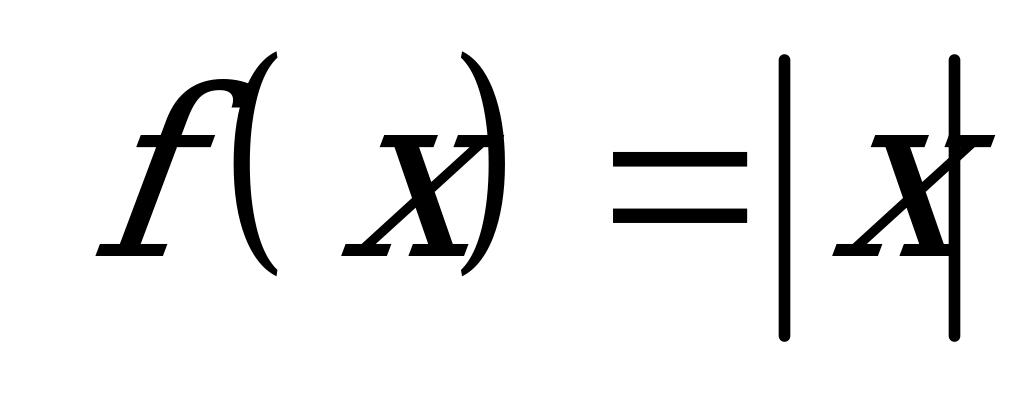 E) E) 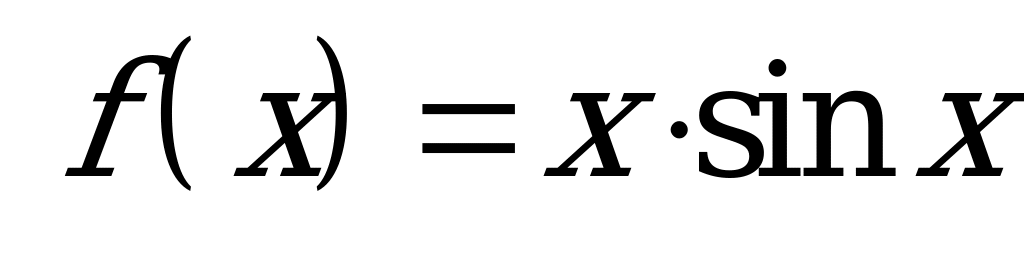 | B |
| В6.14 Какая из функций нечетная ? A) 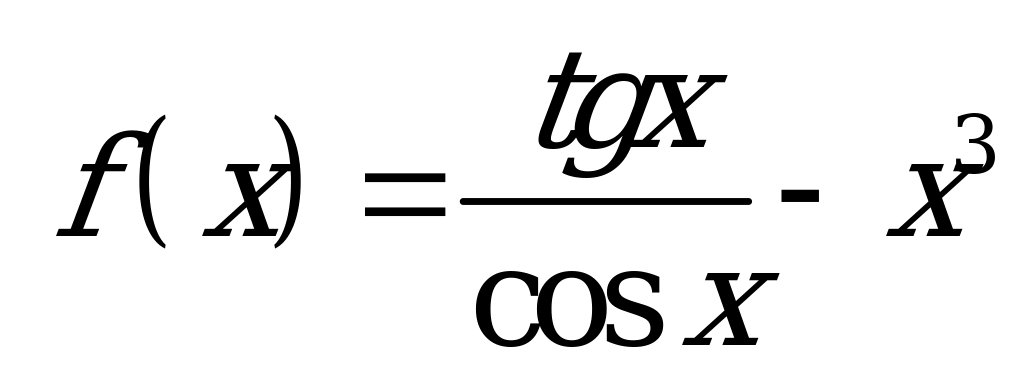 B) B) 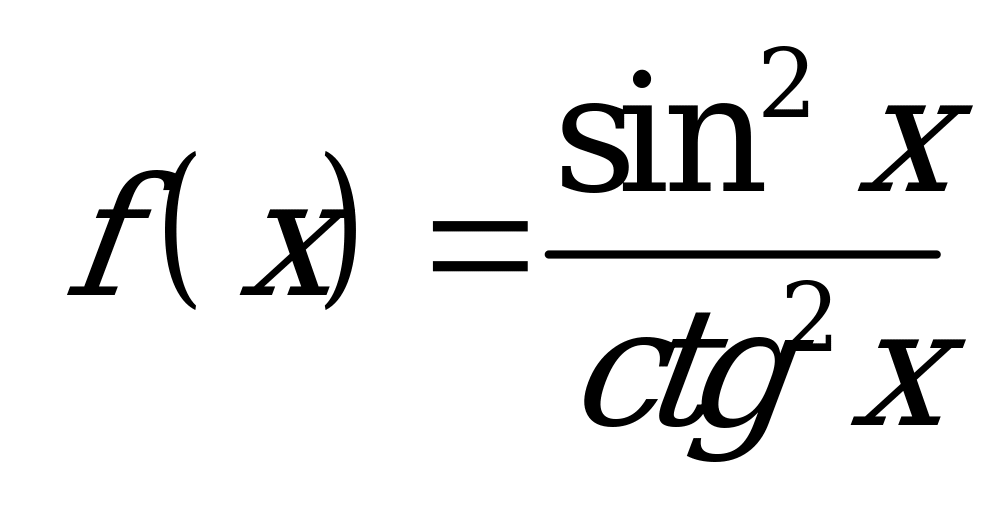 C) 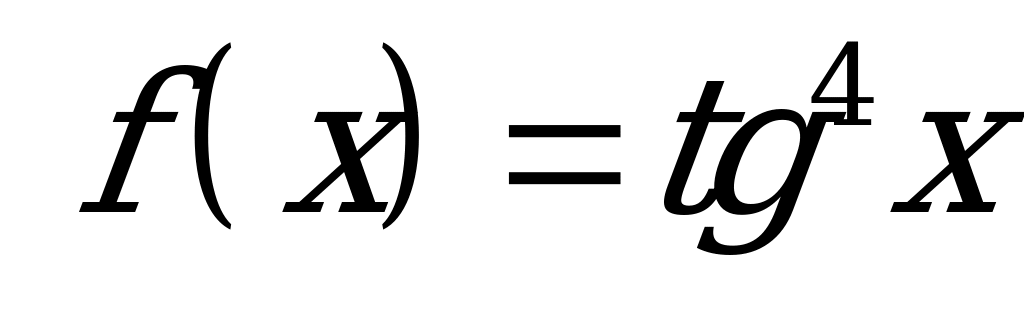 D) D) 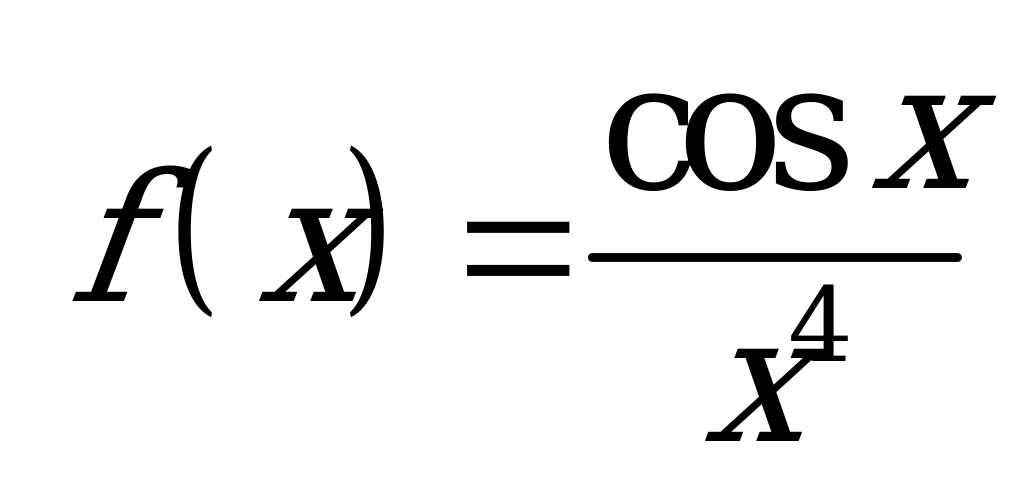 E) E)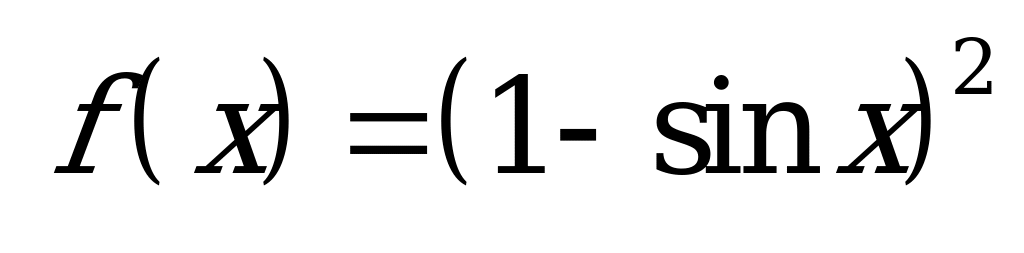 | A |
| В6.15 Какая функция нечётная? A) y = sin3x B) y = sin( x +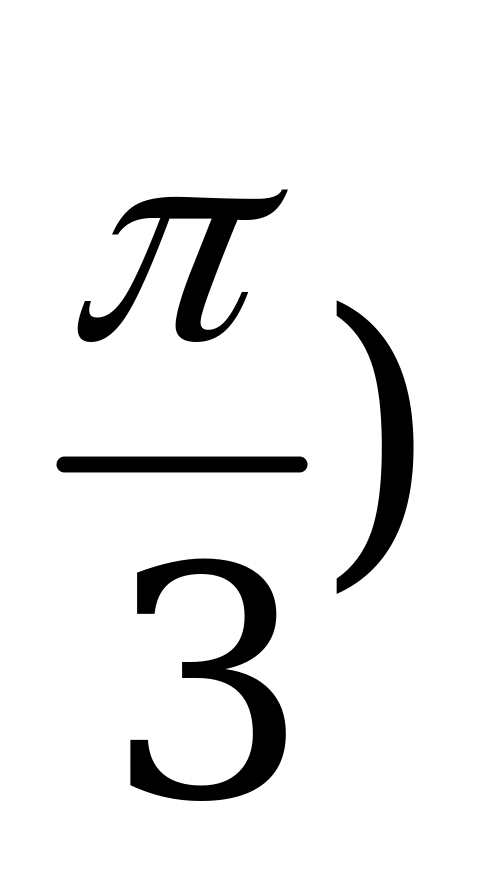 C) y = | sin2x| C) y = | sin2x| D) y = sin|2x| E) y = sinx + 1 | A |
| В6.16 Какая из следующих функций нечетная? A) f(x) = 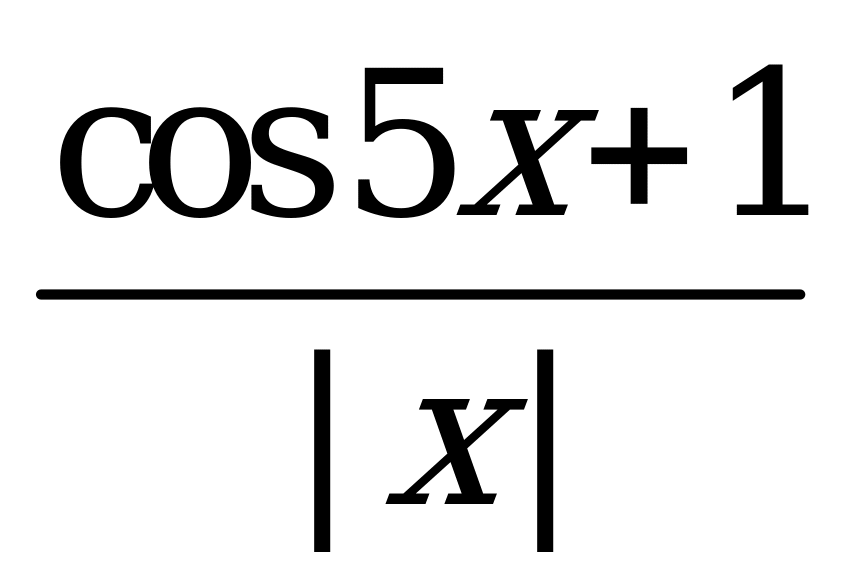 B) f(x) = B) f(x) = 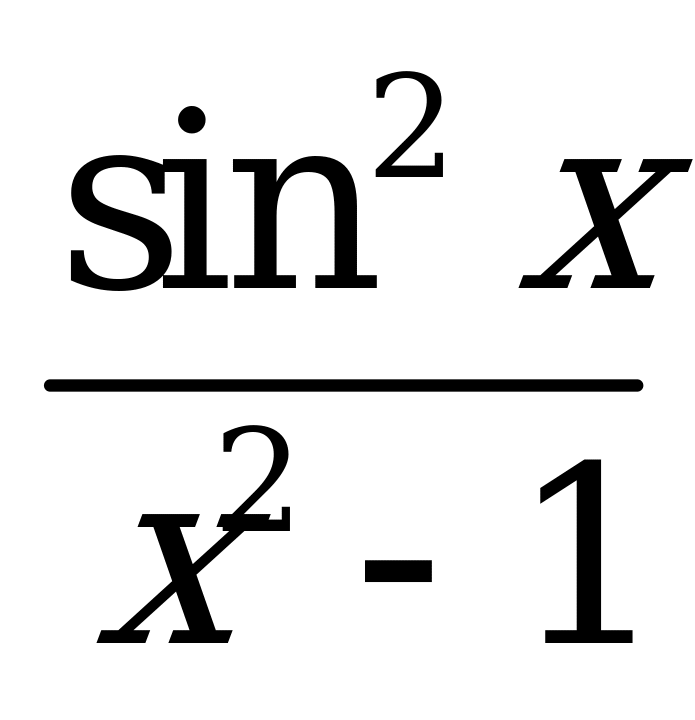 C) f(x) = 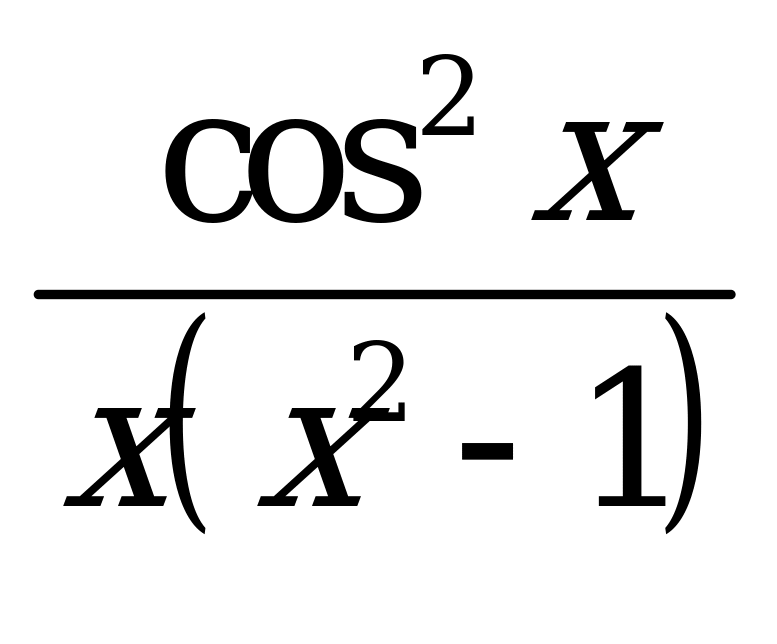 D) f(x) = D) f(x) = 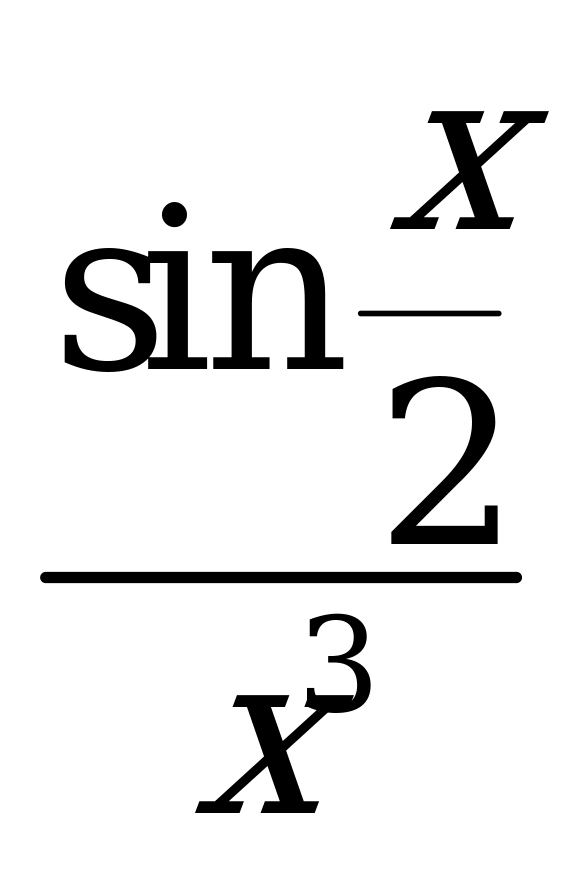 E) f(x) = x4cosx E) f(x) = x4cosx | C |
| В6.17 Какая функция нечетная? A) x3 + x + 4 B) 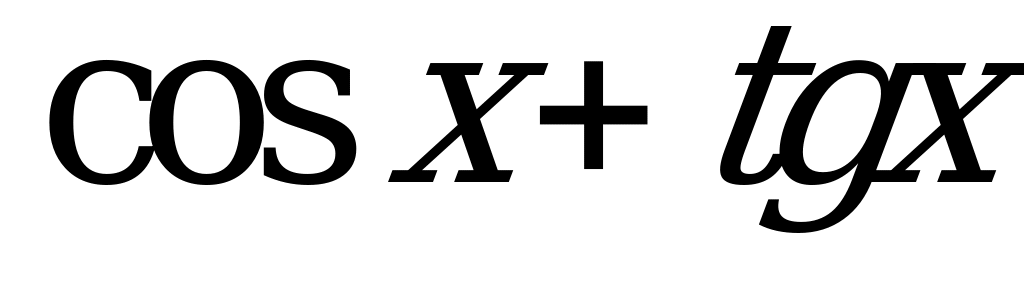 C) C) 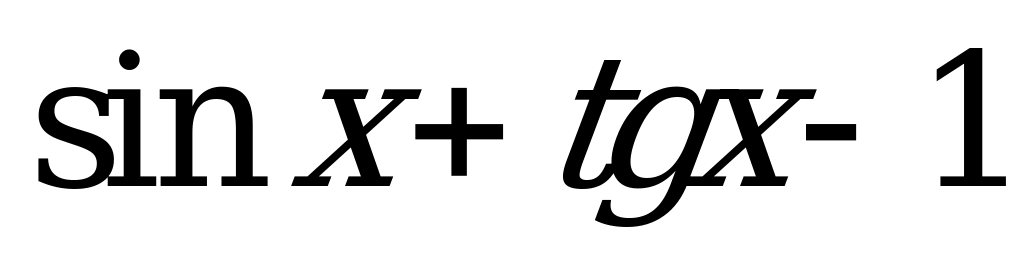 D) 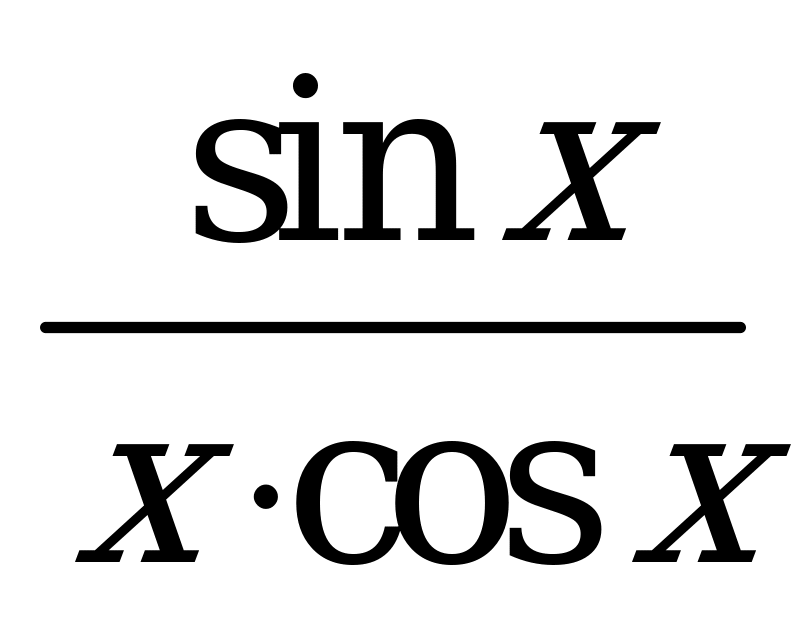 E) E) 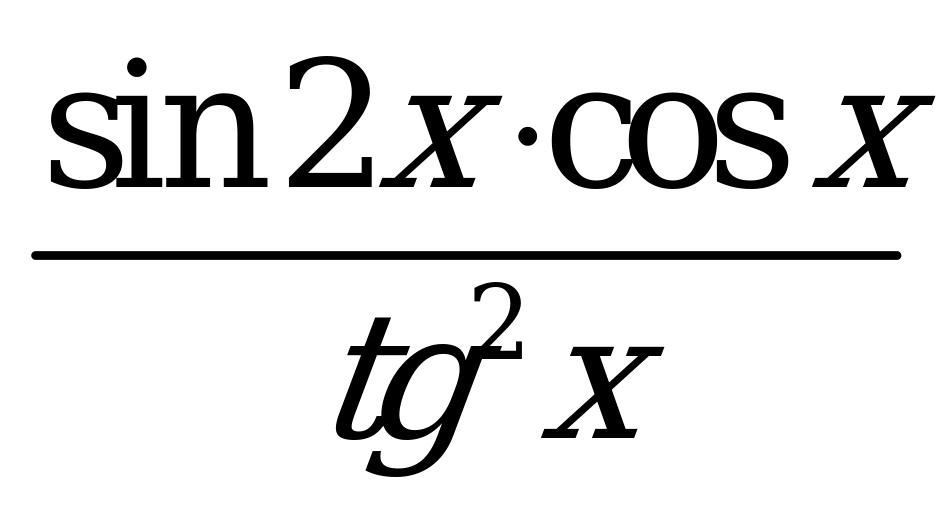 | E |
| В6.18 Найдите область значений функции 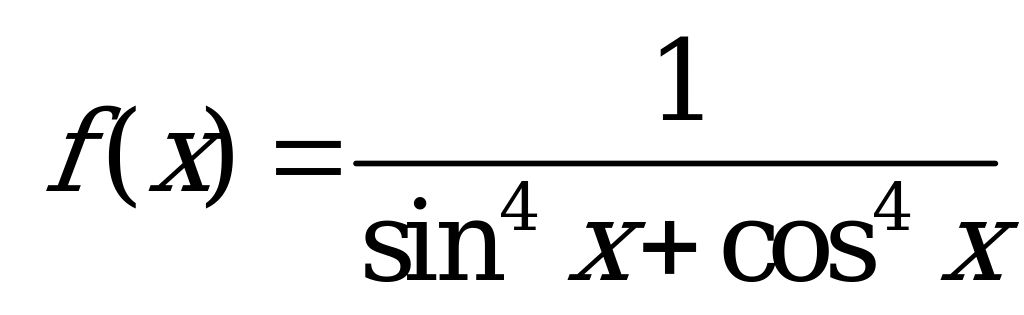 A) [0; 1] B) [0; 2] C) [1; 2] D) [1; 4] E) [0; 4] | C |
| В6.19 График какой из указанных функций изображен на рисунке ? 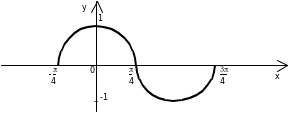 A) 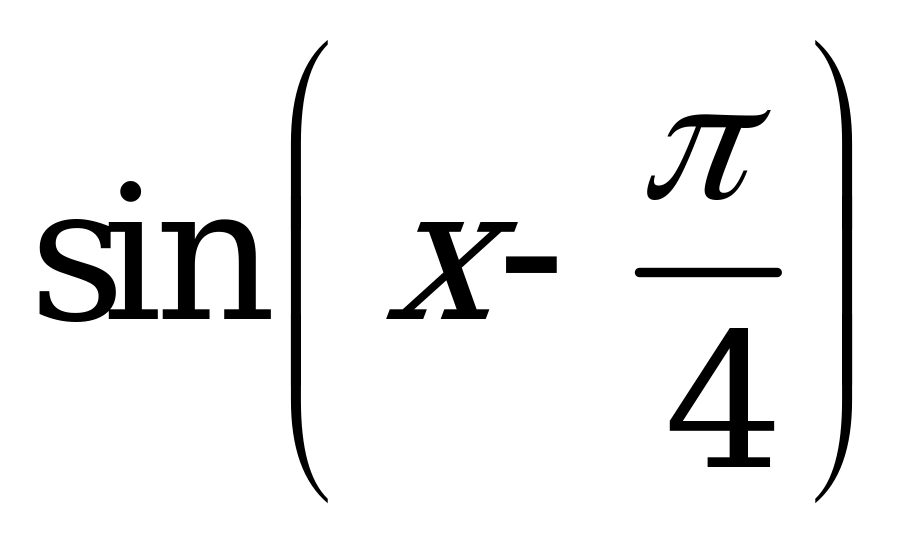 B) B) 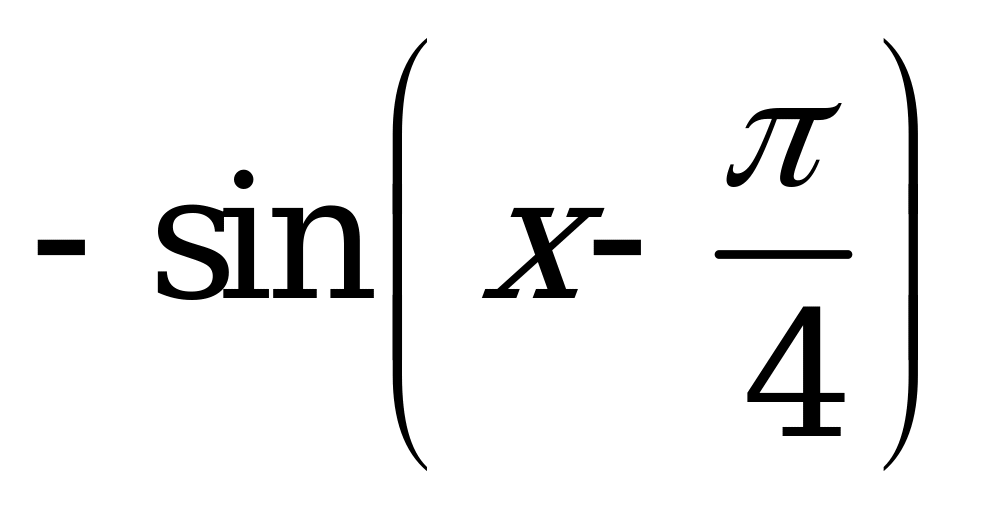 C) C) 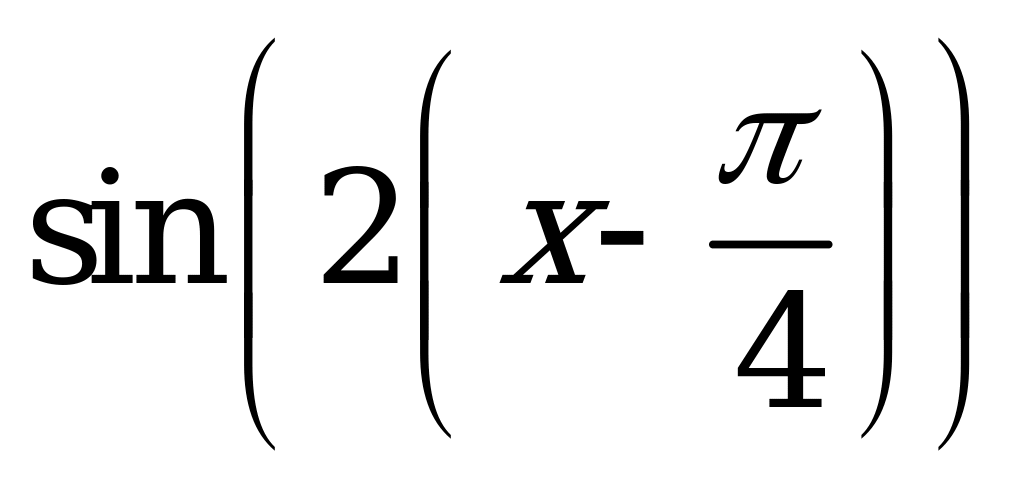 D) нет ответа E) -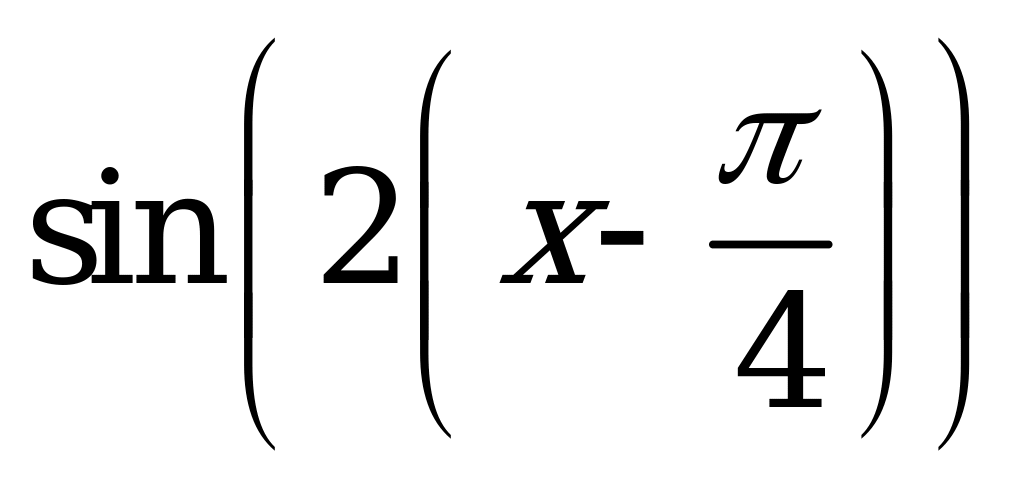 | E |
| В6.20 График какой из указанных функций изображен на рисунке? 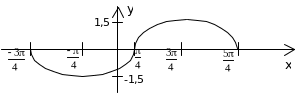 A) -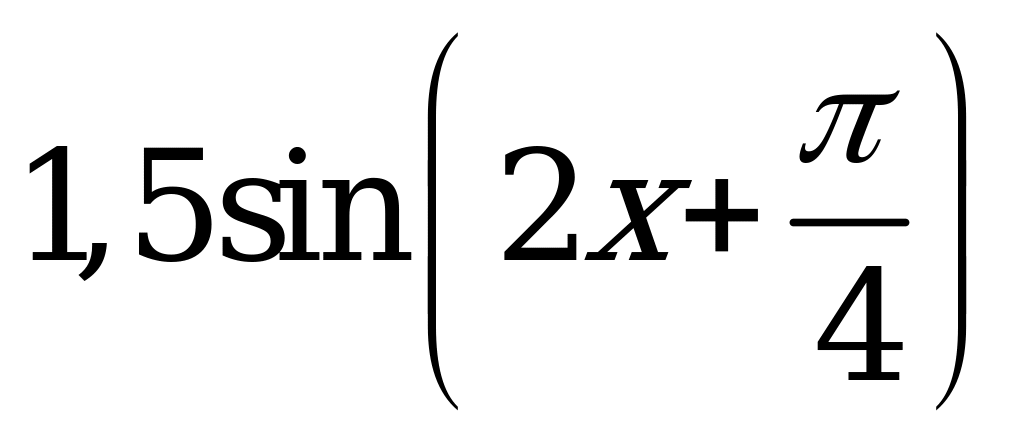 B) - B) -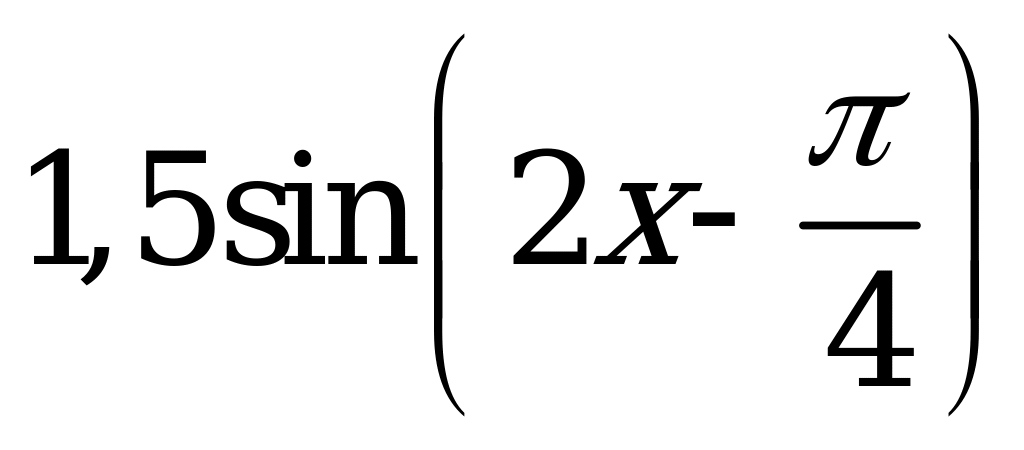 C) 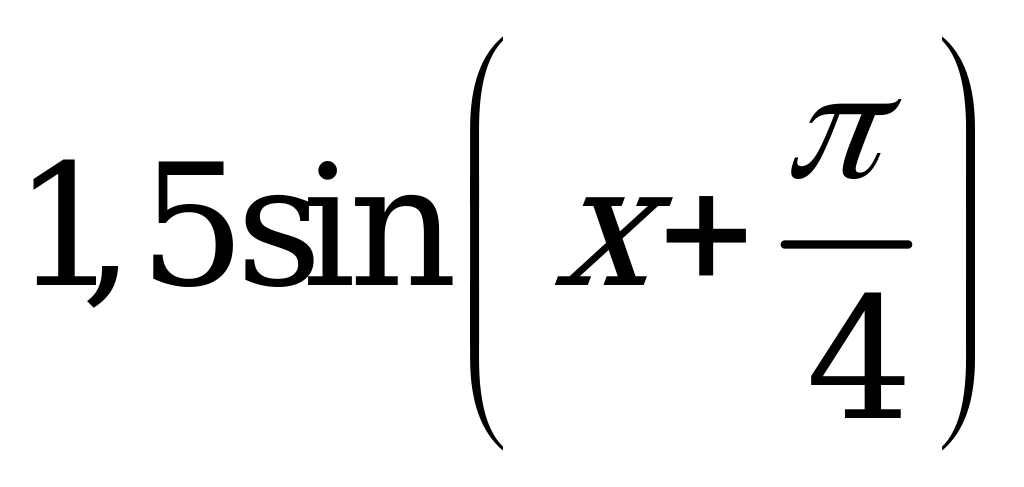 D) D) 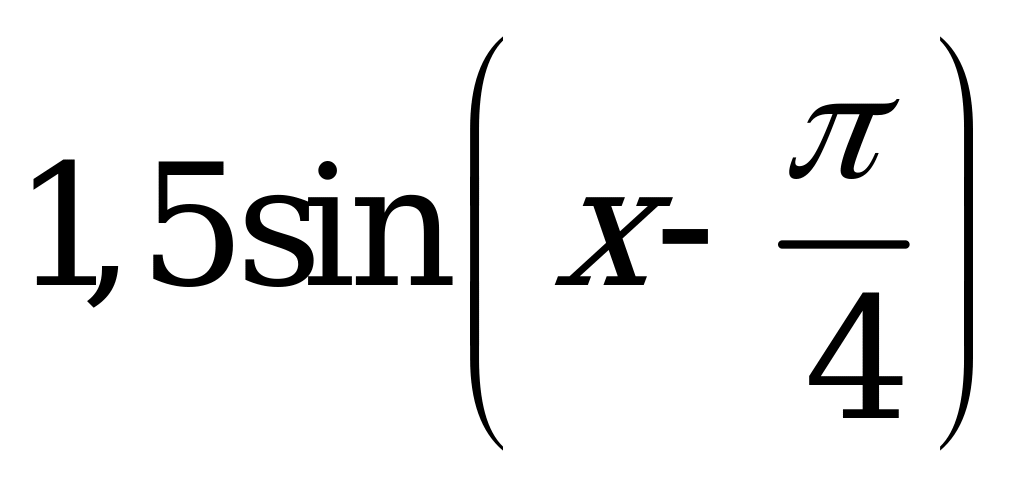 E) - E) -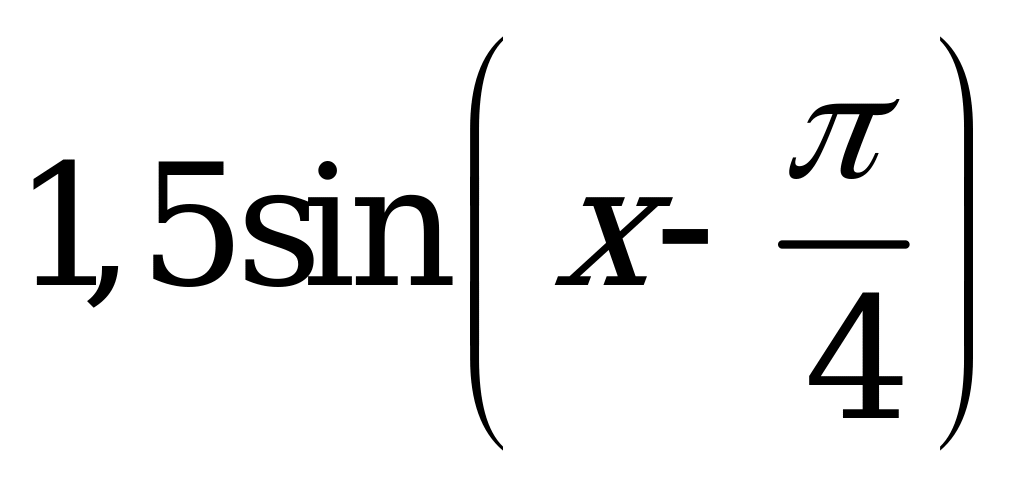 | D |
Тестовые задания наиболее сложного уровня  .
.
| С. Тестовые задания по теме «Тригонометрические функции» | Ответы |
| С1 Найдите 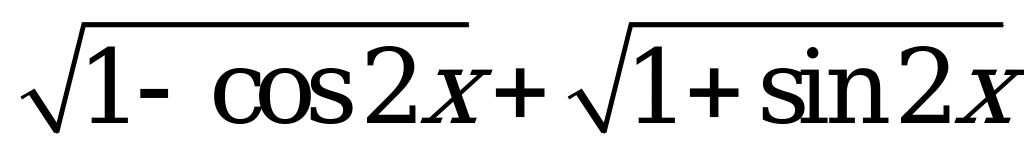 , если , если 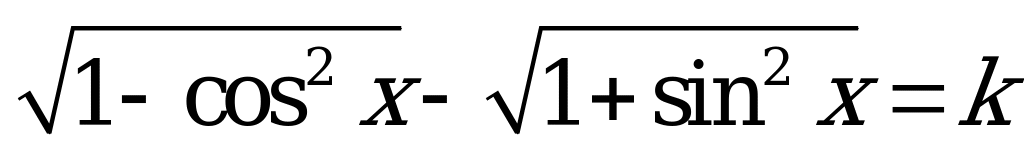 A) 1,5k B) 2k C) 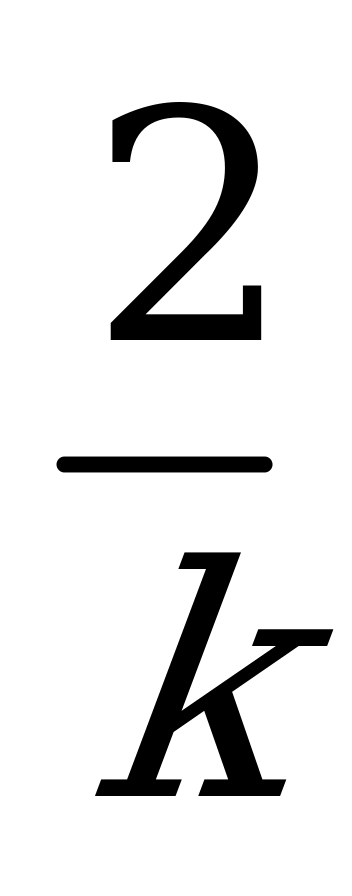 D) - k E) D) - k E) 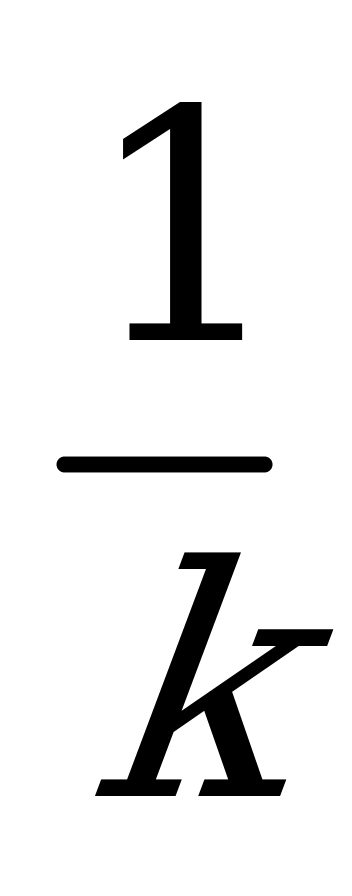 | E |
| С2 Выразите 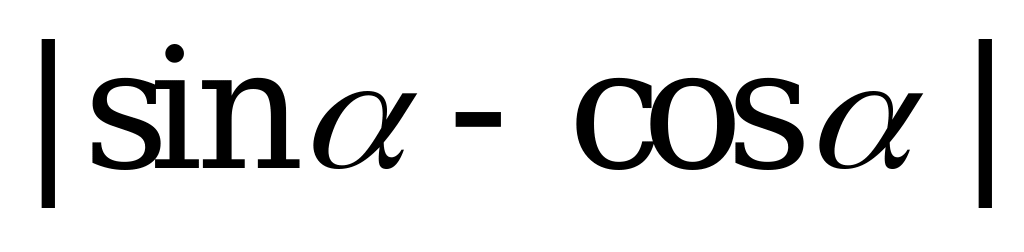 через a, если через a, если 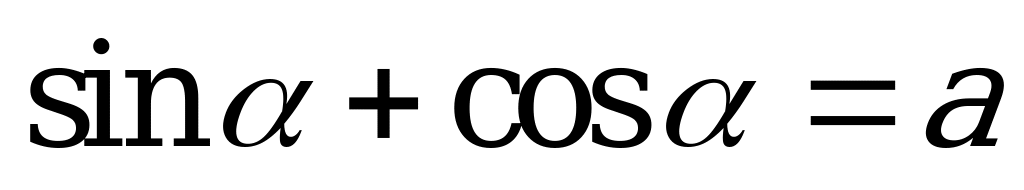 A) 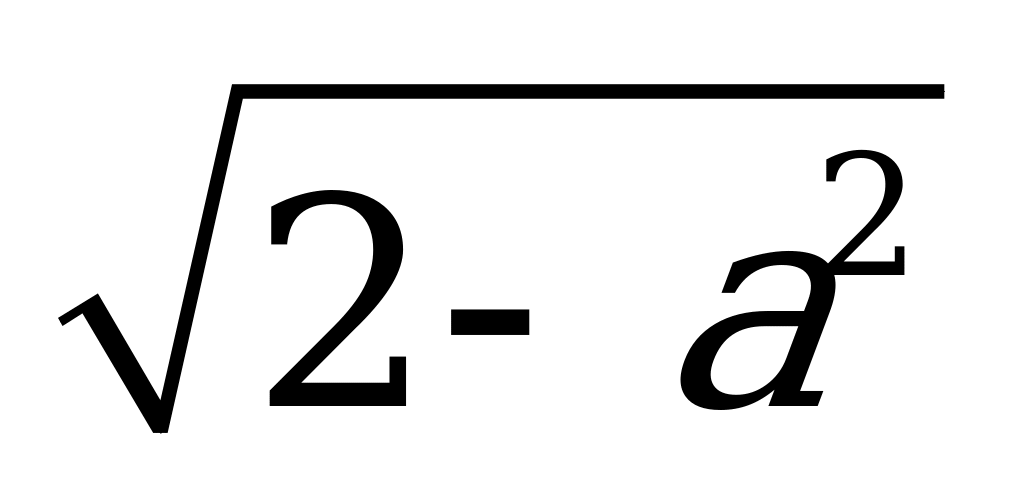 B) B) 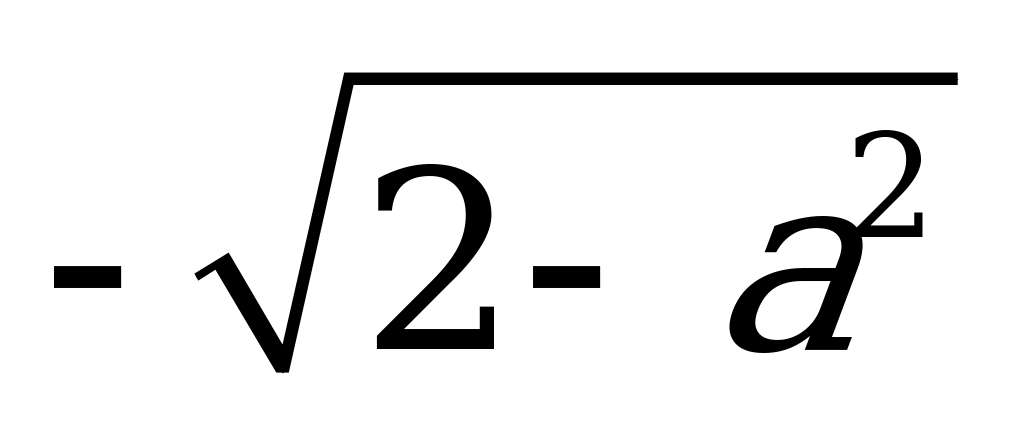 C) C) 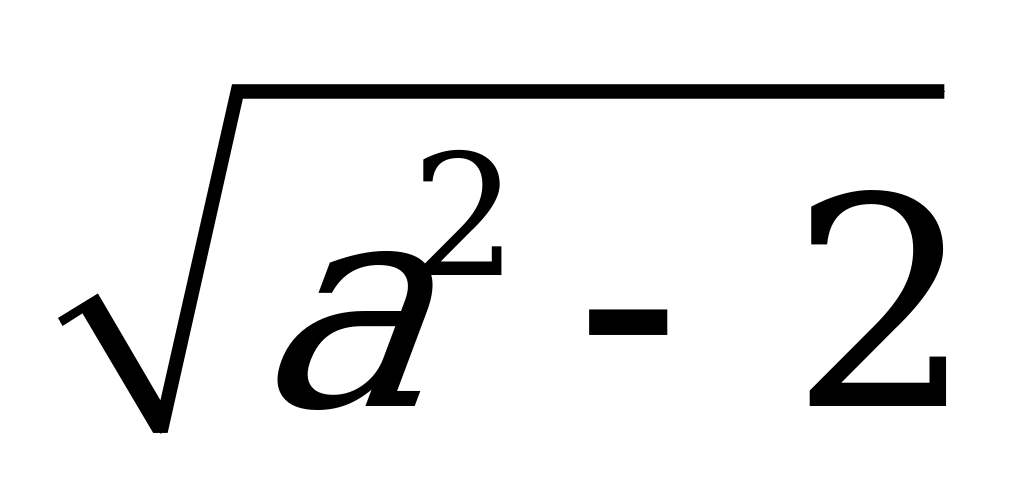 D) D)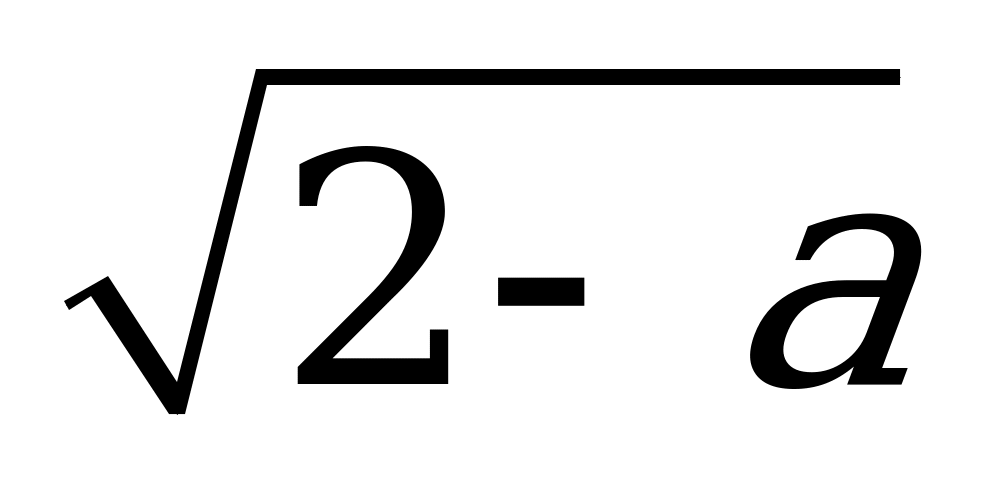 E) E) 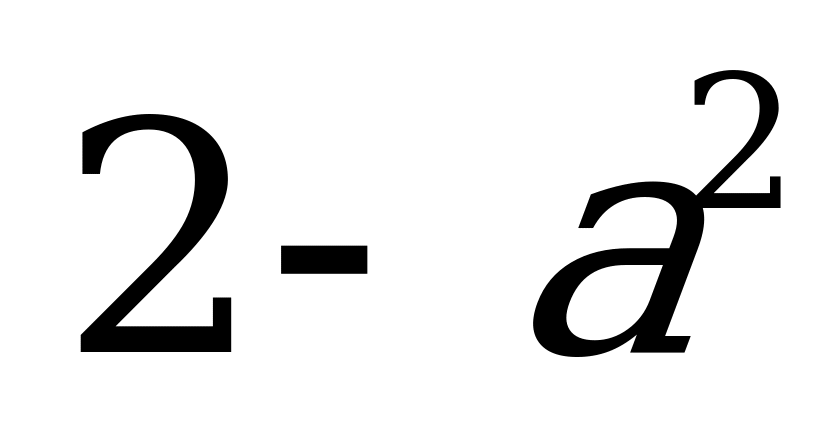 | A |
| С3 Вычислите: 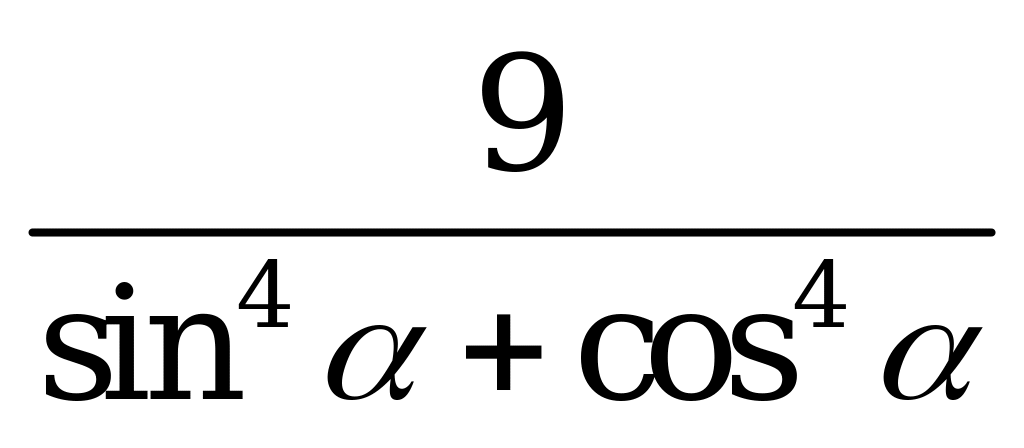 , если , если 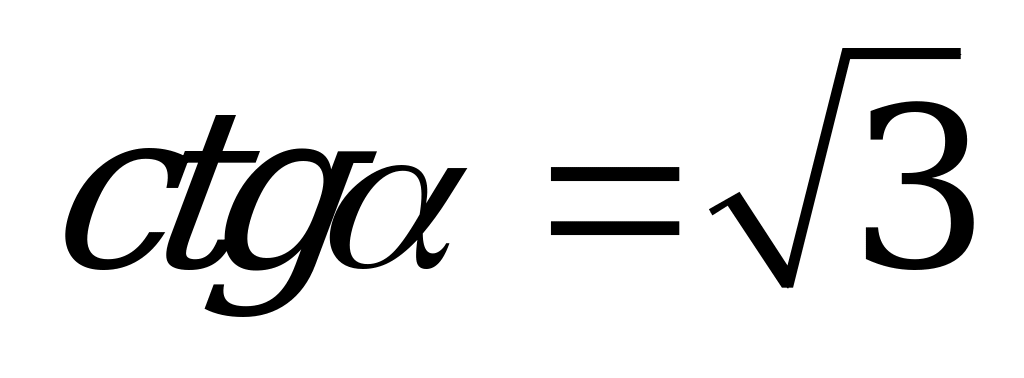 A) 5 B) 4,5 C) 81 D) 4 E) 14,4 | E |
| С4 Решите уравнение 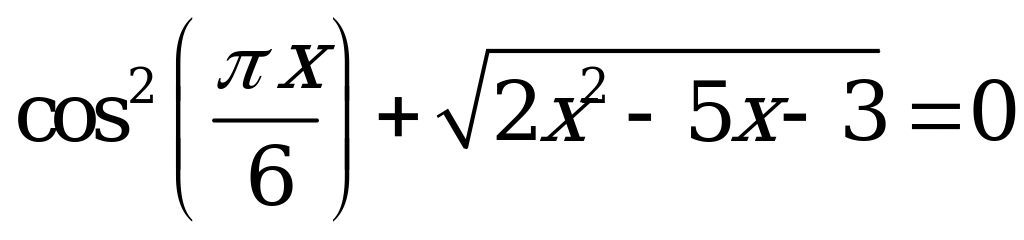 . . A) 3 B) 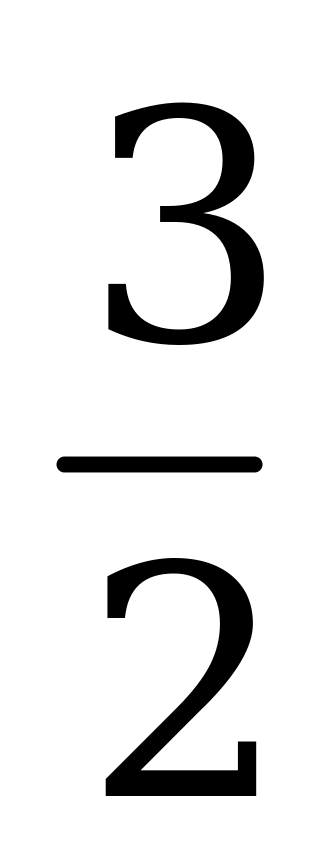 C) - C) -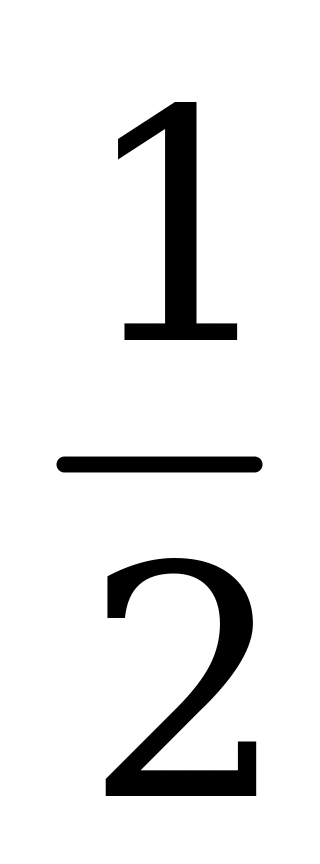 D) -3 E) D) -3 E) 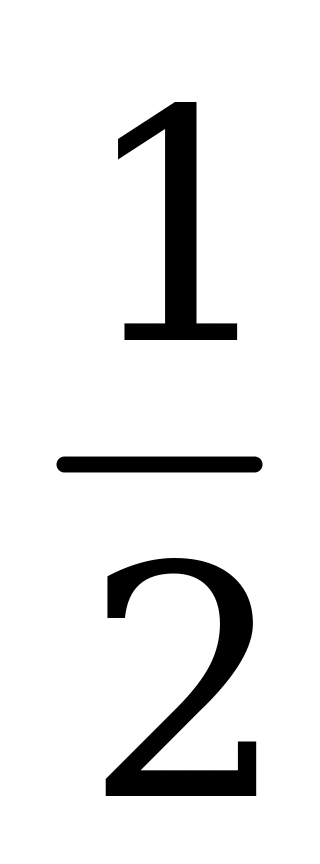 | A |
| С5 Определите число целых корней уравнения sin(10/x) = 0 A) Ни одной B) 8 C) 16 D) 24 E) Бесконечно много | B |
| С6 Какое из указанных чисел не является корнем уравнения 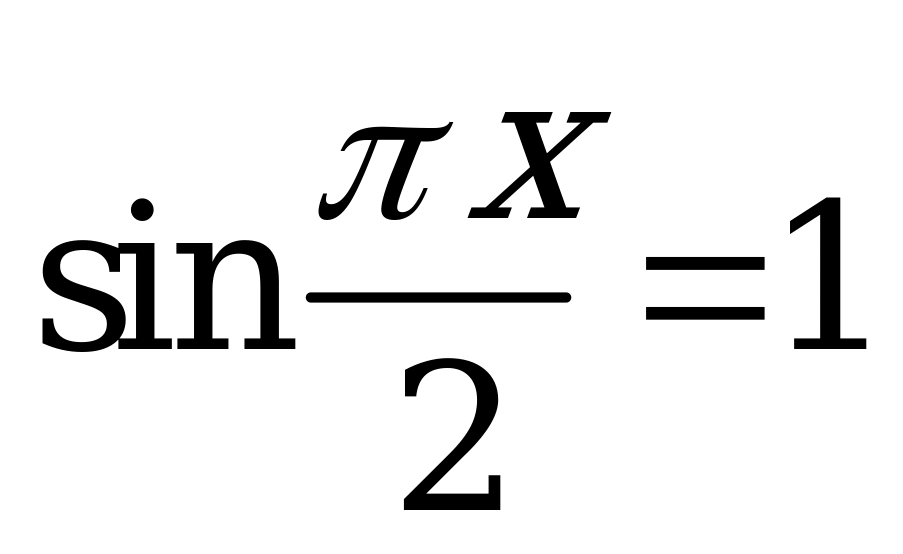 ? ? A) 5 B) 1996 C) 1 D) 9 E) 65 | B |
| С7 Какое из указанных чисел не является корнем уравнения 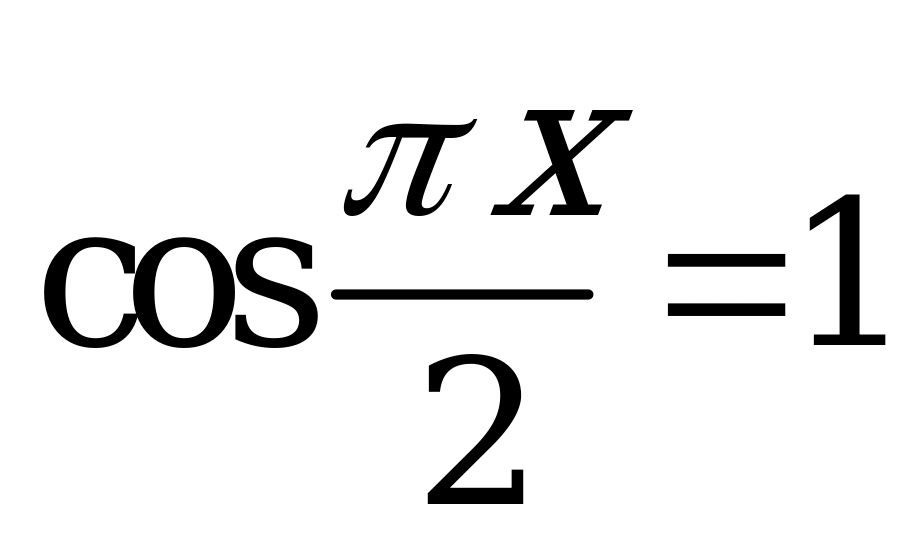 ? ? A) 1996 B) 3 C) 4 D) 40 E) 100 | B |
| С8 Сколько корней имеет уравнение 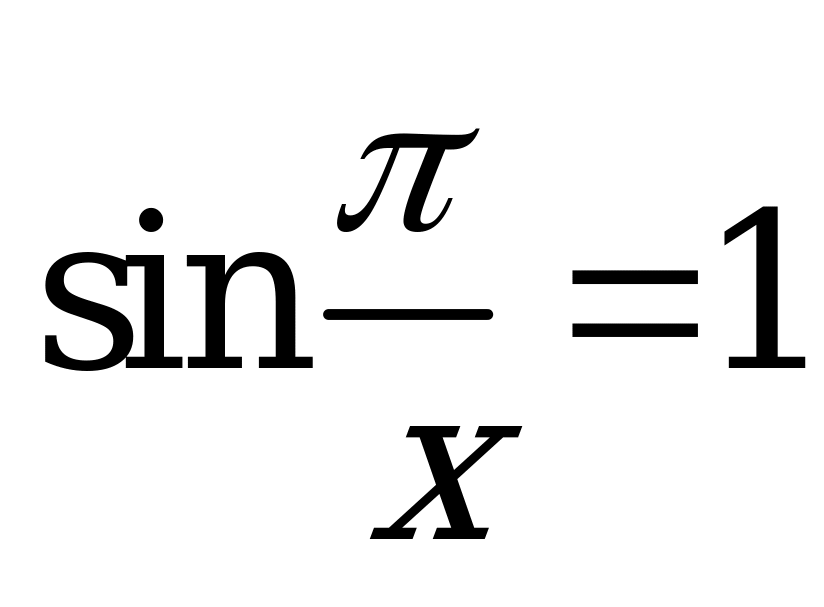 на отрезке на отрезке [0,05; 0,1]? A) 5 B) 1 C) 2 D) 3 E) 4 | A |
| С9 Сколько корней имеет уравнение 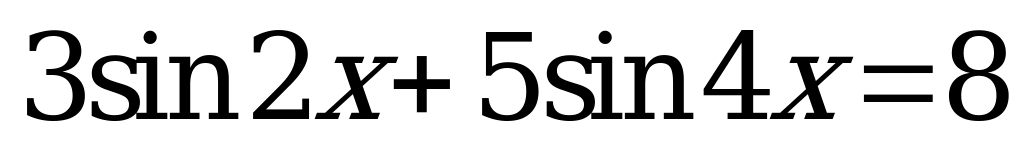 на отрезке [-2; 2]? A) B) 1 C) 2 D) 3 E) 4 на отрезке [-2; 2]? A) B) 1 C) 2 D) 3 E) 4 | A |
| С10 Какая функция в промежутке 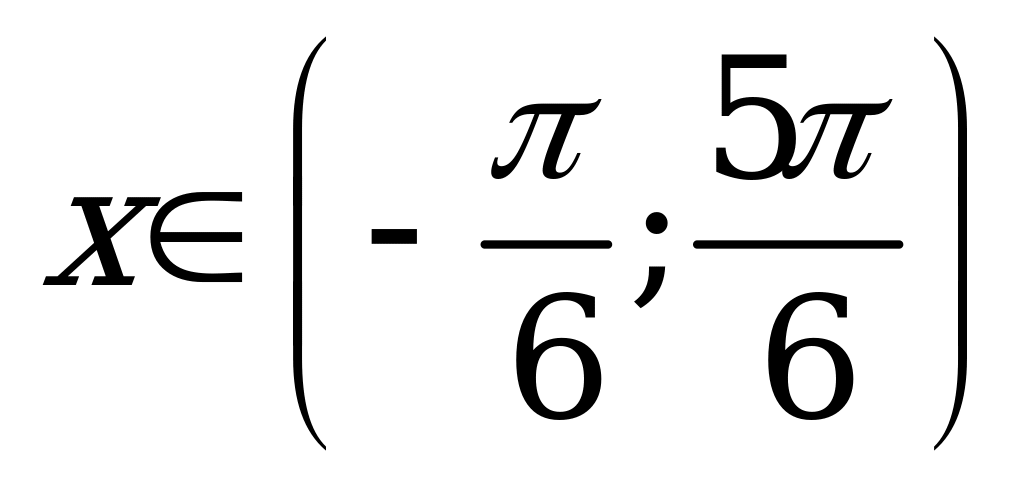 принимает положительные значения? принимает положительные значения? A)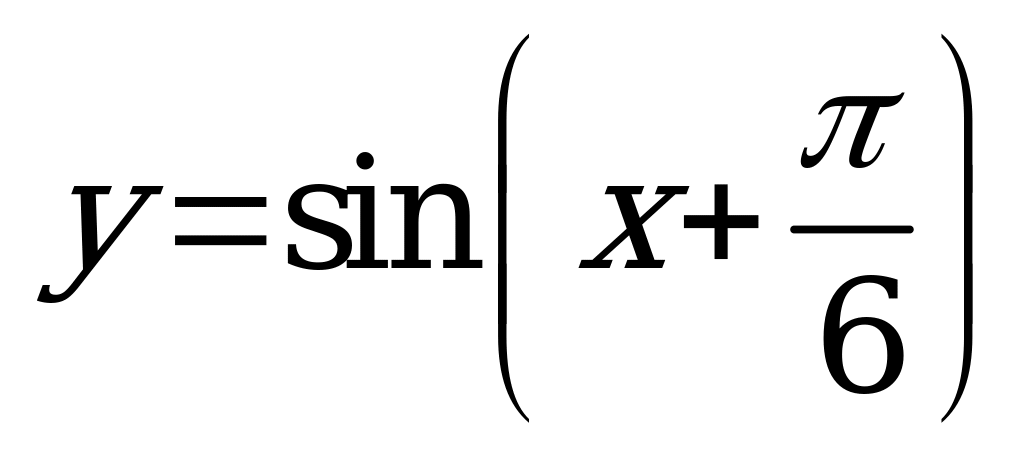 B) B)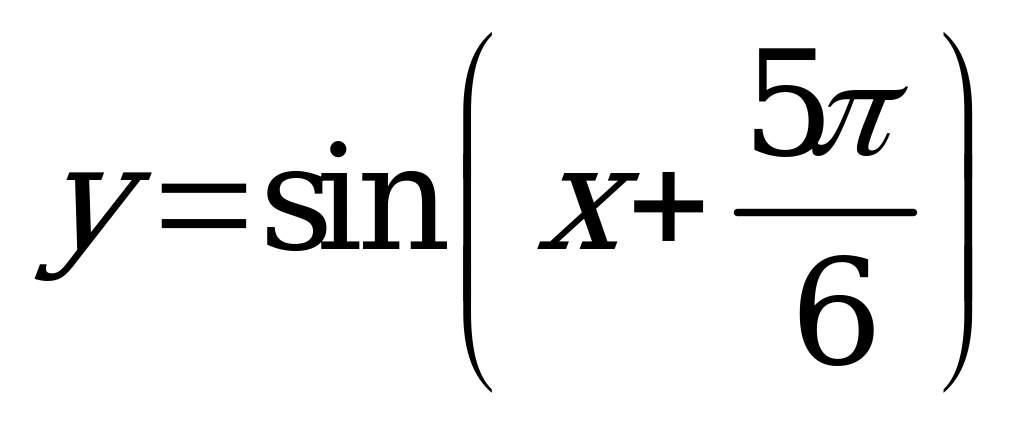 C) C) 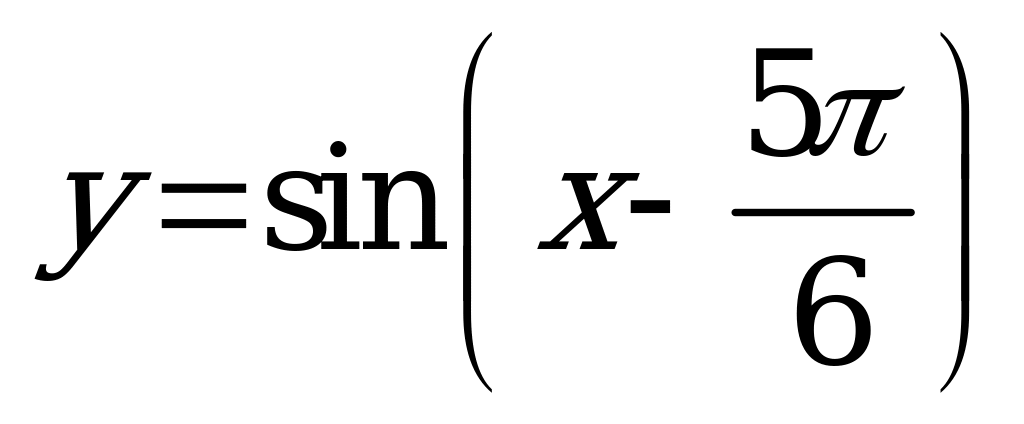 D) 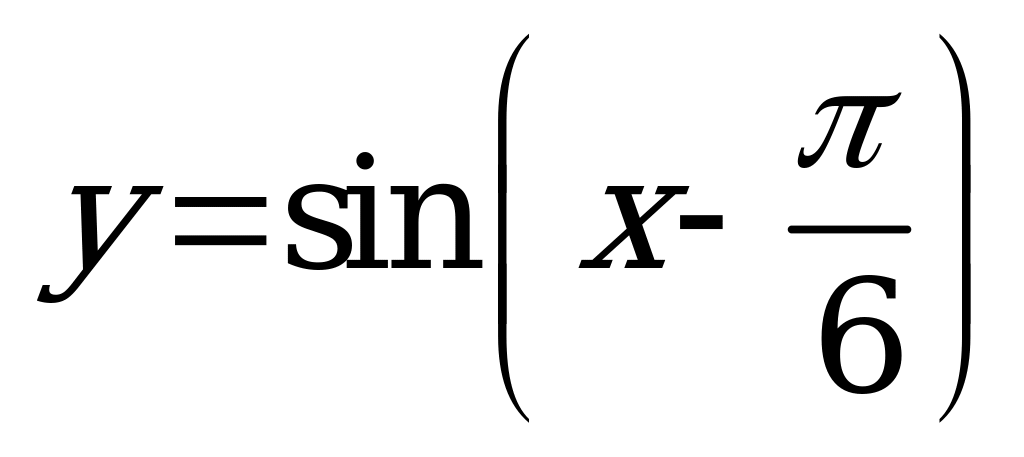 E) E) 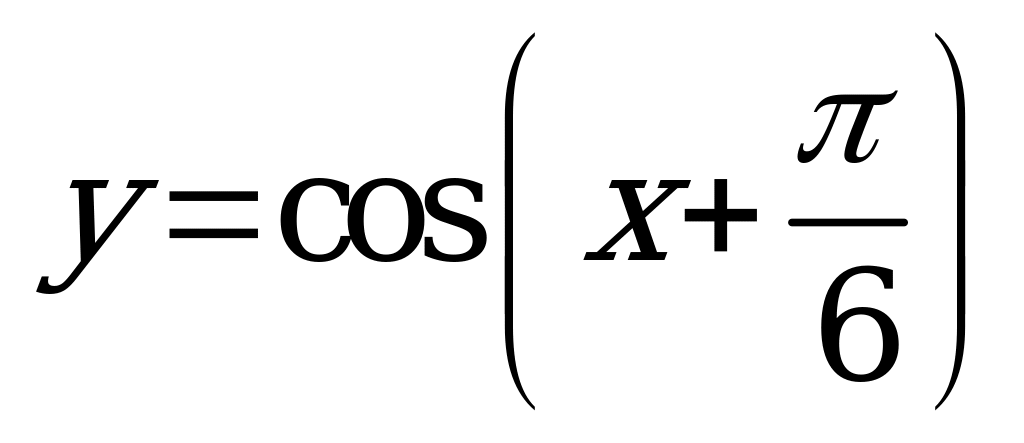 | A |
| С11 Решите неравенство 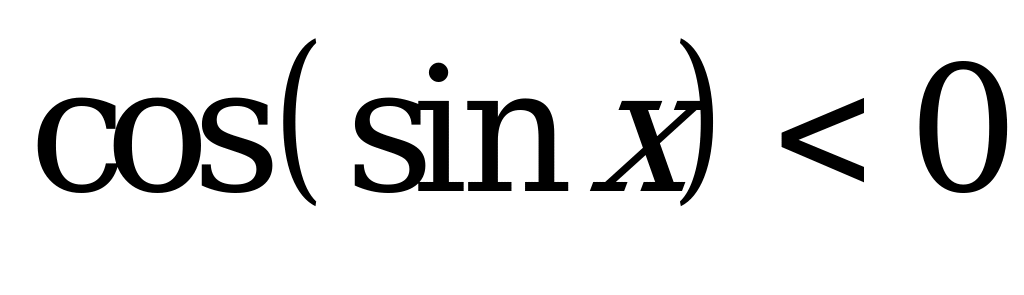 . . A) (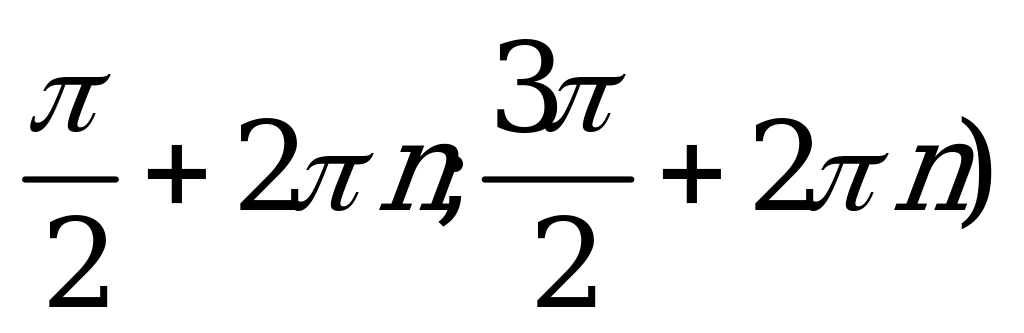 , n , n  Z B) ( Z B) (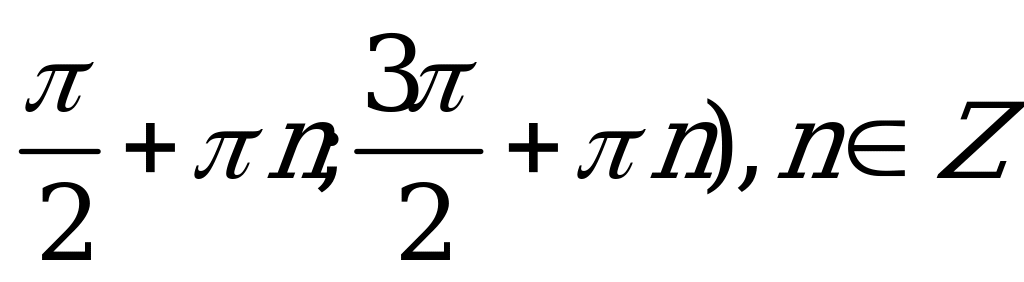 C) (0; 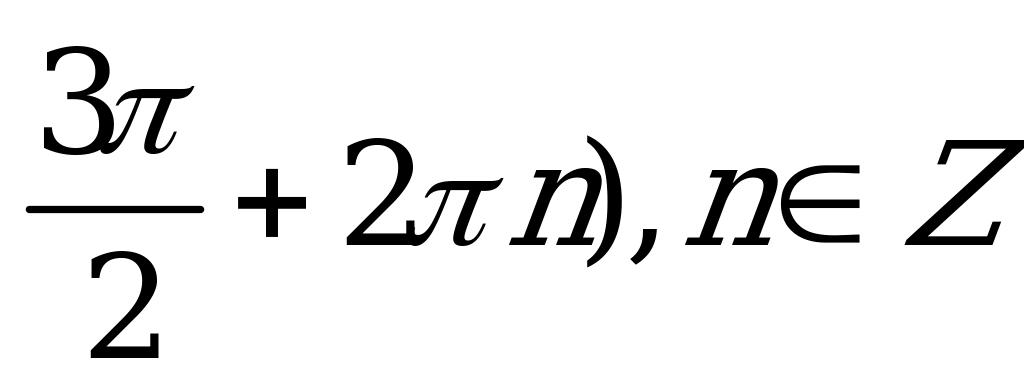 D) (0; D) (0;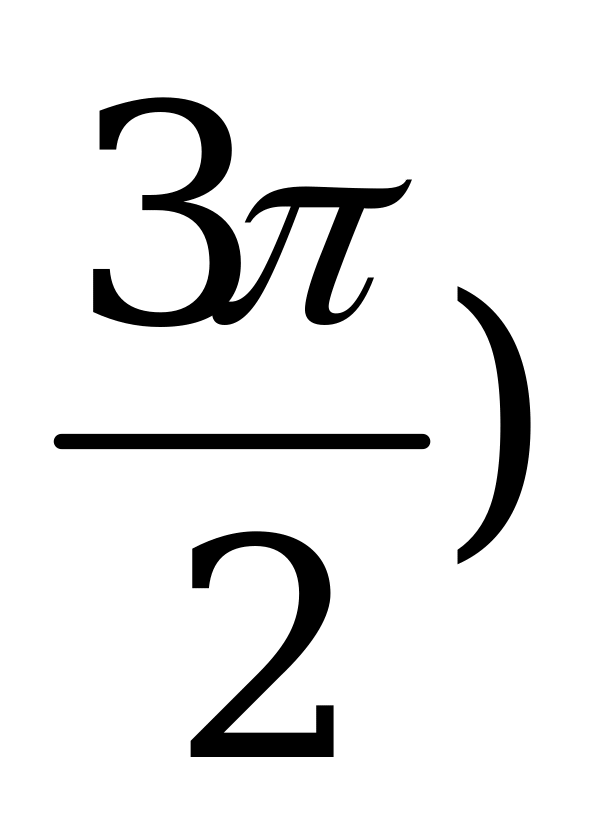 Е) Е)  | E |
| С12 Решите неравенство: 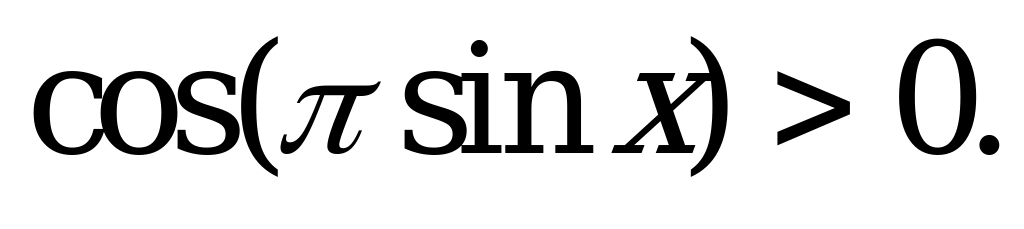 A) 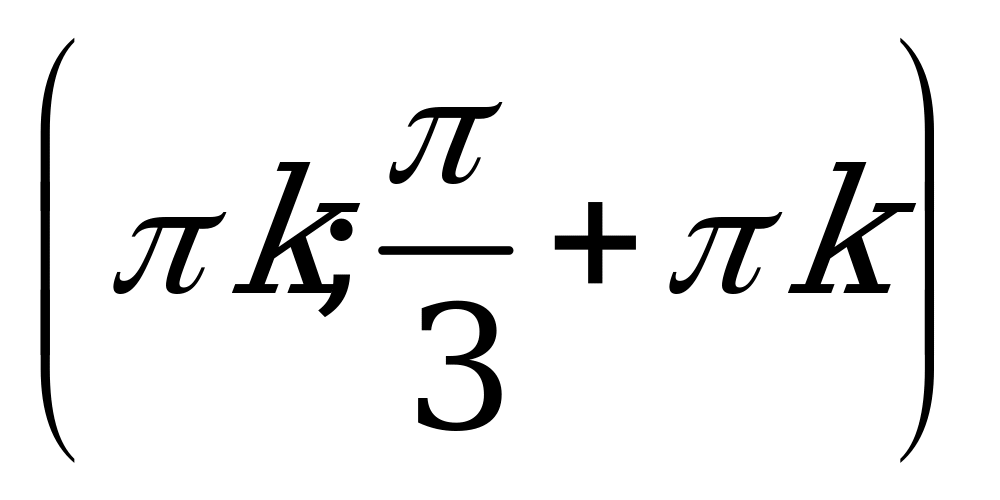 B) B) 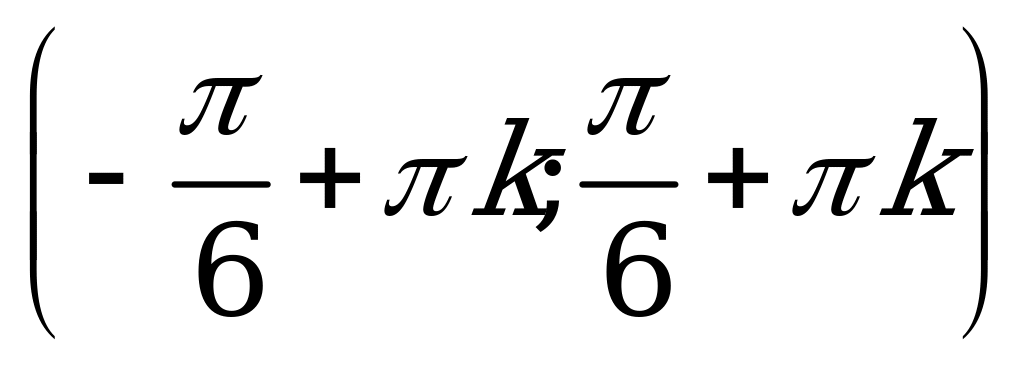 C) 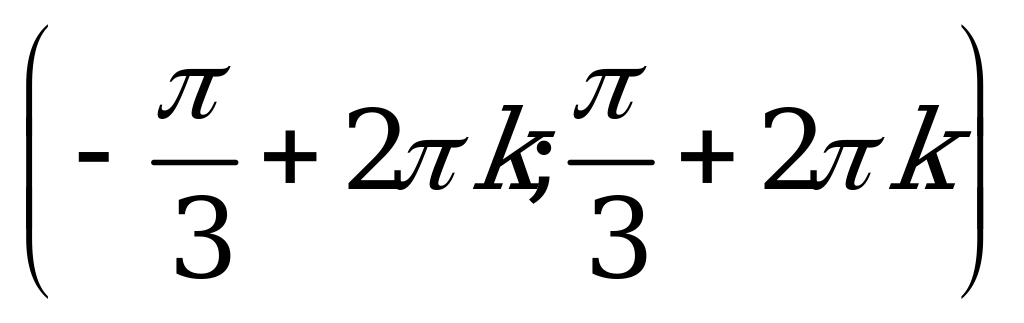 D) D) 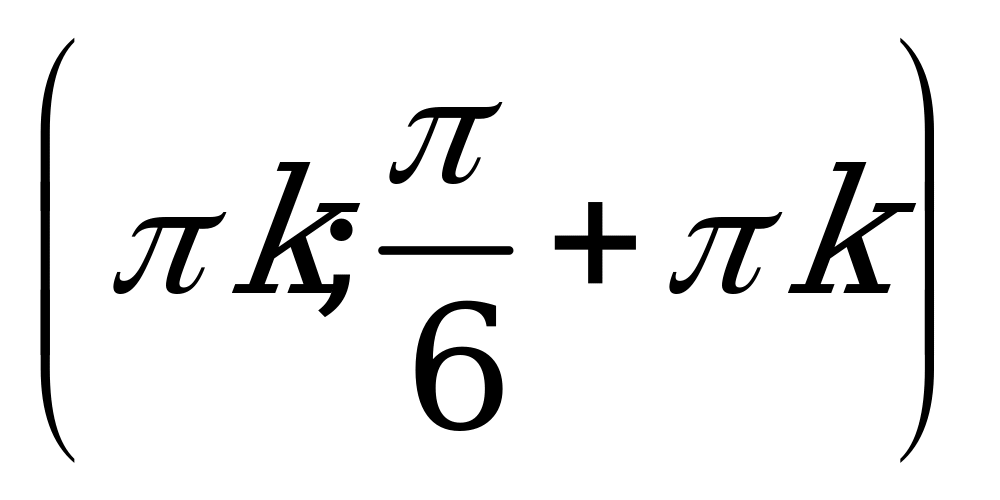 E) 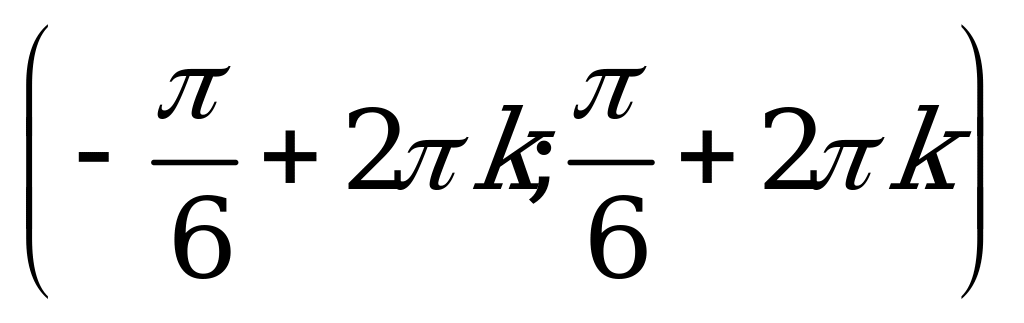 . Везде . Везде 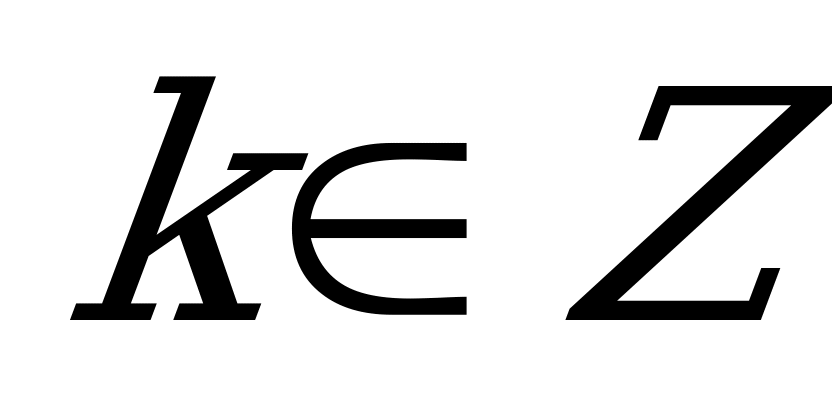 . . | B |
| С13 Укажите верное неравенство A) 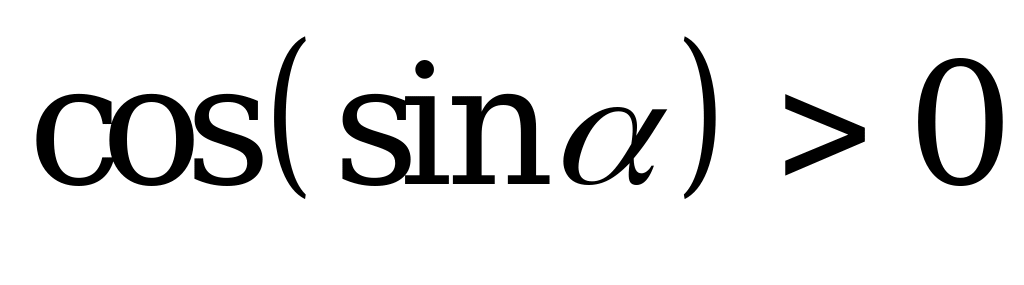 B) B) 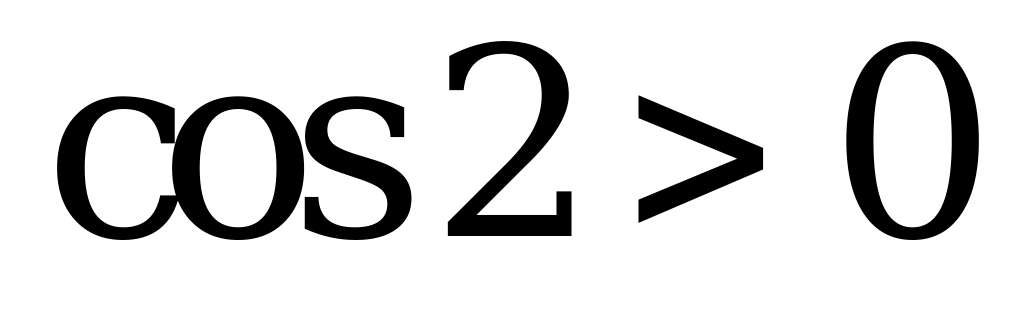 C) - C) -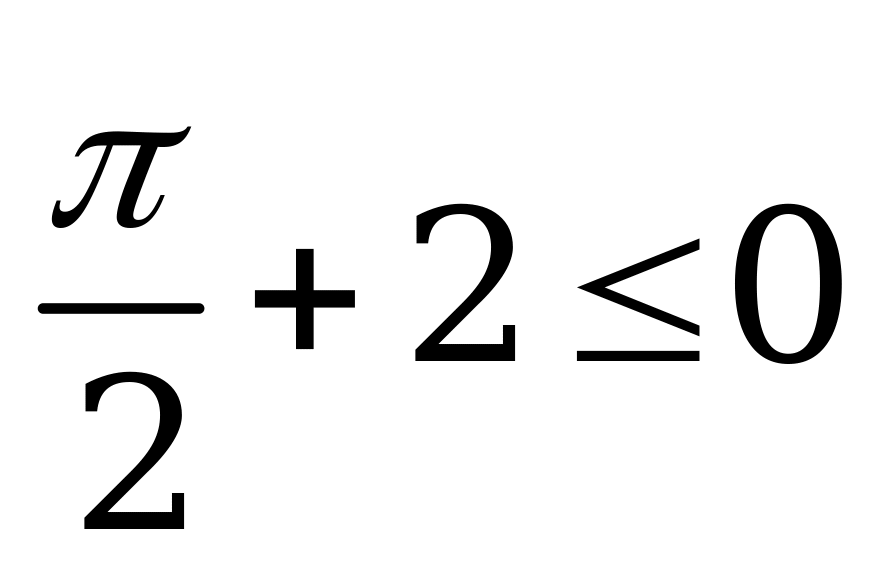 D) 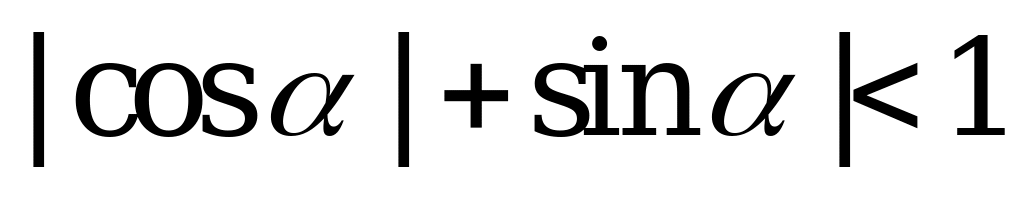 E) E) 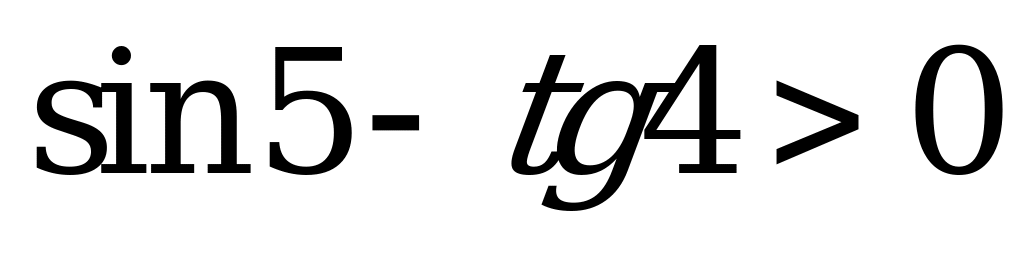 . . | A |
| С14 Найдите абсциссы точек касания графика функции 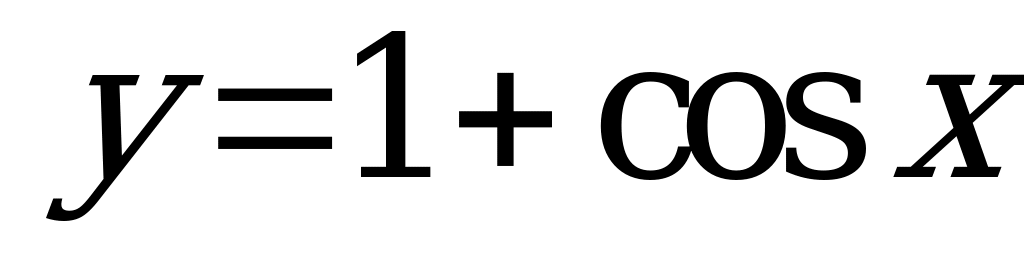 с осью Ox с осью Ox A)  Z B) 2 Z B) 2 Z C) Z C) 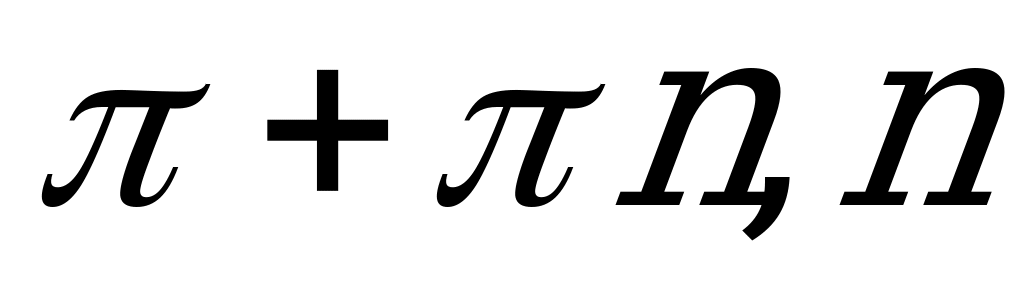 Z Z D) 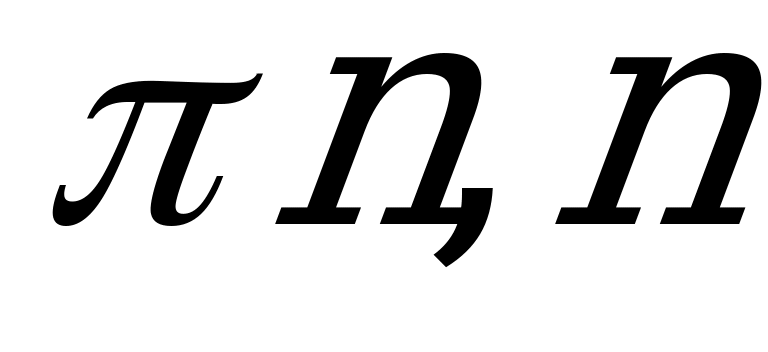 Z E) Z E) 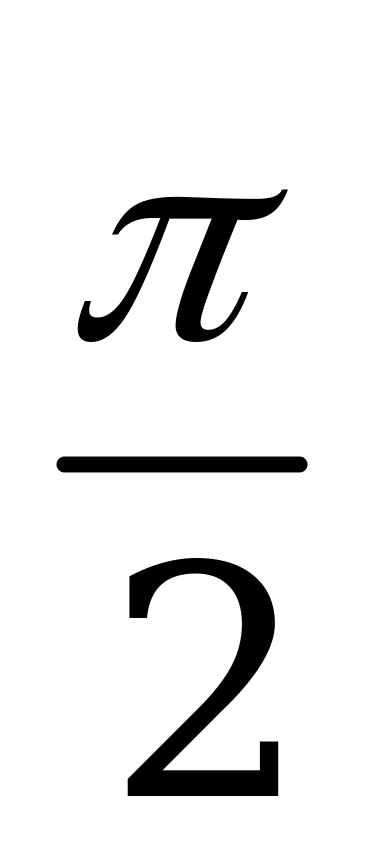 +2 +2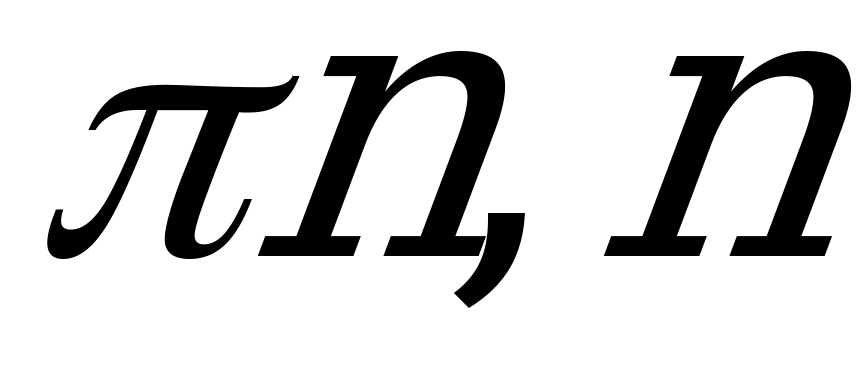 Z Z | A |
| С15 Сколько корней имеет уравнение 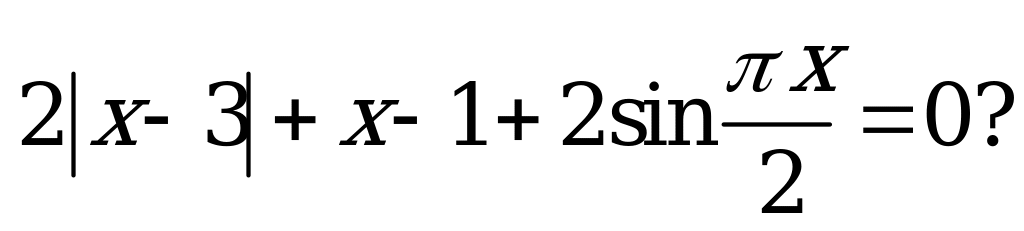 A) B) 1 C) 2 D) 4 E) бесконечно много | B |
| С16 Сколько корней имеет уравнение 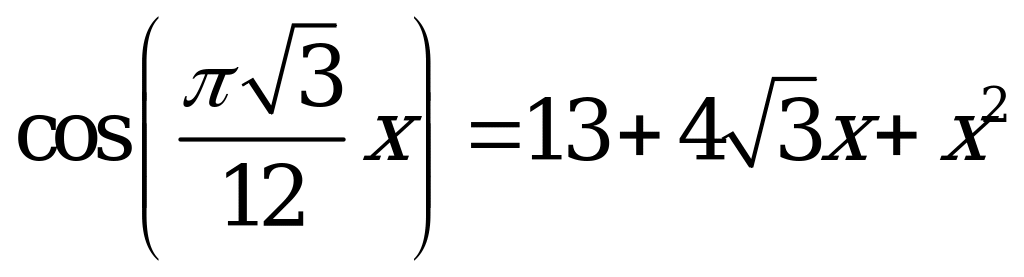 на отрезке на отрезке 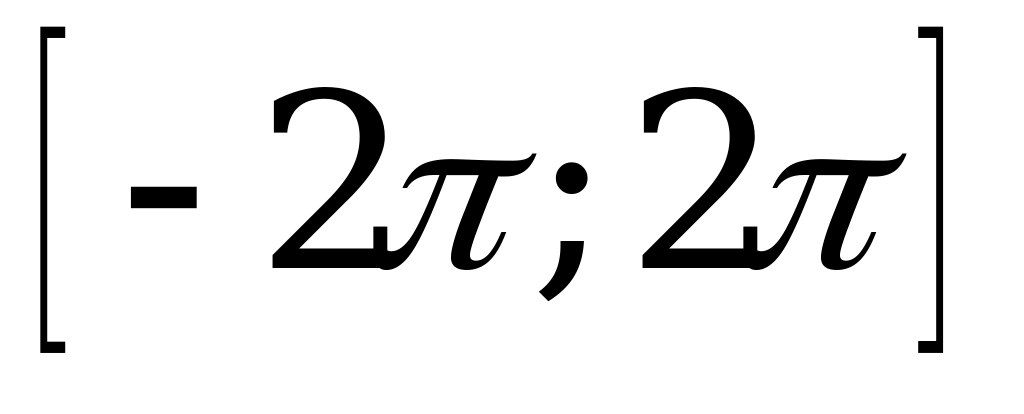 ? ? A) B) 1 C) 2 D) 3 E) 4 | A |
| С17 Сколько корней имеет уравнение 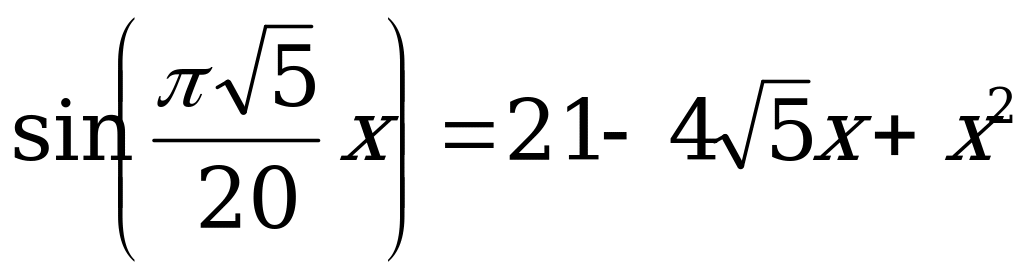 на отрезке на отрезке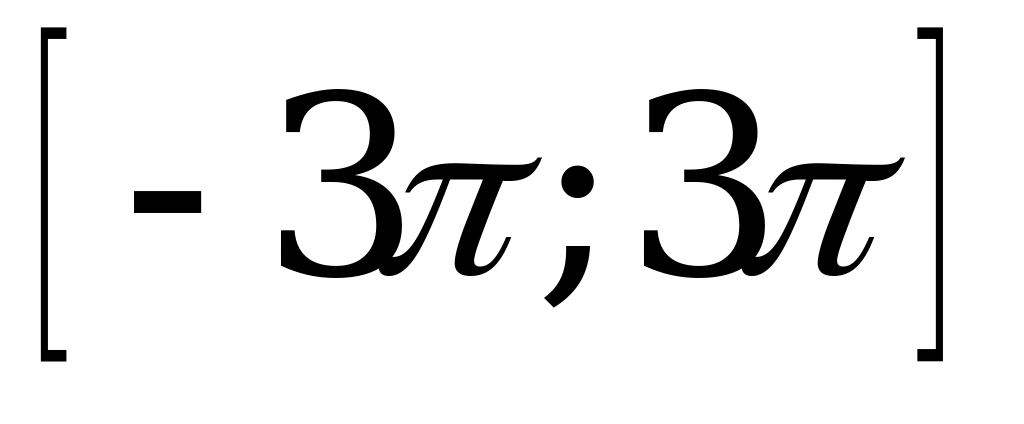 ? ? A) B) 1 C) 2 D) 3 E) 4 | B |
| С18 Решите неравенство 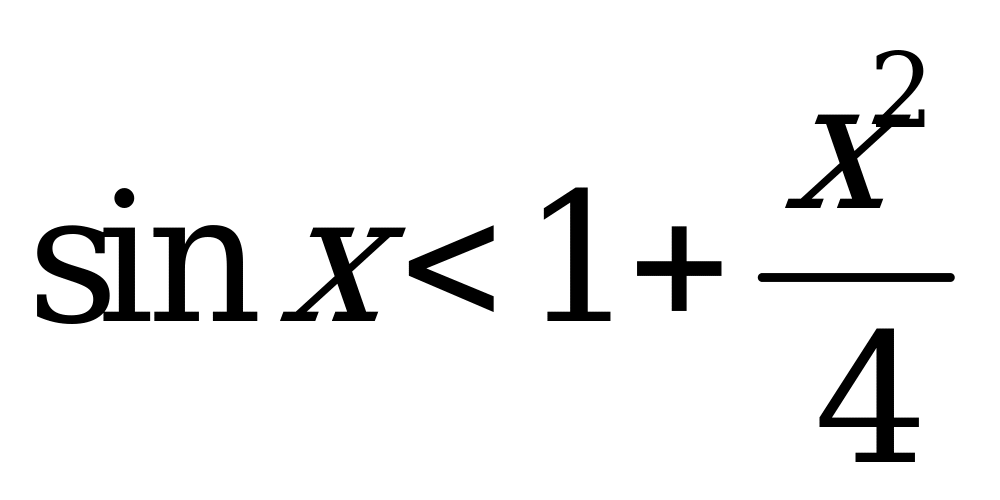 A) B) (-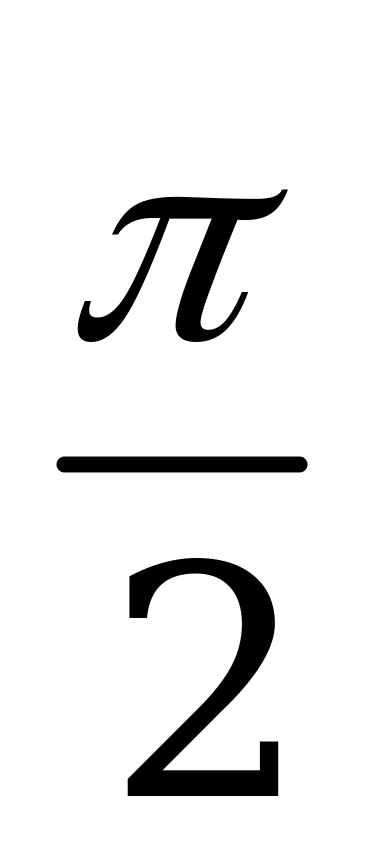 +2n; +2n; 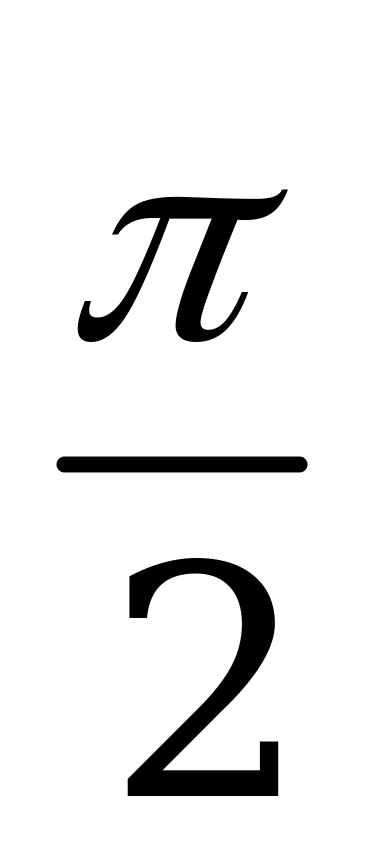 +2n), nZ C) [-; ] +2n), nZ C) [-; ] D) [ -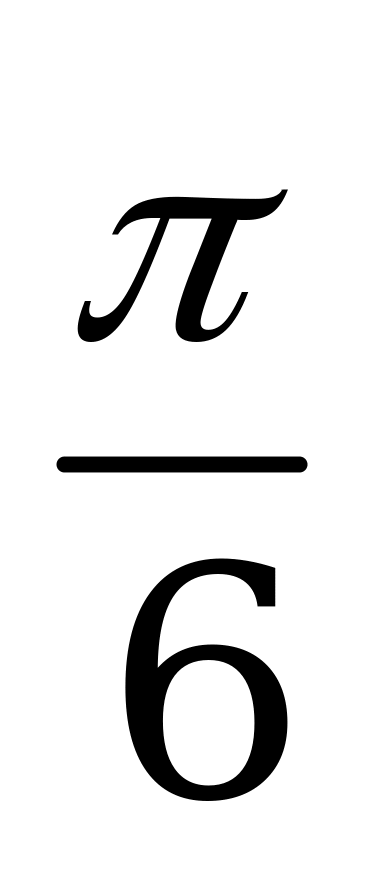 +2n; +2n; 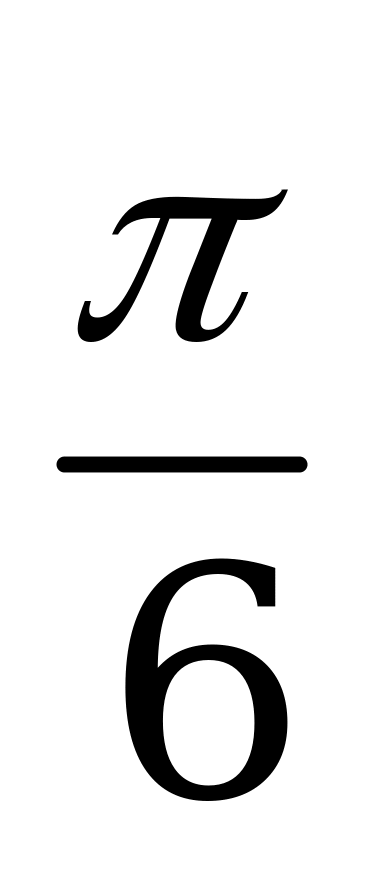 +2n], nZ E) (-; ) +2n], nZ E) (-; ) | E |
| С19 Сколько целых значений входит в область определения функции 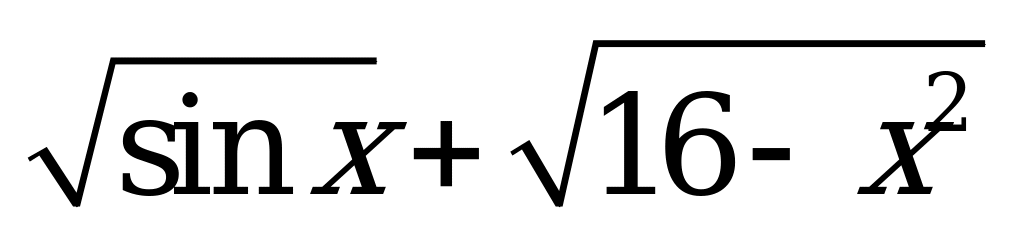 . . A) 3 B) 4 C) 5 D) 2 E) 1 | C |
| С20 Сколько целых чисел из отрезка [-13; 18] принадлежат области определения функции 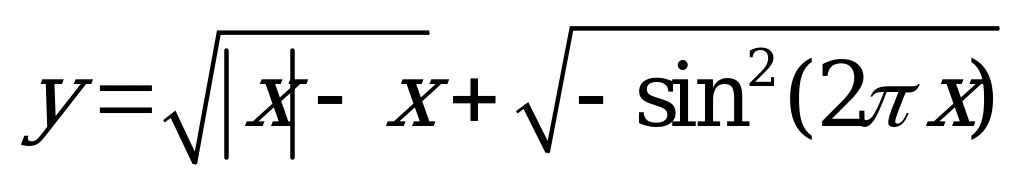 ? ? A) 31 B) 32 C) 22 D) 63 E) 24 | B |
Подведение итогов.
Домашнее задание: составить справочник формул, которые применялись при решении тестовых заданий.
31







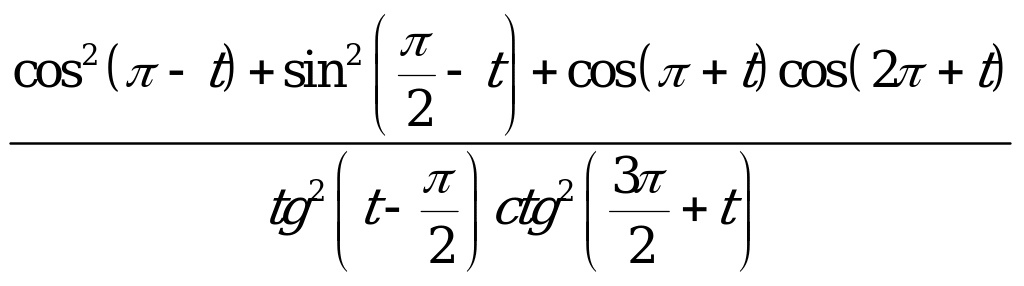 .
.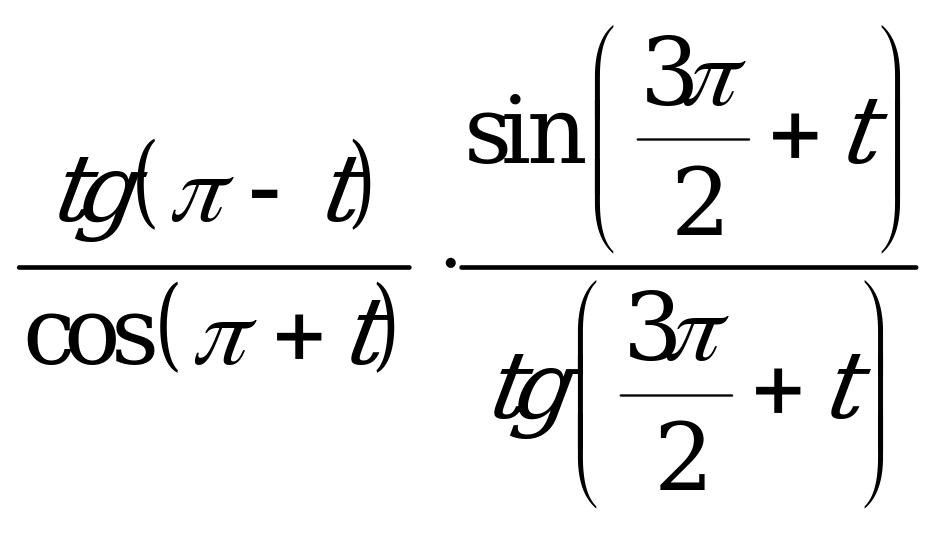
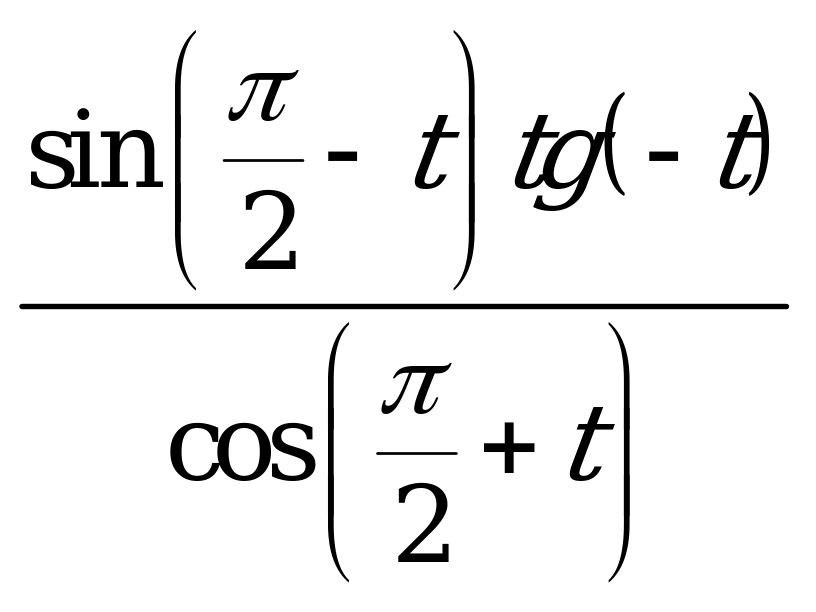 ;
;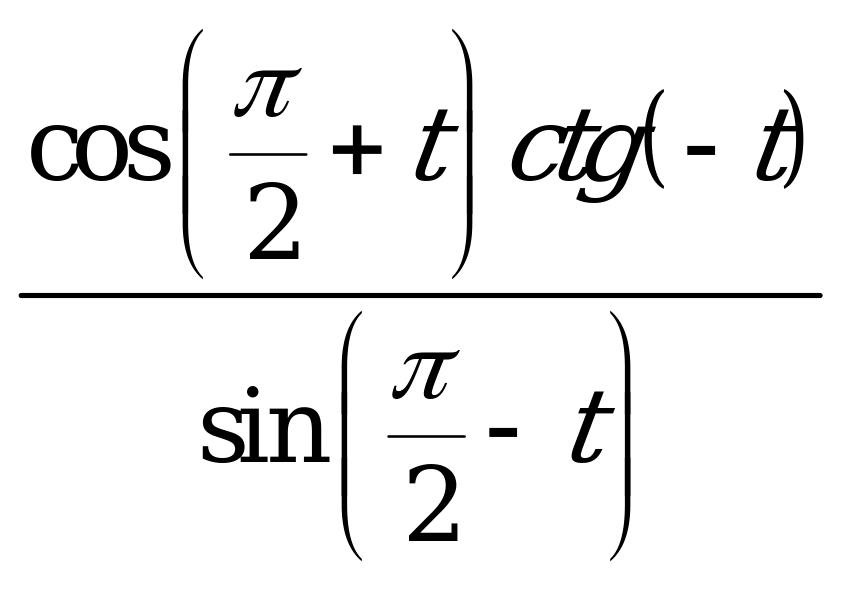 ;
;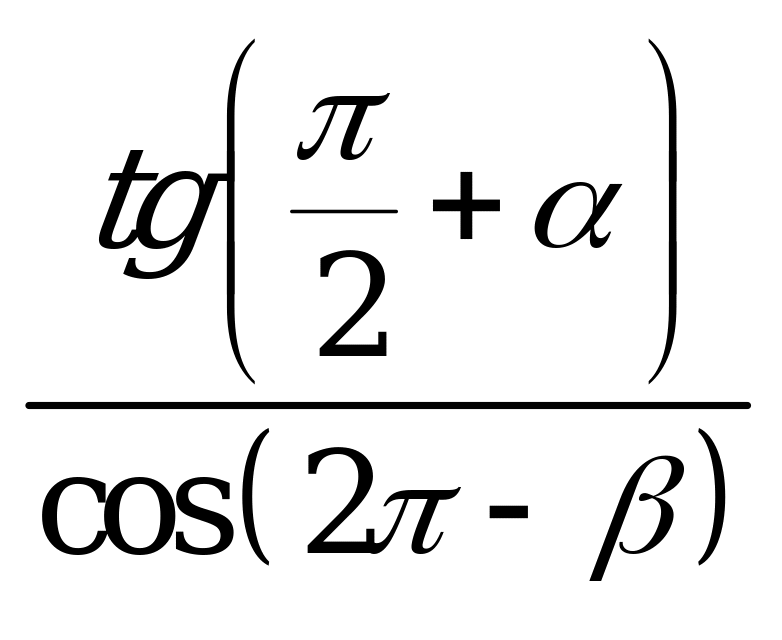 .
.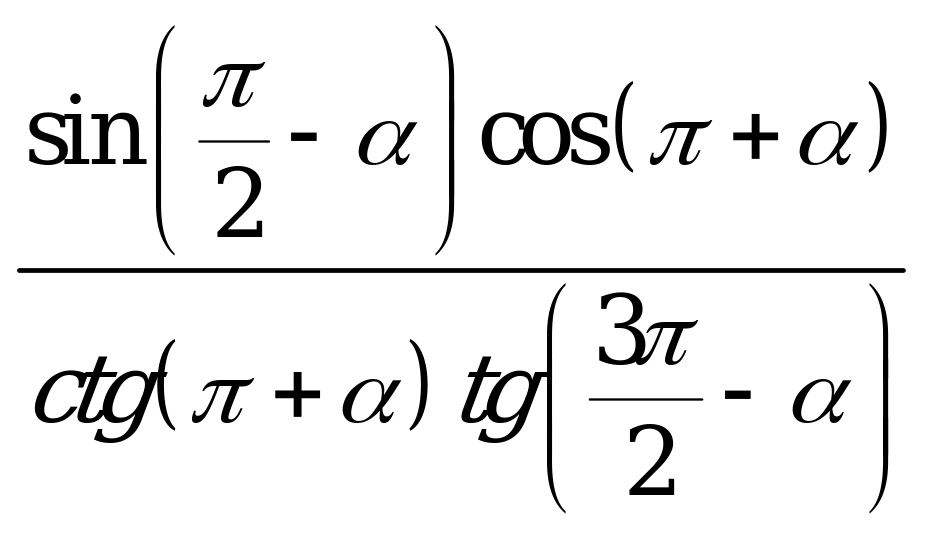
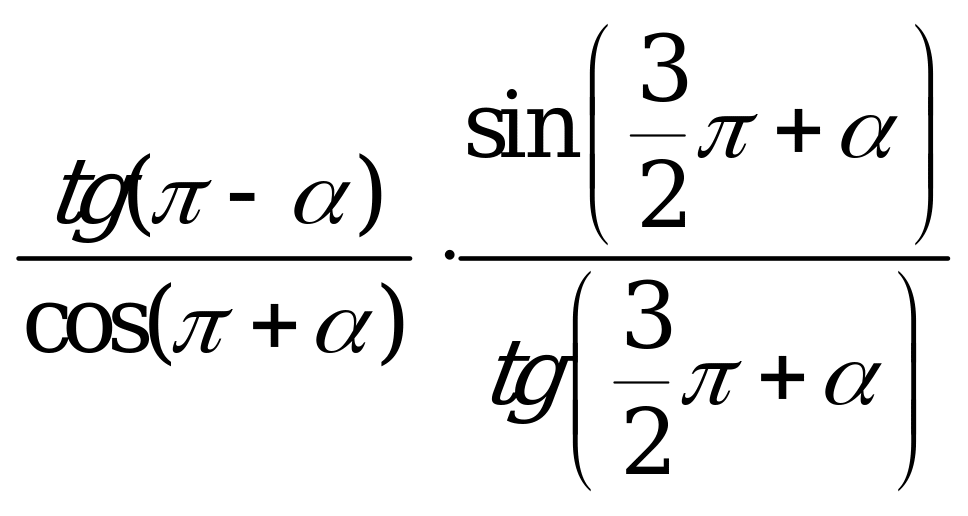 .
.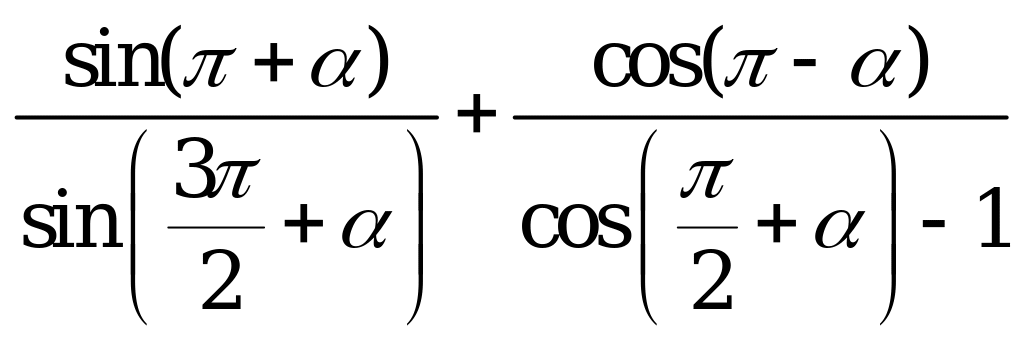
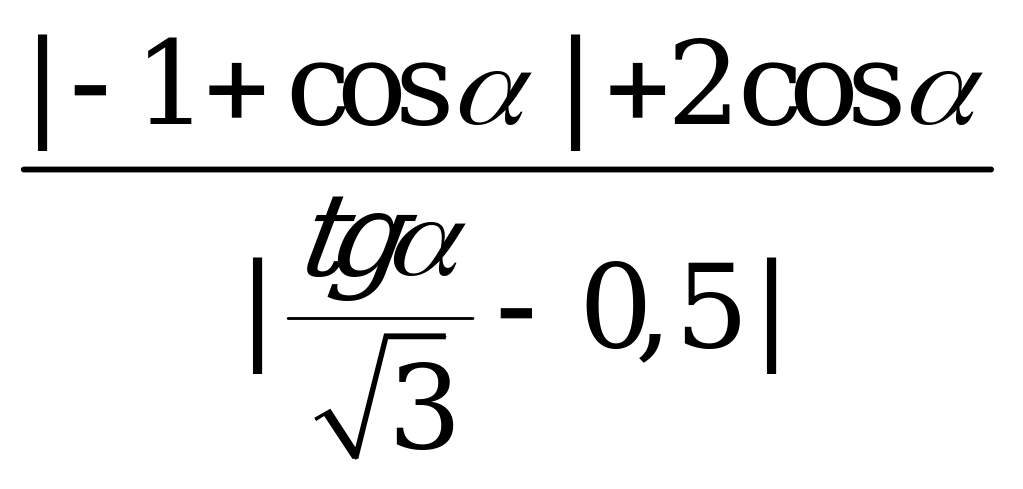 , если
, если