Урок 44. Зачет по теме «Тригонометрические уравнения»
Цели урока: проверить теоретические и практические знания по теме: «Тригонометрические уравнения».
Ход урока:
I. Организационный момент.
Приветствие, сообщение темы и задач урока.
II. Работа в группах.
На уроке, учащиеся объединяются в четыре группы по шесть человек в группе. Учащиеся группы получают карточку с заданиями. Внутри группы учащиеся распределяют между собой задания и, таким образом, каждый учащийся выполняет только одно задание. Решая задания в нутрии группы, можно помогать друг другу, но оценка будет выставляться каждому учащемуся индивидуально.
| Группа №1 |
| задания | №355(в), 357(г), 361(в), 360(а) |
| теория | 1) Арккосинус. Решение уранения 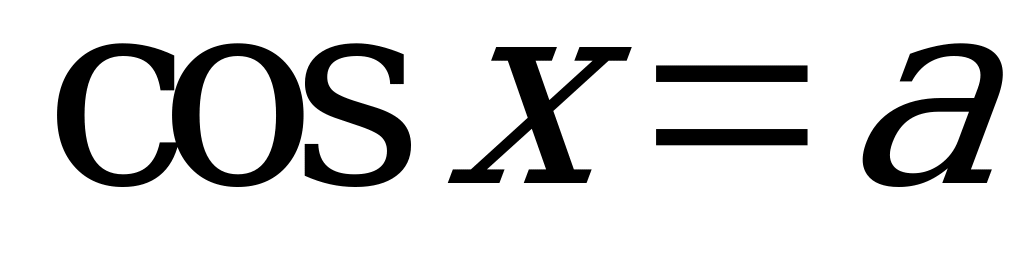 . . 2) Простейшие тригонометрические уравнения. (Составить и решить уравнения) |
| Группа №2 |
| задания | №355(г), 357(в), 361(г), 360(б) |
| теория | 1) Арксинус. Решение уравнения 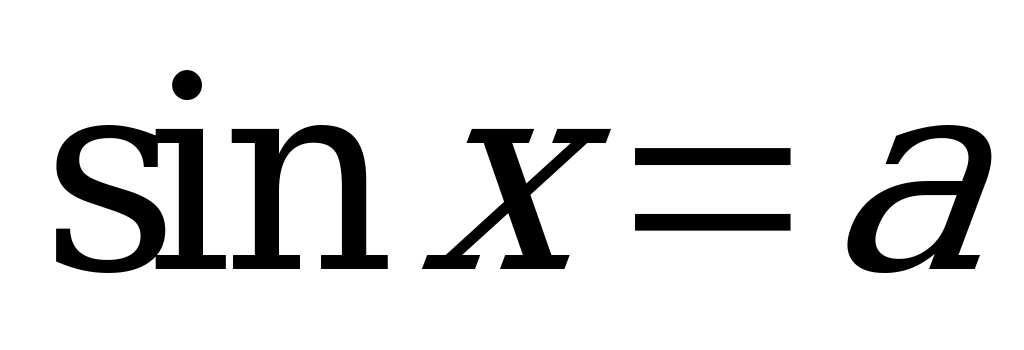 . . 2) Метод введения новой переменной решения тригонометрических уравнений. (Составить и решить уравнения) |
| Группа №3 |
| задания | №356(в), 358(г), 363(в), 360(в) |
| теория | 1) Арктангенс. Решение уравнения 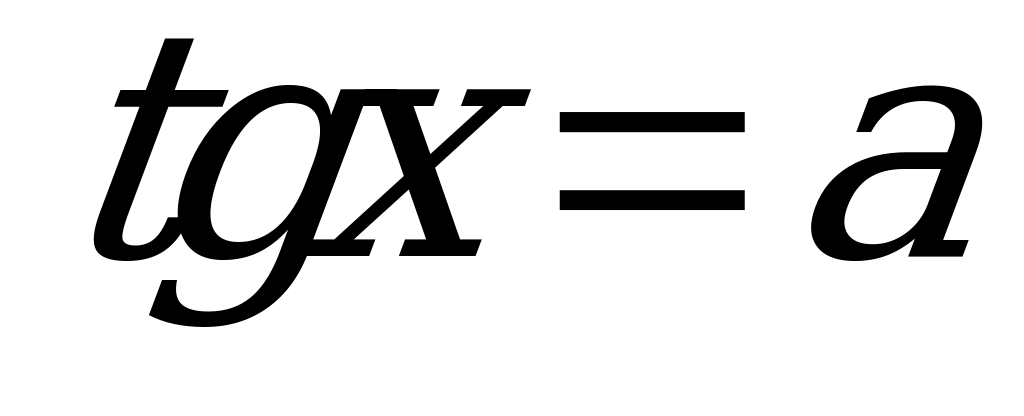 . . 2) Метод разложения на множители решения тригонометрических уравнений. (Составить и решить уравнения) |
| Группа №4 |
| задания | №356(г), 358(в), 363(г), 360(г) |
| теория | 1) Арккотангенс. Решение уравнения 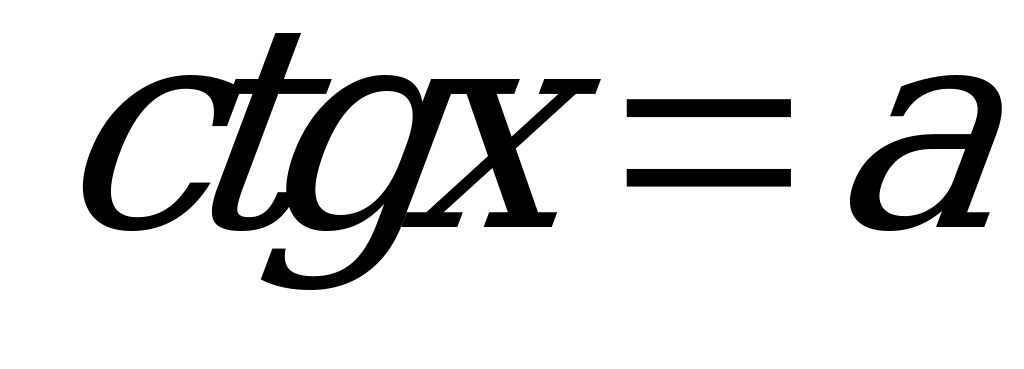 . . 2) Однородные уравнения. (Составить и решить уравнения) |
III. Решение заданий у доски.
Учитель у доски опрашивает учащихся, которые работали над теоретическим вопросом. В процессе ответа у доски учащиеся отвечают на вопросы учеников других групп.
Учащиеся каждой группы сообщают, с каким заданием не справились. Тогда учитель вызывает к доске учащихся из других групп, для решения подобного задания.
Подведение итогов.
Домашнее задание: каждый учащийся в группе решает только
одно задание:
| Группа №1 | а | №365, 372, 373, 375, 378, 387 |
| Группа №2 | б |
| Группа №3 | в |
| Группа №4 | г |
Урок 45. Зачет по теме «Тригонометрические уравнения»
Цели урока: проверить теоретические и практические знания по теме: «Тригонометрические уравнения».
Ход урока:
Организационный момент.
Приветствие, сообщение темы и задач урока.
II. Работа в группах.
На уроке, учащиеся объединяются в шесть групп по четыре
человека в каждой группе по схеме: все учащиеся, решавшие один номер, образуют одну группу.
|
| №365 | №372 | №373 | №375 | №378 | №387 |
| Группа | №1 | №2 | №3 | №4 | №5 | №6 |
Собравшись в группу, учащиеся проверяют совместно домашнее задание и затем сдают учителю на проверку. Каждая группа получает карточки с заданиями.
| Группа №1 | а | №376, 382, 385, 390, 384 | а, б | №394 |
| Группа №2 | б | №376, 382, 385, 390, 384 | в, г | №394 |
| Группа №3 | а | №366, 377, 383, 393, 370 | а, б | №395 |
| Группа №4 | б | №366, 377, 383, 393, 370 | в, г | №395 |
| Группа №5 | а | №367, 381, 386, 392, 371 | а | №396 |
| Группа №6 | б | №367, 381, 386, 392, 371 | б | №396 |
III. Решение заданий у доски.
Доска разделена на 6 частей и учитель в процессе всего урока вызывает к доске учащихся, которые считают, что справились с решением. Учитель, лично, не отвлекая учащихся, проверяет решение у доски.
Подведение итогов.
Домашнее задание: учащиеся выбирают любую группу заданий:
| №389(а) | №389(б) | №389(в) | №389(г) |
| №391(а) | №391(б) | №391(в) | №391(г) |
| №388(а) | №388(б) | №388(в) | №388(г) |
| №397(а) | №397(б) | №398(а) | №398(б) |
Урок 46. Контрольная работа №2
Цели урока: проверить знания и умение учащихся по теме «Тригонометрические уравнения».
Ход урока:
I. Организационный момент.
Приветствие, сообщение темы и задач урока.
II. Решение контрольных заданий.
Уровень  :
:
| Вариант №1 | Вариант №2 |
| 1. Решите уравнения: |
| 1) 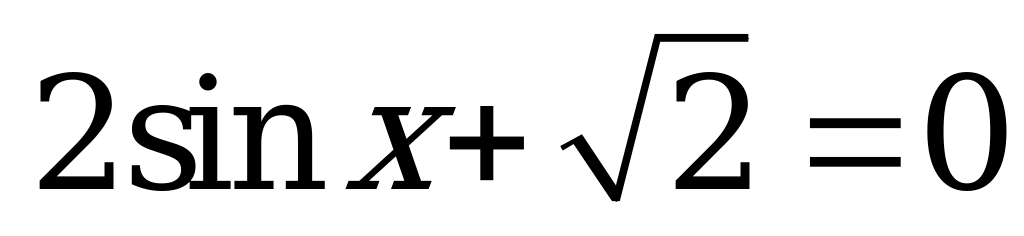 ; ; 2) 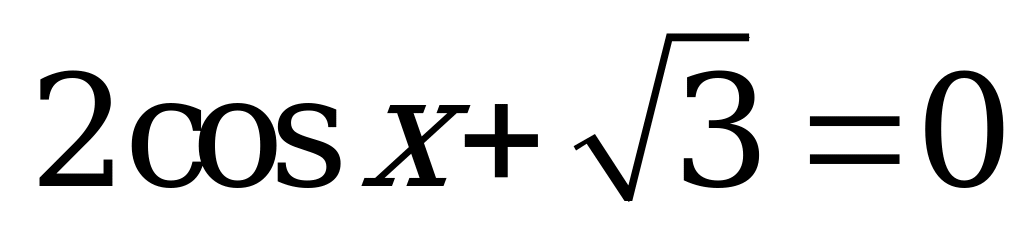 ; ; 3) 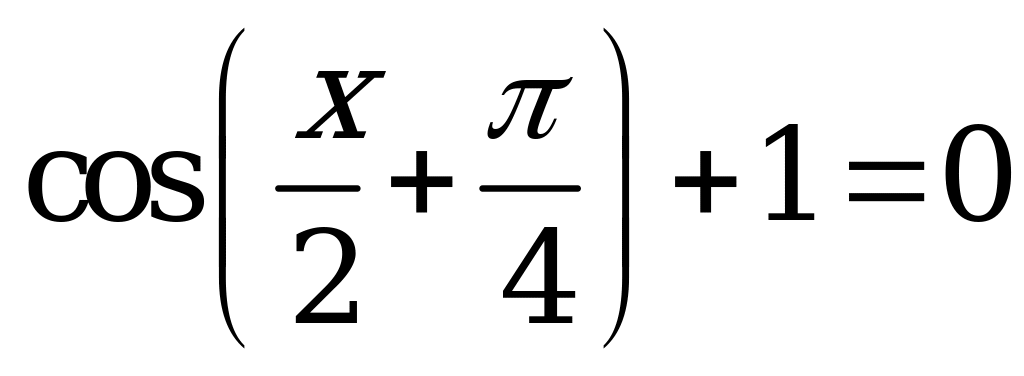 ; ; 4) 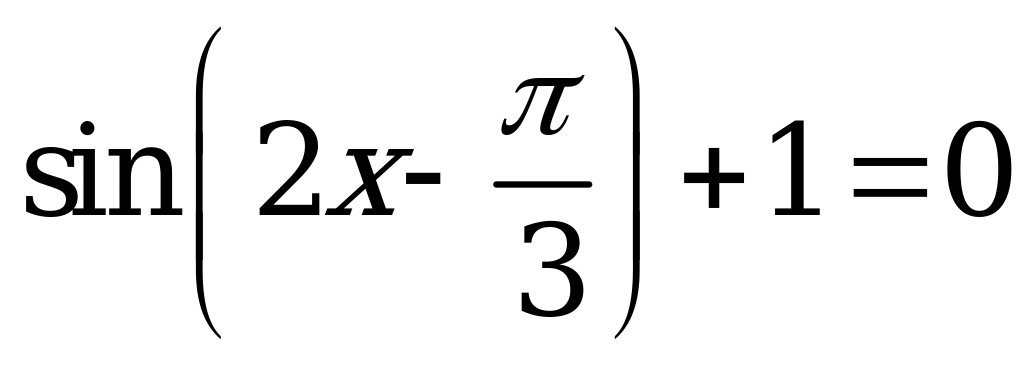 . . | 1) 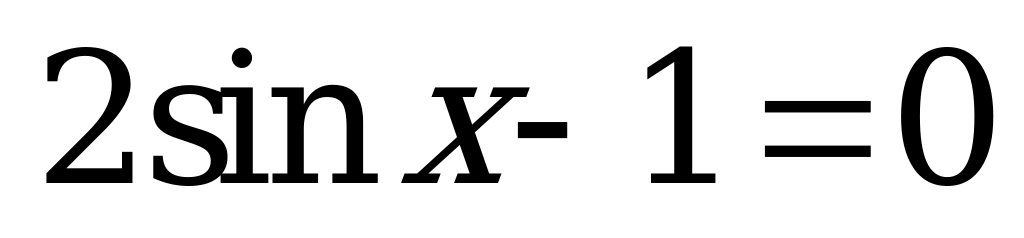 ; ; 2) 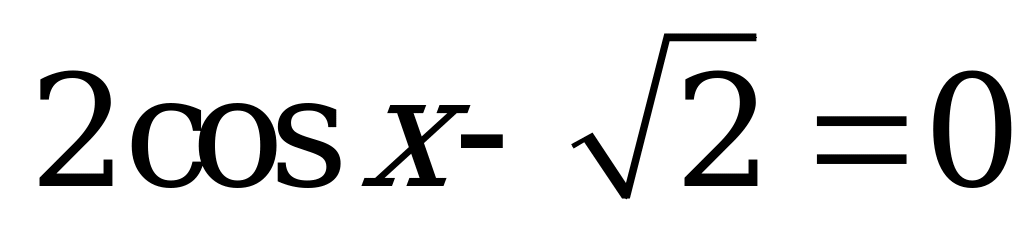 ; ; 3) 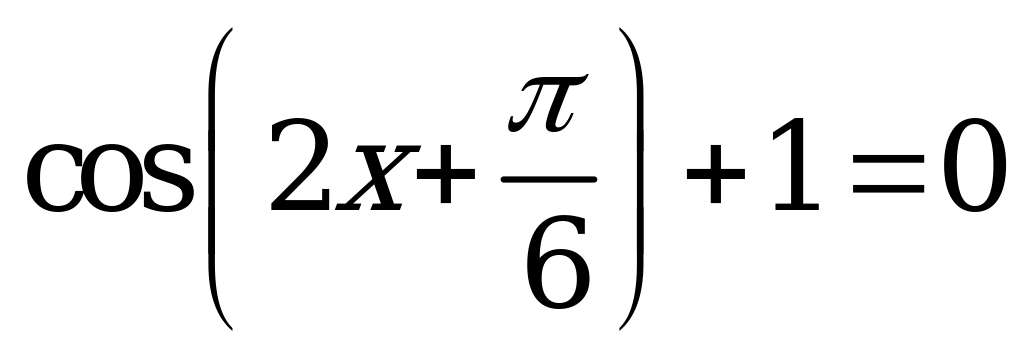 ; ; 4) 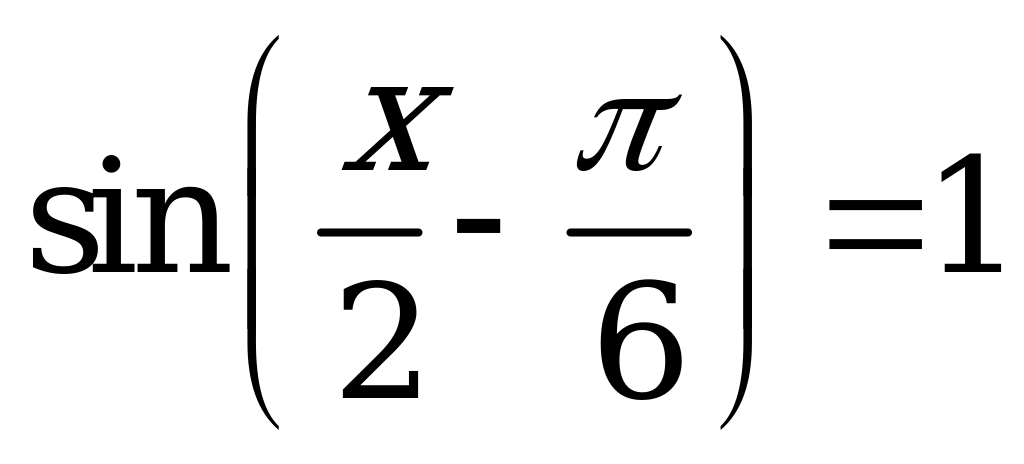 . . |
| 2. Упростить и решить уравнение |
| 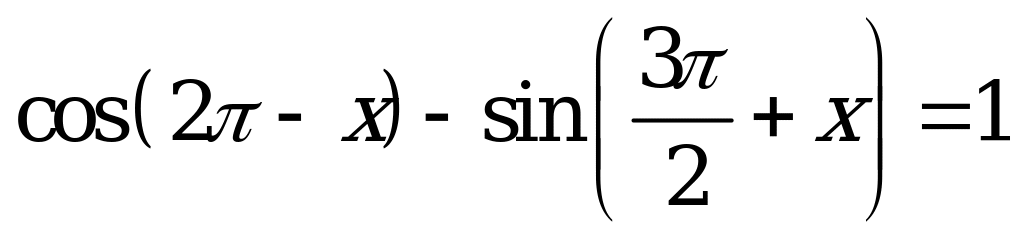
| 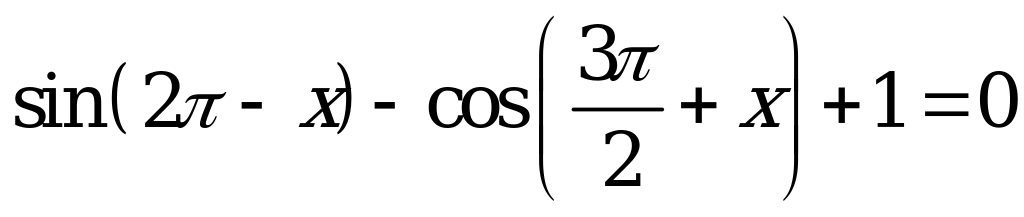
|
Уровень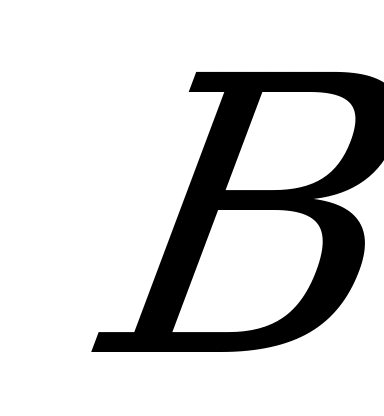 :
:
| Вариант №1 | Вариант №2 |
| 1. Упростить и решить уравнение |
| 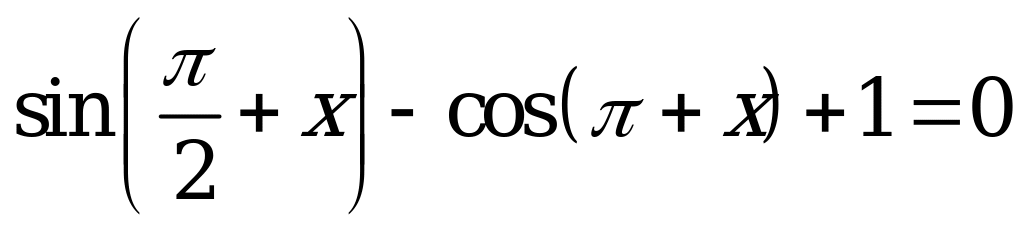
| 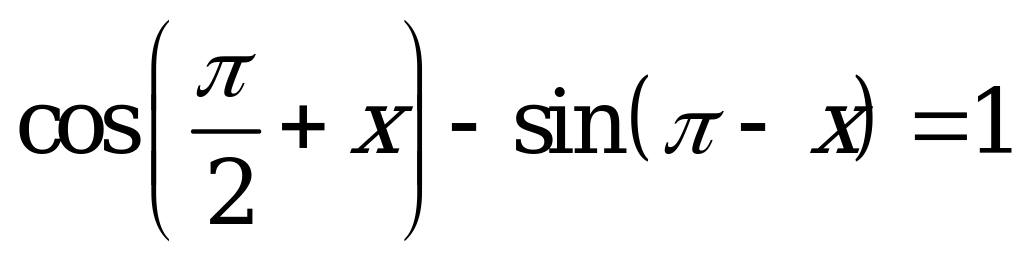
|
| 2. Решите уравнения: |
| 1) ; ; 2) 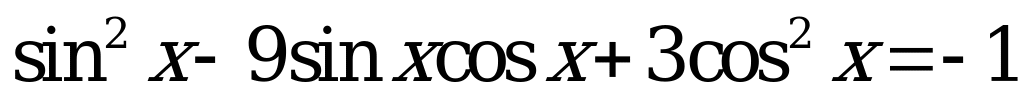 | 1) 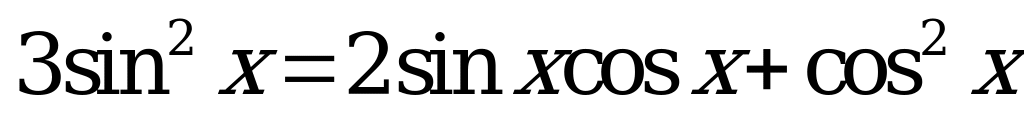 ; ; 2) 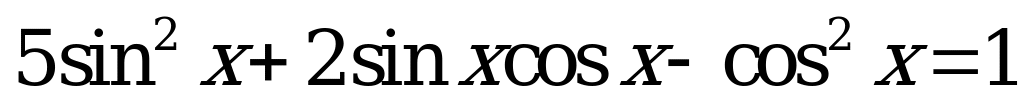 |
| 3. Найдите корни уравнения на отрезке |
| 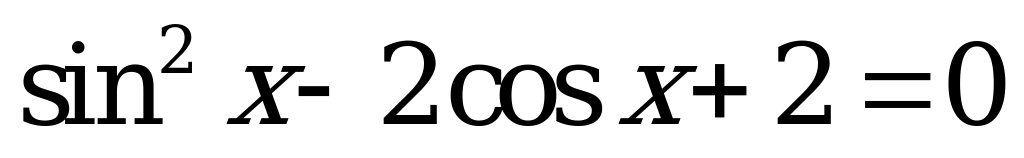 , , 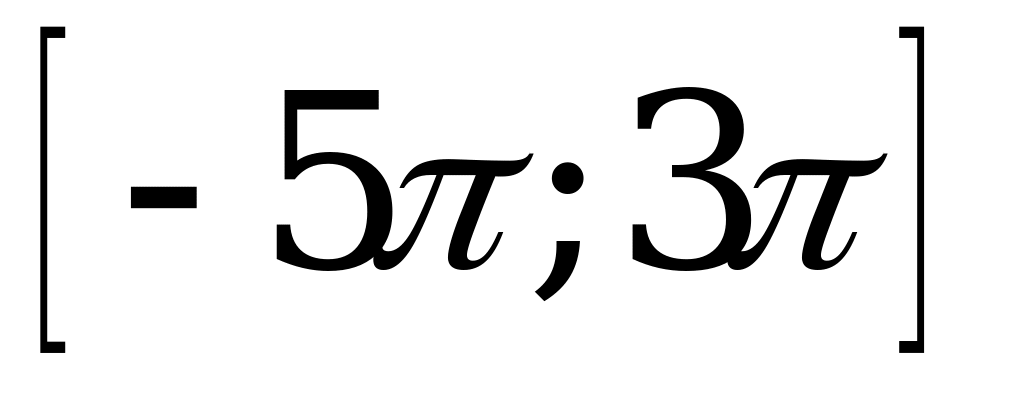
| 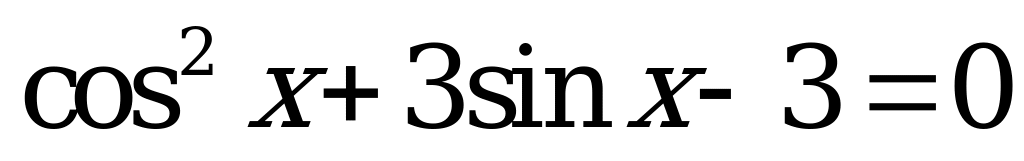 , , 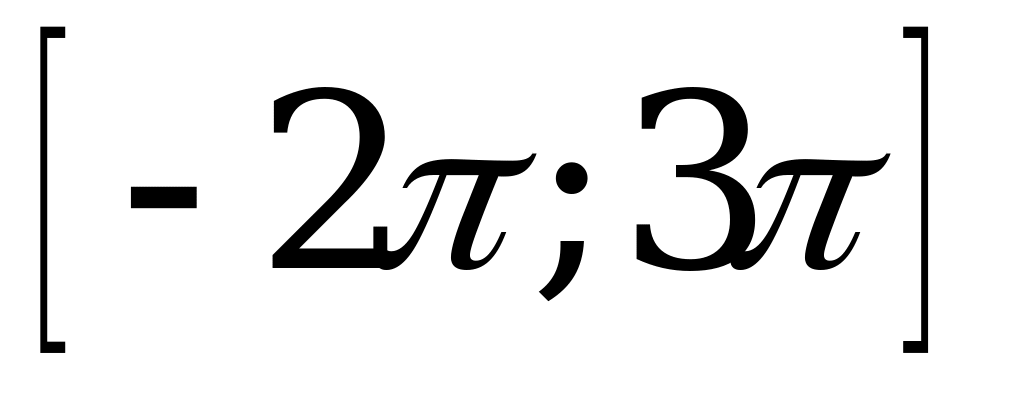
|
Уровень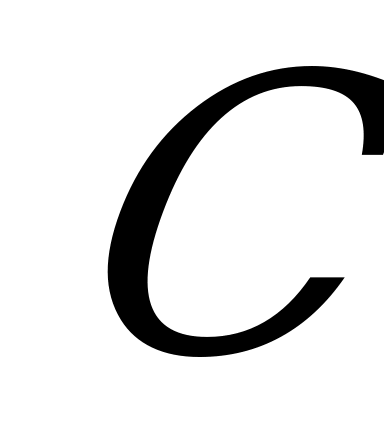 :
:
| Вариант №1 | Вариант №2 |
| 1. Решите уравнения: |
| 1) 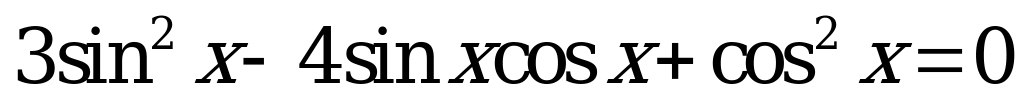 ; ; 2) 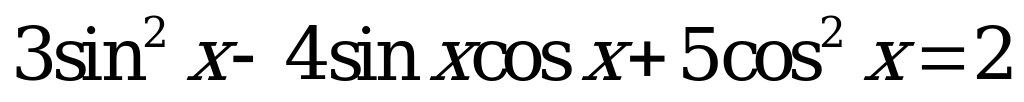 . . | 1) 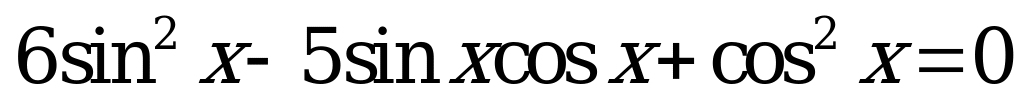 ; ; 2) 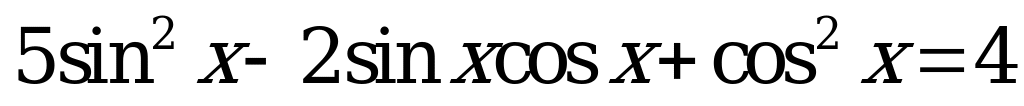 . . |
| 2. Найдите корни уравнений на отрезке: |
| 1) 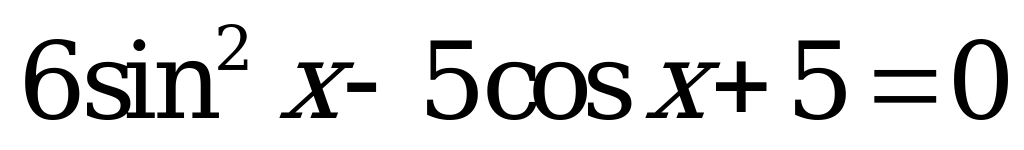 , ,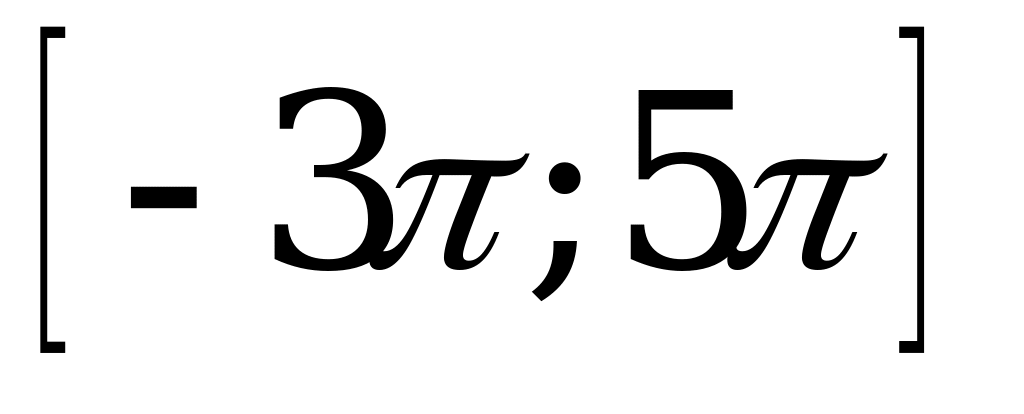 ; ; 2) 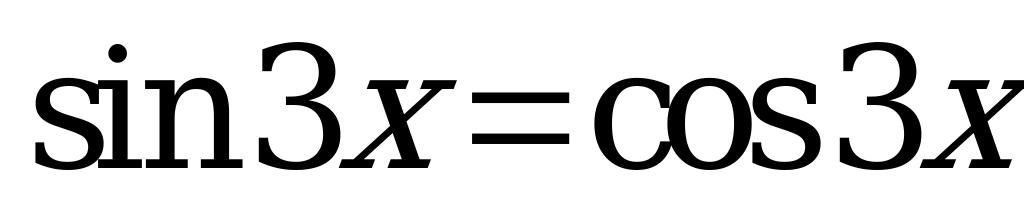 , , 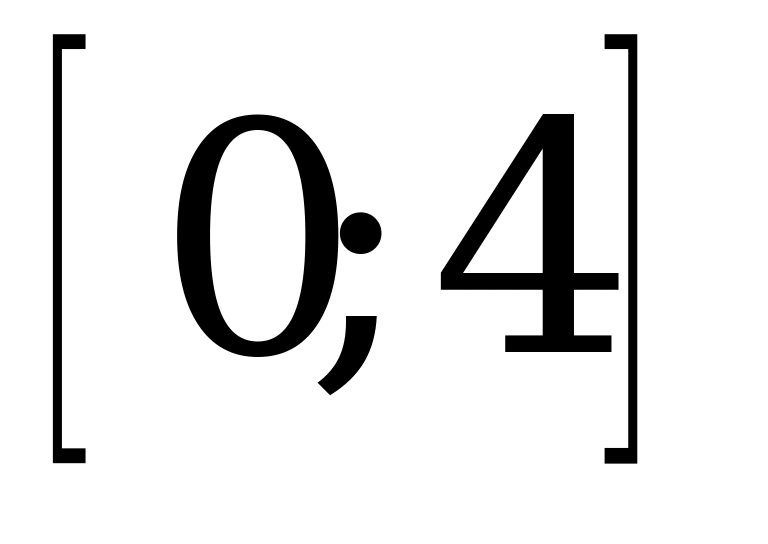 . . | 1) 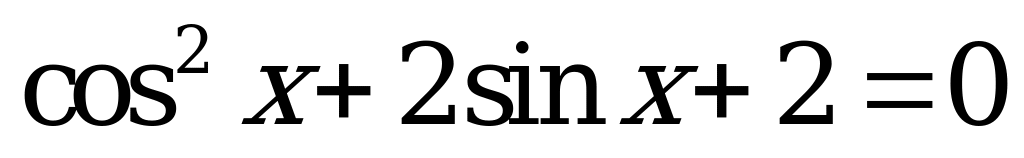 , ,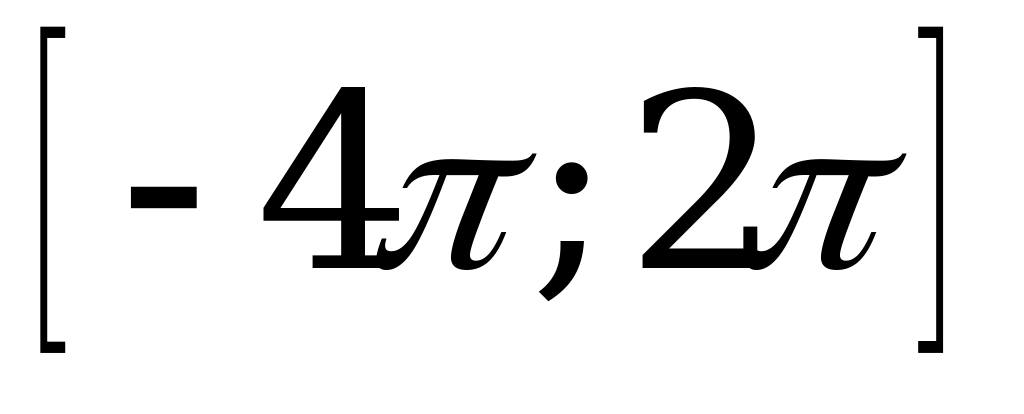 ; ; 2) 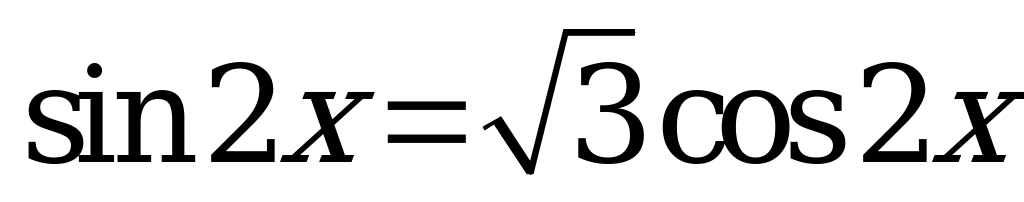 , , 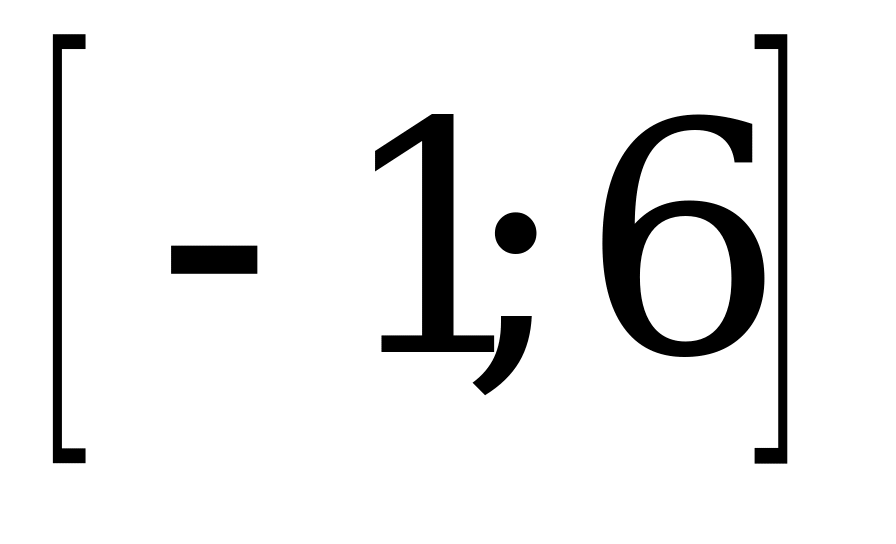 . . |
Подведение итогов.
Домашнее задание: Сделать краткий конспект теории по теме
«Тригонометрические уравнения».
Уроки 47 - 50. Учебно-тренировочные тестовые задания ЕГЭ по теме: «Тригонометрические уравнения»
Цели урока: решение тестовых заданий базового уровня , более сложного уровня
, более сложного уровня 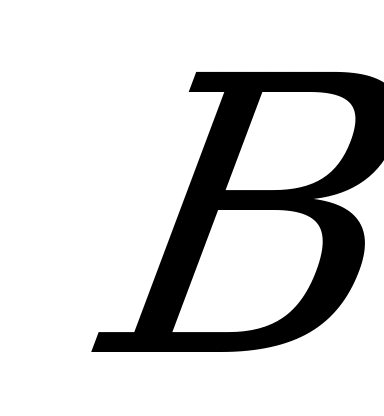 , наиболее сложного уровня
, наиболее сложного уровня 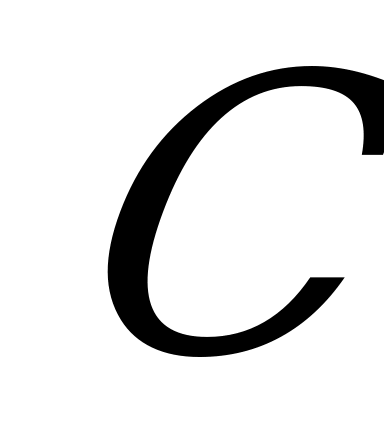 по теме «Тригонометрические уравнения»
по теме «Тригонометрические уравнения»
Ход урока:
I. Организационный момент.
Приветствие, сообщение темы и задач урока.
II. Организация решения тестовых заданий.
Учитель распределяет тестовые задания на четыре урока
следующим образом:
Урок 30. Решение тестовых заданий базового уровня .
.
Урок 31. Решение тестовых заданий базового уровня и тестовых заданий более сложного уровня
и тестовых заданий более сложного уровня 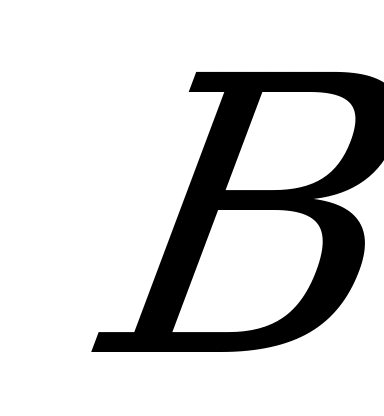 .
.
Урок 32. Решение тестовых заданий более сложного уровня 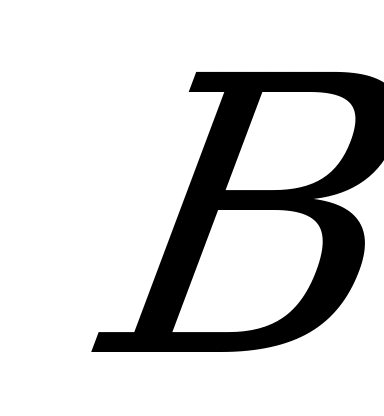 .
.
Урок 33. Решение тестовых заданий наиболее сложного уровня 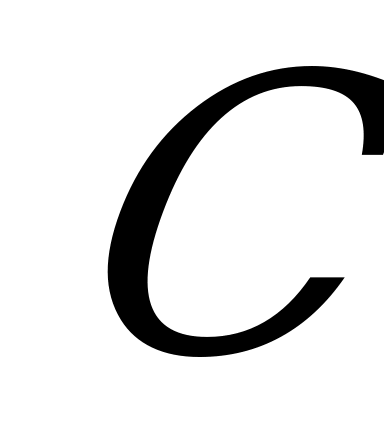 .
.
III. Учебно-тренировочные тестовые задания ЕГЭ
Тестовые задания базового уровня .
.
| А1. Обратные тригонометрические функции | Ответы |
| А1.1 Вычислите: 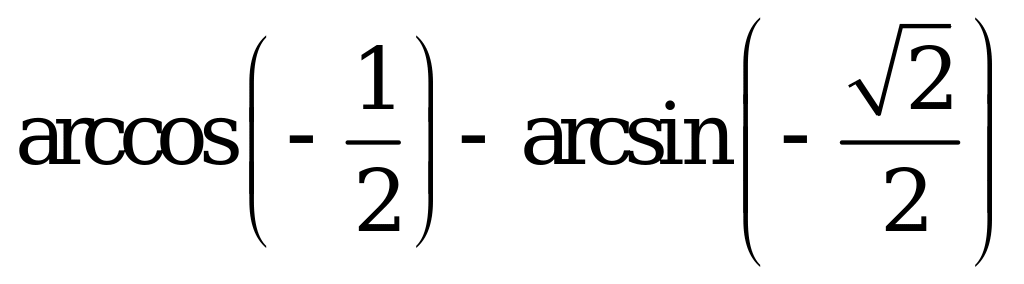 A) 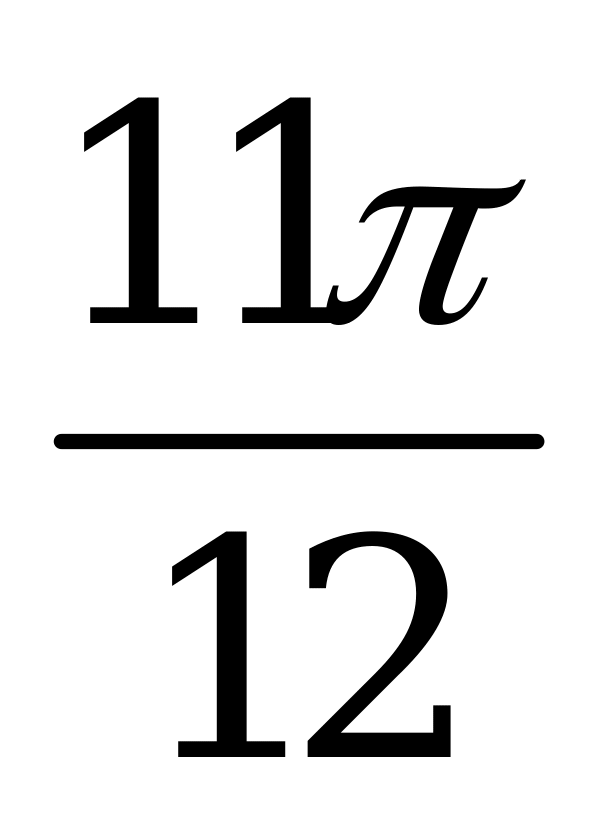 B) B) 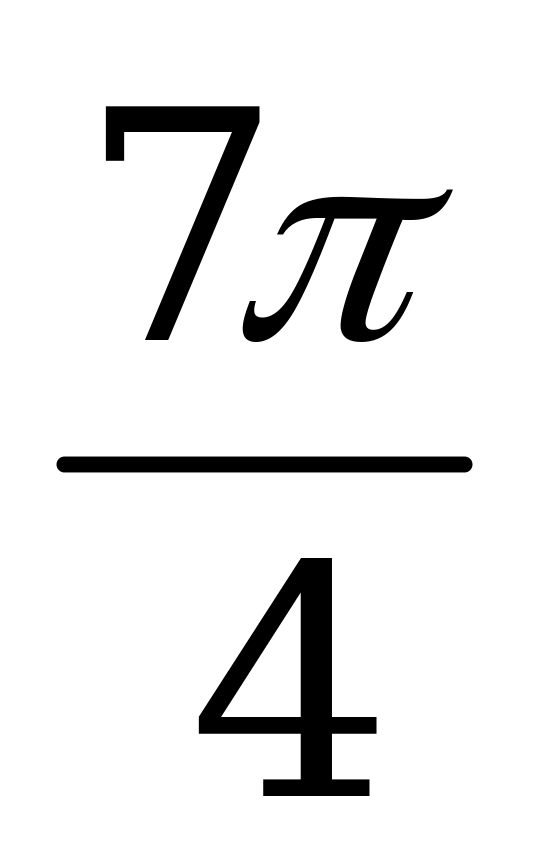 C) C) 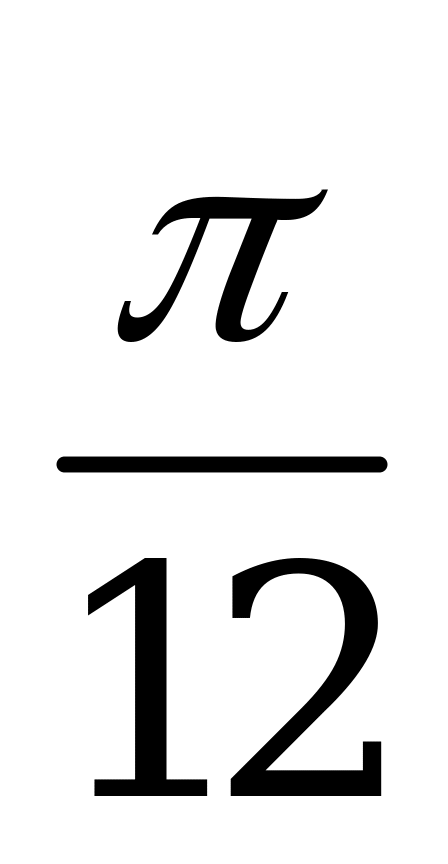 D) D) 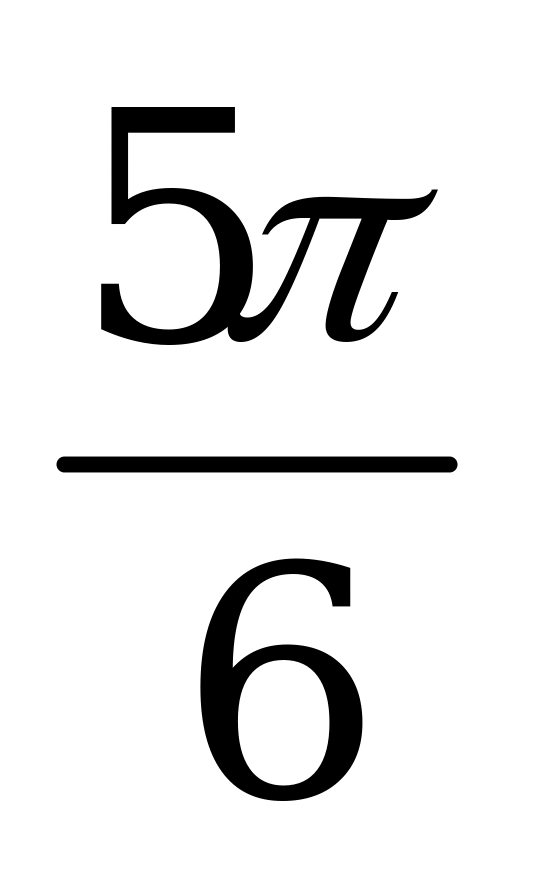 E) E) 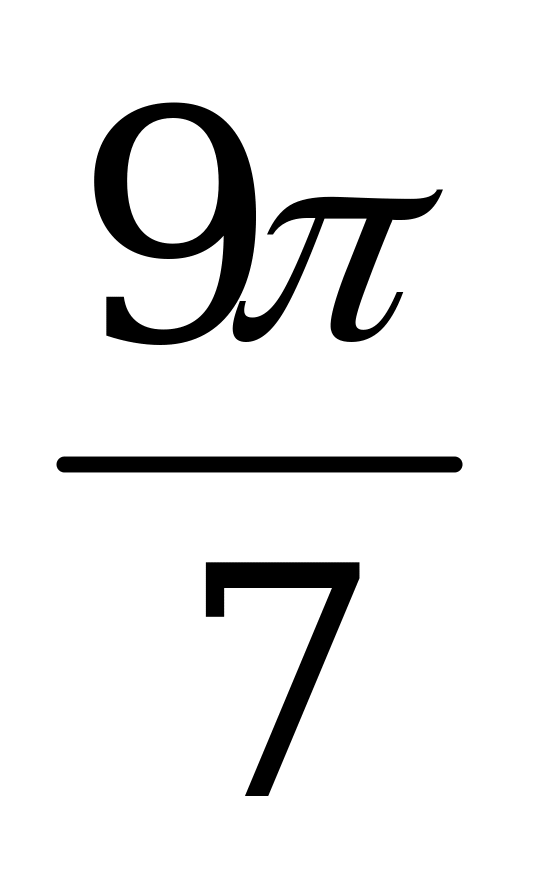 | A |
| А1.2 Вычислите 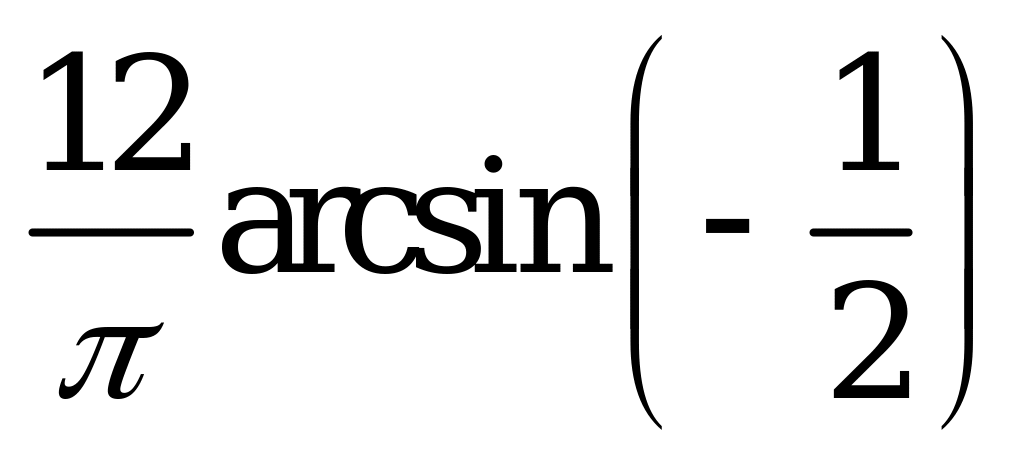 A) 0 B) -2 C) 2 D) 1 E) -1 | B |
| А1.3 Вычислите: 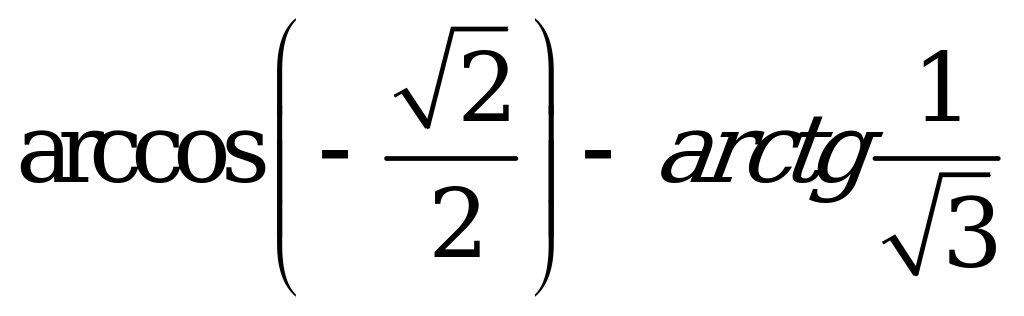 A) -750 B) 750 C) -1050 D) 1650 E) 1050 | E |
| А1.4 Вычислите 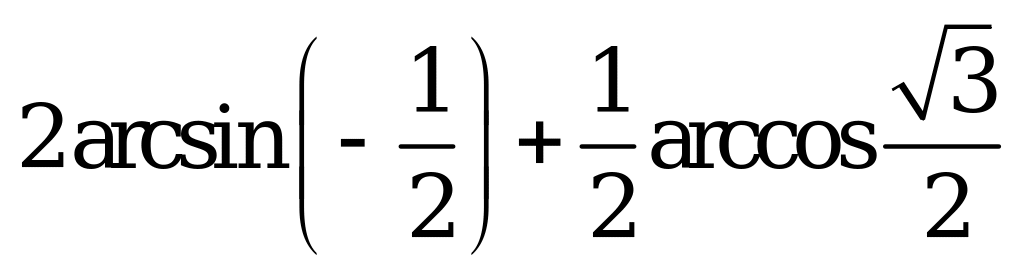 A) -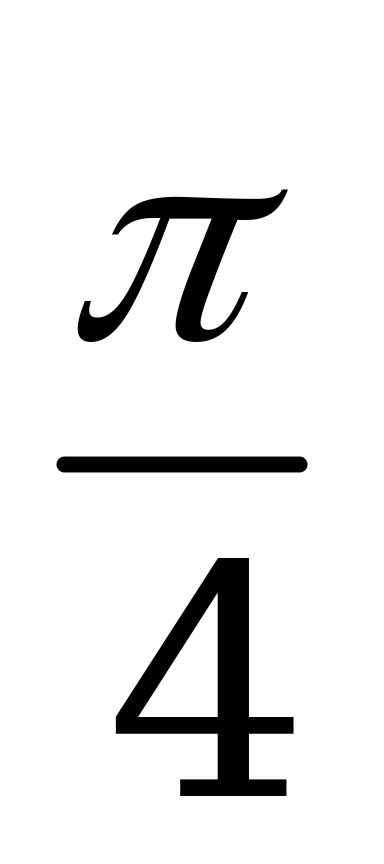 B) B) 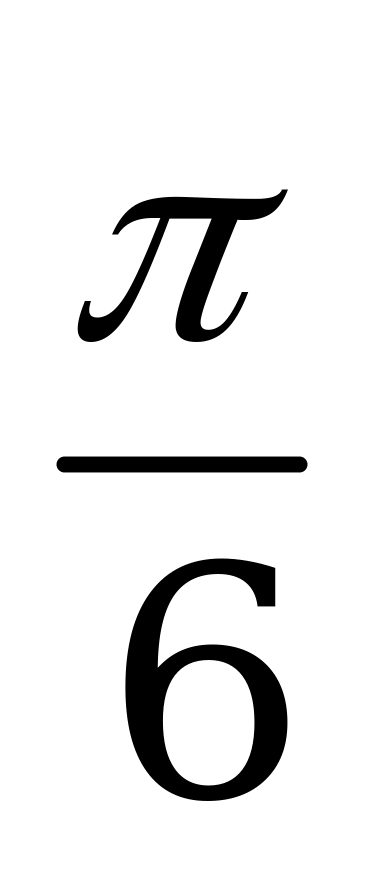 C) 0 D) C) 0 D) 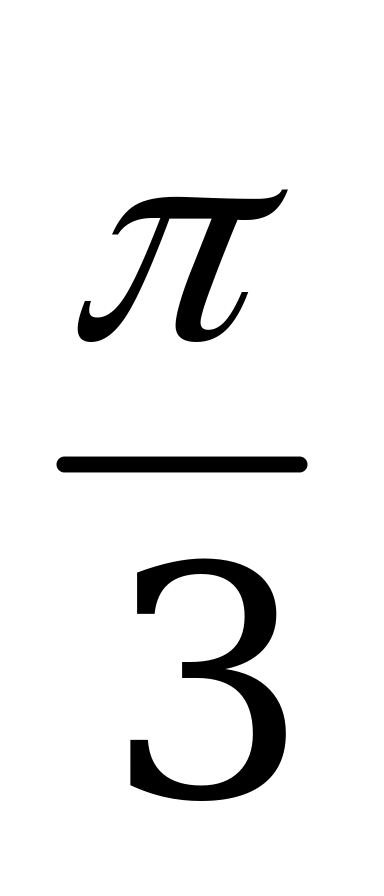 E) - E) -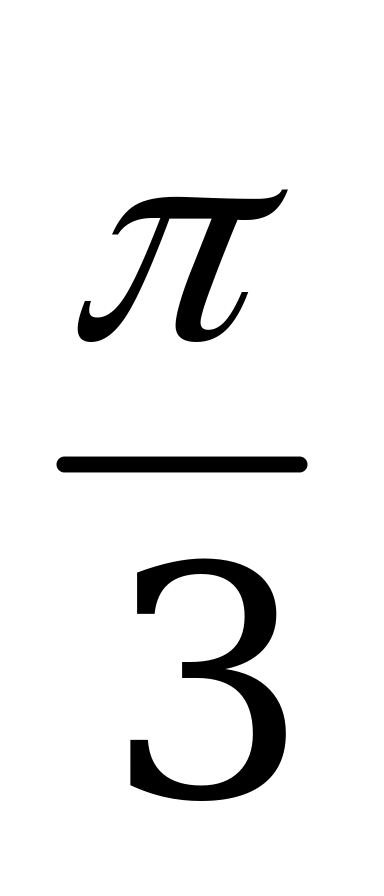 | A |
| А1.5 Вычислите: 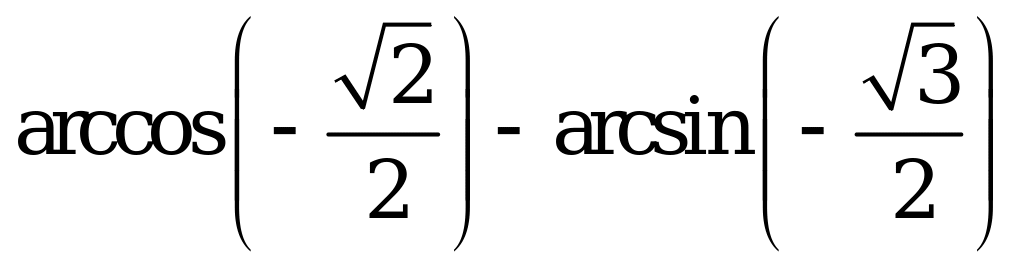 . . A) 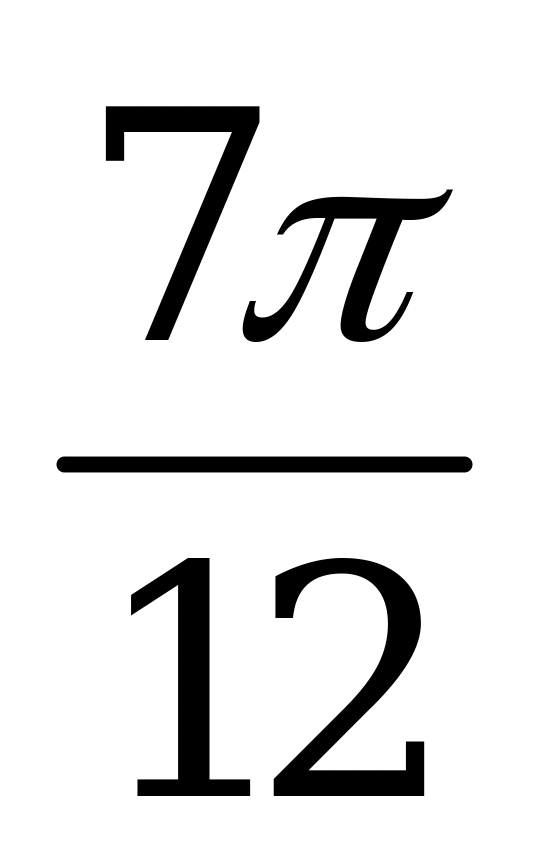 B) B) 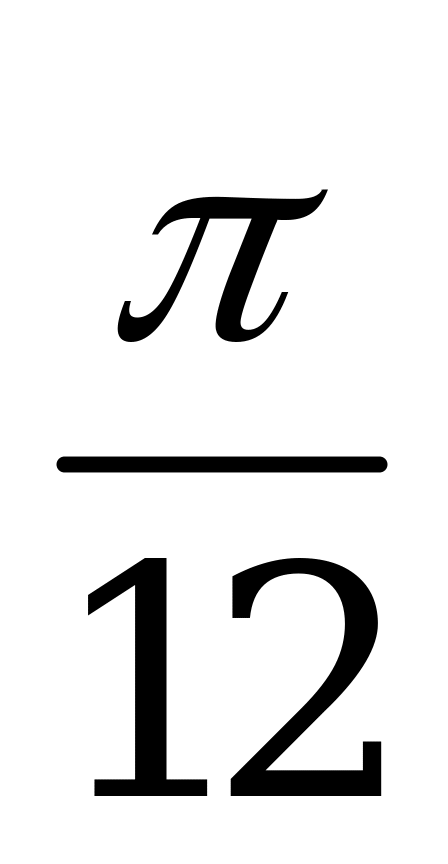 C) C) 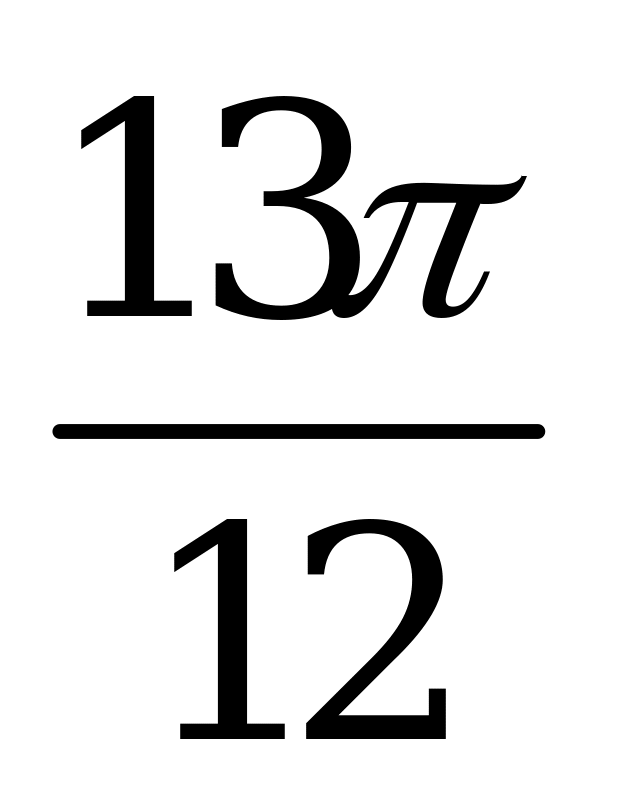 D) D) 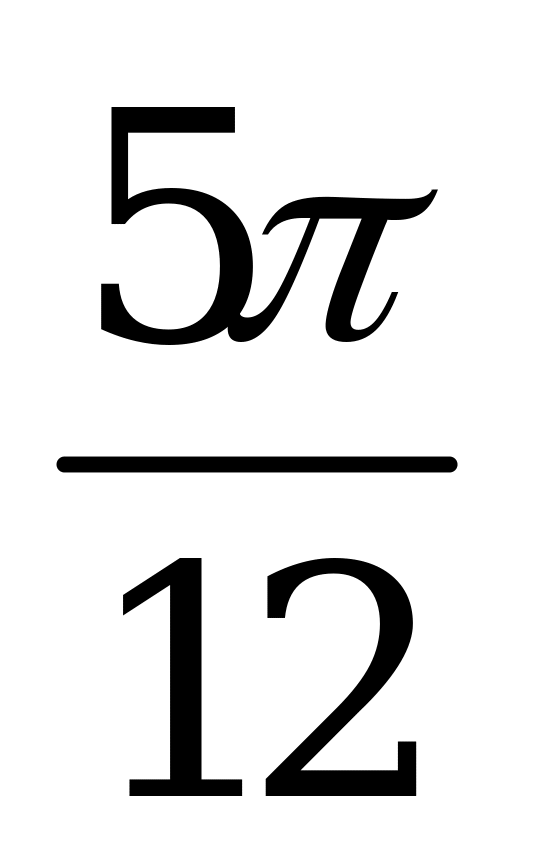 E) - E) -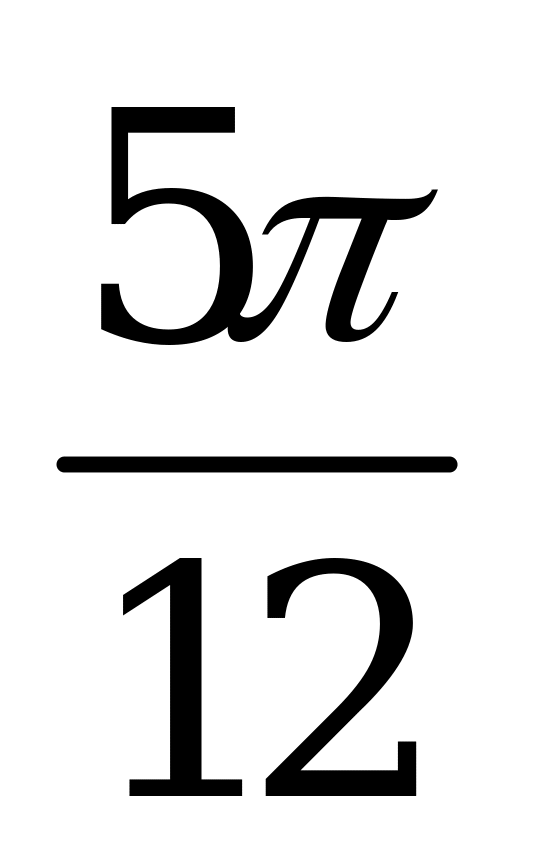 | C |
| А1.6 Вычислите: 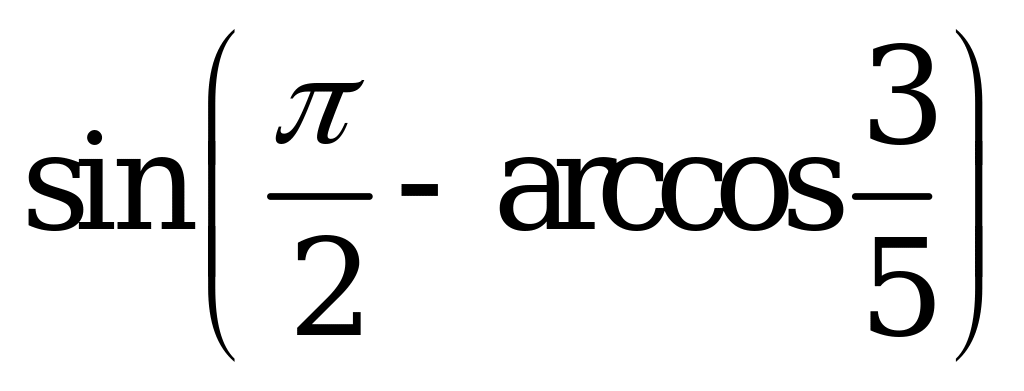 A) 0,8 B) 0,4 C) 0,7 D) 0,5 E) 0,6 | E |
| А1.7 Найдите 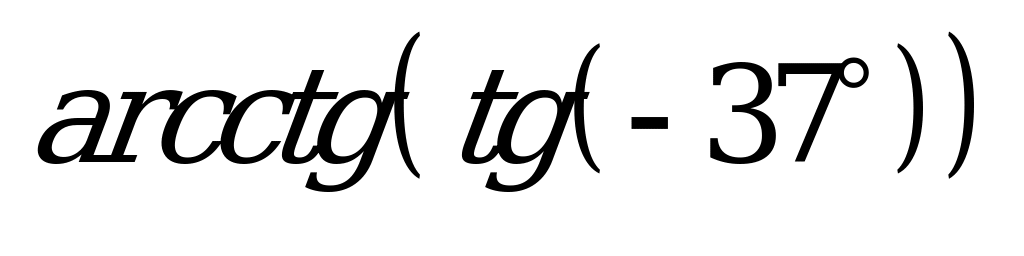 A) 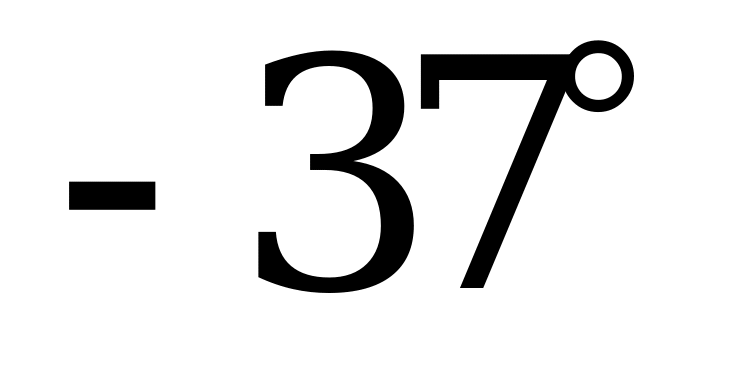 B) B)  C) C) 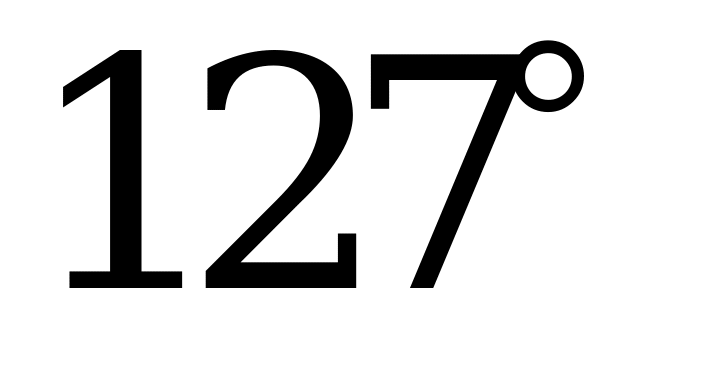 D) D) 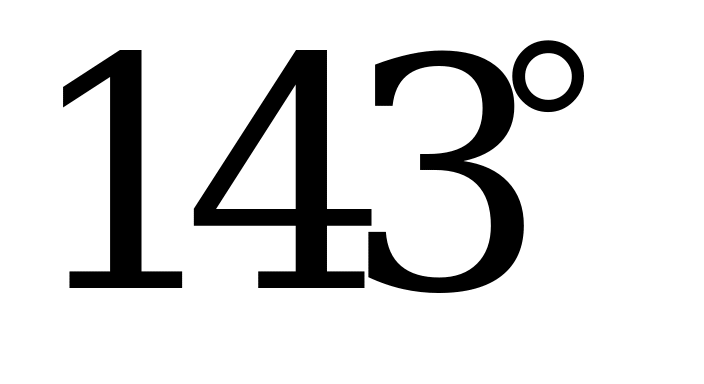 E) E)  | C |
| А1.8 Вычислить: 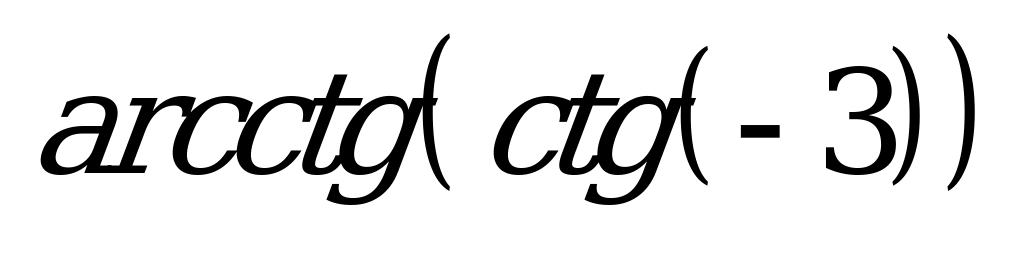 A)  + 3 B) 2 + 3 B) 2 - 3 C) - 3 C) 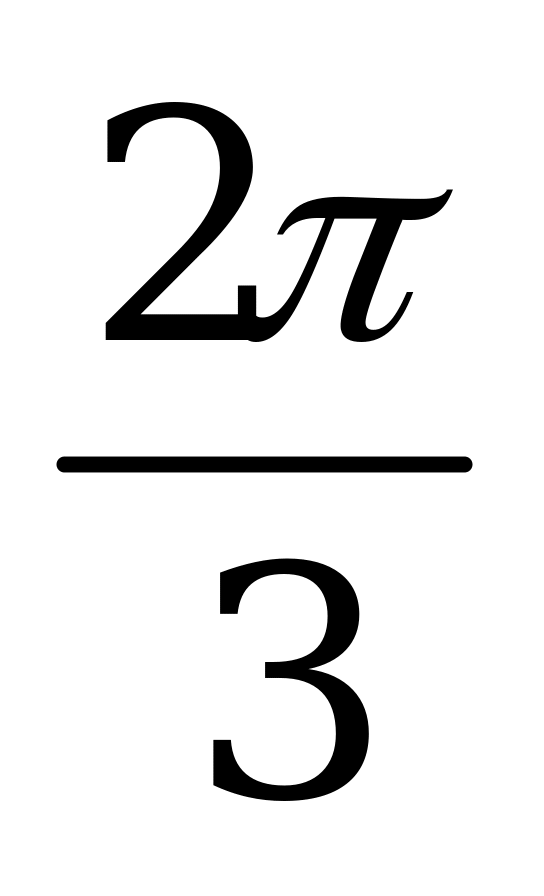 - 3 D) - 3 D) 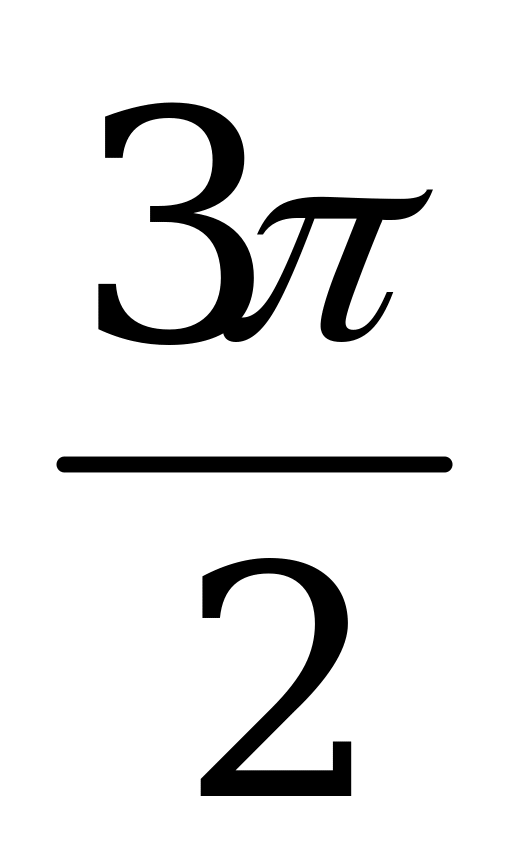 - 3 E) - 3 E)  - 3 - 3 | E |
| А1.9 Расставьте в порядке возрастания числа: x = arccos0,9; y = arccos(-0,7) и z = arccos(-0,2). A) y z x B) x y z C) y x z D) x z y E) z y x | D |
| А1.10 Найдите наибольшее значение выражения аrcos a – 4 аrcsin b, если |a| 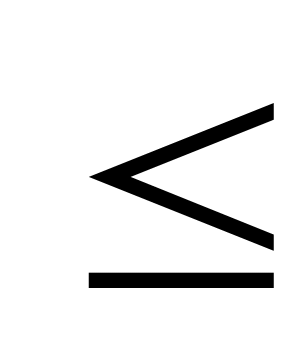 1, |b| 1, |b| 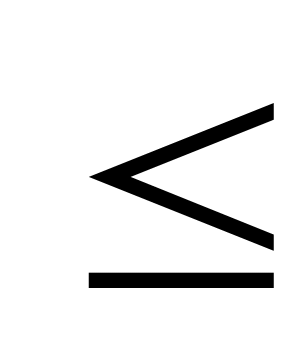 1. 1. A) 2 B) 1 C) 3 B) 1 C) 3 D) 5 D) 5 E) 4 E) 4 | C |
| А2. Решение уравнений | Ответы |
| А2.1 Решите уравнение: 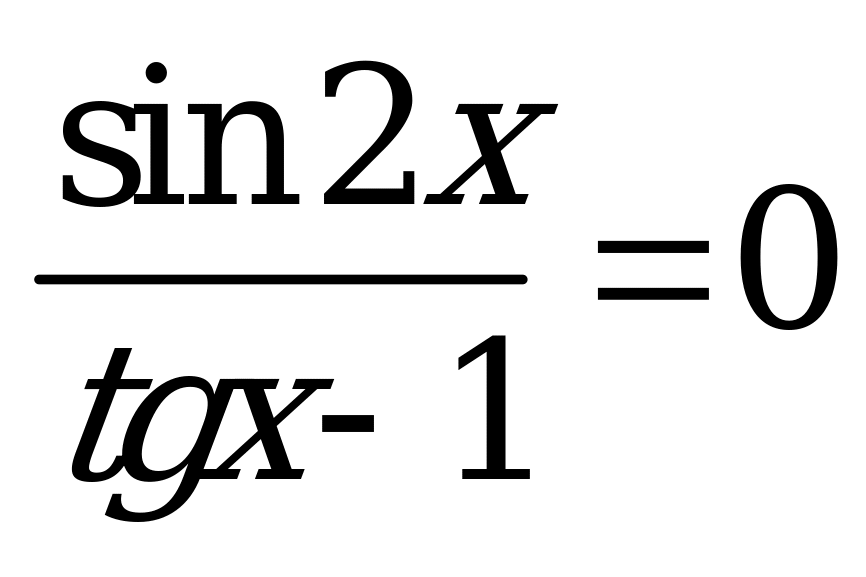 A) 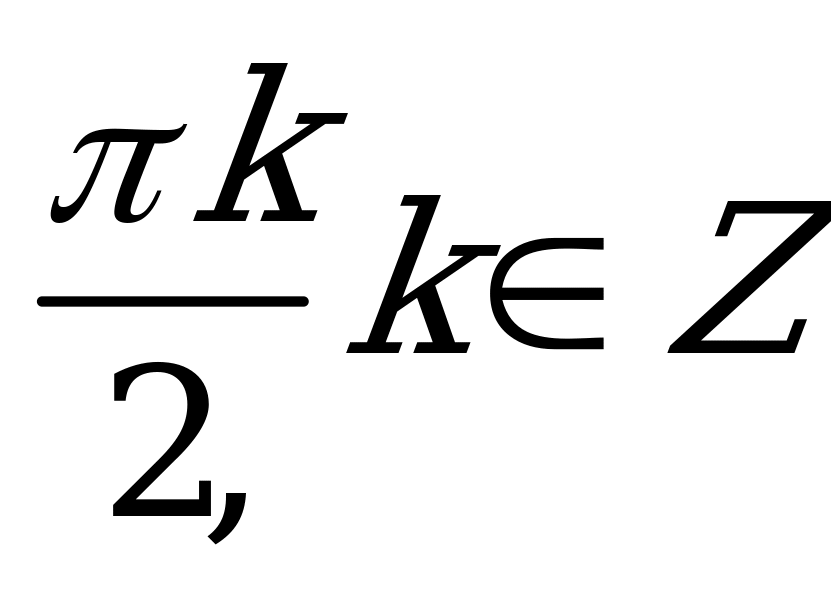 B) B) 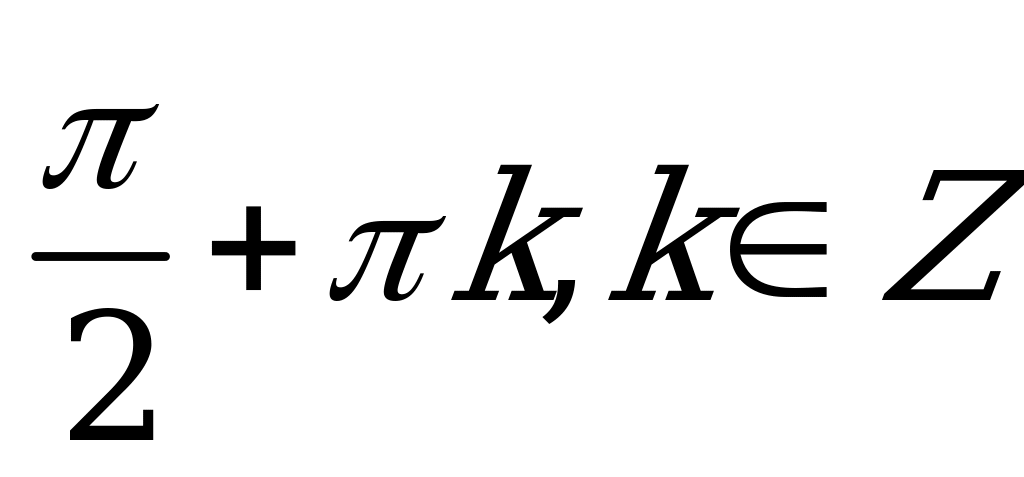 C) 2 C) 2 k, k k, k  Z Z D)  + 2 + 2 k, k k, k  Z E) Z E)  k, k k, k 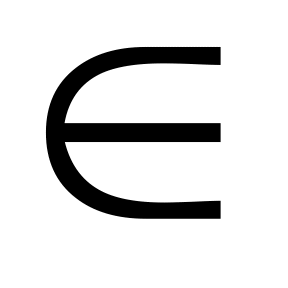 Z Z | E |
| А2.2 Решите уравнение: 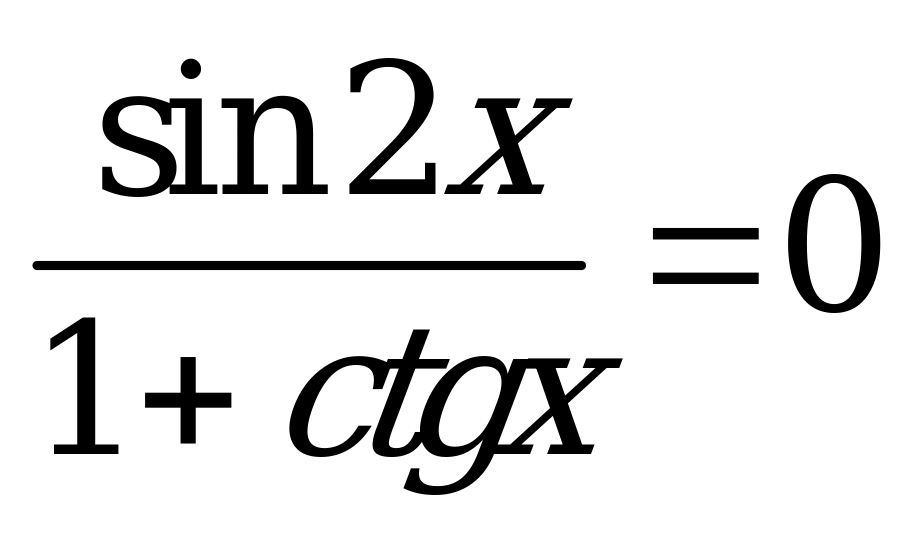 A) 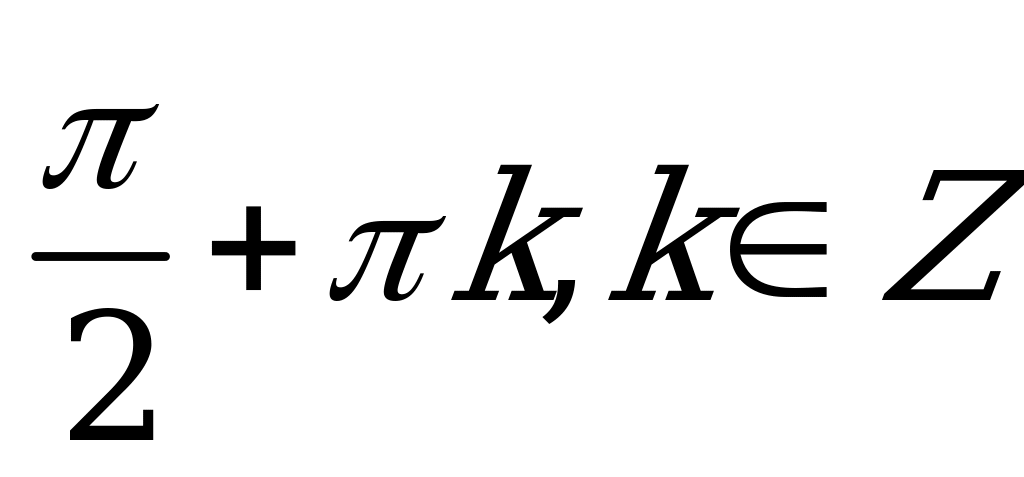 B) B) 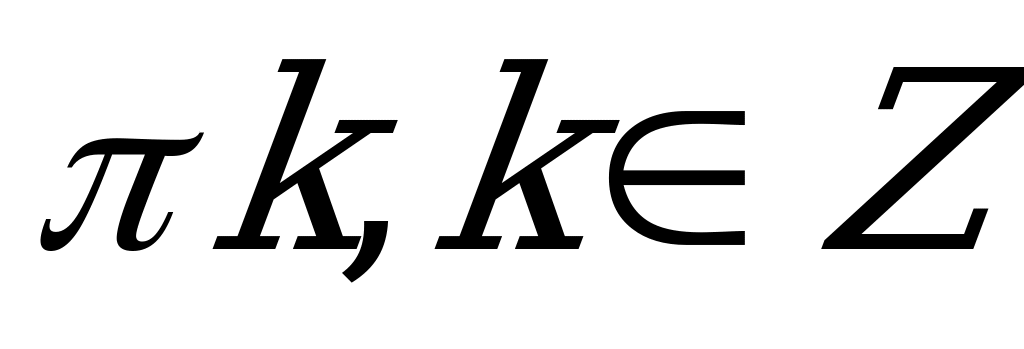 C) C) 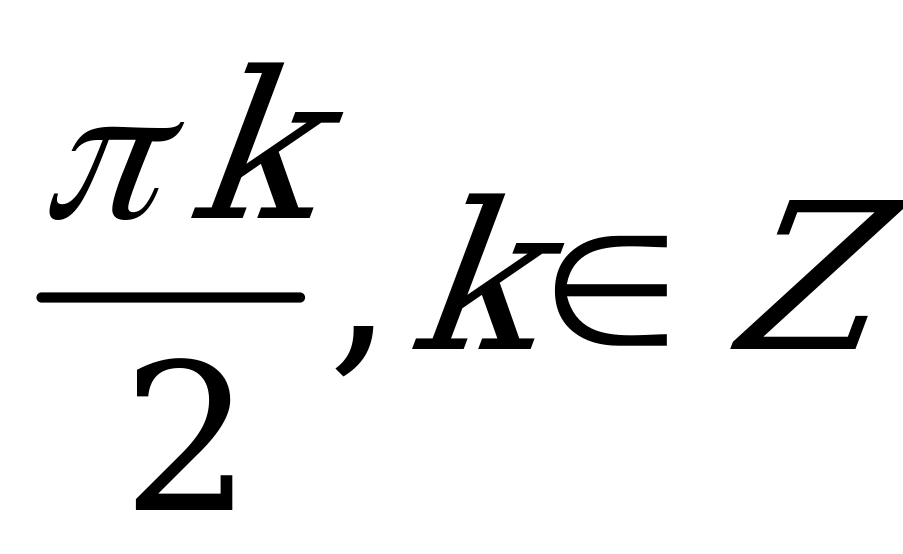 D) 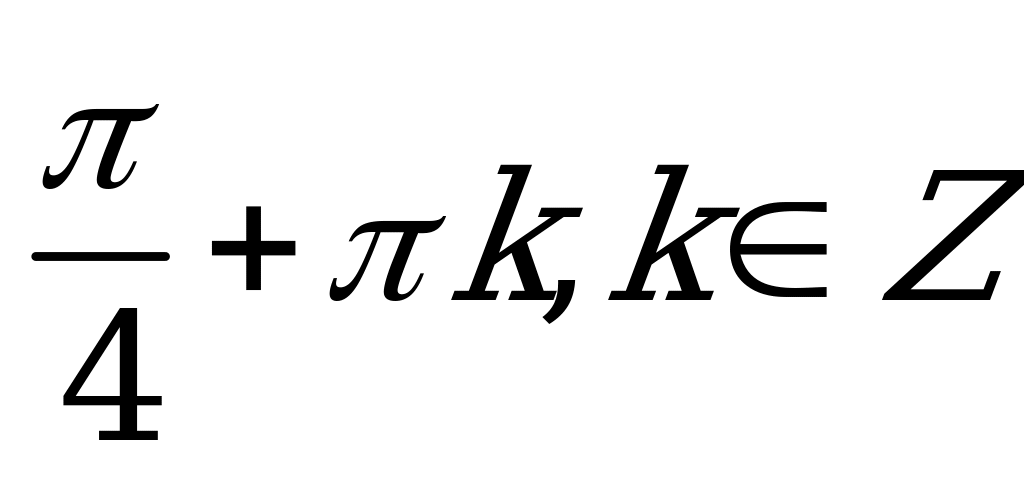 E) E) 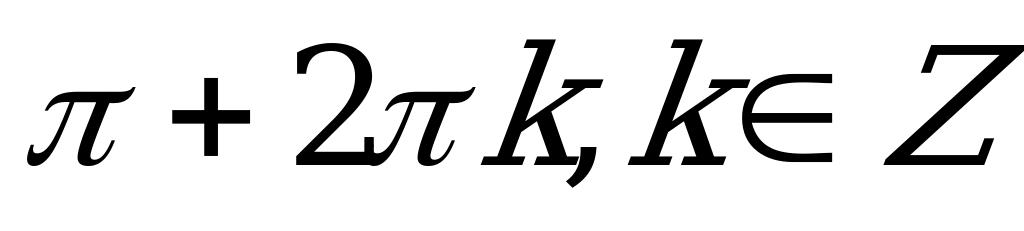 | A |
| А2.3 Решите уравнение:  A) 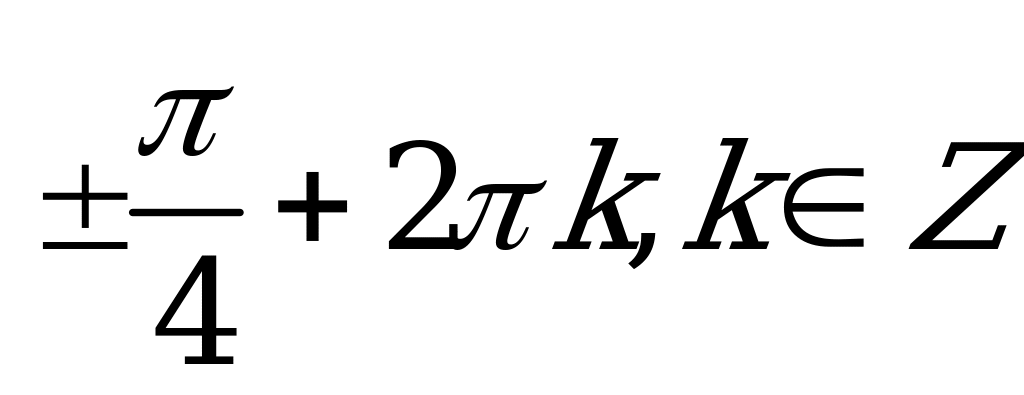 B) B) 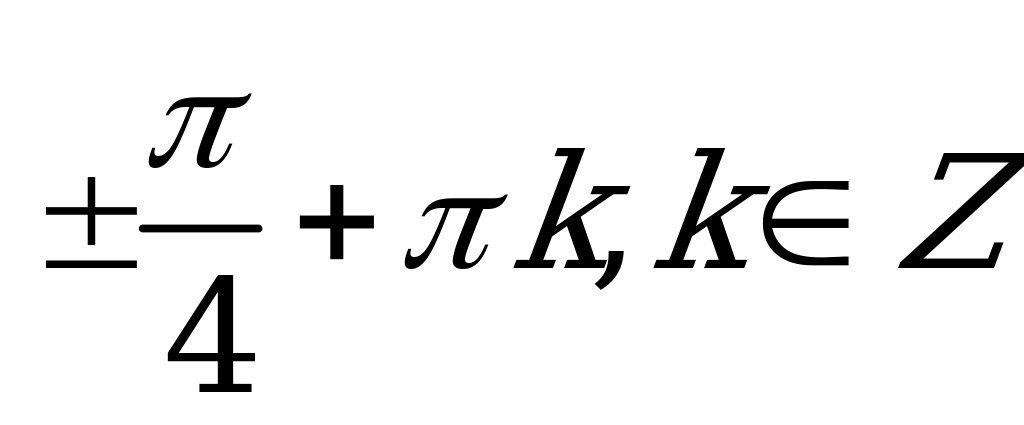 C) 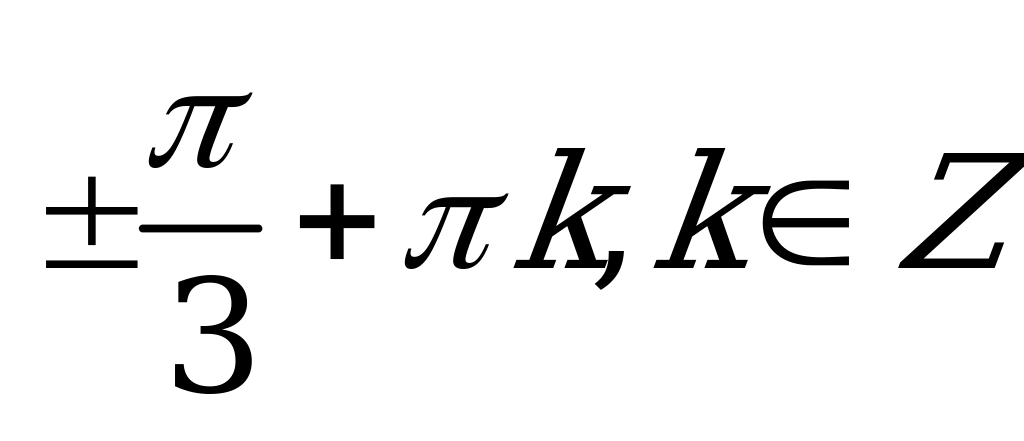 D) D) 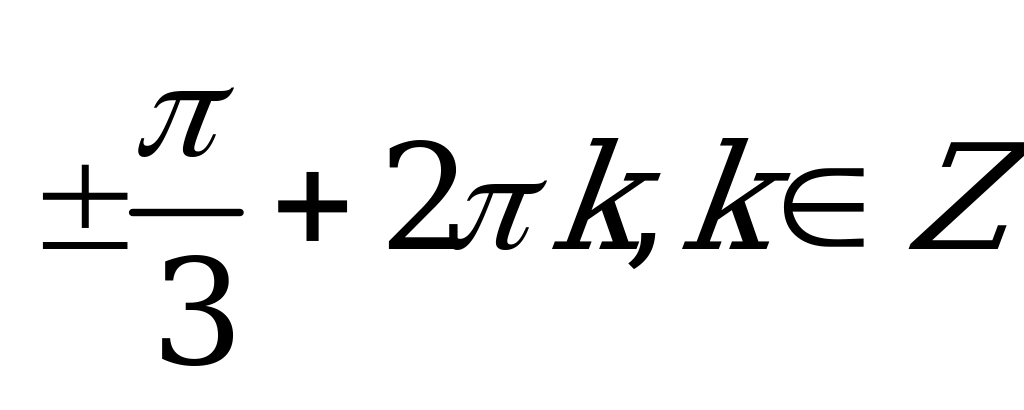 E) 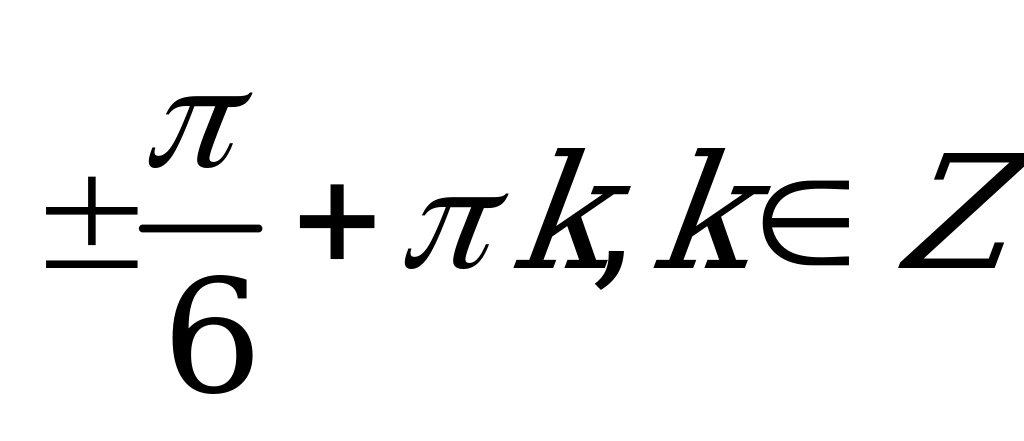 | B |
| А2.4 Решите уравнение: 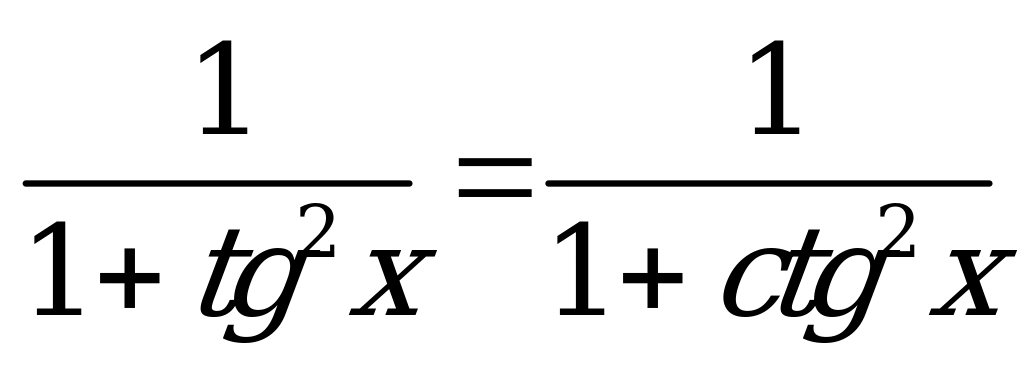 A)  + 2 + 2 k, k k, k 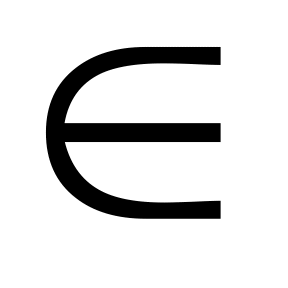 Z B) Z B) 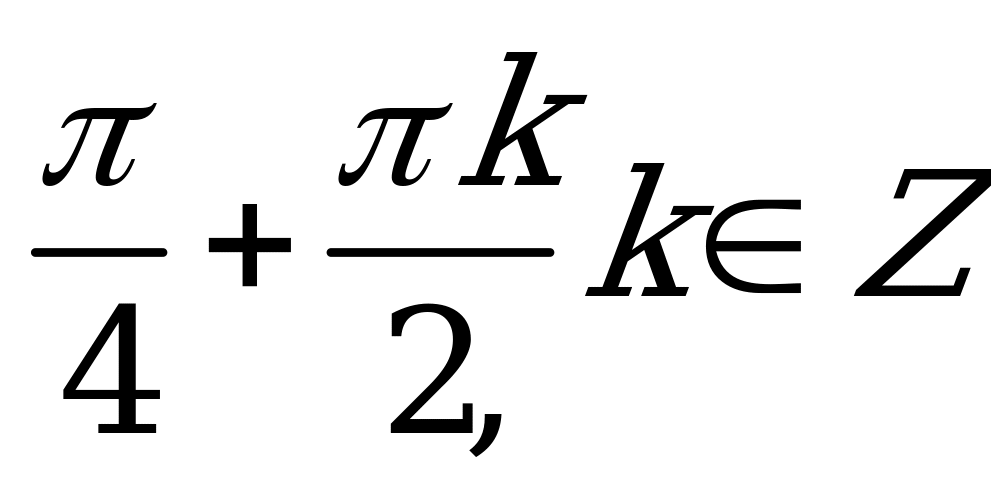 C) 2 k, k k, k 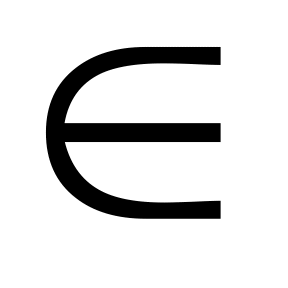 Z D) Z D)  E) E)  k, k k, k  Z Z | B |
| А2.5 Решите уравнение 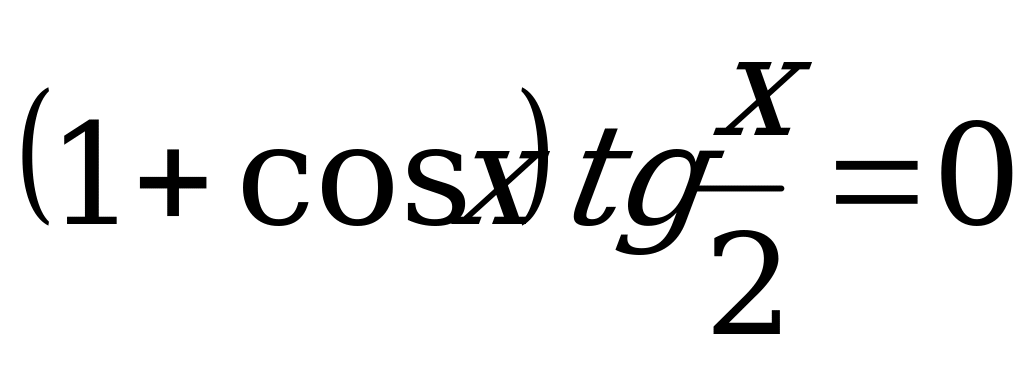 A)  k, k k, k  Z B) Z B)  + 2 + 2 k, k k, k  Z C) 2 Z C) 2 k, k k, k 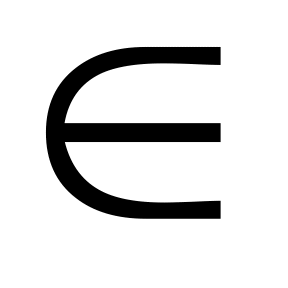 Z Z D)  + +  k, k k, k 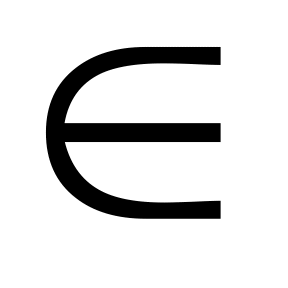 Z E) Z E) 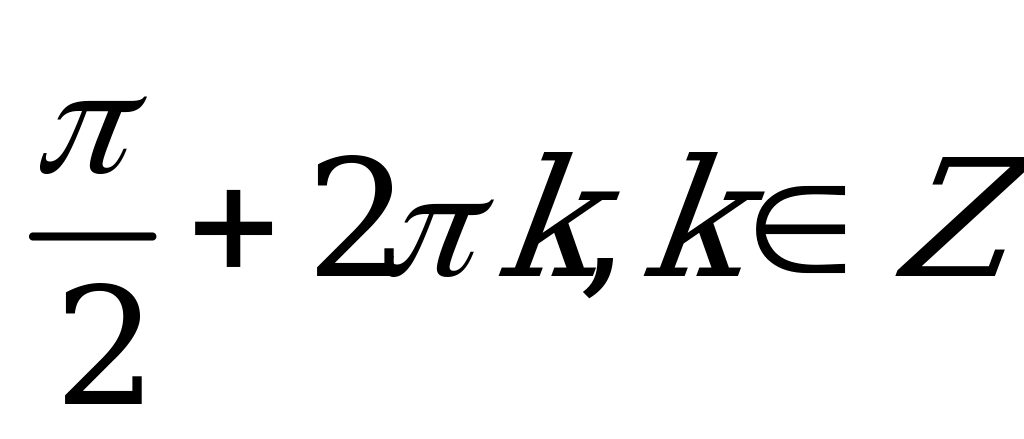 | C |
| А2.6 Решите уравнение 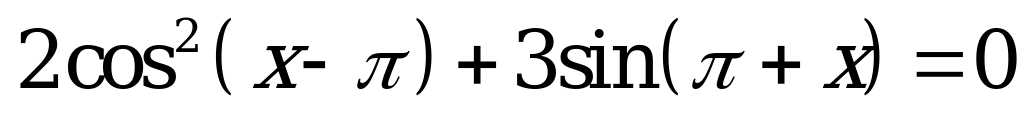 A) 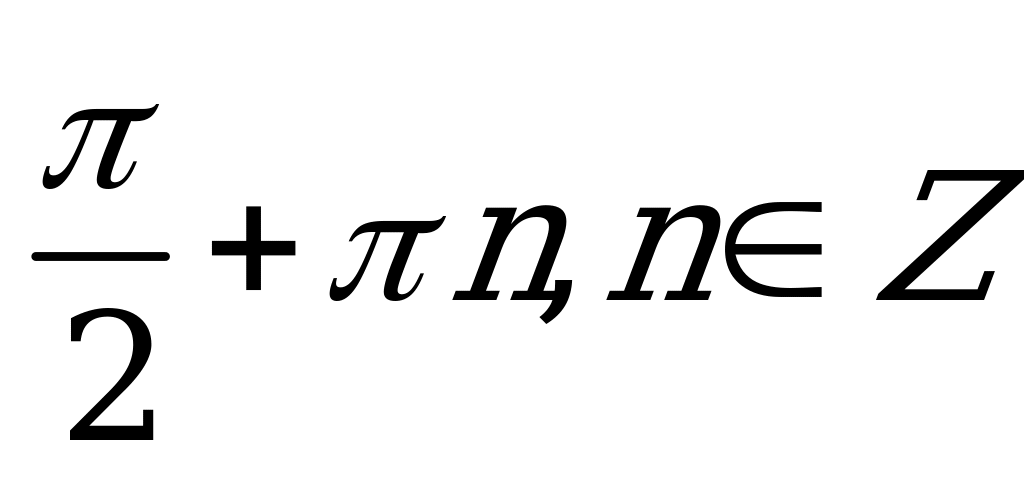 B) B) 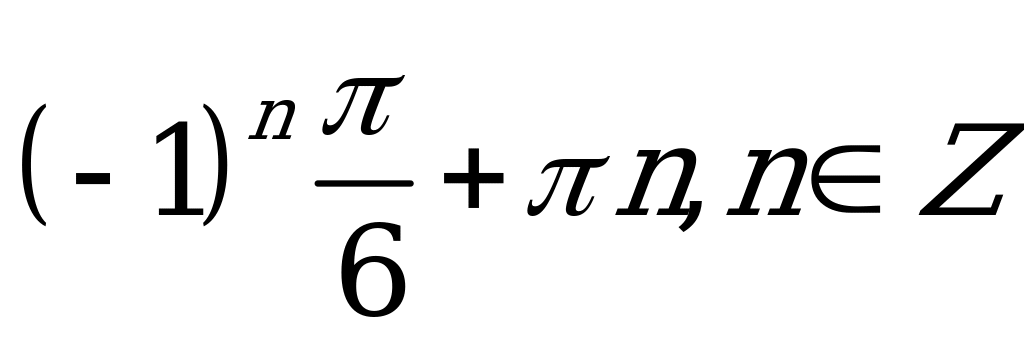 C) 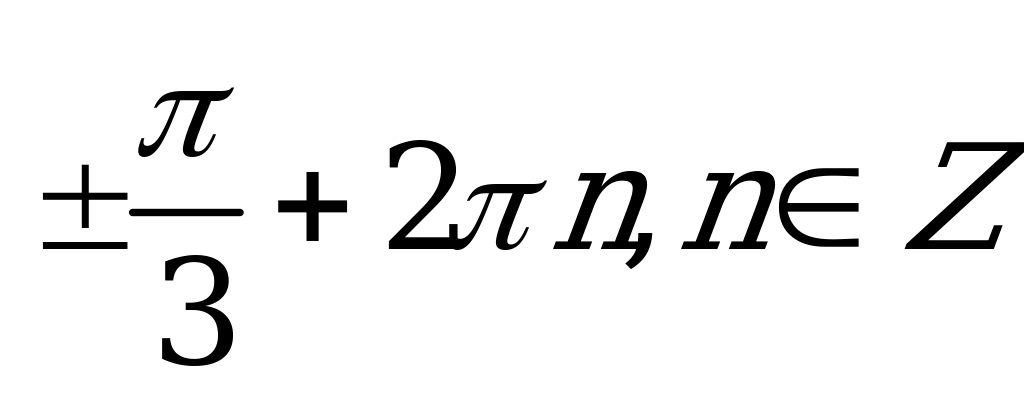 D) D) 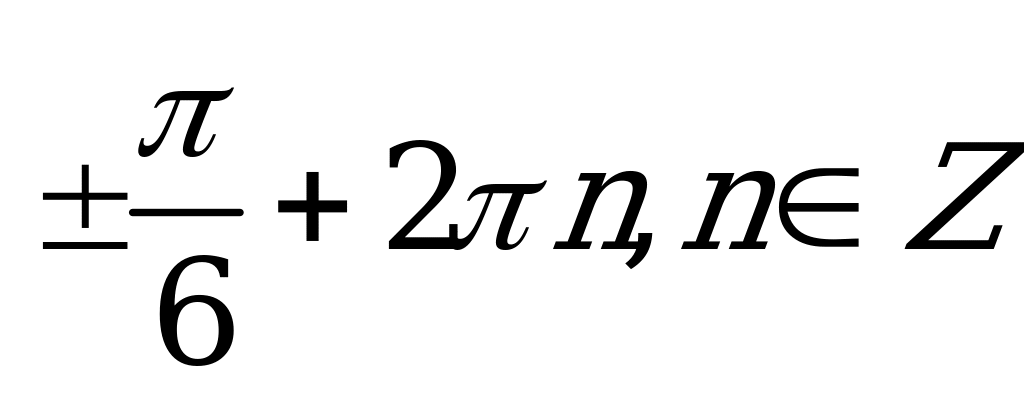 E) E) 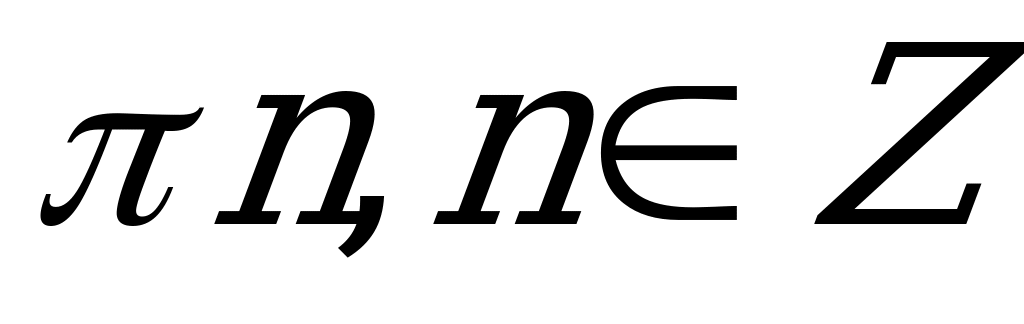 | B |
| А2.7 Решите уравнение: 2sin2x + 5sin(1,5 - x) = 2 - x) = 2 A) 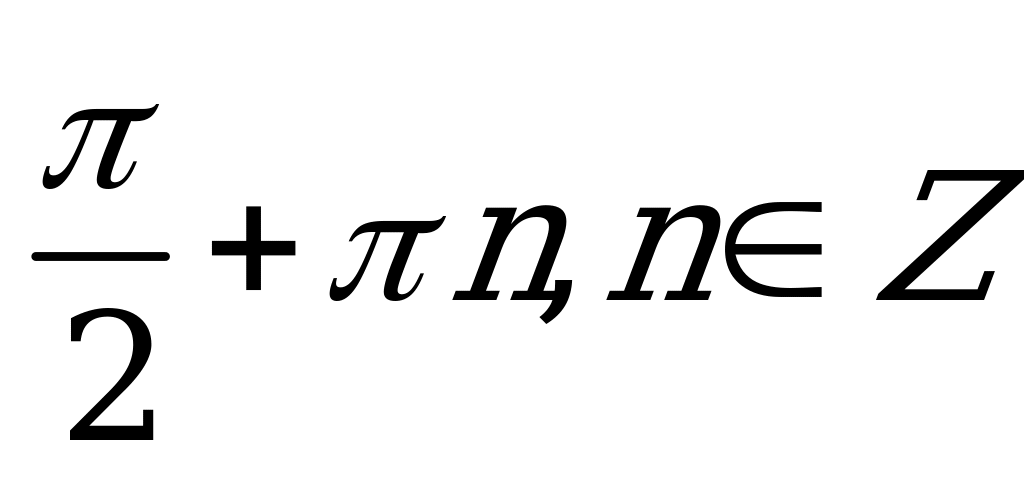 B) B) 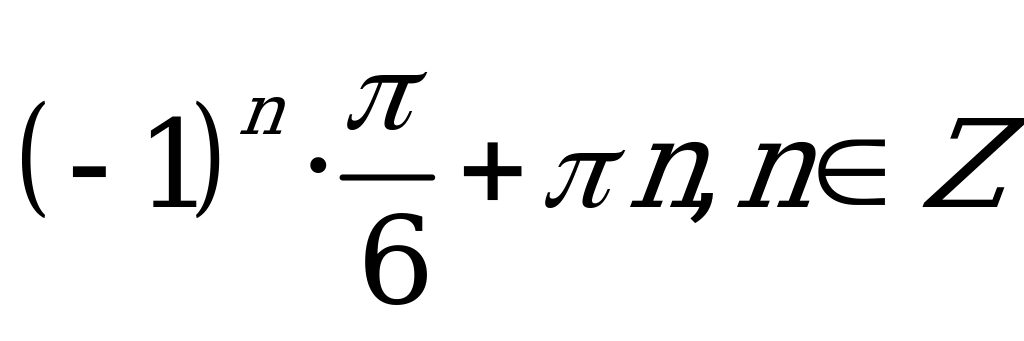 C) 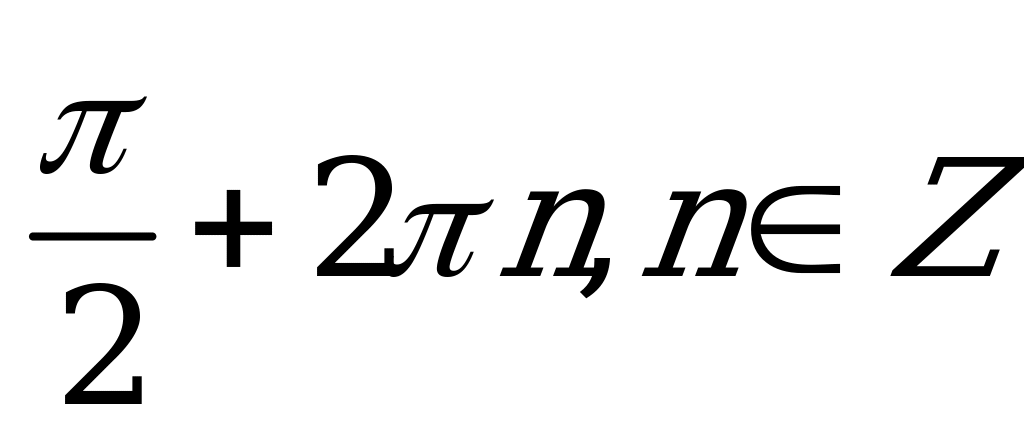 D) D) 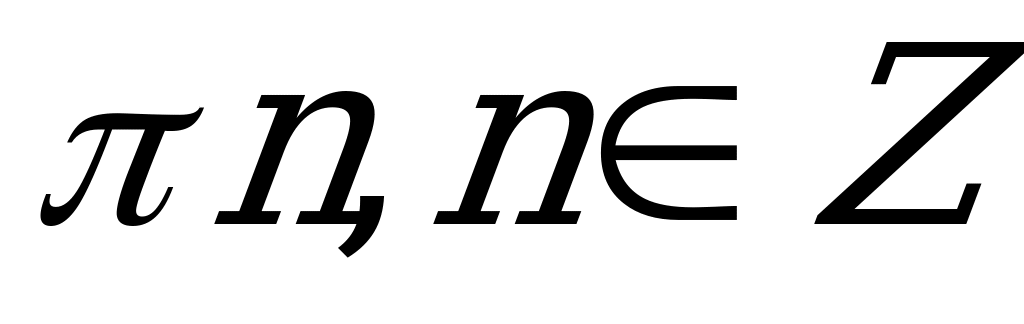 E) E) 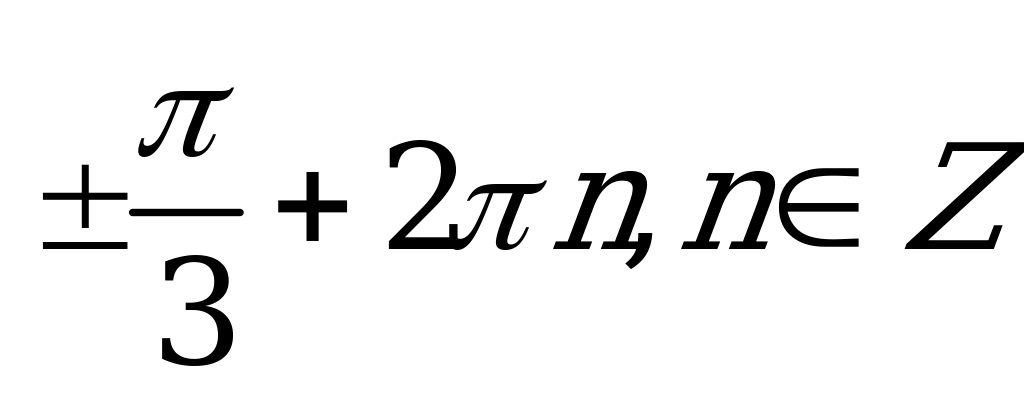 | A |
| А2.8 Решите уравнение: 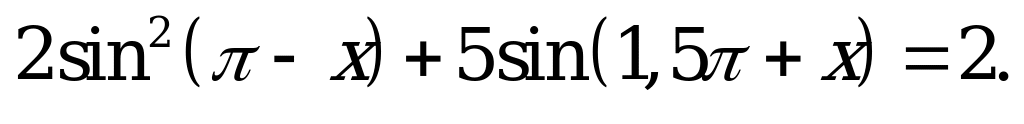 A) 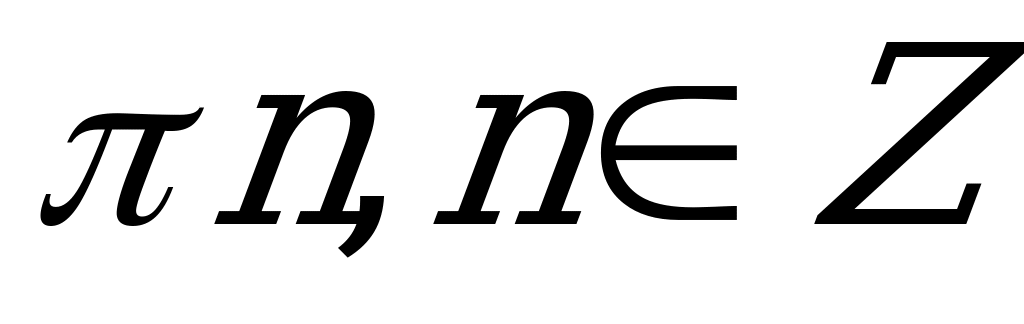 B) B) 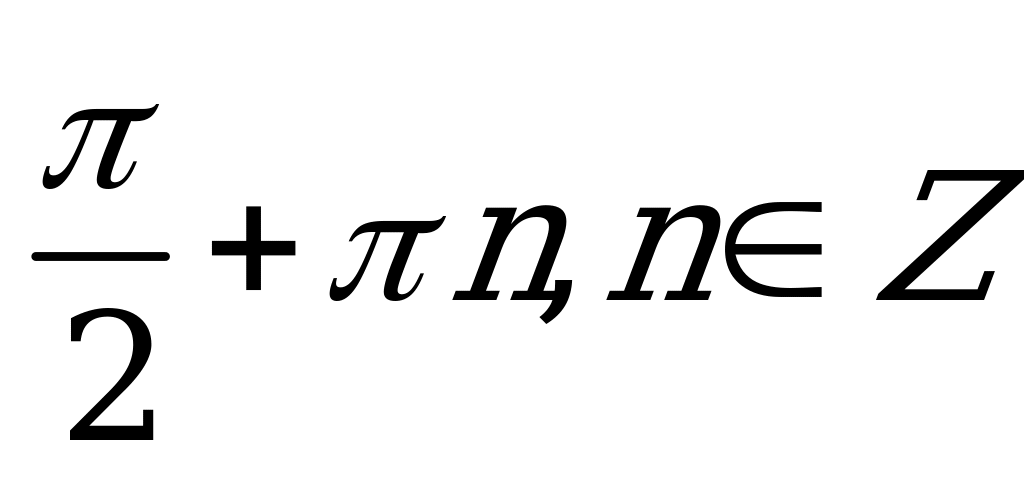 C) C) 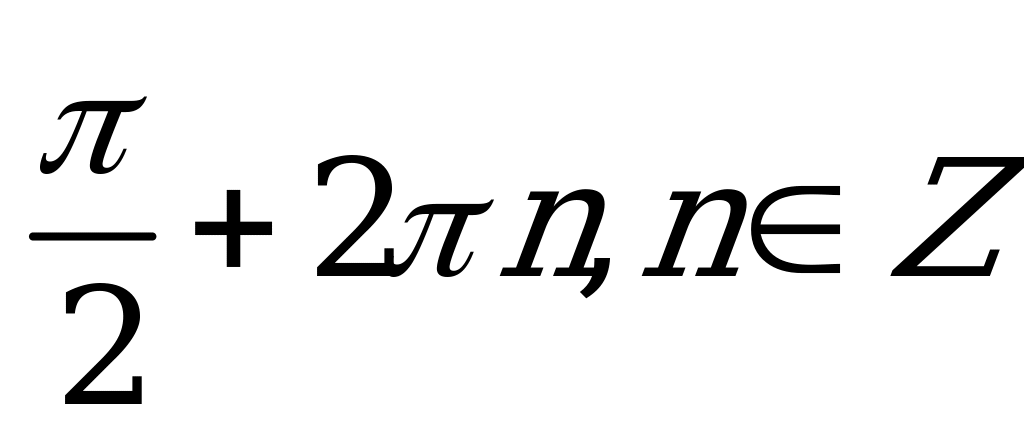 D) 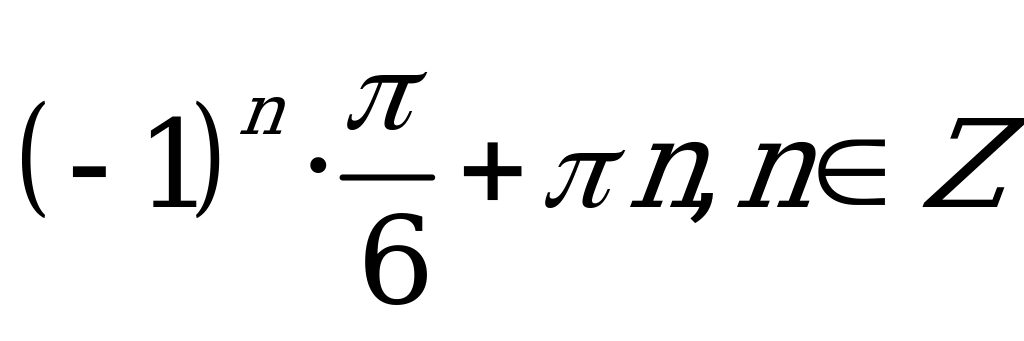 E) E) 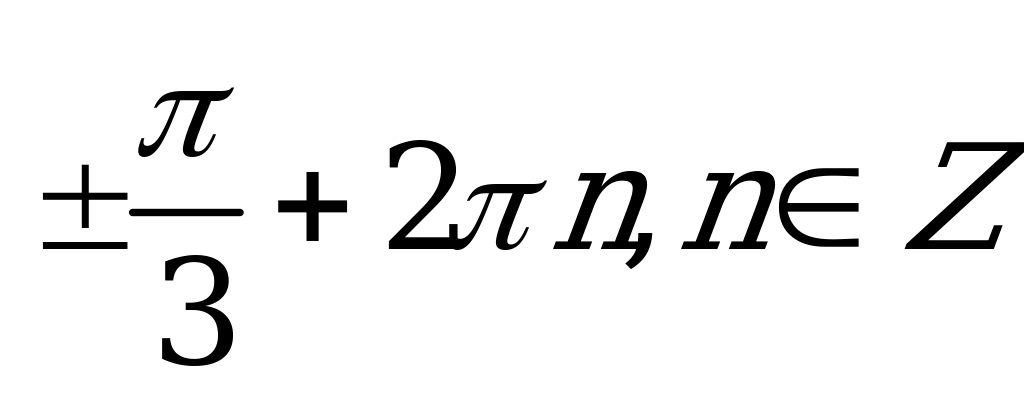 | B |
| А2.9 Решите уравнение: 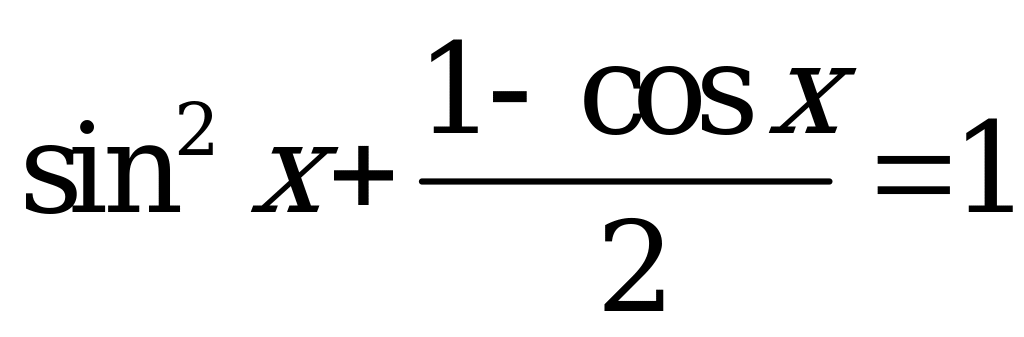 . . A) 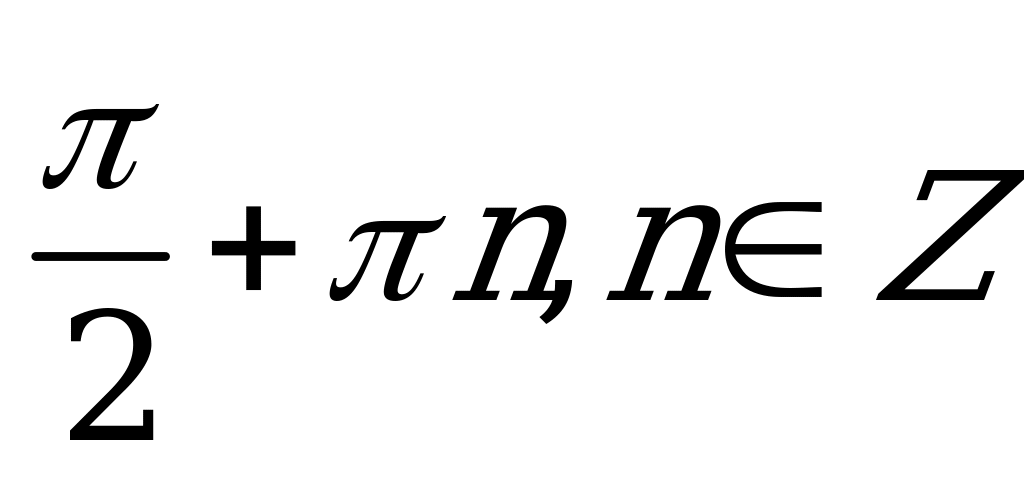 B) B) 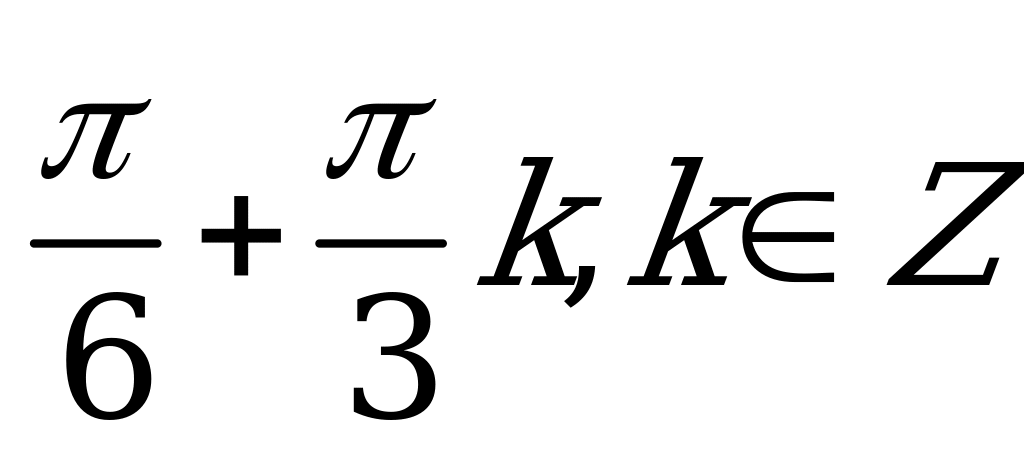 C) C) 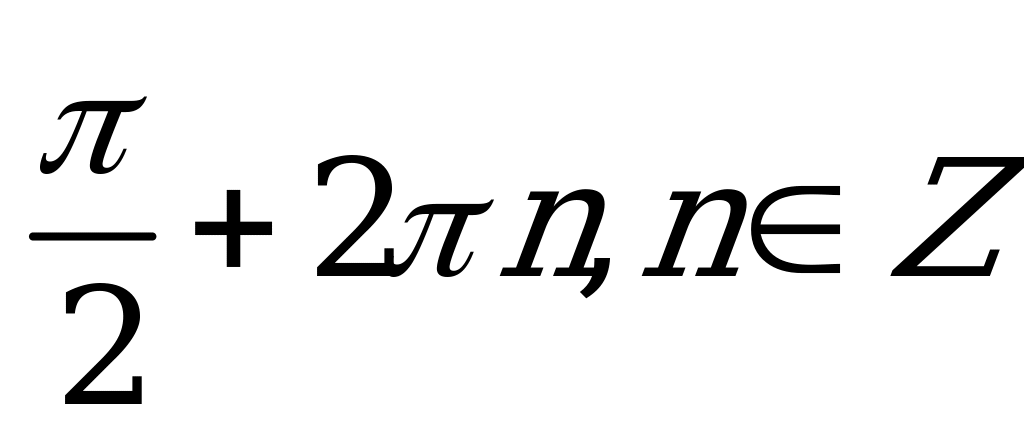 D) 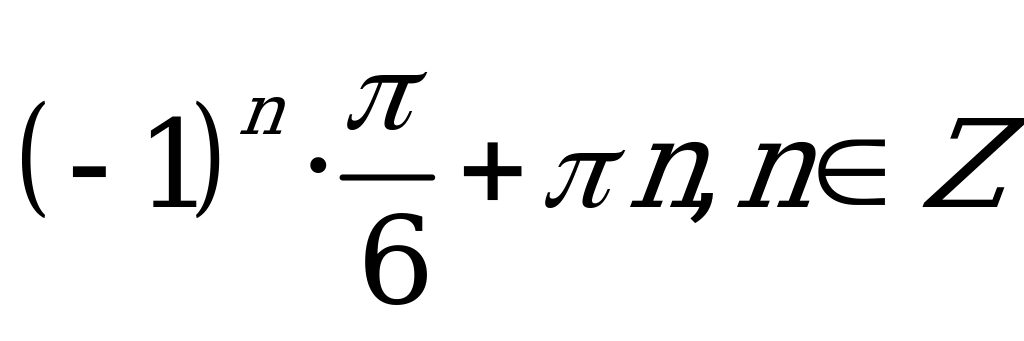 E) E) 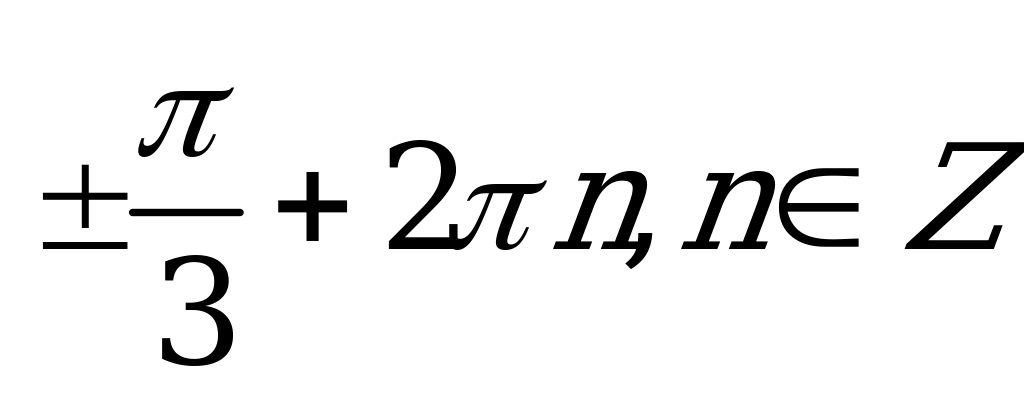 | B |
| А2.10 Решите уравнение: 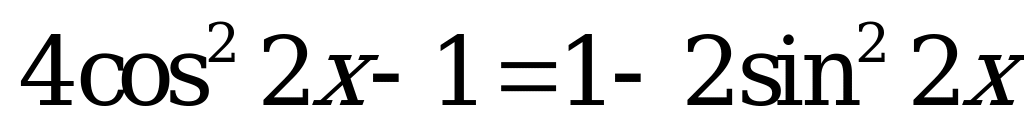 A) 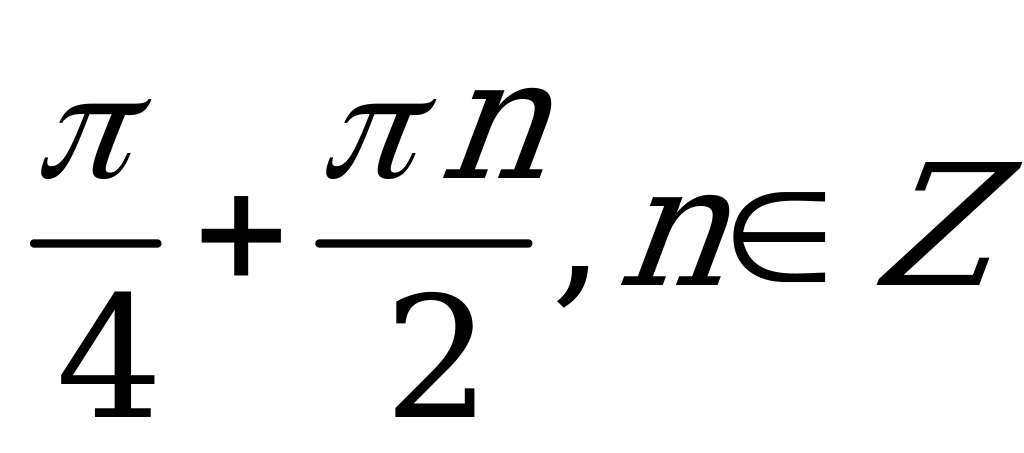 B) B) 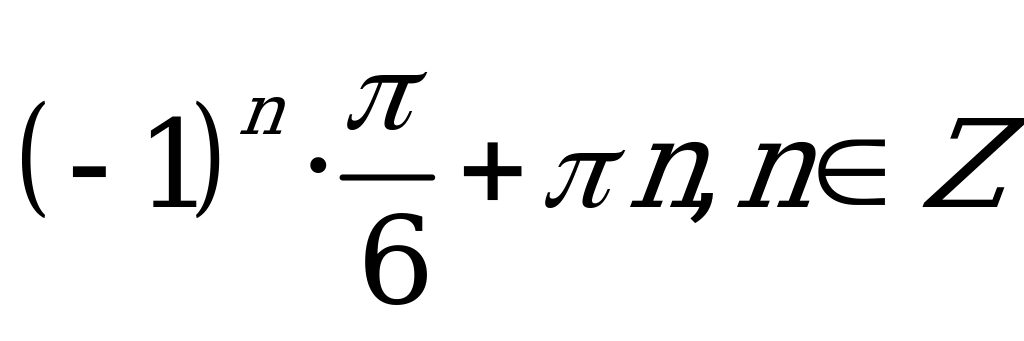 C) 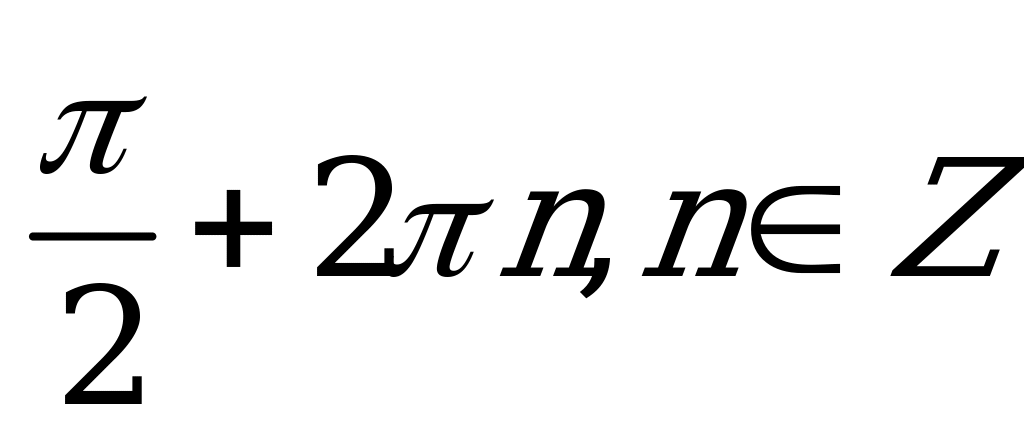 D) D) 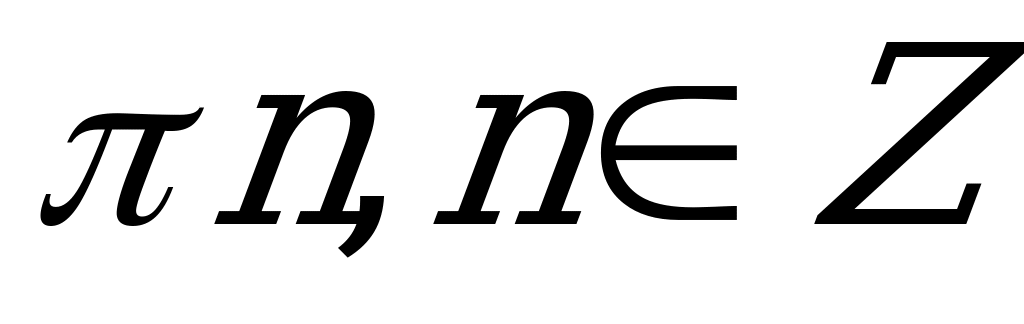 E) E) 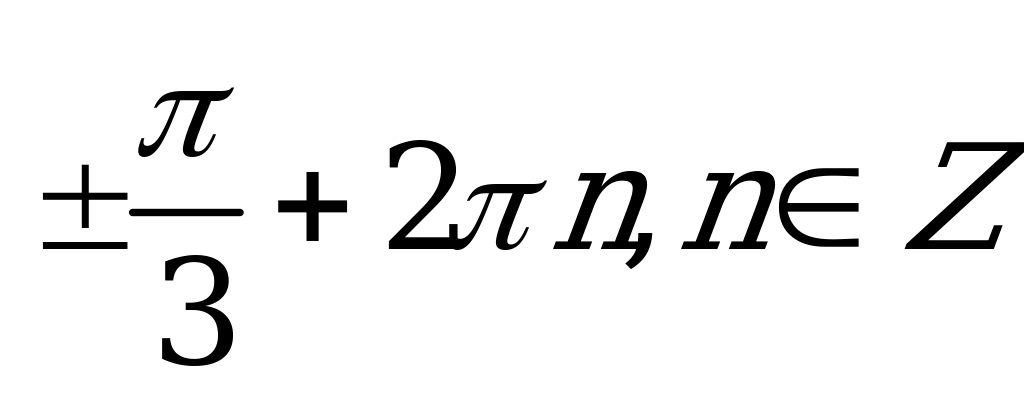 | A |
| А3. Тригонометрические уравнения на интервале | Ответы |
| А3.1 Сколько нулей имеет функция 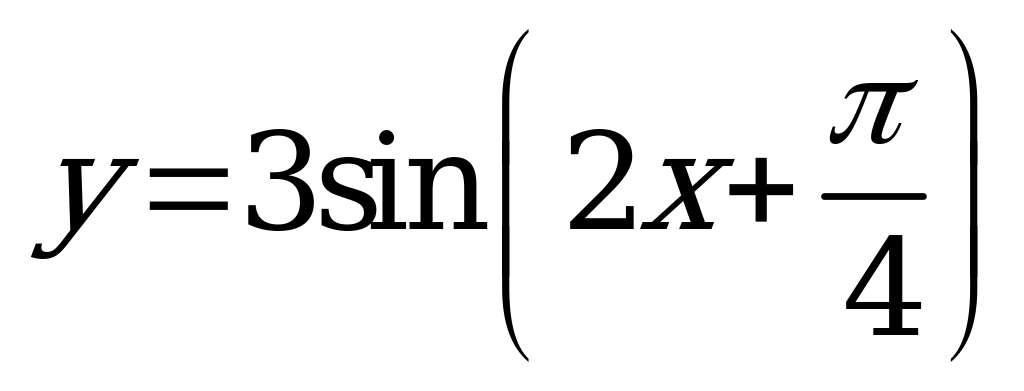 на отрезке [0; 2 на отрезке [0; 2 ]? A) 4 B) 5 C) 3 D) 2 E) 1 ]? A) 4 B) 5 C) 3 D) 2 E) 1 | A |
| А3.2 Сколько корней уравнения cos2x = 1 удовлетворяет условию x2 10? A) 1 B) 2 C) 3 D) 4 E) 5 | C |
| А3.3 Найдите решение уравнения 1 + 2sin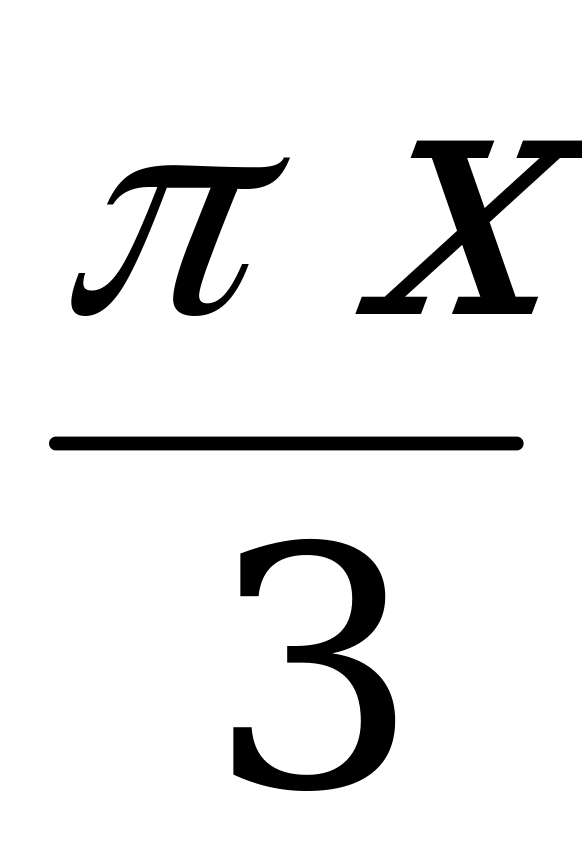 = 0 = 0 (2 x A) 2,5; 3,5 B) 3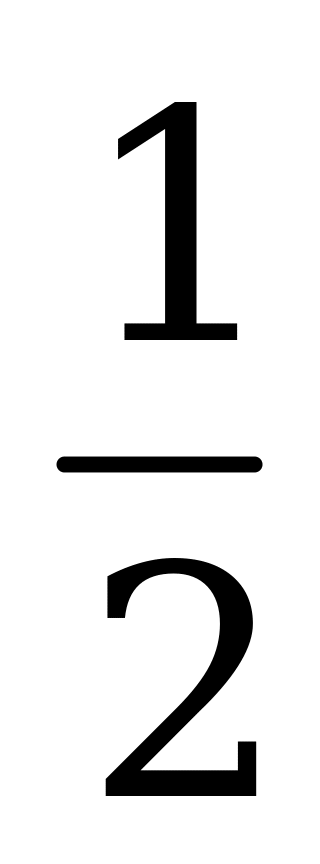 C) 3 C) 3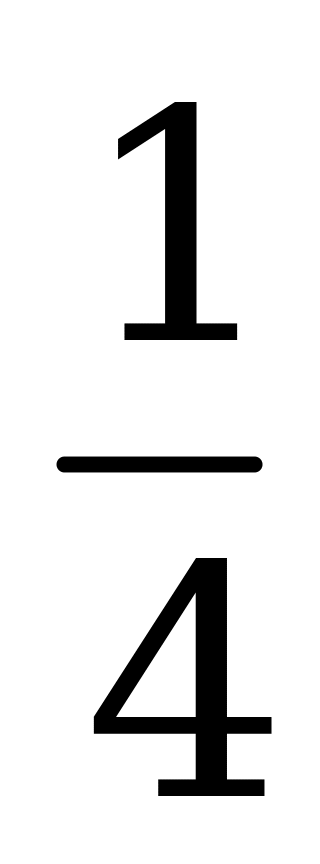 ; 4 D) 3 E) ; 4 D) 3 E) | B |
| А3.4 Сколько корней имеет уравнение (8x – 1)(x + 2)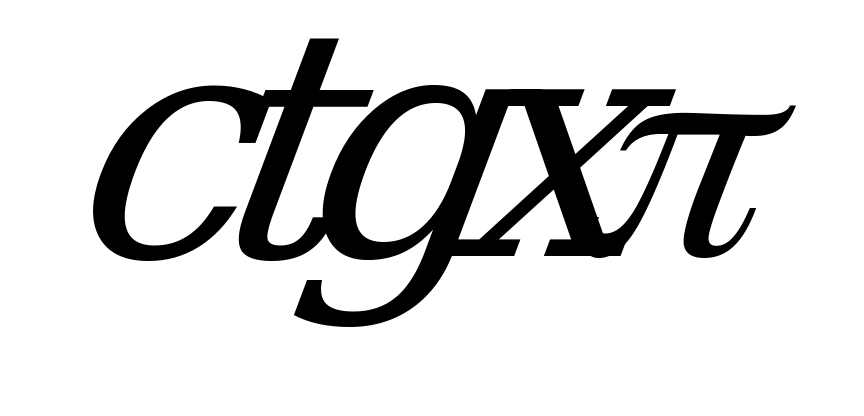 = 0 на отрезке [-2; 2]? = 0 на отрезке [-2; 2]? A) 5 B) 4 C) 6 D) 7 E) 3 | A |
| А3.5 Сколько корней имеет уравнение: 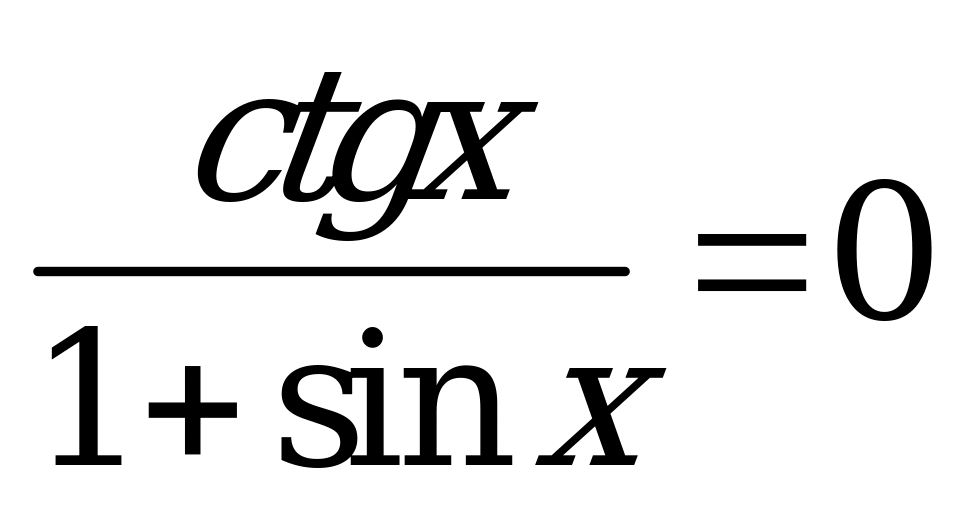 на промежутке [0; 5 на промежутке [0; 5 ] ? ] ? A) 5 B) 4 C) 3 D) 2 E) 6 | C |
| А3.6 Сколько корней на отрезке [ 0; 4 ] имеет уравнение ] имеет уравнение 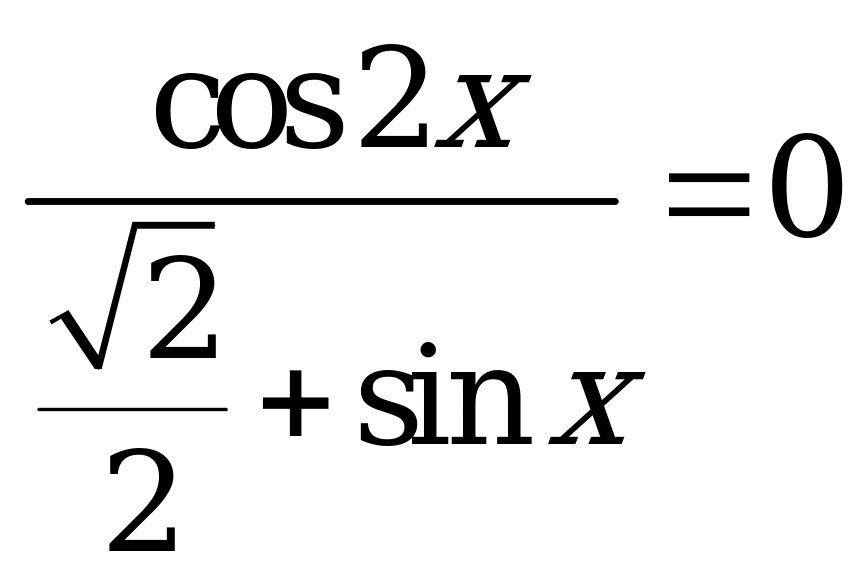 A) 8 B) 6 C) 4 D) 2 E) 12 | C |
| А3.7 Сколько корней имеет уравнение 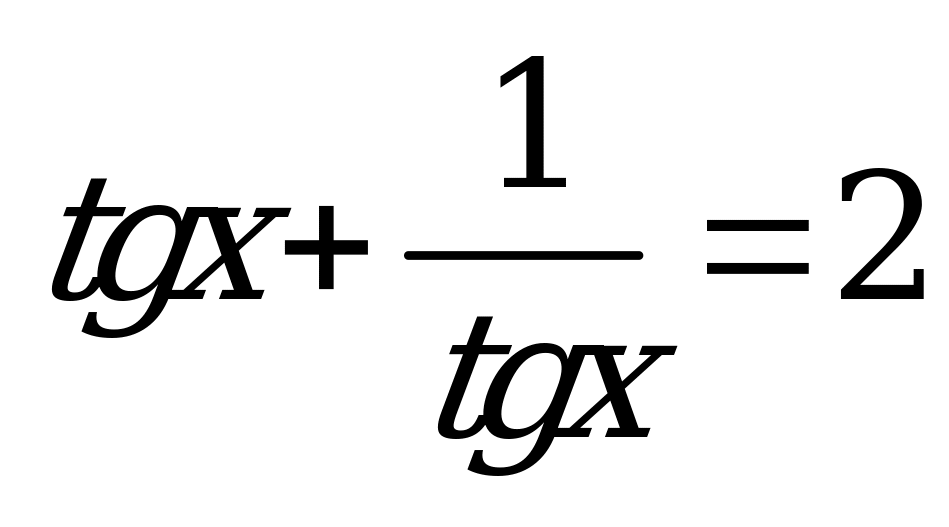 на отрезке [-2; ]? A) 3 B) 5 C) 4 D) 6 E) 2 на отрезке [-2; ]? A) 3 B) 5 C) 4 D) 6 E) 2 | A |
| А3.8 Сколько корней имеет уравнение sinx + cosx = 1 на отрезке [- ; 2 ; 2 ] ? ] ? A) 0 B) 1 C) 2 D) 3 E) 4 | D |
| А3.9 Сколько корней уравнения 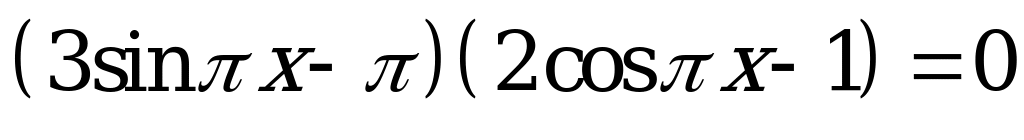 промежутке [0; 3] ? промежутке [0; 3] ? A) 1 B) 2 C) 3 D) 4 E) бесконечно много | C |
| А3.10 Найдите наименьший положительный корень уравнения 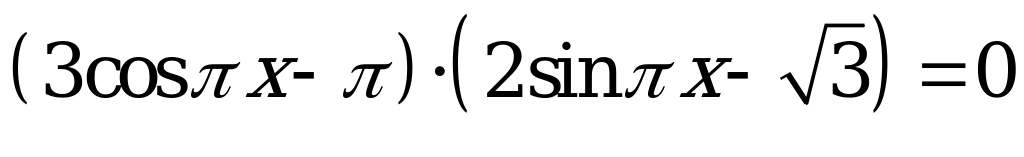 A) 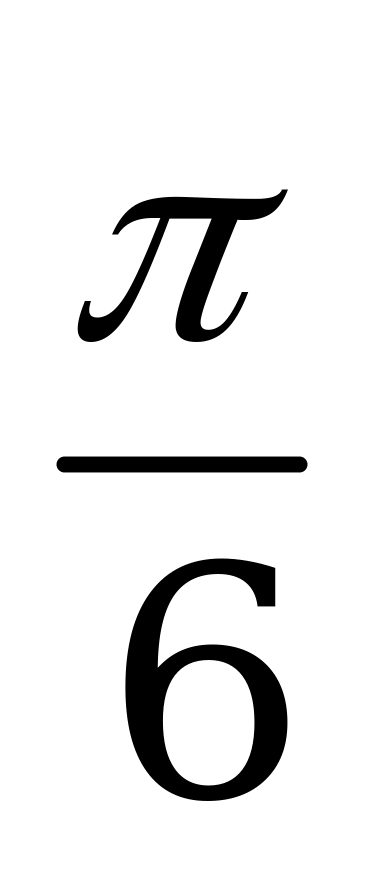 B) B) 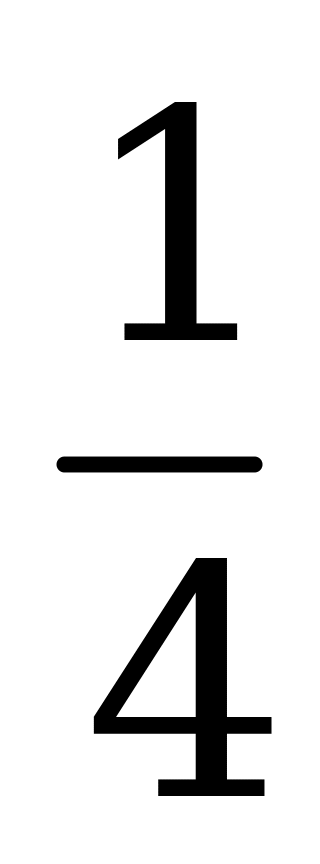 C) C) 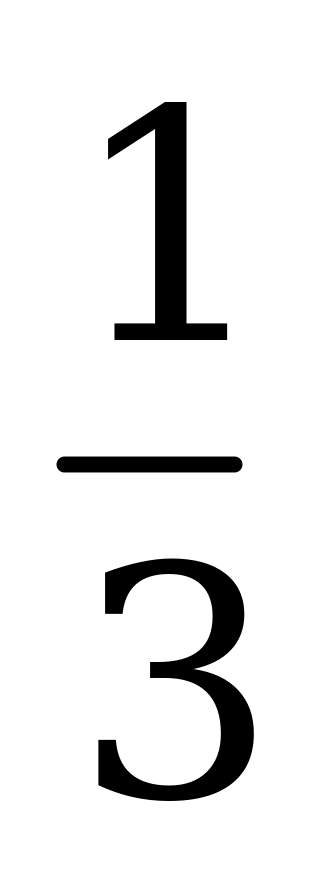 D) D) 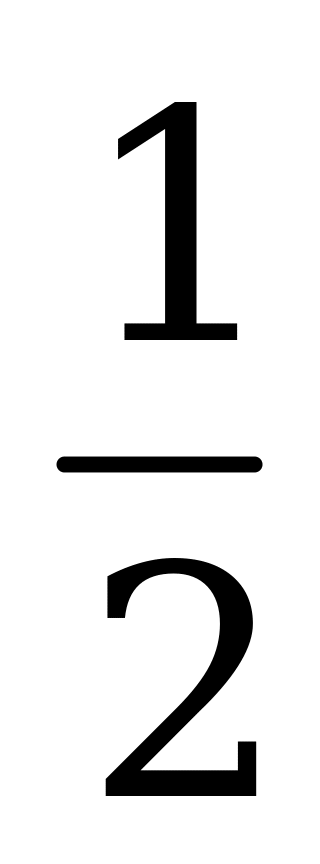 E) нет верного ответа E) нет верного ответа | C |
| А4. Задачи с обратными тригонометрическими функциями | Ответы |
| А4.1 Найдите 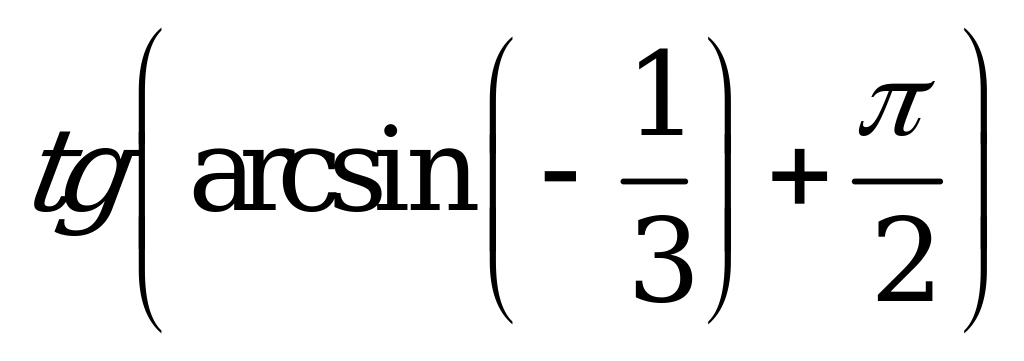 A) 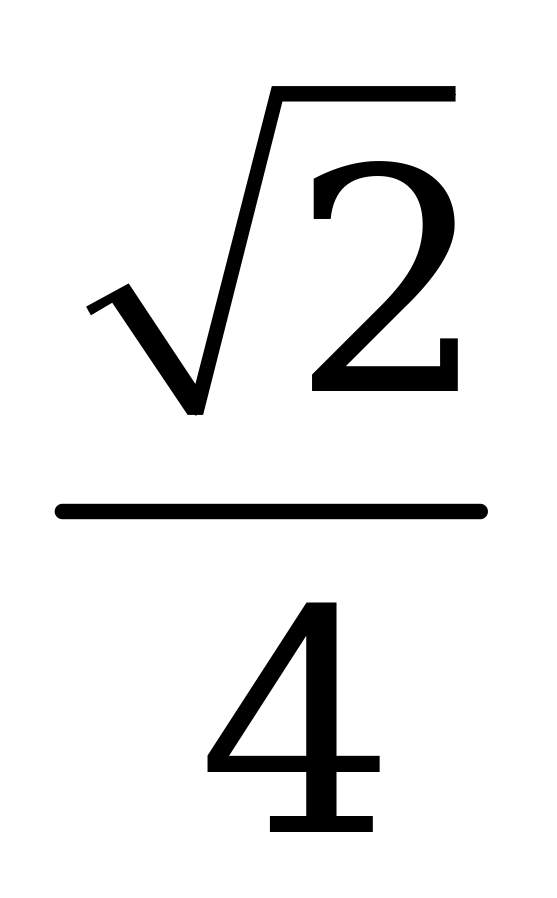 B) - B) -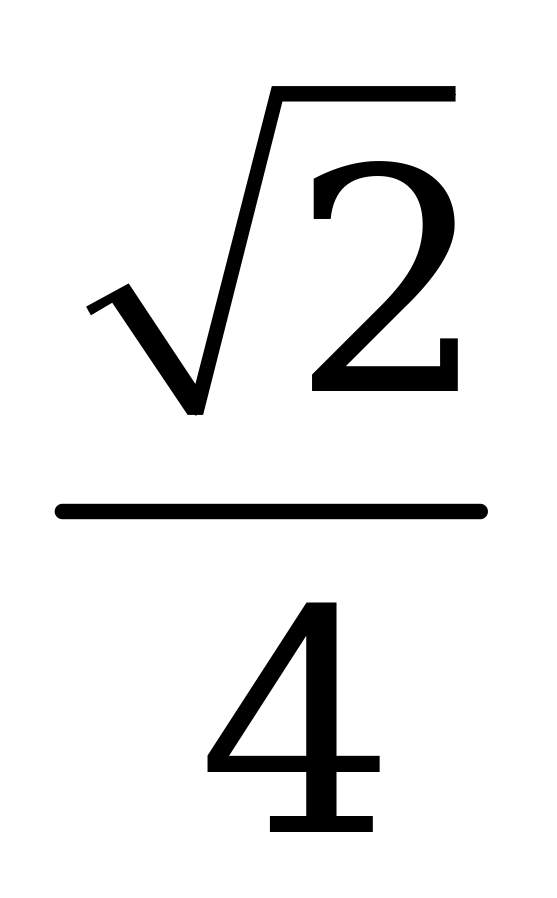 C) C) 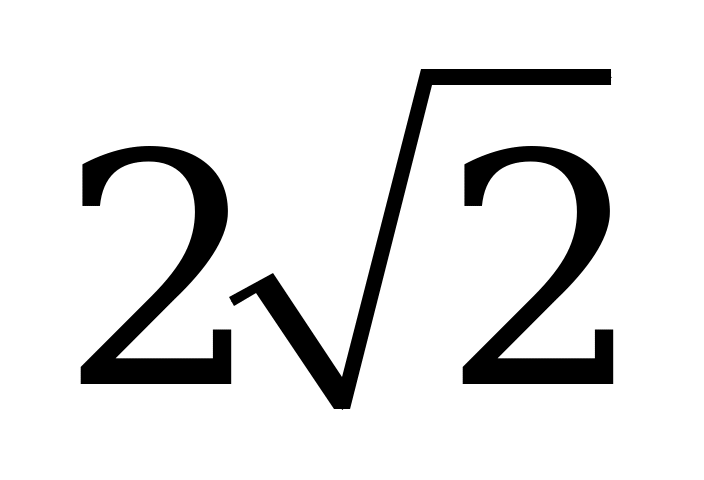 D) - D) -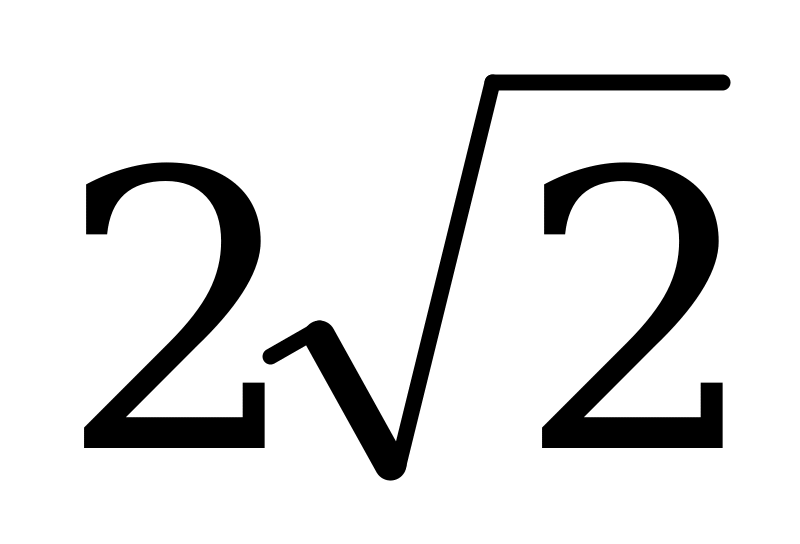 E) E) 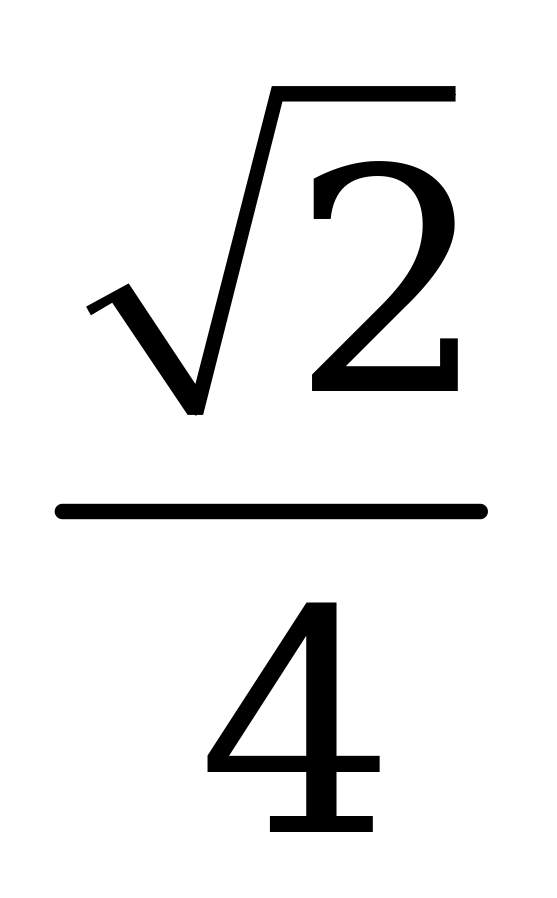 | C |
| А4.2 Вычислите  A) 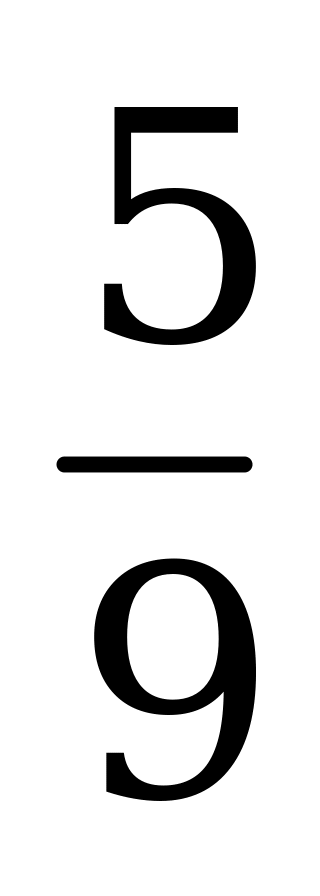 B) B) 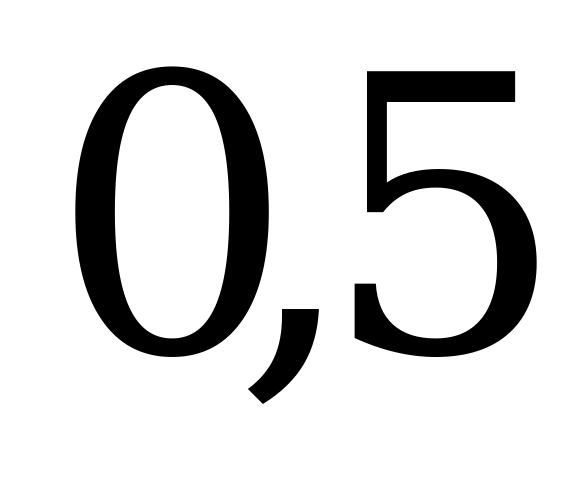 C) C) 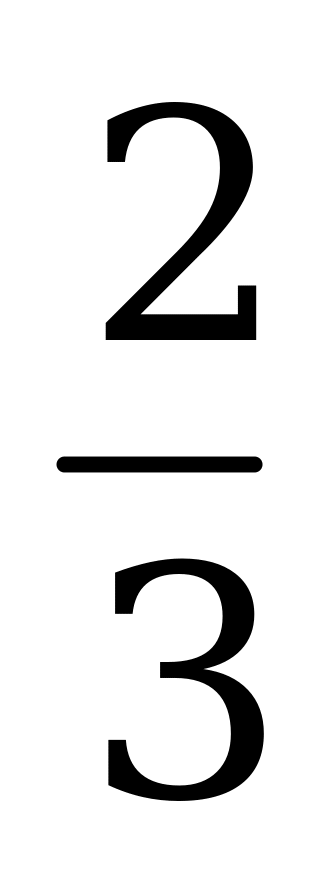 D) D) 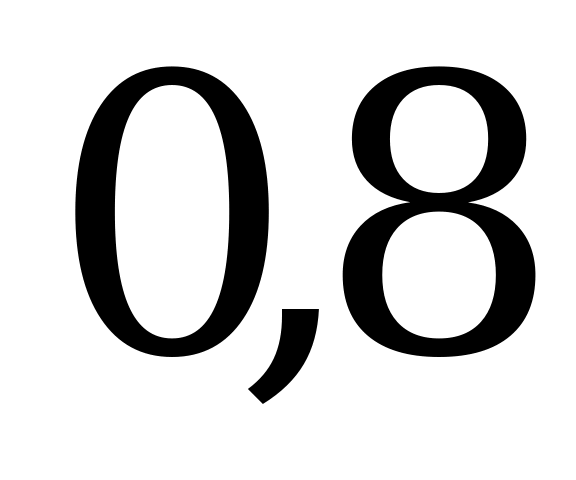 E) E) 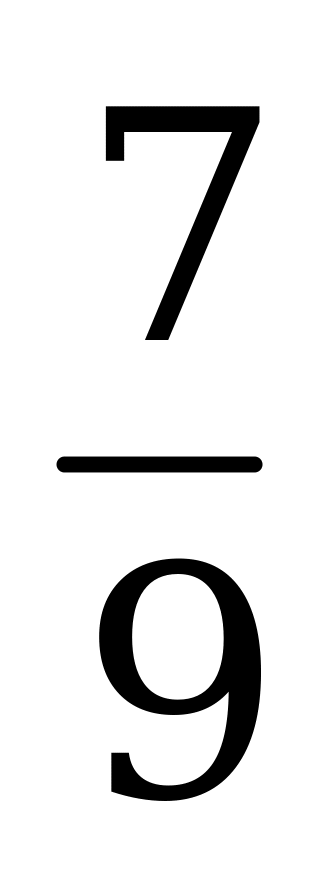 | E |
| А4.3 Найдите 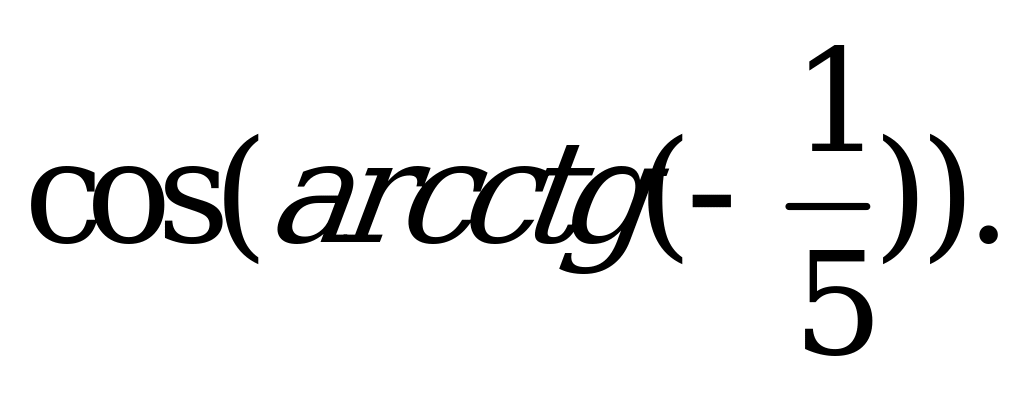 A) 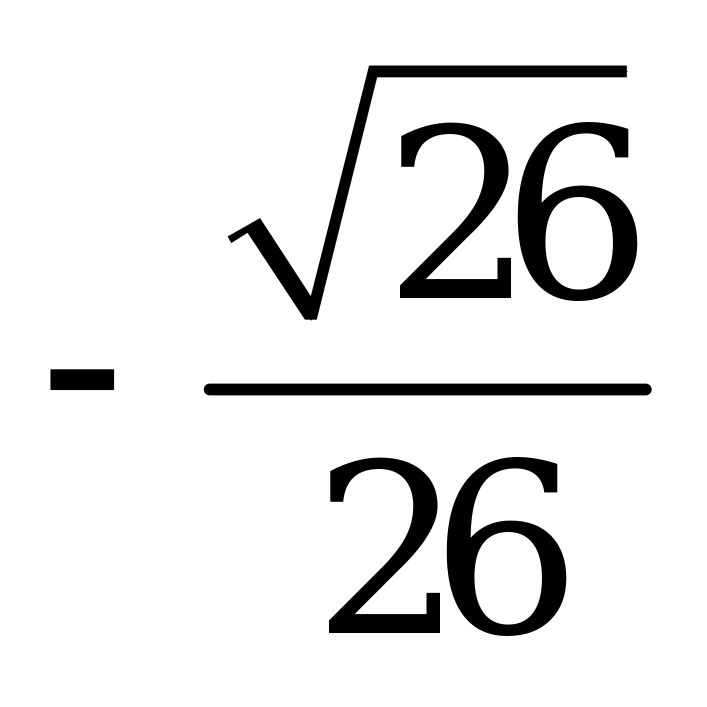 B) B) 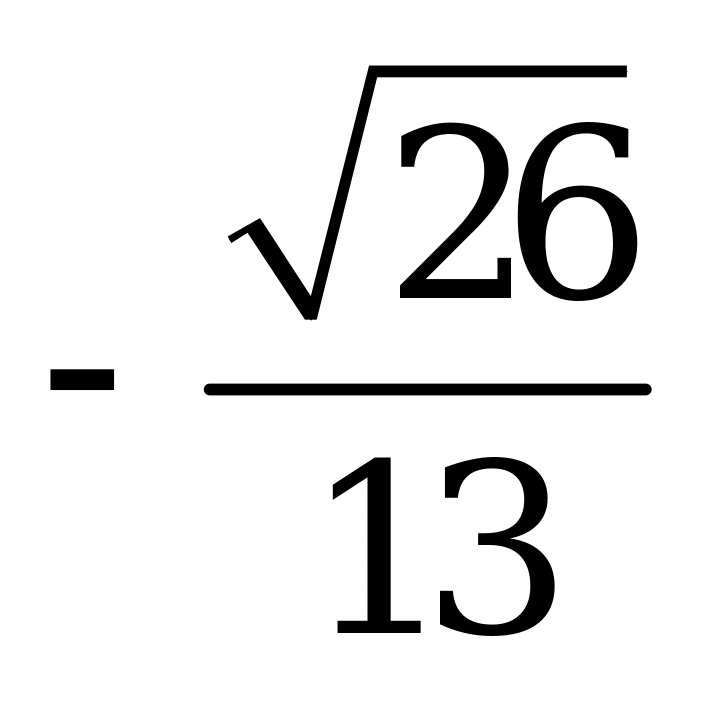 C) C) 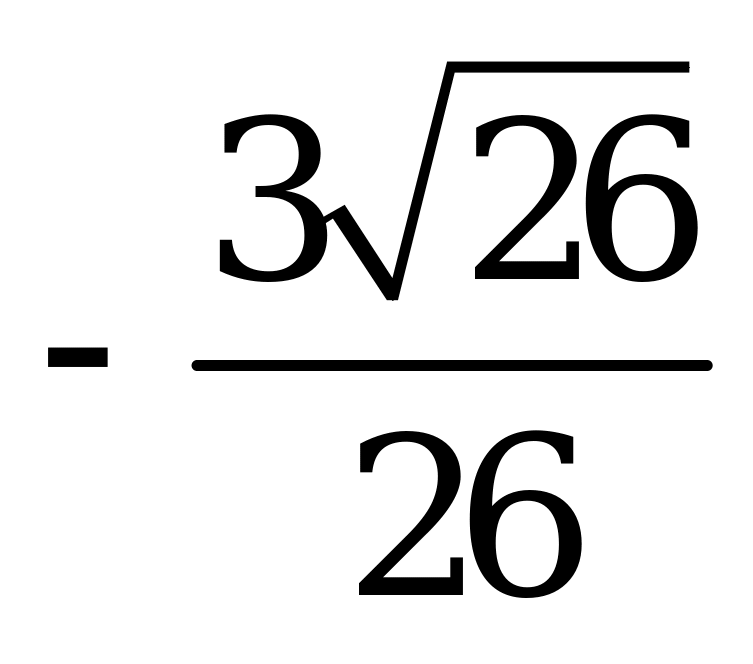 D) D) 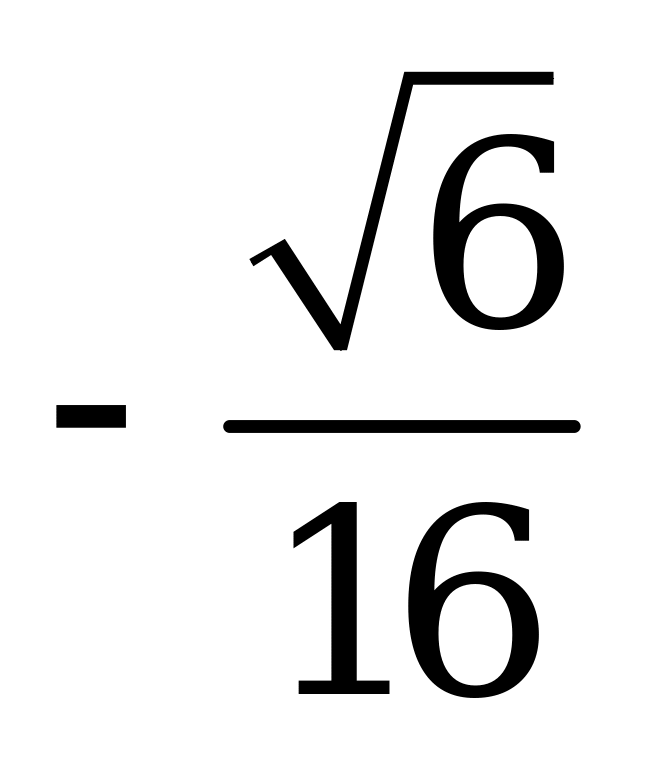 E) E) 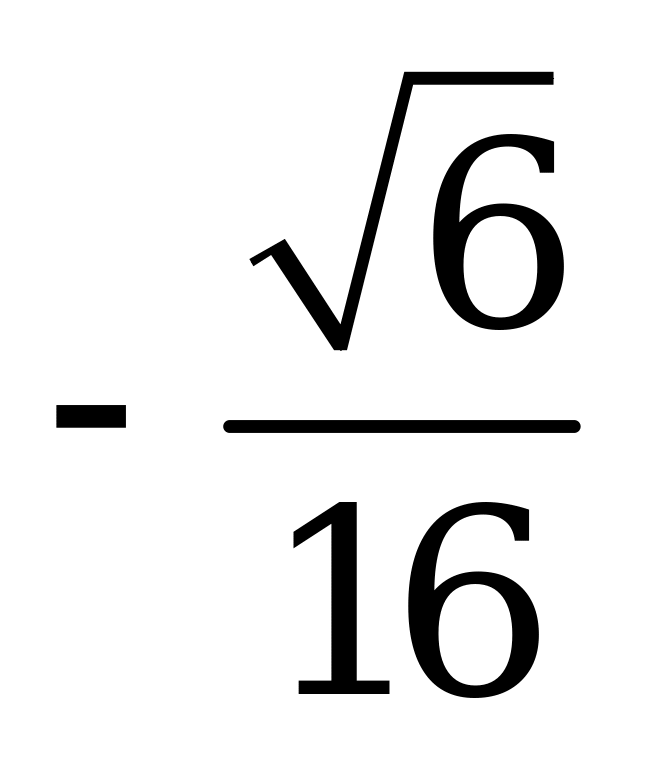 | A |
| А4.4 Вычислите 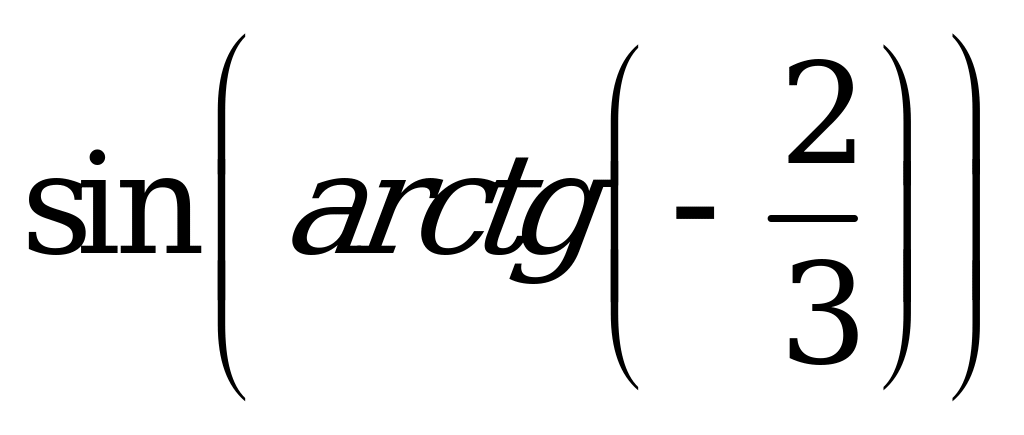 A) -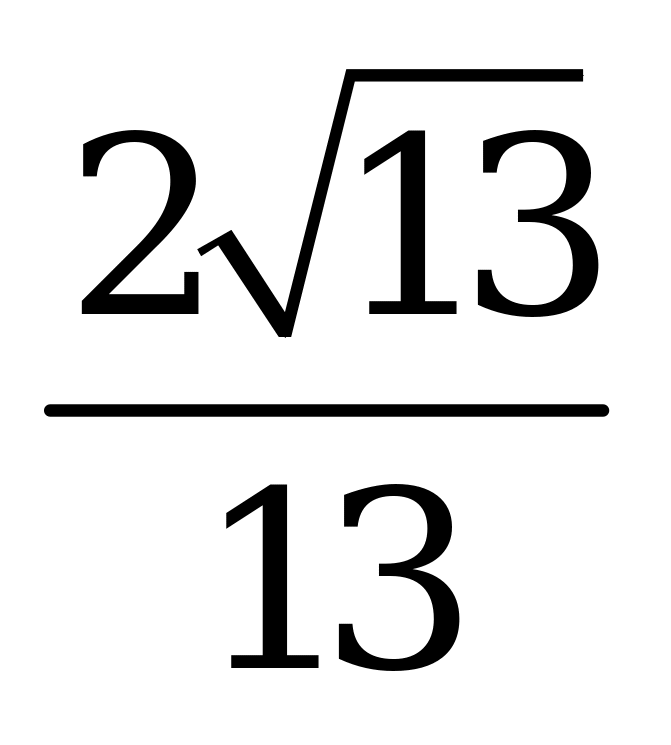 B) - B) -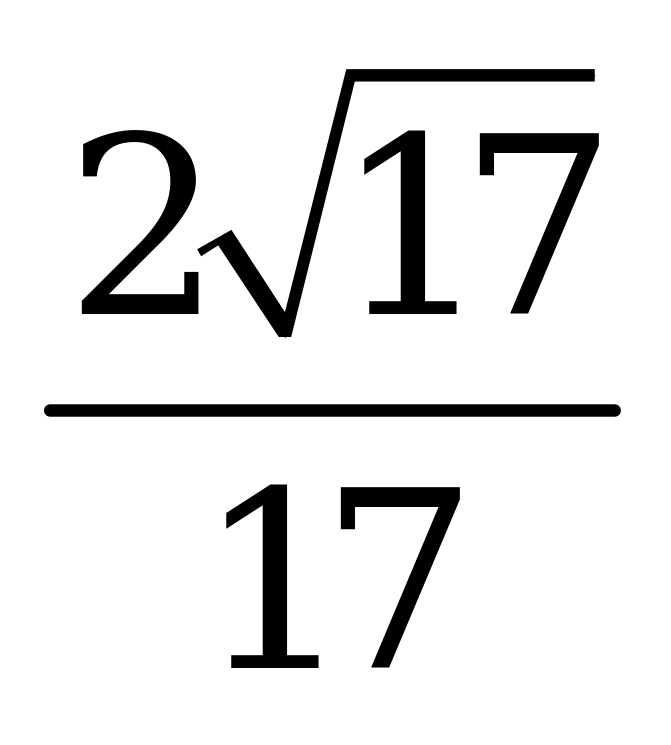 C) - C) -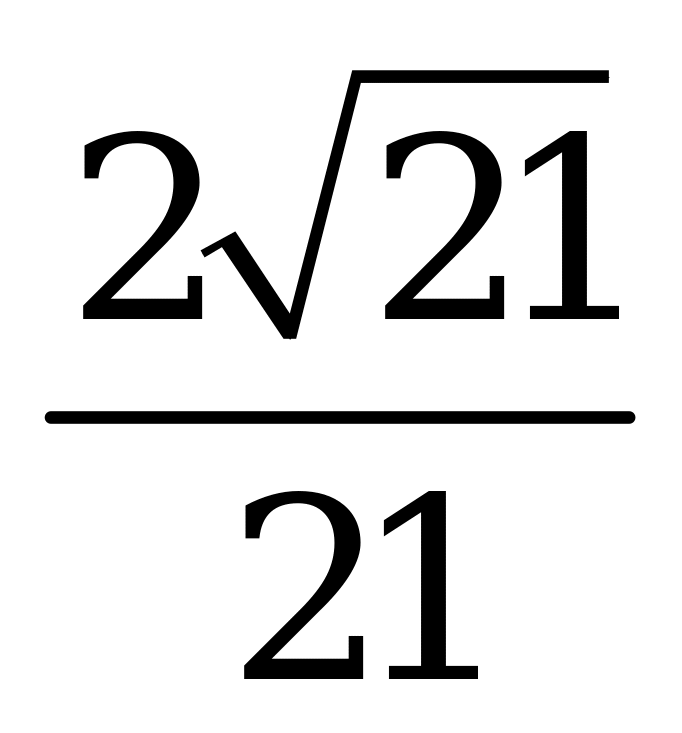 D) - D) -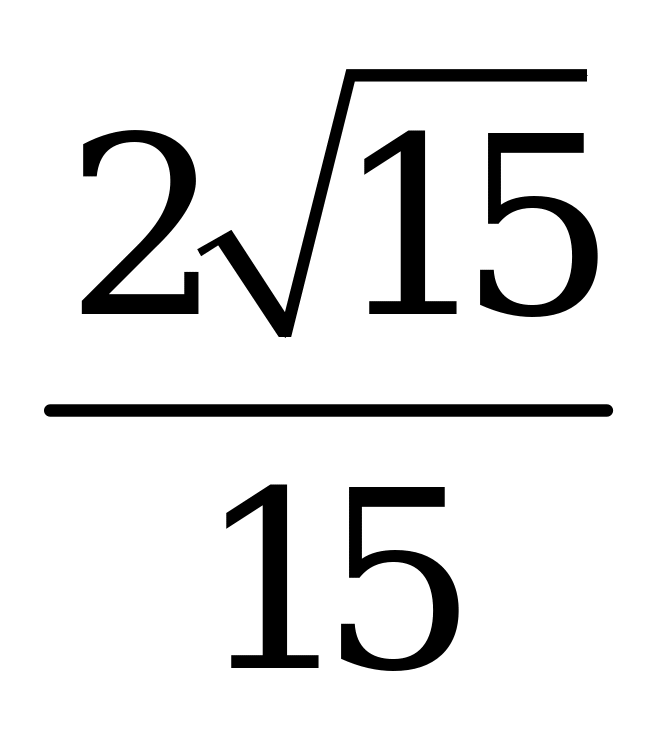 E) - E) -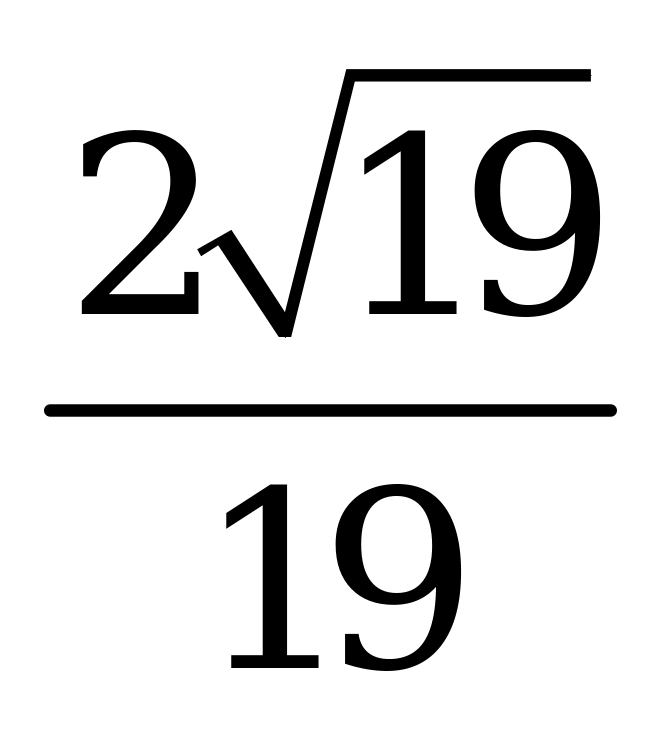 | A |
| А4.5 Найдите произведение корней уравнения 4arctg(x2 – 3x + 3) - = 0. A) 2 B) 3 C) -3 D) 1 E) 0 | A |
| А4.6 Вычислите  A) -0,28 B) 0,28 C) -0,26 D) 0,26 E) -0,24 | A |
| А4.7 Вычислите: 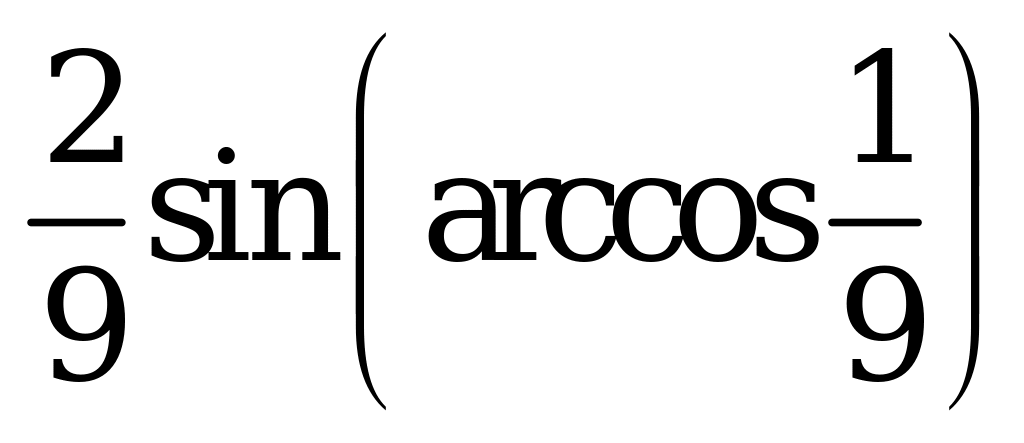 A) 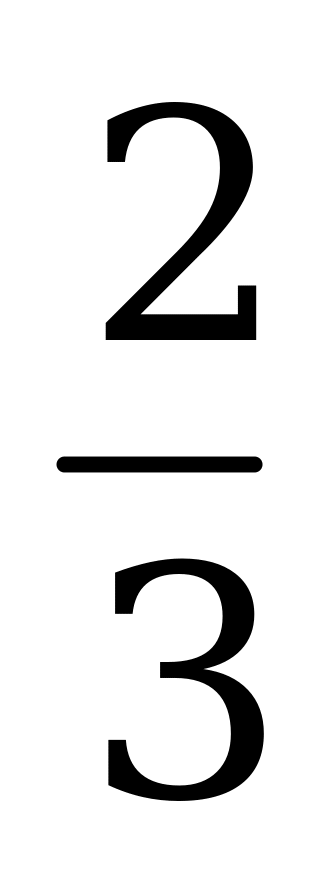 B) B) 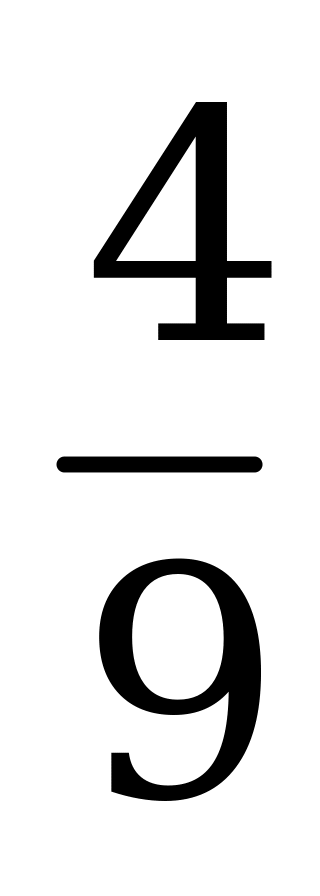 C) C) 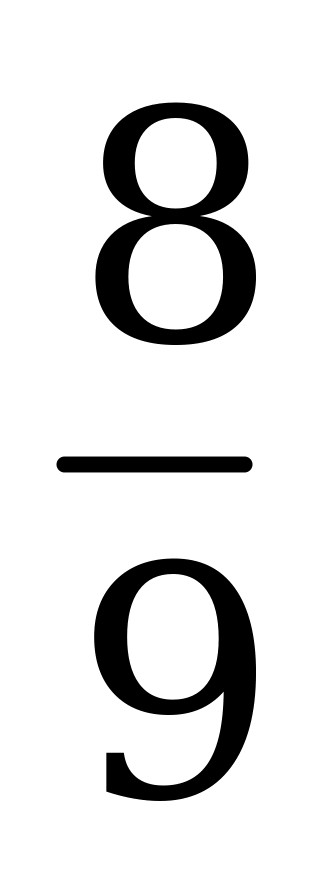 D) D) 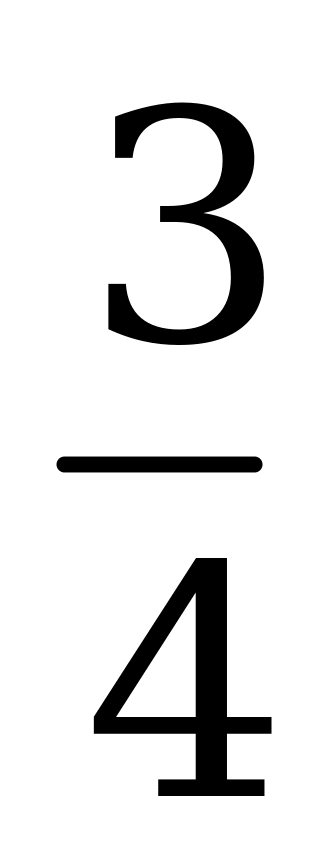 E) E) 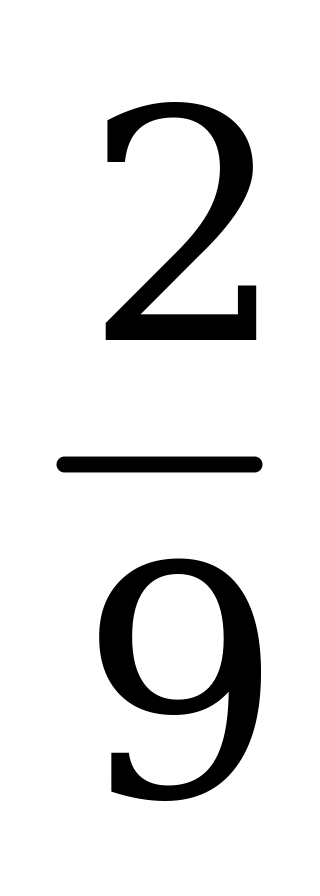 | A |
| А4.8 Найдите значение 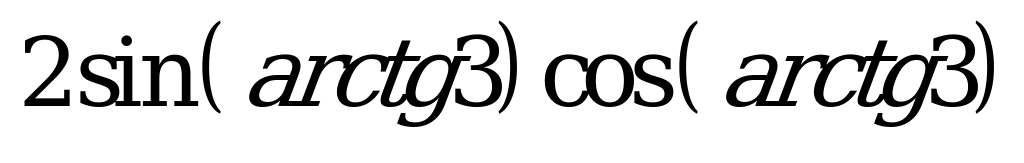 . . A) 0,6 B) 0,8 C) 0,75 D) 0,36 E) 0,9 | A |
| А4.9 Вычислите: 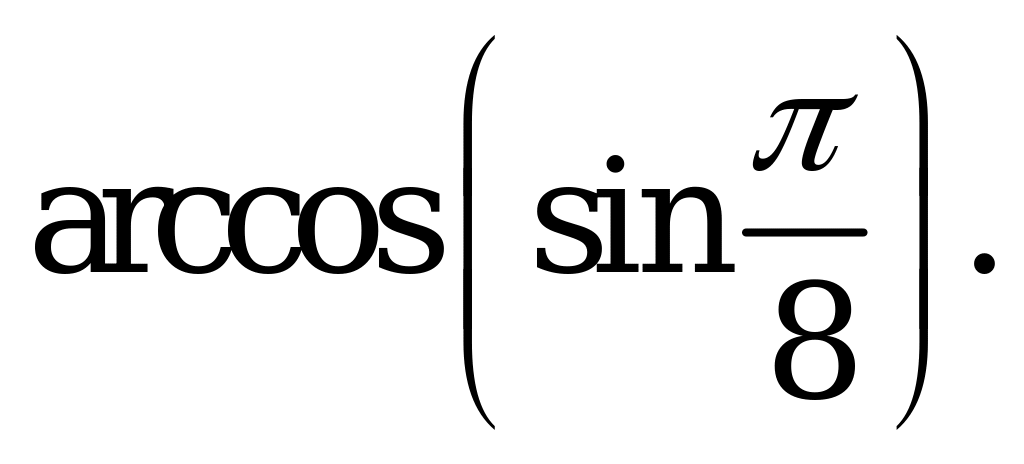 A) 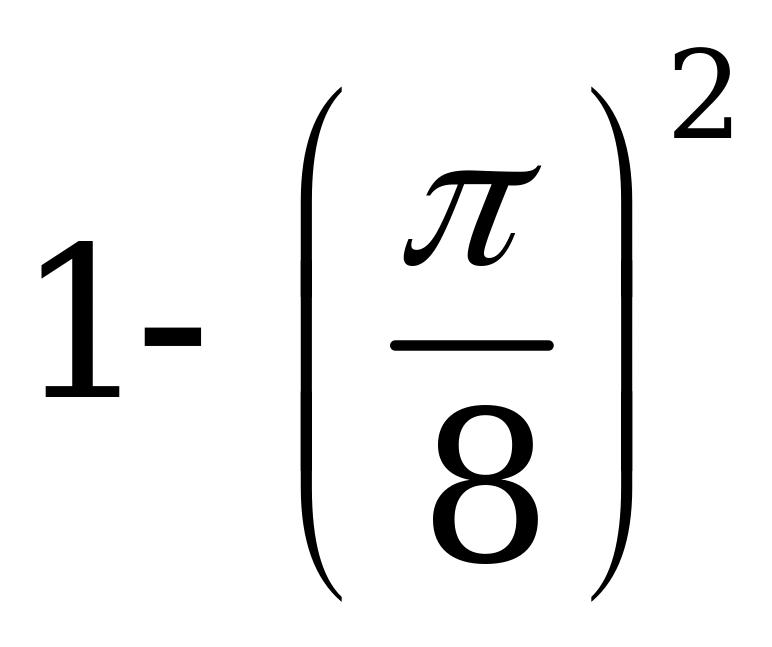 B) B) 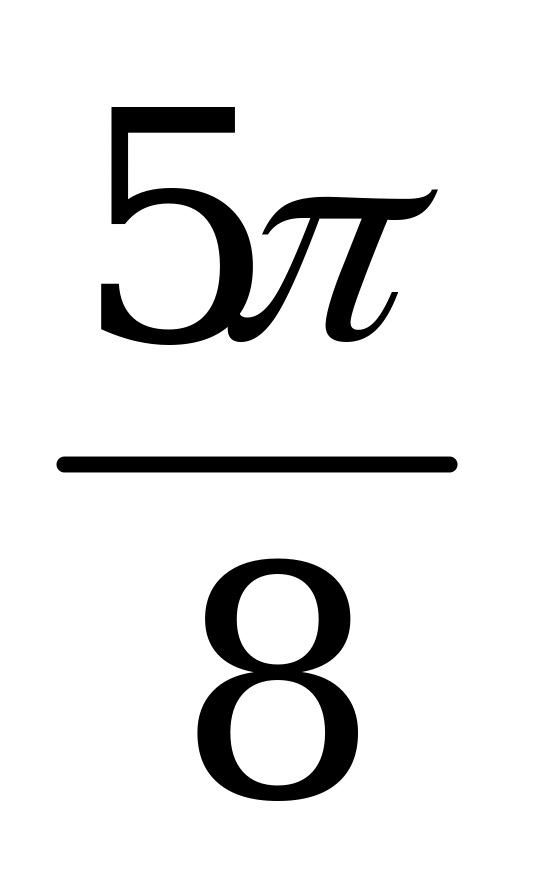 C) C) 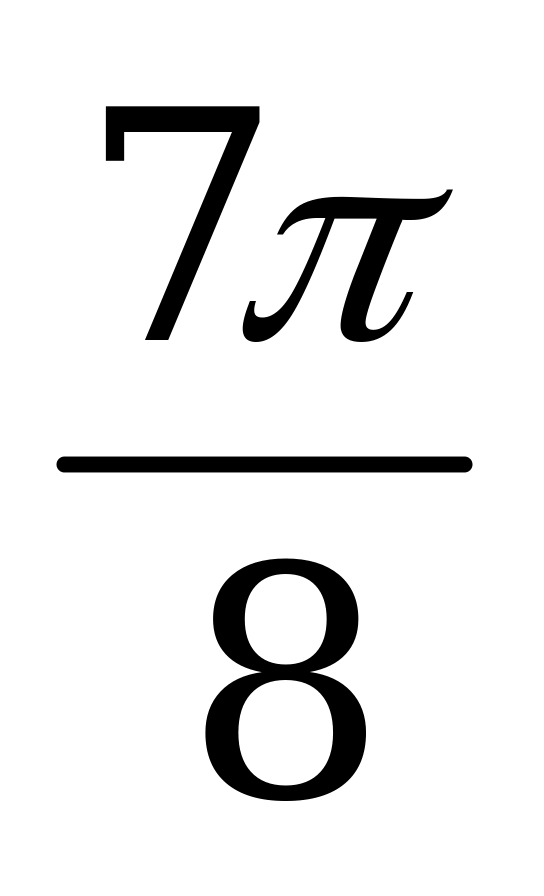 D) D) 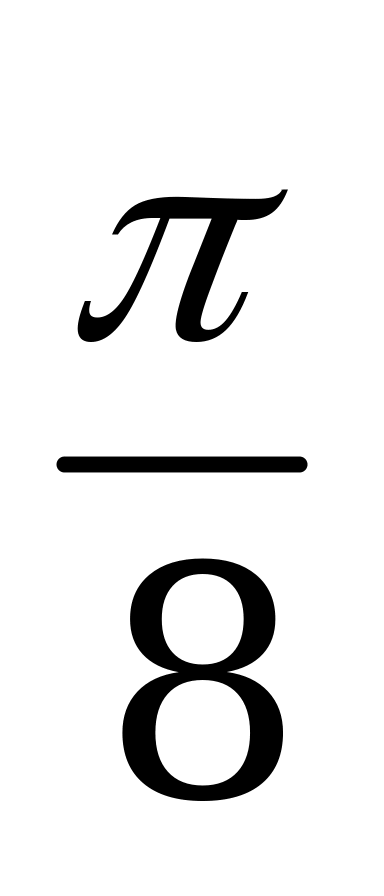 E) E) 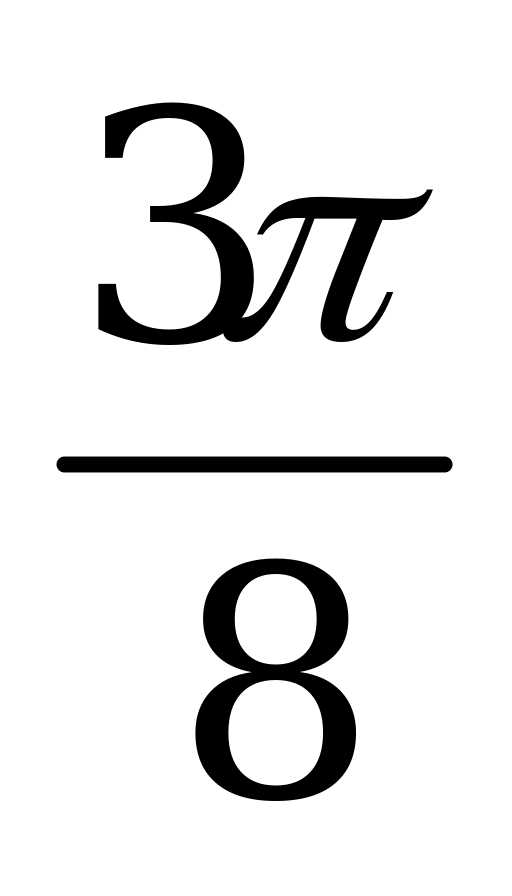 | E |
| А4.10 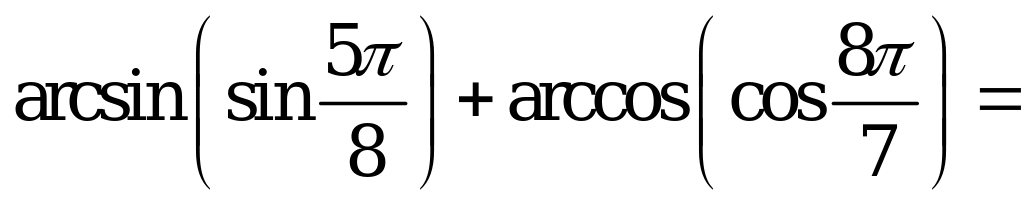 ? ? A) 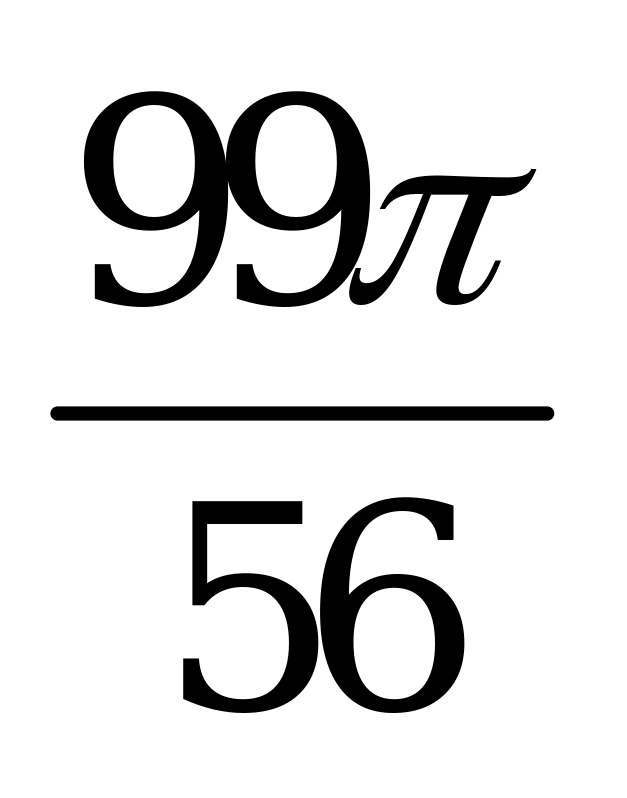 B) B) 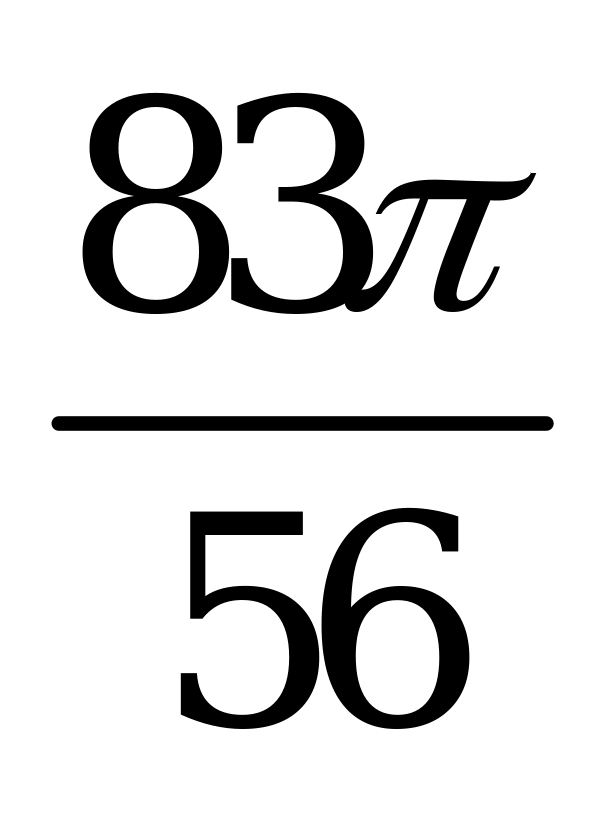 C) C) 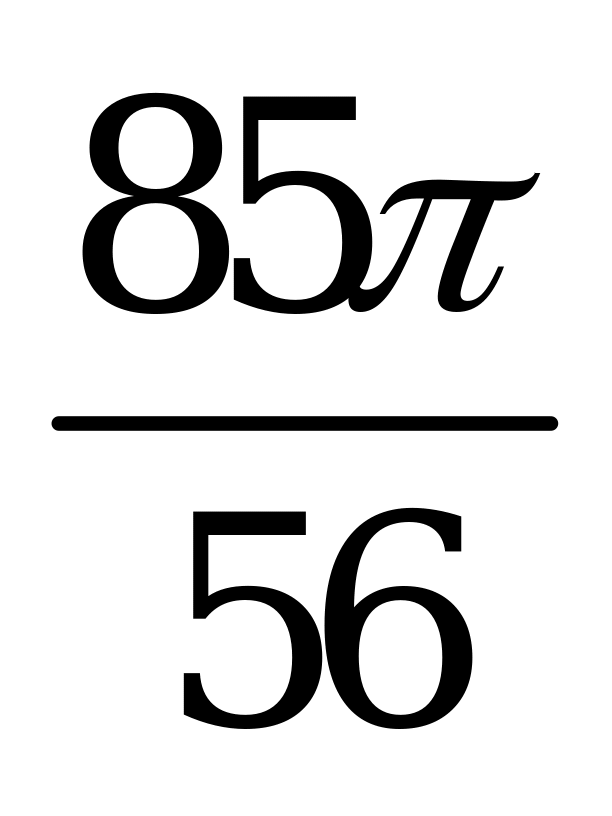 D) D) 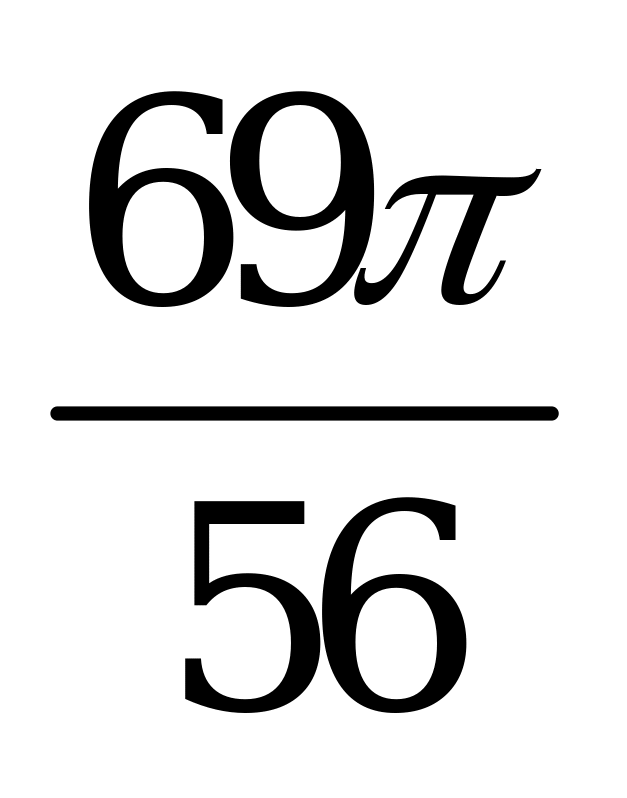 E) E) 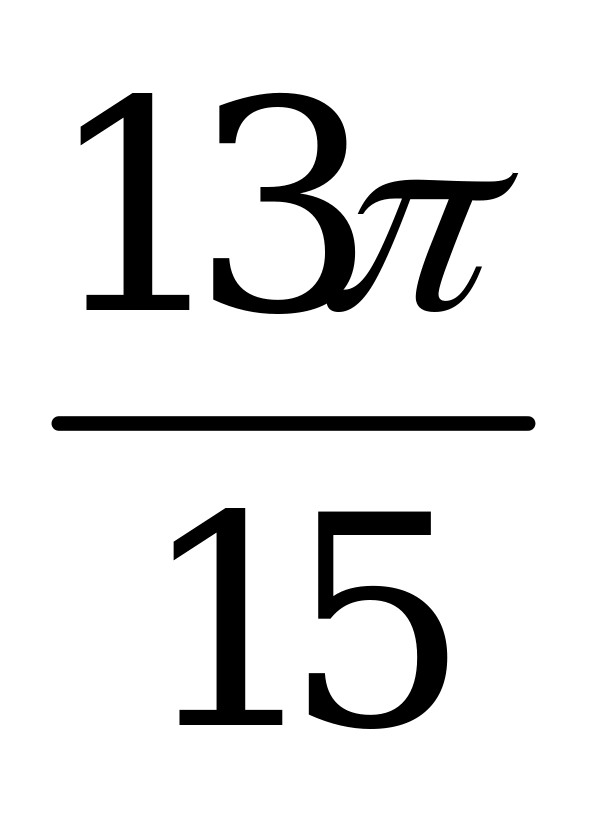 | D |
Тестовые задания более сложного уровня 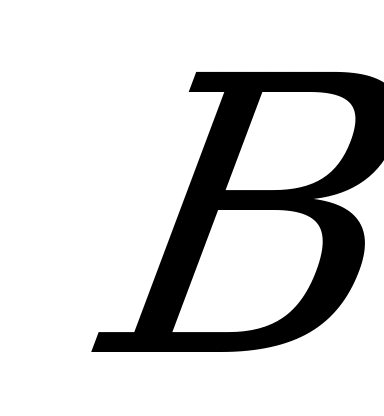 .
.
| В1. Обратные тригонометрические функции | Ответы |
| В1.1 Решите уравнение 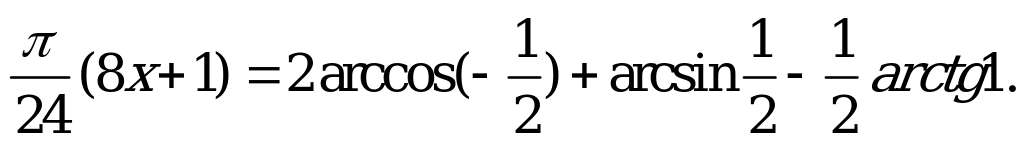 A) 4 B) 6 C) 5 D) 3 E) 2 | A |
| В1.2 Расставьте в порядке убывания числа: 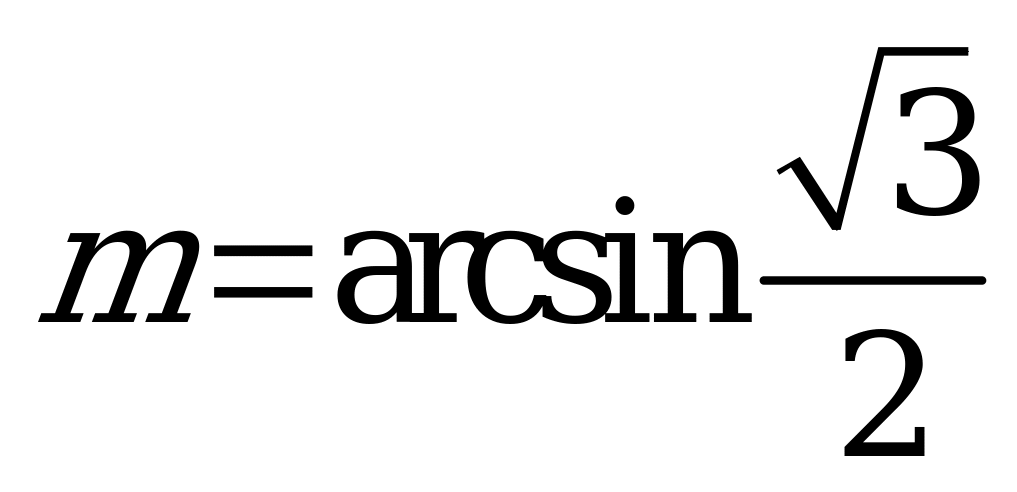 , , 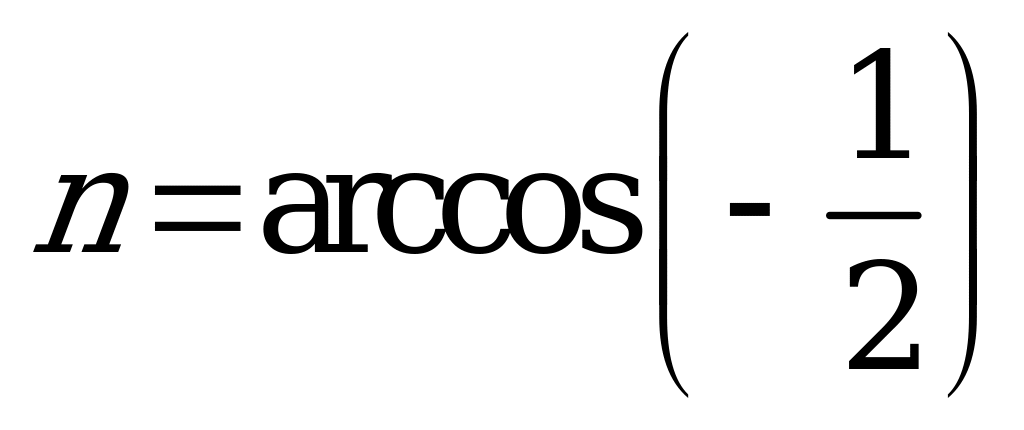 и и 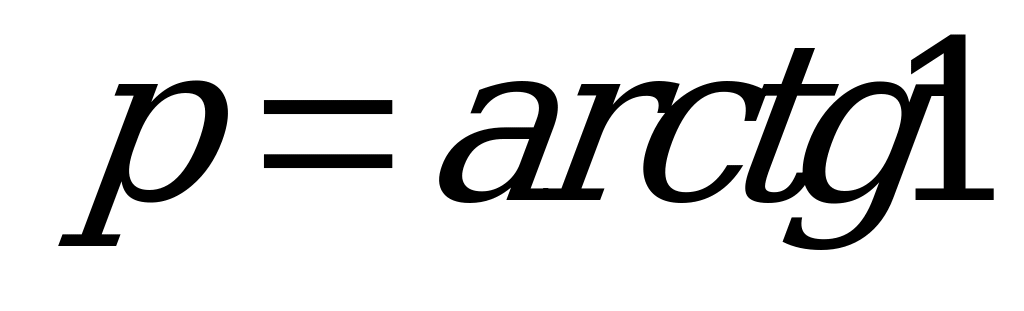 . . A) m p n B) m n p C) n m p D) p n m E) p m n | C |
| В1.3 Вычислите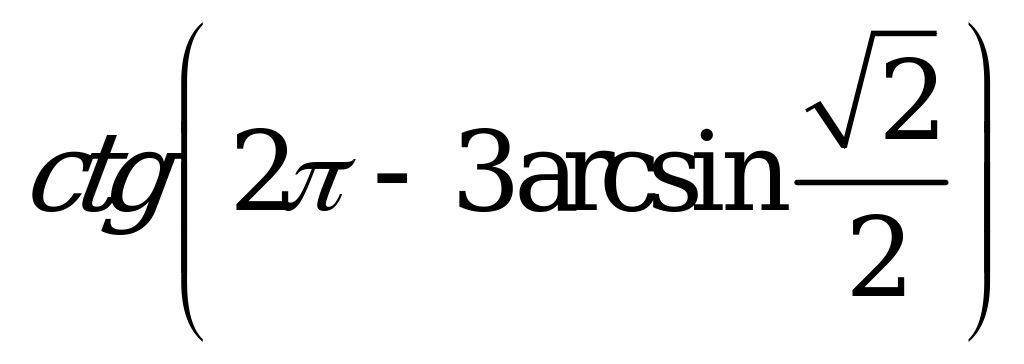 . . A) 1 B) -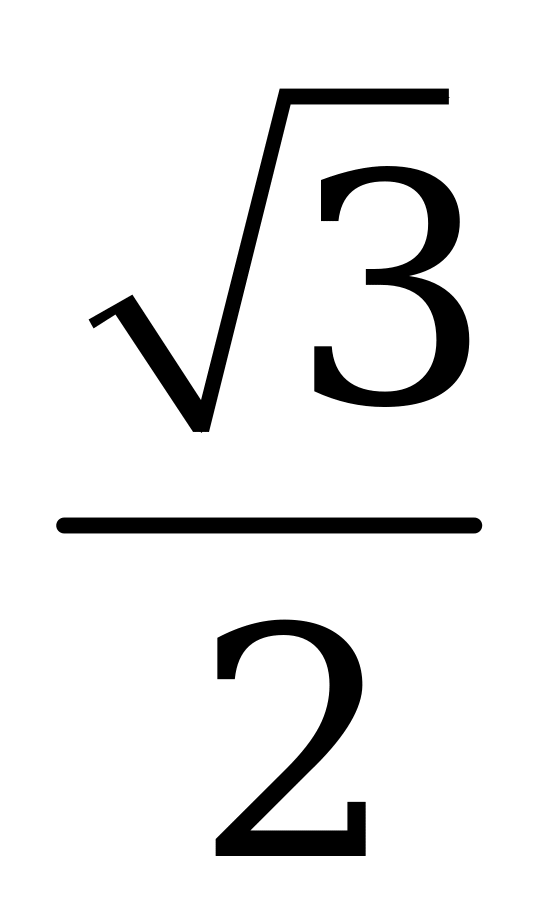 C) - C) -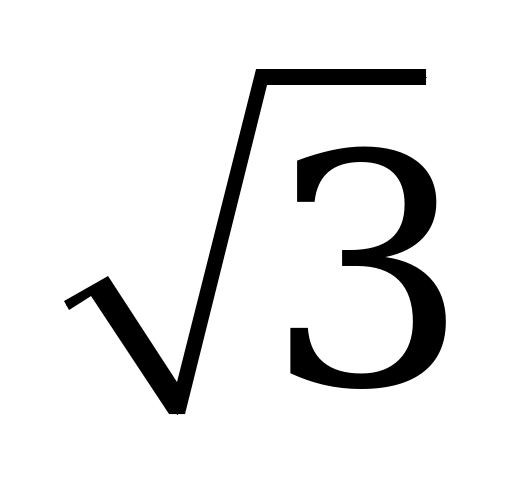 D) D) 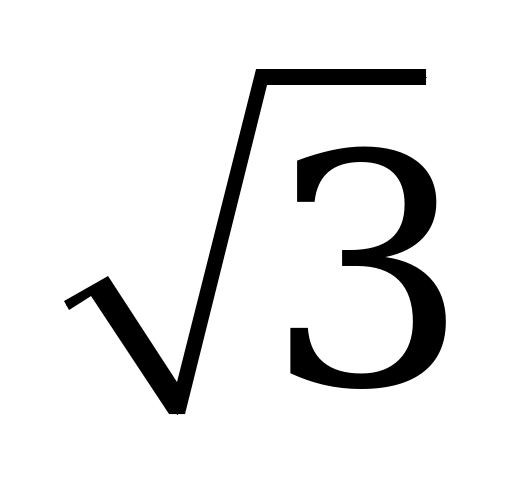 E) E) 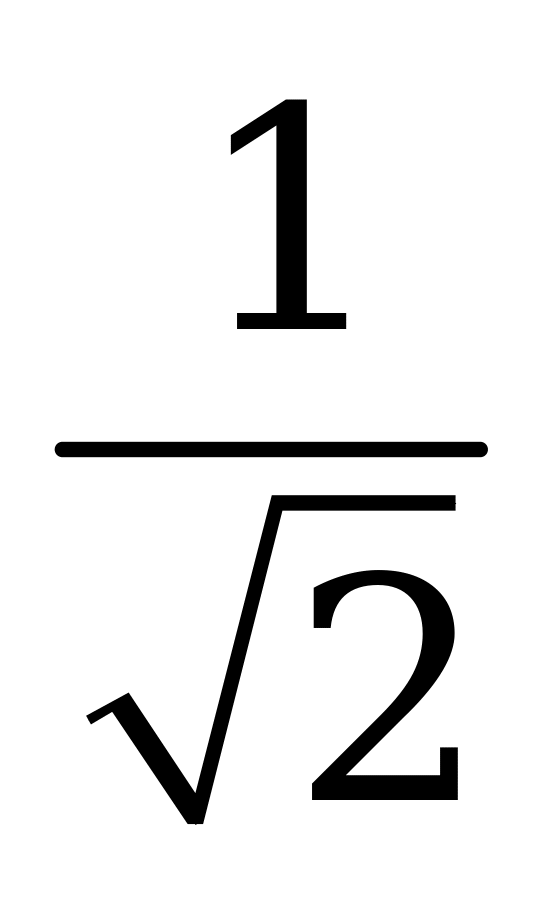 | A |
| В1.4 Вычислите: 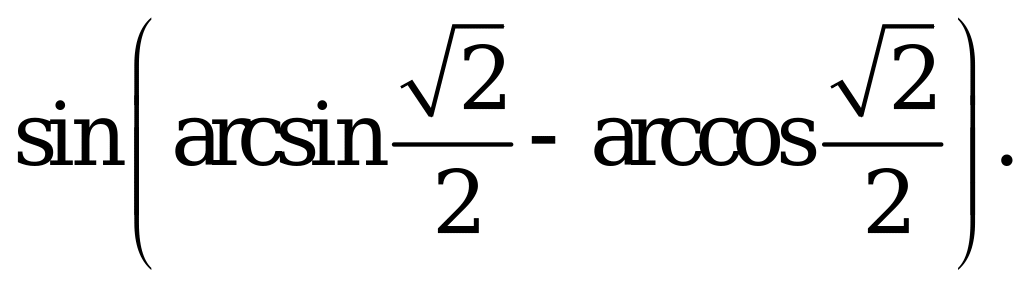 A) 0 B) 1 C) 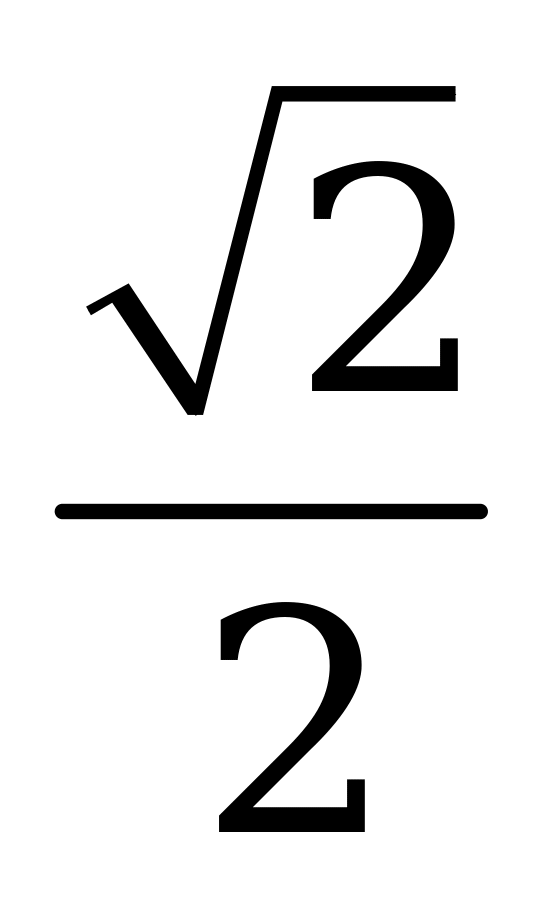 D) D) 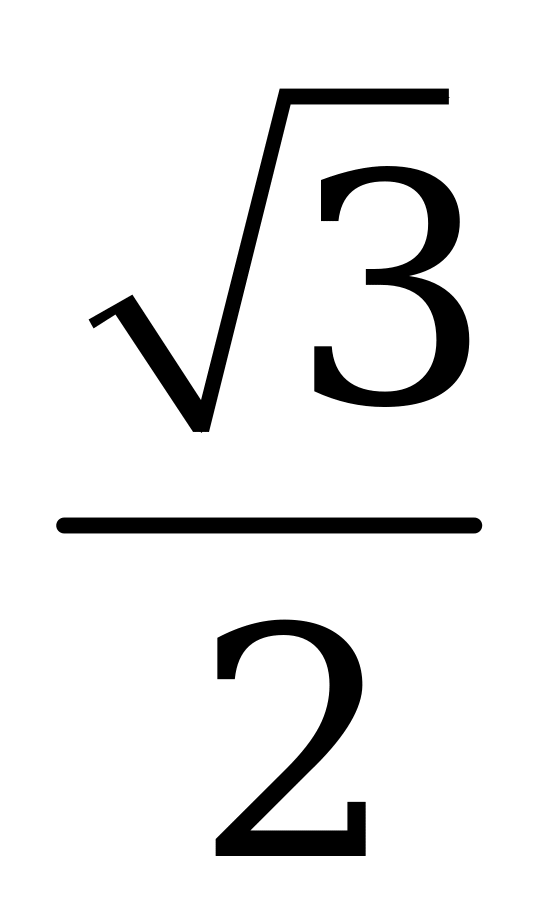 E) E) 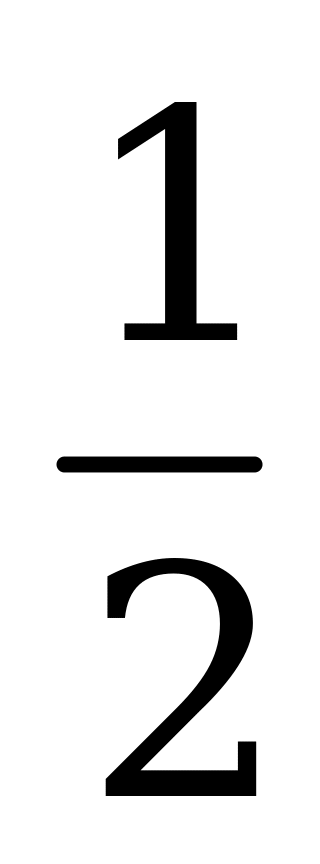 | A |
| В1.5 Вычислите 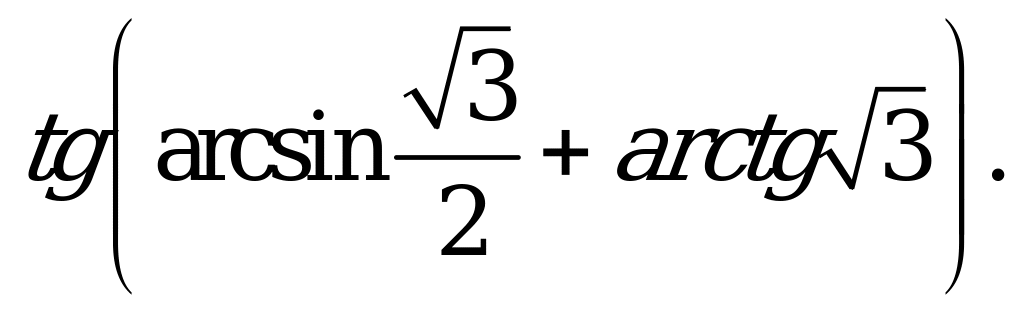 A) 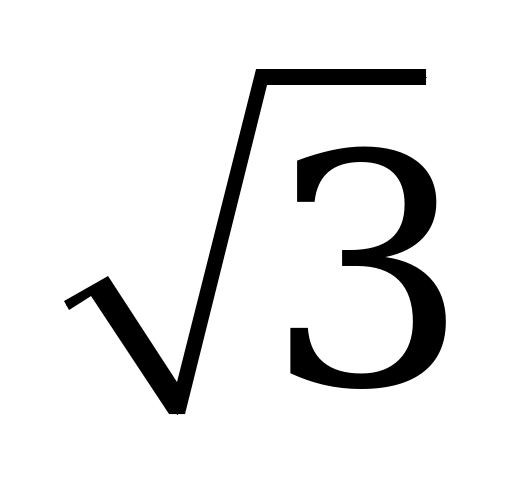 B) - B) -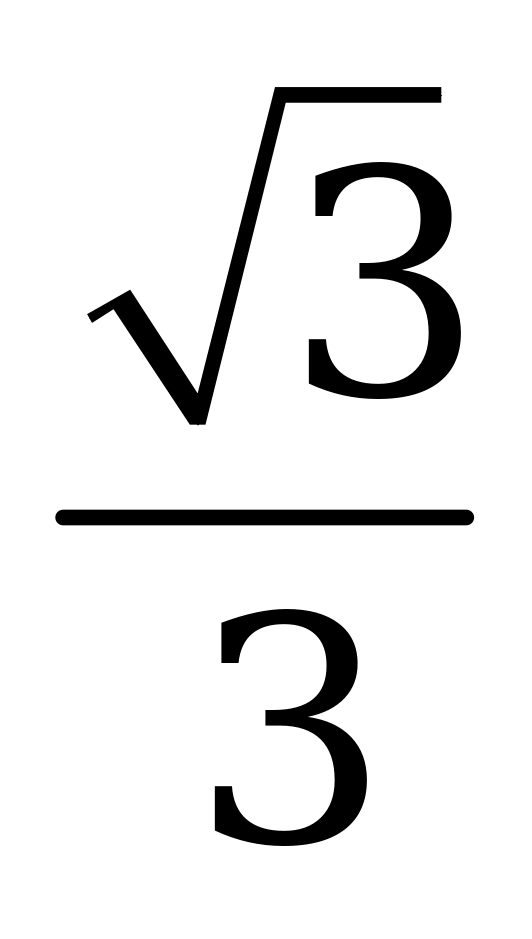 C) - C) -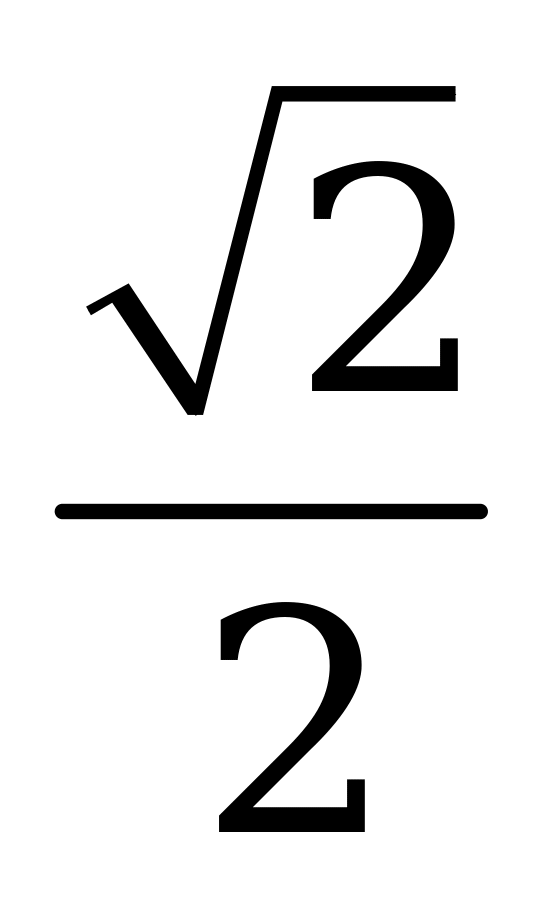 D) - D) -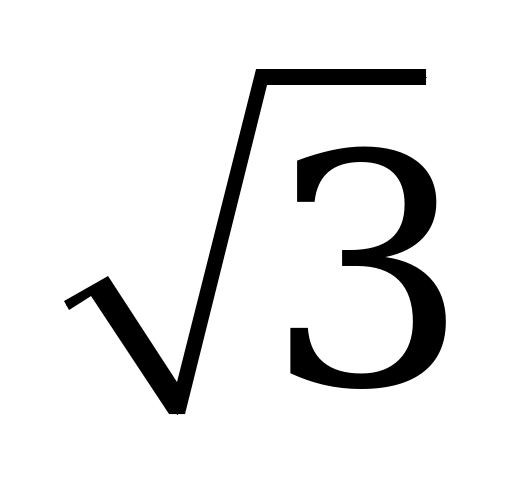 E) -1 E) -1 | D |
| В1.6 Вычислите 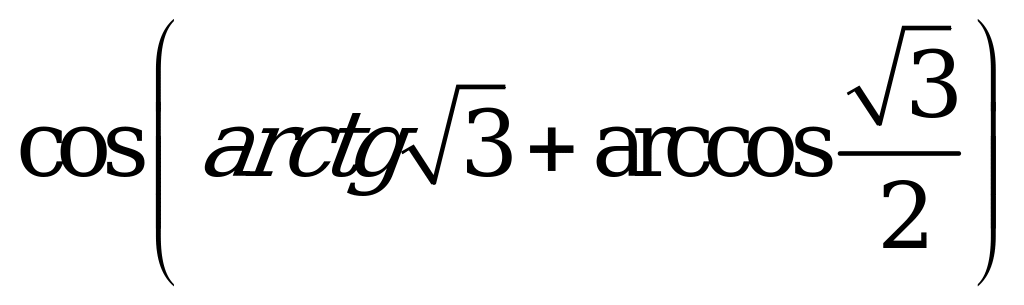 А) 1 B) 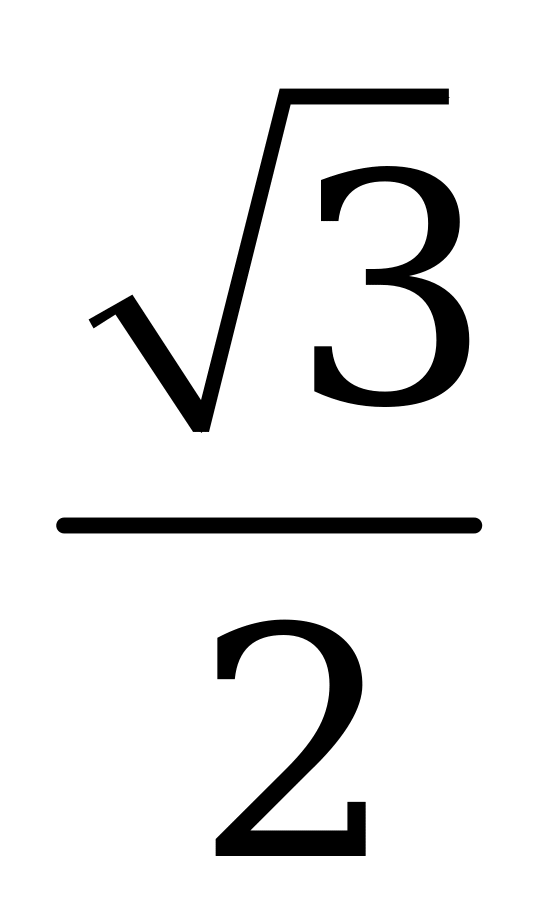 C) C) 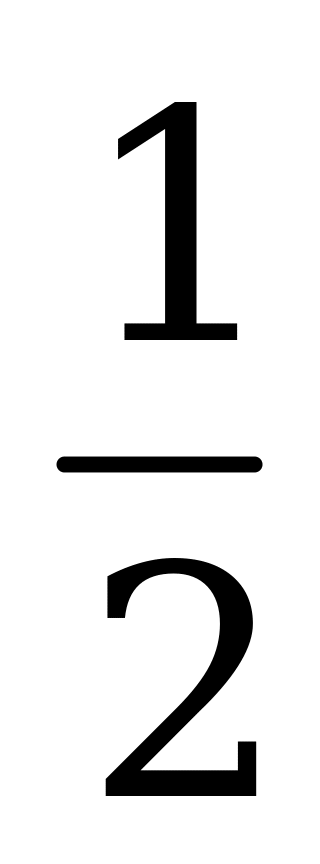 D) D) 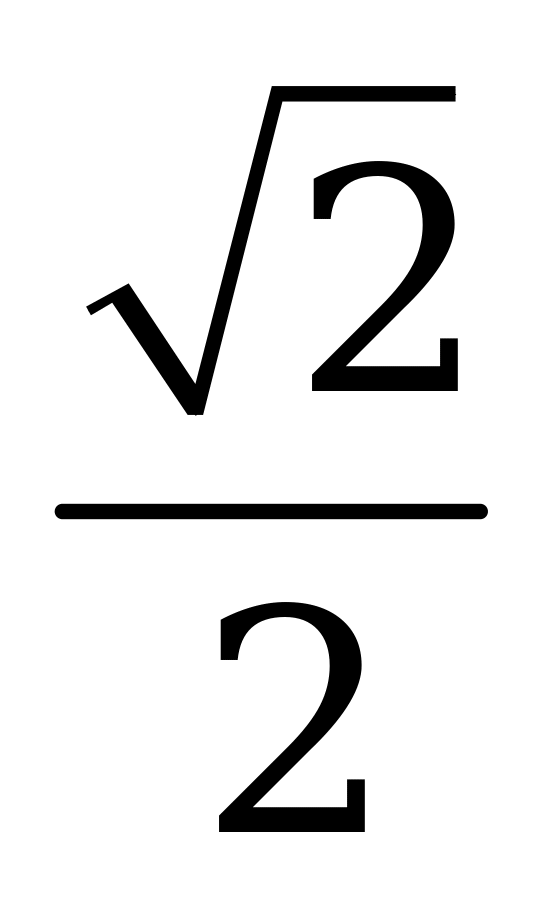 E) 0 E) 0 | E |
| В1.7 Вычислите 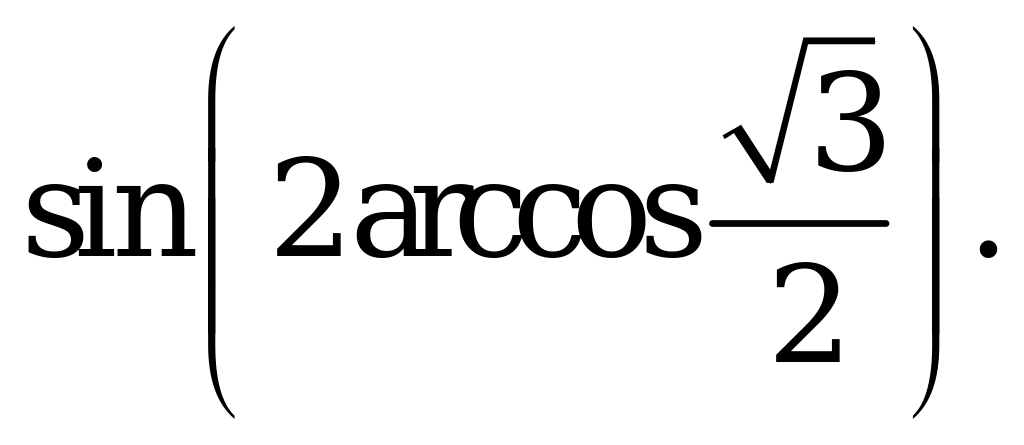 A) 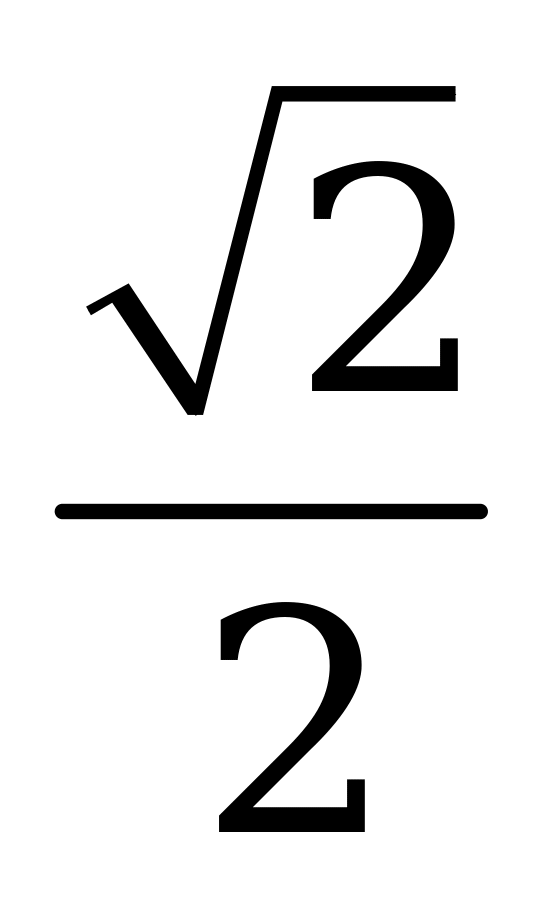 B) B) 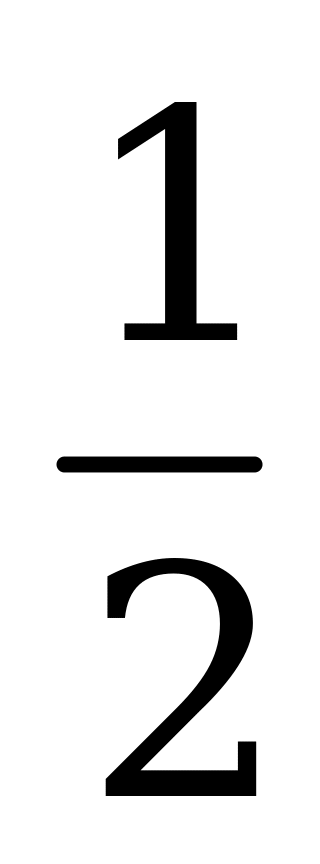 C) C) 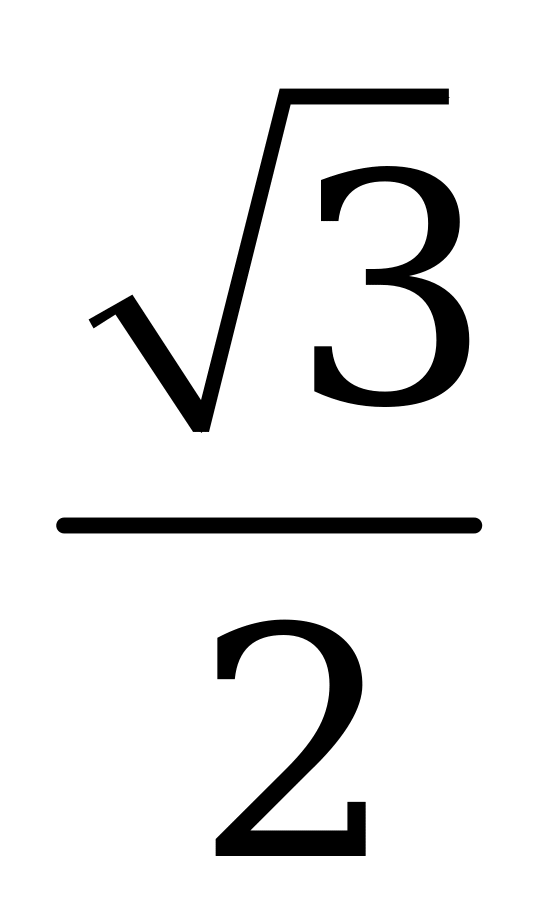 D) D) 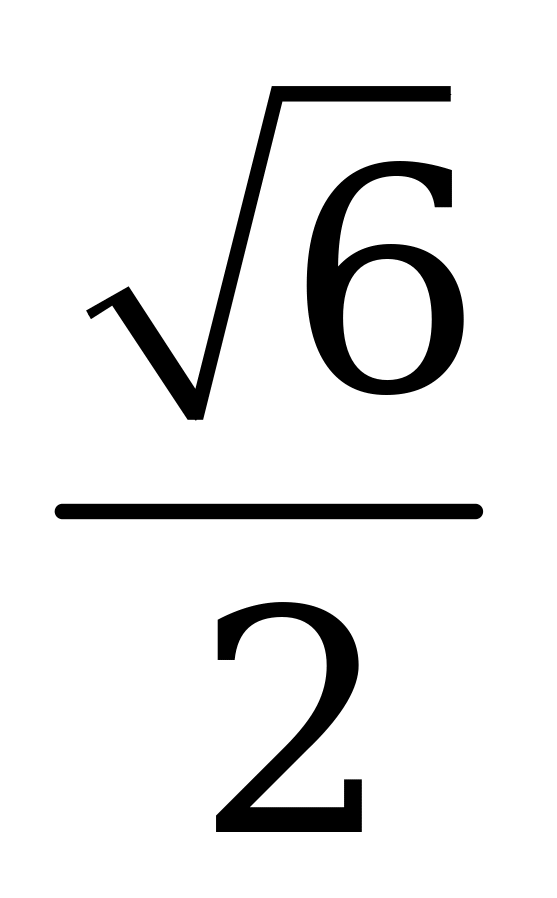 E) E) 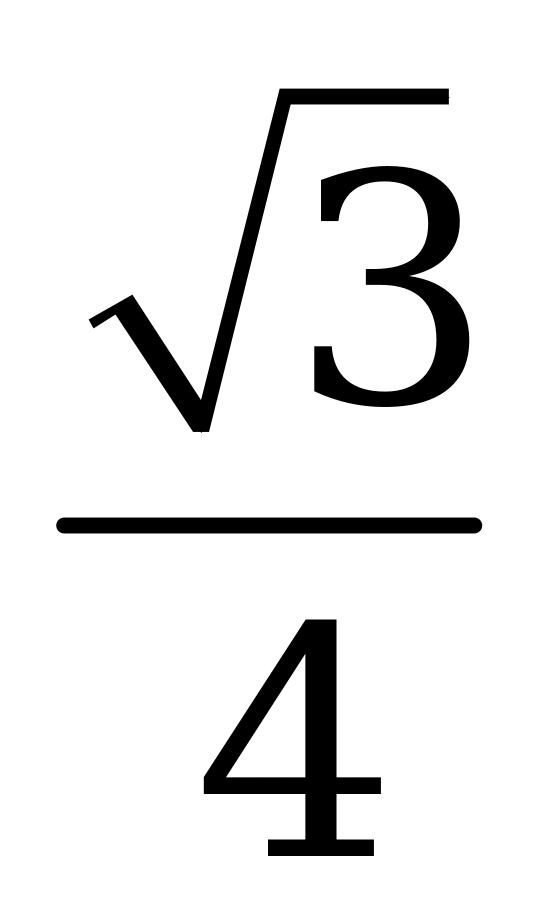 | C |
| В1.8 Найдите sin3 , если , если  =2 =2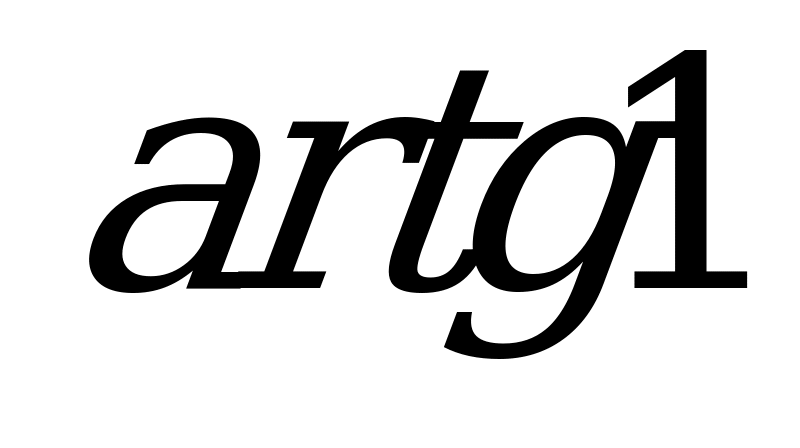 - - 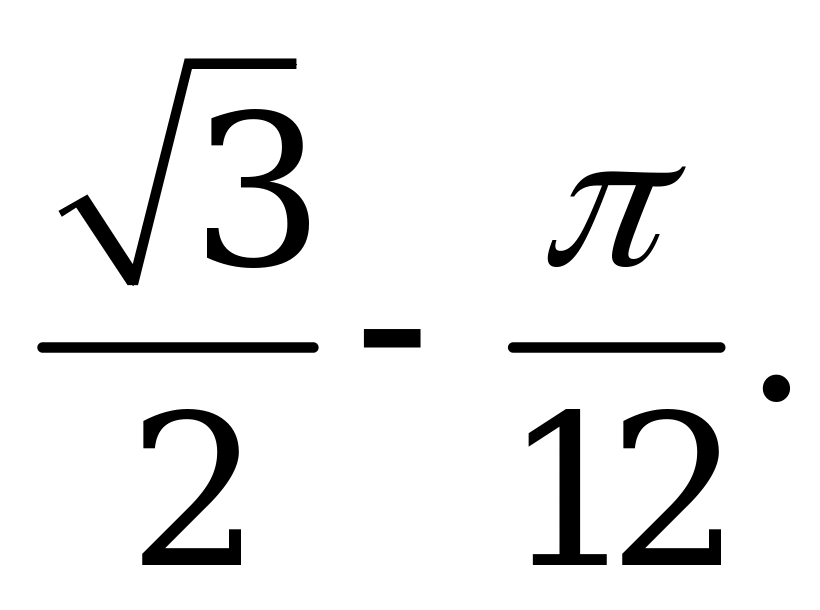 A) 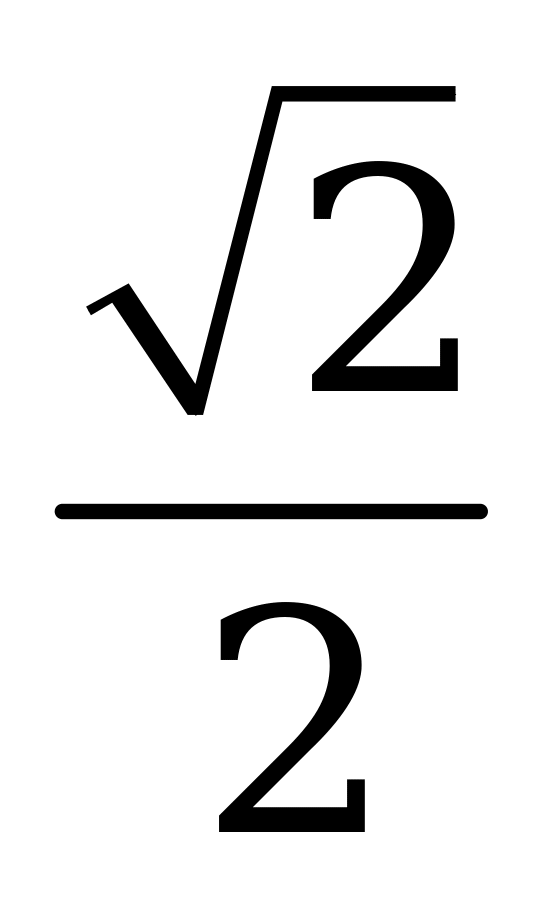 B) – 0,5 C) - B) – 0,5 C) -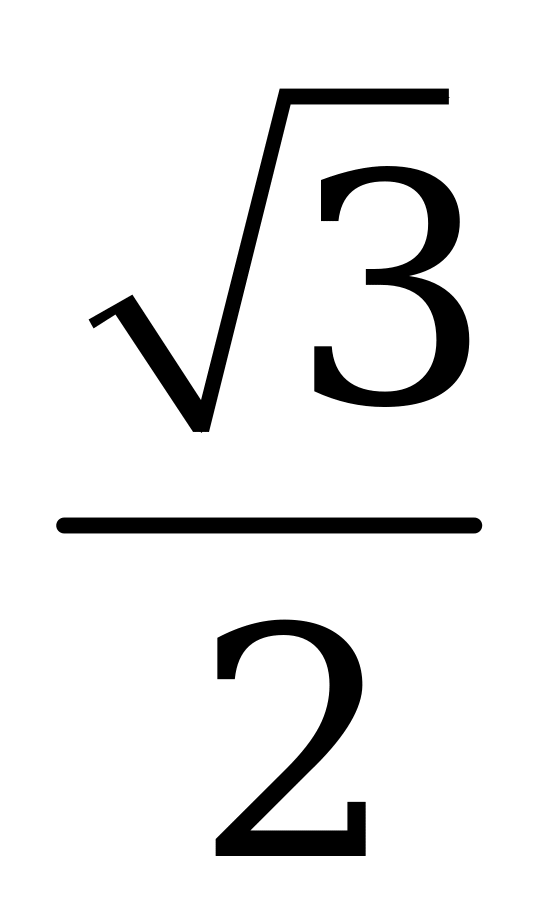 D) D) 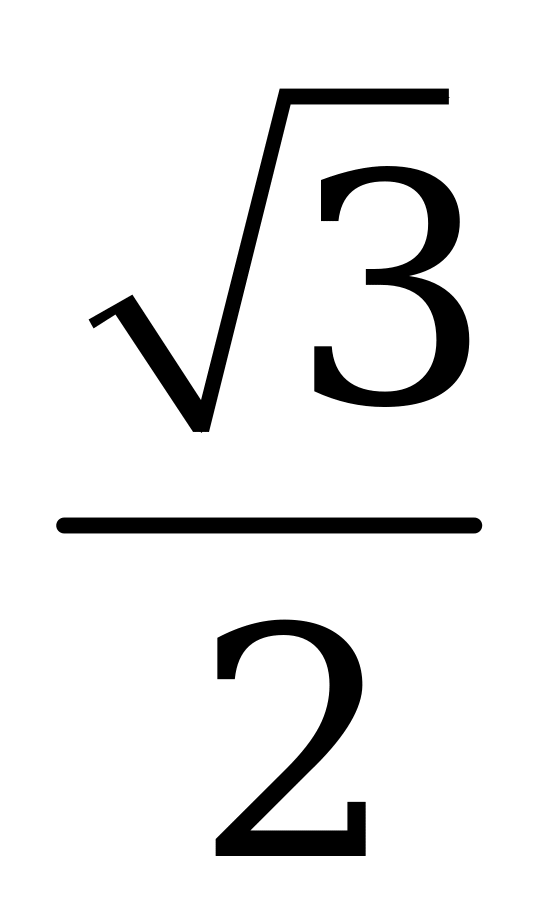 E) 1 E) 1 | A |
| В1.9 Вычислите 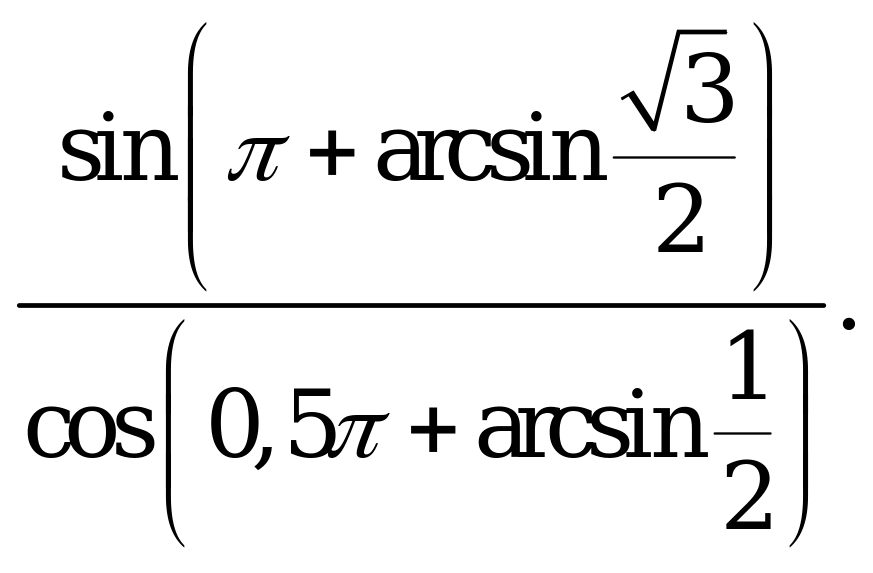 A) 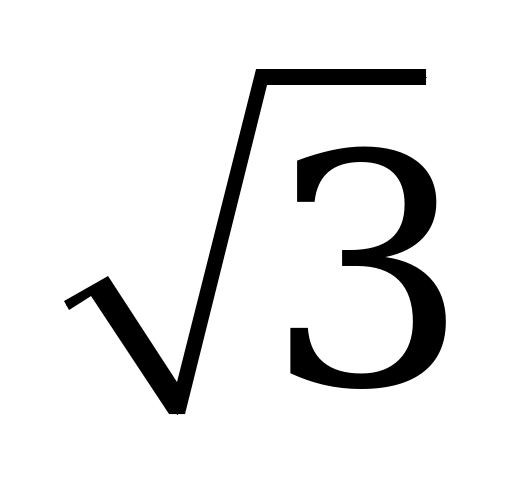 B) B) 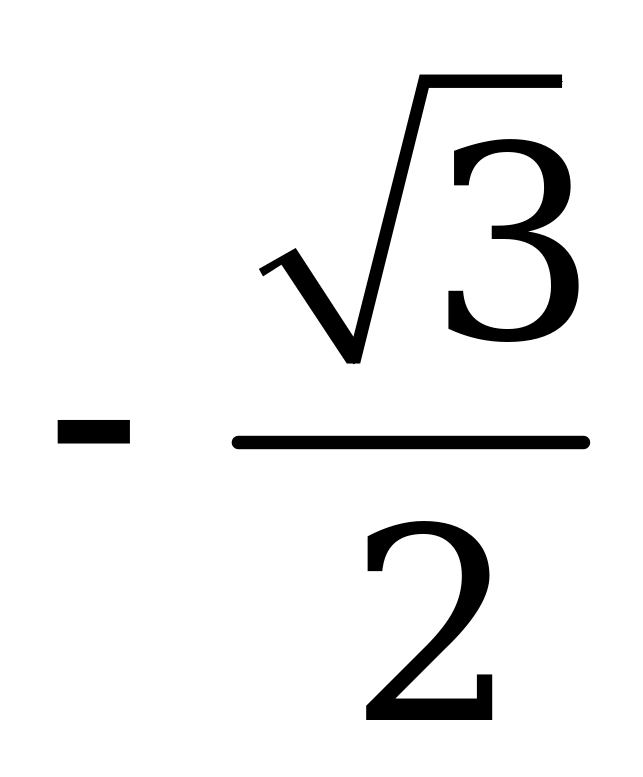 C) C) 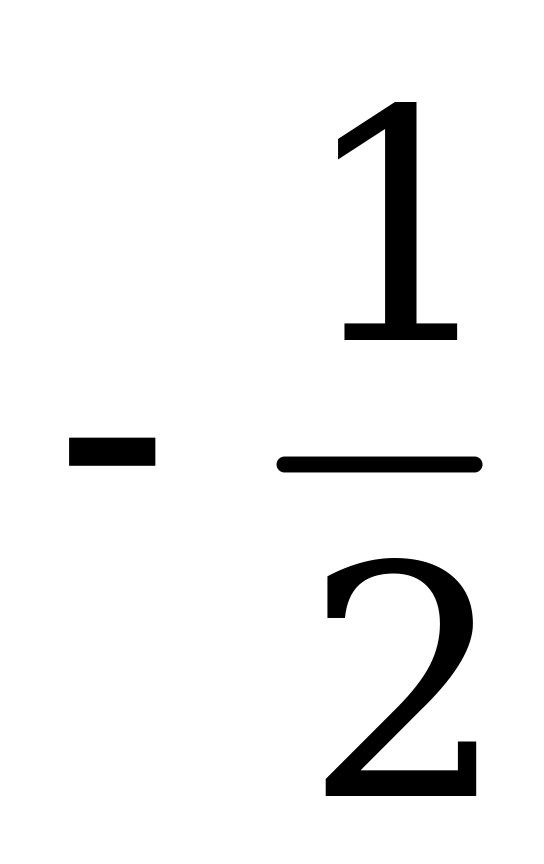 D) D) 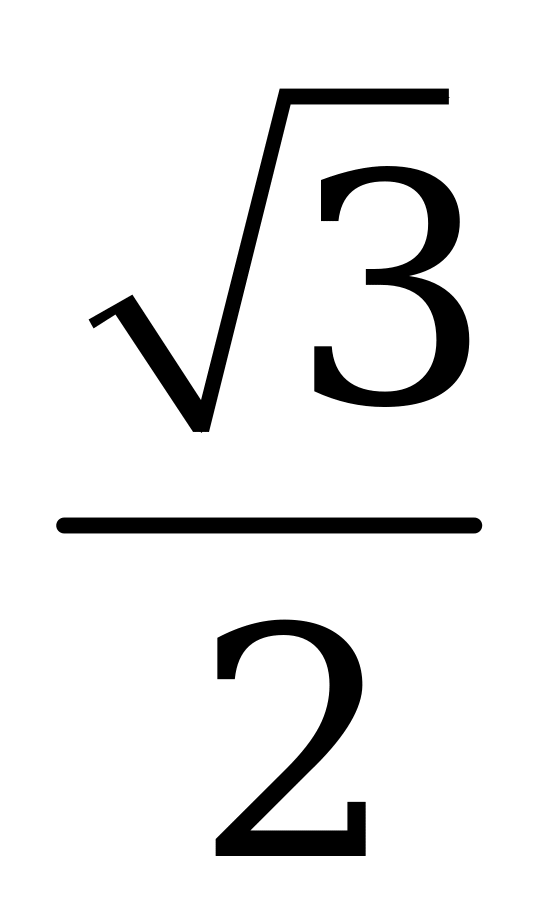 E) 1 E) 1 | A |
| В1.10 Вычислите sin( 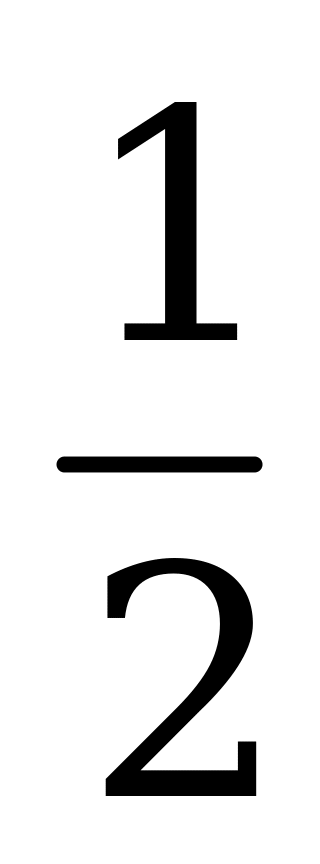 + +  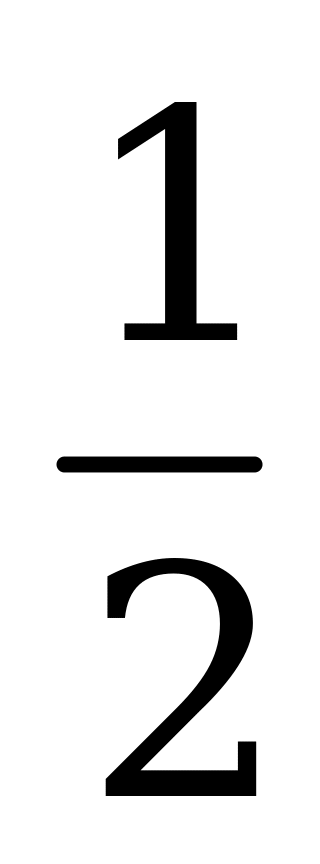 ) ) A 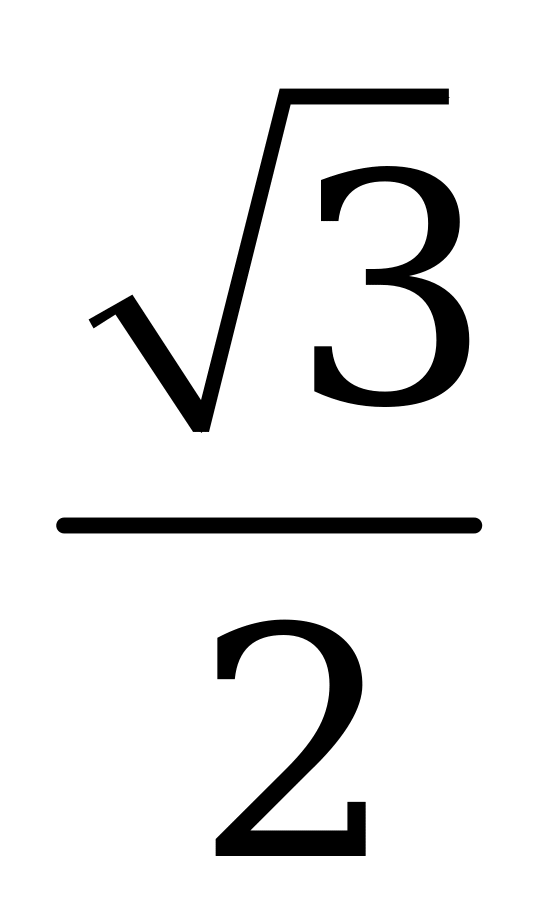 B) B) 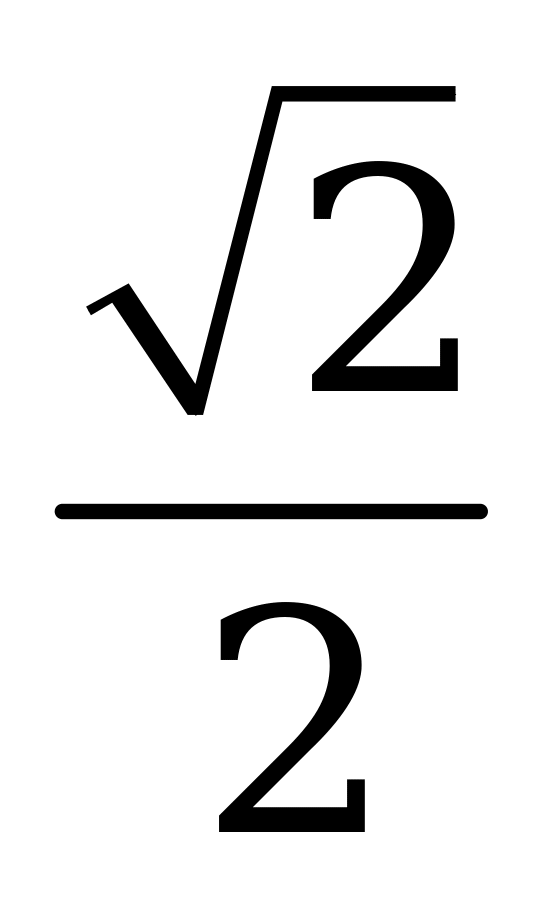 C) 1 D) C) 1 D) 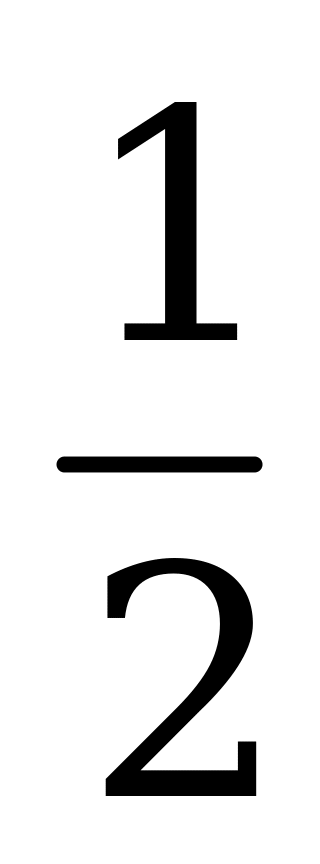 E) E) 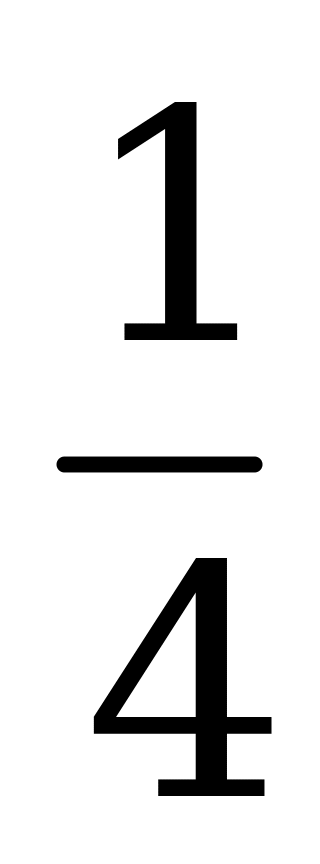 | C |
| В2. Решение уравнений |
|
| В2.1 Решите уравнение: 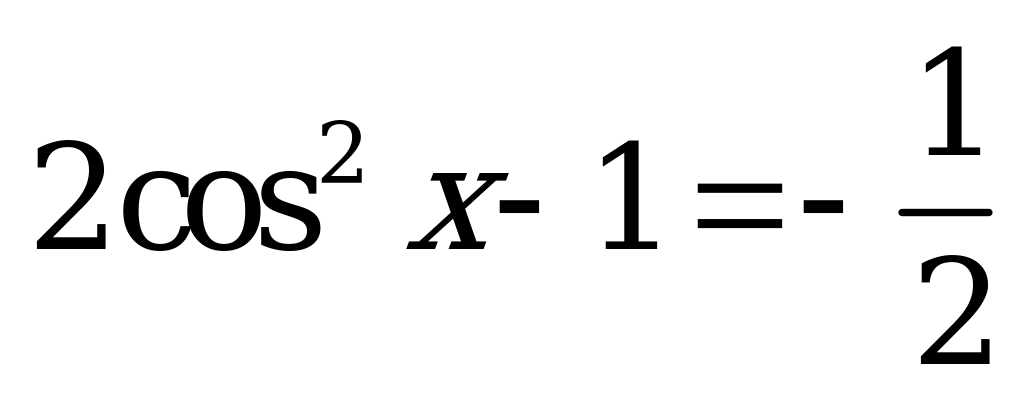 A) 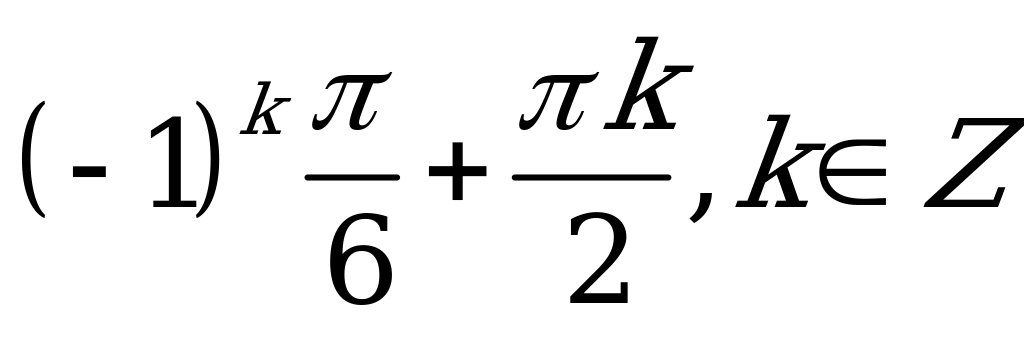 B) B) 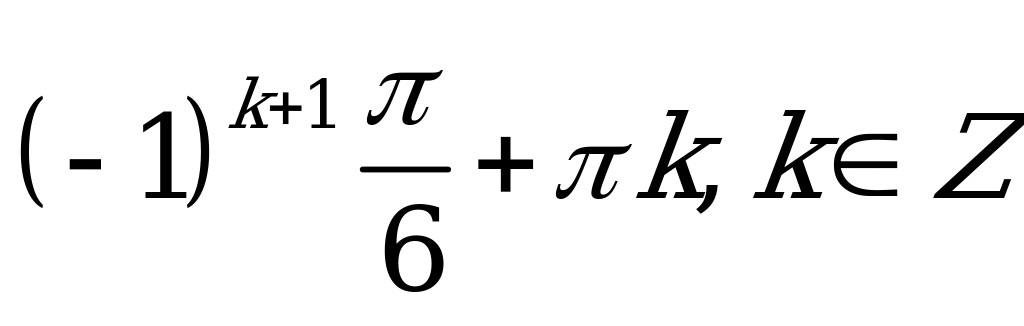 C) ±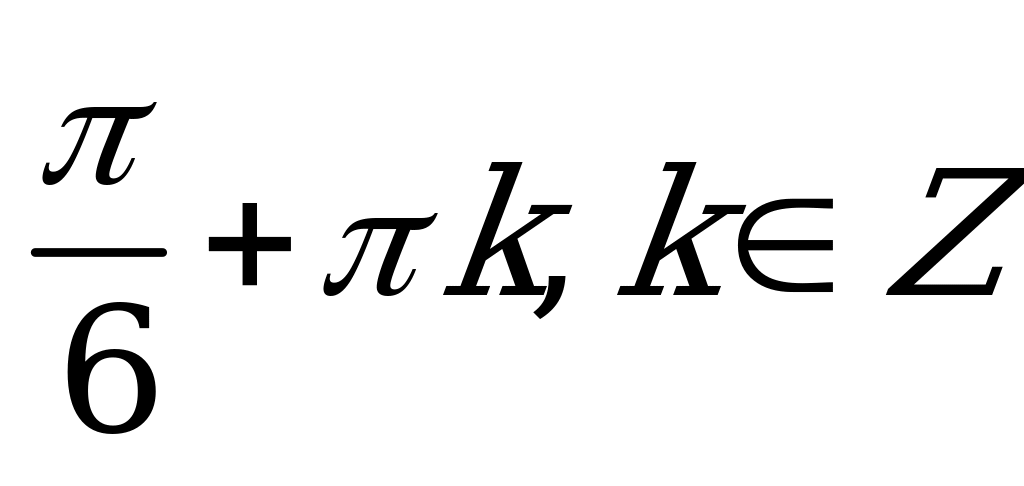 D) D) 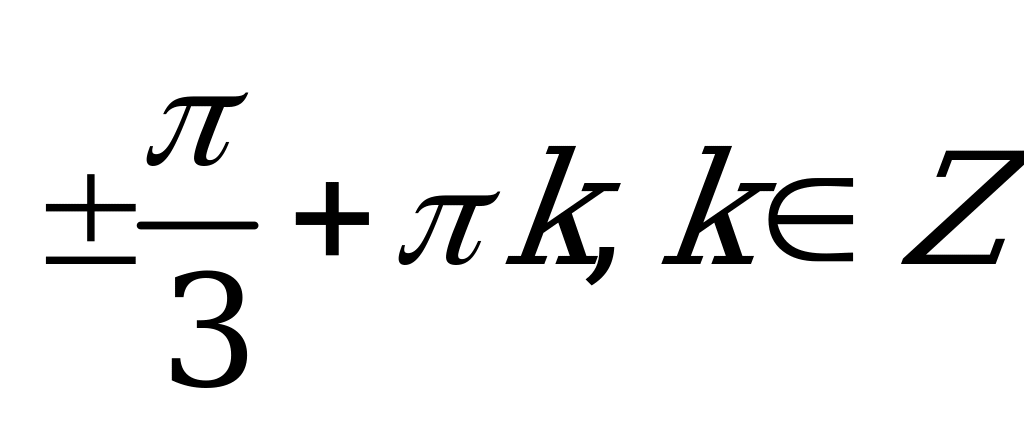 E) E)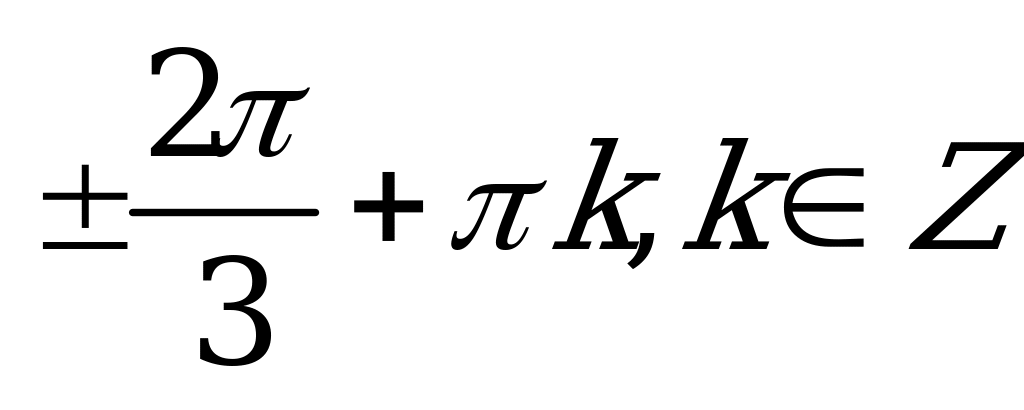 | D |
| В2.2 Решите уравнение: 4sin22x = 3 A) 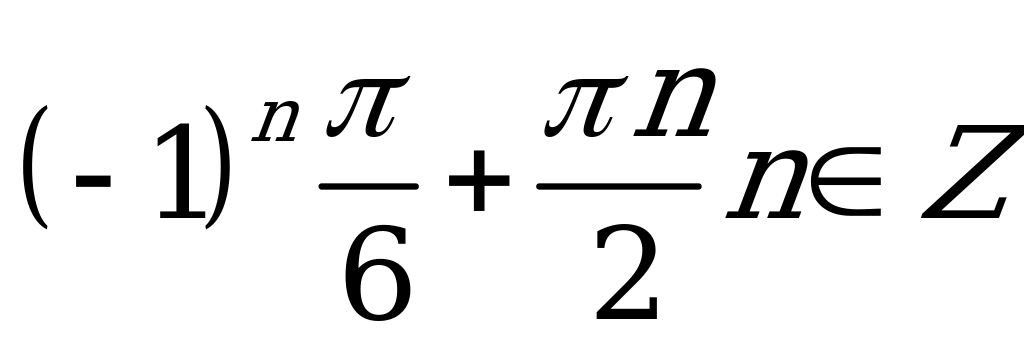 B) B) 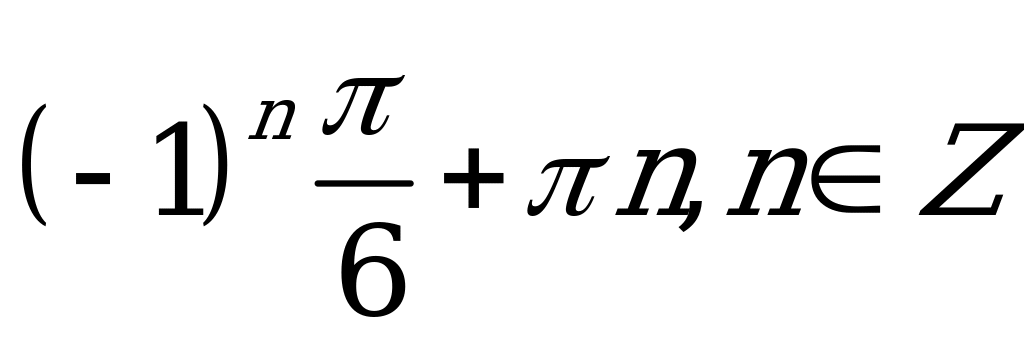 C)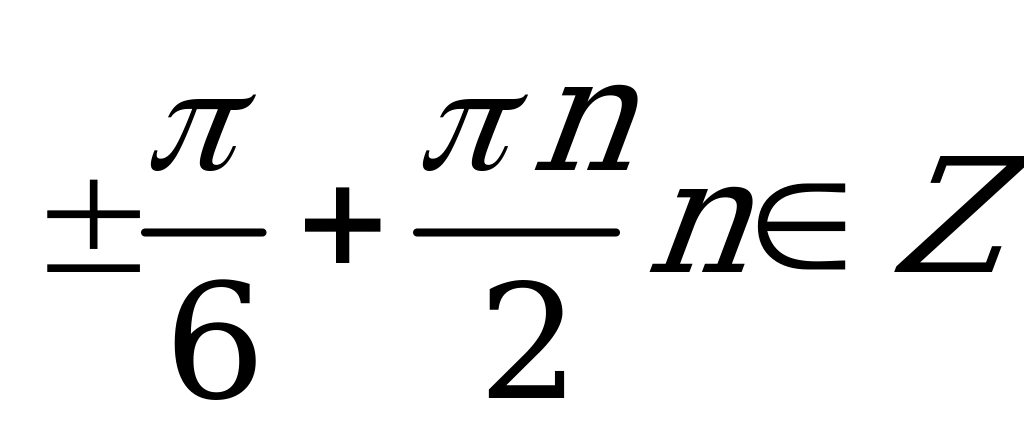 D) D)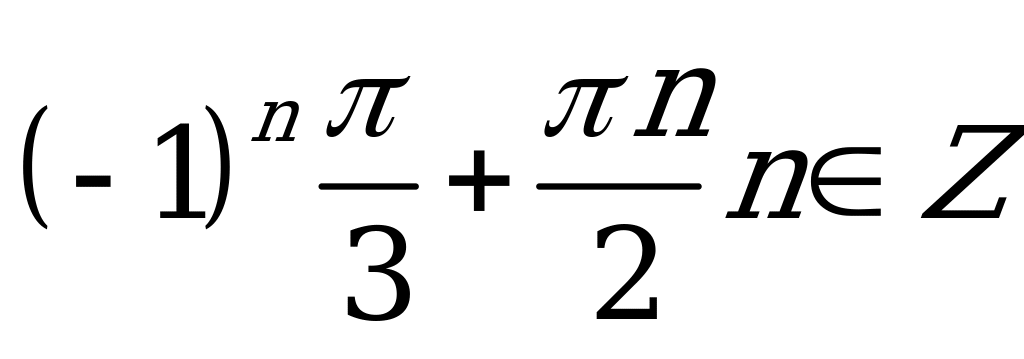 E) E) 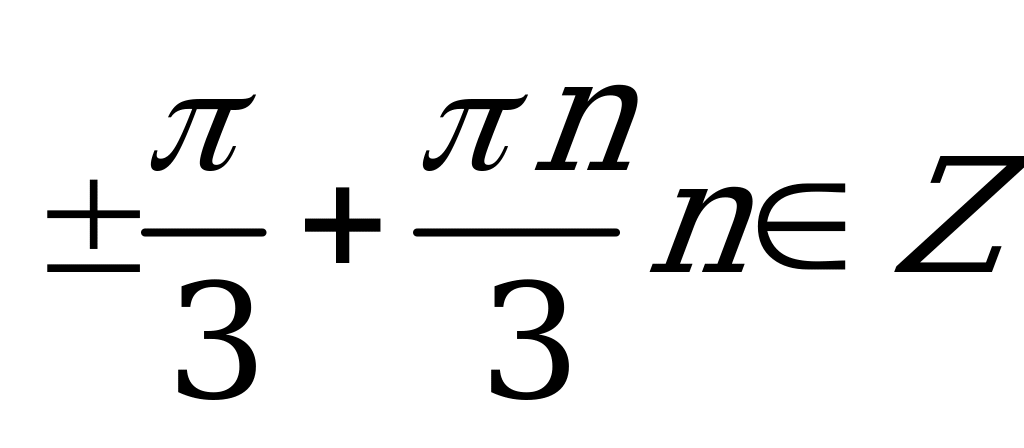 | C |
| В2.3 Решите уравнение 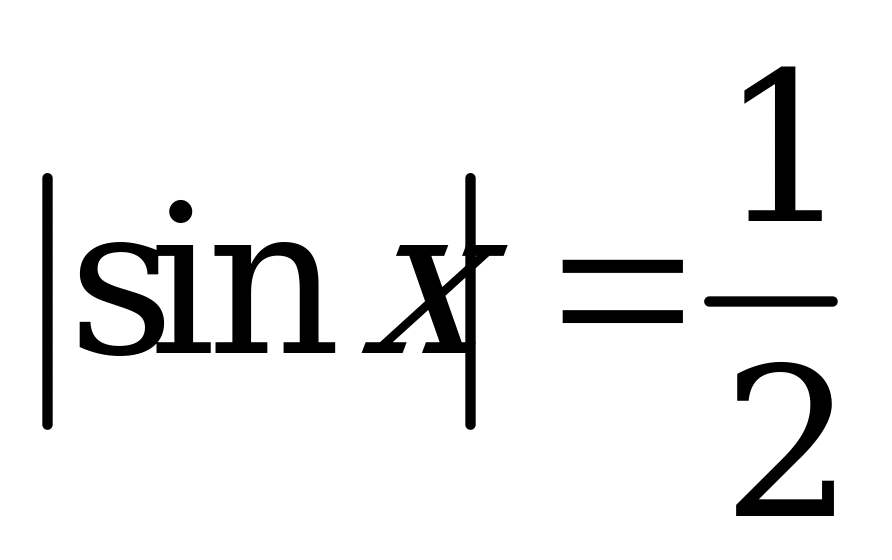 A) 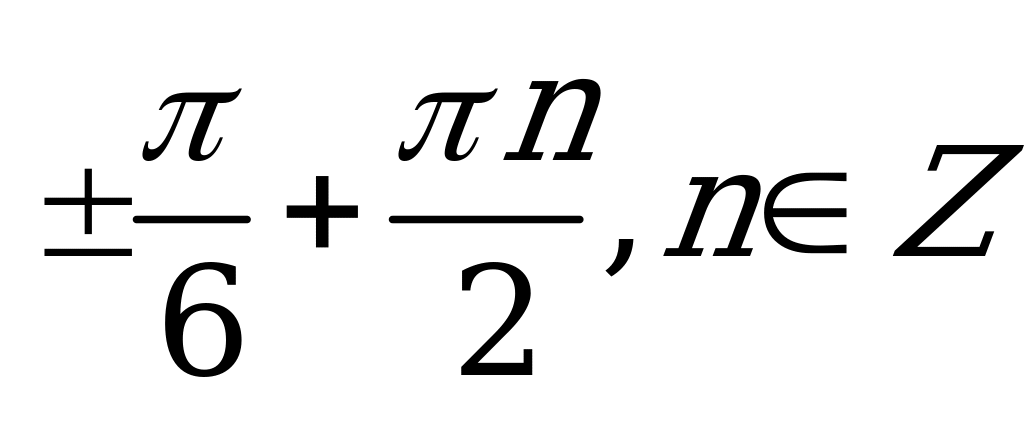 B) B) 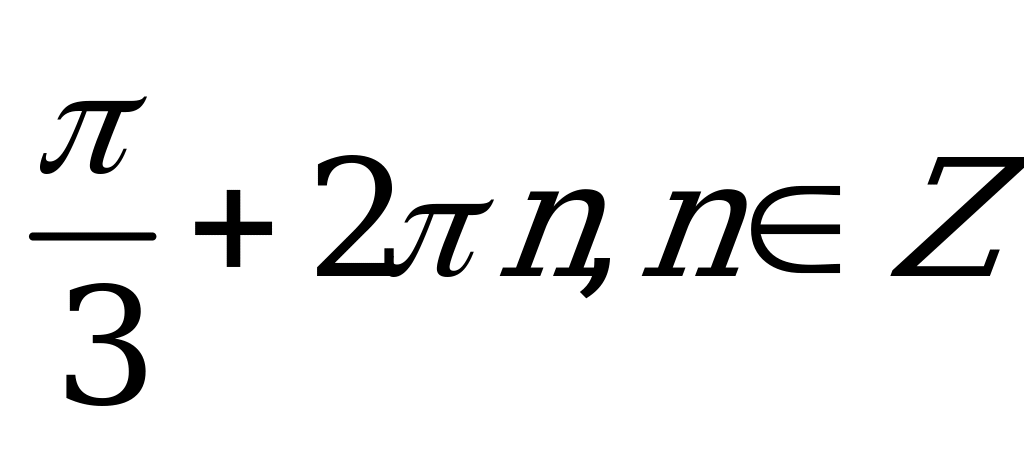 C) 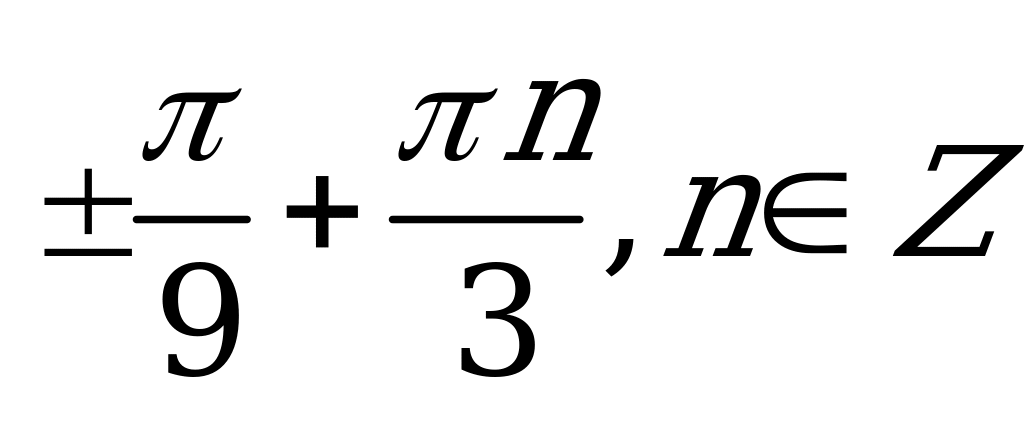 D) D) 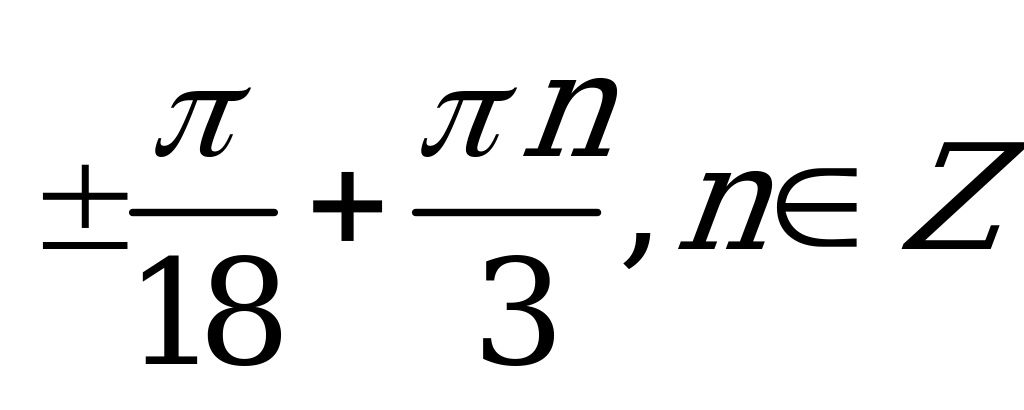 E) E) 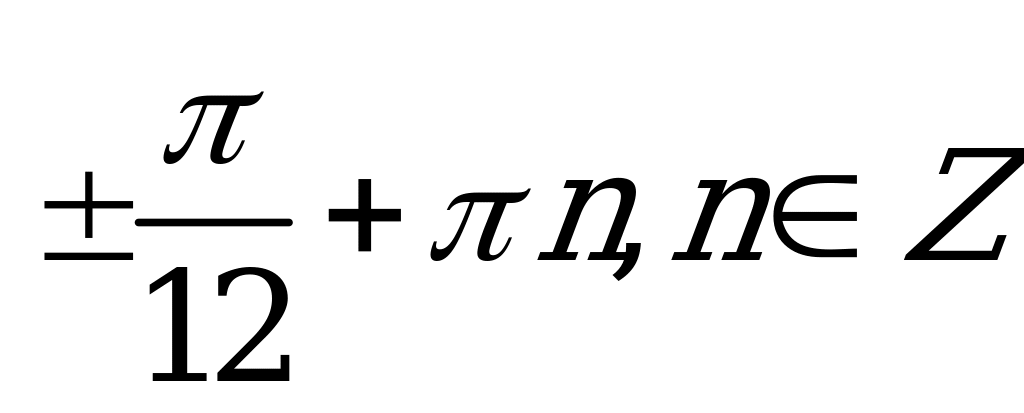 | D |
| В2.4 Решите уравнение: 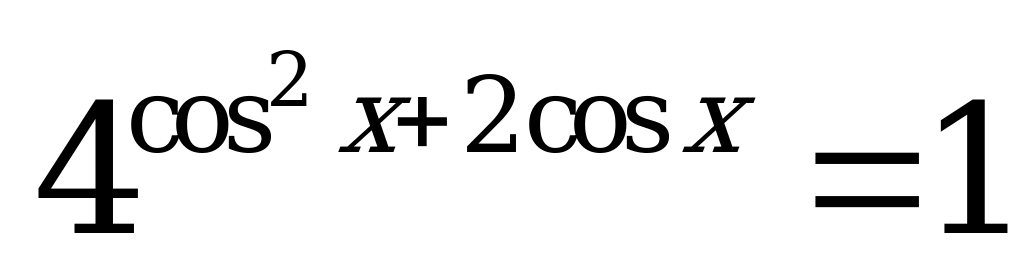 A) 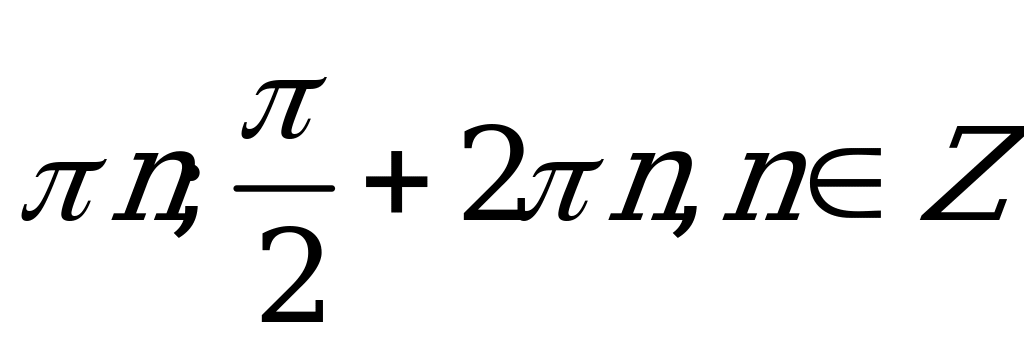 B) B) 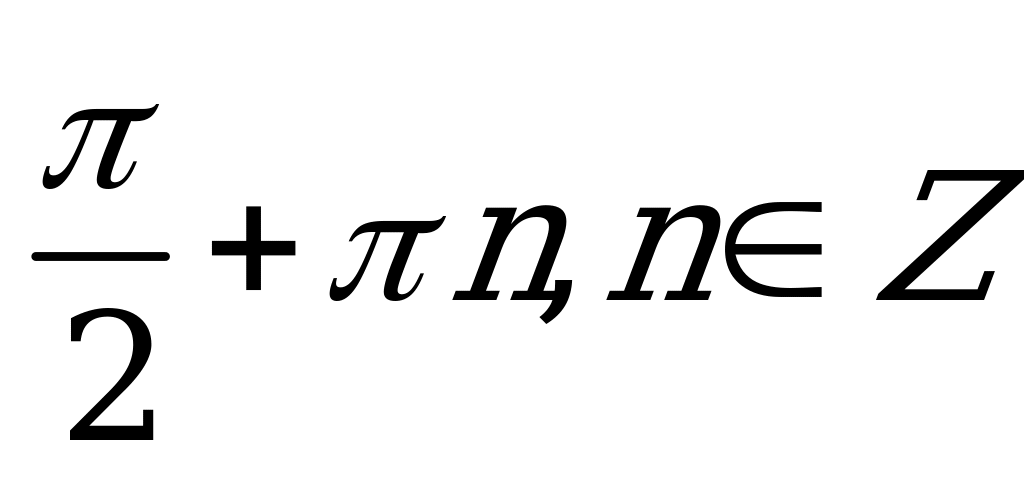 C) 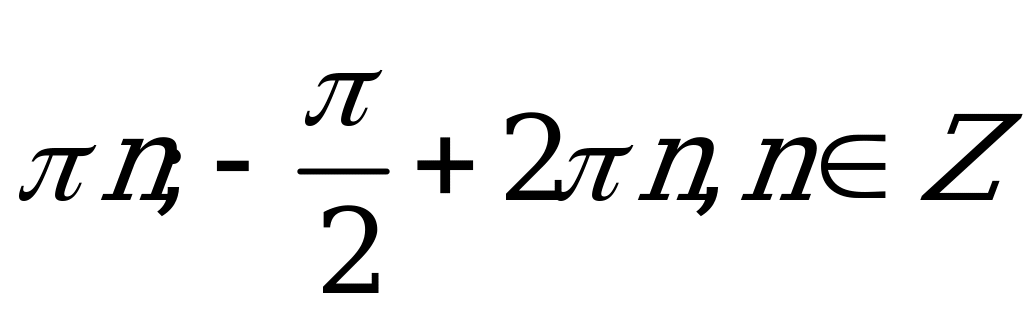 D) D) 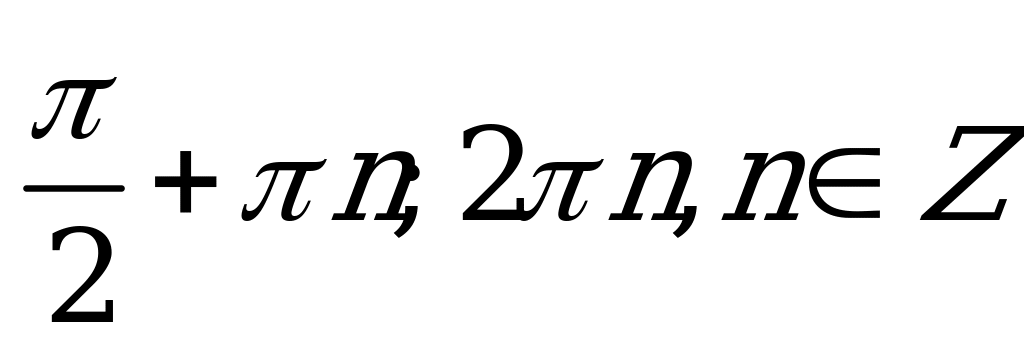 E) 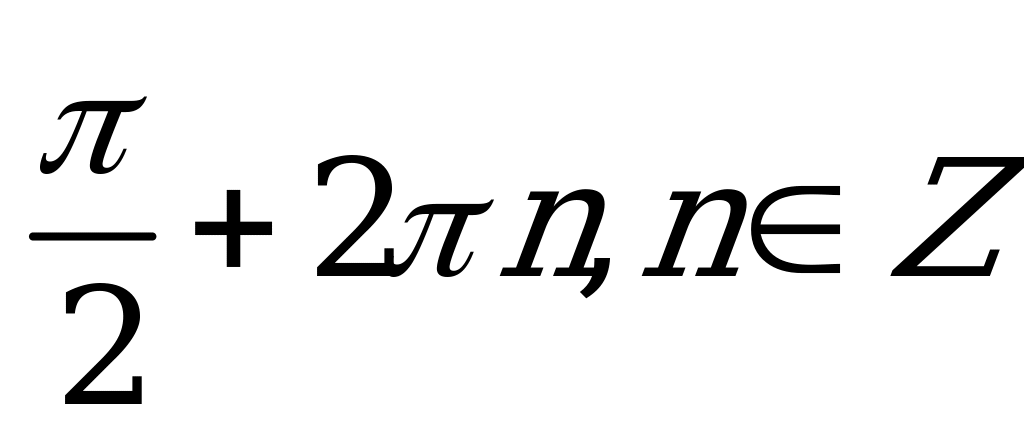 | B |
| В2.5 Решите уравнение 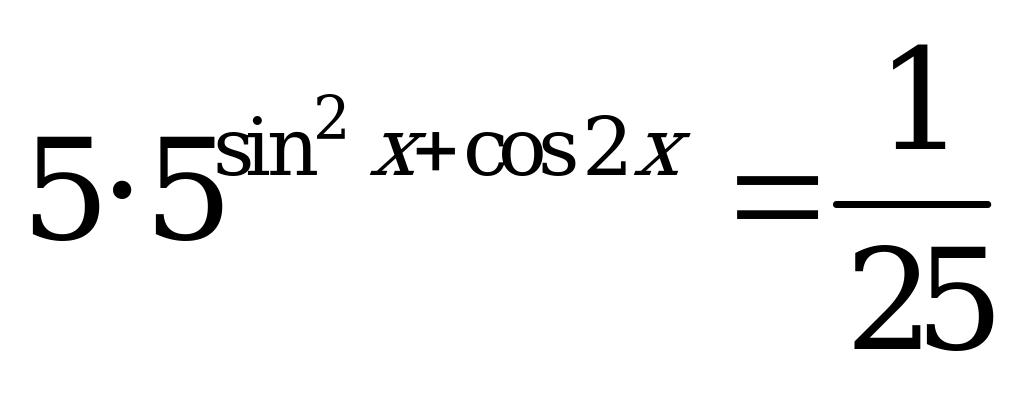 A)  B) B)  n, n n, n 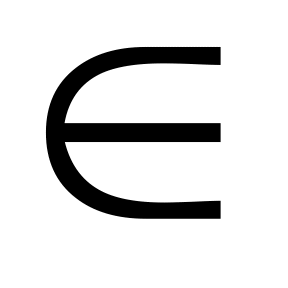 Z C) Z C) 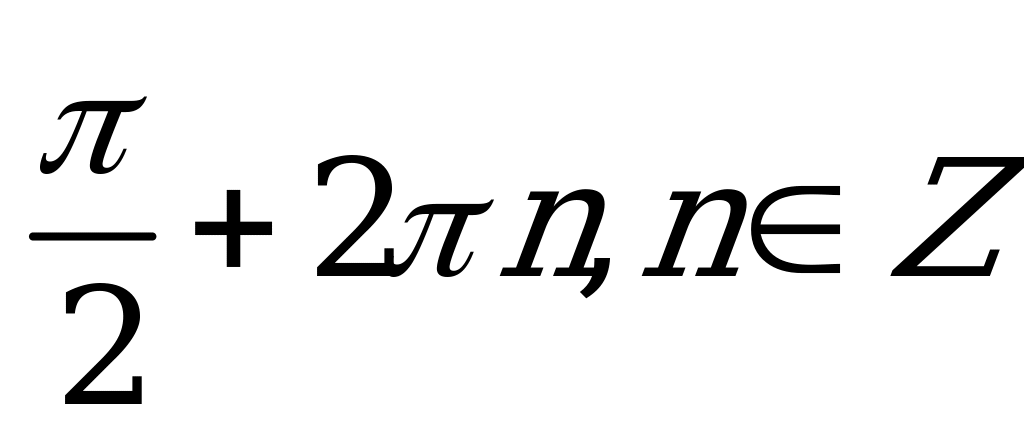 D) 2 n, n n, n  Z E) Z E) 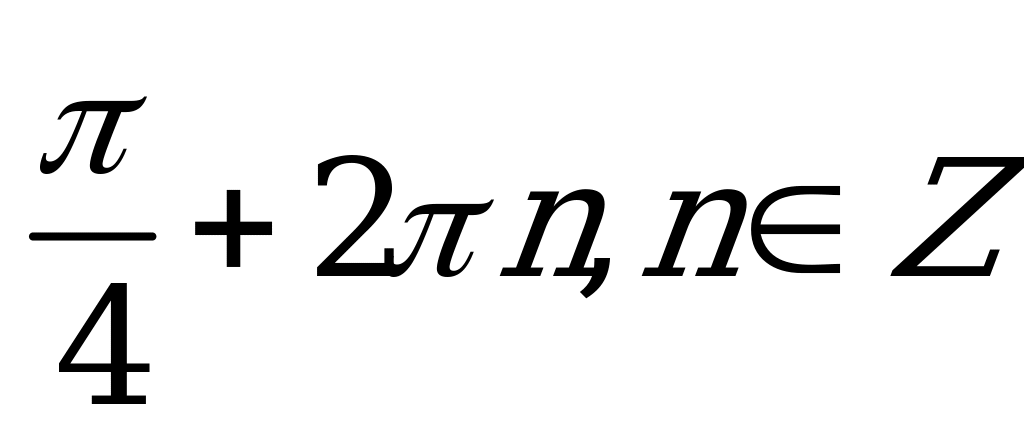 | A |
| В2.6 Решите уравнение 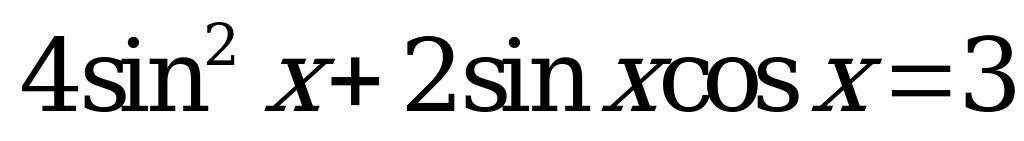 . . A) -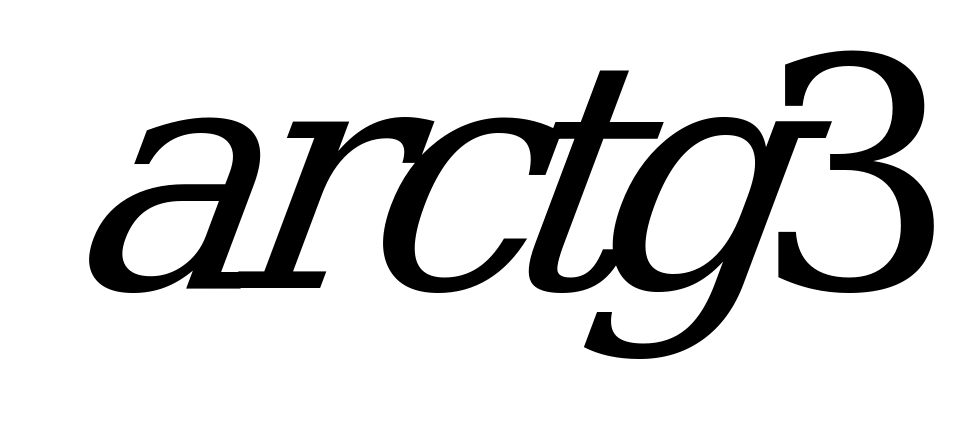 + k; + k; 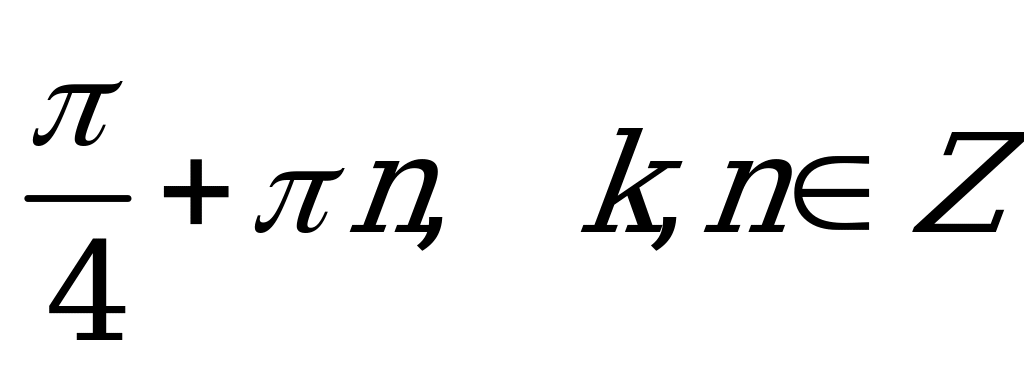 B) B) 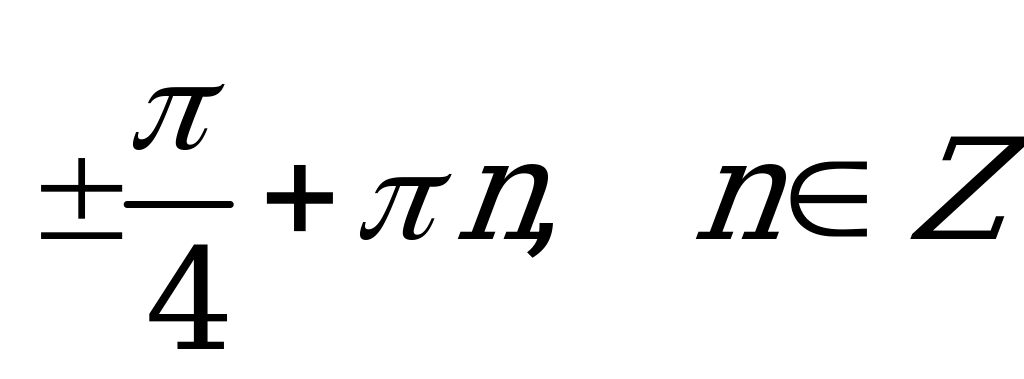 C) 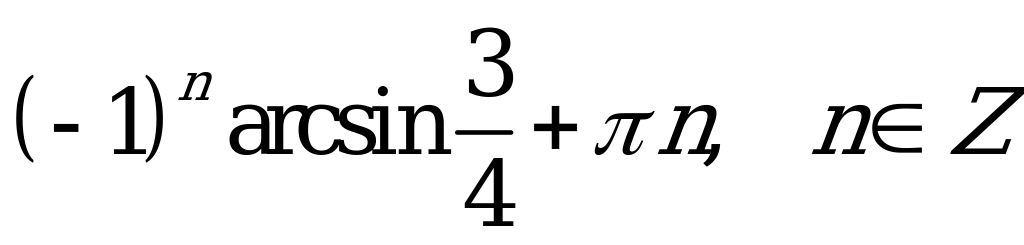 D) 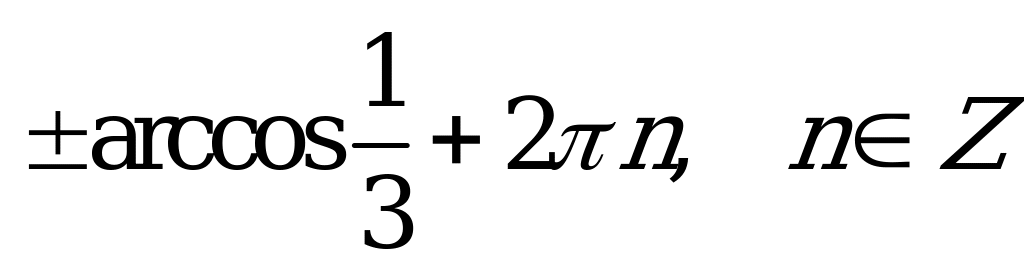 E) E) 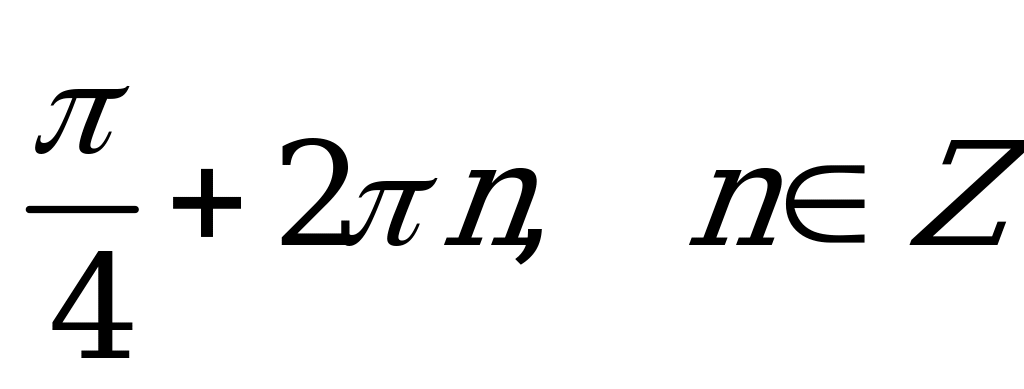 | A |
| В2.7 Решите уравнение 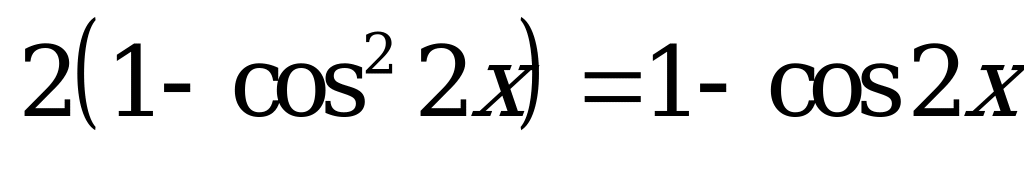 . . A) 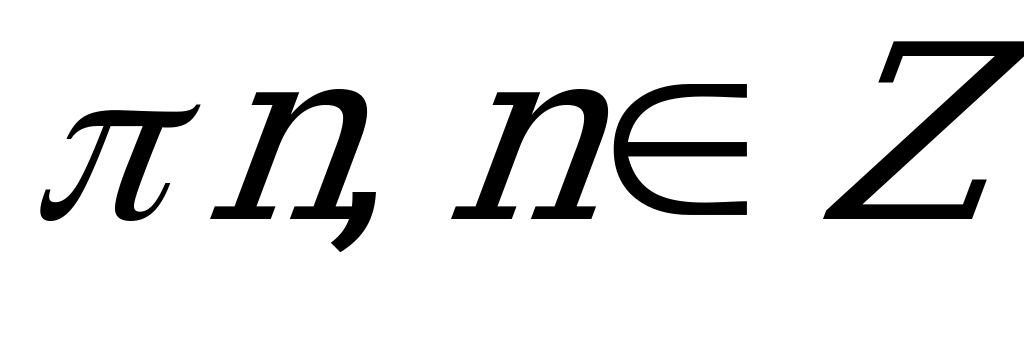 B) B) 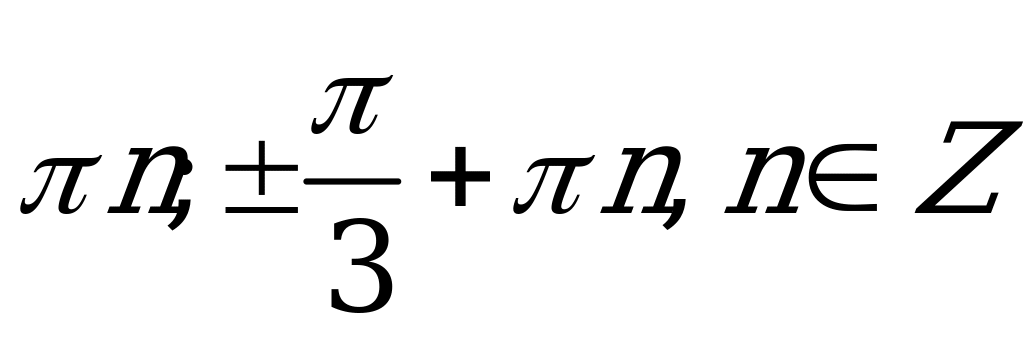 C) C) 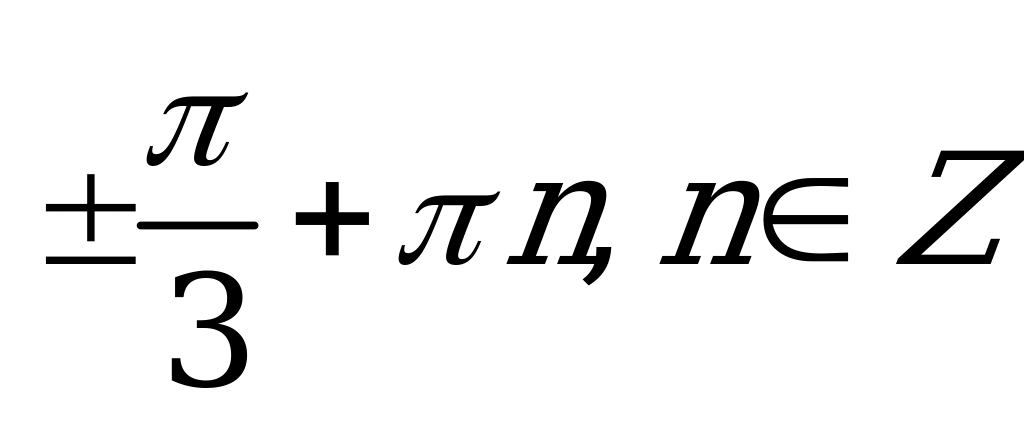 D) D) 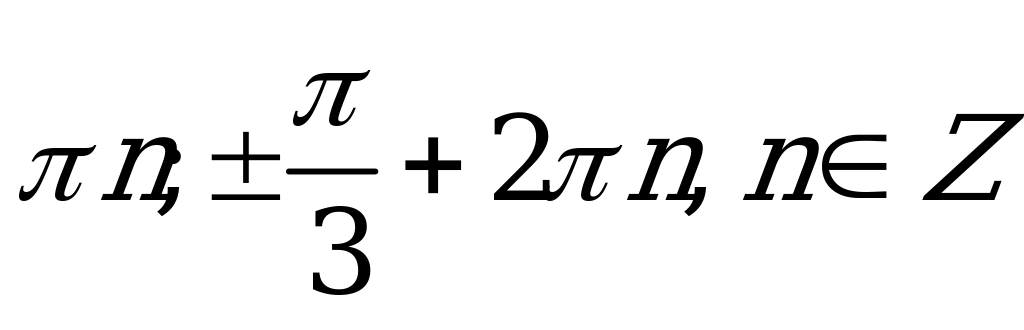 E) E) 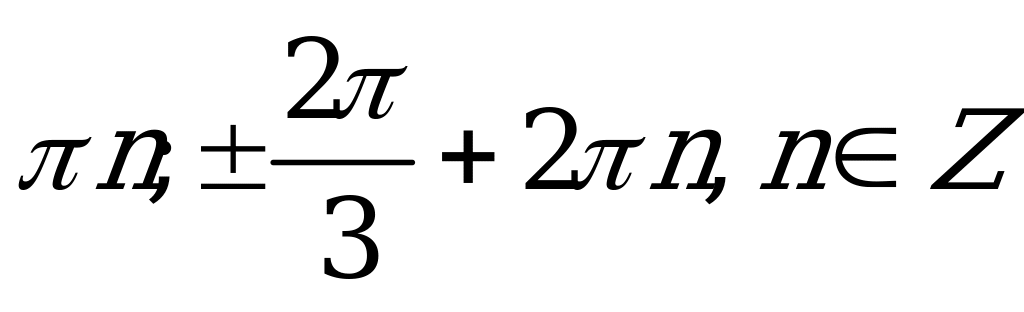 | B |
В2.8 Решите уравнение: 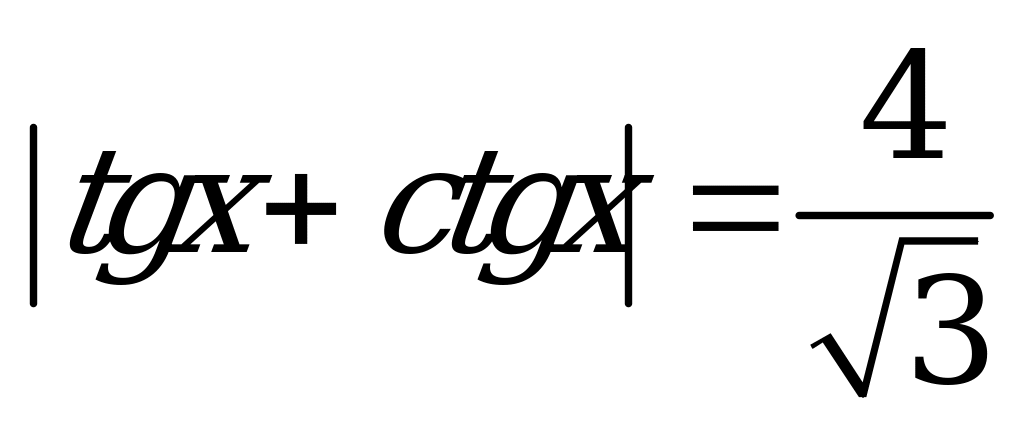 A) 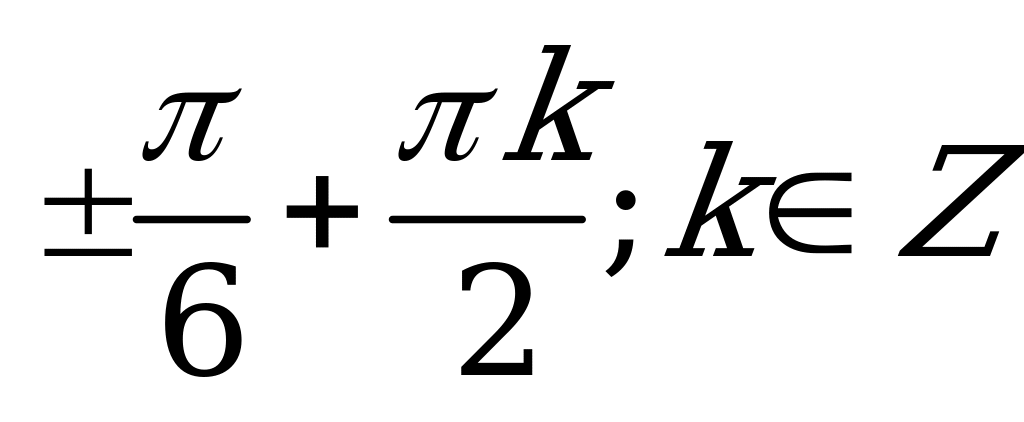 B) B)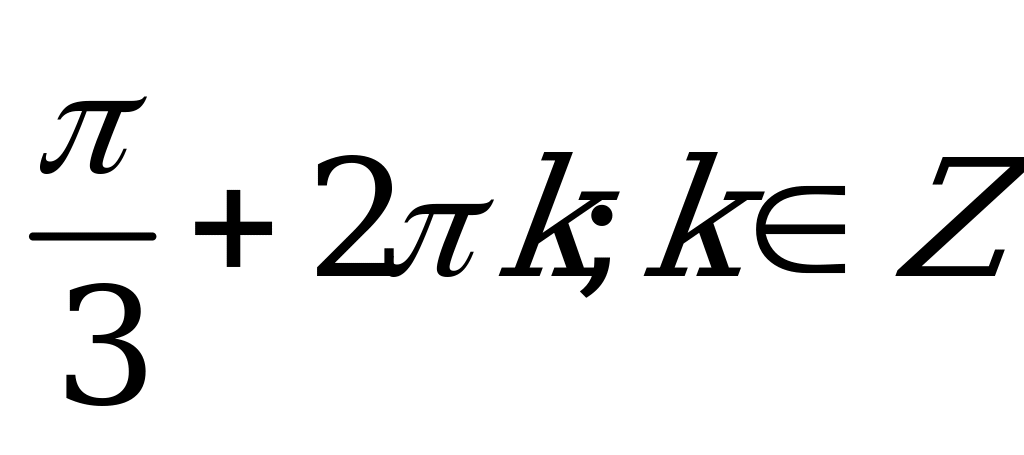 D) D)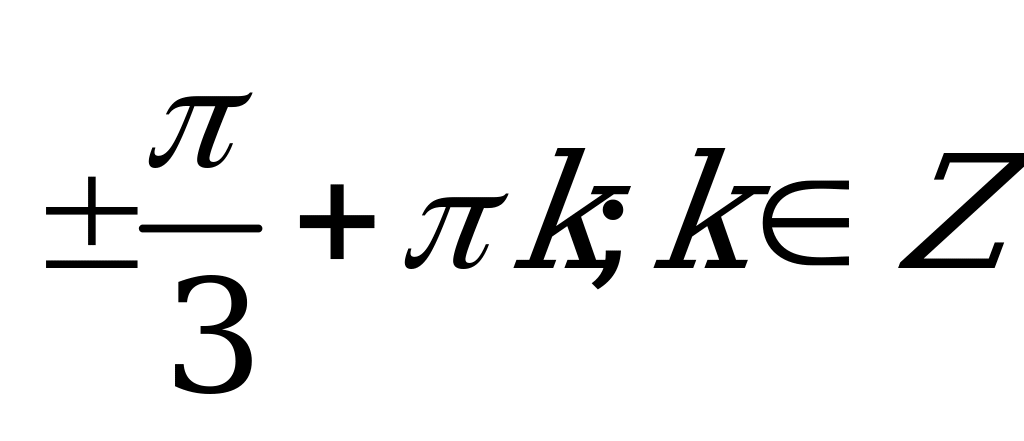 C) C)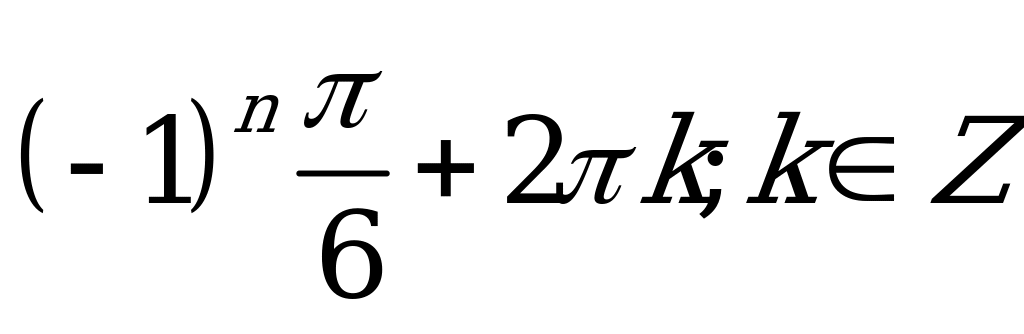 E) E) 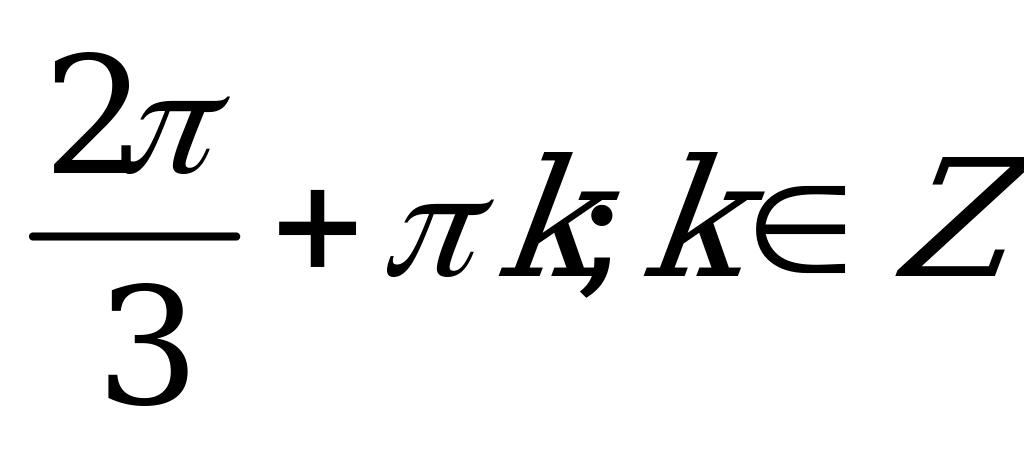 | A |
| В2.9 Решить уравнение: sin1995x + cos1995x = 1 A) 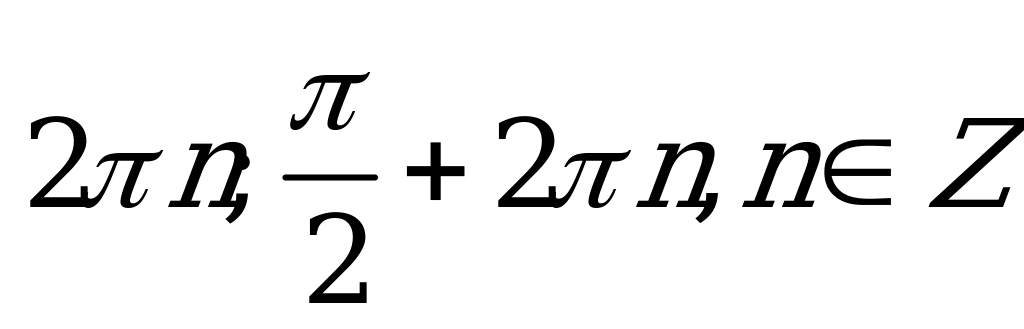 B) B) 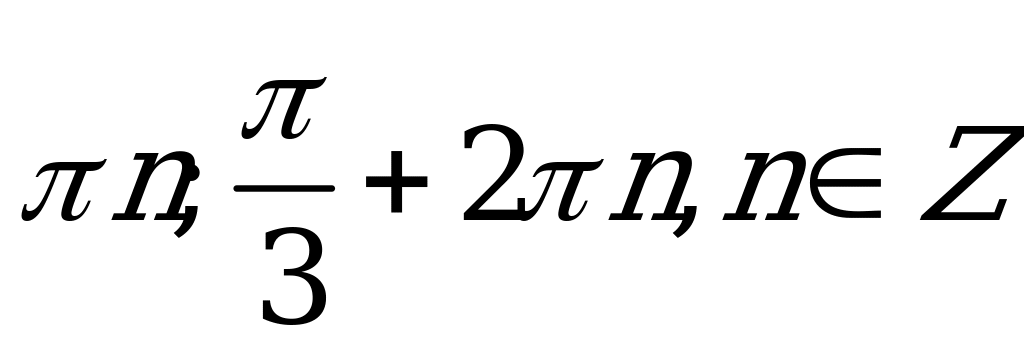 C) 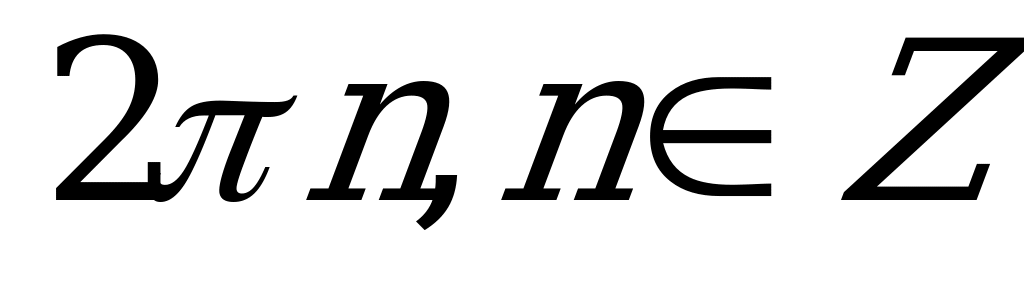 D) D) 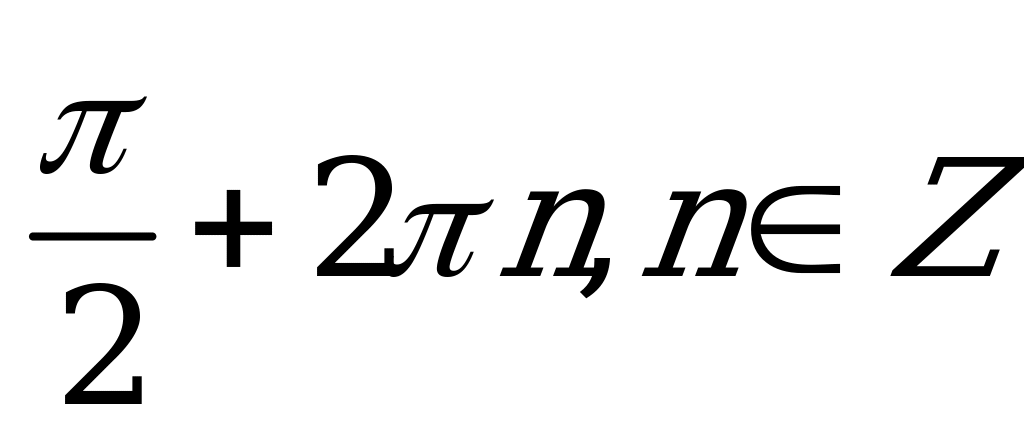 E) E) 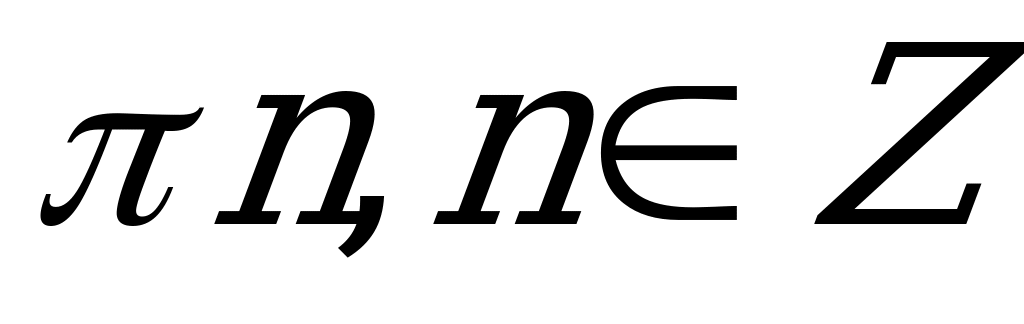 | A |
| В2.10 Решить уравнение: sin1993x + cos1993x = 1 A) 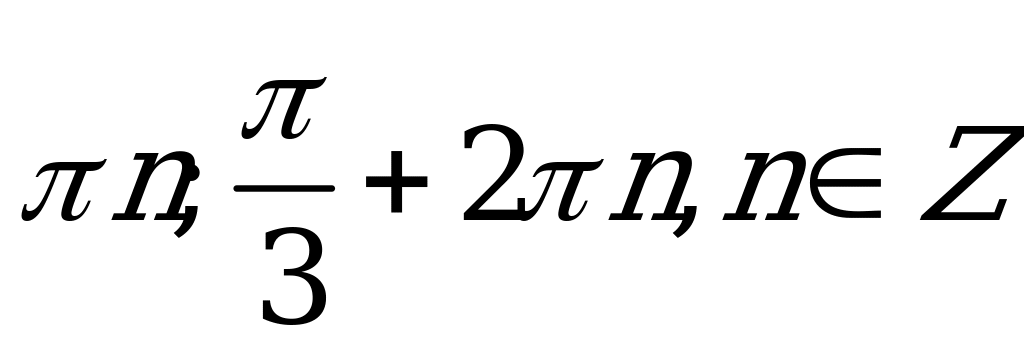 B) B) 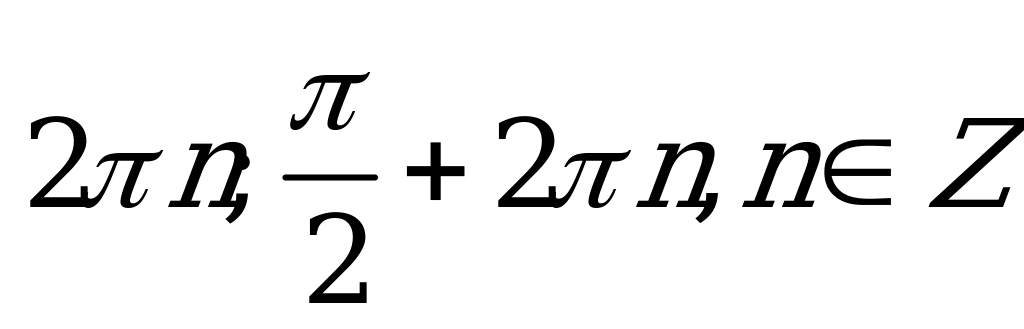 C) 2 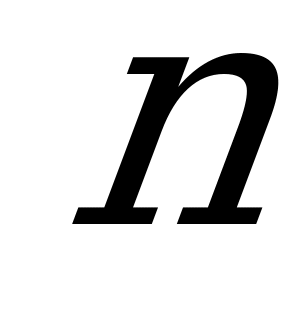 , , 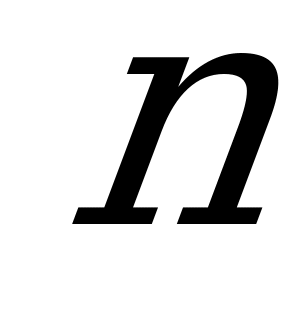 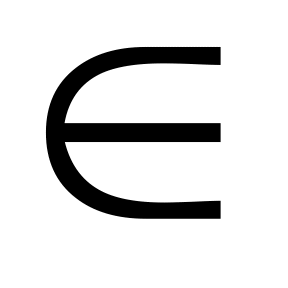 Z D) Z D)  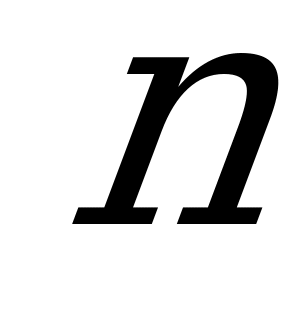 , , 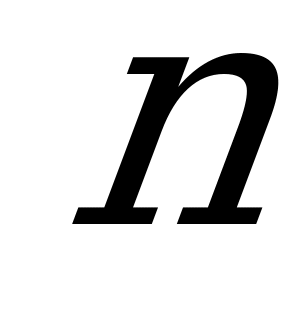 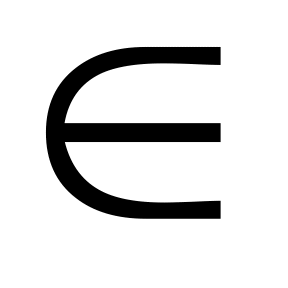 Z E) Z E) 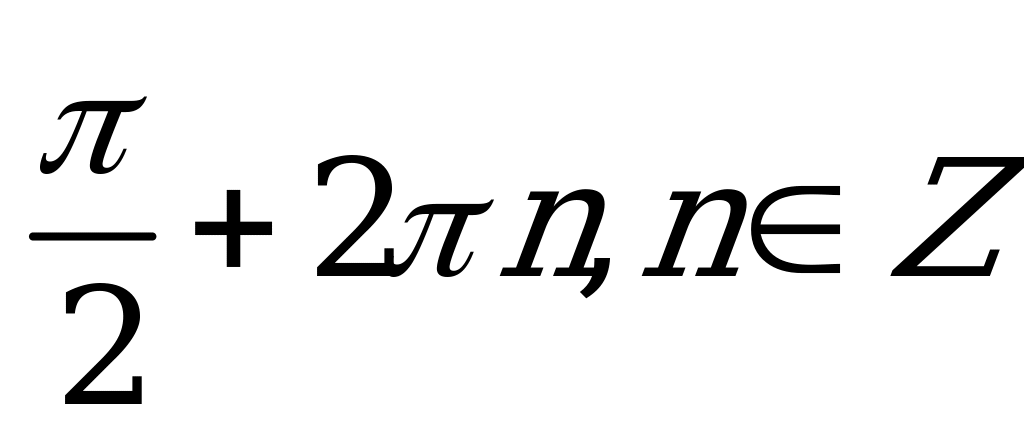 | B |
| В3. Тригонометрические уравнения на интервале | Ответы |
| В3.1 Сколько корней уравнения 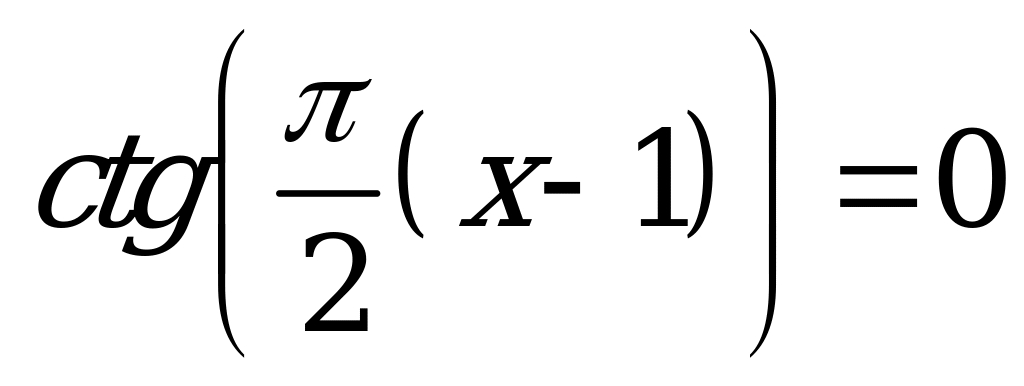 принадлежат интервалу (1, 5)? принадлежат интервалу (1, 5)? A) 1 B) 2 C) 3 D) 4 E) 5 | B |
| В3.2 Сколько корней имеет уравнение 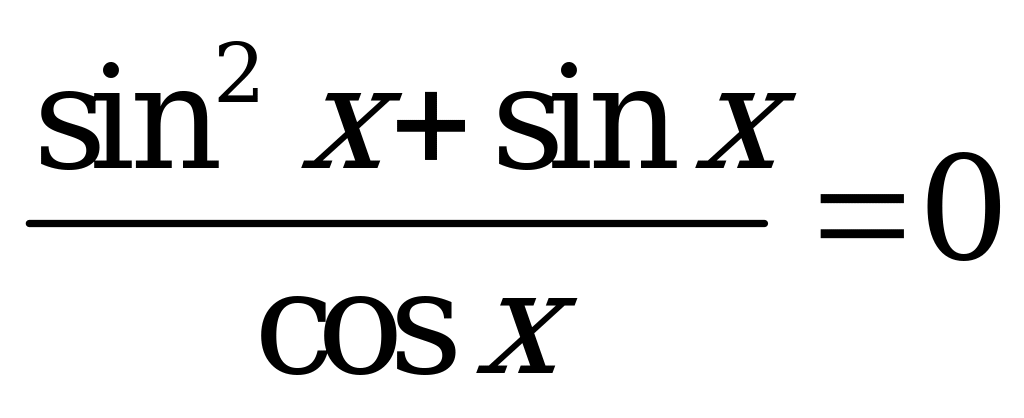 на промежутке [0; 4 на промежутке [0; 4 ] ? ] ? A) 5 B) 4 C) 7 D) 2 E) 6 | A |
| В3.3 Найдите сумму корней уравнения 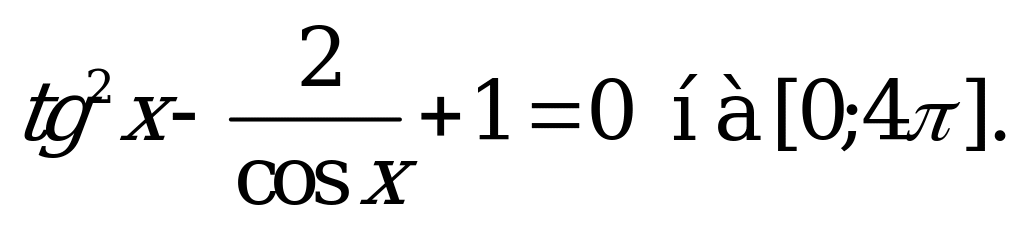 A) 7 B) 7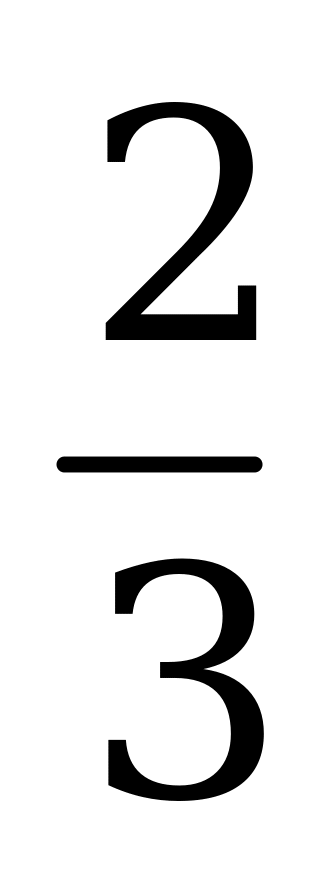 C) 8 D) 7 C) 8 D) 7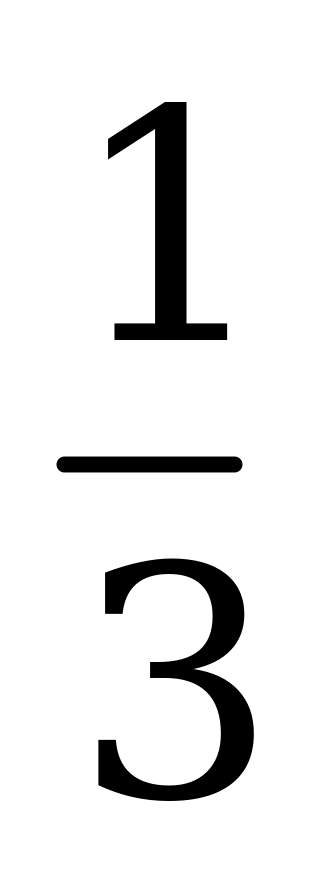 E) 8 E) 8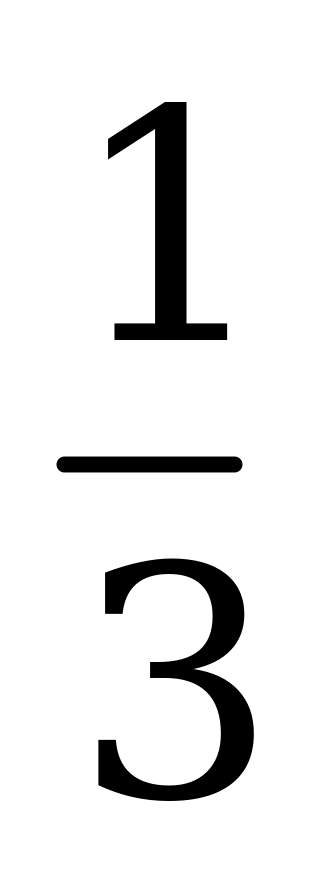 | C |
| В3.4 Найдите сумму корней уравнения 3sin22x + 7cos2x – 3 = 0, принадлежащих интервалу (-900; 1800). A) 900 B) 1050 C) 1800 D) 1350 E) 1500 | D |
| В3.5 Сколько корней на отрезке 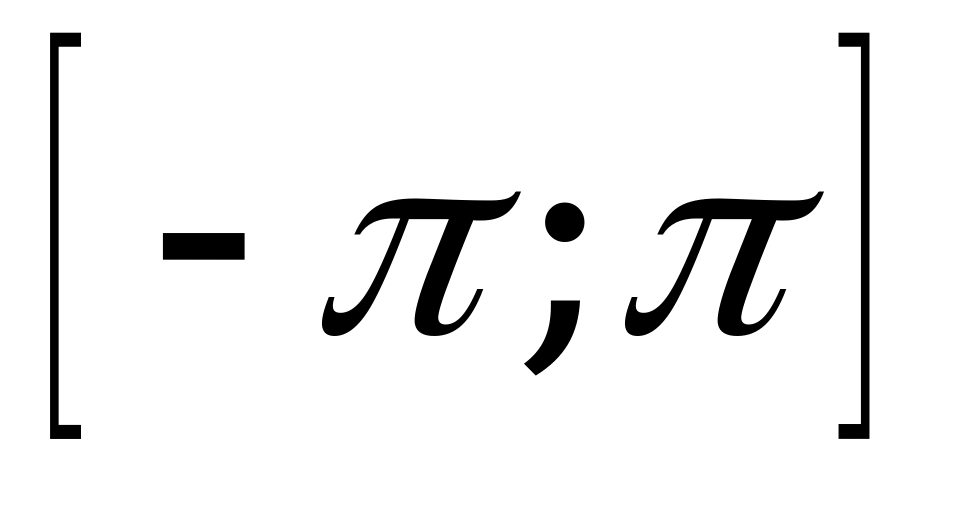 имеет уравнение имеет уравнение cos3x + sin4x = 1? A) 1 B) 2 C) 3 D) 4 E) 5 | C |
| В3.6 Сколько корней на отрезке 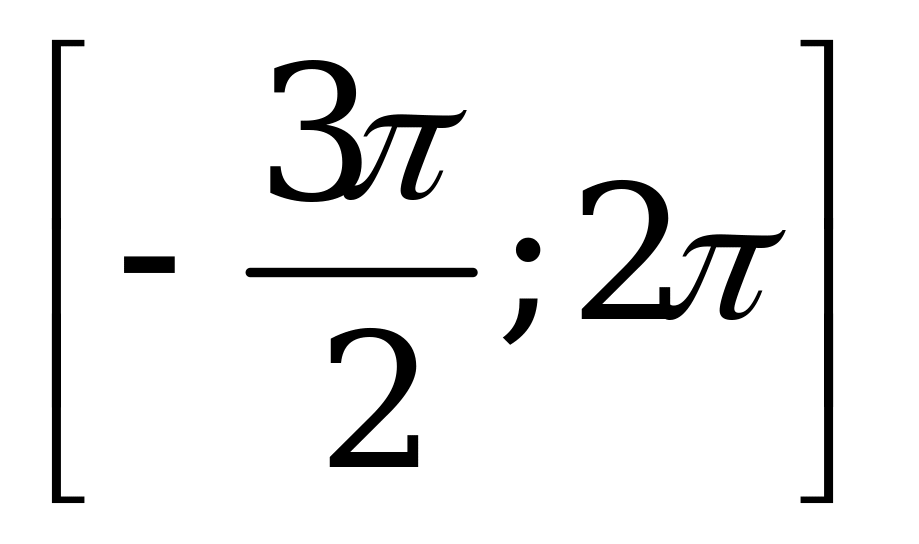 имеет уравнение cos4x + sin3x = 1? имеет уравнение cos4x + sin3x = 1? A) 4 B) 8 C) 6 D) 7 E) 5 | C |
| В3.7 Сколько корней на промежутке [-2 ; 2 ; 2 ] имеет уравнение ] имеет уравнение  A) 6 B) 5 C) 4 D) 2 E) 1 | B |
| В3.8 На отрезке [-3; ] найдите сумму всех корней уравнения 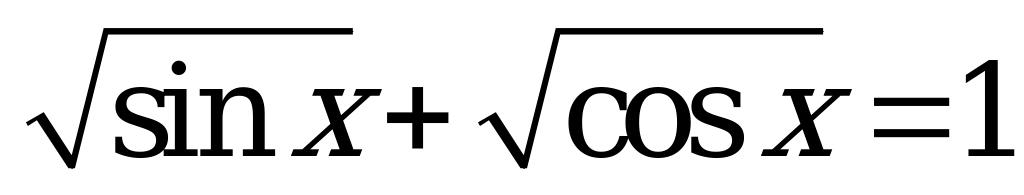 . . A) -3 B) -2 C) - D) 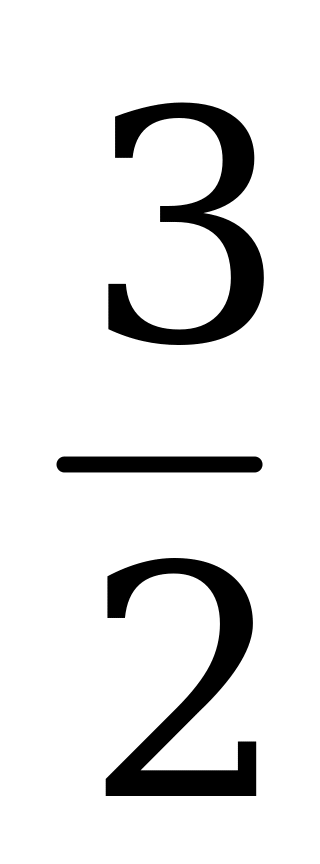 E) 3 E) 3 | A |
| В3.9 Найдите сумму корней уравнения 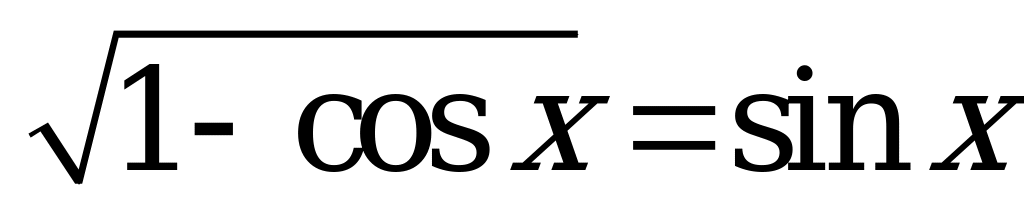 при x при x 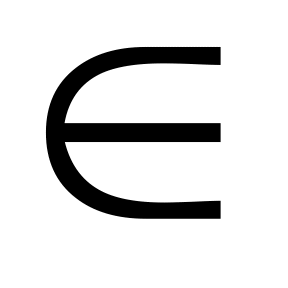 [ [ ; 3 ; 3 ]. ]. A) 2 B) 5 B) 5 C) 6 C) 6 D) 3,5 D) 3,5 E) 4,5 E) 4,5 | E |
| В3.10 Найдите модуль разности корней уравнения 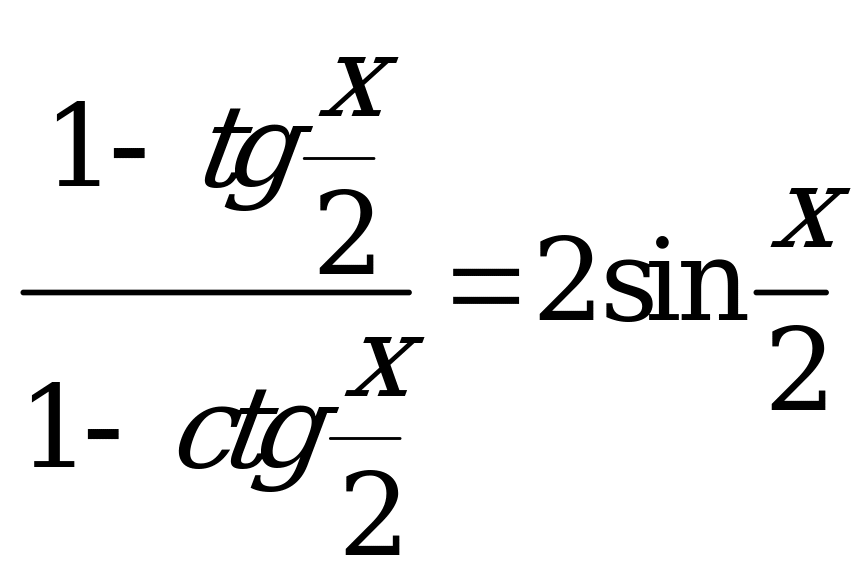 принадлежащих интервалу принадлежащих интервалу (1800; 5400). A) 1200 B) 1350 C) 2400 D) 1800 E) 3600 | A |
| В4. Задачи с обратными тригонометрическими функциями | Ответы |
| В4.1 Вычислите tg( - arcsin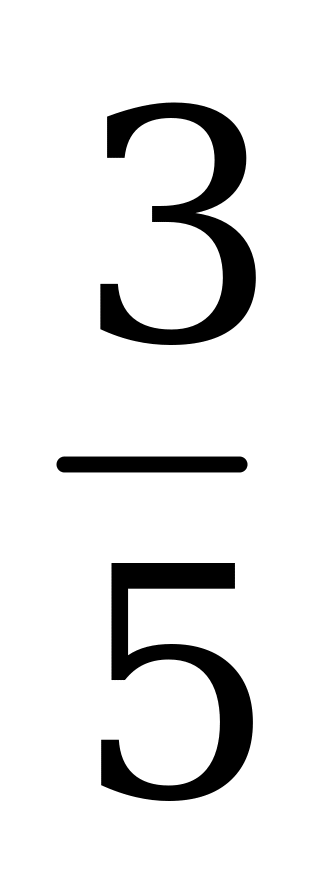 ) ) A) 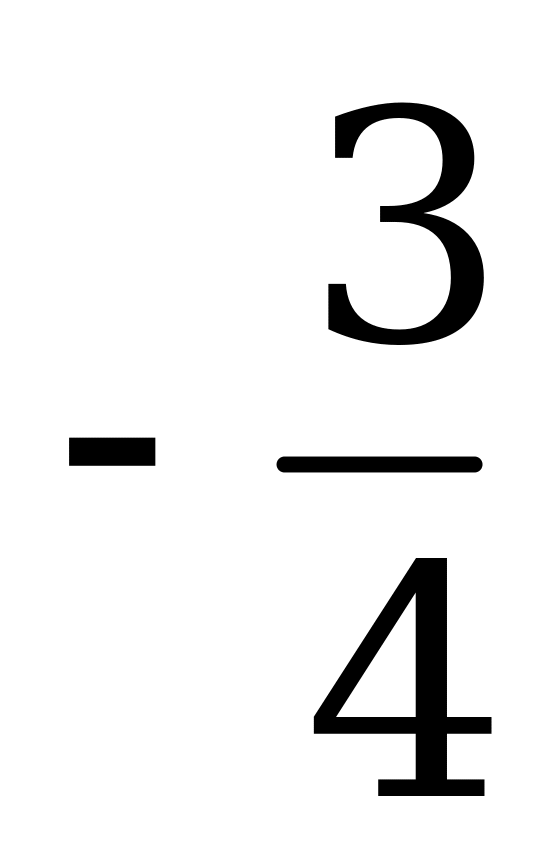 B) B) 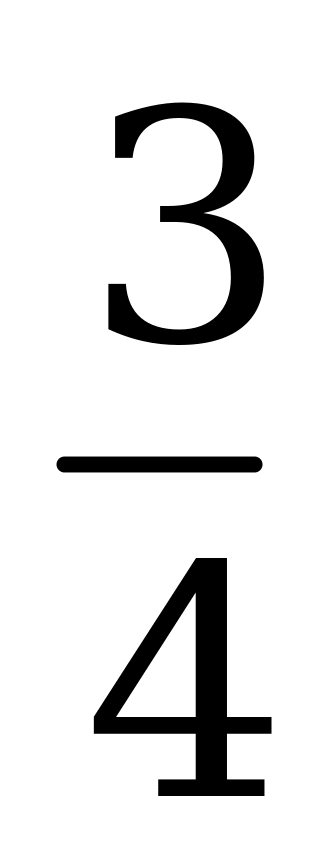 C) C) 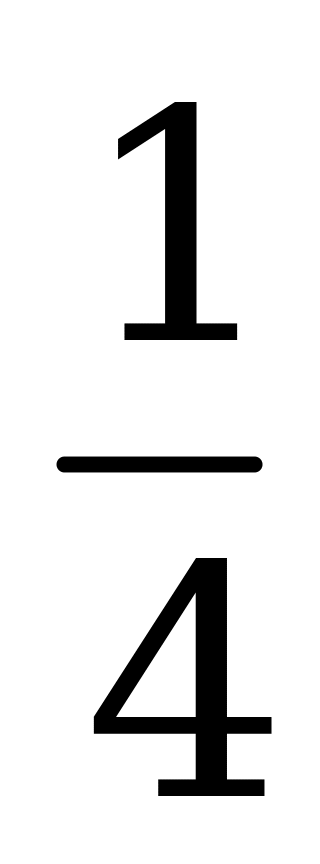 D) D) 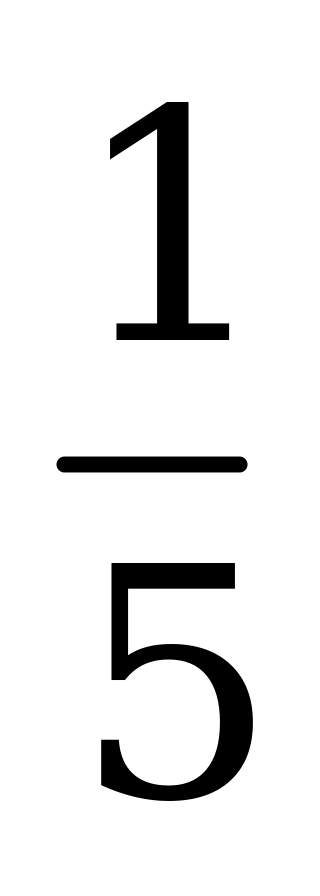 E) E) 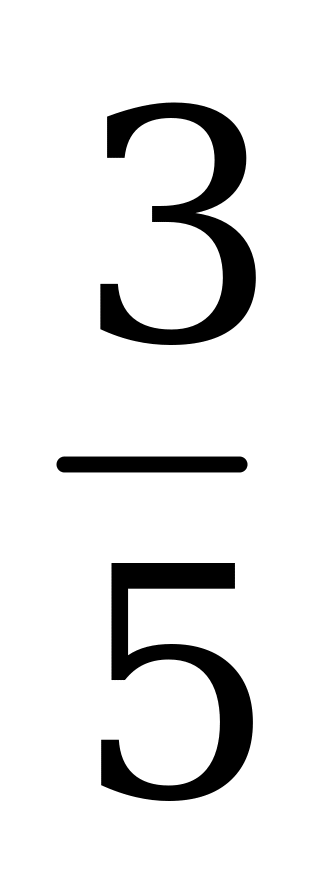 | A |
| В4.2 Найдите 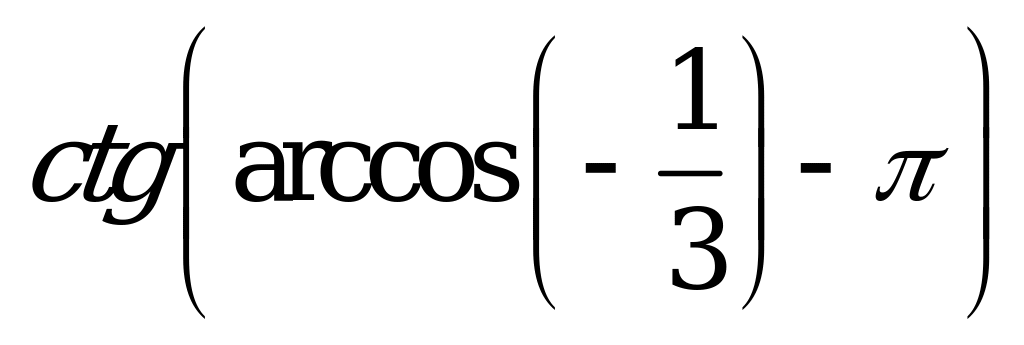 A) 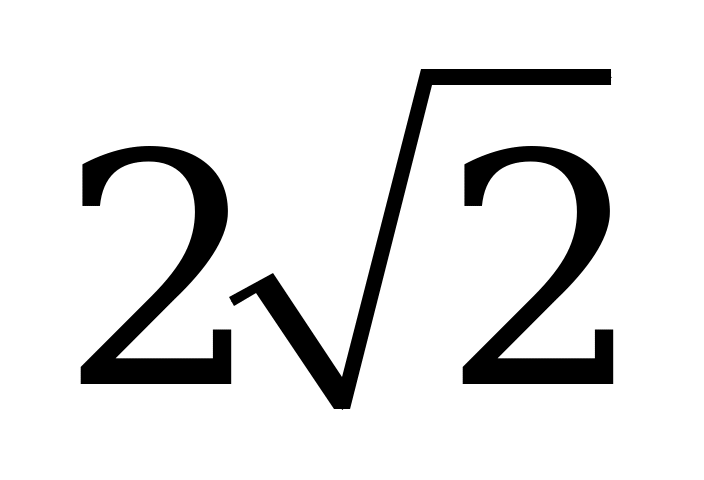 B) - B) -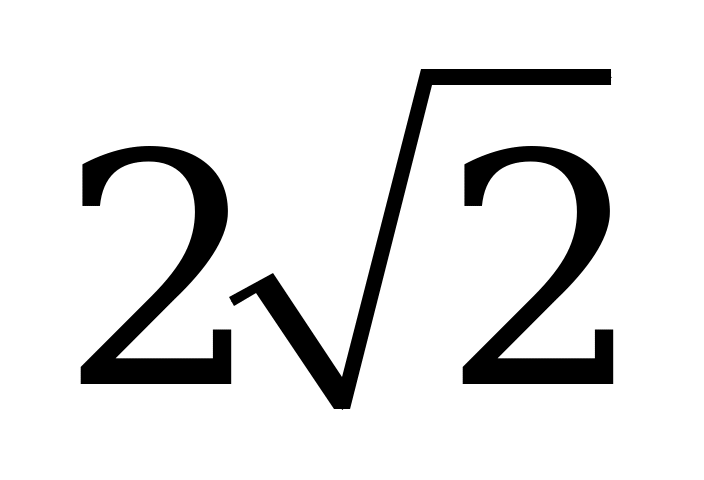 C) C) 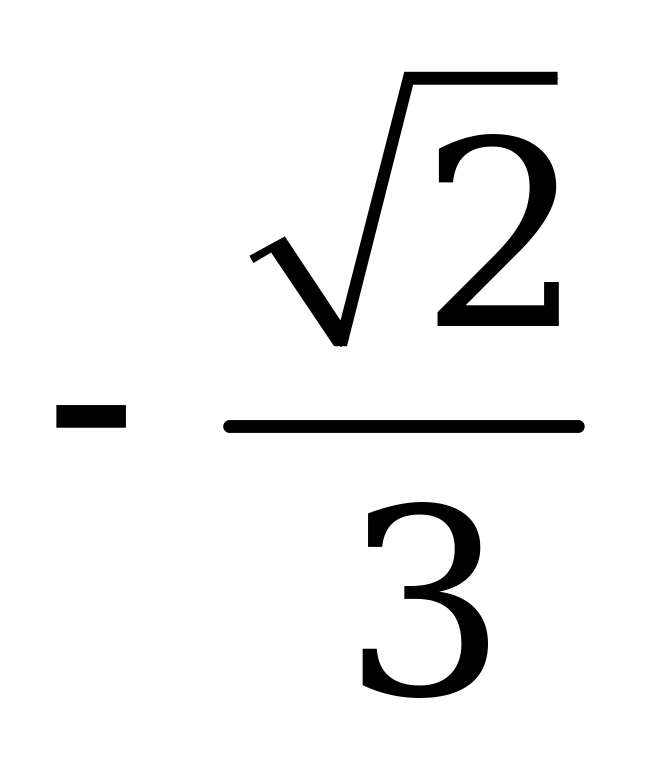 D) D) 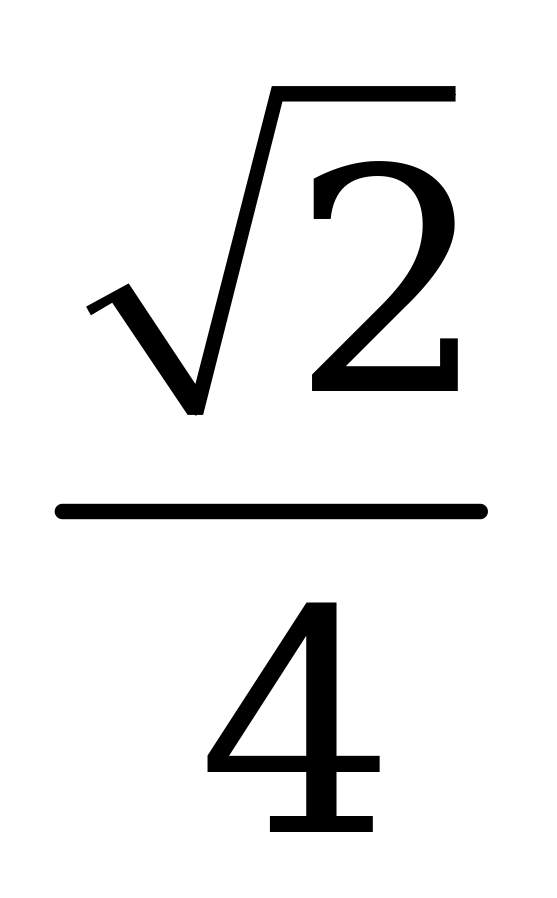 E) E) 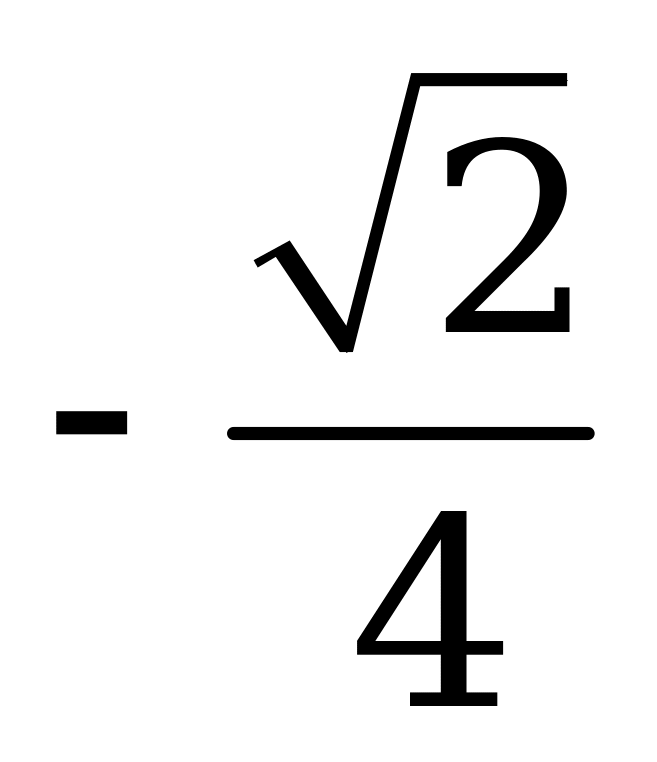 | E |
| В4.3 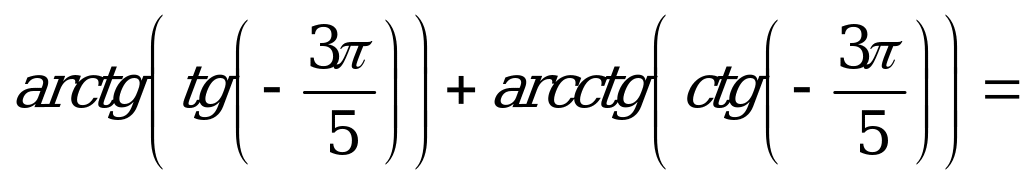 ? ? A) 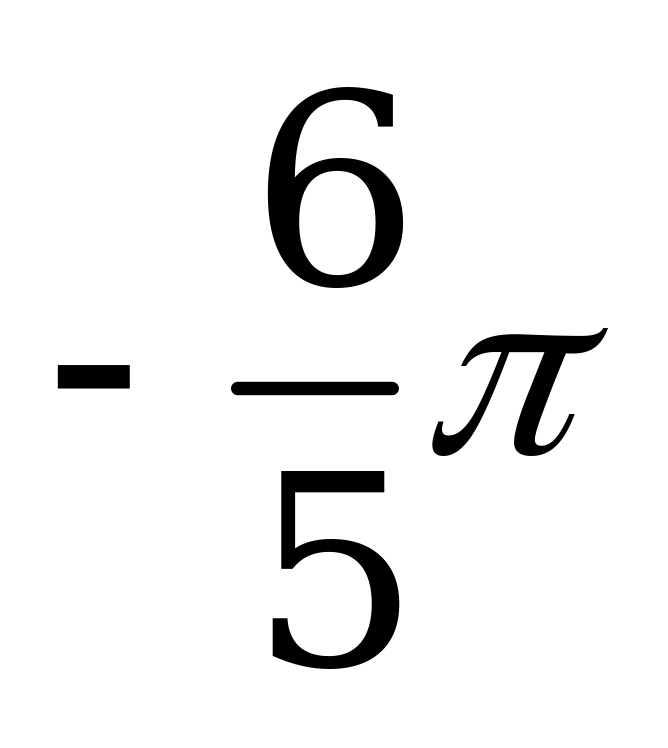 B) B) 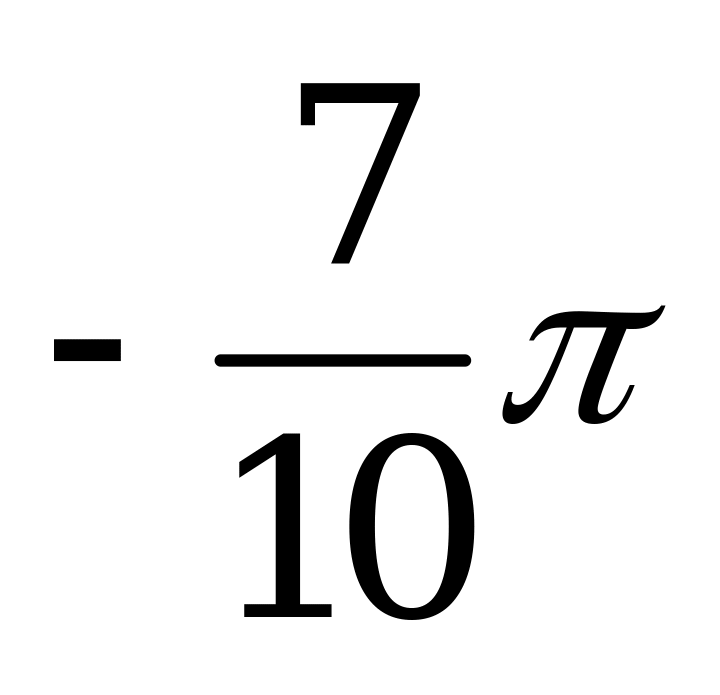 C) C) 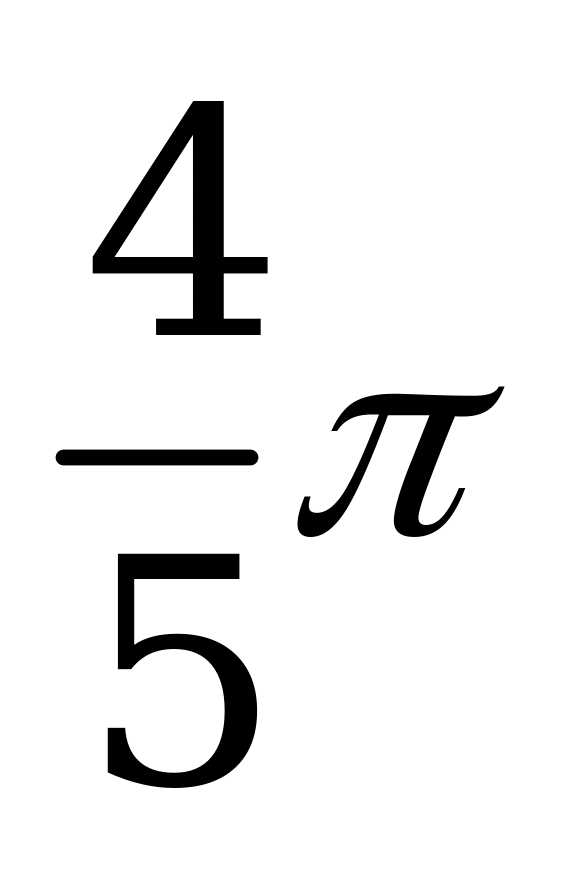 D) D) 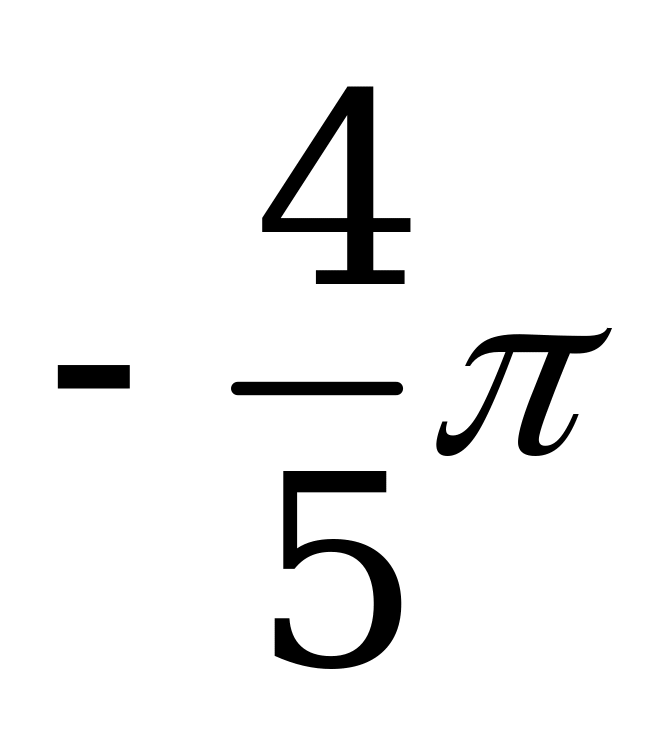 E) E) 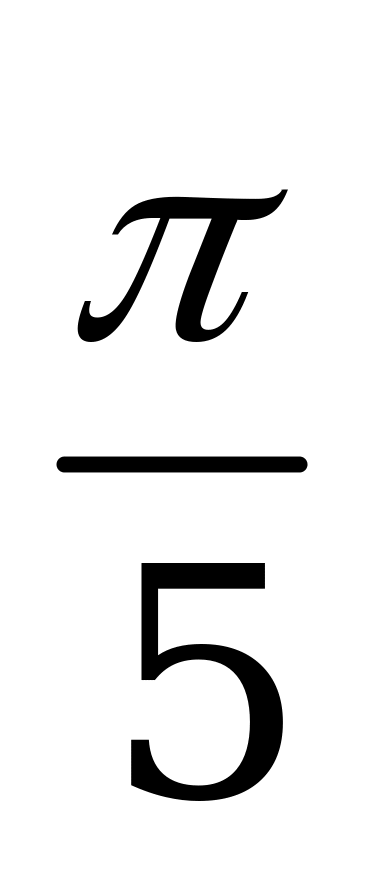 | C |
| В4.4 Найдите множество значений функции  A) [0; A) [0;  ] B) ] B) 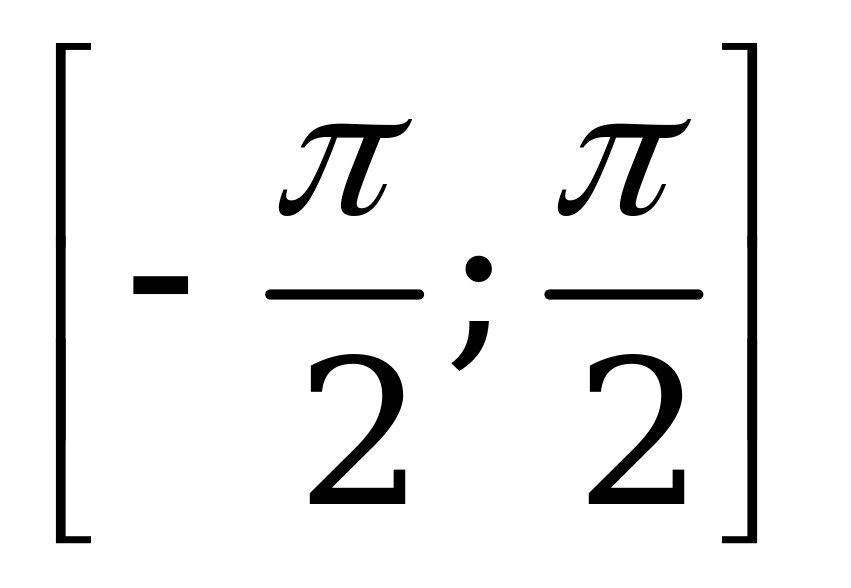 C) 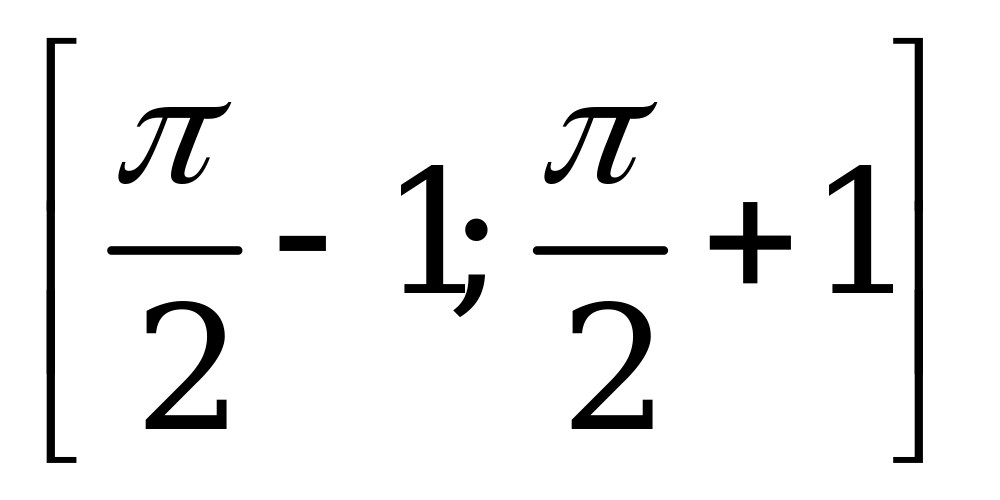 D) D) 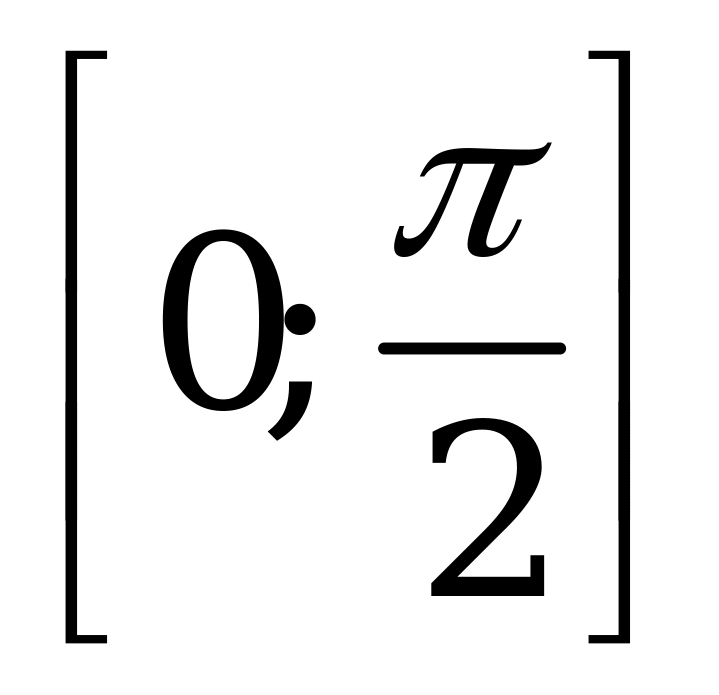 E) (0; E) (0;  ) ) | A |
| В4.5 Найдите наименьшее значение функции 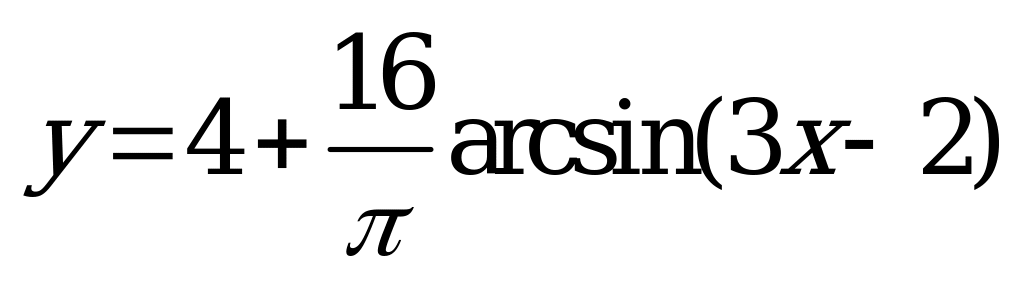 A) -4 B) 4 C) -2 D) 0 E) -6 | A |
| В4.6 4 arcsinx + arccosx =  . Вычислите 3x2 . Вычислите 3x2 A) 0 B) 1 C) 3 D) 0,75 E) 1,5 | D |
| В4.7 3 arccosx + 2 arcsinx =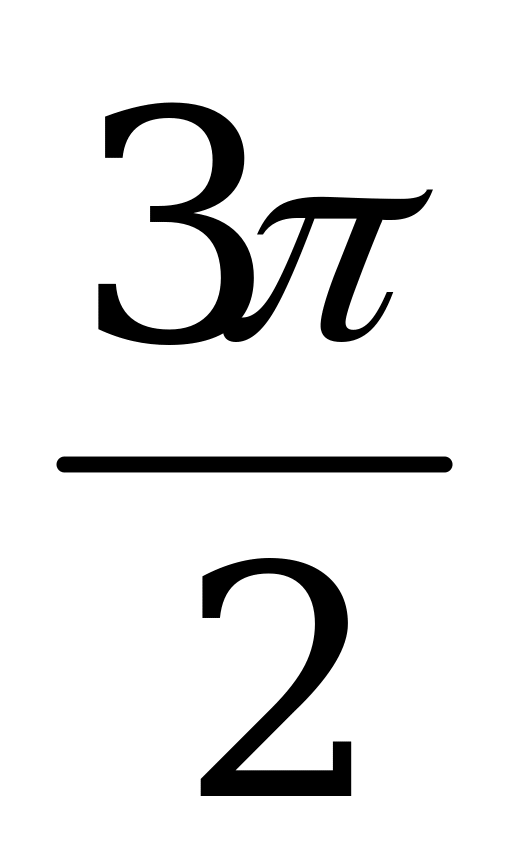 . Вычислите . Вычислите 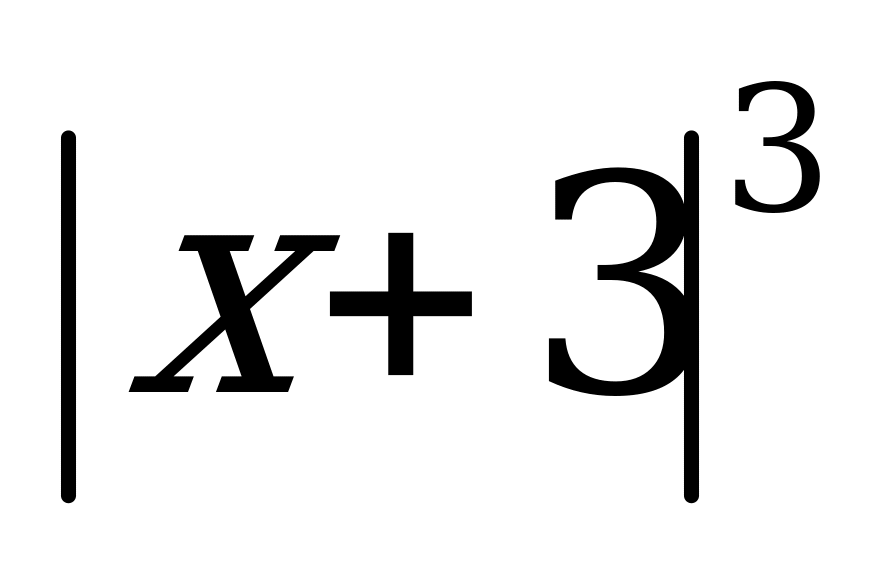 A) 1 B) 8 C) 27 D) 64 E) 0 | C |
| В4.8 Сколько решений имеет уравнение: 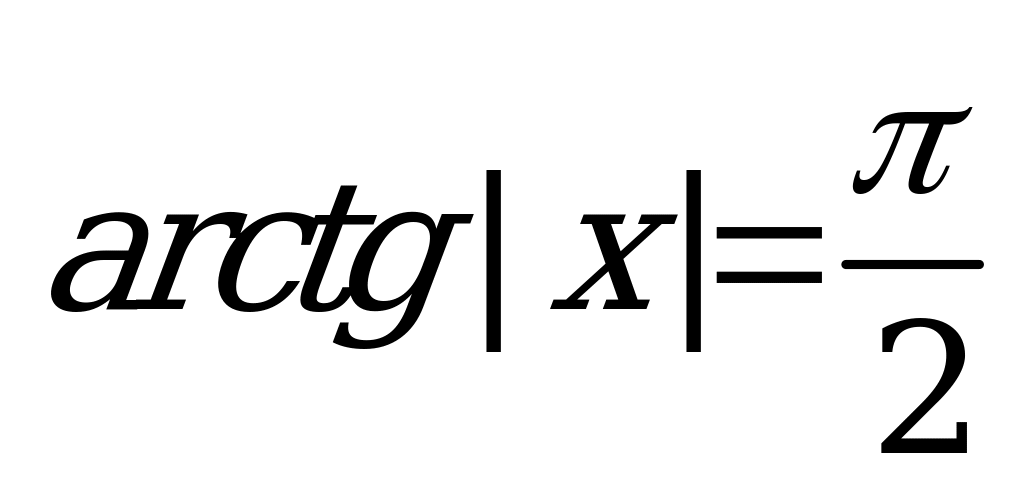 A) 2 B) 1 C)  D) бесконечно много E) 3 D) бесконечно много E) 3 | C |
| В4.9 Сколько решений имеет уравнение: 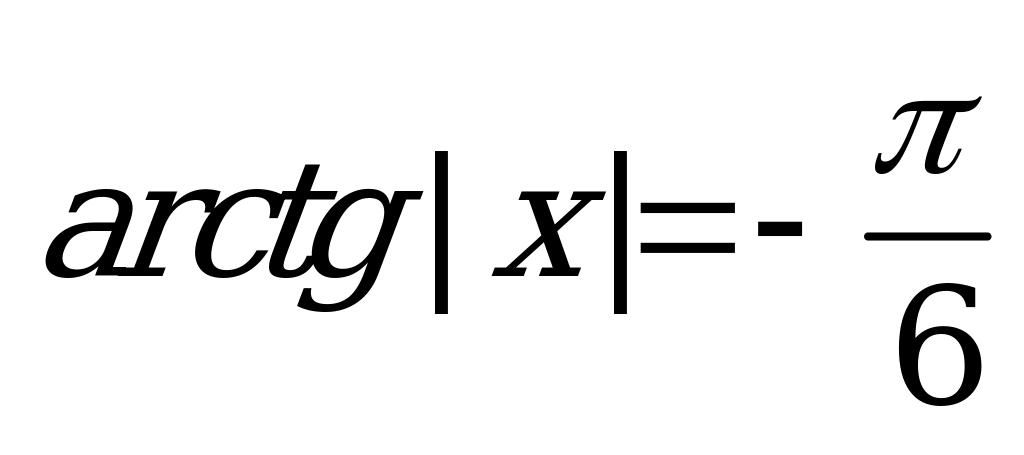 ? ? A) 1 B)  C) 2 D) бесконечно много E) 3 C) 2 D) бесконечно много E) 3
| B |
| В4.10 Вычислите:  A) 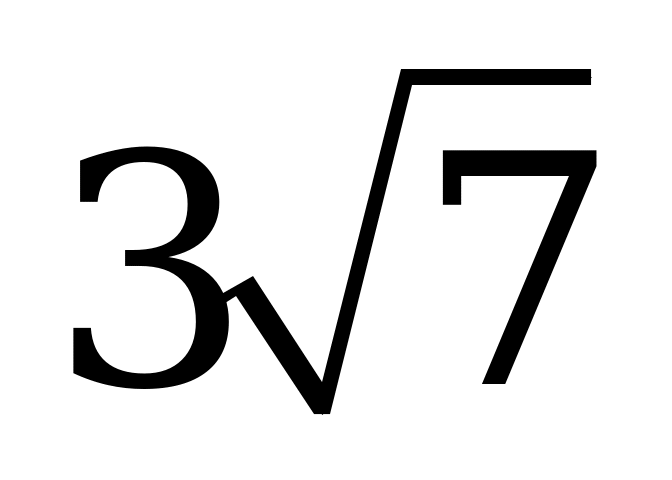 B) B) 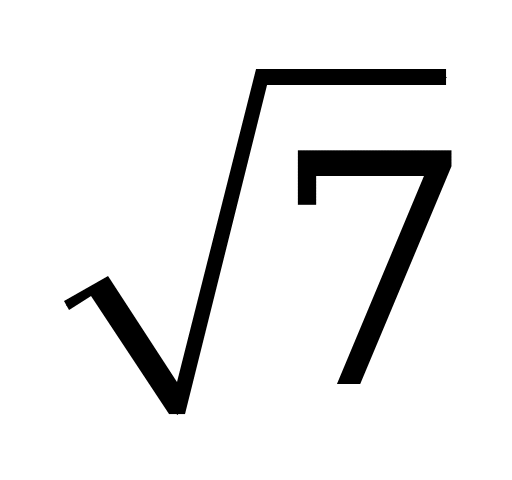 C) - C) -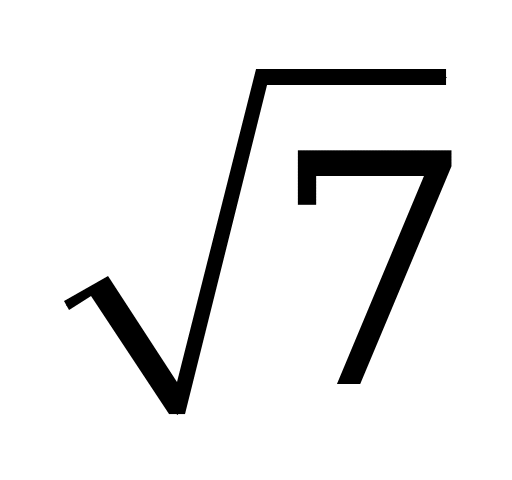 D) D) 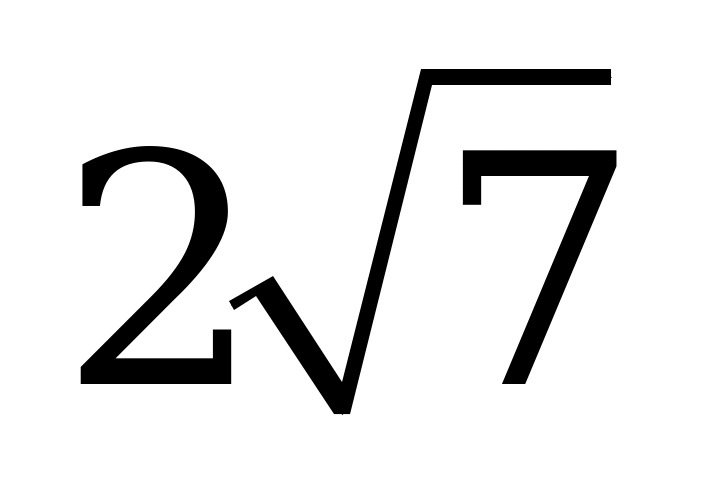 E) E) 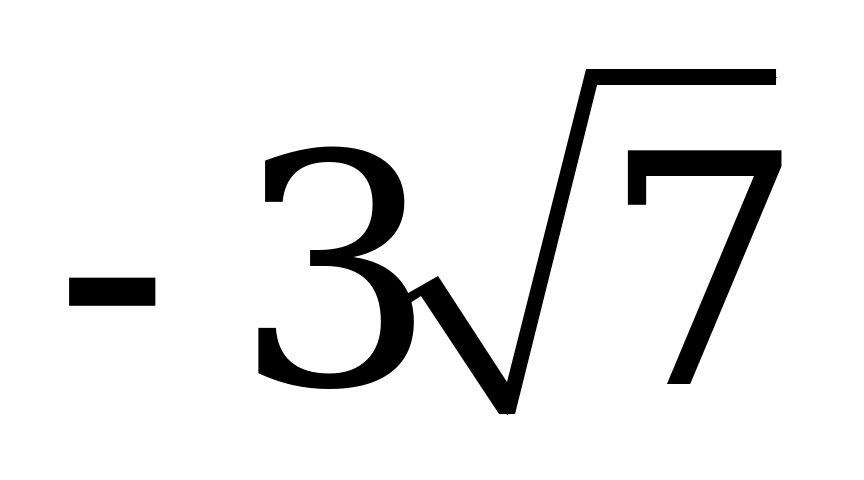 | E |
Тестовые задания наиболее сложного уровня 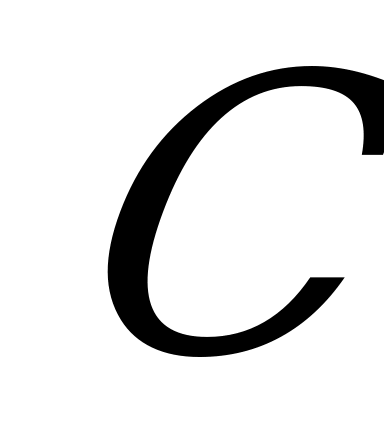 .
.
|
| Ответы |
| С1. Решите уравнение 3cosx – 4sinx = -3 A) 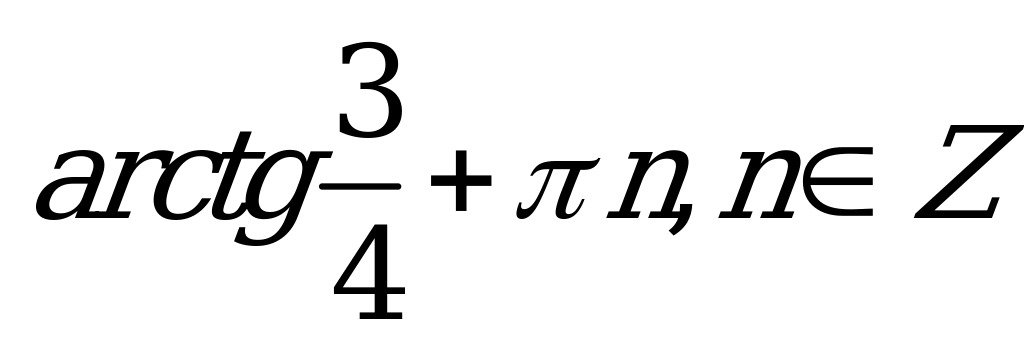 B) B) 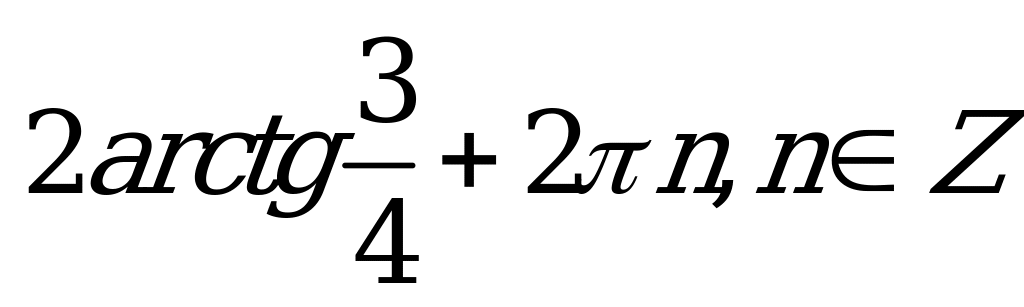 C) 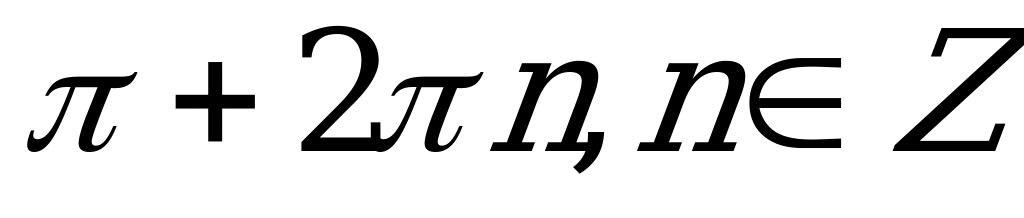 D) D) 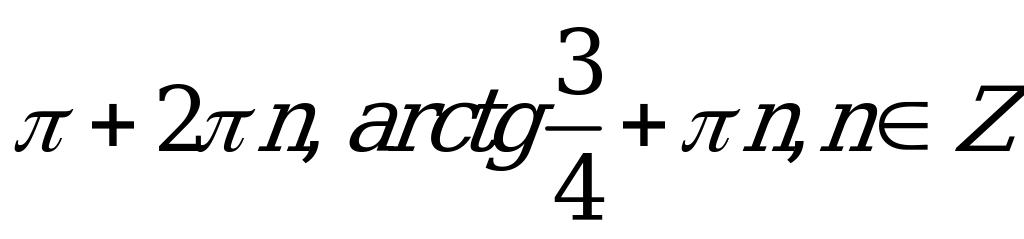 E) 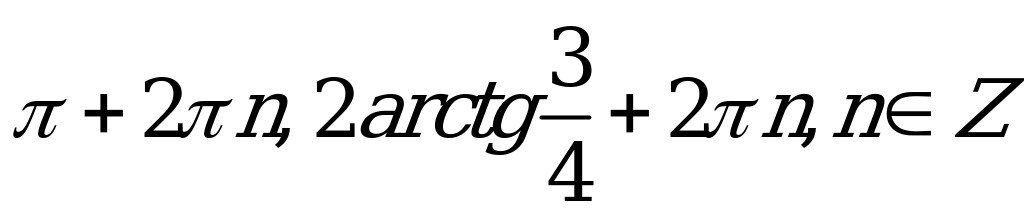 | E |
| С2. Для уравнения sin5x + cos6x = 1 найдите разность между наибольшим и наименьшим корнями на отрезке 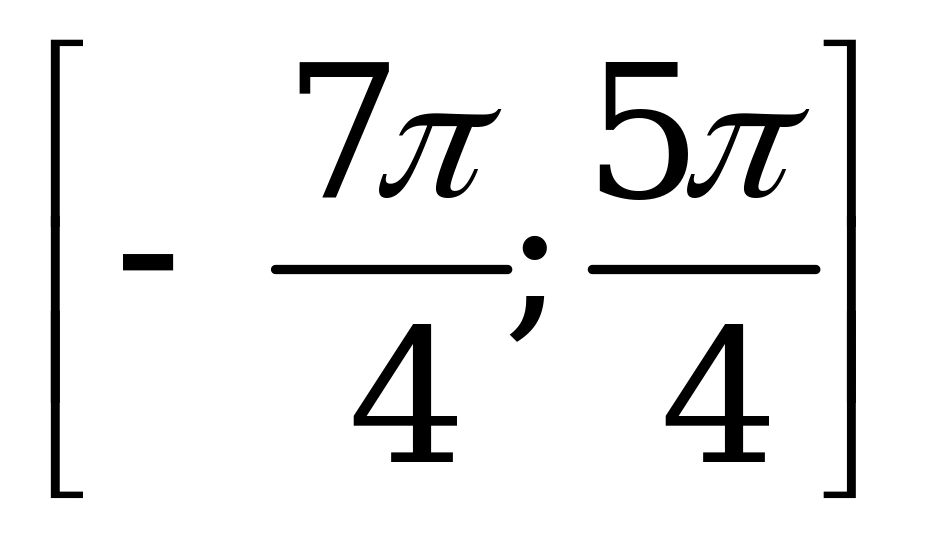 . A) 2 B) 1,5 C) 3,5 D) 3 E) 2,5 . A) 2 B) 1,5 C) 3,5 D) 3 E) 2,5 | E |
| С3. Найдите наименьший положительный корень уравнения 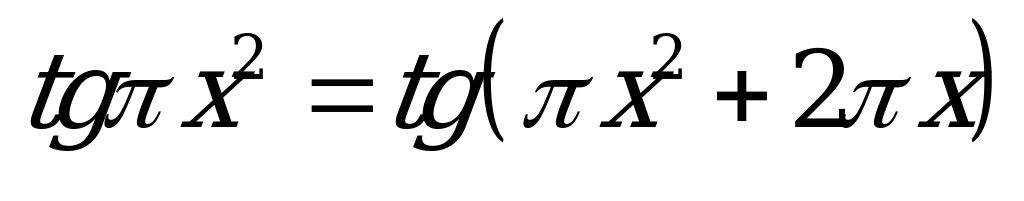 A) 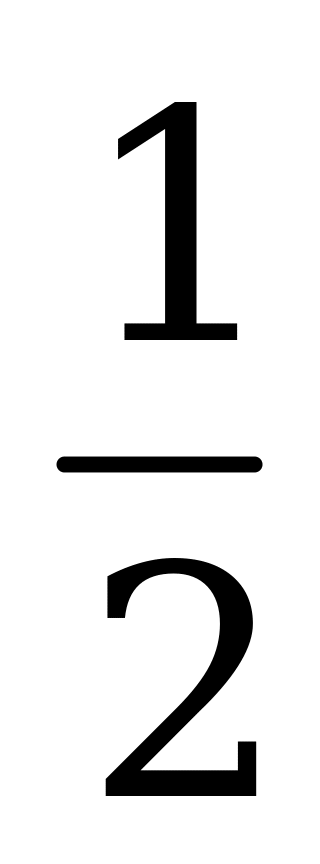 B) B) 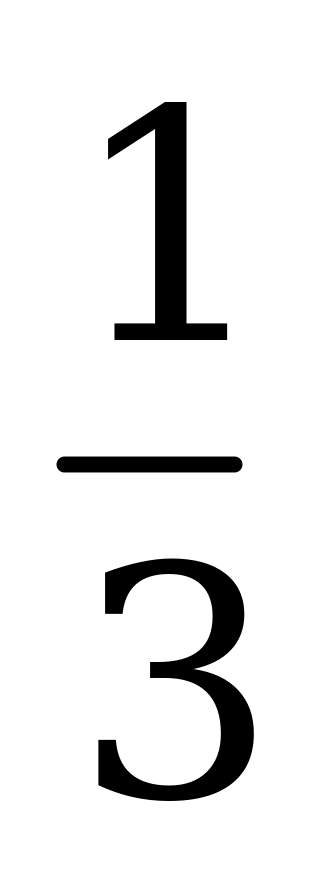 C) 1 D) C) 1 D) 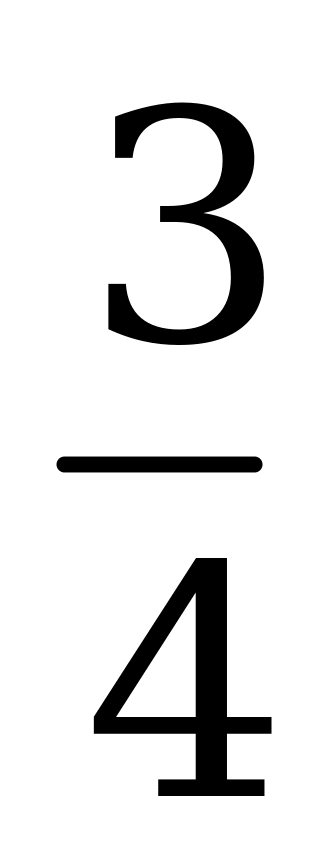 E) E) 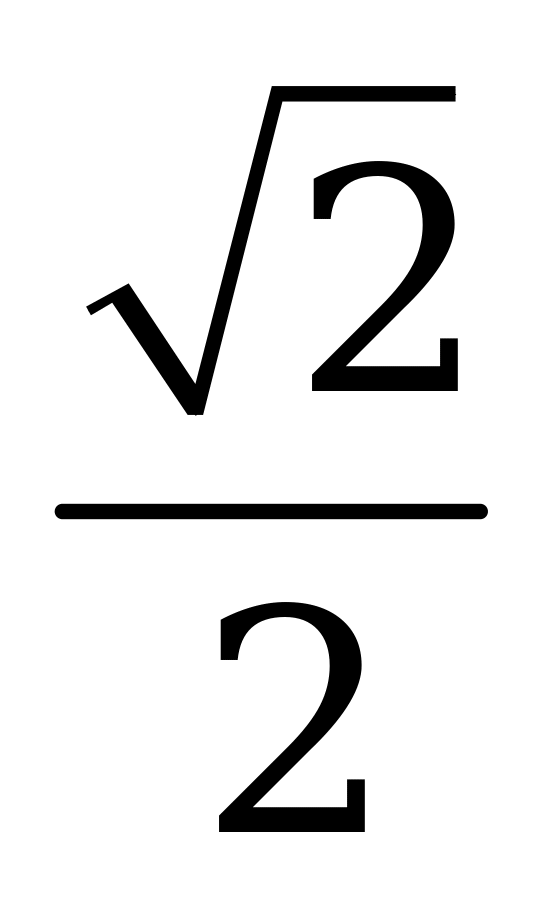 | A |
| С4. Решите уравнение 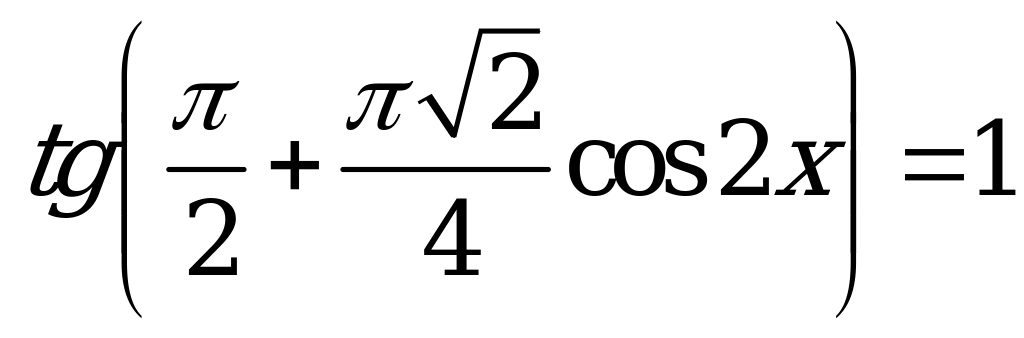 A) 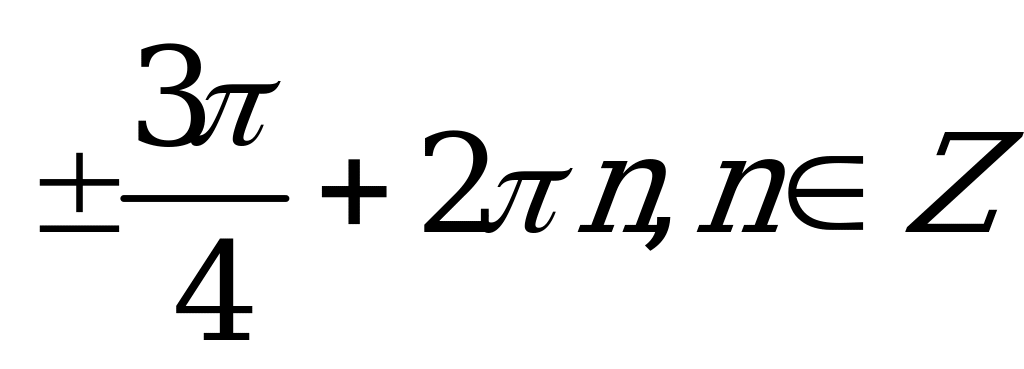 B) B) 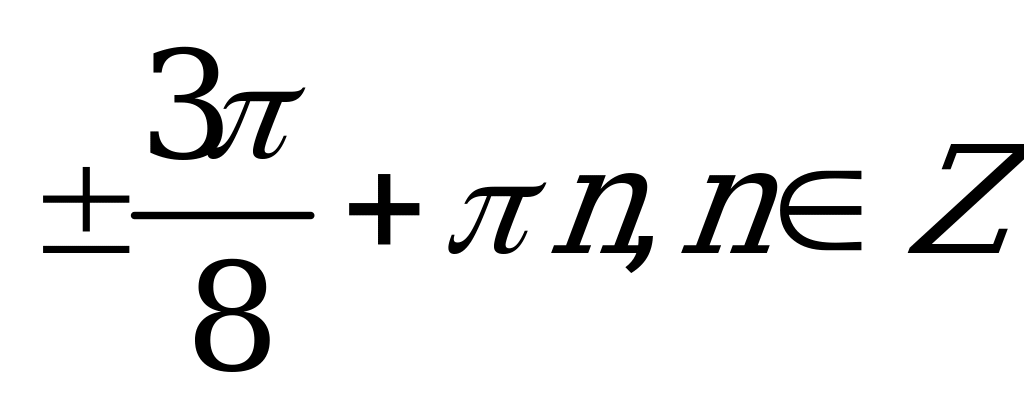 C) 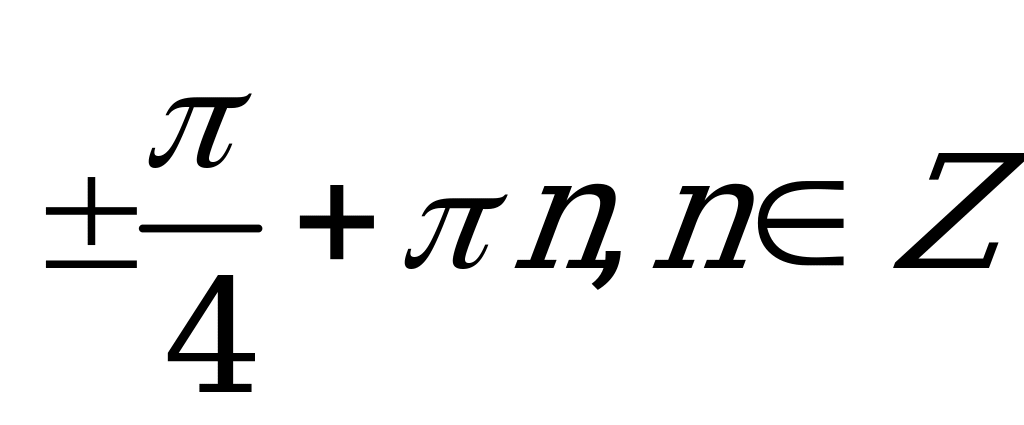 D) D) 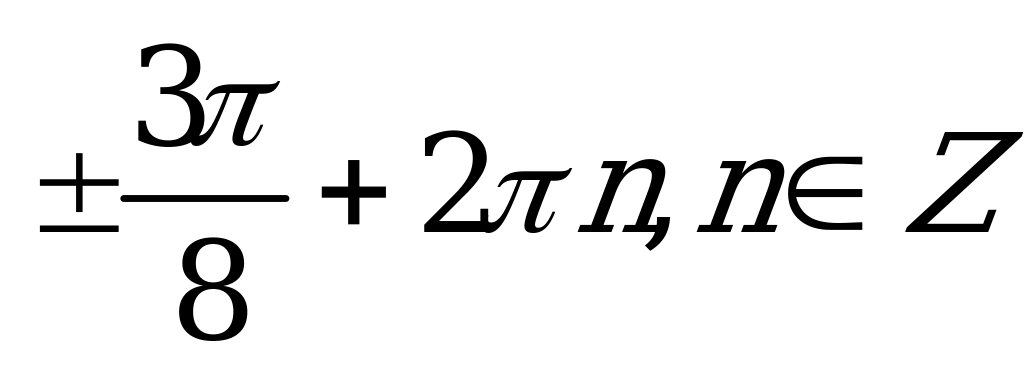 Е) Е)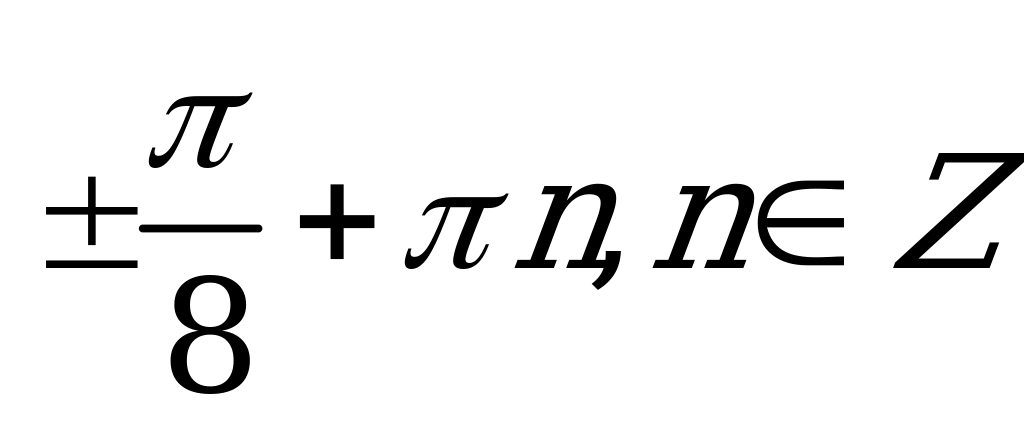 | B |
| С5. Решите уравнение: sin( cosx) = 0 cosx) = 0 A) 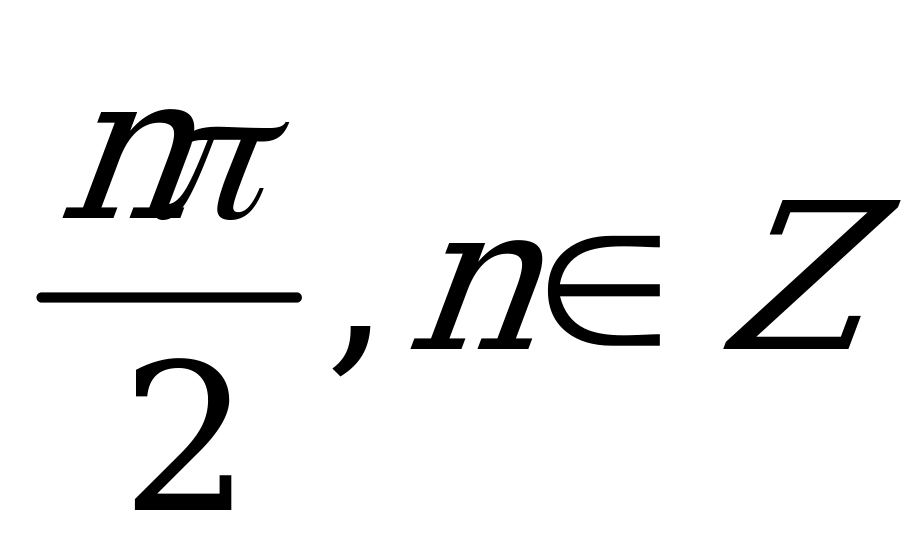 B) B) 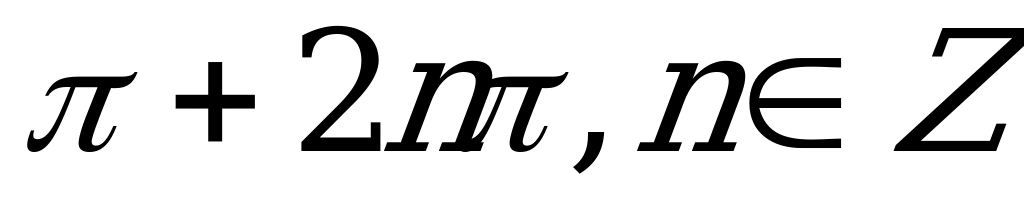 C) 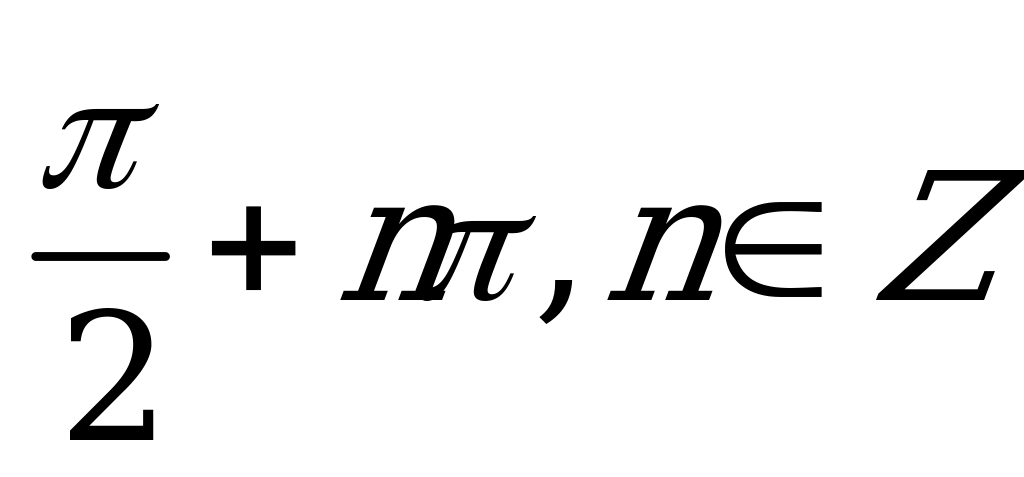 D) D) 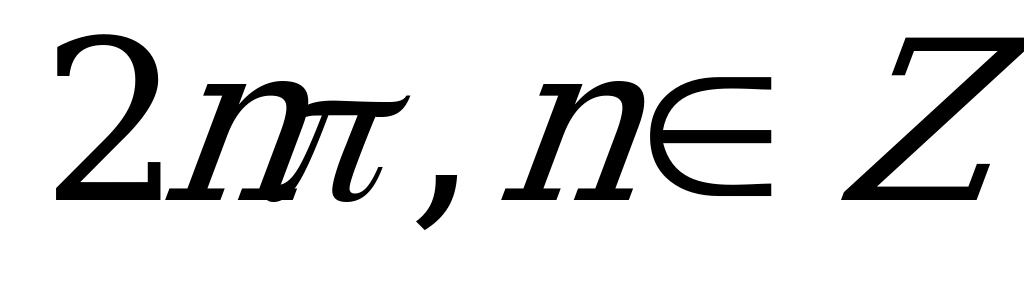 E) E) 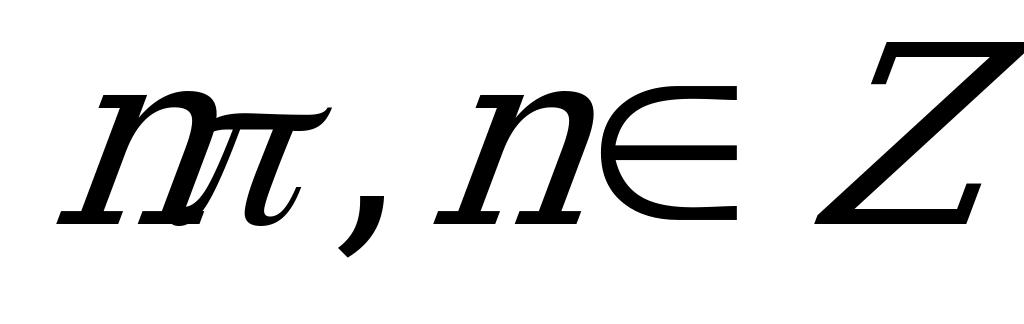 | A |
| С6. Решите уравнение sin( cos3x) = 1. A) 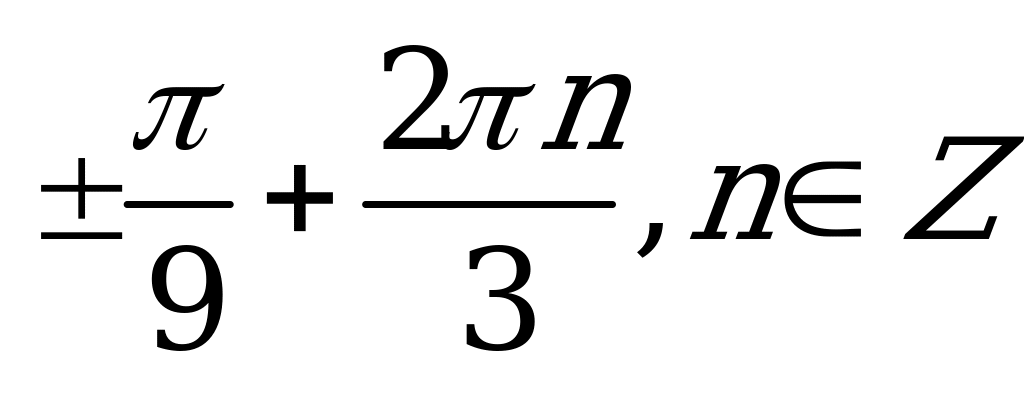 B) B) 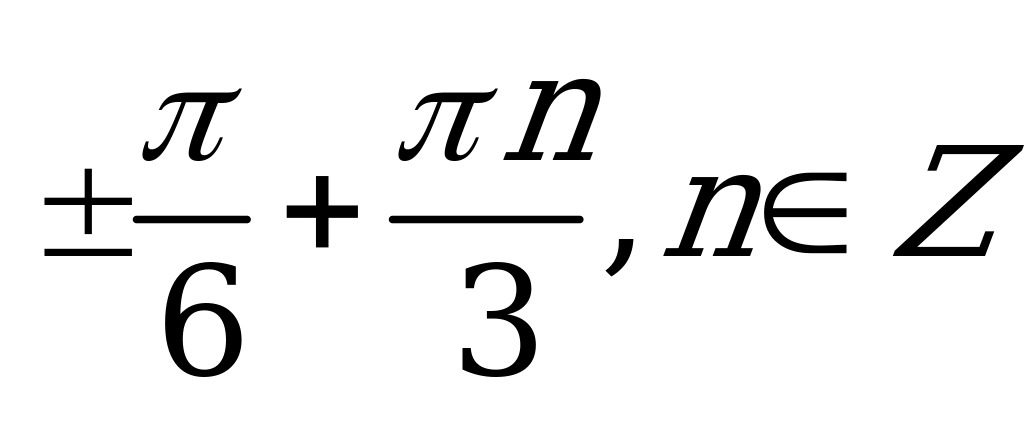 C)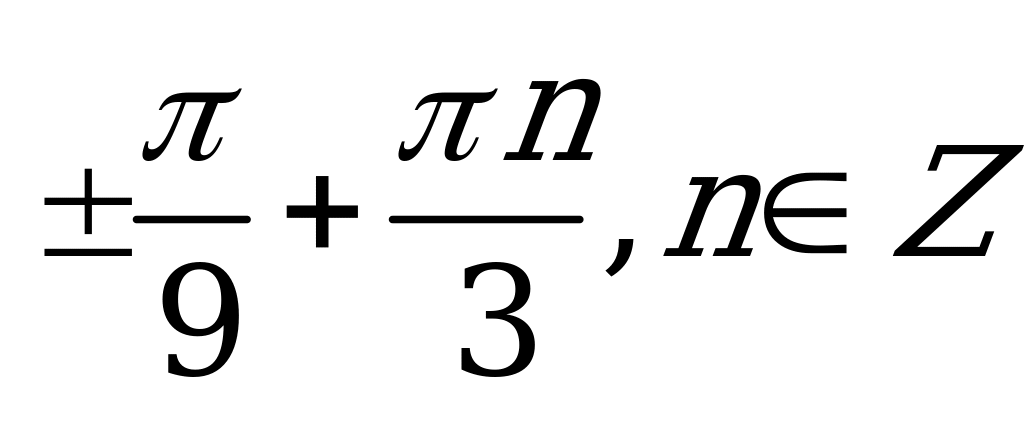 D) D)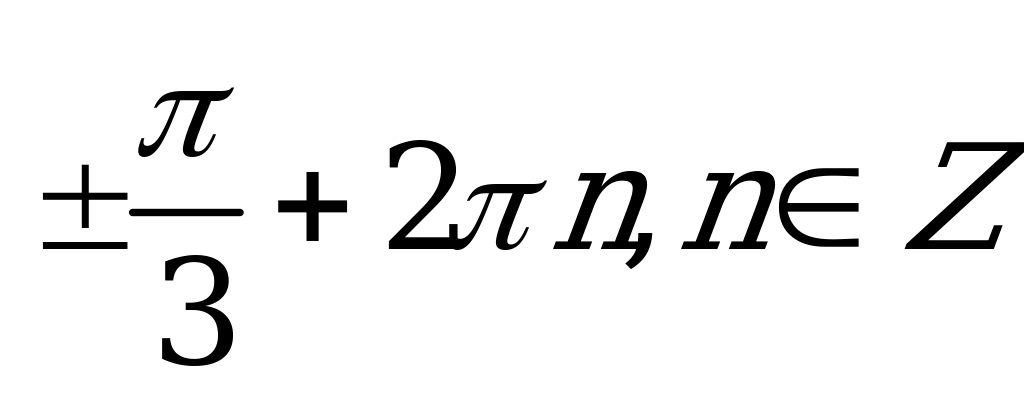 E) E)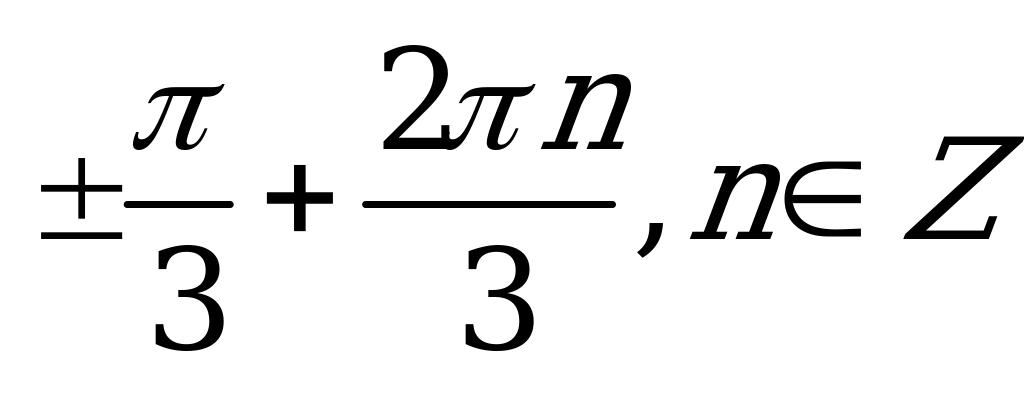 | A |
| С7. Решите неравенство 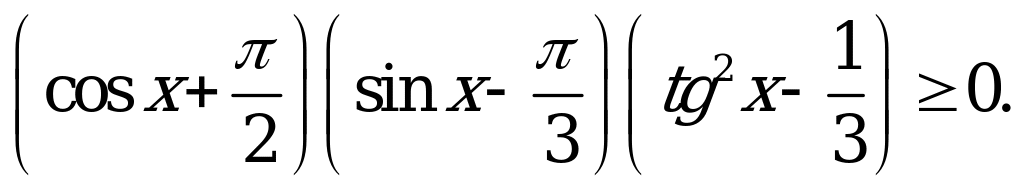 A)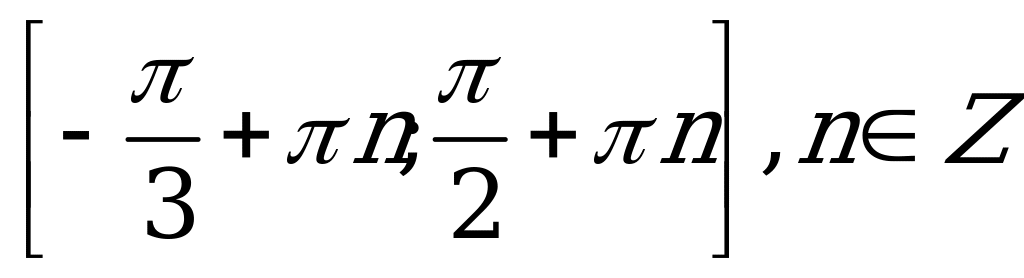 B) B)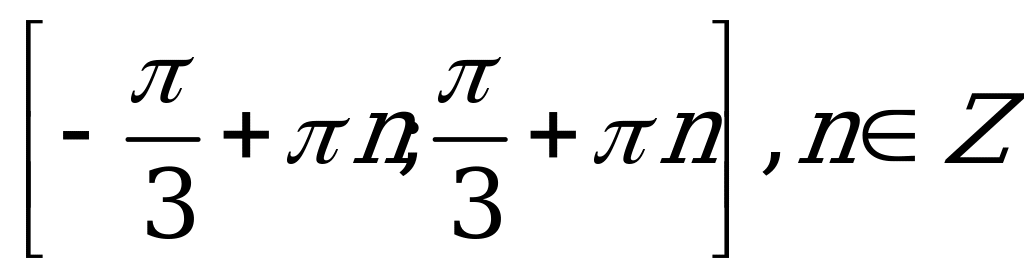 C) C)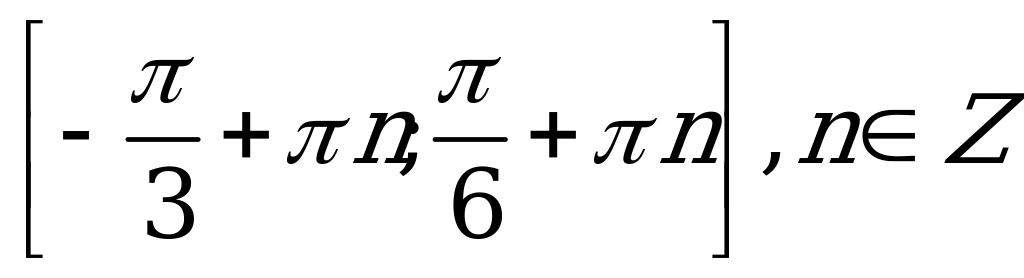 D) D) 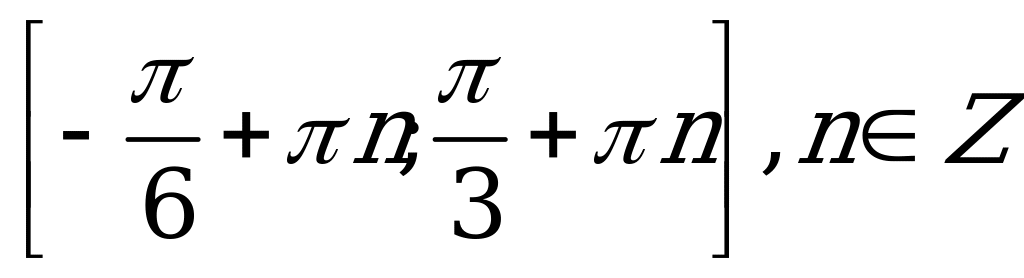 E) 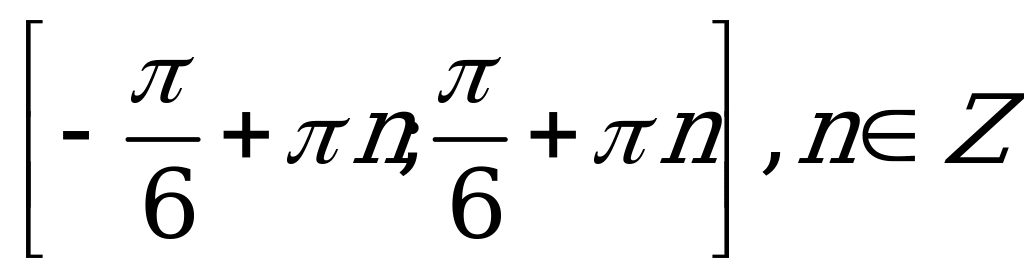 | E |
| С8. При каких значениях x выполняется неравенство sin2x - 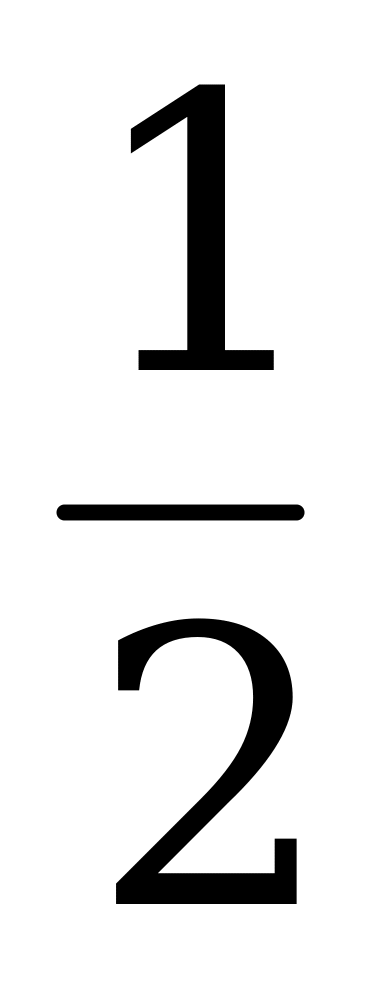 sin2x - 2cos2x sin2x - 2cos2x 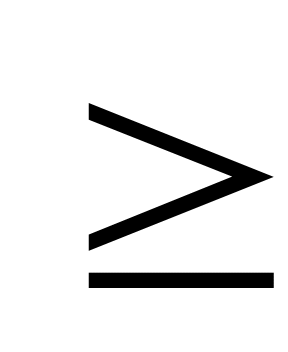 0, если x 0, если x 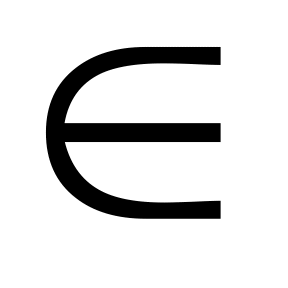 [0; 2 [0; 2 ] ? ] ? A) 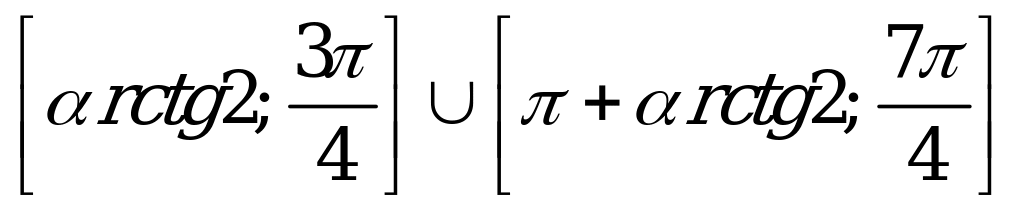 E) [ E) [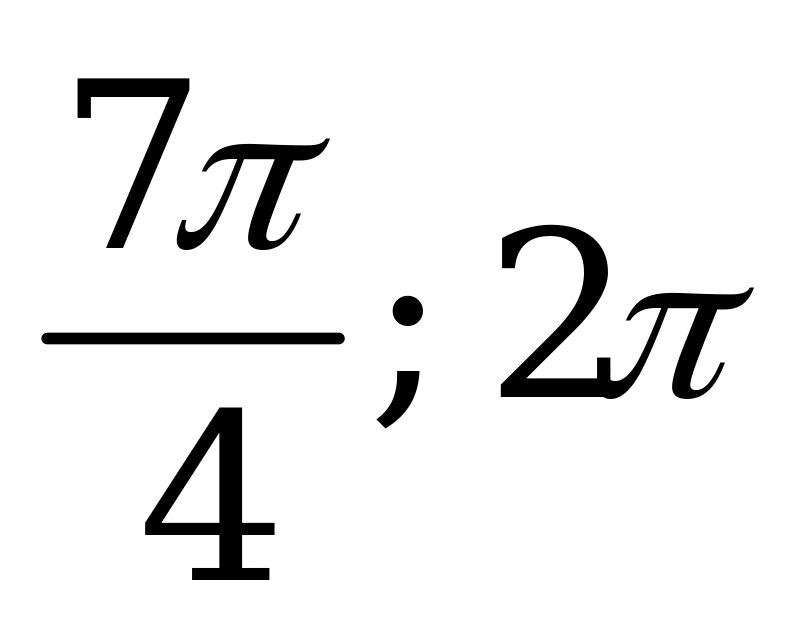 ] ] B) [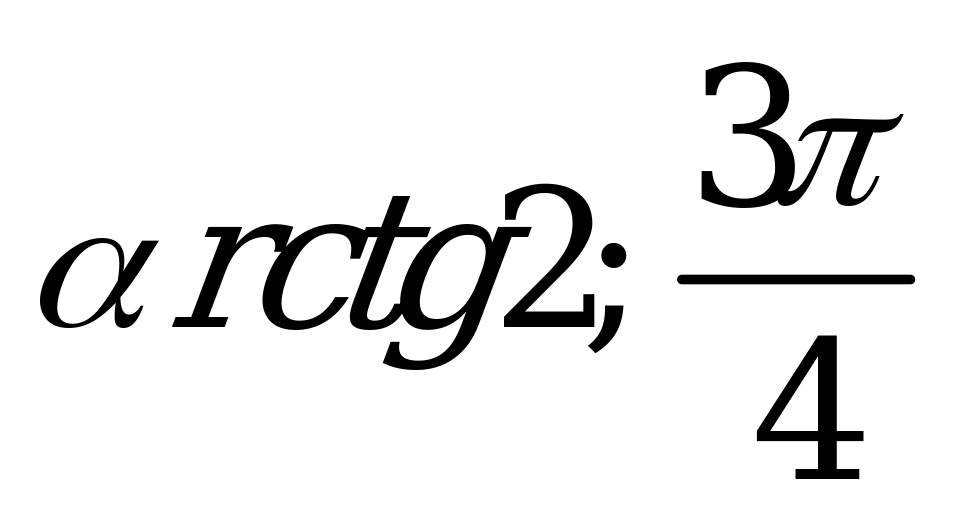 ] C) [ ] C) [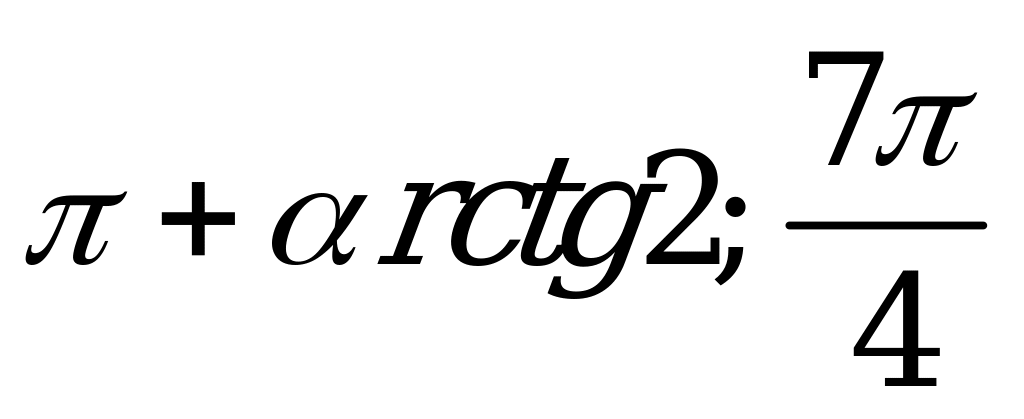 ] ] D) [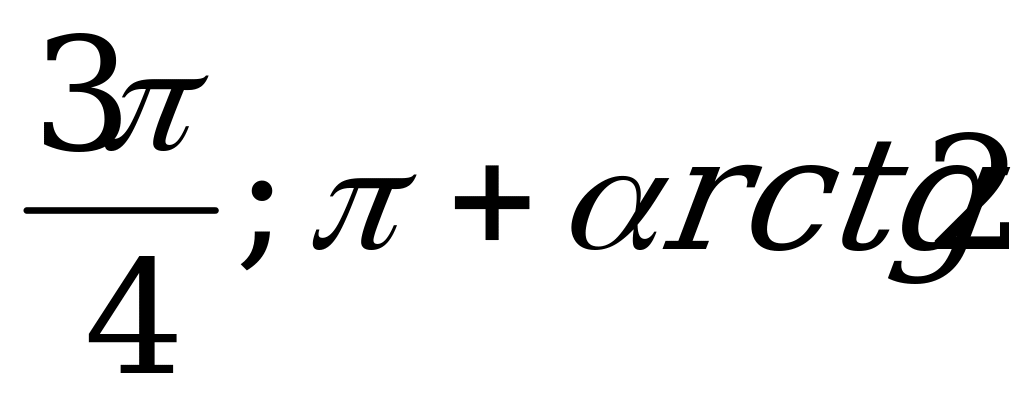 ] ] | A |
| С9. При каких значениях x выполняется неравенство sin2x - sin2x - 8cos2x 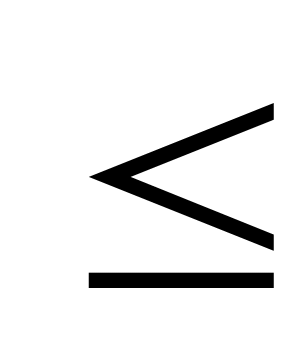 0, если x 0, если x  [0; 2 [0; 2 ]? ]? A) [arctg4;  – arctg2] E) [0; arctg4] – arctg2] E) [0; arctg4] B) [arctg4;  – arctg2] – arctg2]  [ [ + arctg4; 2 + arctg4; 2 – arctg2] – arctg2] C) [ + arctg4; 2 + arctg4; 2 – arctg2] D) [arctg2; – arctg2] D) [arctg2;  ] ] | B |
| С10. Решите неравенство 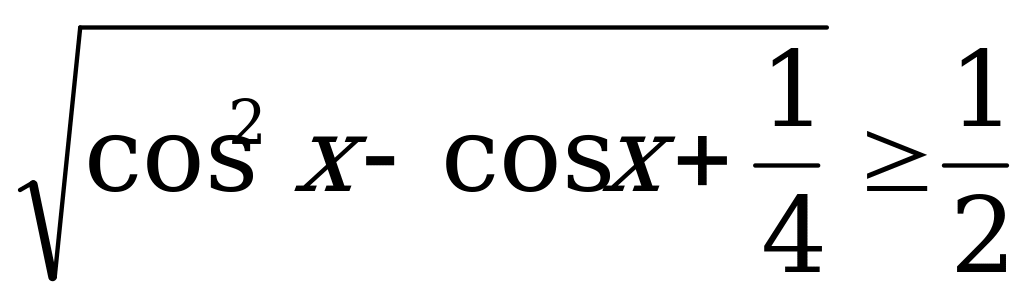 A) 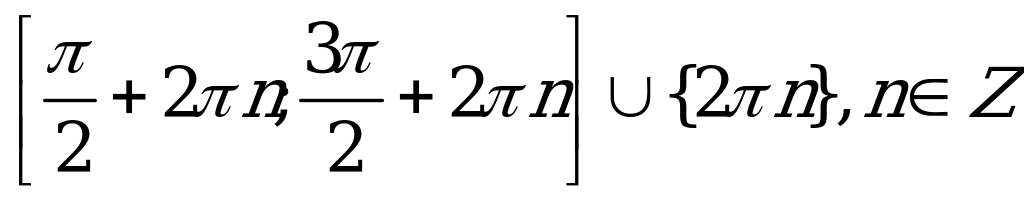 B) 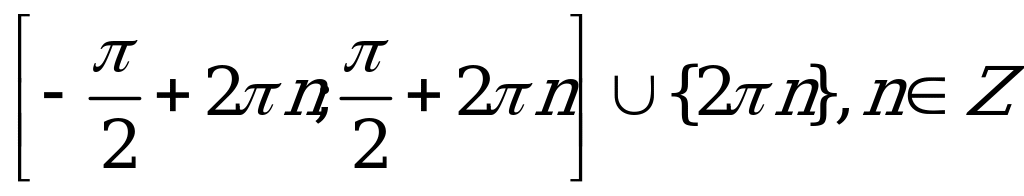 C) 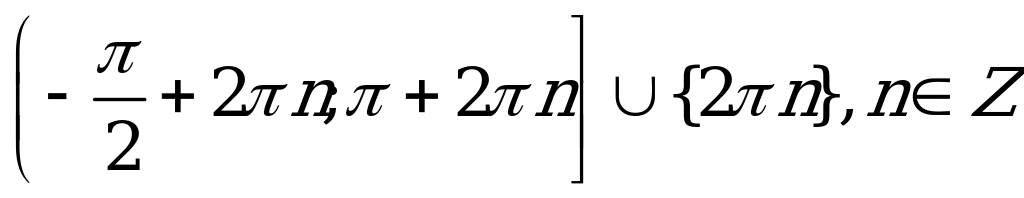 D) 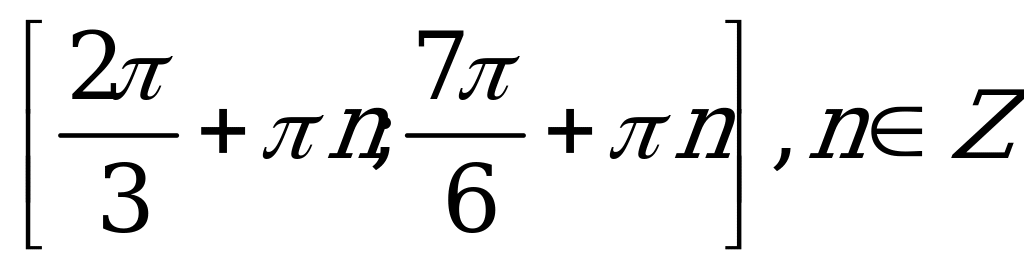 E) E) 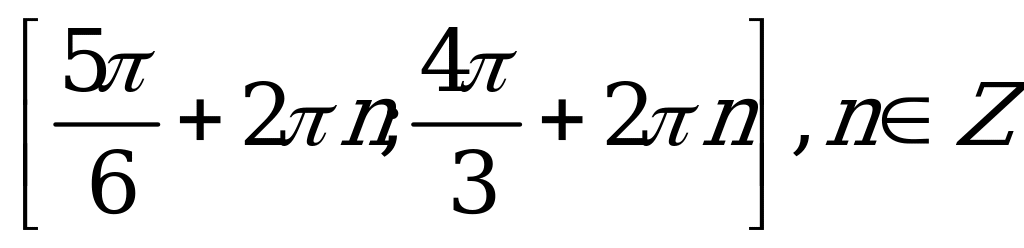 | A |
| С11. Решите неравенство cos(sinx). A) (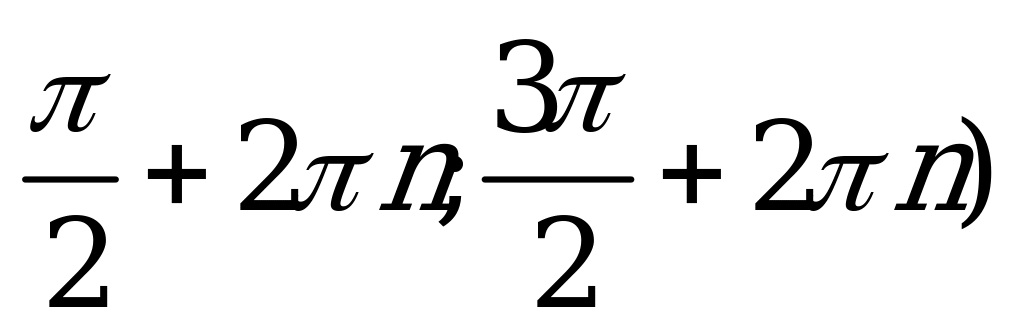 , n , n 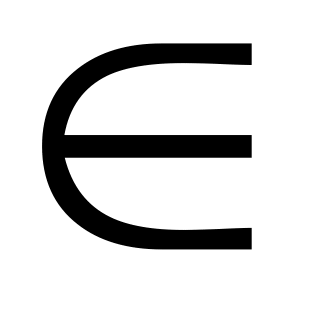 Z B) ( Z B) (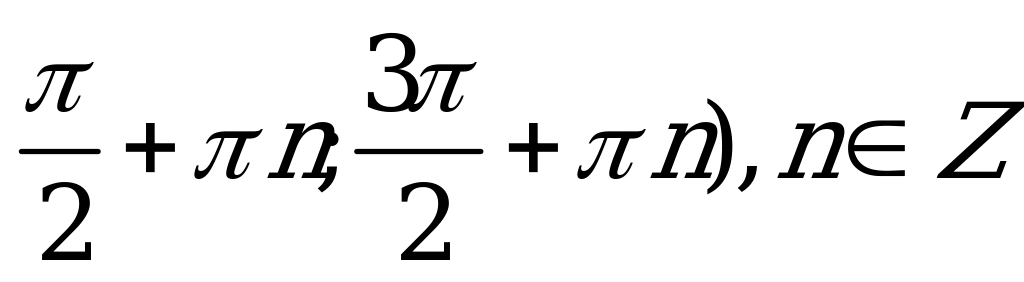 C) (0; 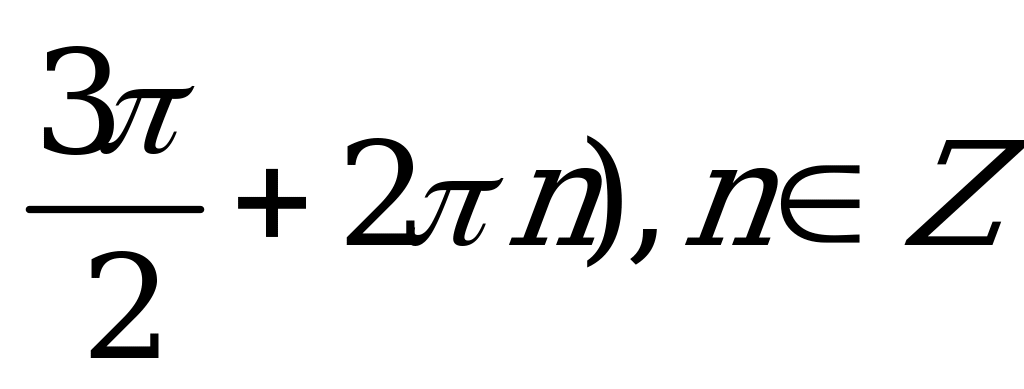 D) (0; D) (0;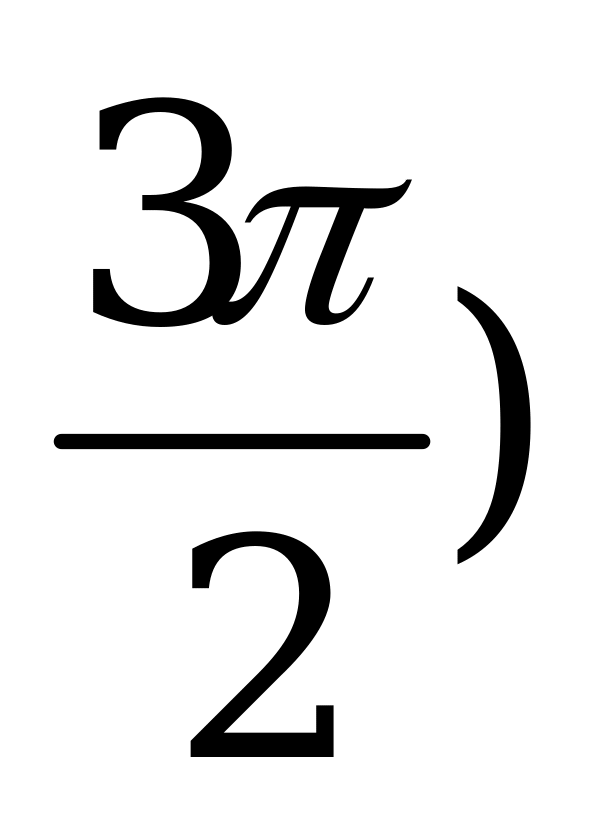 Е) Е)  | Е |
| С12. Решите неравенство: 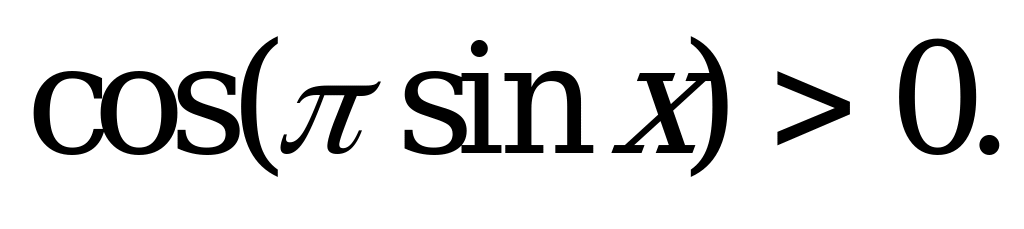 A) 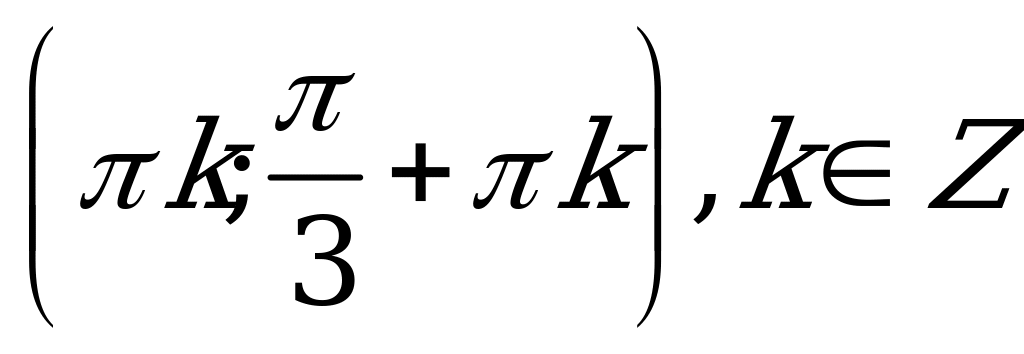 B) B) 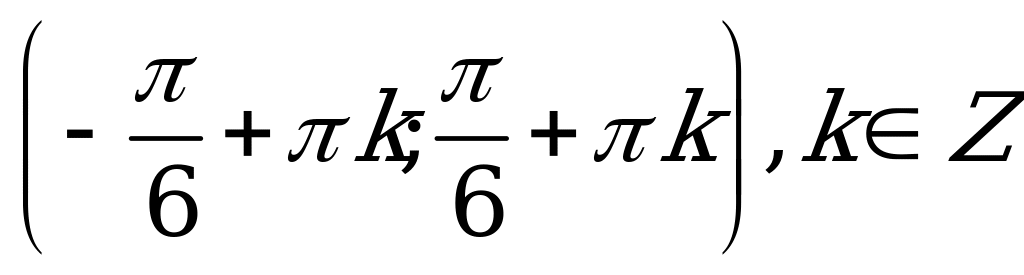 C) 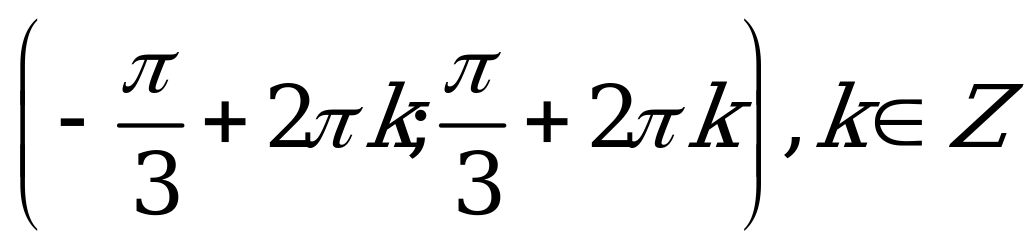 D) 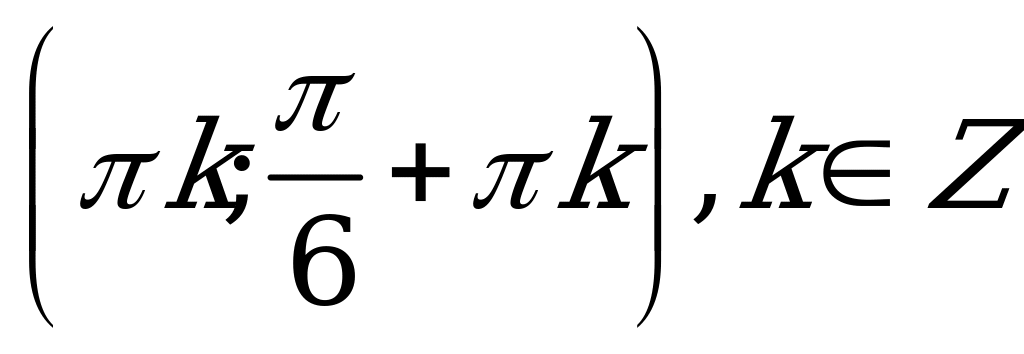 E) E) 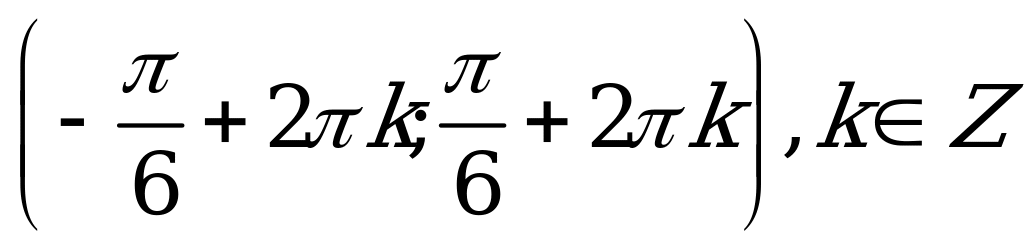 | B |
| С13. Сколько корней имеет уравнение arcsin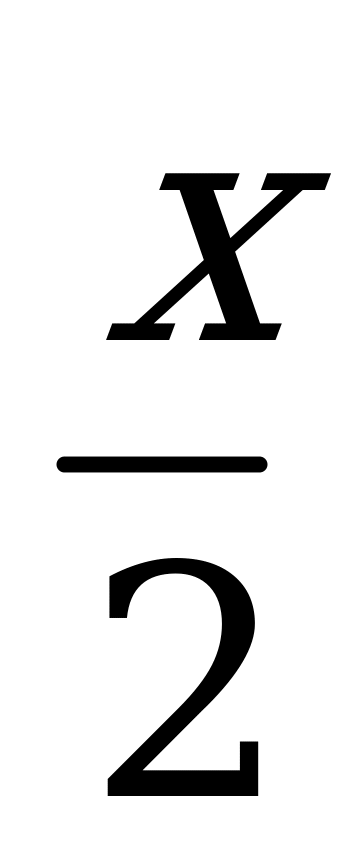 +2arccosx= +2arccosx= ? ? A) 1 B) 2 C)  D) 3 E) бесконечно много D) 3 E) бесконечно много | A |
| С14. Найдите наименьший положительный корень уравнения 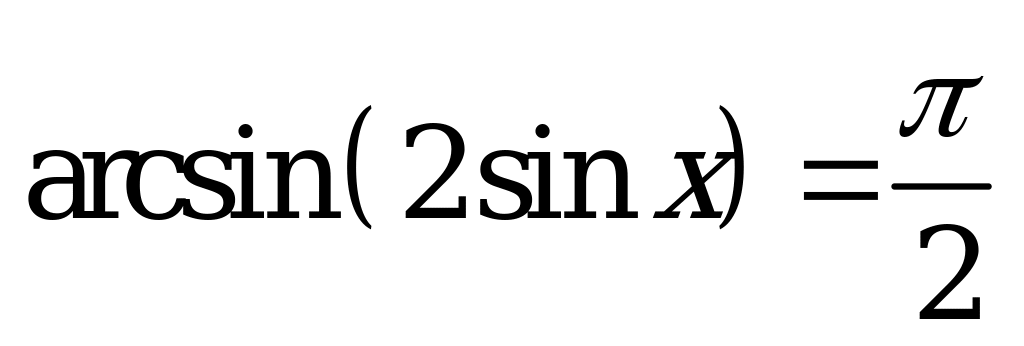 . . A) 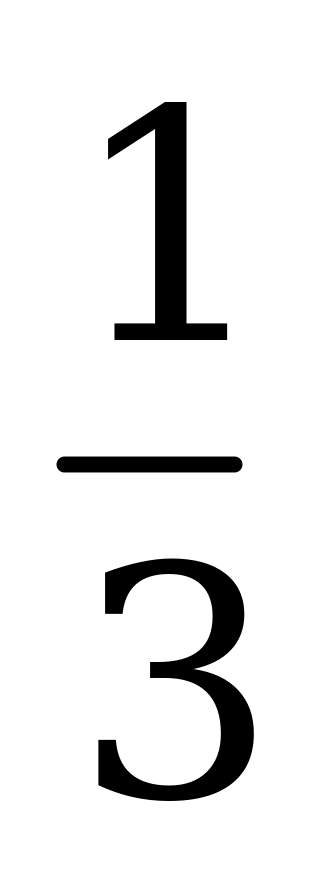 B) B) 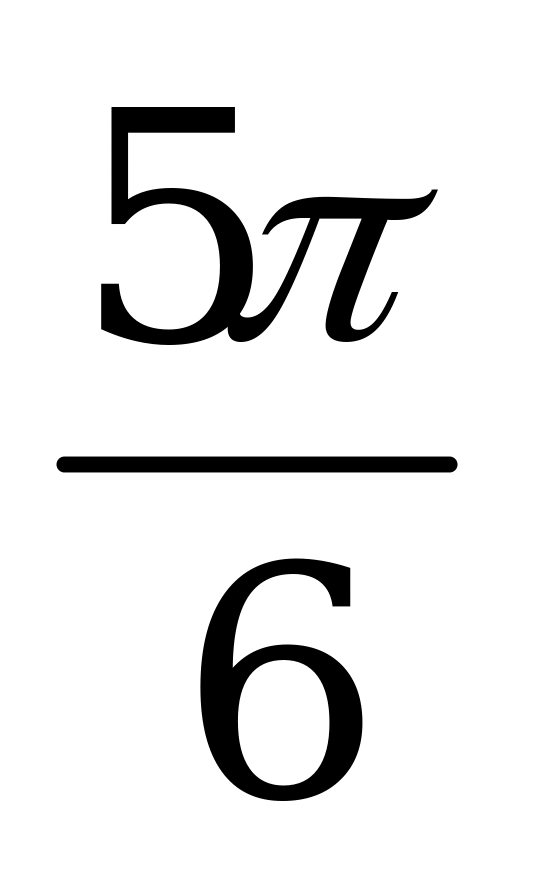 C) C) 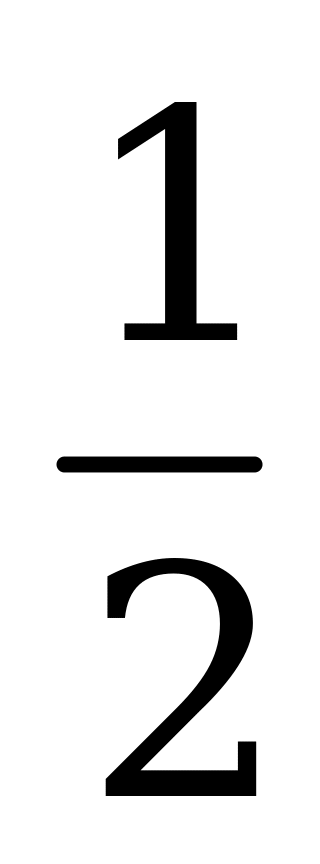 D) D) 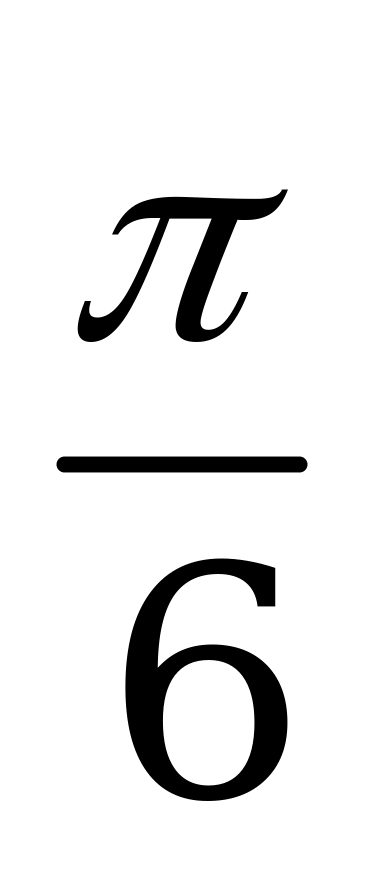 E) E) 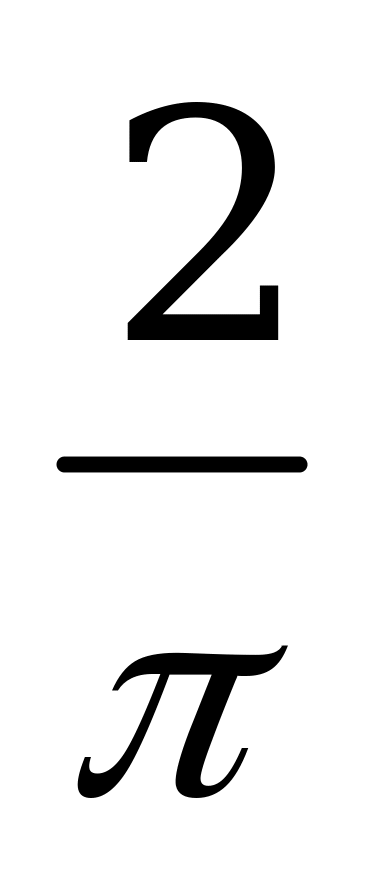 | D |
| С15. Найдите сумму корней уравнения 2(arc2cosx) +  2 = 3 2 = 3 arccosx arccosx A) 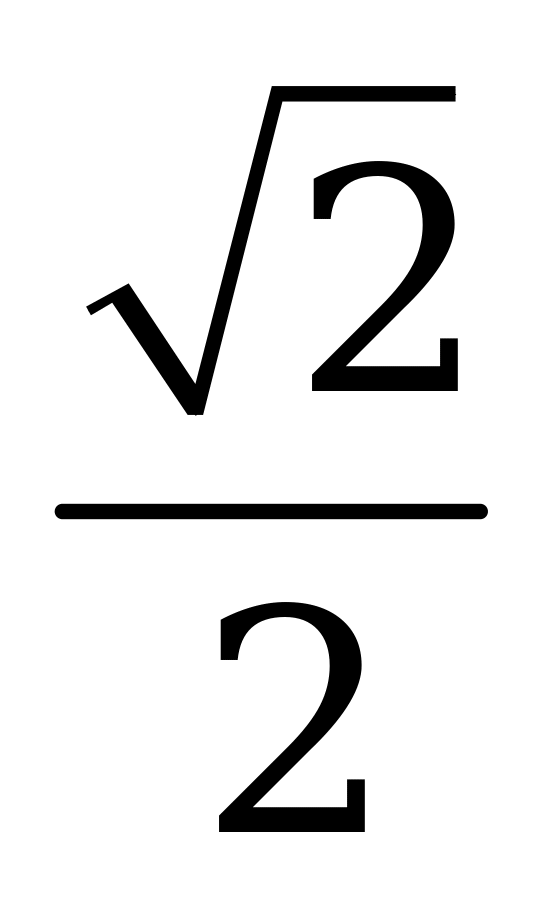 B) -1 C) 1 D) B) -1 C) 1 D) 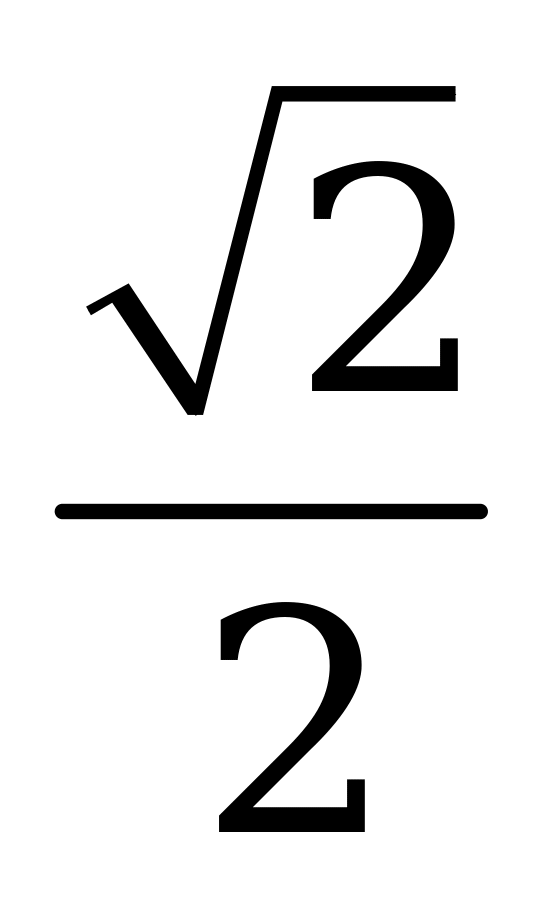 E) E) 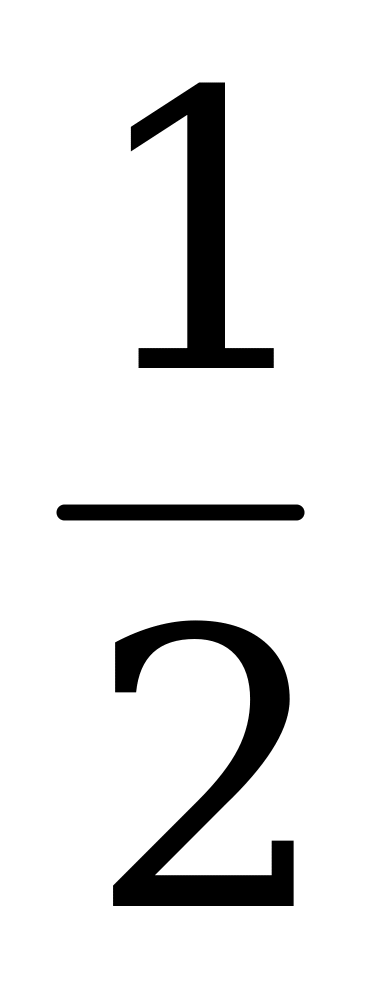 | B |
| С16. Вычислить: arcsin(sin10) A)  - 10 B) 2 - 10 B) 2 - 10 C) 3 - 10 C) 3 - 10 D) - 10 D) 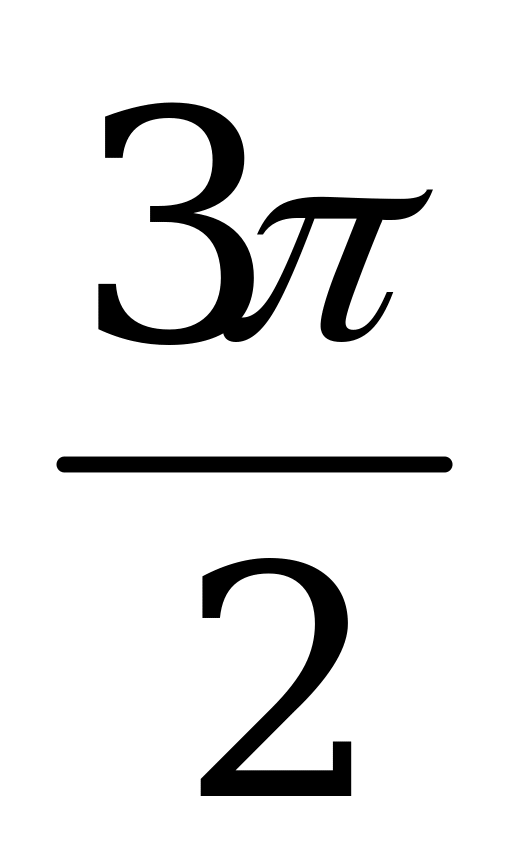 - 10 E) - 10 E) 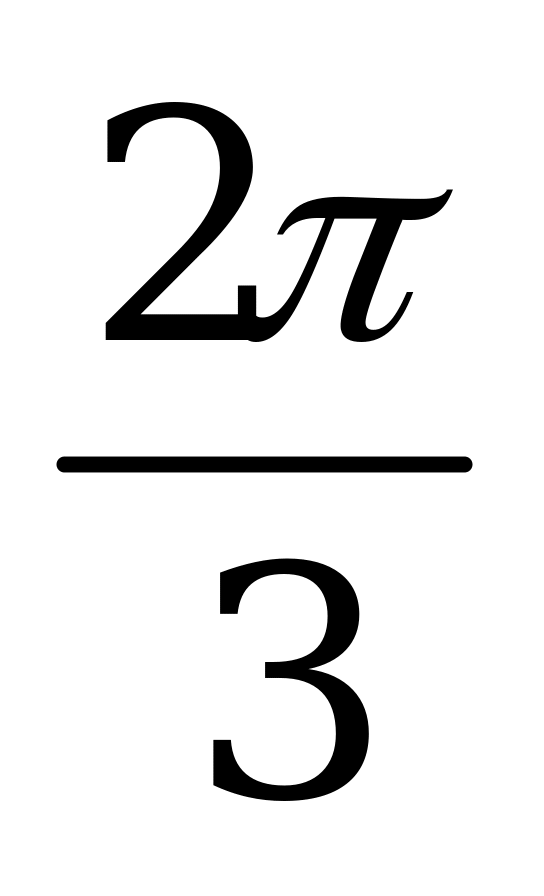 - 10 - 10 | C |
| С17. Сколько корней имеет уравнение cos(10arctgx) = 1? A) 5 B) бесконечно много C) 1 D) 3 E)  | A |
| С18. Найдите произведение корня уравнения arccosx = arctgx на 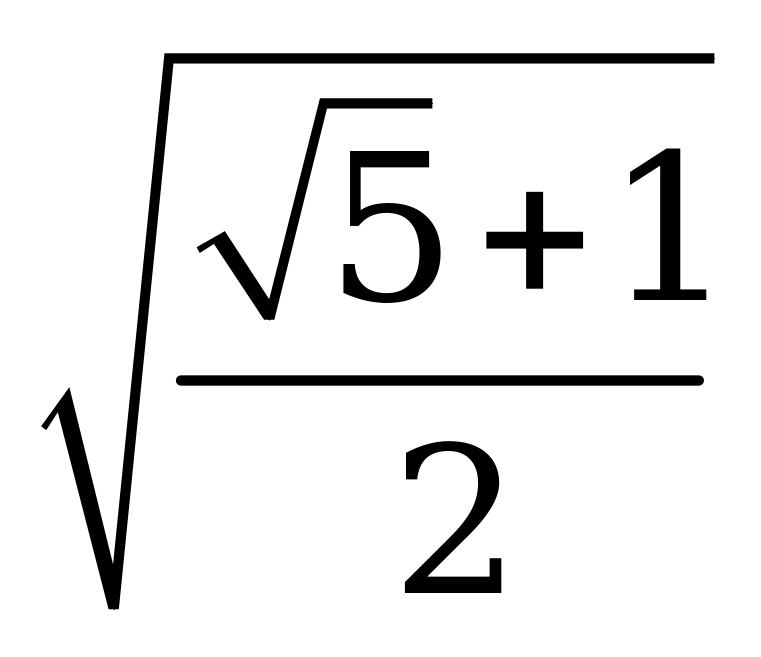 . . A) 1 B) 2 C) 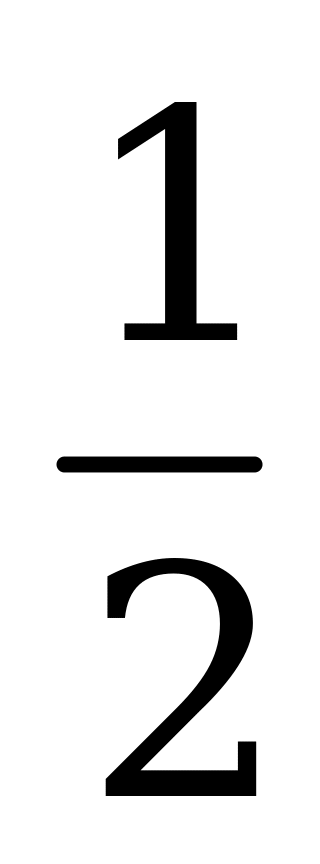 D) D) 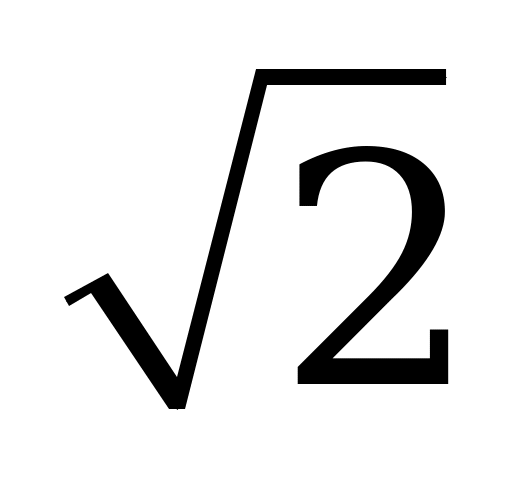 E) E) 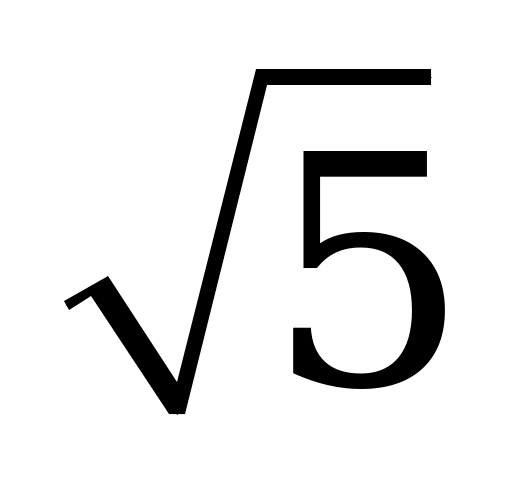 | A |
| С19. Решите уравнение 2x = arcctg(tgx) A) 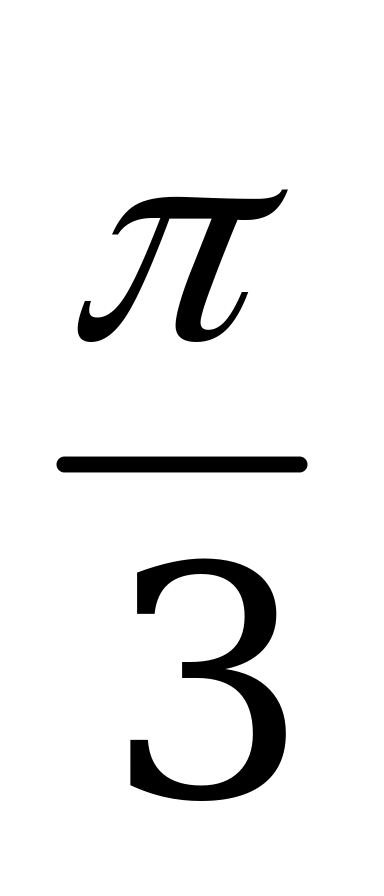 B) B) 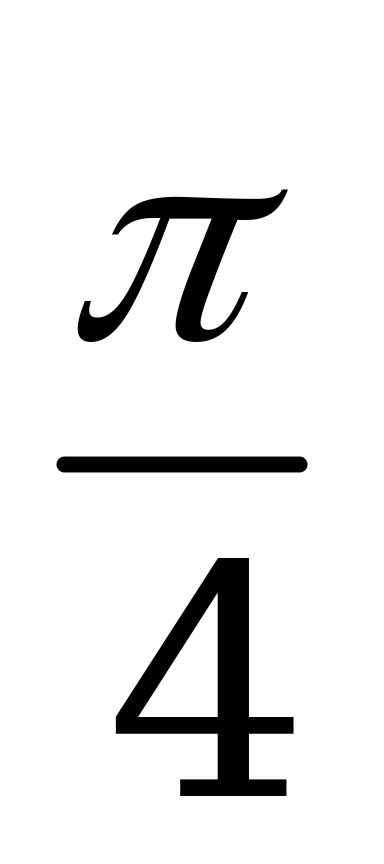 C) C) 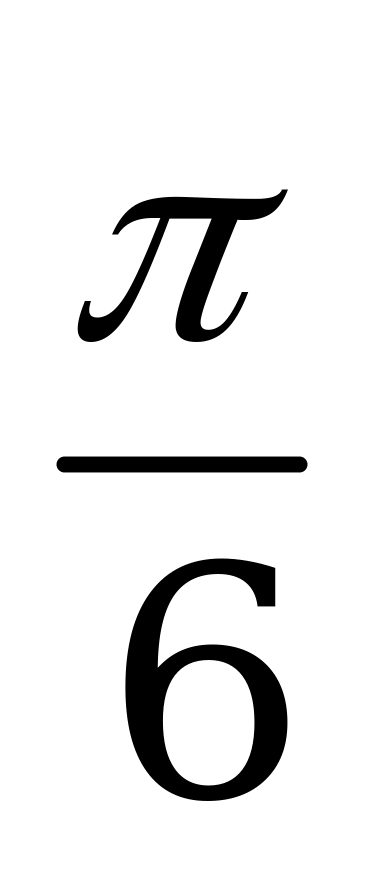 D) D) 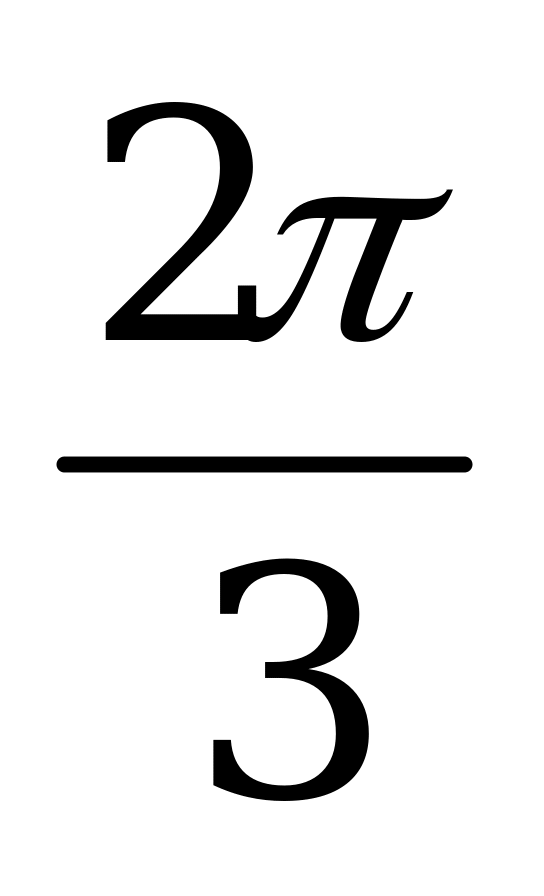 E) E) 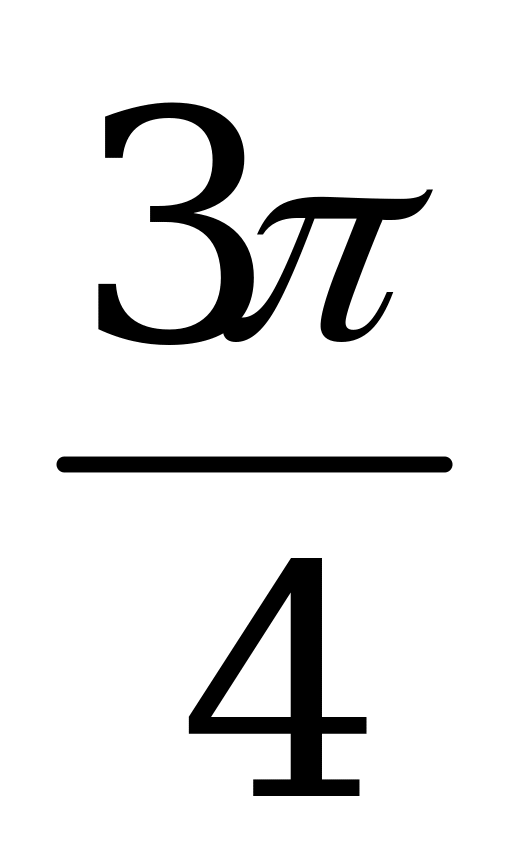 | C |
| С20. Найдите наибольшее целое значение x, удовлетворяющее неравенству arctgx A) -2 B) -1 C) 0 D) 1 E) 2 | B |
Подведение итогов.
Домашнее задание: составить справочник формул, которые применялись при решении тестовых заданий.
24







 принадлежащих интервалу
принадлежащих интервалу 









