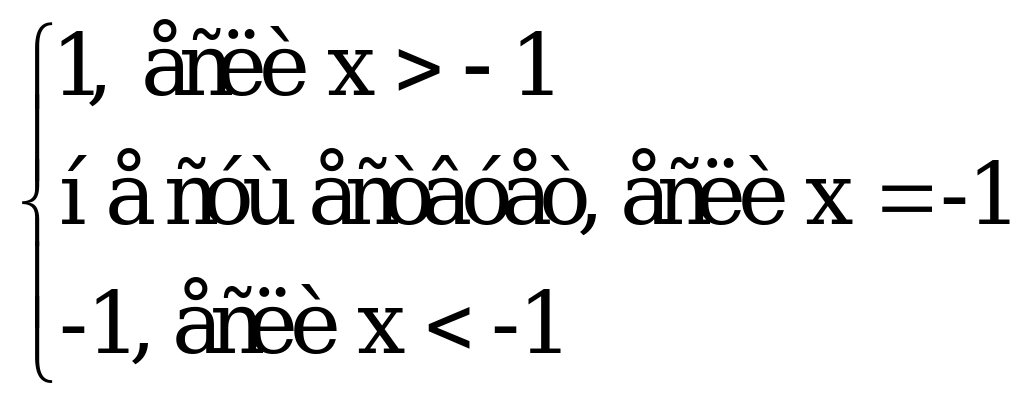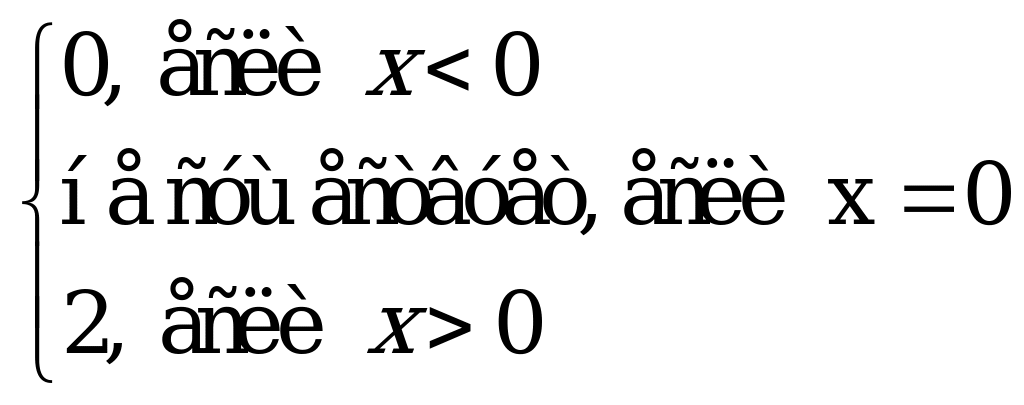Урок 90. Зачет по теме «Производная»
Приветствие, сообщение темы и задач урока.
На уроке, учащиеся объединяются в четыре группы по шесть человек в группе. Каждая группа получает карточку с теоретическими заданиями. Учащиеся распределяют между собой задания и, таким образом, каждый учащийся выполняет только одно задание. Решая задания в нутрии группы, можно помогать друг другу, но оценка будет выставляться каждому учащемуся индивидуально.
Учитель у доски опрашивает учащихся, которые работали над формулировкой алгоритма. В процессе ответа у доски учащиеся отвечают на вопросы учеников других групп.
Урок 91. Зачет по теме «Производная»
Приветствие, сообщение темы и задач урока.
На уроке, учащиеся объединяются в четыре группы по шесть человек в каждой группе случайным образом. Каждой группе предлагается на выбор задания трех уровней А, В, С.
Урок 92. Контрольная работа №4
Приветствие, сообщение темы и задач урока.
«Производная».
Урок 93-96. Учебно-тренировочные тестовые задания ЕГЭ по теме: «Производная»
Приветствие, сообщение темы и задач урока.
| А1. Производная элементарной функции | Ответы |
| А1.1 Вычислите 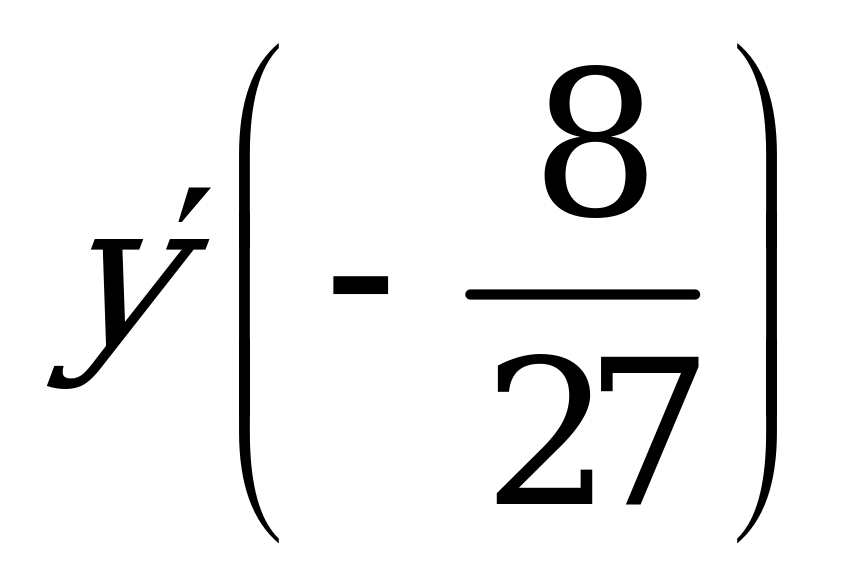 , если , если 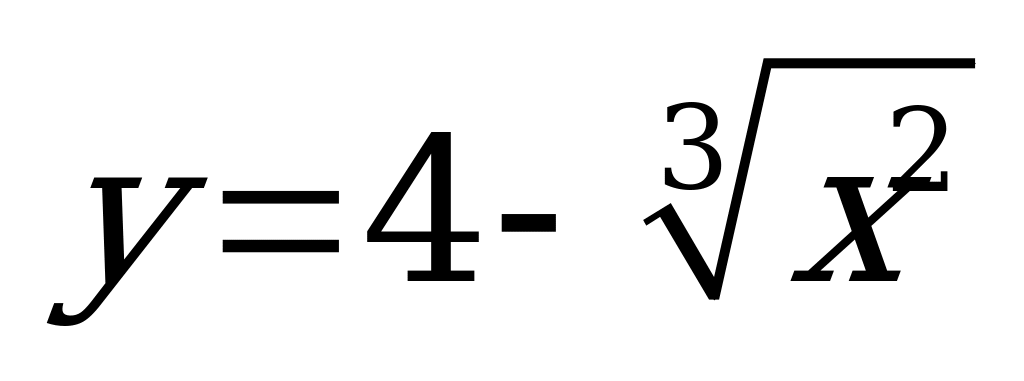 . . A) 1 B) 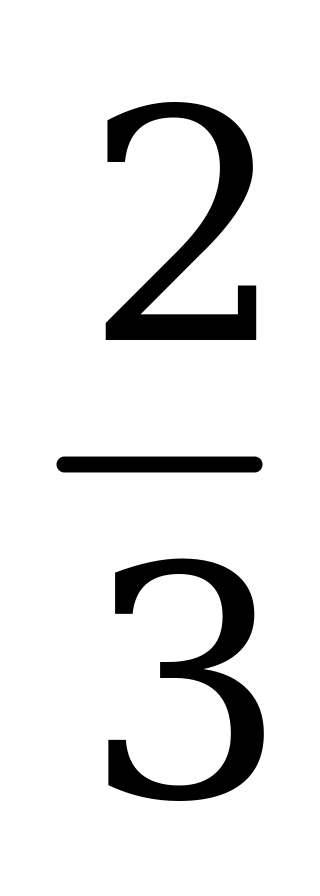 C) -1 D) - C) -1 D) -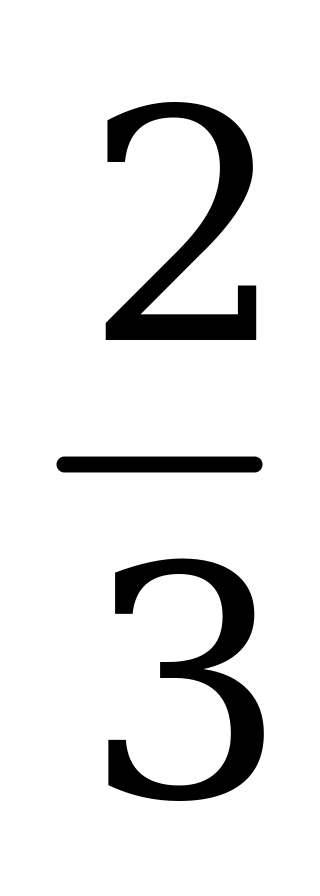 E) 3 E) 3 | А |
| А1.2 Найдите 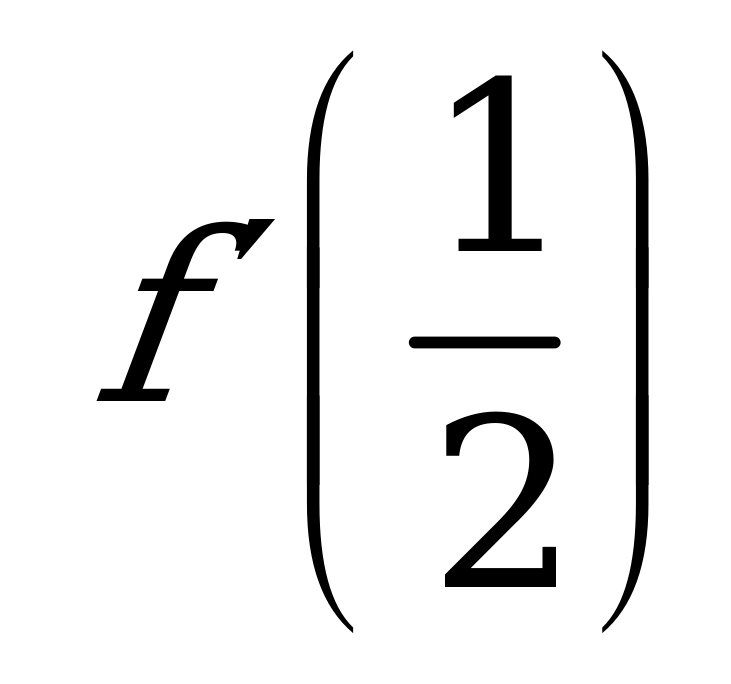 , если , если 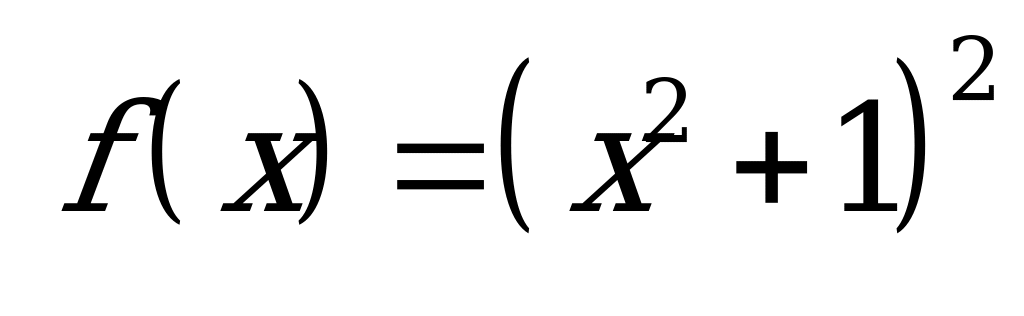 A) 2,5 B) -1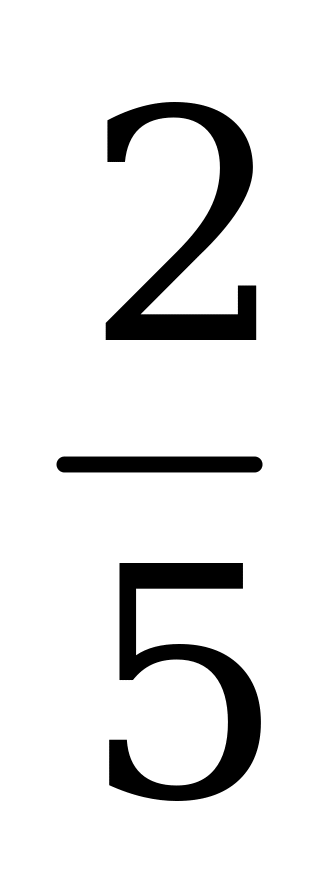 C) -1 C) -1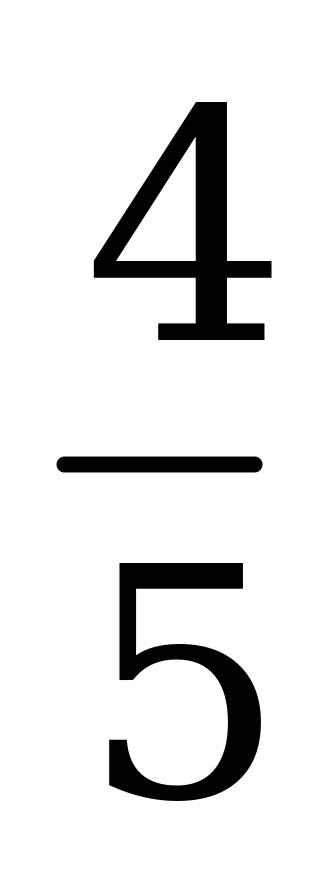 D) D) 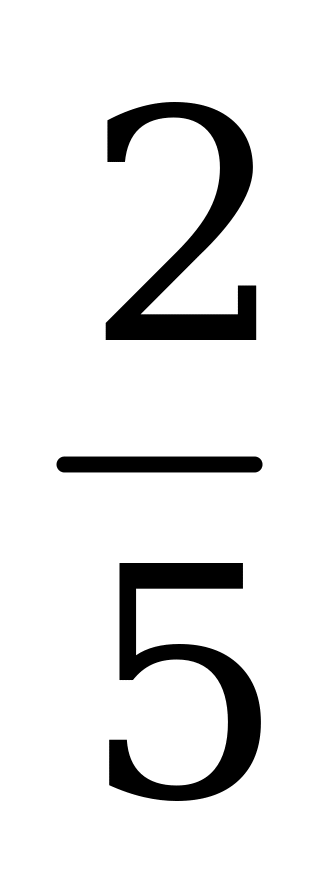 E) 1 E) 1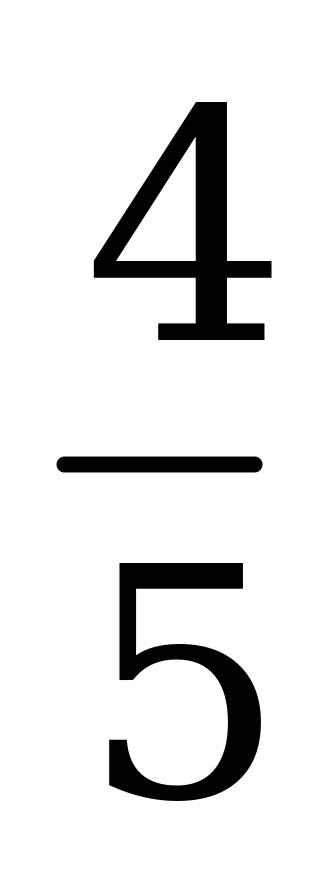 | А |
| А1.3 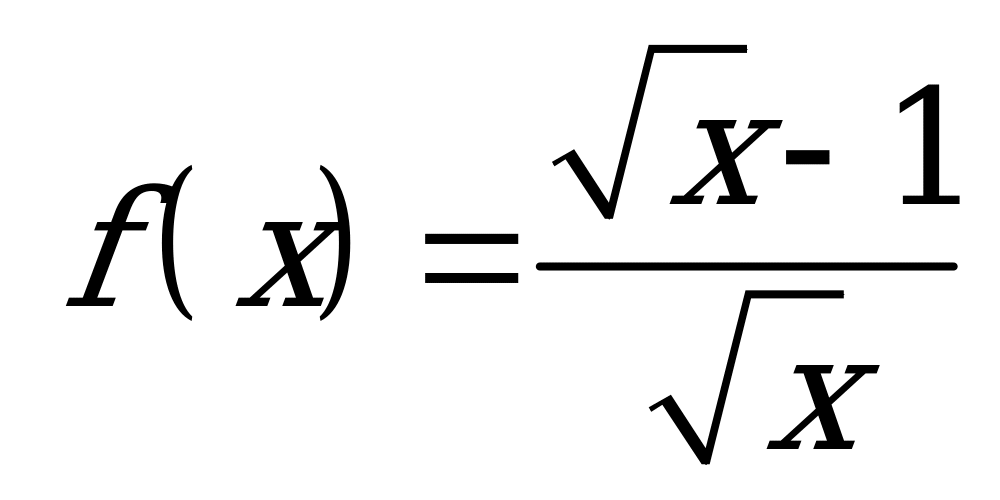 , ,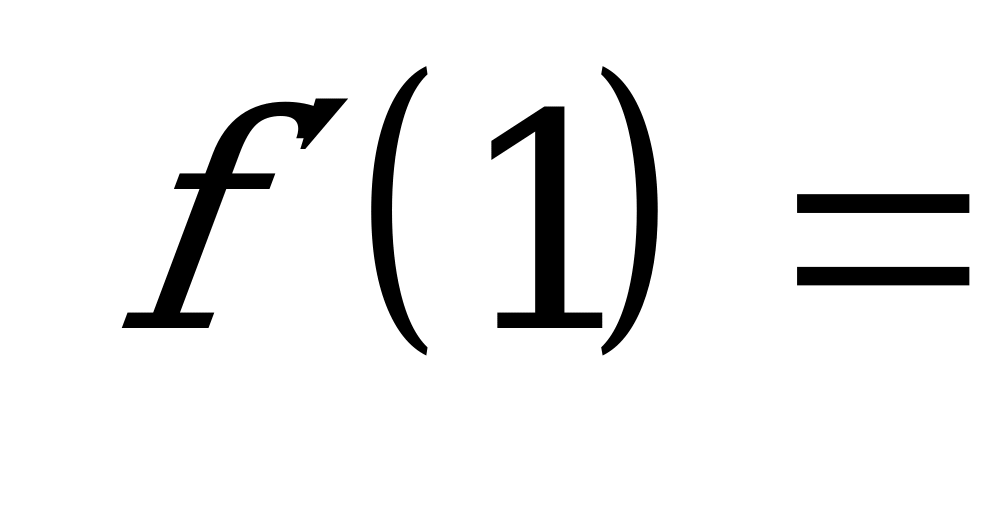 ? A) ? A)  B) 2 C) 1 D) B) 2 C) 1 D) 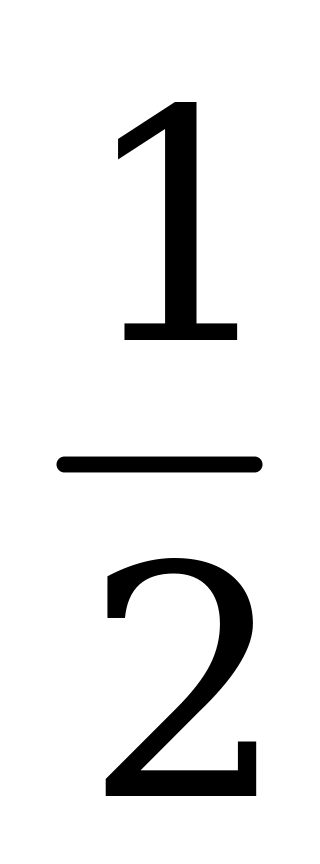 E) 3 E) 3 | Д |
| А1.4 Найдите производную функции y = sin2x + cos2x A) 2sin2x B) 0 C) 4sinx D) sin4x E) 1 | В |
| А1.5 Найти f’(), если 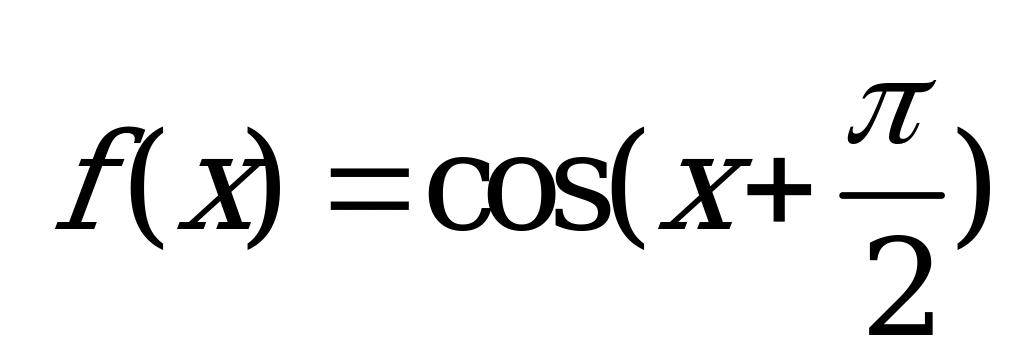 и и 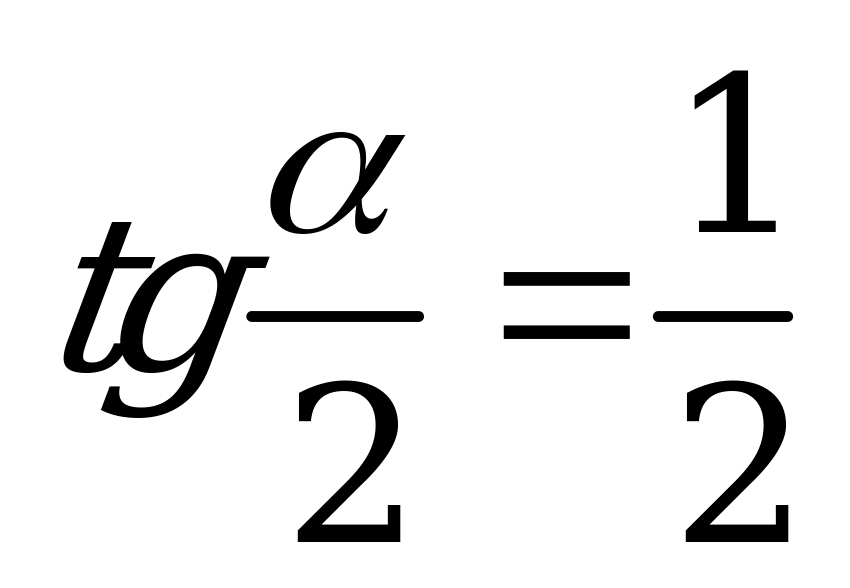 A) -0,6 B) 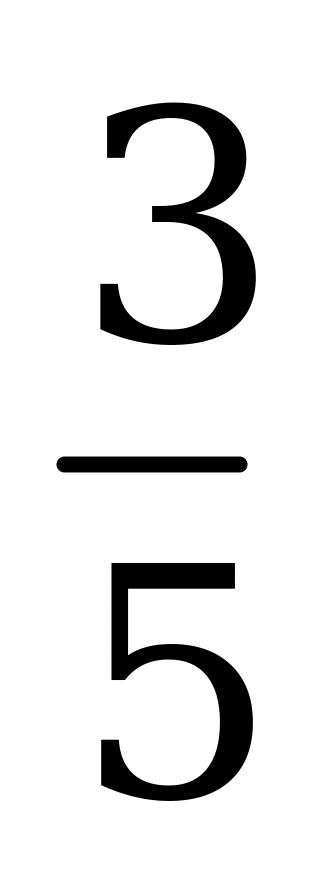 C) 0,8 D) C) 0,8 D) 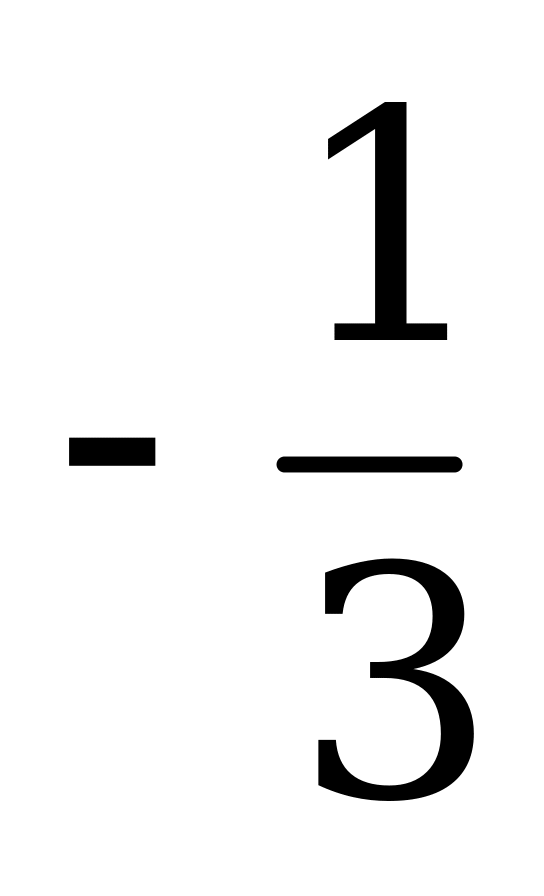 E) 0,4 E) 0,4 | А |
| А1.6 Найдите 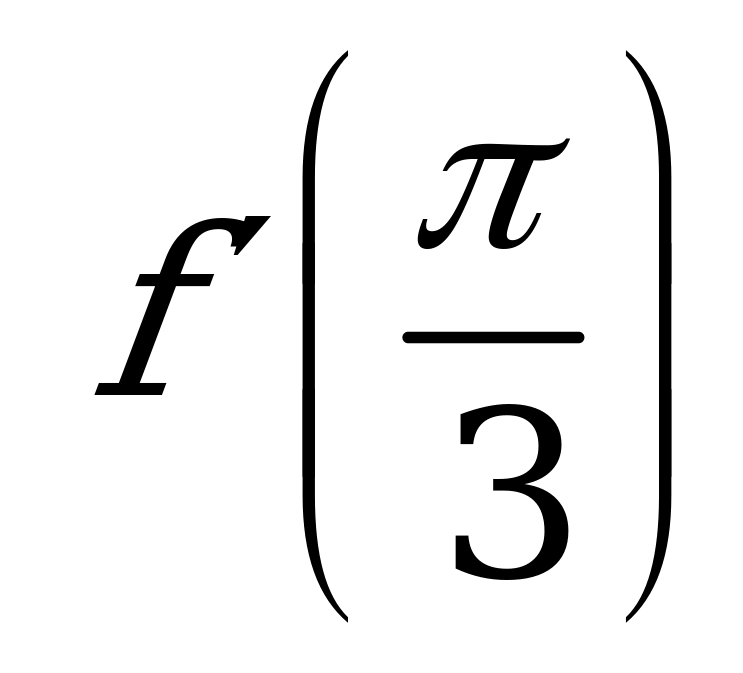 , если , если 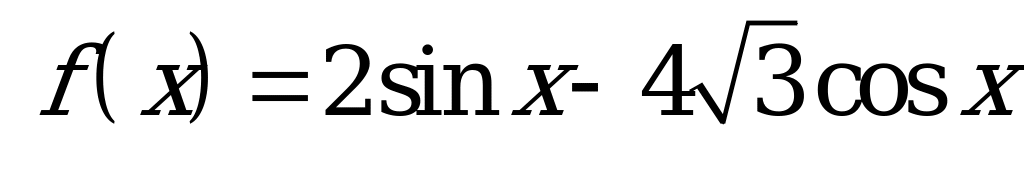 A) 7 B) -5 C) 2 + 4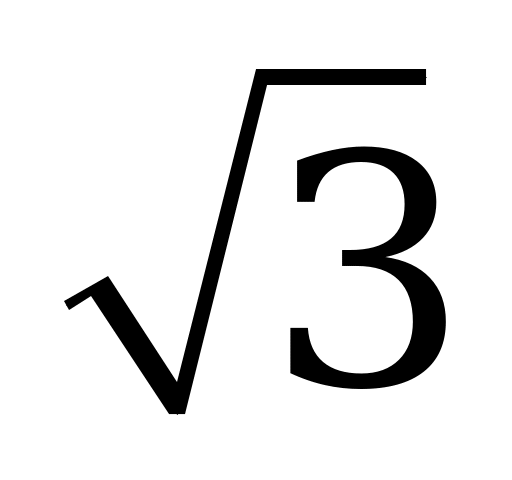 D) 2 D) 2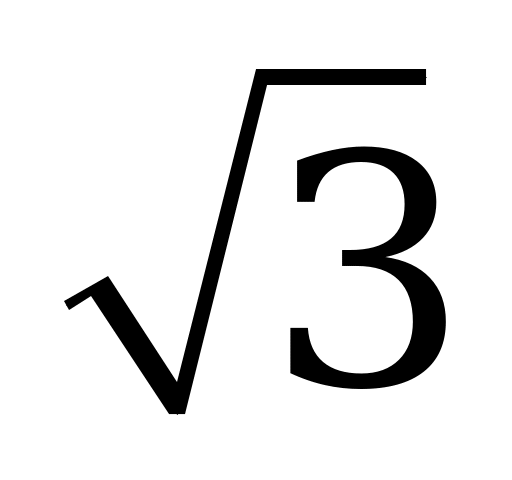 - 2 E) 5 - 2 E) 5 | А |
| А1.7 Найдите производную функции: y = - 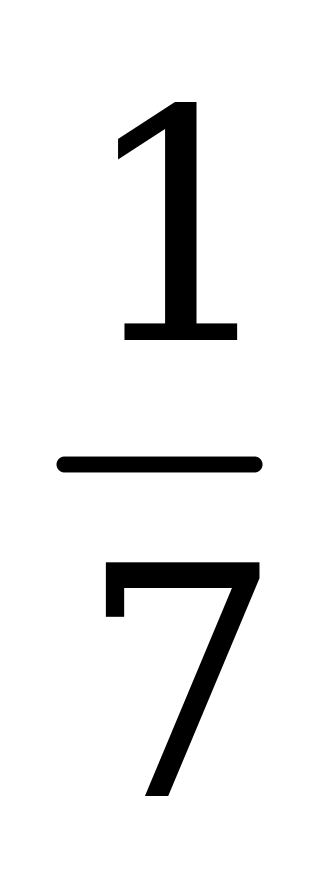 sin(7x - 5) sin(7x - 5) A) -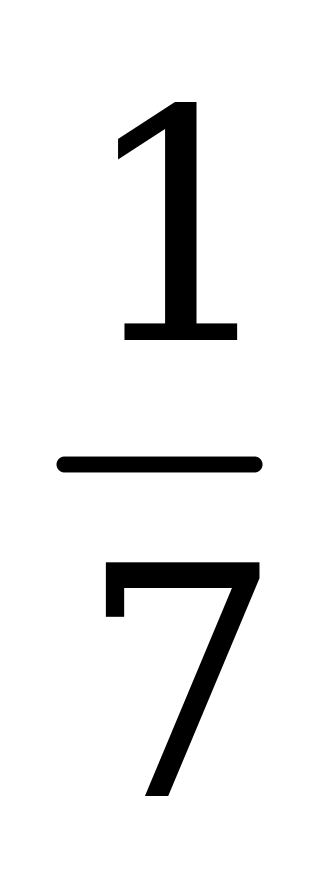 cos(7x - 5) B) -7cos(7x – 5) C) cos(7x - 5) cos(7x - 5) B) -7cos(7x – 5) C) cos(7x - 5) D) -cos(7x - 5) E) -7cos7x | Д |
| А1.8 y = 2 - cos2x. y ' = ? A) 2sin2x B) sin2x C) 4cos2x D) -sin2x E) -2sin2x | А |
| А1.9 Найдите 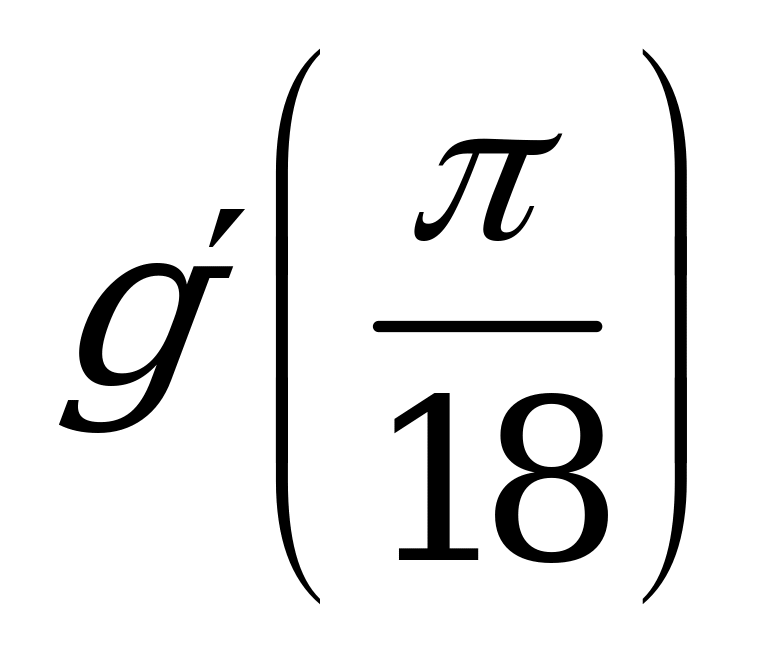 , если , если 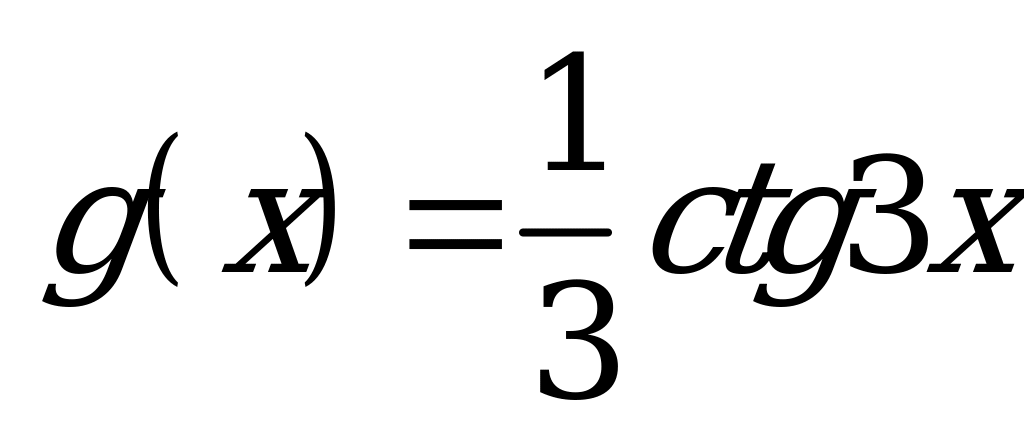 A) -2 B) 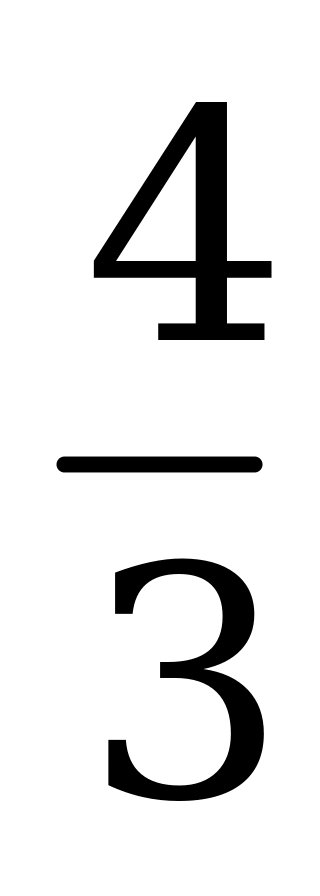 C) 4 D) - C) 4 D) -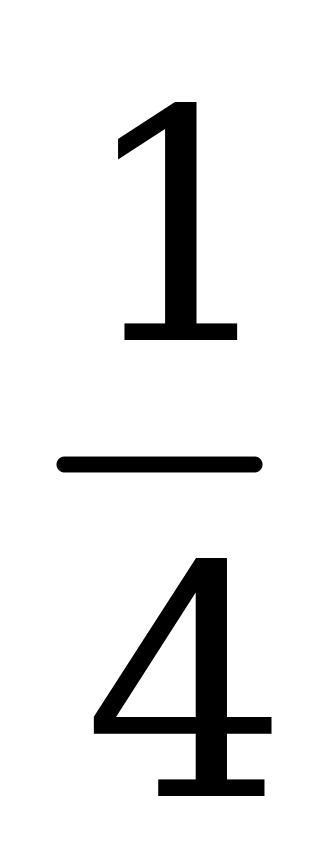 E) -4 E) -4 | Е |
| А1.10 Найдите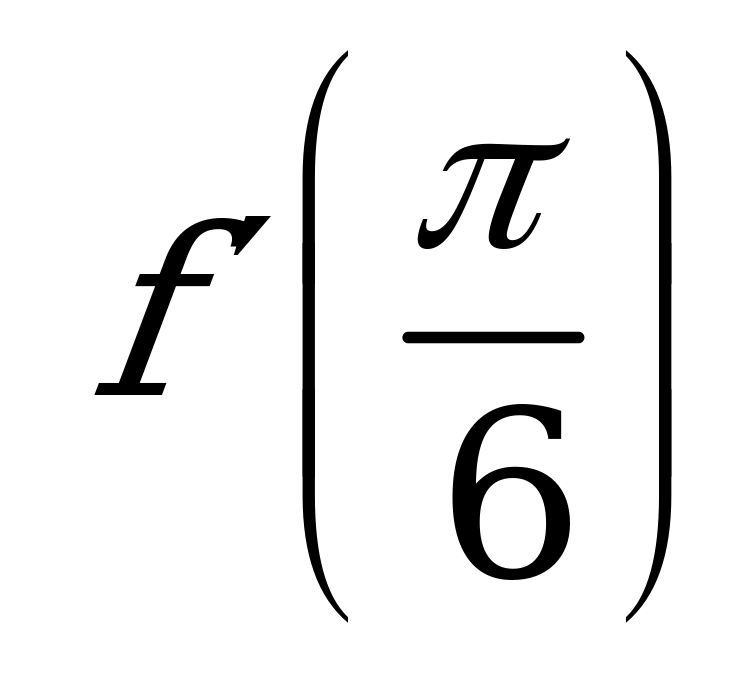 , если , если 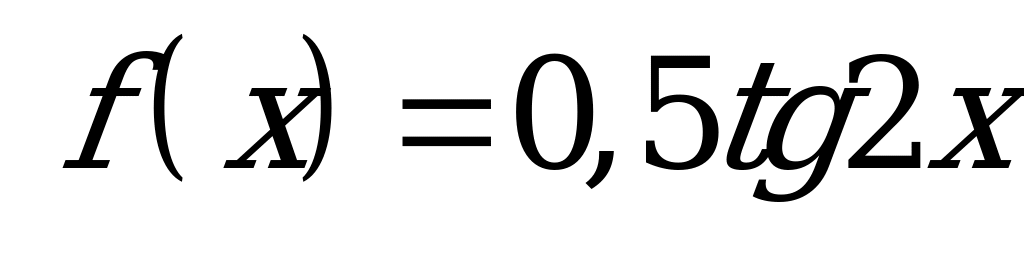 A) 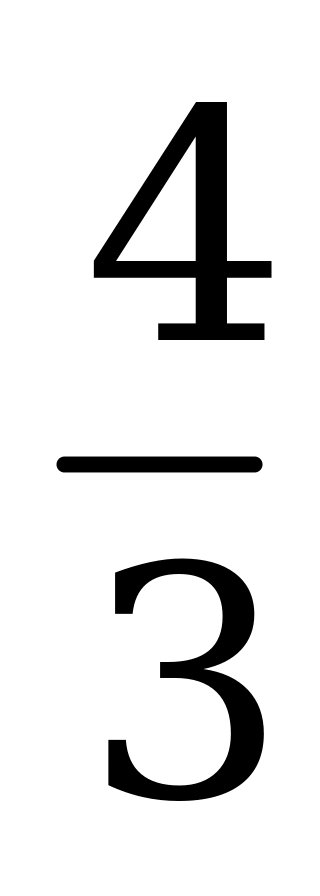 B) - B) -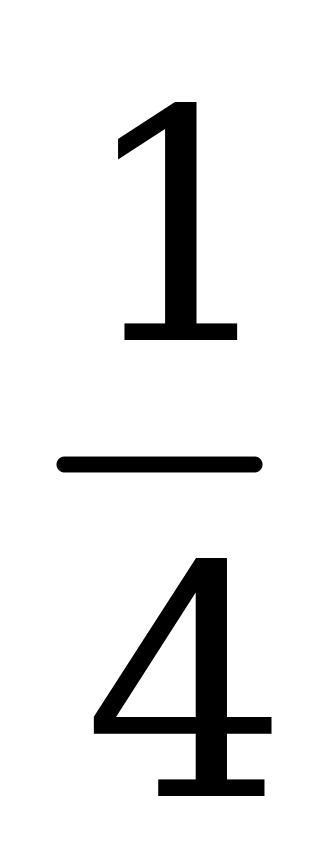 C) 4 D) 2 E) - C) 4 D) 2 E) -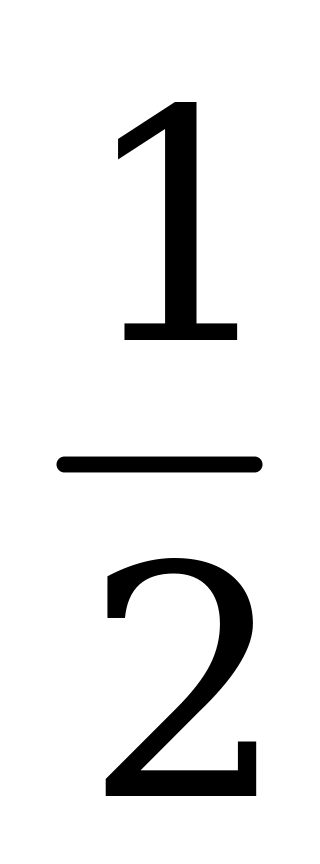 | С |
| А2. Производная сложной функции | Ответы |
| А2.1 Найдите 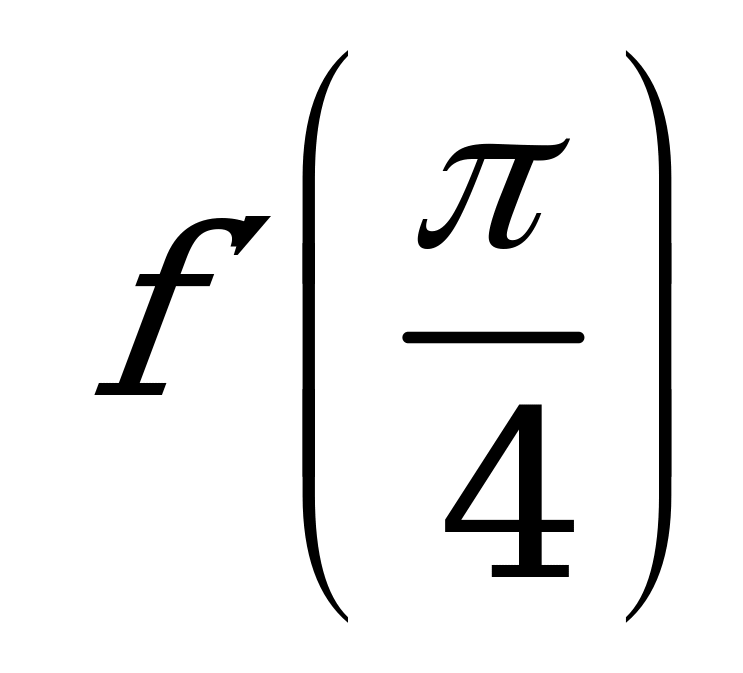 , если , если 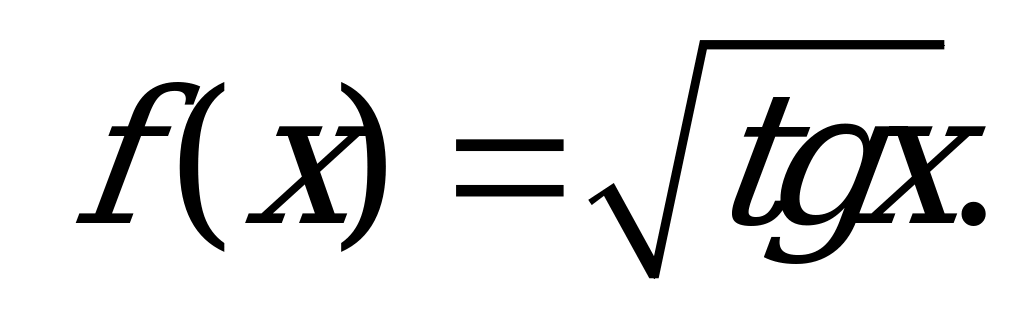 A) 1 B) 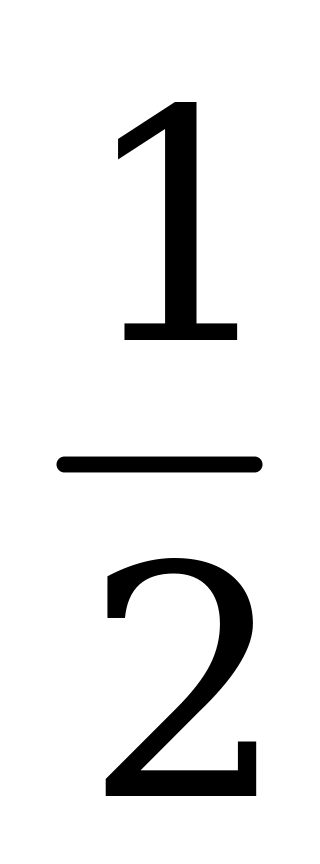 C) C) 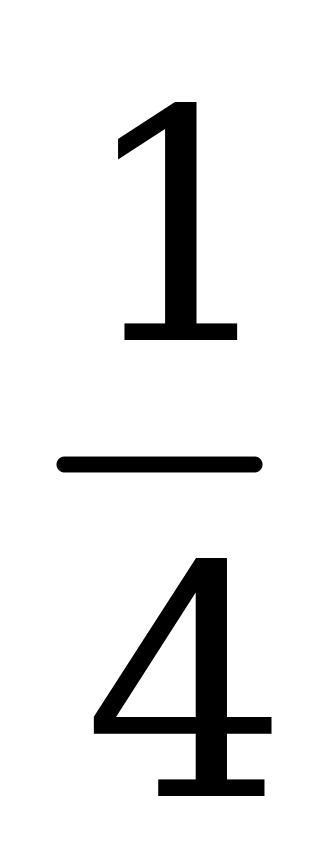 D) D) 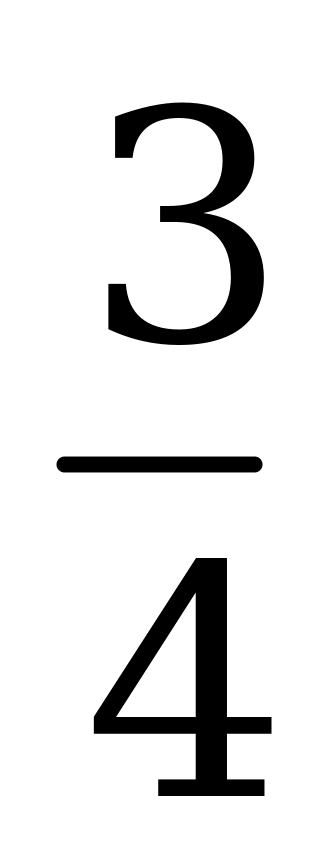 E) E) 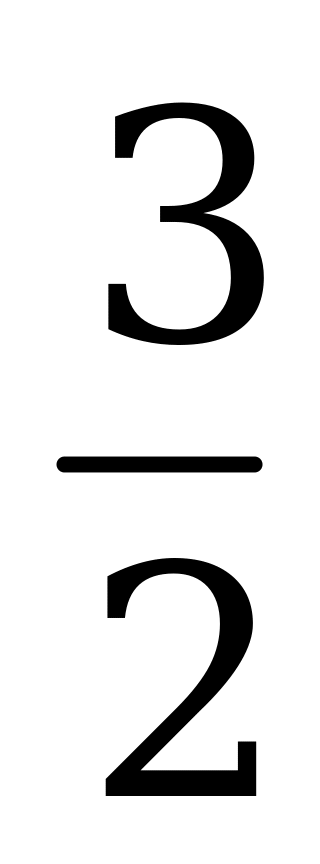 | А |
| А2.2 Найти 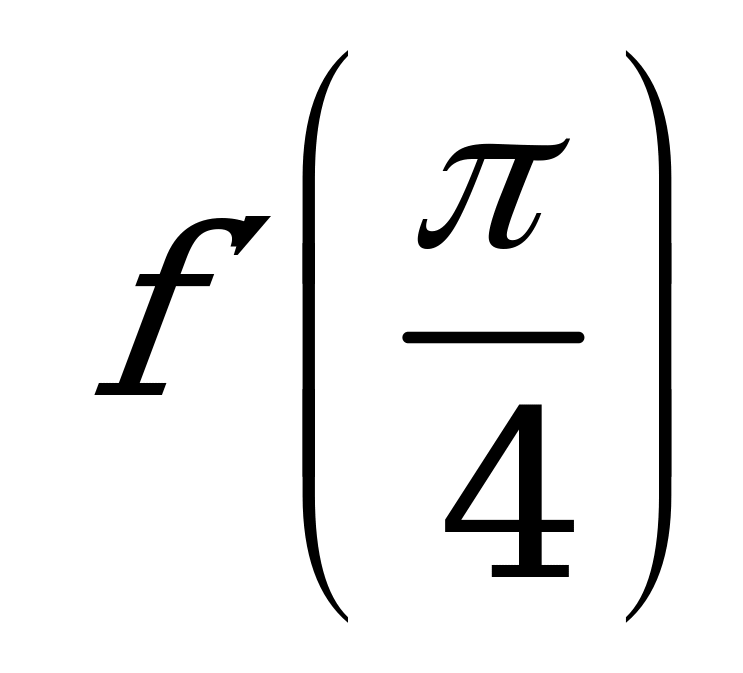 , если , если 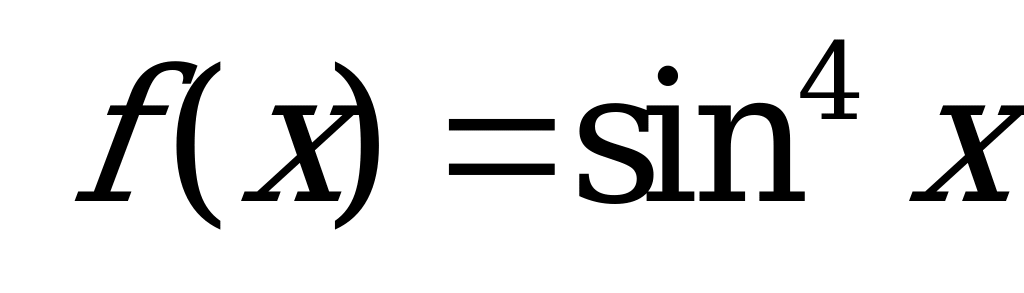 . . A) 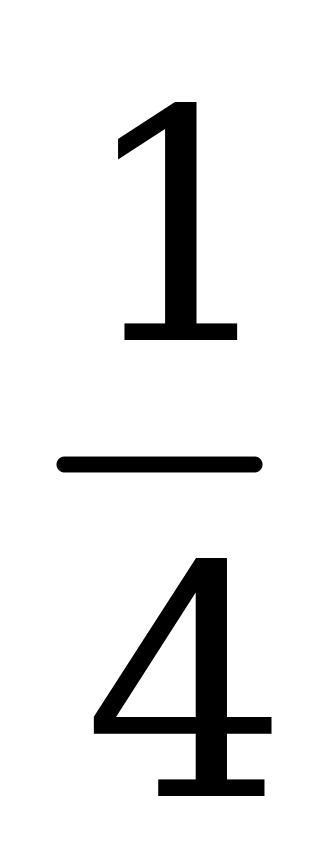 B) 1 C) B) 1 C) 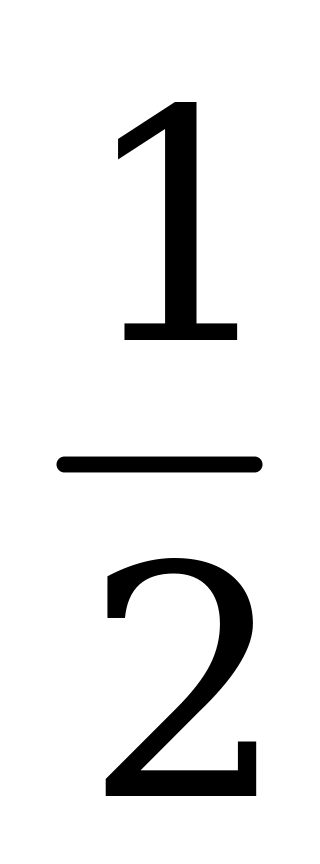 D) D) 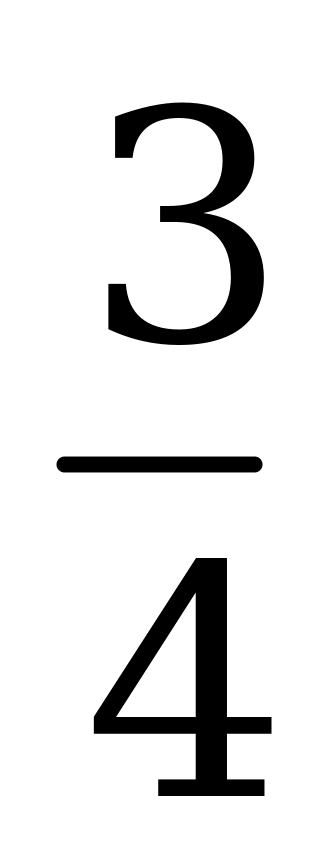 E) E) 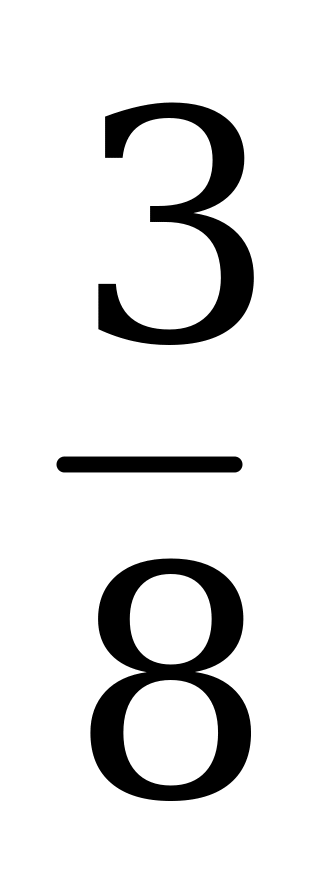 | В |
| А2.3 Найдите 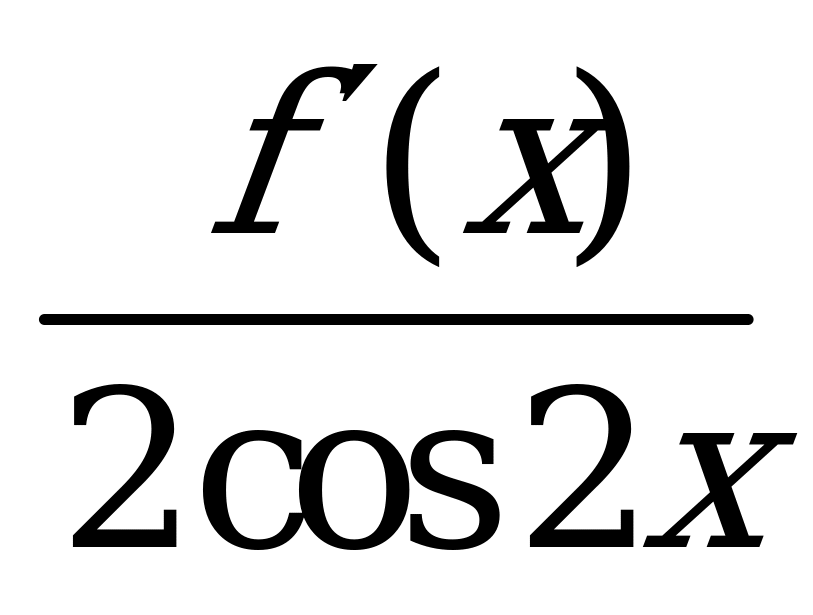 , если f(x) = sin22x , если f(x) = sin22x A) sin2x B) cos2x C) -sin2x D) -cos2x E) 2sin2x | E |
| А2.4 Найдите 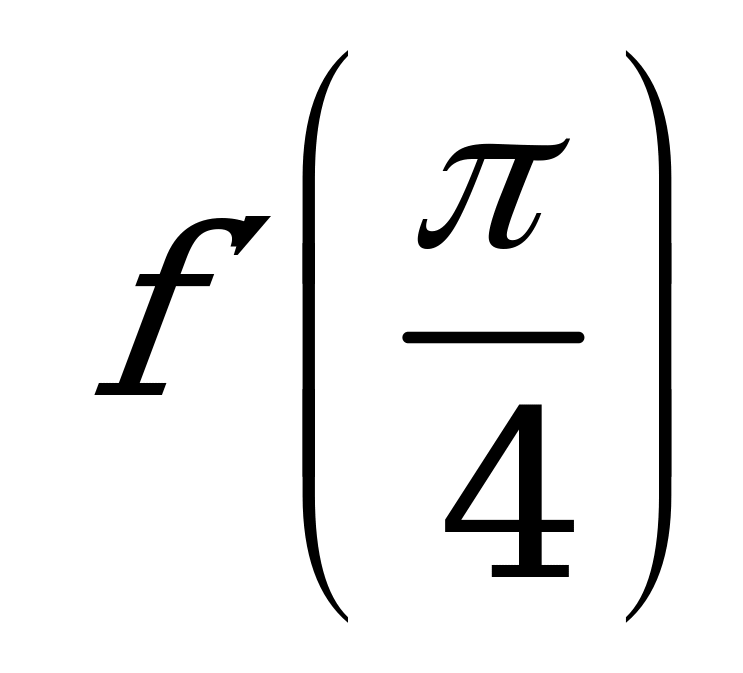 , если , если 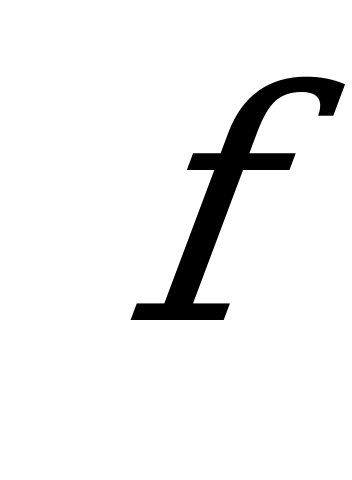 (x)= (x)=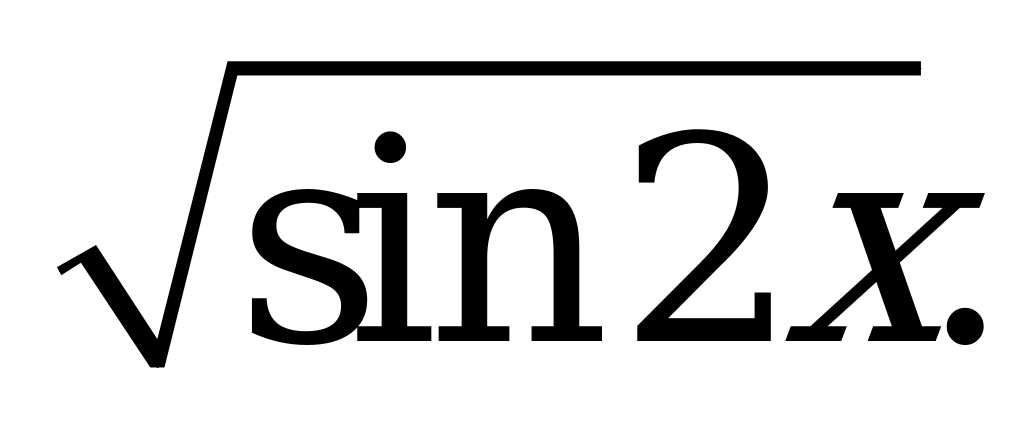 A) 0 B) 1 C) 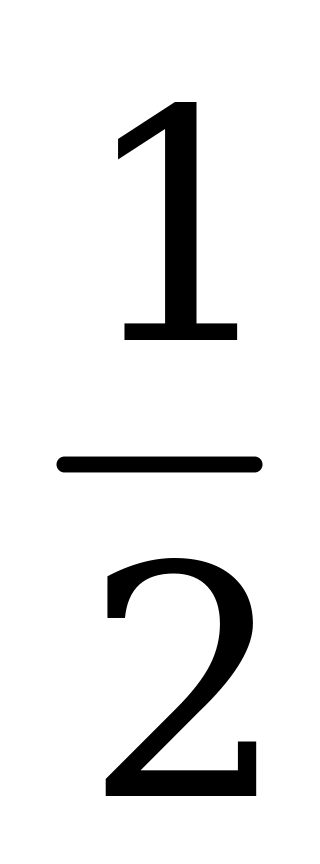 D) D) 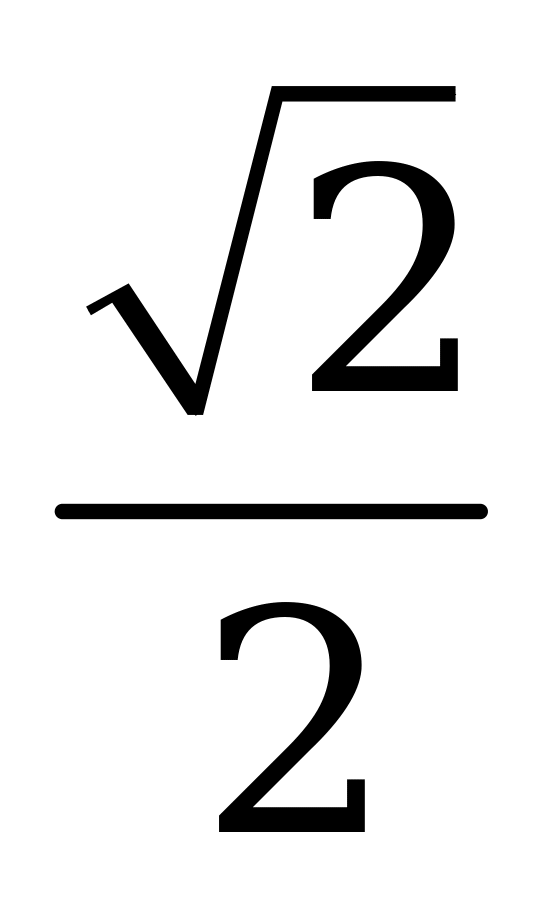 E) -1 E) -1 | А |
| А2.5 y=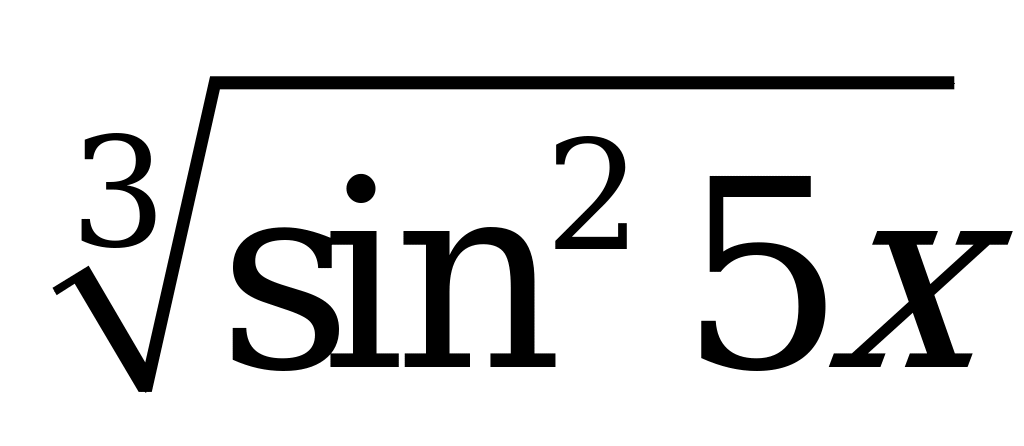 y( y(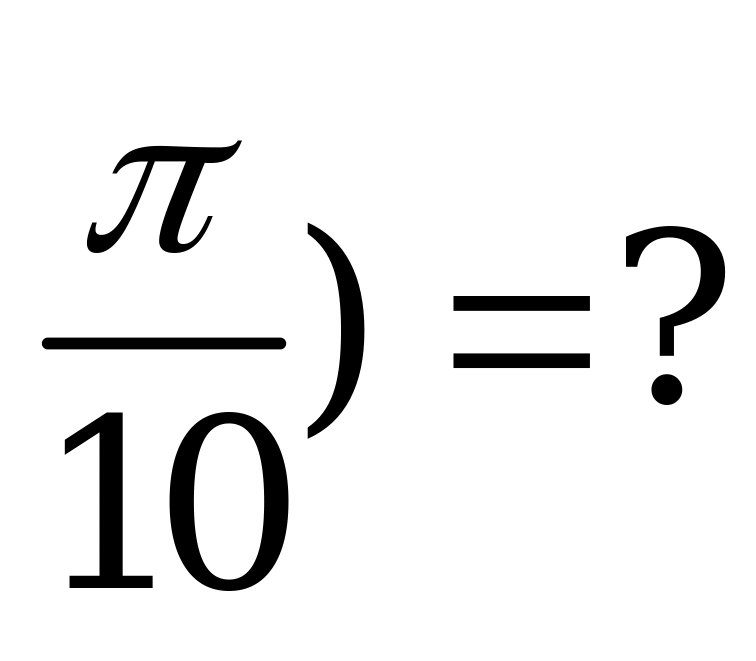 A) 3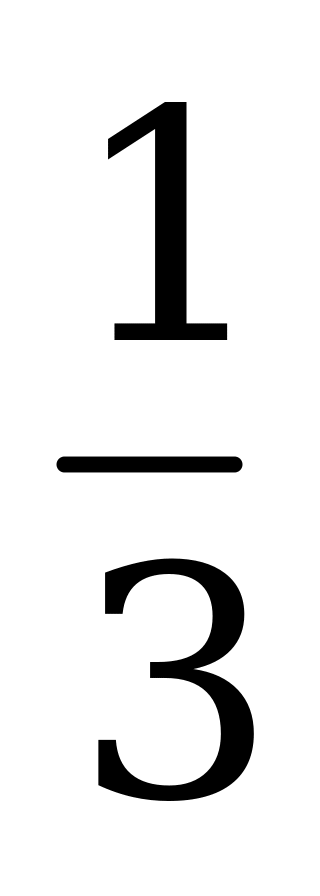 B) 1 B) 1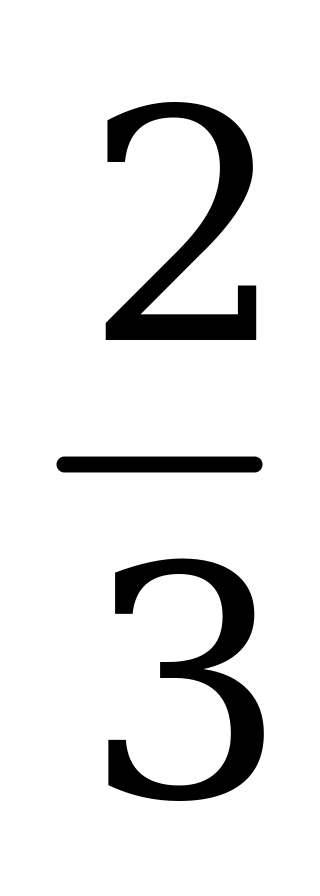 C) 2 D) 0 E) 2 C) 2 D) 0 E) 2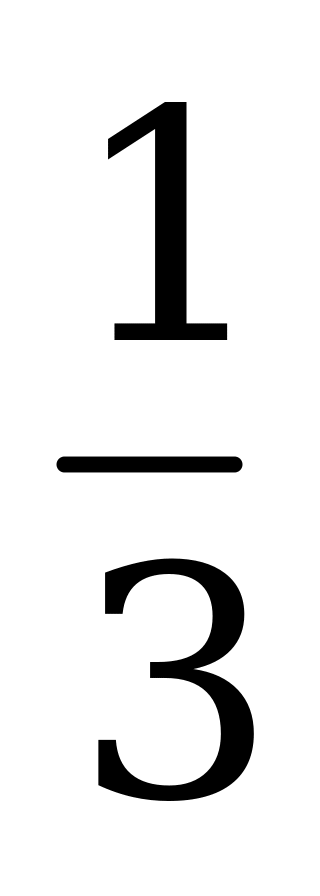 | Д |
| А2.6 Найдите производную функции: 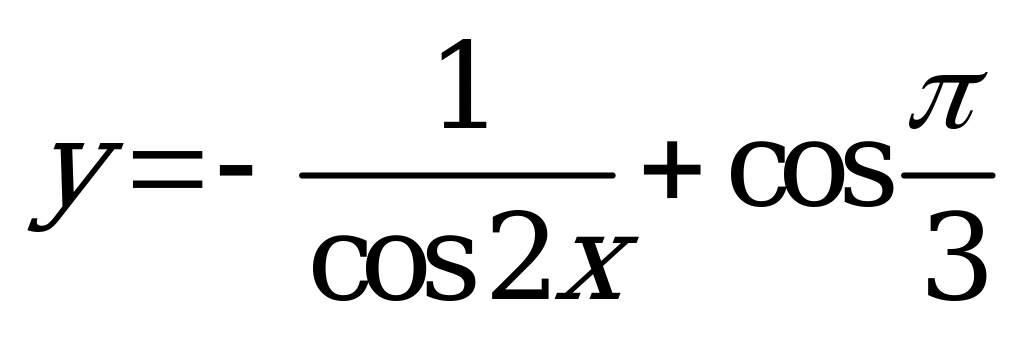 в точке в точке 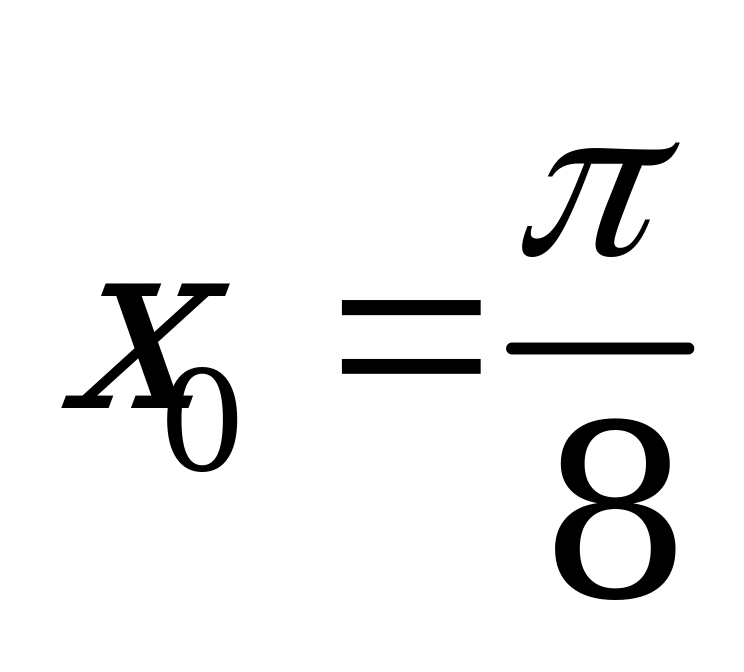 . A) . A) 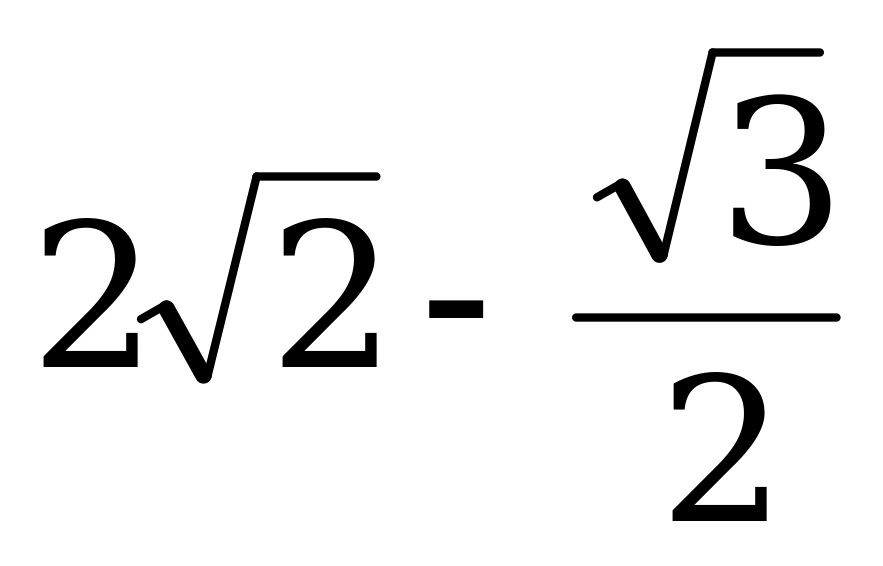 B) 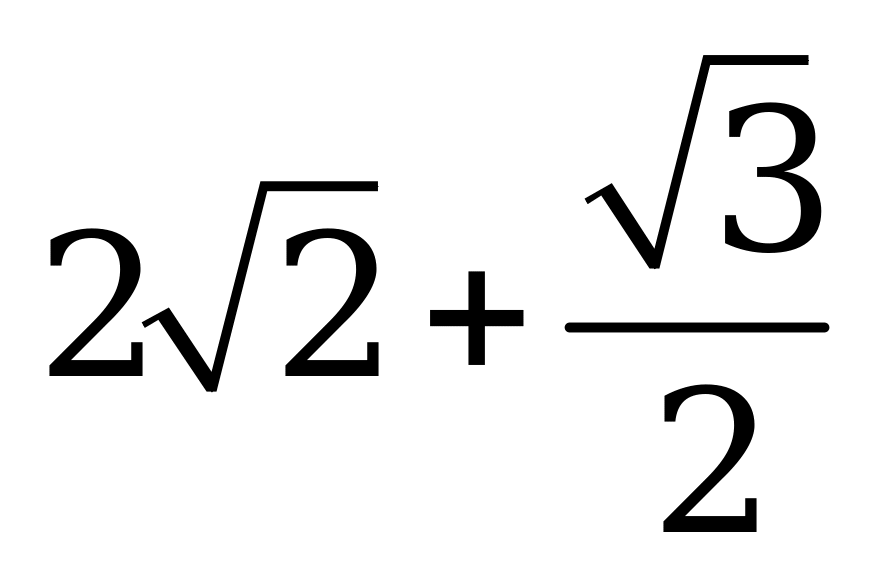 C) C) 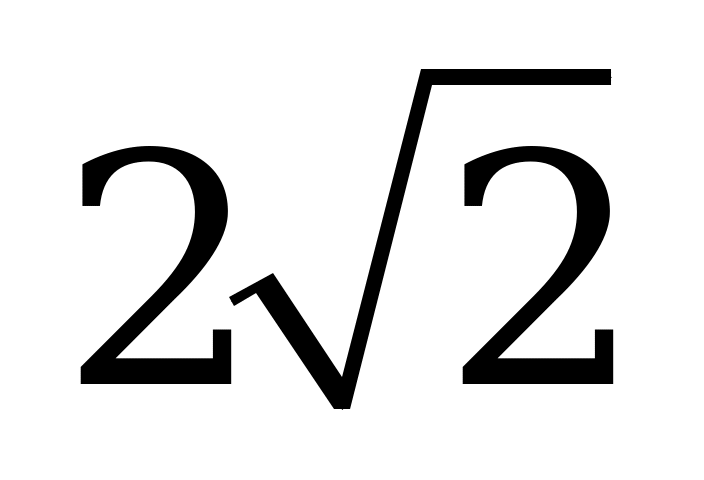 D) - D) -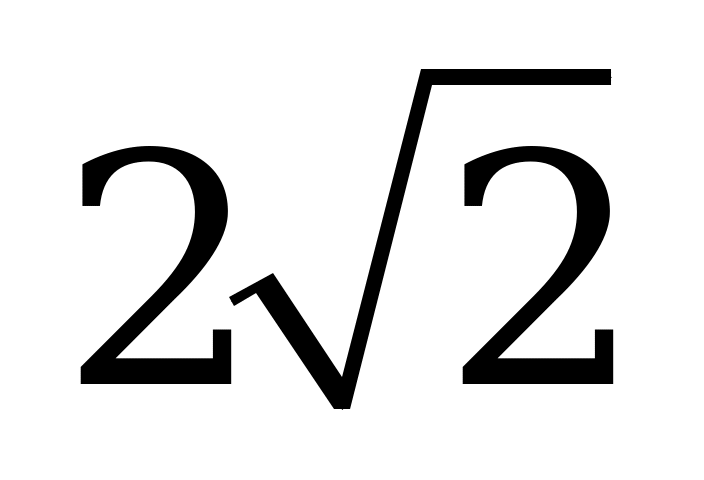 E) E) 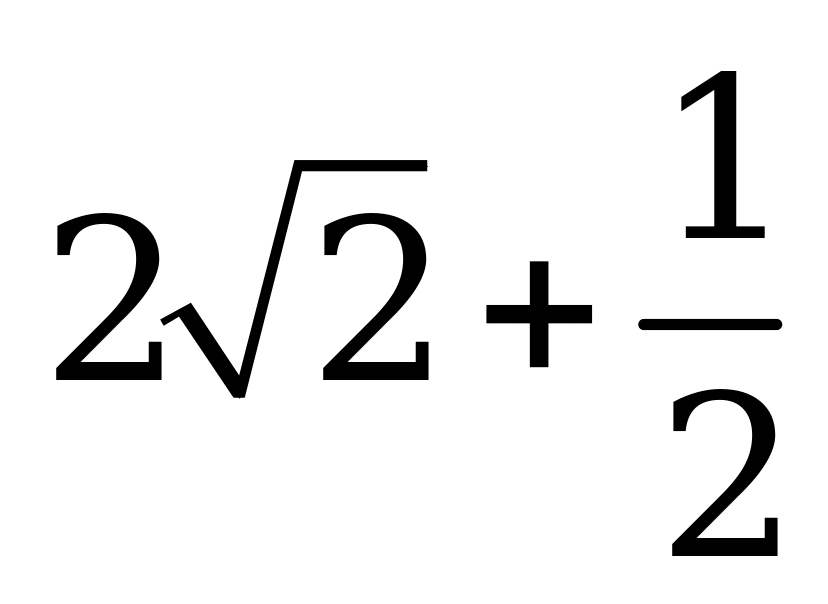 | Д |
| А2.7 Вычислите 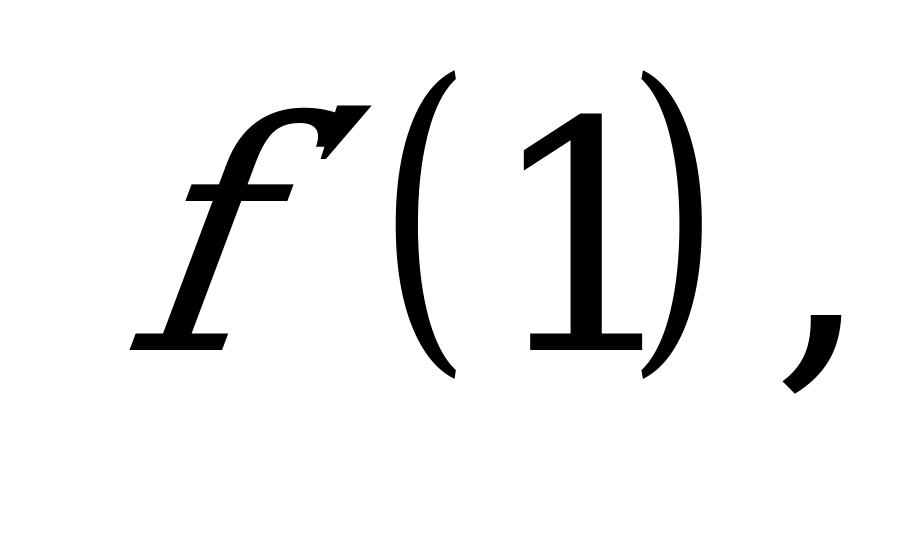 если если 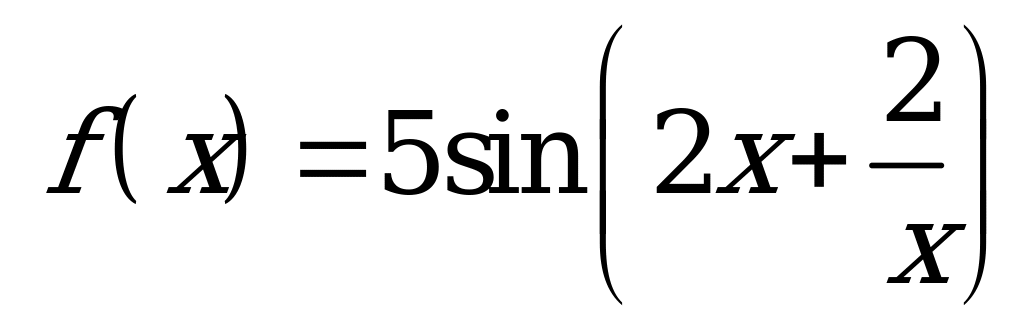 A) 5 B) 0 C) 2,5 D) - 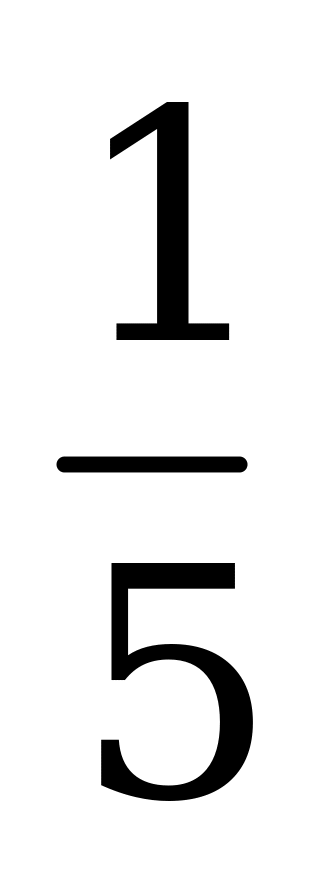 E) E)  | В |
| А2.8 Найдите производную функции 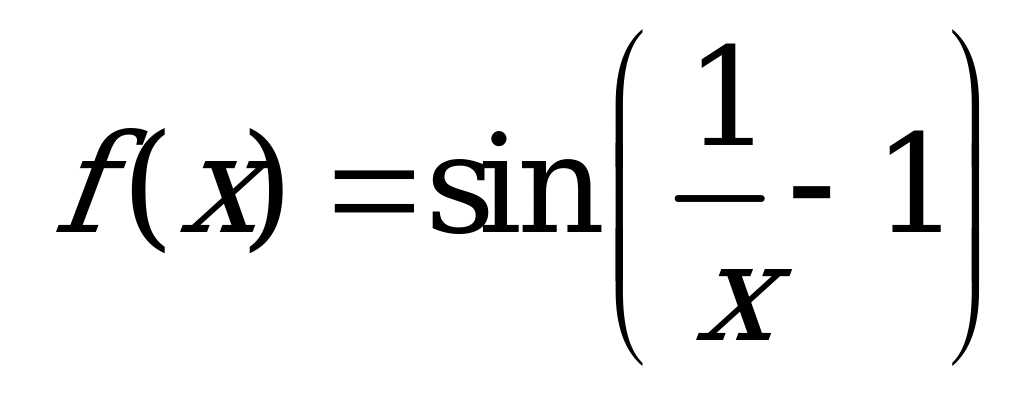 . . A) 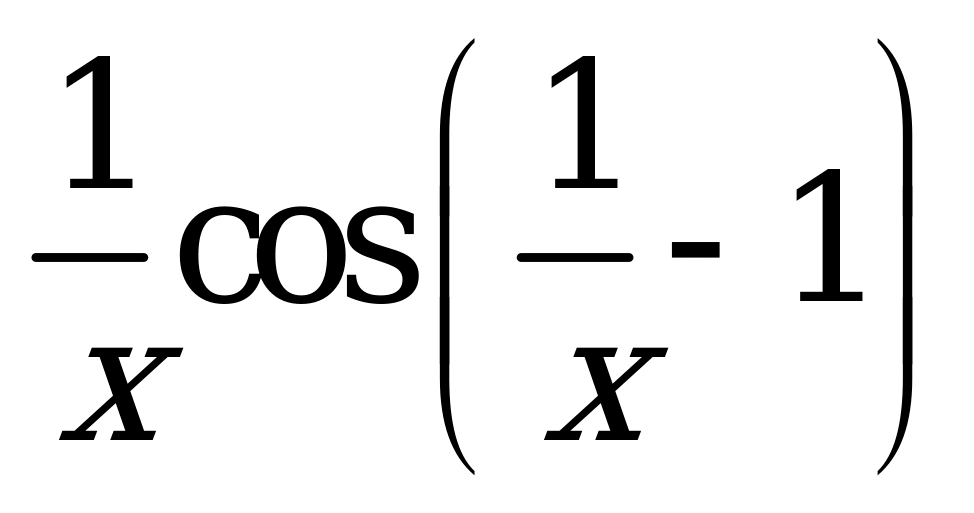 B) B) 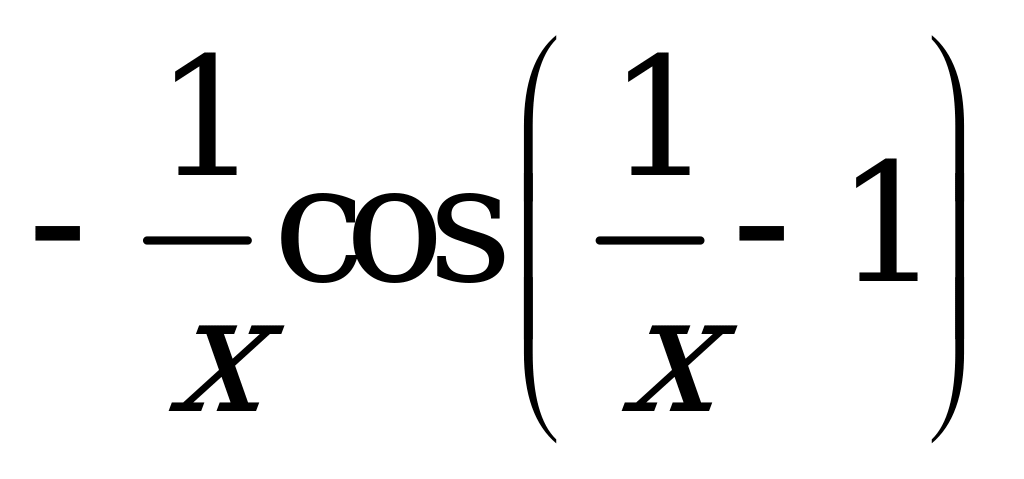 C) C) 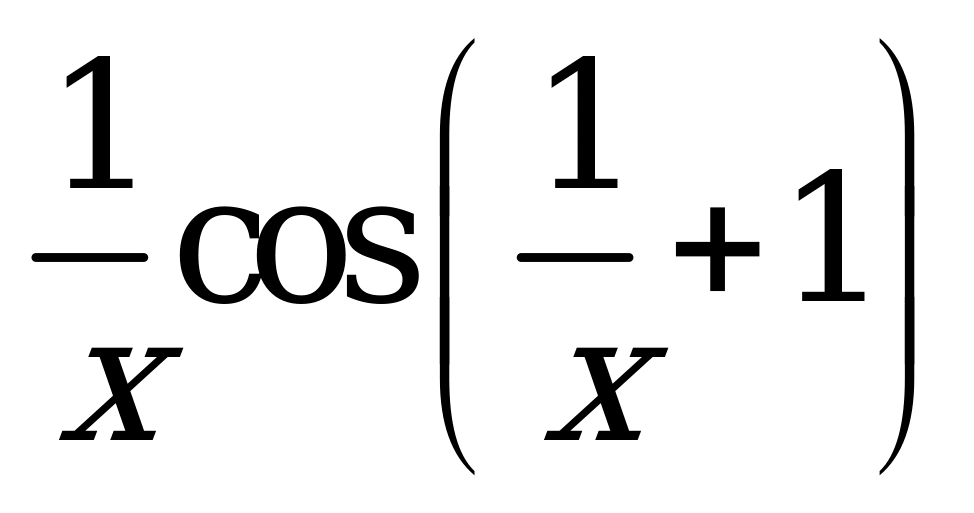 D) D) 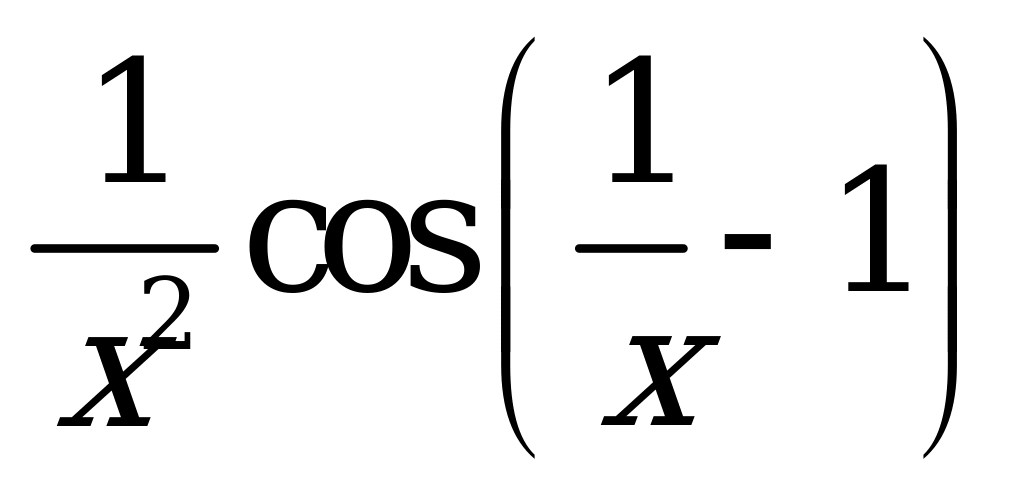 E) - E) -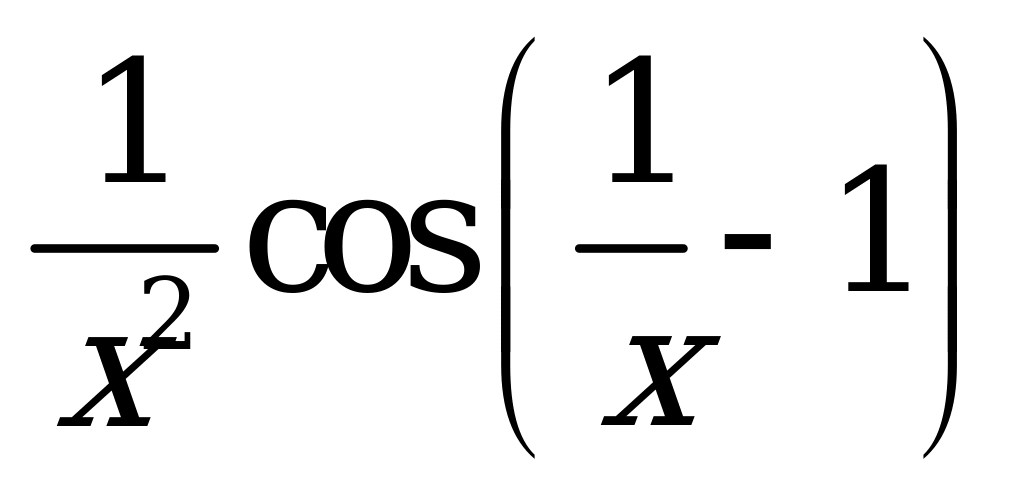 | Е |
| А2.9 Найдите 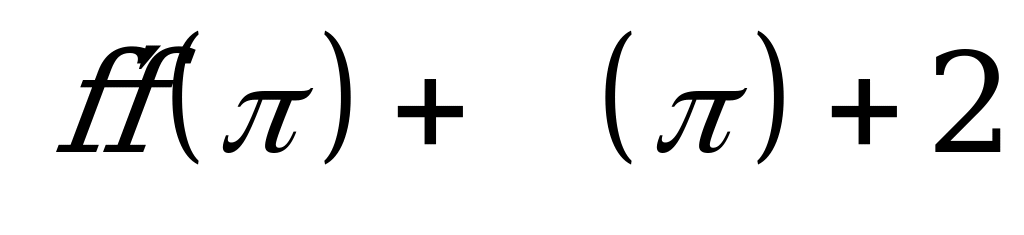 , если ƒ(x)=x·sin2x. , если ƒ(x)=x·sin2x. A) 2 B) 2 C) 2+2 D) 2-2 Е) 4 | С |
| А2.10 Найдите 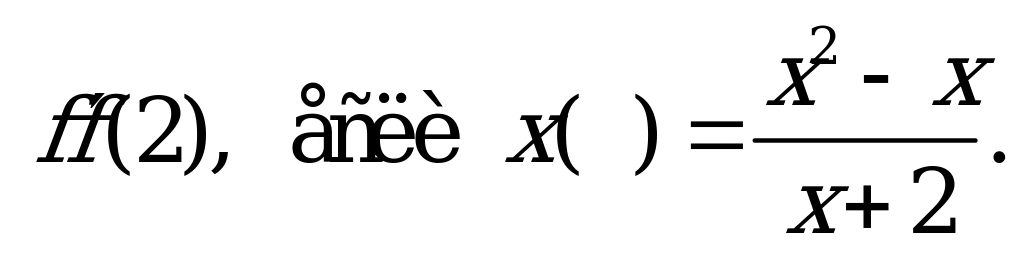 A) 0,625 B) 0,5 C) 0,25 D) -0,5 E) 1 | А |
| А3. Критические точки, интервалы монотонности функции | Ответы |
| А3.1 Найдите все интервалы убывания функции: 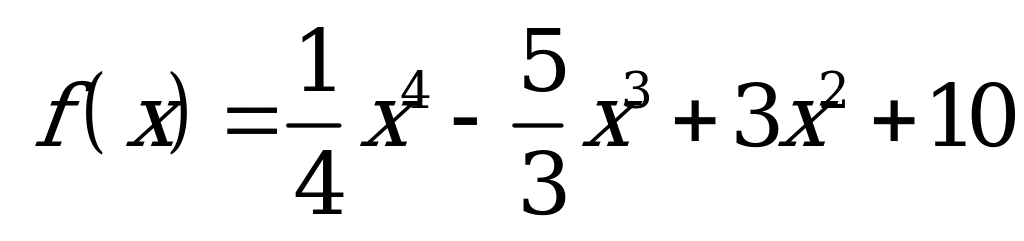 A) (2; 3) B) (- ; 0] и [2; 3] C) (- ; 0] и [2; 3] C) (- ; 3) ; 3) D) (- ; 0) и (3; ; 0) и (3; ) E) (- ) E) (- ; 0) и (2; ; 0) и (2;  ) ) | В |
| А3.2 Найдите промежутки возрастания функции 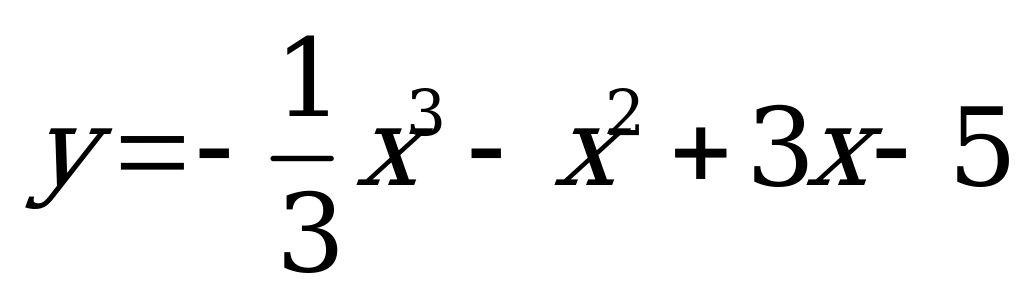 . A) (- . A) (- ; -1] и [3; ; -1] и [3;  ) ) B) [-1; 3] C) [-3; 1] D) [1; 3] E) (- ; -3] и [1; ; -3] и [1;  ) ) | С |
| А3.3 Чему равна сумма всех целых значений аргумента функции f(x)=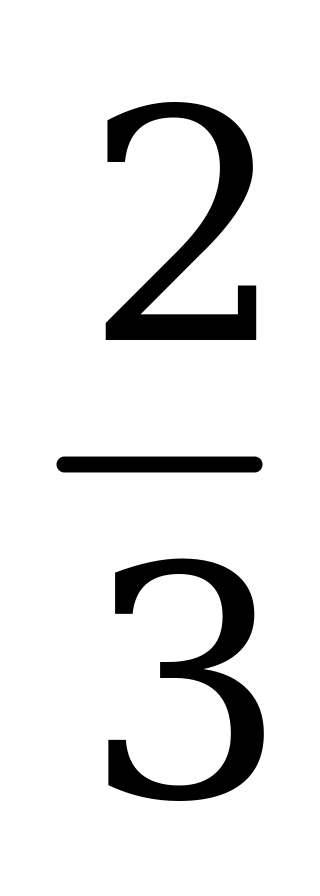 x3 - 4x2 + 3, при которых эта функция убывает? A) 9 B) 8 C) 10 D) 7 E) 11 x3 - 4x2 + 3, при которых эта функция убывает? A) 9 B) 8 C) 10 D) 7 E) 11 | С |
| А3.4 Найти длину отрезка, на котором функция f(x) = -2x3 + 15x2 + 12 возрастает. A) 5 B) 4 C) 6 D) 4,5 E) определить нельзя | А |
| А3.5 Найдите суммарную длину промежутков возрастания функции y = f(x), если ее производная равна f (x) = x(1 – x)(x2 – 7x + 10) A) 1 B) 3 C) 4 D) 6 E) 8 | С |
| А3.6 Все значения аргумента функции f(x) = 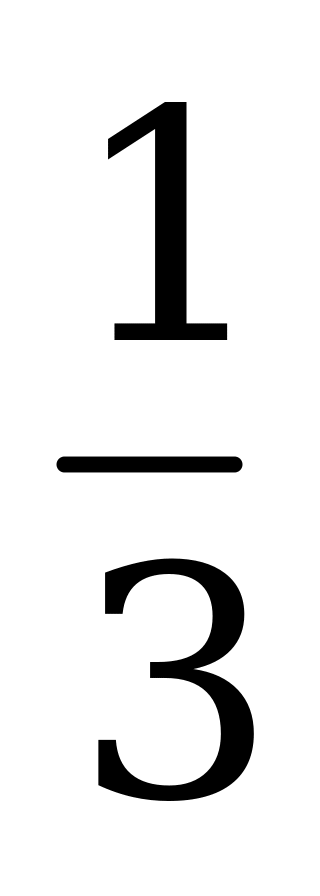 x3 + 3x2, для которых эта функция убывает, отложены на оси ОХ. Какова длина получившегося отрезка? x3 + 3x2, для которых эта функция убывает, отложены на оси ОХ. Какова длина получившегося отрезка? A) 4 B) 5 C) 6 D) 3 E) 7 | С |
| А3.7 Найдите значение функции f(x) = x3 + 2,5x2 - 2x в точке максимума. A) -8 B) 6 C) 10,5 D) -12 E) 14 | В |
| А3.8 Найдите сумму значений функции f(x) = 0,6x5 – 2x3 – 1 в точках максимума и минимума. A) -3 B) -2 C) -1 D) 1 E) 2 | В |
| А3.9 Найдите разность между наименьшим и наибольшим значениями функции 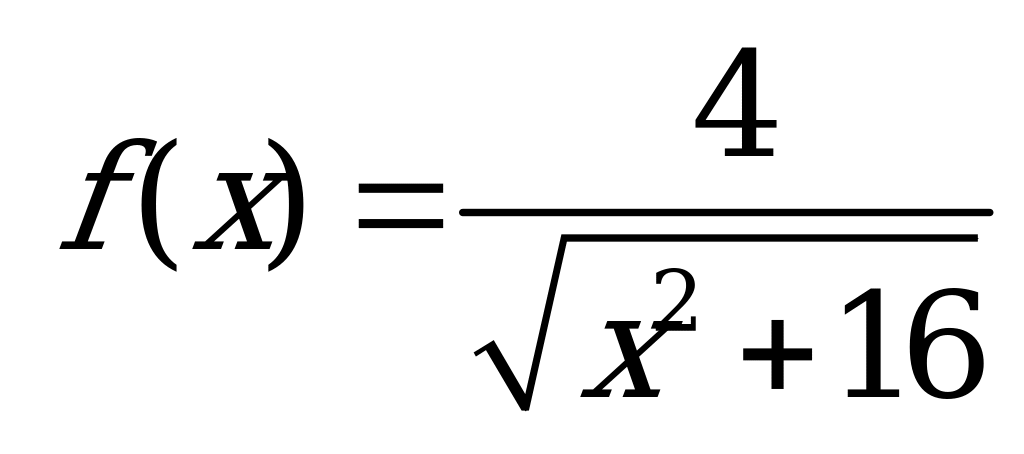 , заданной на отрезке [-3; 3]. , заданной на отрезке [-3; 3]. A) -0,2 B) 0,2 C) 0,4 D) -0,8 E) 0,8 | А |
| А3.10 Найдите сумму значений функции y = 3x5 – 5x3 – 3 в точках экстремума. A) -9 B) -6 C) -8 D) -4 E) -2 | В |
| А4. Наибольшее, наименьшее значение функции | Ответы |
| А4.1 Найти наибольшее значение функции f(x) = 3x2 - 4x - 4 на отрезке [0; 3]. A) 10 B) 20 C) 11 D) 16 E) 18 | С |
| А4.2 Найдите наибольшее значение функции 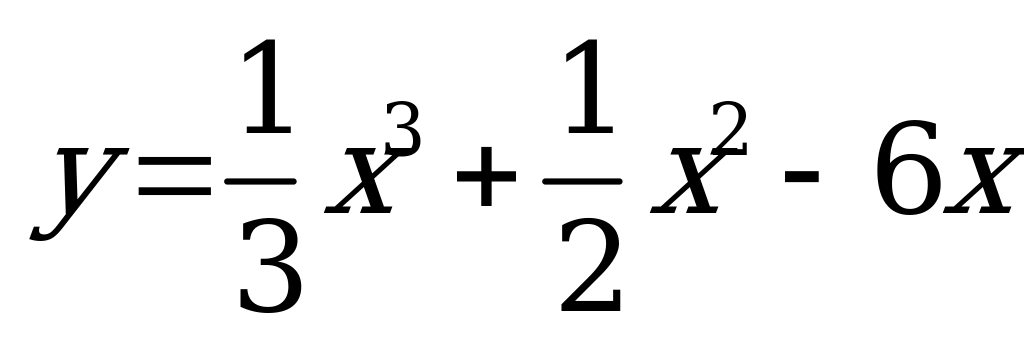 на отрезке [-1; 3]. на отрезке [-1; 3]. A) 6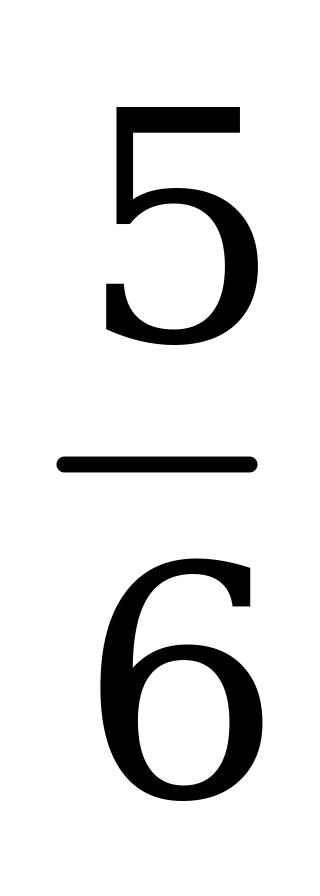 B) 6 B) 6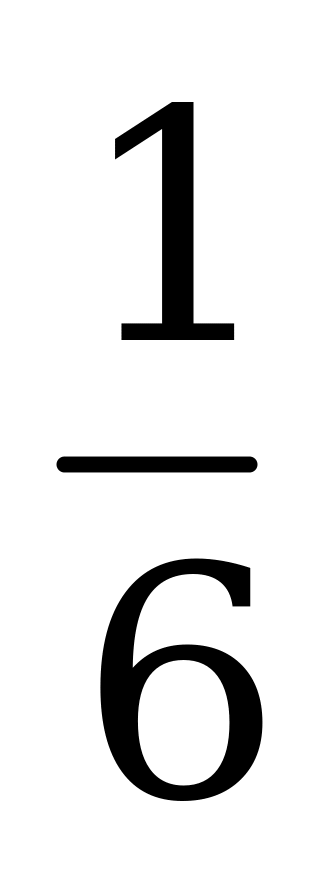 C) 6 D) 6,5 E) 6 C) 6 D) 6,5 E) 6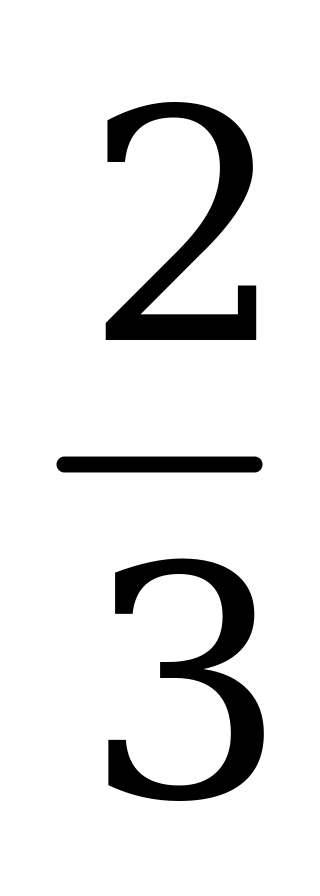 | В |
| А4.3 Чему равна разность между наибольшим и наименьшим значениями функции f(x) = x3 + 2x - 5 на отрезке [-1; 1] ? A) -6 B) 6 C) -5 D) 5 E) 4 | В |
| А4.4 Найдите наибольшее значение функции y = -2x2 + 5x – 3. A) 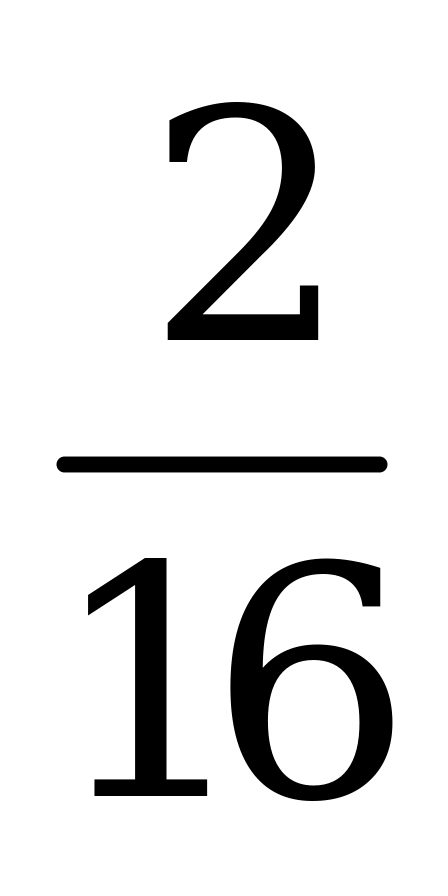 B) B) 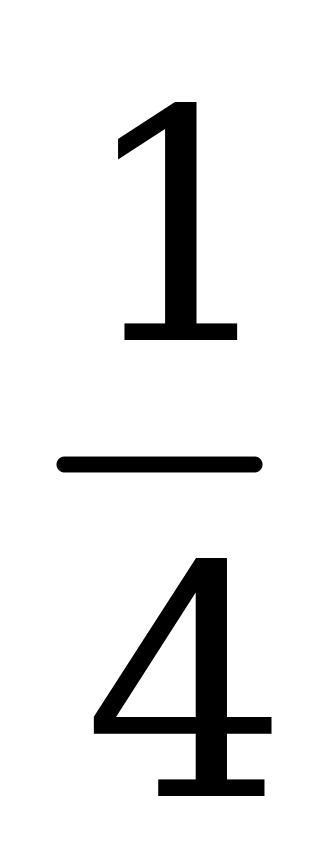 C) 5 D) -3 E) C) 5 D) -3 E) 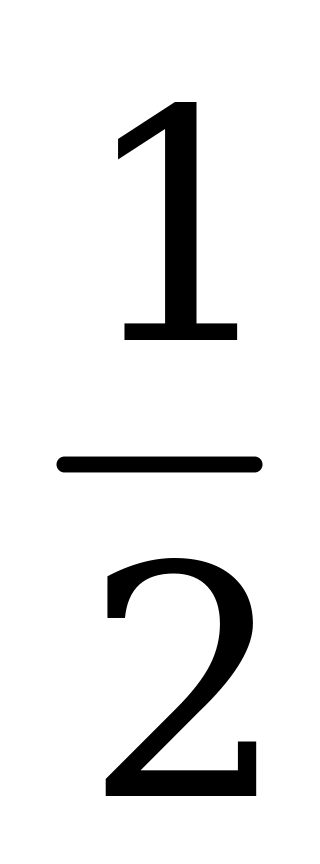 | А |
| А4.5 Найдите наименьшее значение функции y = 2x3 + 3x2 - 12x на отрезке [0; 2]. A) 0 B) -2 C) -5 D) -7 E) -8 | Д |
| А4.6 Найдите разность между наибольшим и наименьшим значениями функции y = x3 - 3x2 + 1, заданной на отрезке [-1;4]. A) 20 B) 14 C) 15 D) 18 E) 16 | А |
| А4.7 Найдите наименьшее значение функции 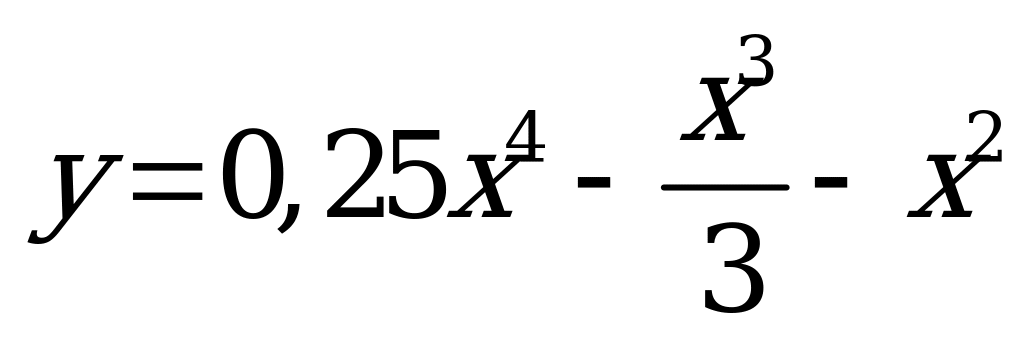 на луче [-2,5; на луче [-2,5;  ). ). A) -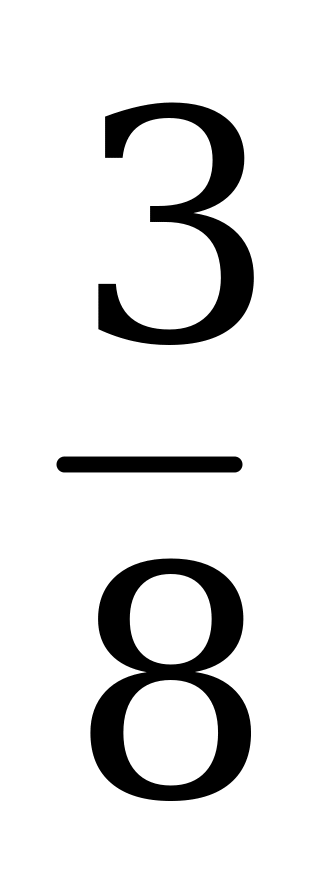 B) B) 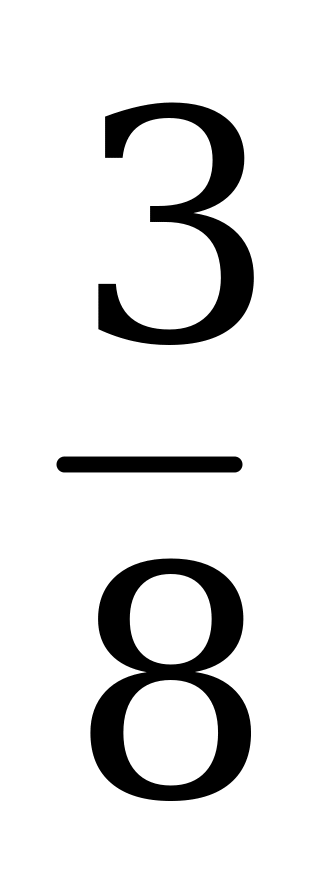 C) C) 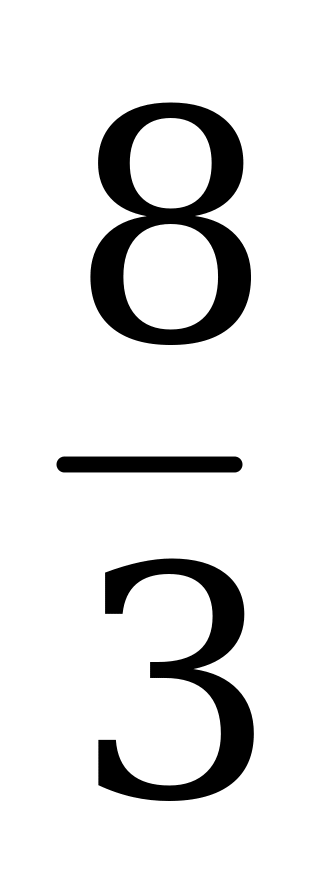 D) - D) -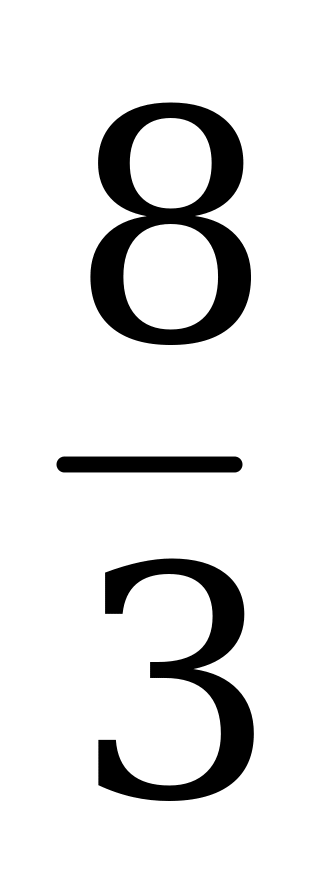 E) найти нельзя E) найти нельзя | Д |
| А4.8 Найдите наибольшее значение функции 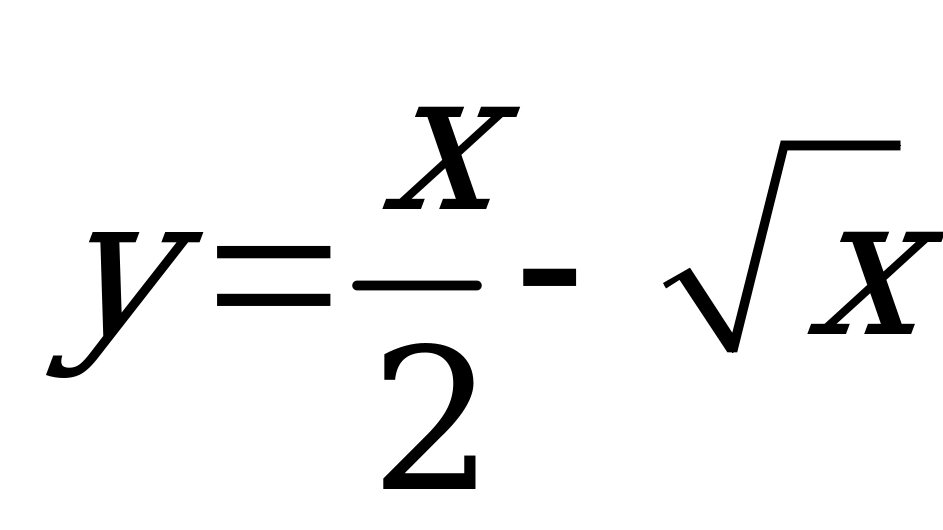 на отрезке [0; 16]. A) 4 B) 8 C) -3 D) 5 E) 12 на отрезке [0; 16]. A) 4 B) 8 C) -3 D) 5 E) 12 | А |
| А4.9 Найдите наибольшее и наименьшее значение функции ƒ(x)=x2(x-6) на отрезке [-1; 3] A) 2; -4 B) 0; -32 C) 6; -21 D) 0; -27 Е) 6; -20 | Д |
| А4.10 Найдите наименьшее значение функции y=3x2-12x-16 на отрезке [3; 8]. A) 18 B) -22 C) -25 D) -28 E) -30 | С |
| А5. Уравнение касательной функции | Ответы |
| А5.1 Угловой коэффициент касательной, проведенной к графику функции y = sin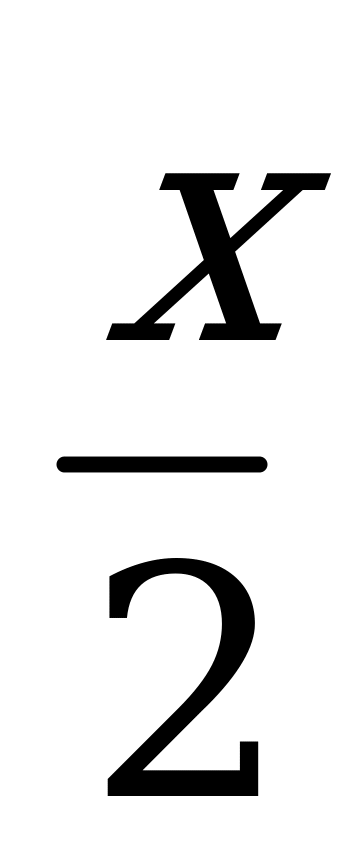 (x (0; )), в точке (x0, y0) равен (x (0; )), в точке (x0, y0) равен 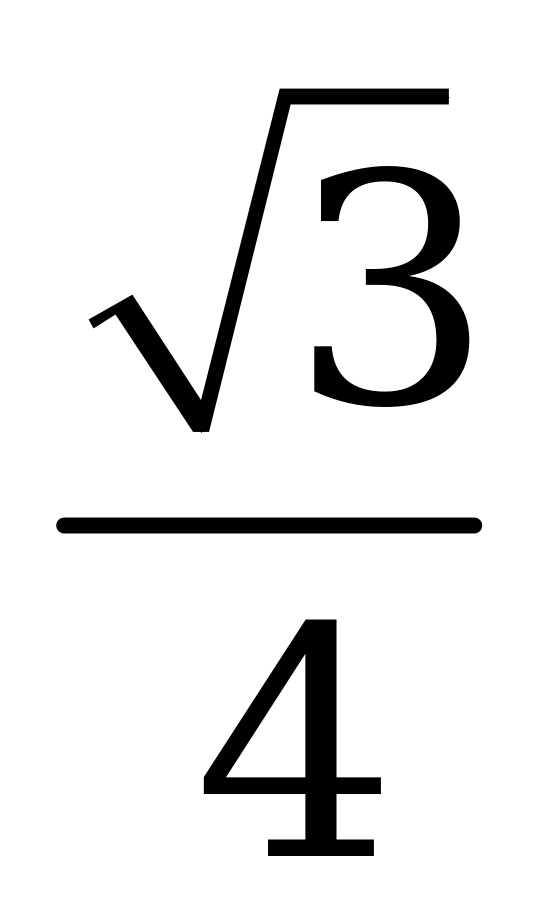 . Найдите x0 y0. . Найдите x0 y0. A) 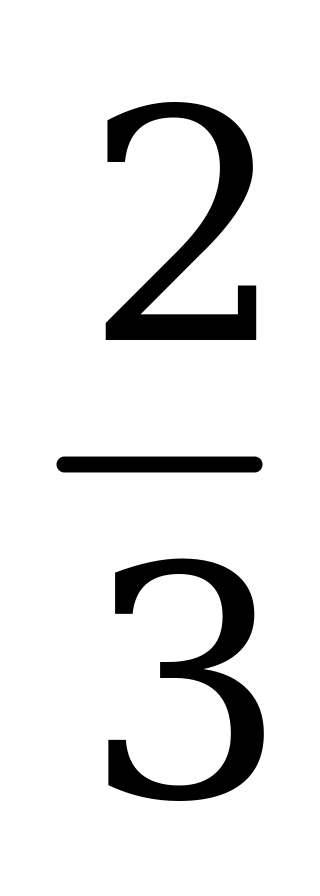 B) B) 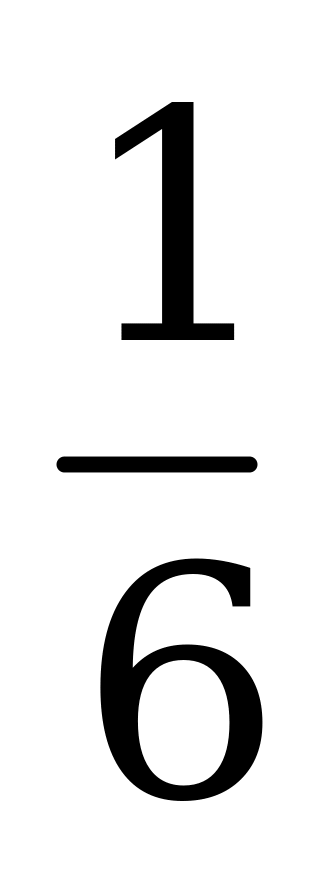 C) C) 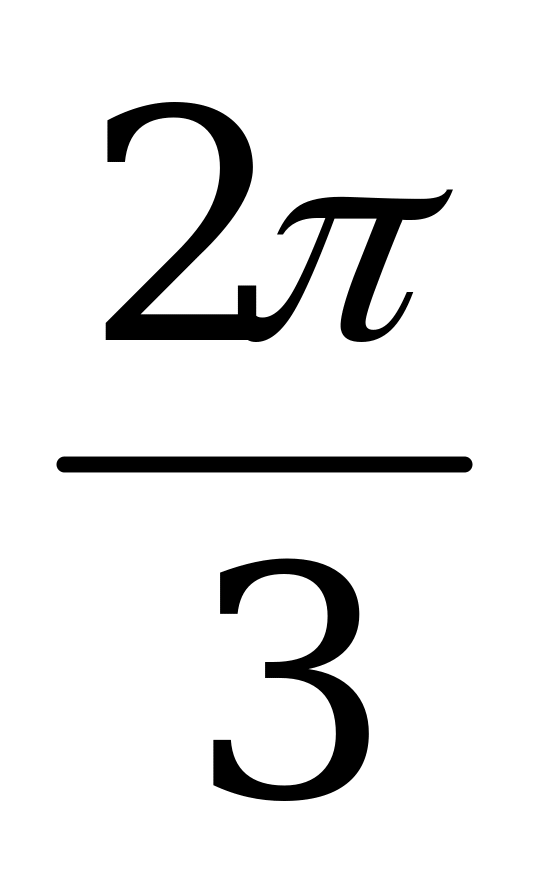 D) - D) -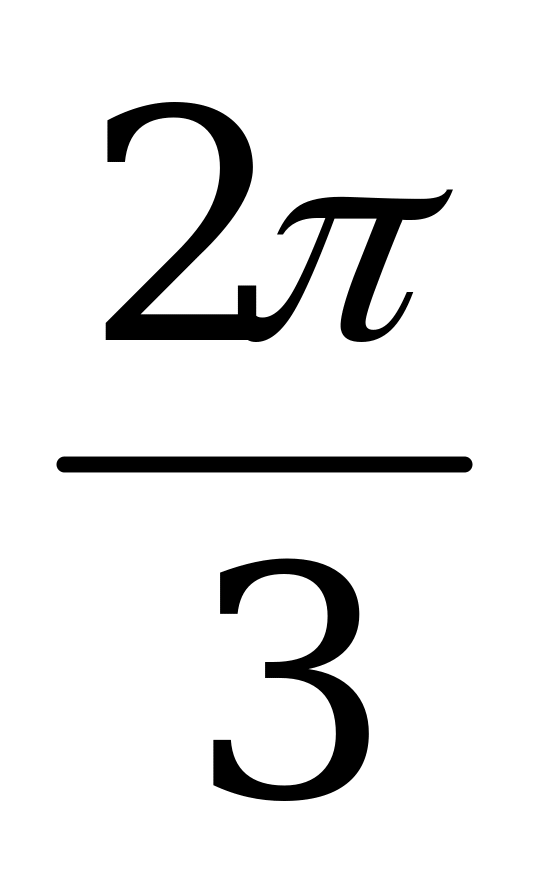 E) E) 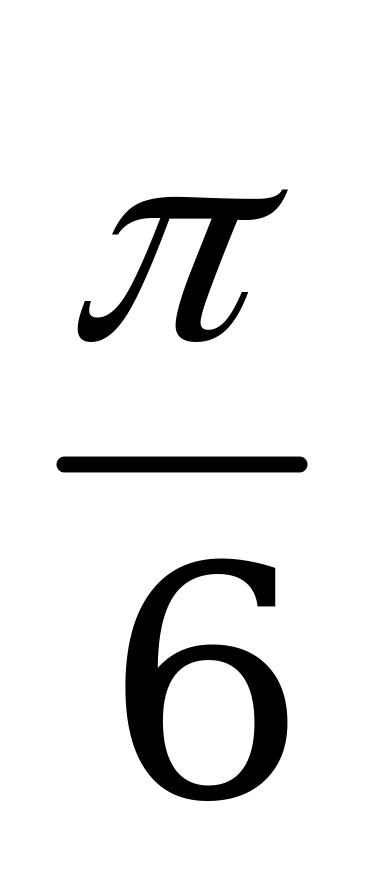 | Е |
| А5.2 Какая из прямых параллельна касательной к кривой y = 4 – x2 в точке x0 = 2? A) y = 4 – 4x B) y = 2x + 8 C) y = x + 8 D) y = 4x + 8 E) y = 8 – 4x | А |
| А5.3 При каких значениях x касательная к графику функции y = 2x3 + 3x2 - 6x параллельна прямой y = 6x + 1 ? A) -2 и 3 B) 1 и 3 C) -2 и 1 D) 2 и -1 E) -1 и 3 | С |
| А5.4 В какой точке касательная, проведенная к графику функции y = x2 - 2x + 1, параллельна прямой y = -4(x + 1)? A) (-1;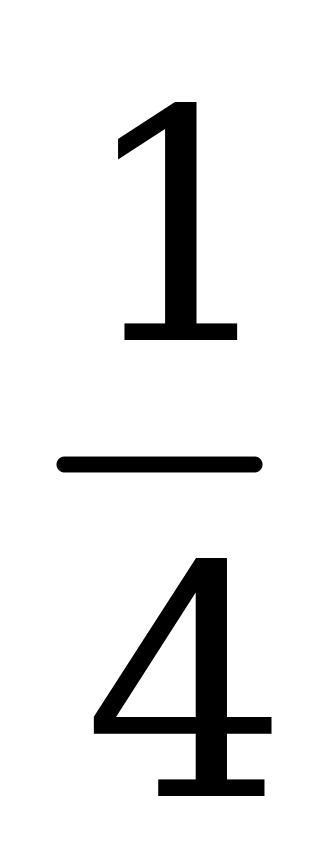 ) B) (-1; 4) C) (1; ) B) (-1; 4) C) (1; 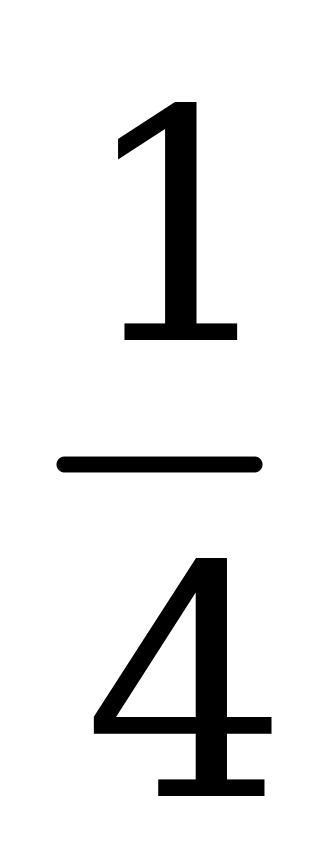 ) ) D) (1; 4) E) (0; 4) | В |
| А5.5 Через точку A(1; 4) проходят две касательные к графику функции 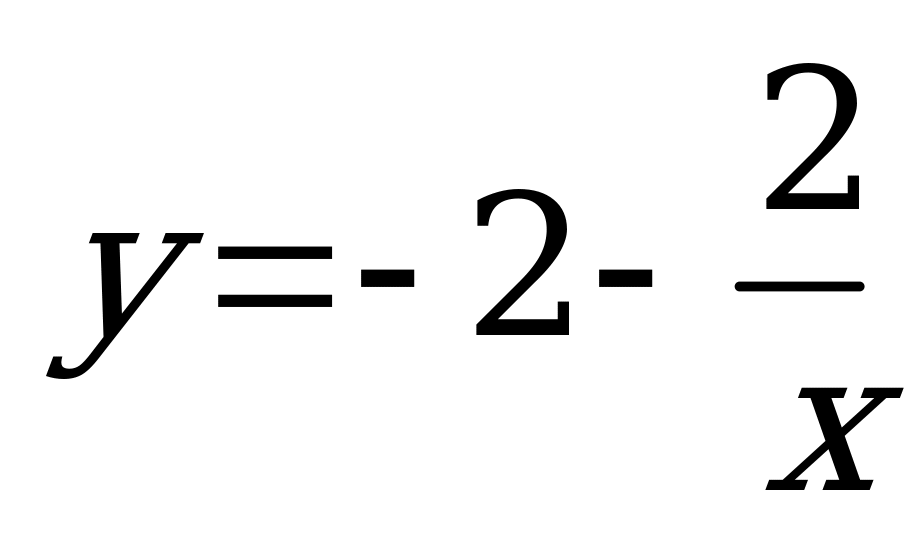 . Найдите сумму абсцисс точек касания. . Найдите сумму абсцисс точек касания. A) -1 B) 1 C) 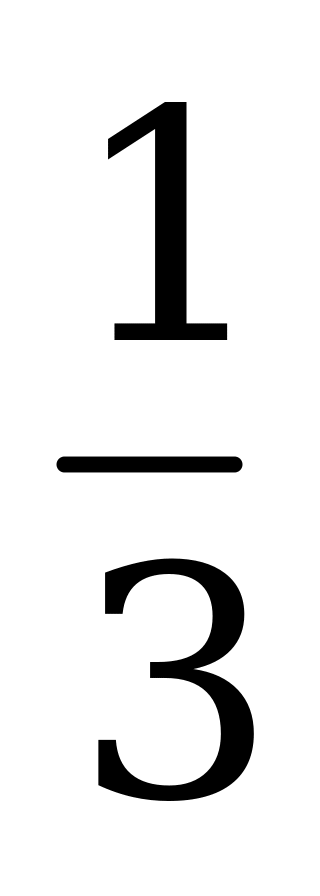 D) D) 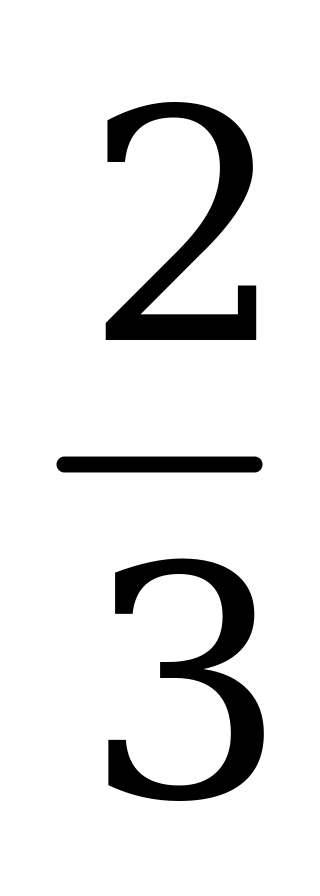 E) - E) -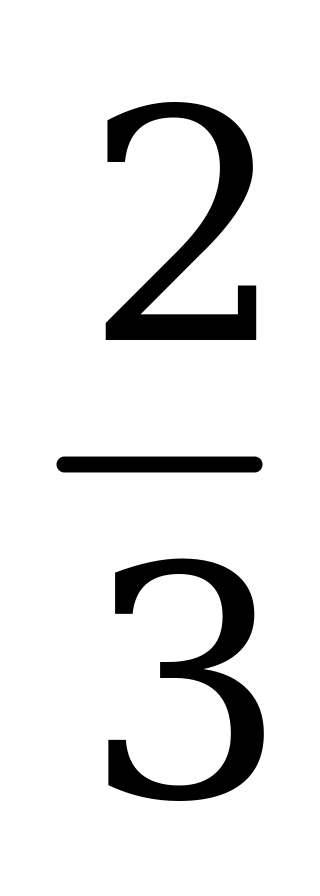 | Е |
| А5.6 Угловой коэффициент касательной, проведенной к параболе y = x2 – 2x в ее точке (x0; y0), равен 4. Напишите уравнение этой касательной. A) y = 4x - 4 B) y = 4x + 9 C) y = 4x + 4 D) y = 4x - 5 E) y = 4x - 9 | Е |
| А5.7 В какой точке графика функции 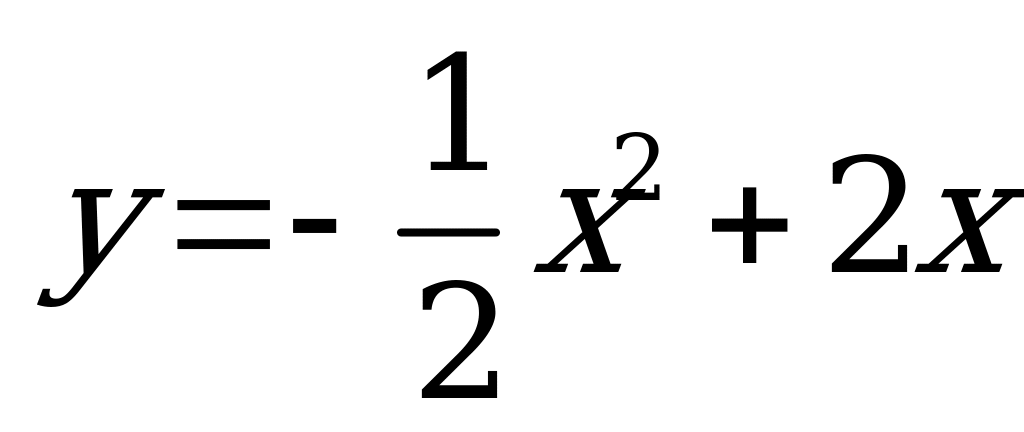 касательная к графику будет параллельна прямой, заданной уравнением y = -2x ? касательная к графику будет параллельна прямой, заданной уравнением y = -2x ? A) (-4; 0) B) (0; 4) C) (4; 0) D) (0; -4) E) (2; 4) | С |
| А5.8 Найдите угловой коэффициент касательной, проведенной к окружности (x + 3)2 + (y – 5)2 = 45 в ее точке A(0; 11). A) -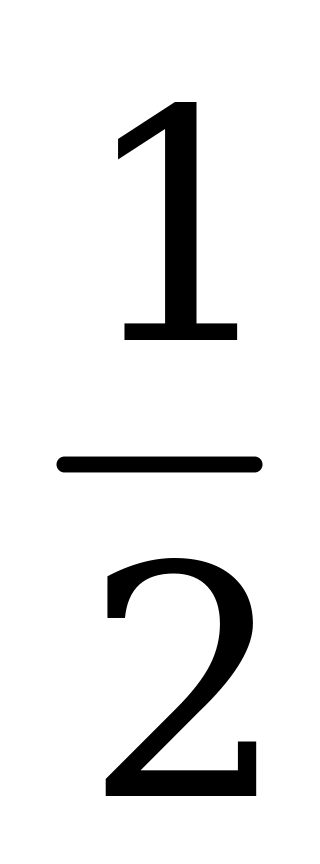 B) -2 C) B) -2 C) 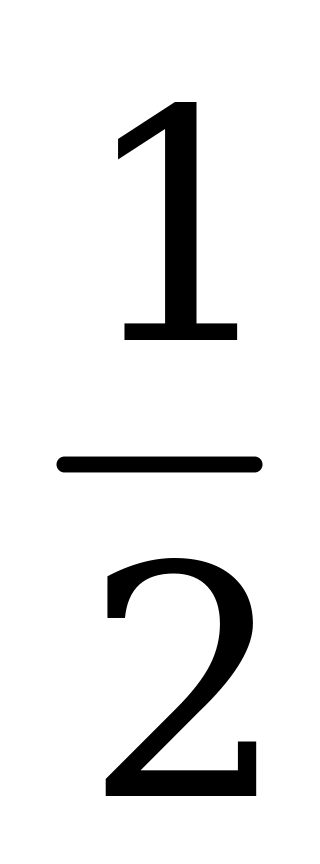 D) 2 E) D) 2 E) 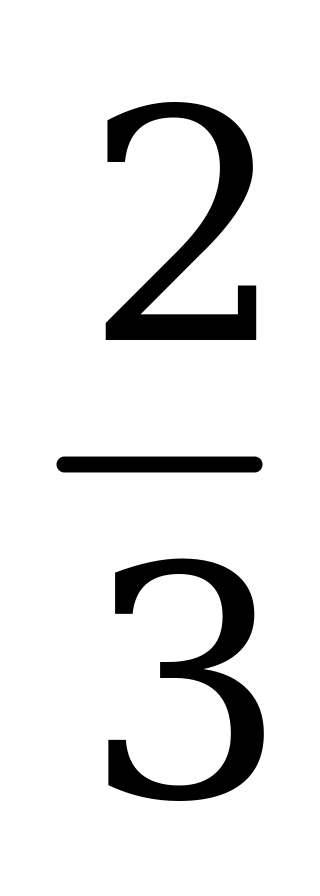 | А |
| А5.9 В какой точке касательная, проведенная к графику функции y = x2 + 2x + 8, параллельна прямой y + 2x - 8 = 0? A) (-2; 8) B) (2; 8) C) (-2; -8) D) (2; -8) E) (0; 8) | А |
| А5.10 Прямая y = -5x + 3 параллельна касательной к графику функции f(x) = x2 - x. Найдите координаты точки касания. A) (-2; 6) B) (1; 0) C) (2; 4) D) (0; 0) E) (2; 2) | А |
| А6. Уравнения движения материальной точки | Ответы |
| А6.1 Тело движется прямолинейно по закону 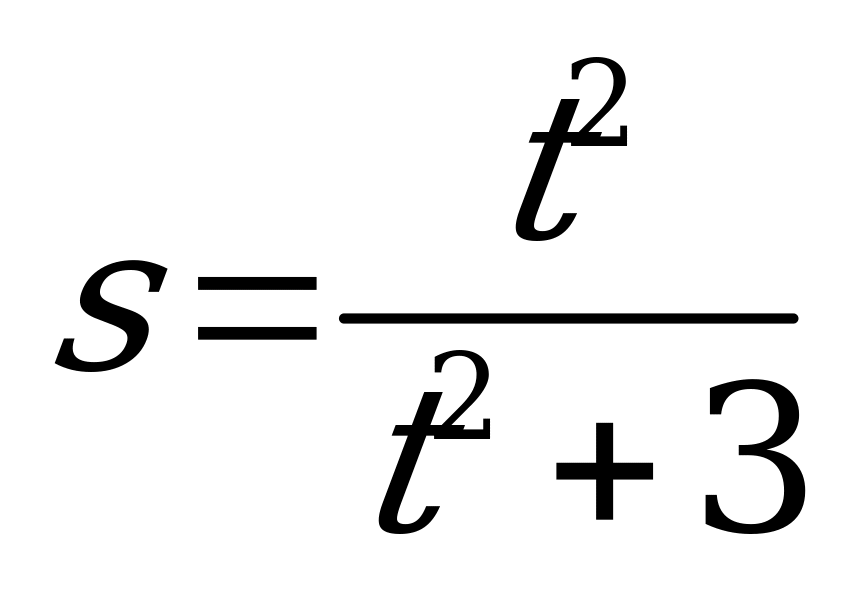 . Найдите скорость тела в момент t = 1 . Найдите скорость тела в момент t = 1 A) 0,4 B) 0,5 C) 0,225 D) 0,375 E) 0,45 | Д |
| А6.2 Найдите скорость (м/сек) материальной точки в момент t =2 сек, если точка движется прямолинейно по закону 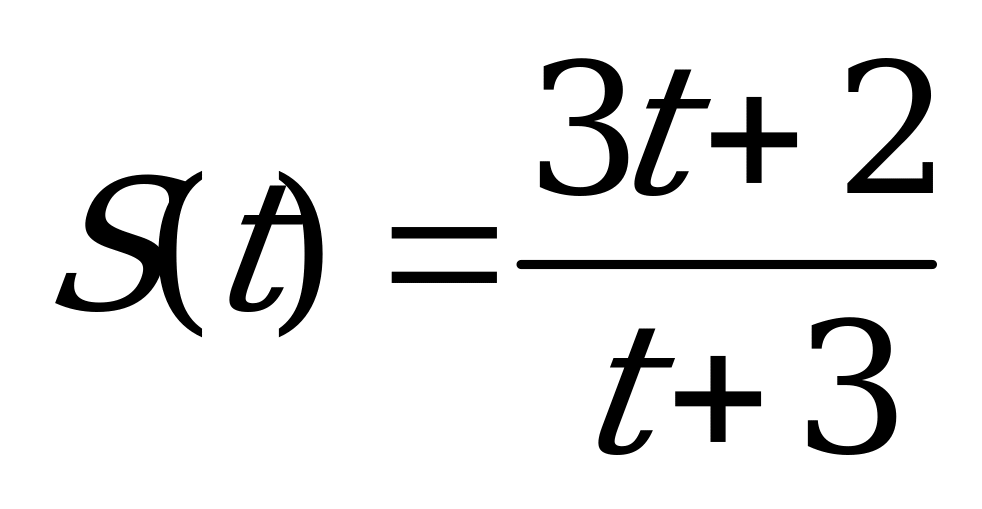 . . A) 0,2 B) 0,25 C) 0,28 D) 0,32 E) 0,5 | С |
| А6.3 Две материальные точки движутся прямолинейно по законам S1(t) = 2,5t2 - 6t + 1 и S2(t) = 0,5t2 + 2t - 3. В какой момент скорость первой точки будет в три раза больше скорости второй ? A) 2 B) 3 C) 4 D) 5 E) 6 | Е |
| А6.4 Две материальные точки движется по законам S1(t) = 2t3 – 5t2 – 3t (м) и S2(t) = 2t3 – 3t2 – 11t + 7 (м). Найдите ускорение (м/с2) первого тела в момент, когда скорости этих тел равны. A) 10 B) 8 C) 14 D) 9 E) 11 | С |
| А6.5 Материальная точка движется прямолинейно по закону 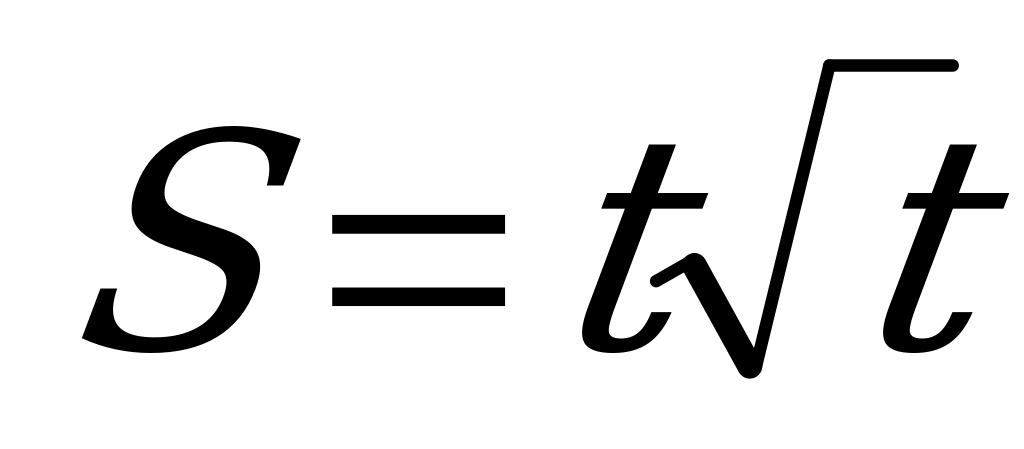 . Найдите ускорение этой точки в момент t = 2 сек (S в метрах). . Найдите ускорение этой точки в момент t = 2 сек (S в метрах). A) 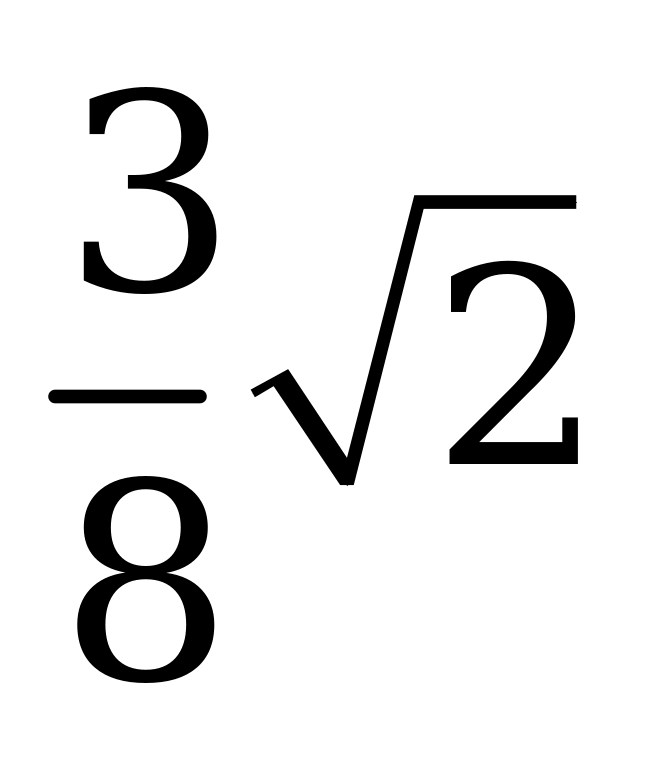 B) B) 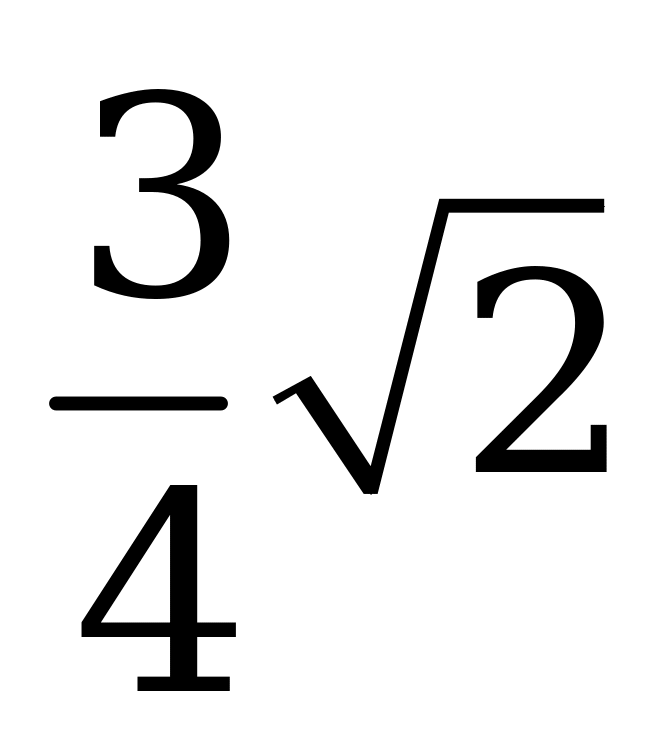 C) C) 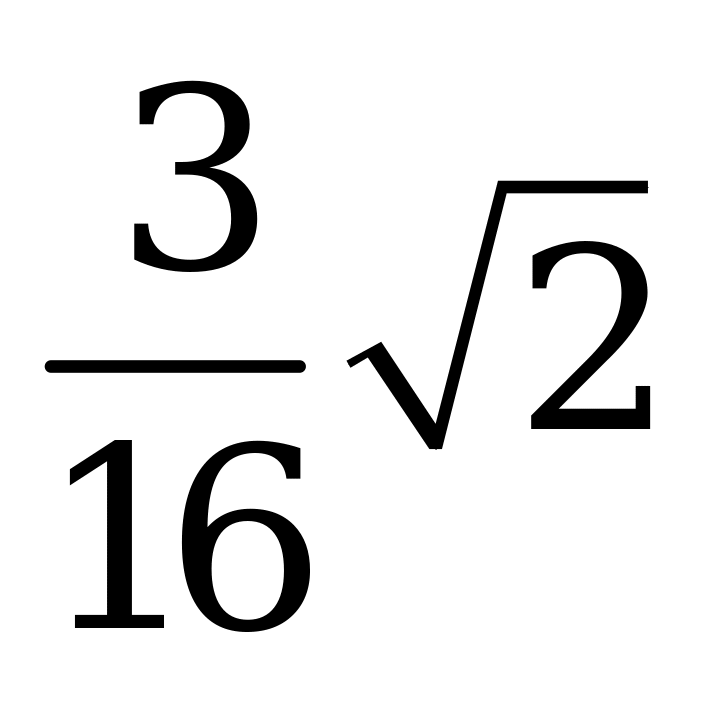 D) D) 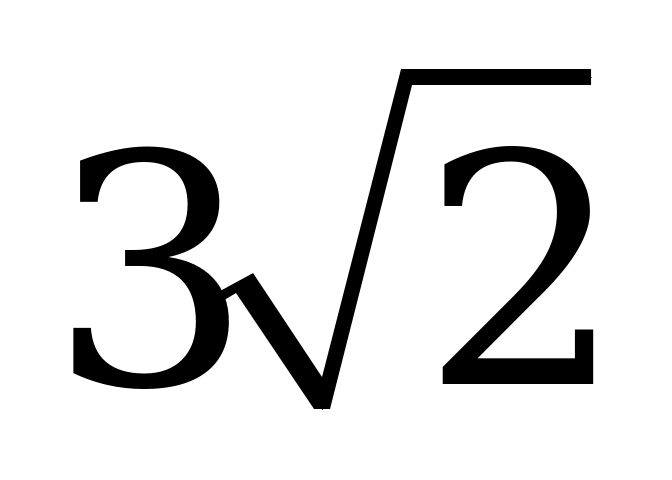 E) E) 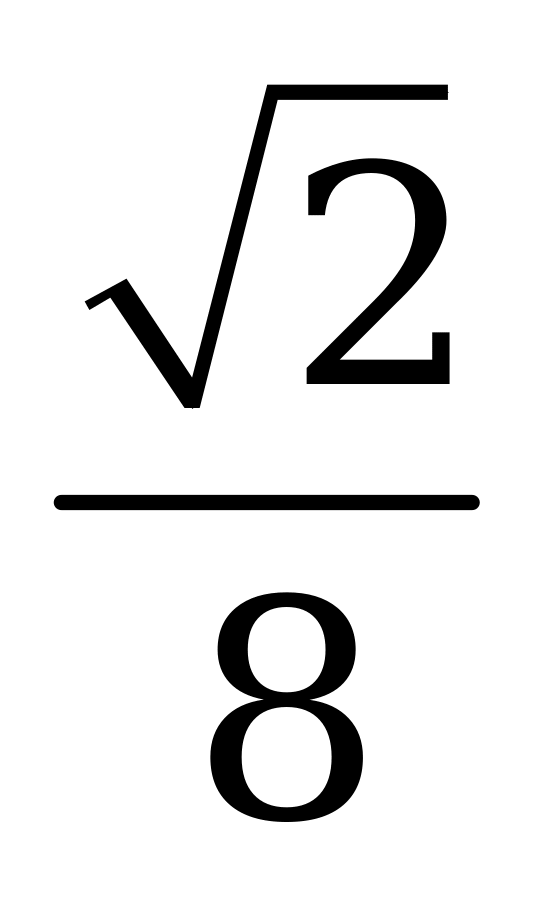 | А |
| А6.6 Материальная точка движется по закону 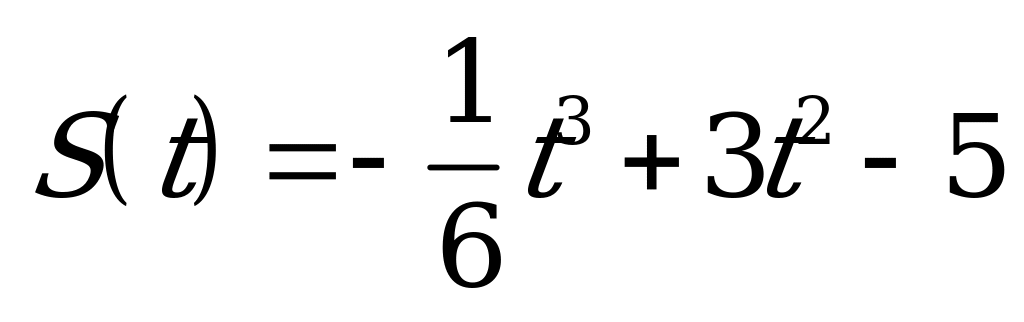 . С какой скоростью движется точка в момент, когда ее ускорение равно нулю ? . С какой скоростью движется точка в момент, когда ее ускорение равно нулю ? A) 24 B) 18 C) 12 D) 6 E) 15 | В |
| А6.7 Два тела, которые находились в начале координат, одновременно начали движение в положительном направлении оси ОХ. Первое тело движется со скоростью V1(t) = 3t2 – 5 (м/с), а второе со скоростью V2(t) = 3t2 + 2t + 1 (м/с). Чему будет равно расстояние (м) между этими телами через 4 секунды? A) 38 B) 42 C) 40 D) 36 E) 44 | С |
| А5.8 Материальная точка движется прямолинейно согласно закону S(t) = 3t3 - 3t2 + 12t (м). Чему равна ее скорость (м/мин) в момент, когда ее ускорение равно 0. A) 8 B) 7 C) 9 D) 11 E) 10 | Д |
| В1. Производная элементарной функции | Ответы |
| В1.1 Дана функция 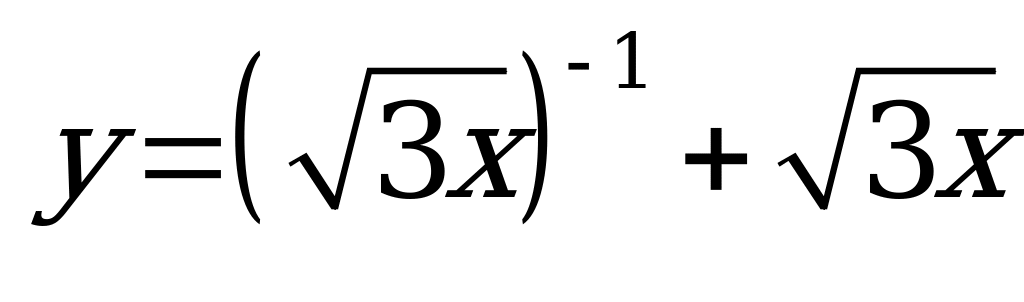 . Вычислите . Вычислите 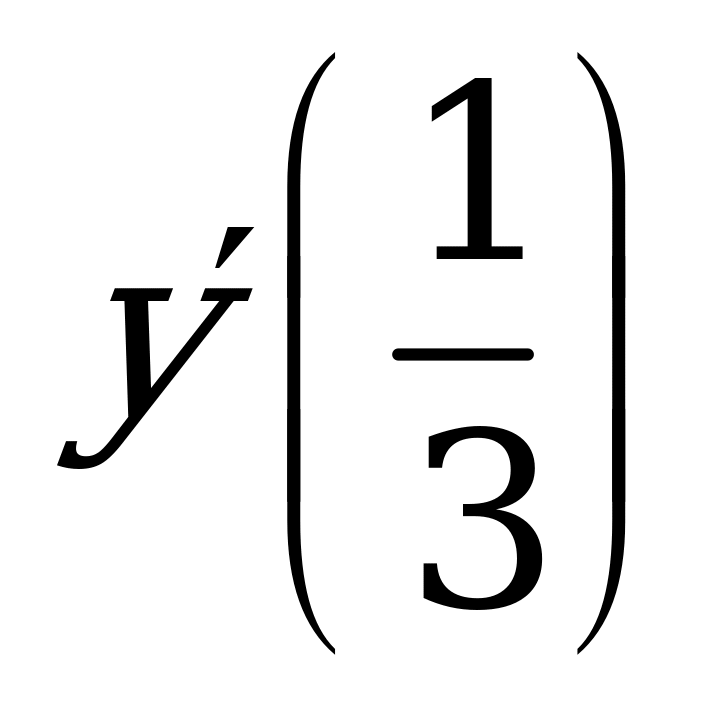 A) 0 B) 1,5 C) 0,5 D) -0,5 E) 1 A) 0 B) 1,5 C) 0,5 D) -0,5 E) 1 | А |
| В1.2 В скольких точках функции f (x)= x3 равна своей производной? A) 2 B) 1 C) 0 D) 3 E) 4 | А |
| В1.3 Сколько целых решений имеет неравенство f'(x) 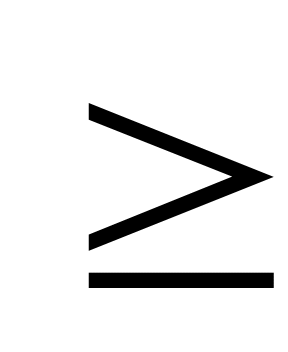 0, где f(x) = -4x3 - 11x2 - 8x + 7? 0, где f(x) = -4x3 - 11x2 - 8x + 7? A) 4 B) 3 C) 2 D) 1 E)  | Д |
| В1.4 Решите неравенство ƒ’(x)f(x)=3x+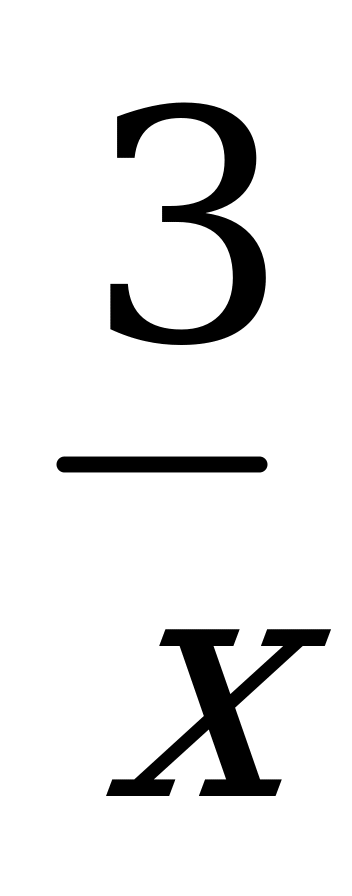 . . A) (-1; 0) U (0; 1) B) (-; -1) C) ( 1; ) D) (0; 1) E) (-1; 0) | А |
| В1.5 Сколько целых решений имеет неравенство 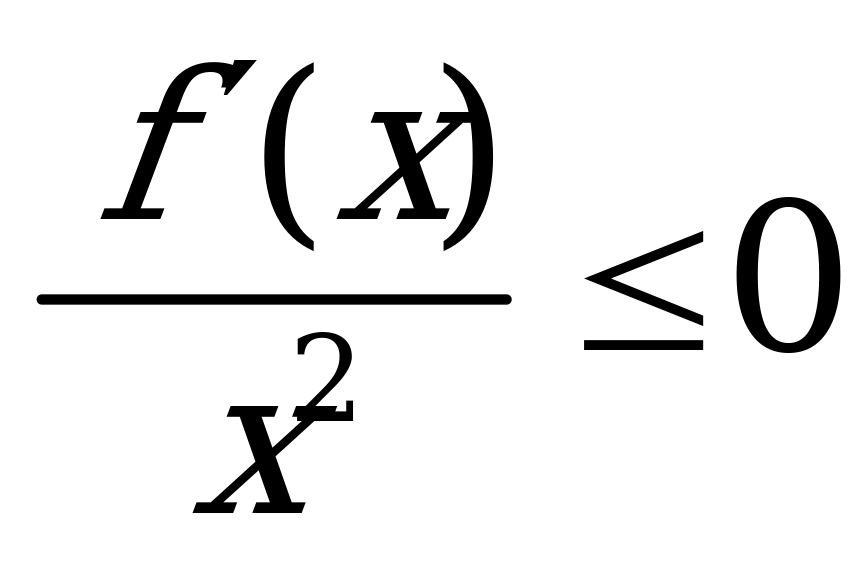 , где , где 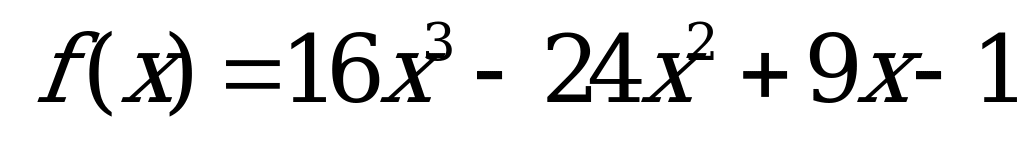 ? ? A) 4 B) 3 C) 2 D) 1 E) ни одного | Е |
| В1.6 Сколько целых решений имеет система неравенств 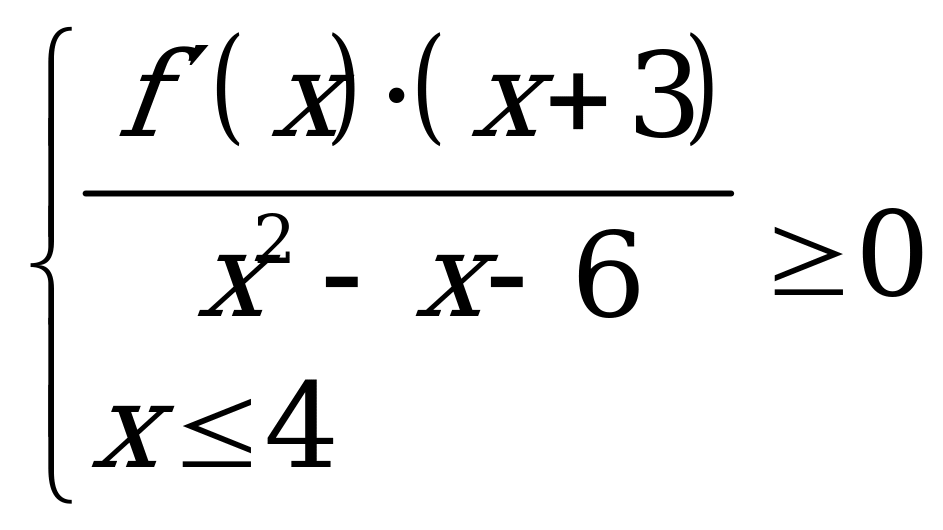 если если 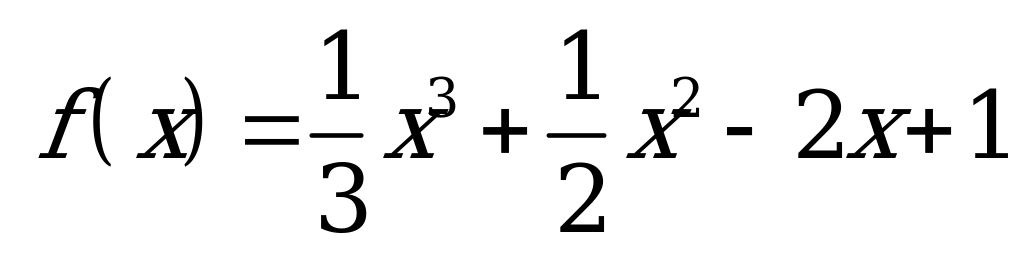 A) 6 B) 5 C) 4 D) 7 E) бесконечно много | В |
| В1.7 При каких значениях х f ' (x) g ' (x), если f(x) = 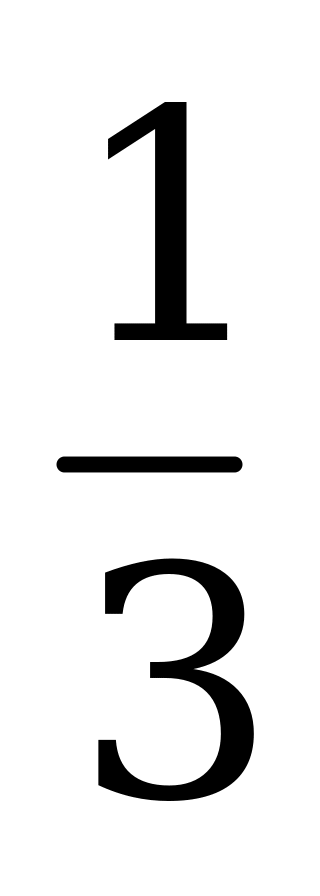 x3 и g(x) = -x2 + 3x ? A) (- x3 и g(x) = -x2 + 3x ? A) (- ; -3) ; -3) 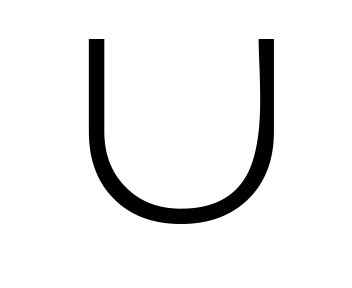 (1; (1;  ) ) B) (-3; 1) C) (1;  ) D) (- ) D) (- ; -3) E) (-3; ; -3) E) (-3;  ) ) | В |
| В1.8 Найдите наименьшее натуральное решение неравенства 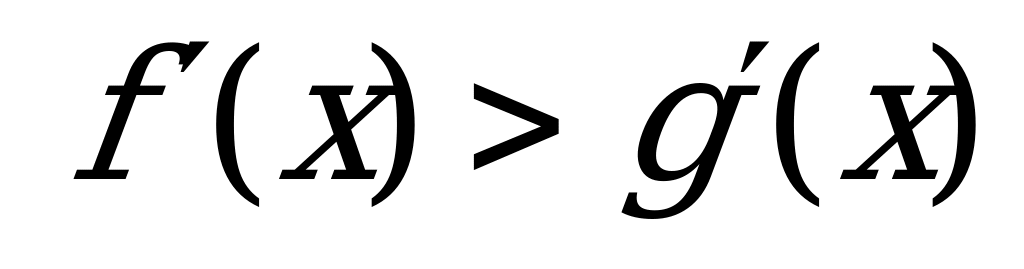 , если , если 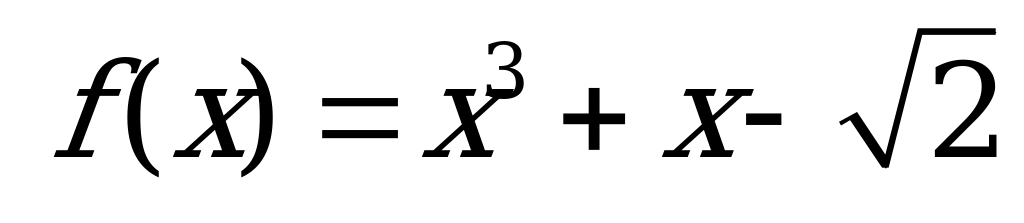 и и 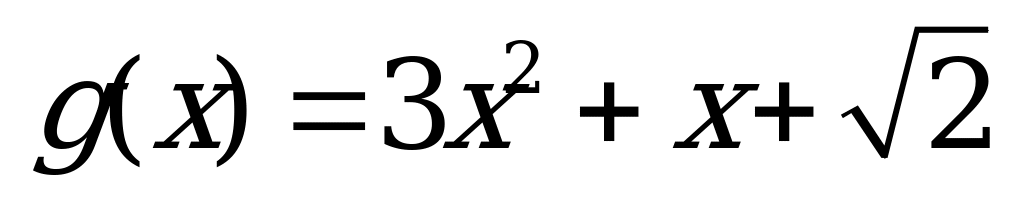 . A) 3 B) 2 C) 6 D) 5 E) 1 . A) 3 B) 2 C) 6 D) 5 E) 1 | А |
| В1.9 Найти 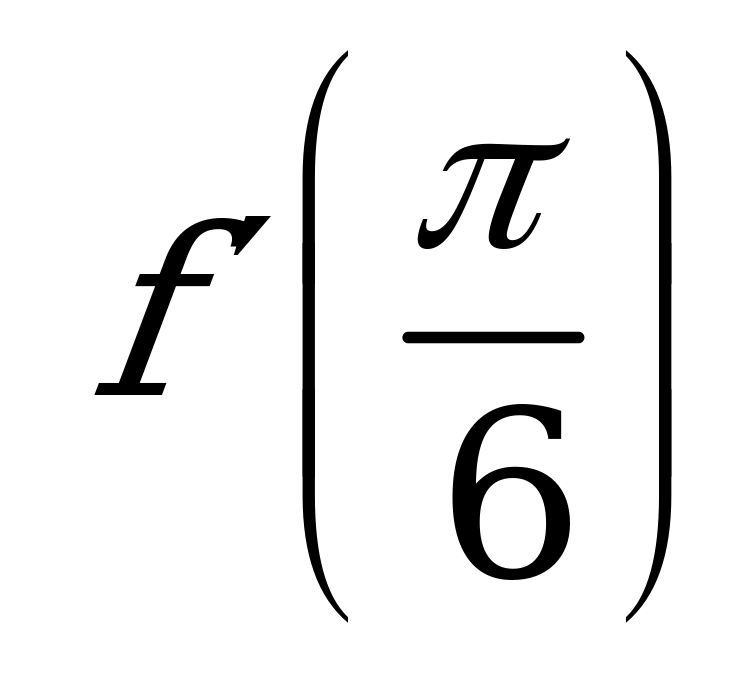 , если , если 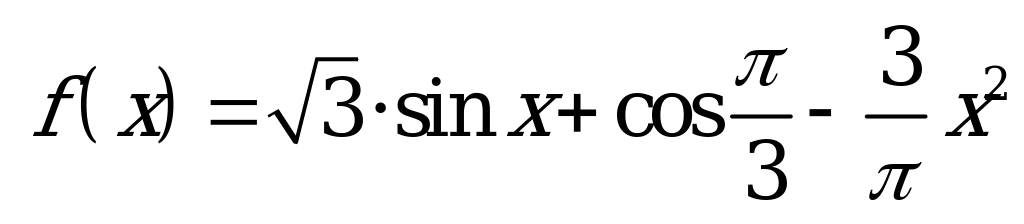 A) 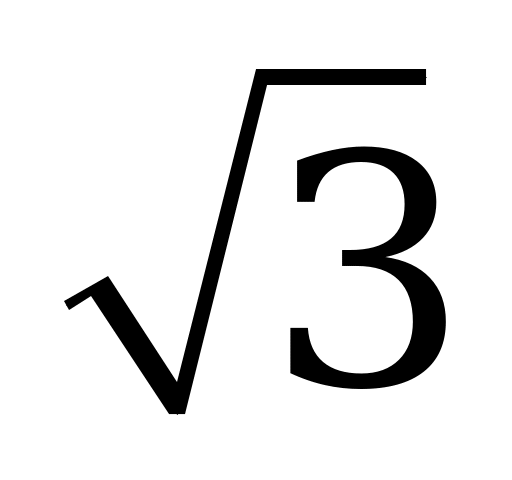 B) 0,5 C) B) 0,5 C) 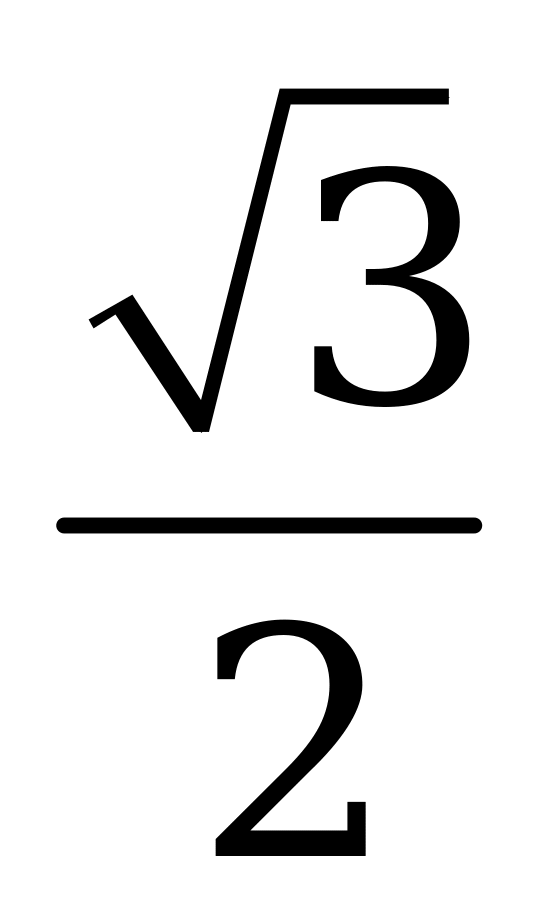 D) 0 E) D) 0 E) 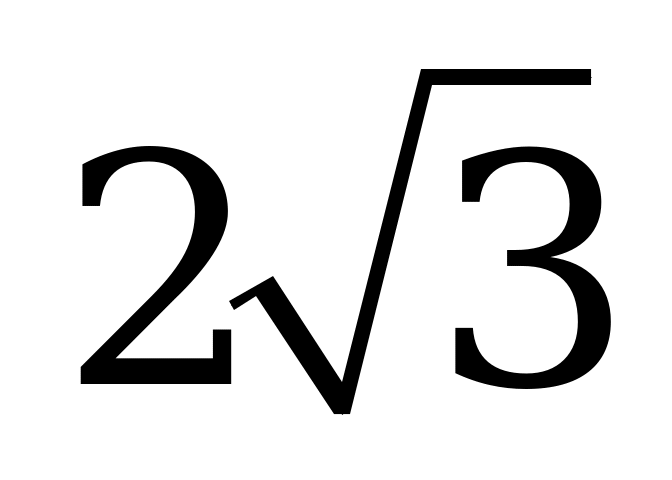 | В |
| В1.10 Найти 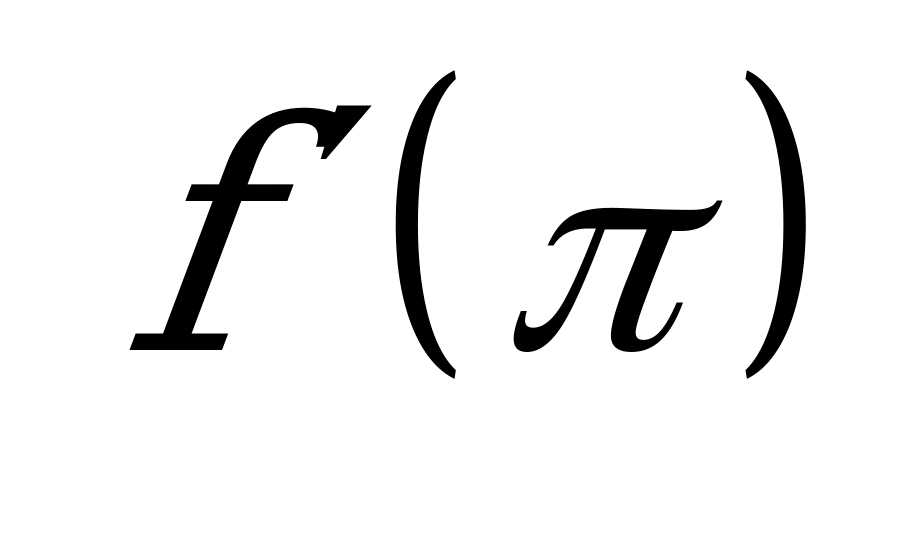 , если , если 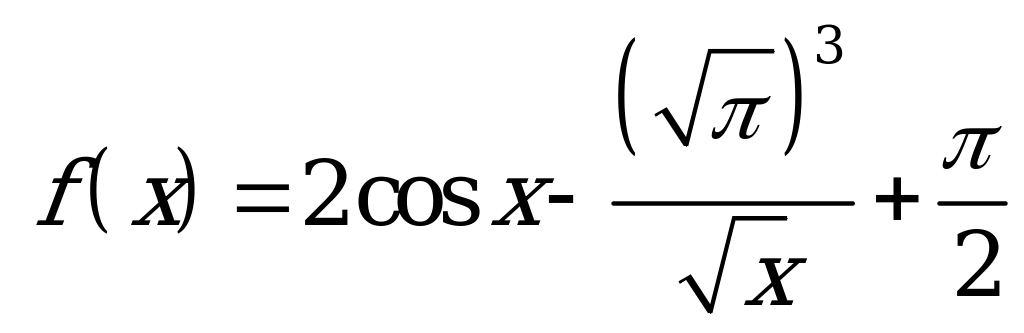 A) 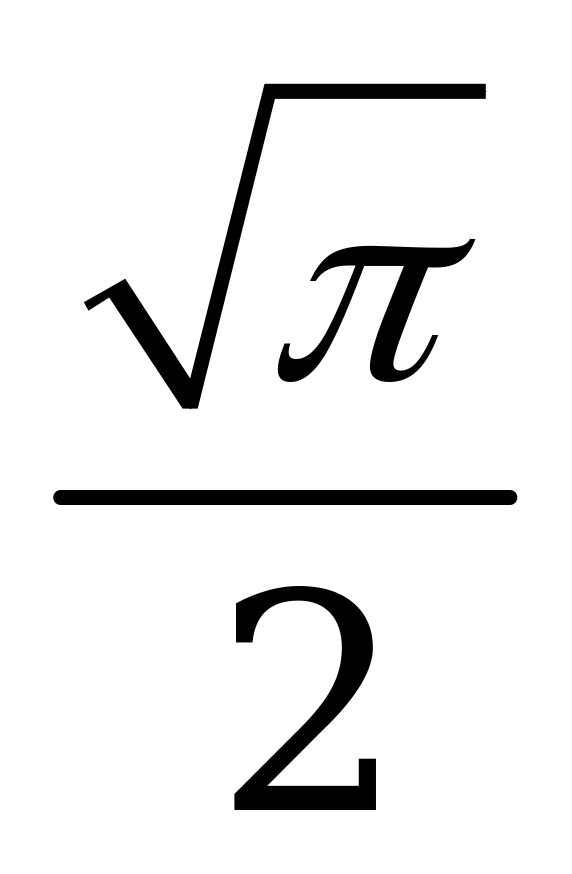 B) -1,5 C) 0,5 D) 2,5 E) - B) -1,5 C) 0,5 D) 2,5 E) -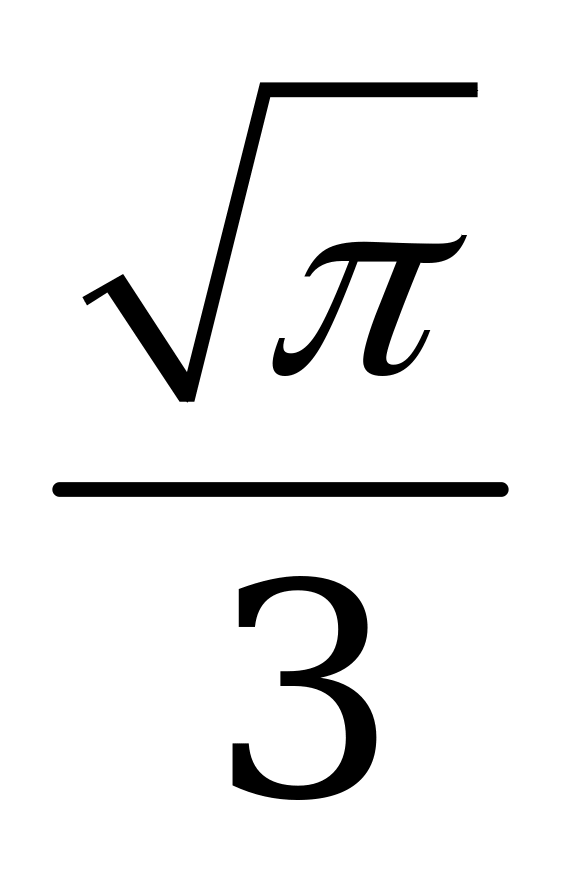 | С |
| В2. Производная сложной функции | Ответы |
| В2.1 Найти производную функции: y = sin(cosx) A) sinx cos(cosx) B) cosx cos(cosx) B) cosx sin(cosx) C) -sinx sin(cosx) C) -sinx cos(cosx) cos(cosx) D) -cosx sin(cosx) E) cosx sin(cosx) E) cosx cos(sinx) cos(sinx) | С |
| В2.2 Найти производную функции: y = sin(sinx) A) sin(sinx)  cosx B) cos(cosx) cosx B) cos(cosx)  cosx cosx C) sin(cosx)  sinx D) cos(sinx) sinx D) cos(sinx)  sinx E) cos(sinx) sinx E) cos(sinx)  cosx cosx | Е |
| В2.3 Решите неравенство 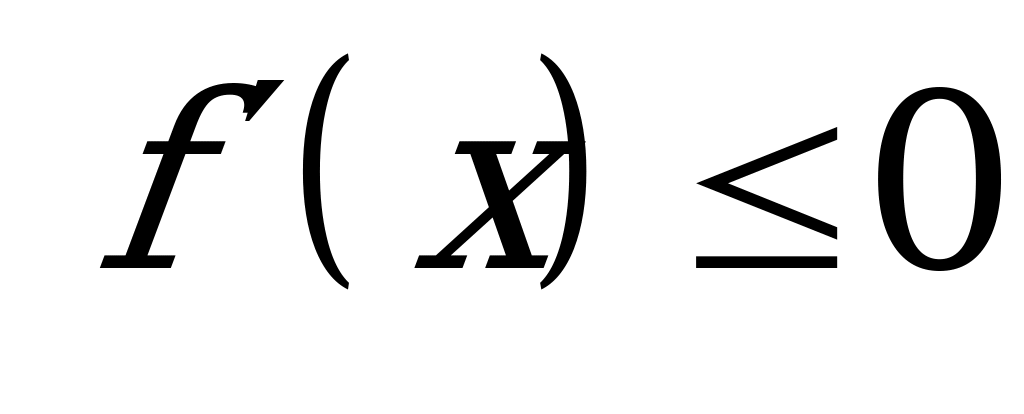 для функции для функции f(x) = (x-2)2(x+4) A) [ -4; 2 ] B) [ 2; 4 ] C) [ -2; 2 ] D) [ -3; 2 ] E) [ 2; 6 ] | С |
| В2.4 Решите уравнение g(x) = 0, где g(x) = 3x(2x-1)5. A) 12-1; 2-1 B) 2; 12 C) D) 1; 2 E) 3; 4 | А |
| В2.5 Вычислите f (0) + f 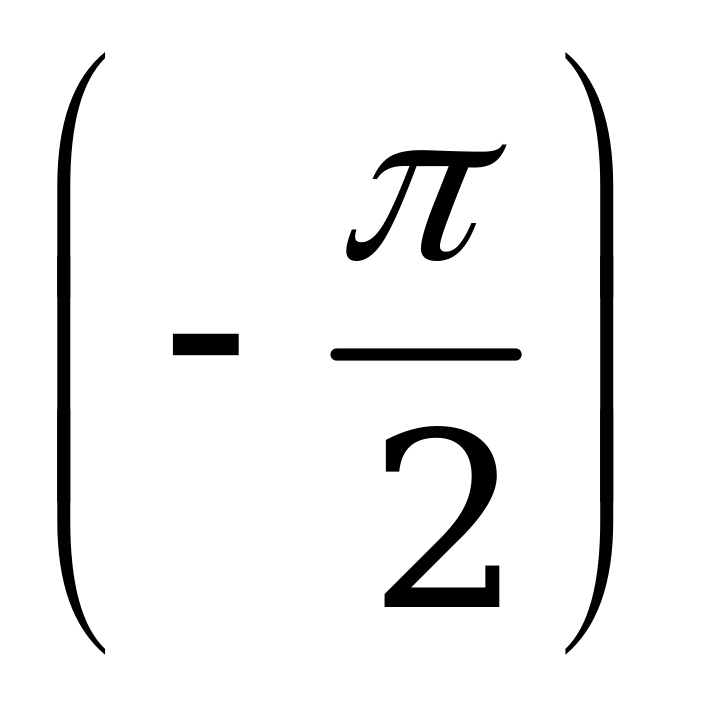 , если f(x) = (3x2 + x)cos2x , если f(x) = (3x2 + x)cos2x A) -3+2 B) 0 C) 3 D) 3-1 E) 32+ | С |
| В2.6 Вычислите значение производной функции y = x2cos3x + 2x + 1 в точке 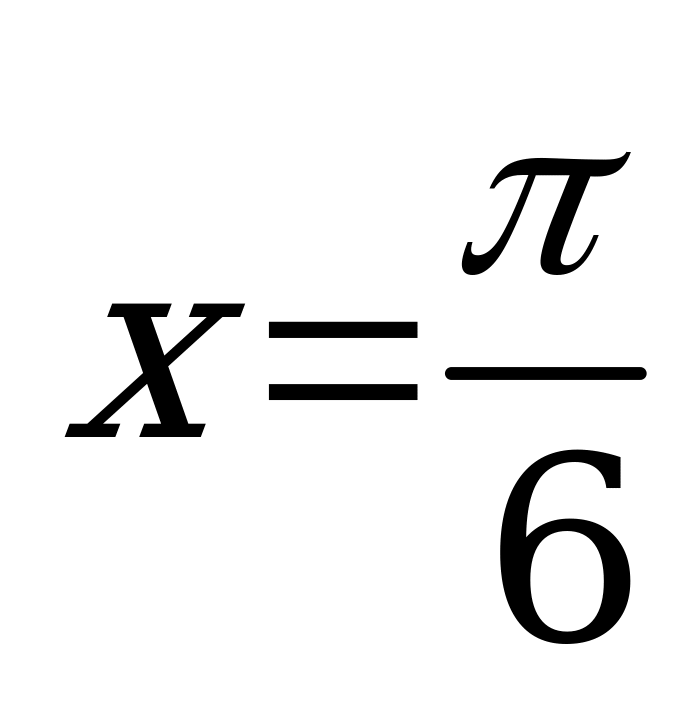 . . A) 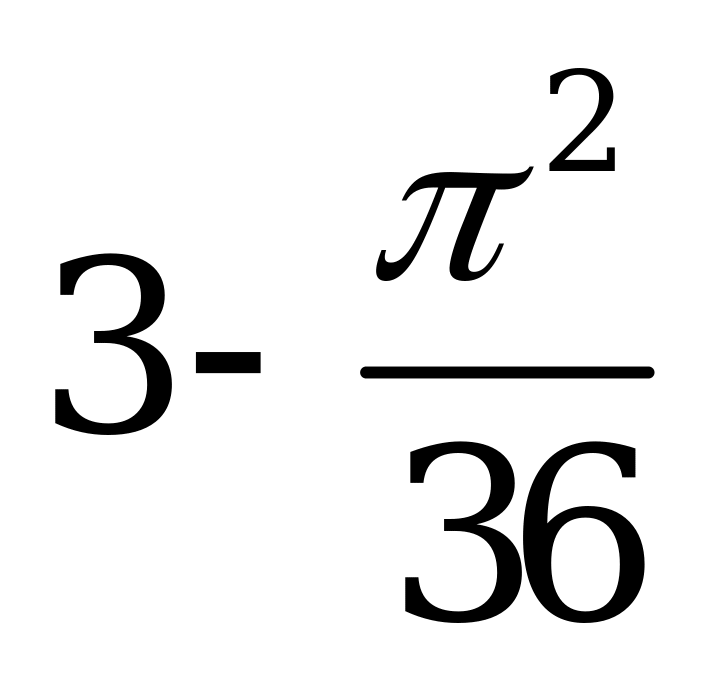 B) B) 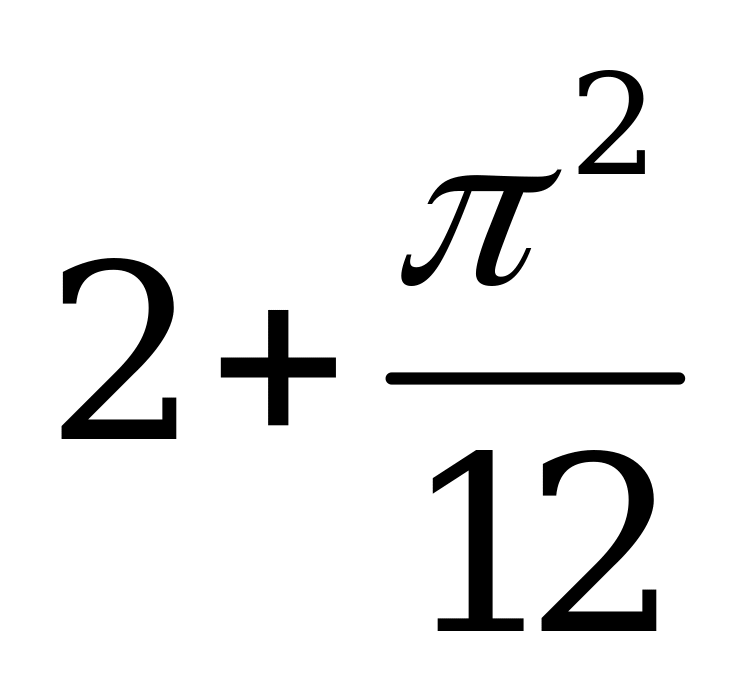 C) 2 D) C) 2 D) 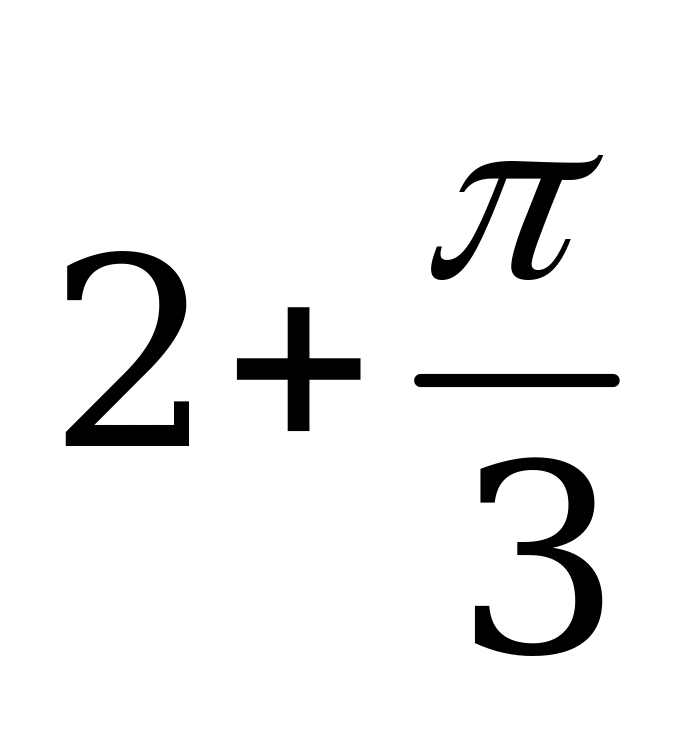 E) E) 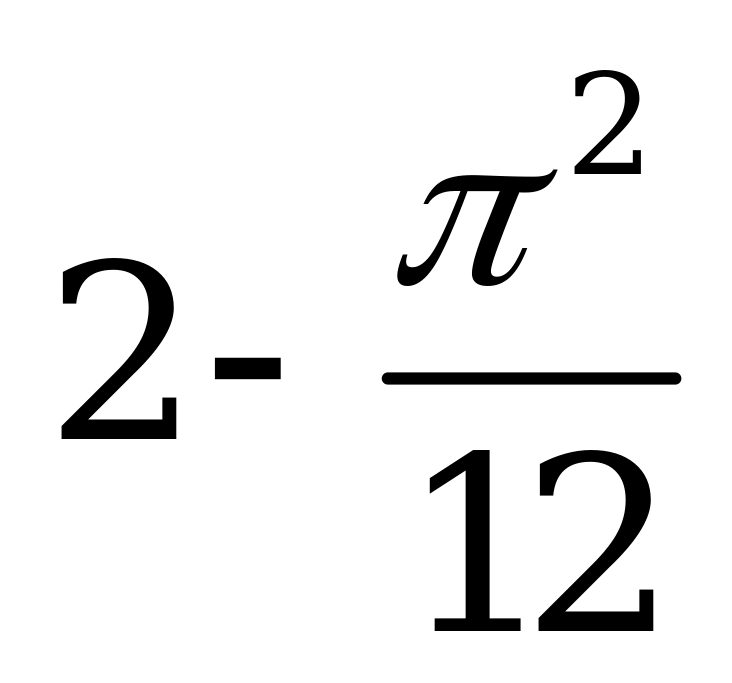 | Е |
| В2.7 Вычислите: ý(2), если y=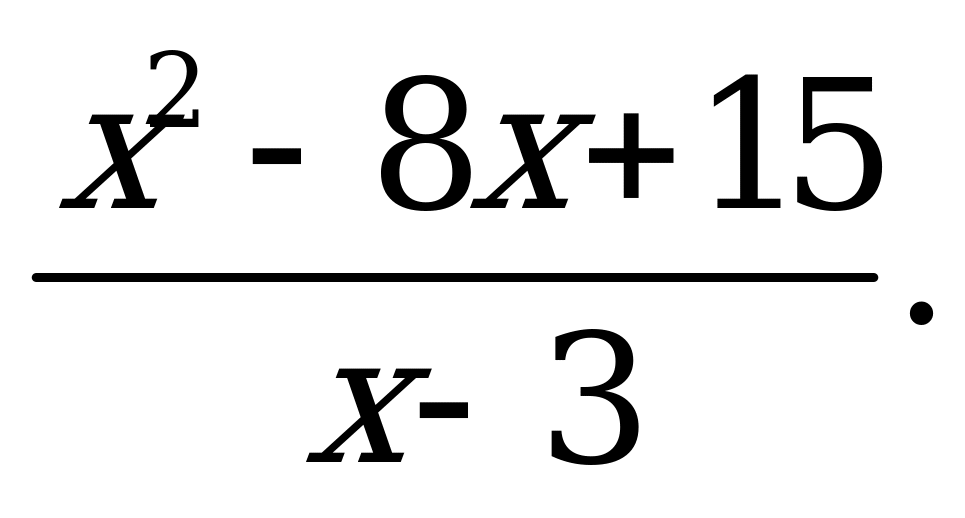 A) 5 B) 3 C) 2 D) -5 E) 1 | Е |
| В2.8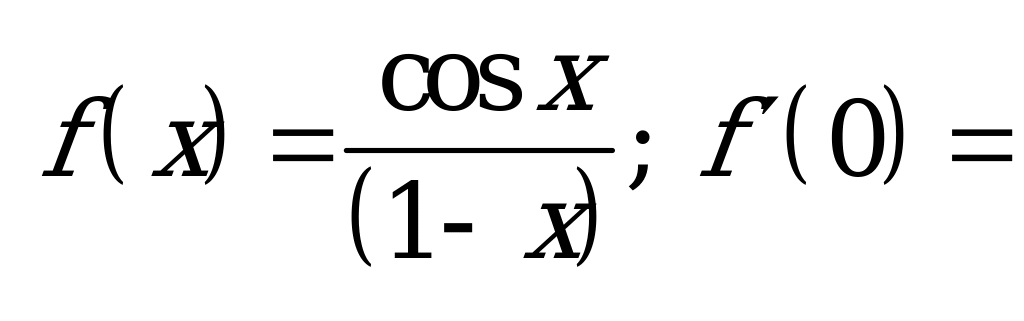 ? ? A) 4 B) 2 C) 3 D) 0 E) 1 | Е |
| В2.9 Найдите производную функции 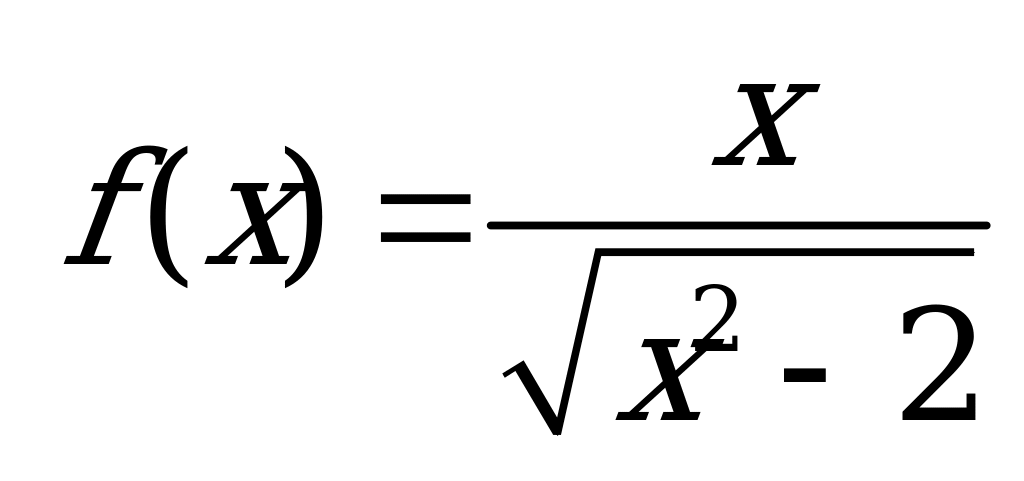 A) 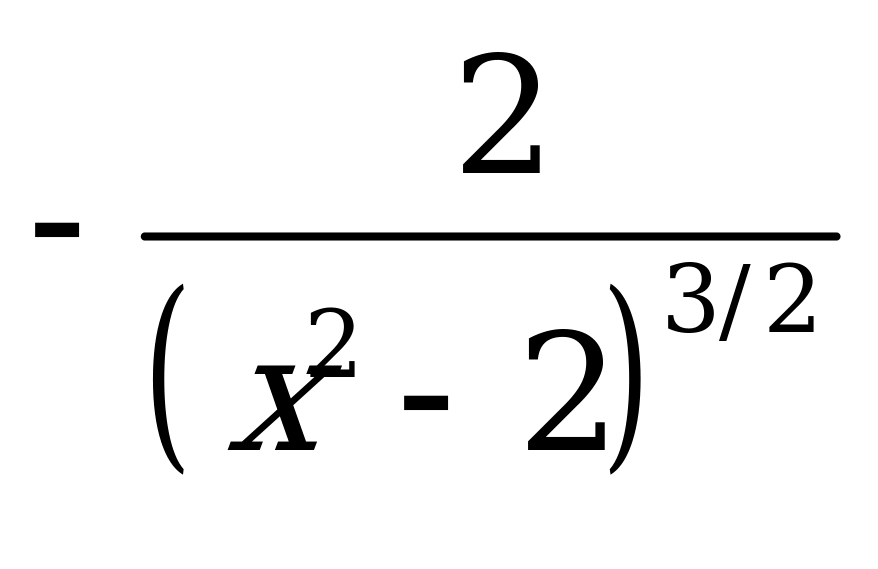 B) B) 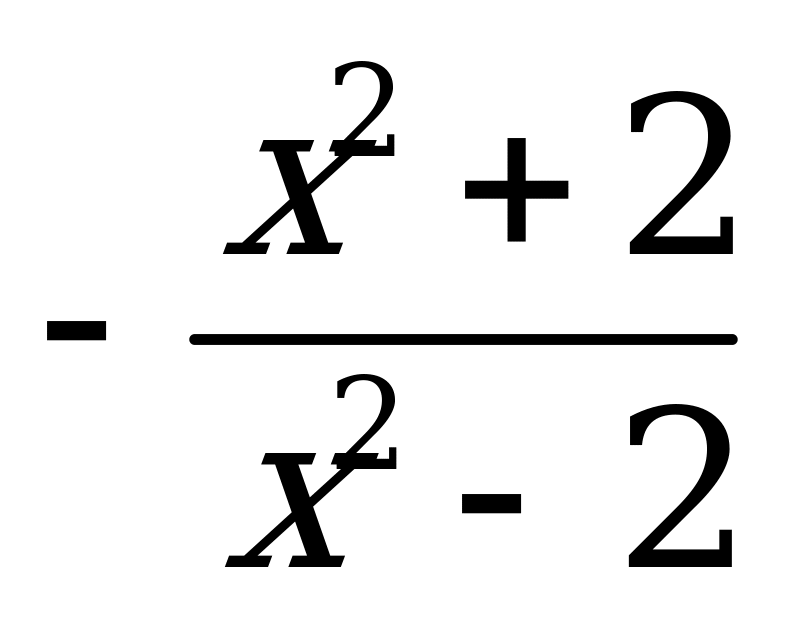 C) C) 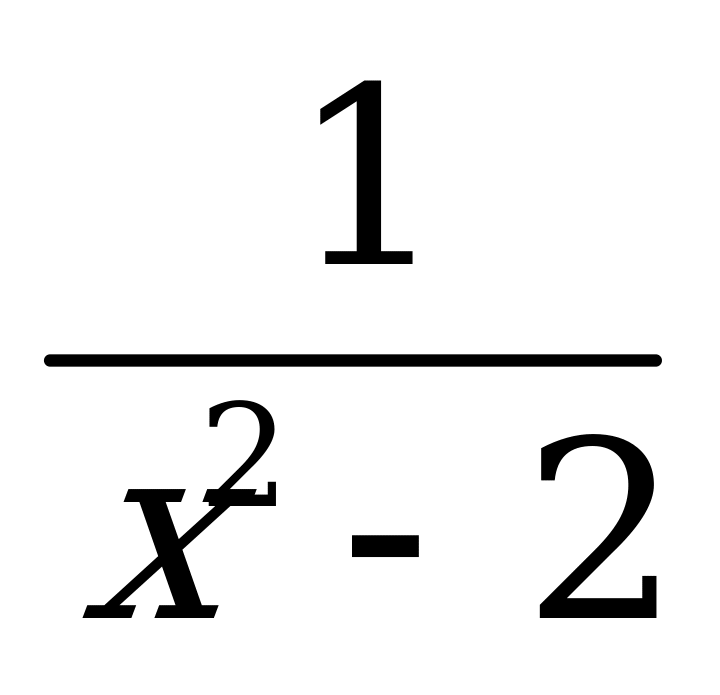 D) 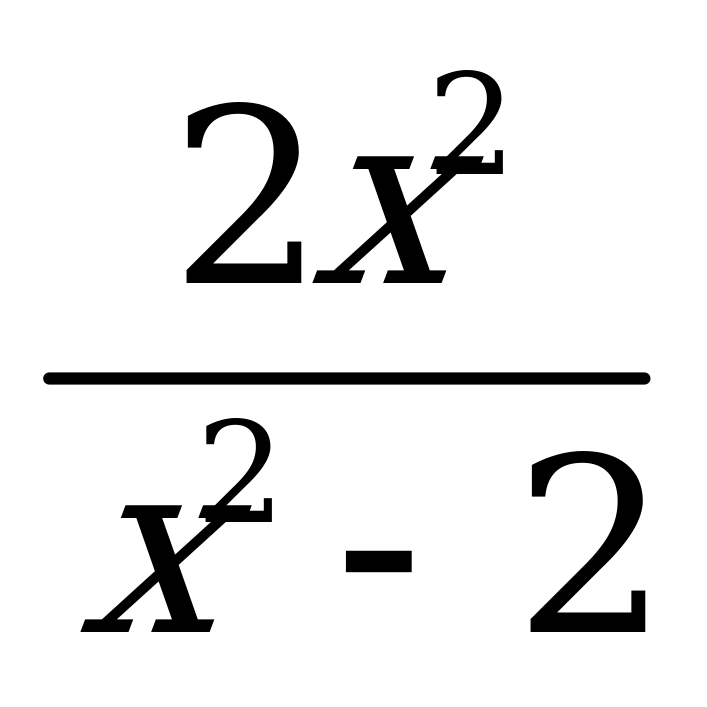 E) E) 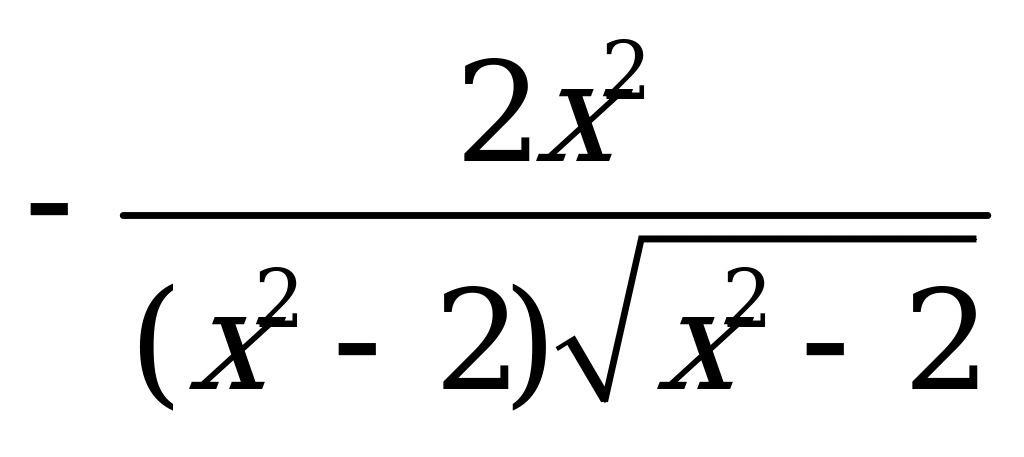 | А |
| В2.10 Найдите 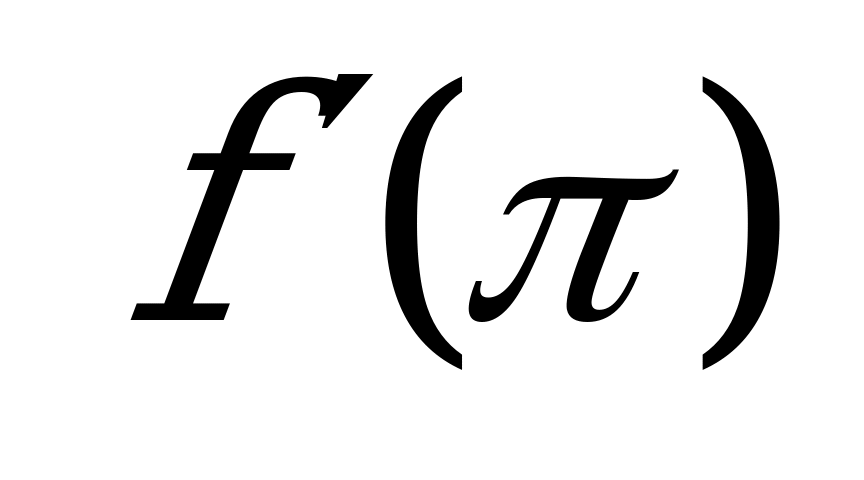 , если , если 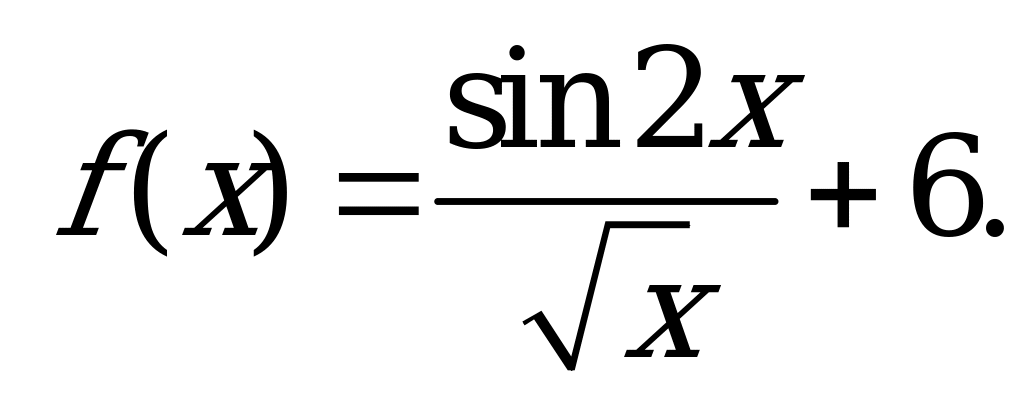 A) 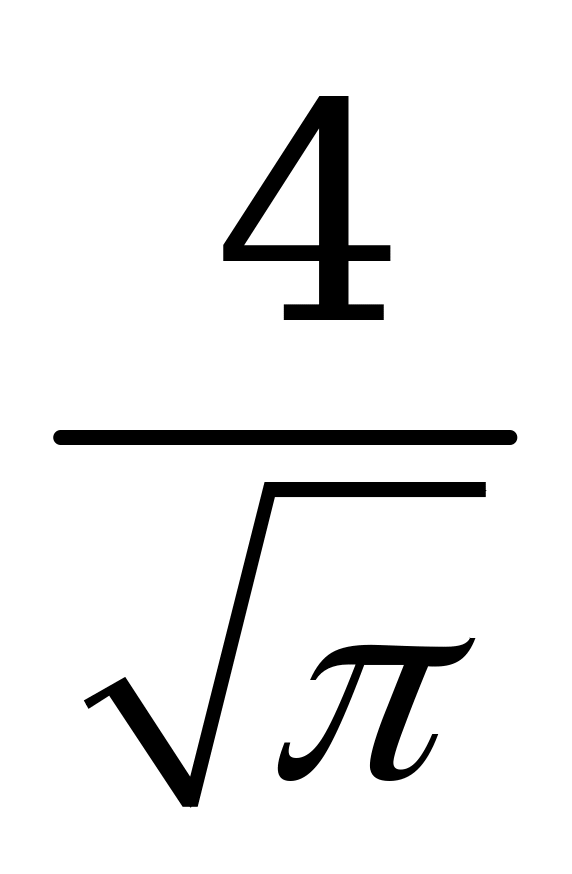 B) B) 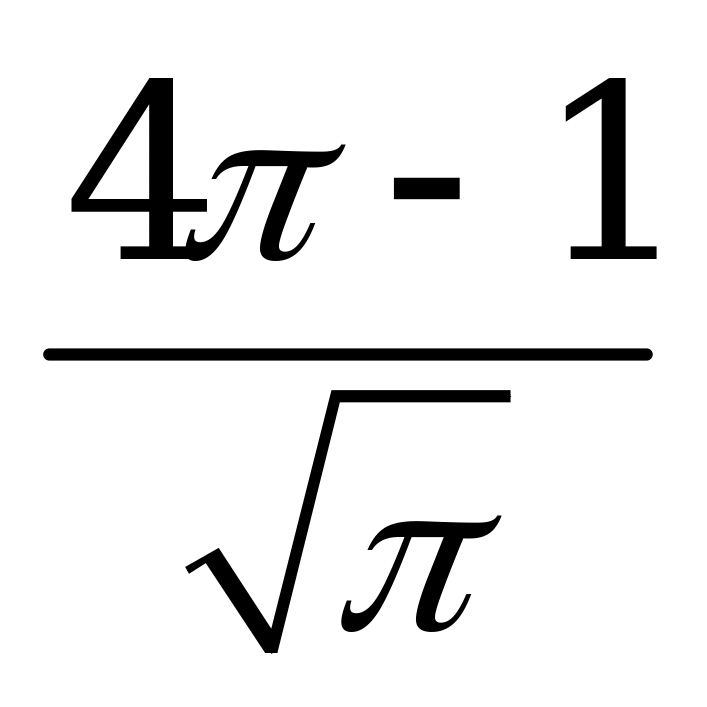 C) C) 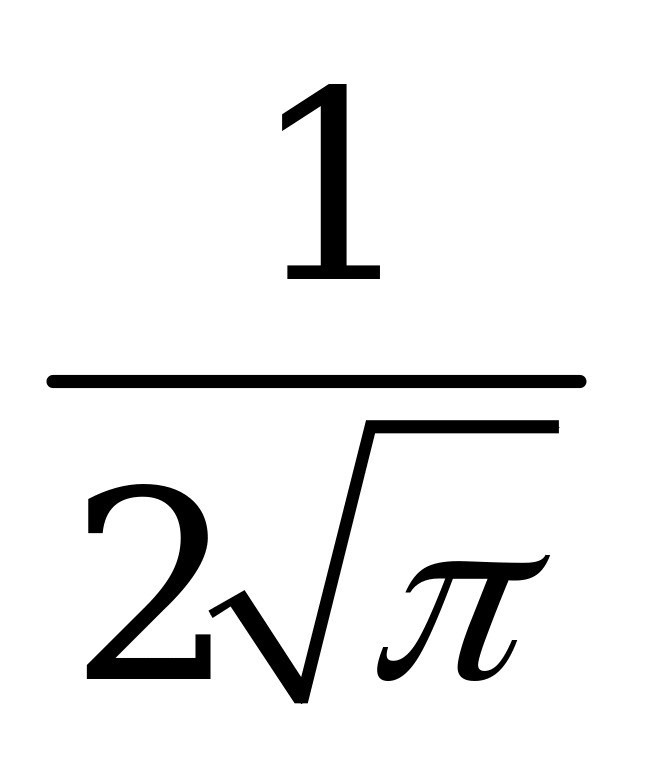 D) D) 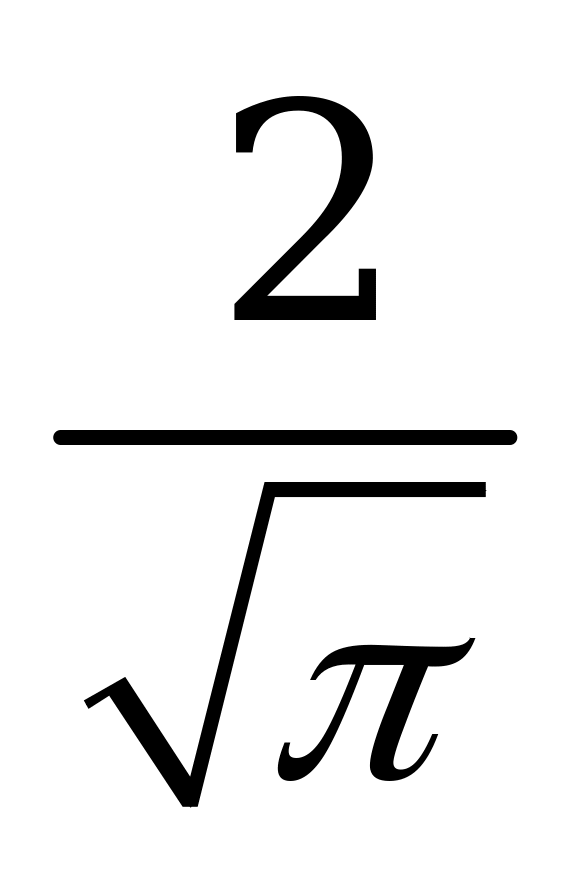 E) E) 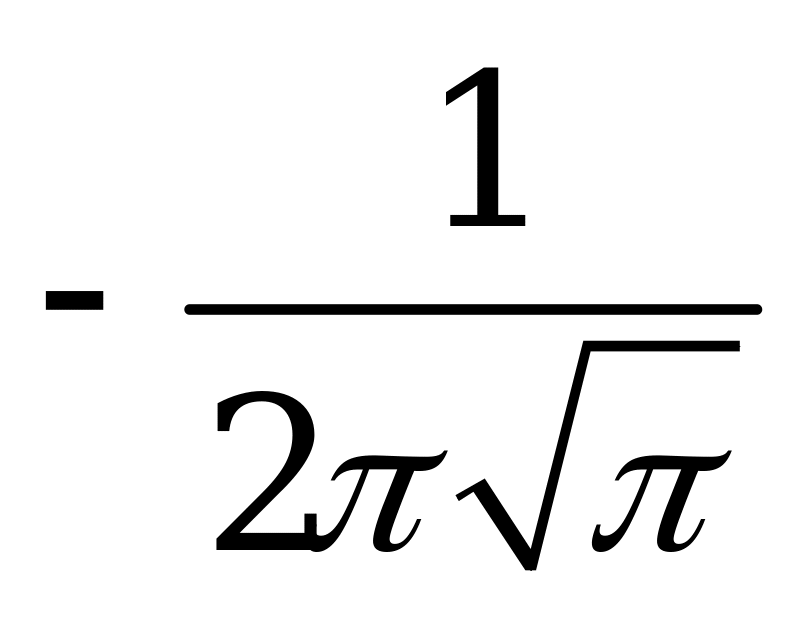 | Д |
| В3. Критические точки, интервалы монотонности функции | Ответы |
| В3.1 Найдите значение функции 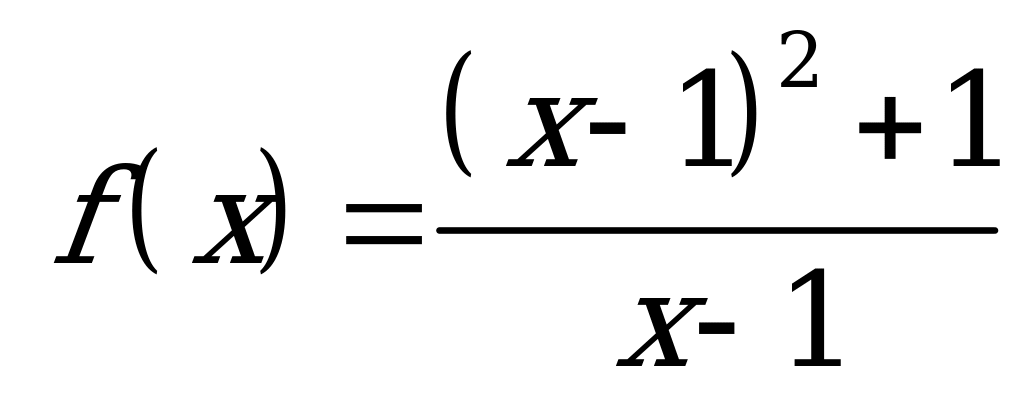 , в точке ее минимума. A) -1 B) 2 C) -2 D) 0 E) 1 , в точке ее минимума. A) -1 B) 2 C) -2 D) 0 E) 1 | В |
| В3.2 Найдите значение m – 2M, если m и M – значения функции 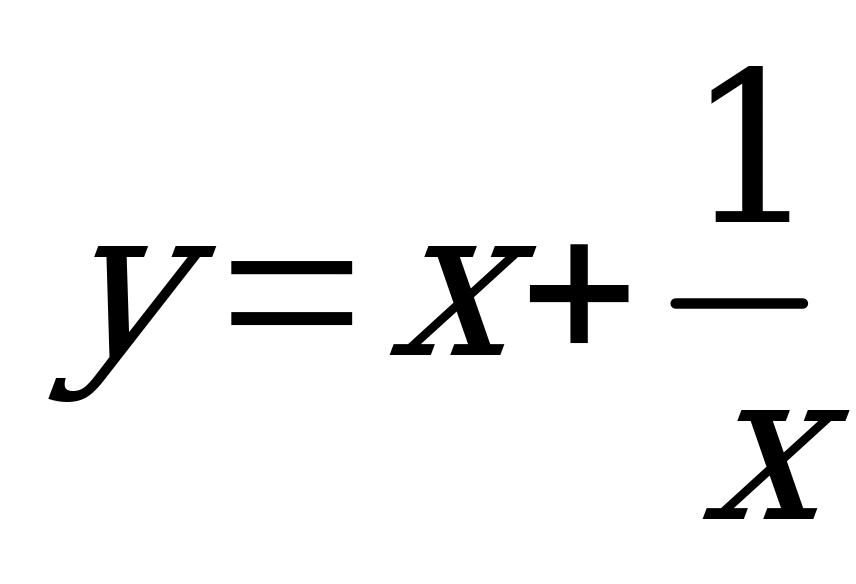 в точке минимума и максимума, соответственно. A) -6 B) 6 C) -4 D) 4 E) 3 в точке минимума и максимума, соответственно. A) -6 B) 6 C) -4 D) 4 E) 3 | В |
| В3.3 Найдите промежуток убывания функции y = x +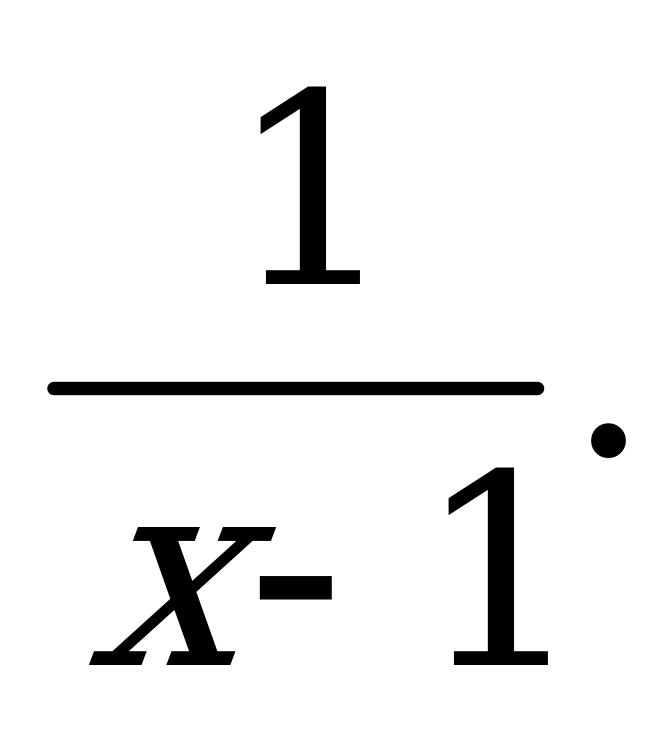 A) [0; 1)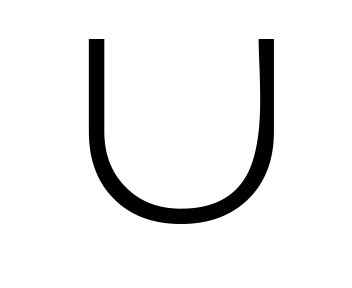 (1; 2] B) (0; 2) C) (0; 1) D) (1;2) E) (-; 0) (1; 2] B) (0; 2) C) (0; 1) D) (1;2) E) (-; 0)  (2; ) (2; ) | А |
| В3.4 Найдите разность между максимумом и минимумом функции 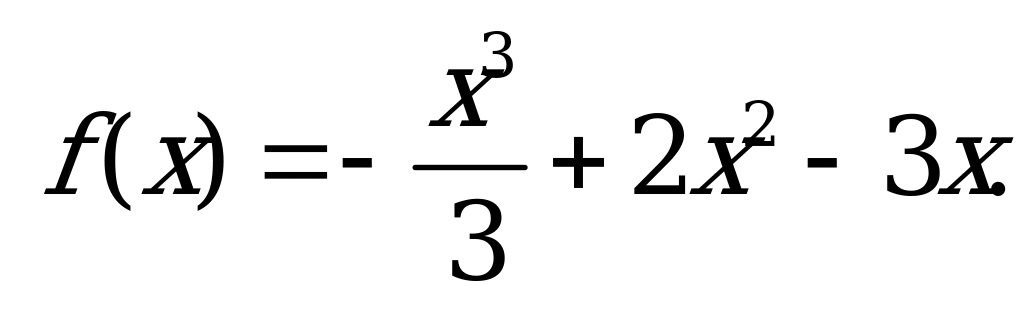 A) -1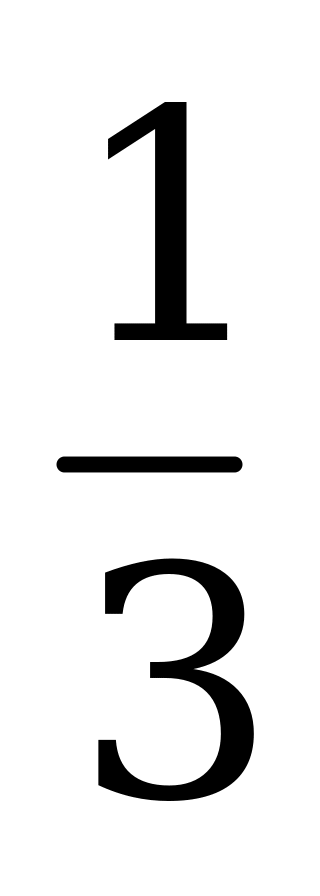 B) 1 B) 1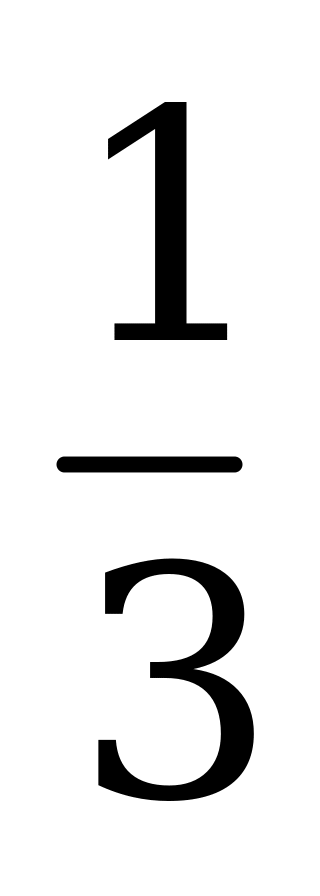 C) 1 C) 1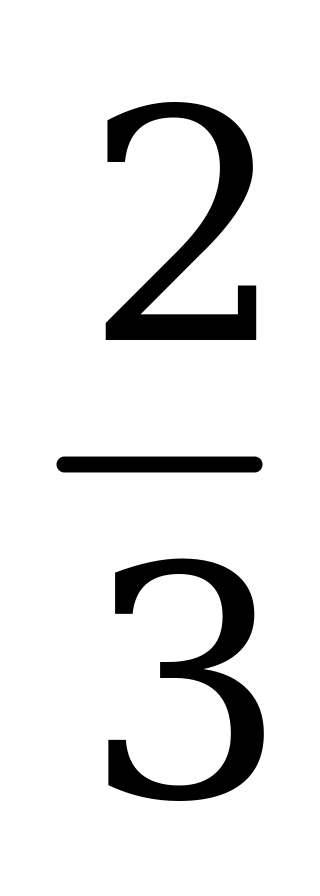 D) -1 D) -1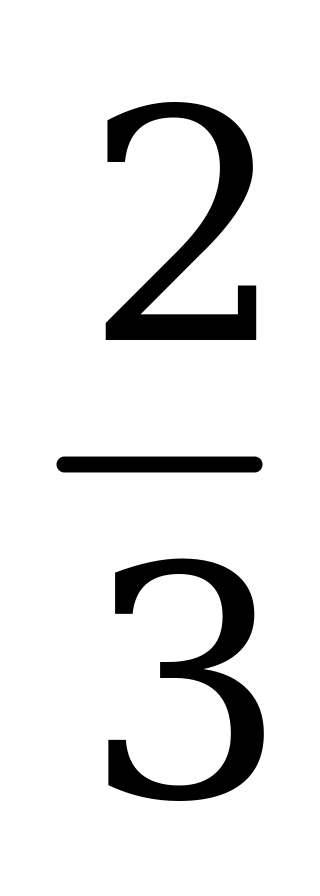 E) 1,5 E) 1,5 | В |
| В3.5 Найдите сумму критических точек функции Y =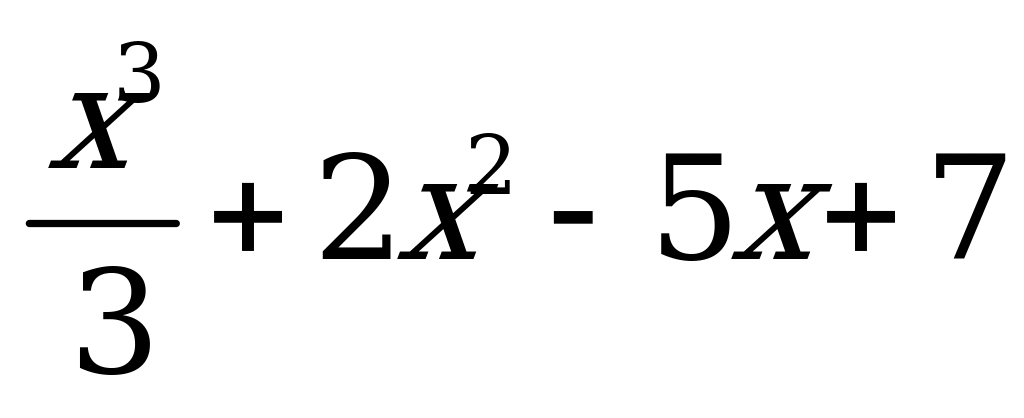 . A) –4 B) –5 C) 5 D) 4 E) -3 . A) –4 B) –5 C) 5 D) 4 E) -3 | А |
| В3.6 Найдите сумму минимумов функции f(x) = 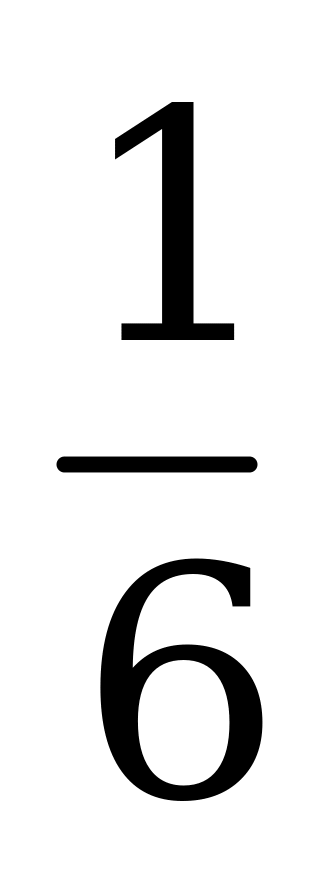 x6 – x6 – 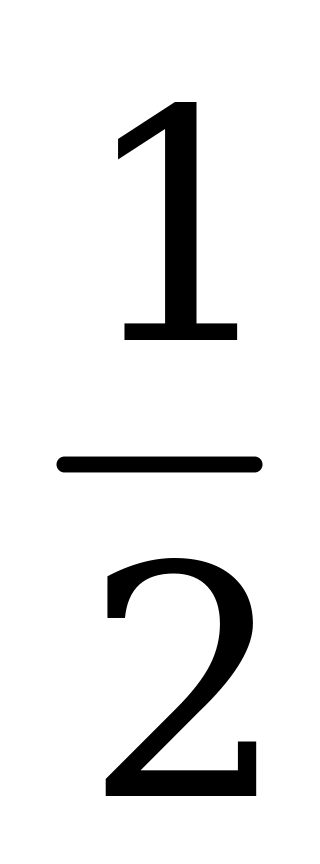 x2 + 4 x2 + 4 A) 4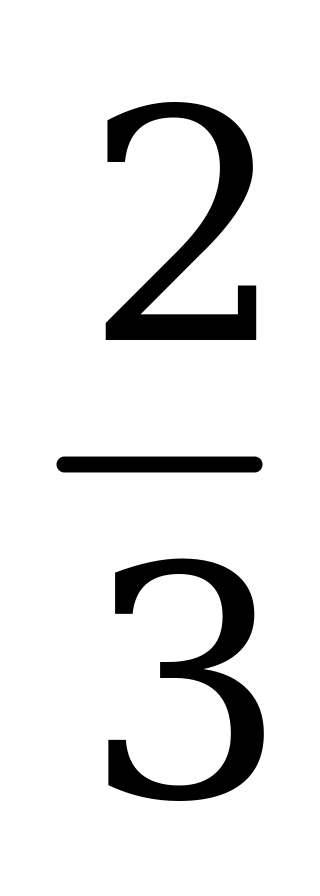 B) 7 B) 7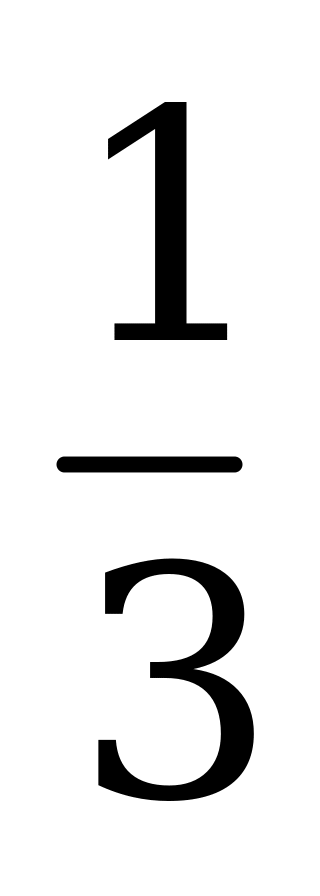 C) 6 C) 6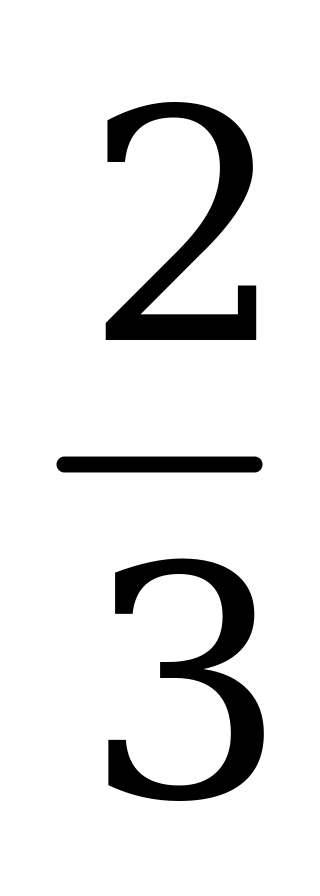 D) 3 D) 3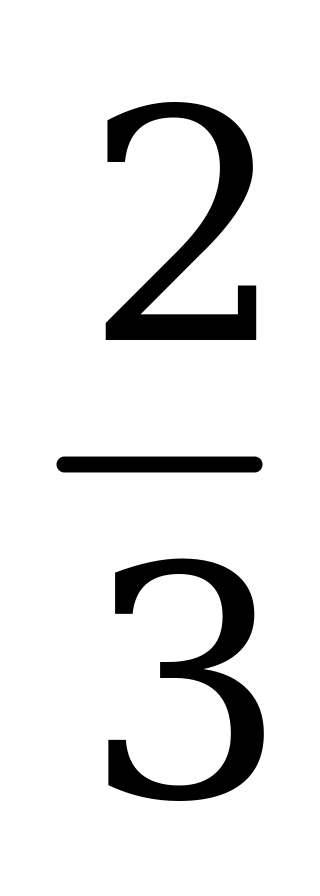 E) 5 E) 5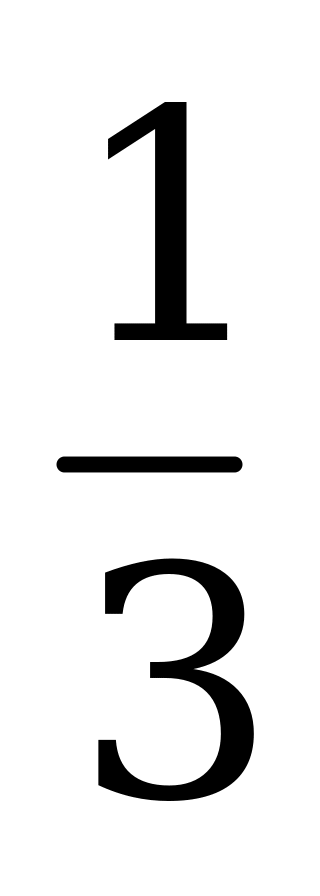 | В |
| В3.7 Найдите промежутки возрастания функции 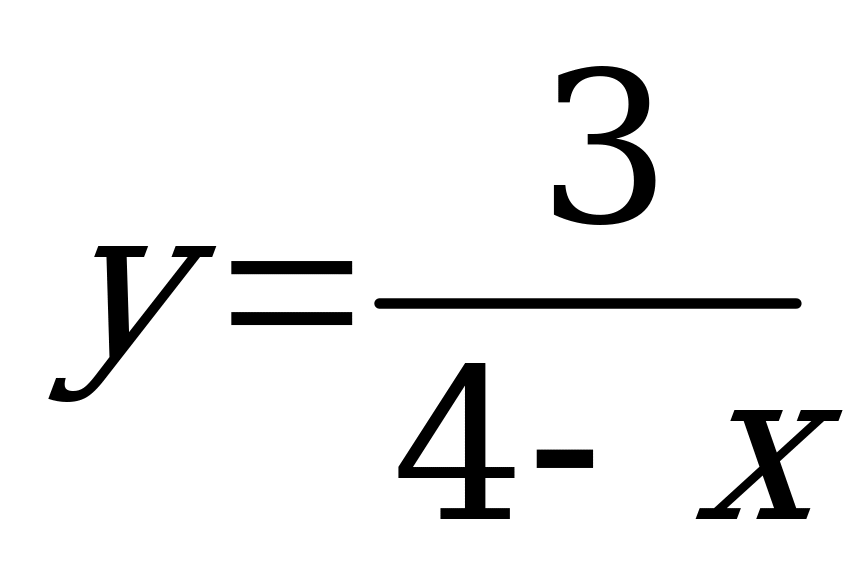 . A) (- . A) (- ; 4) ; 4)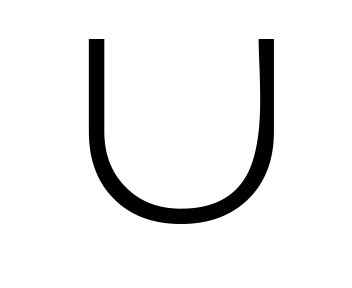 (4; (4;  ) B) R ) B) R C) (- ; ;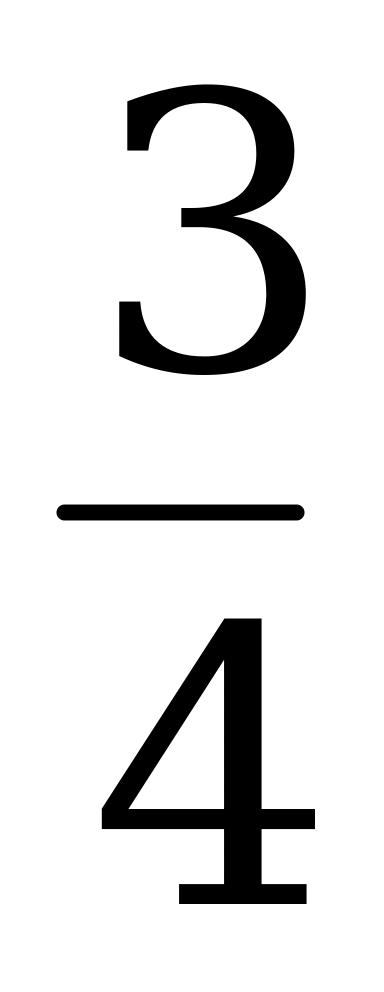 ) )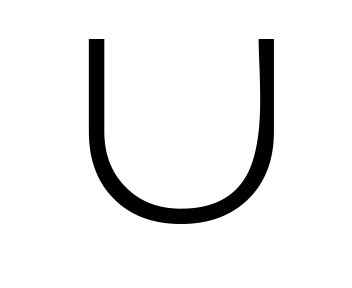 ( (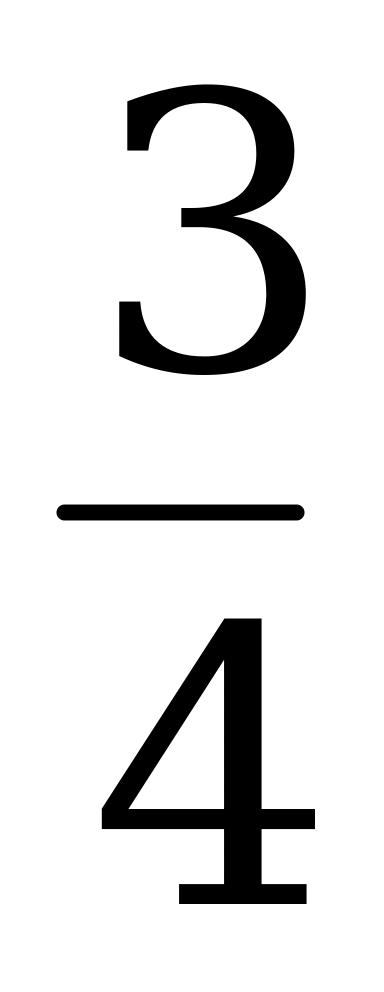 ; ; ) D) R+ E) [4; ) D) R+ E) [4;  ) ) | А |
| В3.8 Найдите точку минимума x=x0 функции f(x) = 0,9x5–4,5x3+4. A) -1 B) 1 C) 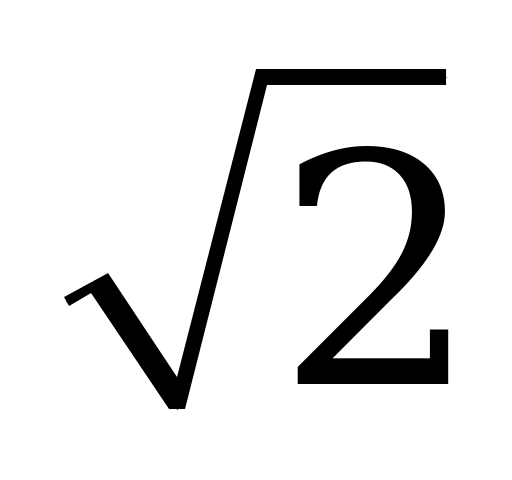 D) - D) -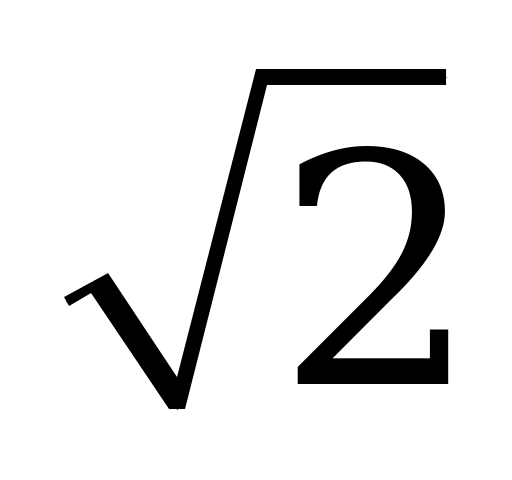 E) E) 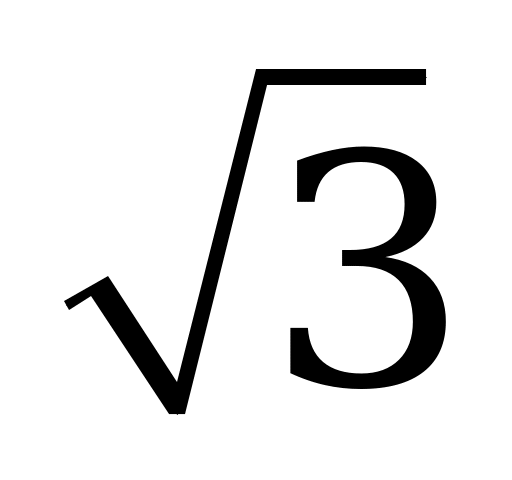 | Е |
| В3.9 Укажите промежутки возрастания функции 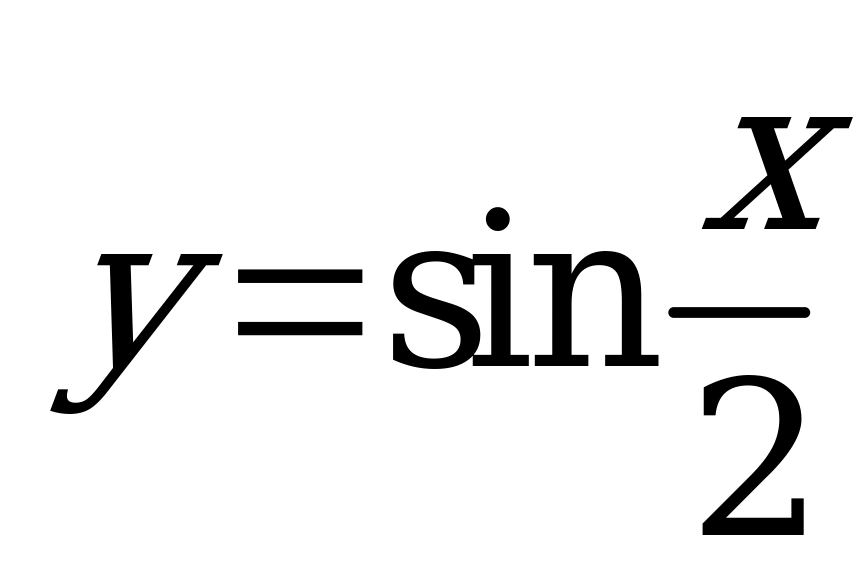 . . A)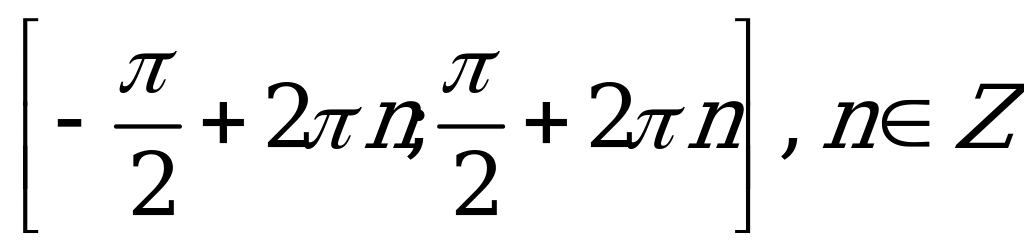 B) B) 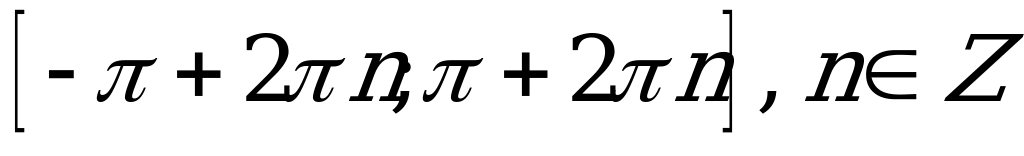 C)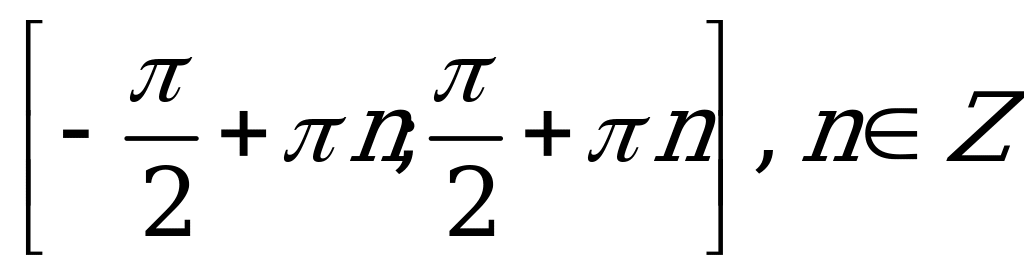 D) D) 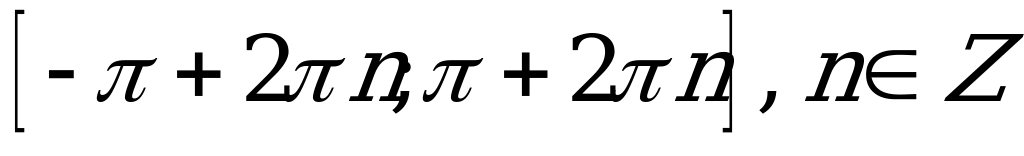 E) 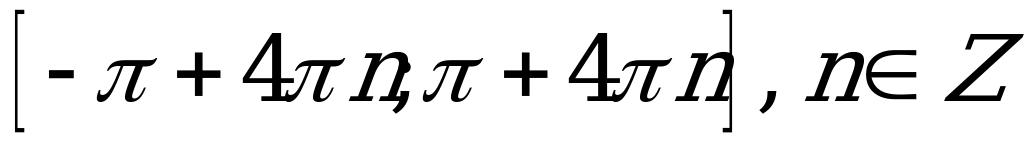 | Е |
| В3.10 Найдите модуль разности экстремальных значений функции y = x3 – 3x2 – 9x + 12 A) 20 B) 12 C) 4 D) 2 E) 32 | Е |
| В4. Наибольшее, наименьшее значение функции | Ответы |
| В4.1 Найдите сумму значений функции 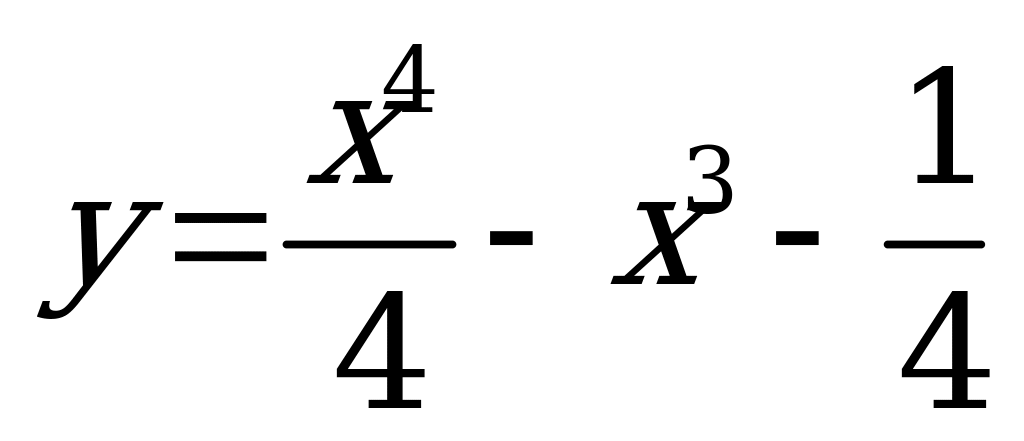 в точках экстремумов функции. в точках экстремумов функции. A) 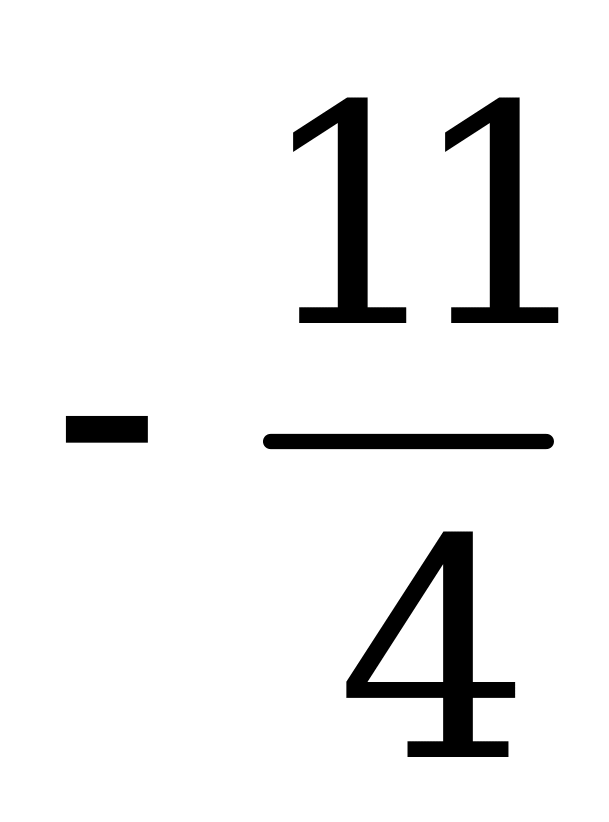 B) -9 C) -7 D) -5 E) B) -9 C) -7 D) -5 E) 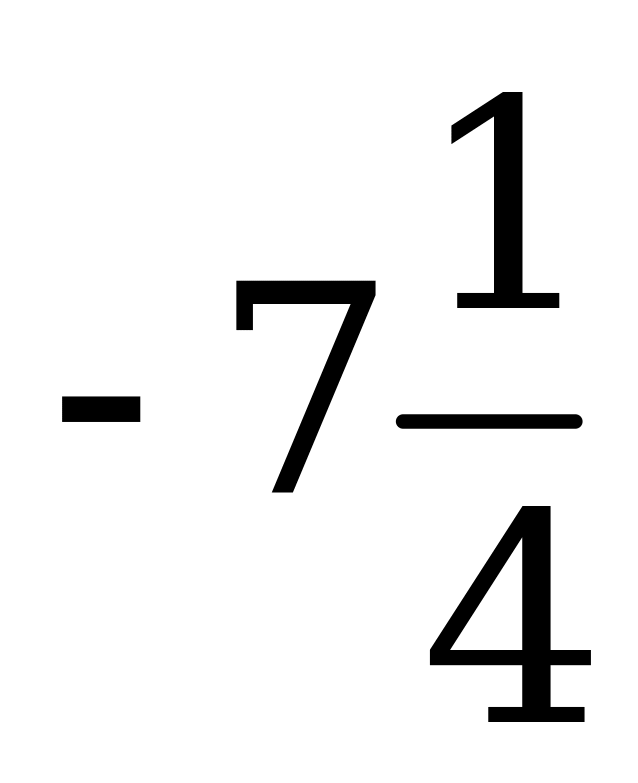 | С |
| В4.2 На отрезке [0,25; 1] найдите наибольшее значение функции 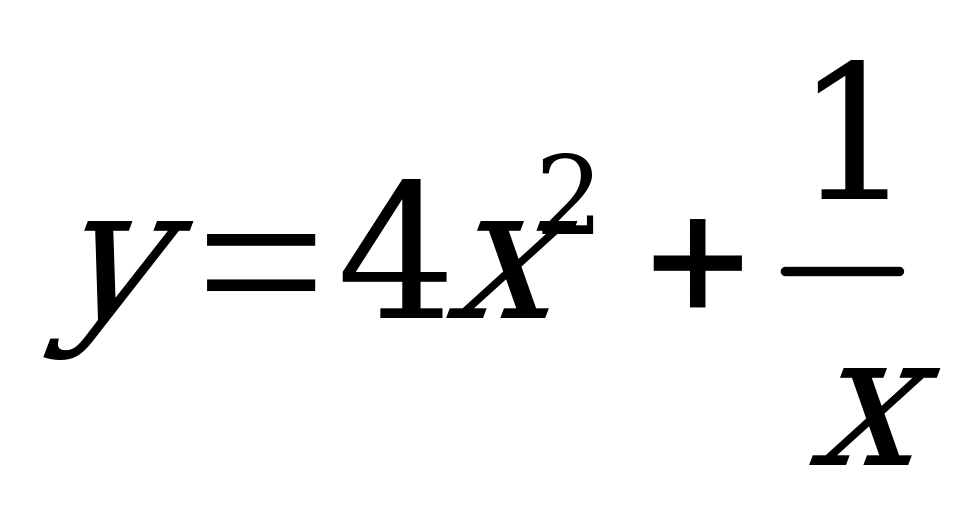 A) 3 B) 4,25 C) 4,5 D) 5 E) 5,25 | Д |
| В4.3 Найдите сумму наименьшего и наибольшего значений функции 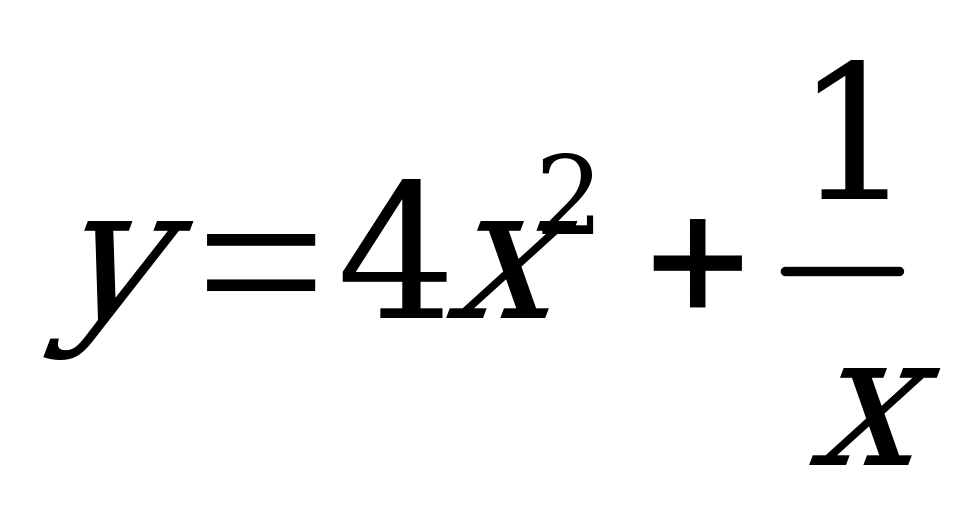 на отрезке на отрезке 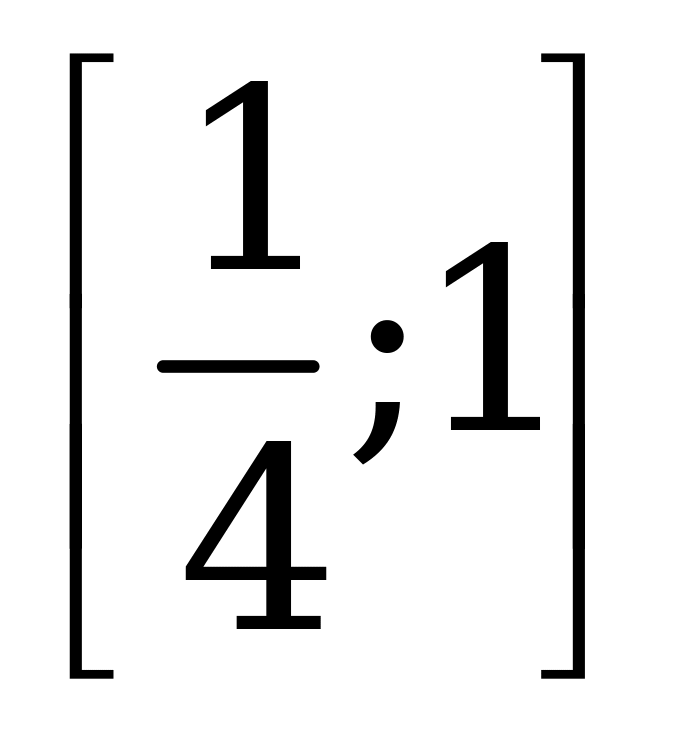 A) 7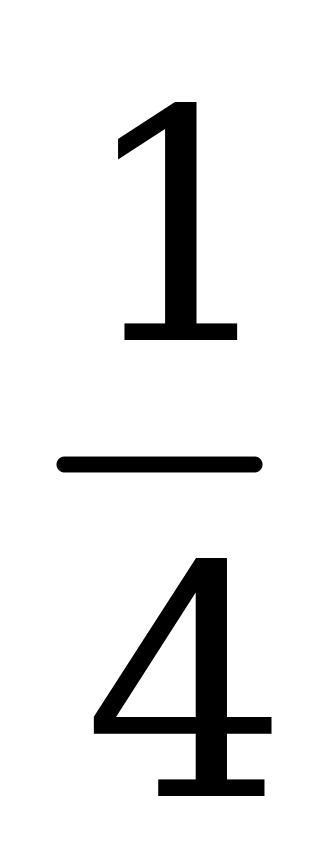 B) 9 B) 9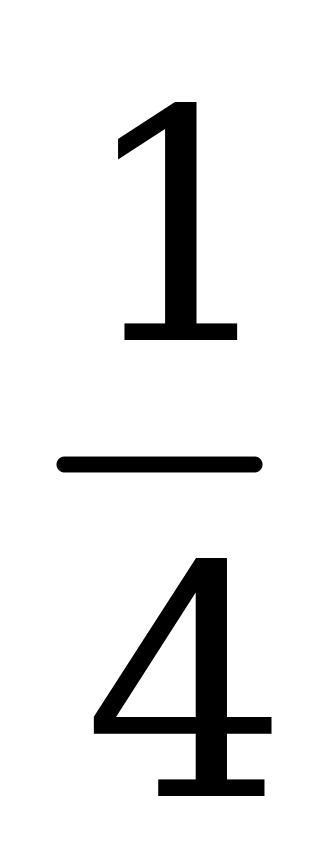 C) 10 C) 10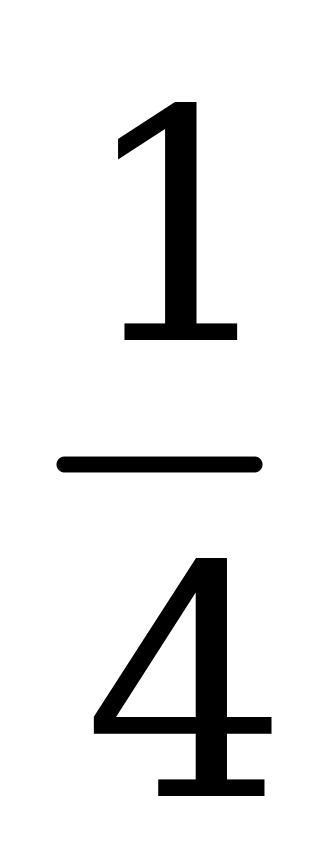 D) 6 E) 8 D) 6 E) 8 | Е |
| В4.4 Укажите наименьшее значение выражения 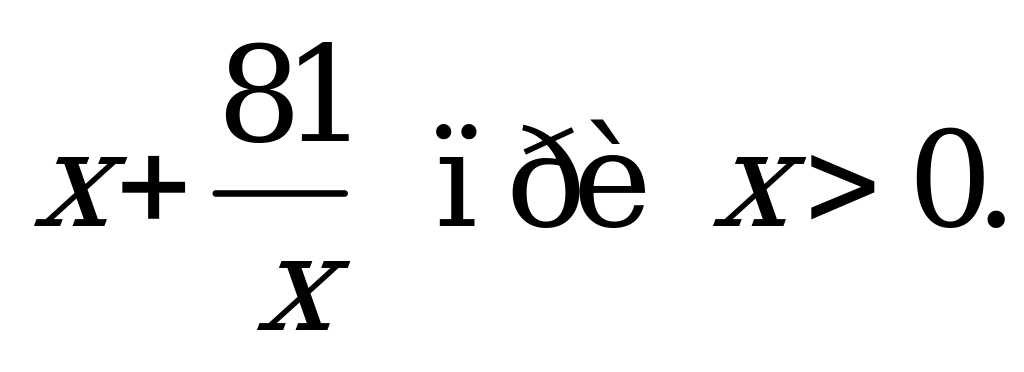 A) 30 B) 24 C) 6 D) 12 E) 18 A) 30 B) 24 C) 6 D) 12 E) 18 | Е |
| В4.5 Найдите наименьшее значение функции 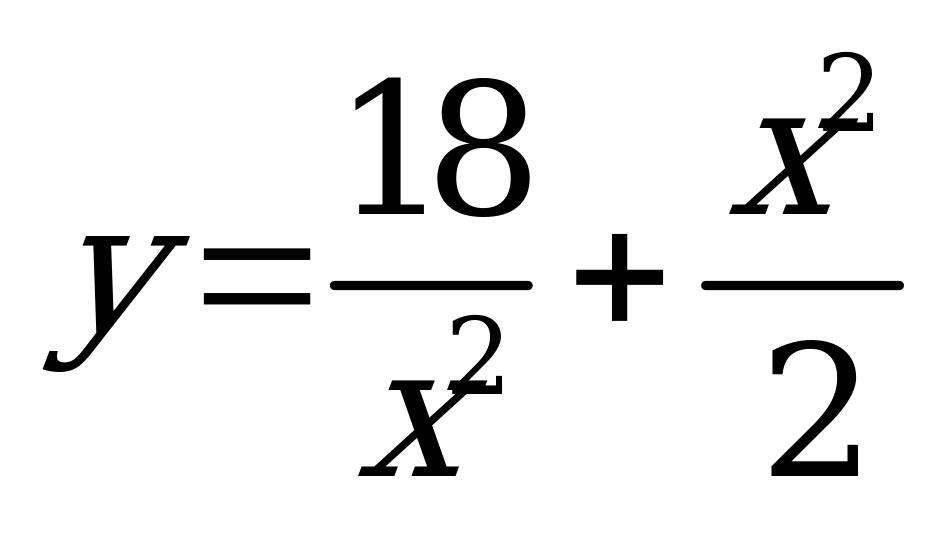 . . A) 6 B) 5 C) 4 D) 3 E) 2 | А |
| В4.6 Найти наименьшее значение функции: 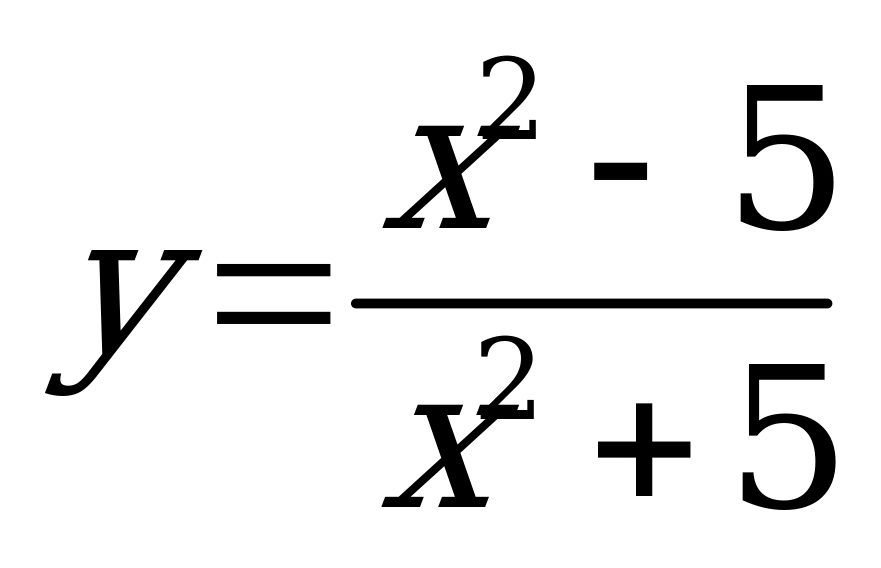 . . A) 5 B) -5 C) -1 D) 1 E) 0 | С |
| В4.7 Укажите наибольшее значение функции f(x)= sin 2x – 2 cosx на отрезке cosx на отрезке 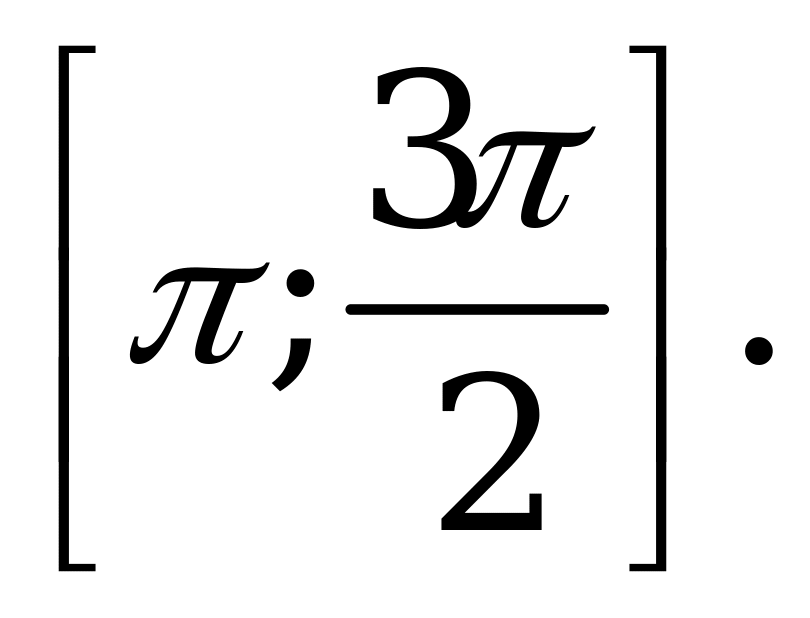 A) 1,5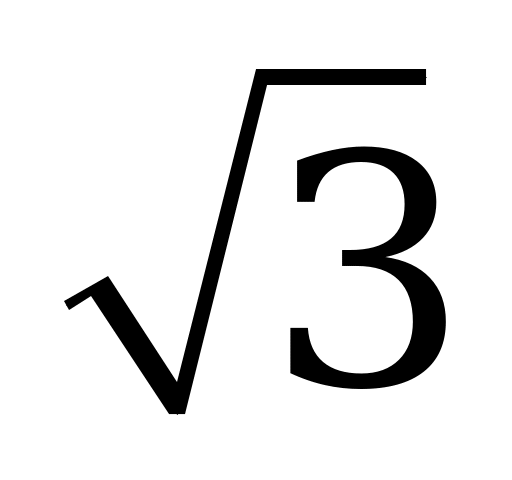 B) 0 C) 3 D) 2 E) 2 B) 0 C) 3 D) 2 E) 2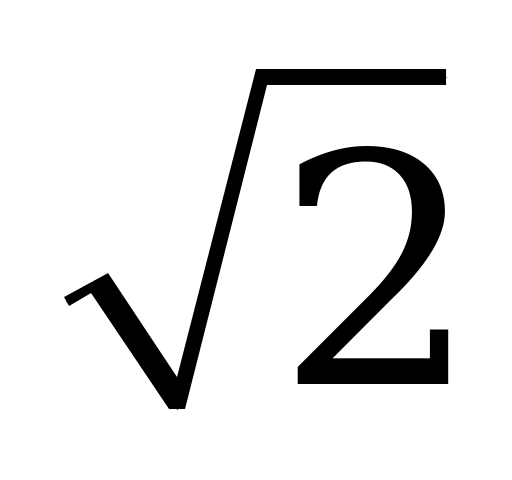 | А |
| В4.8 Найдите сумму наибольшего и наименьшего значений функции 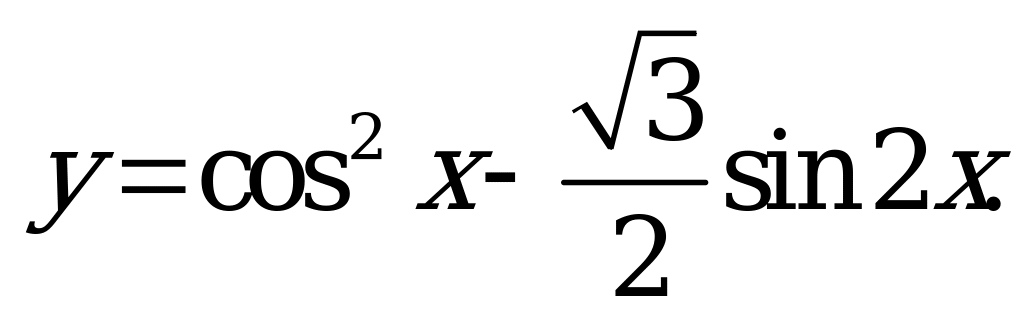 A) 1,5 B) 0,5 C) 1 D) 2 E) 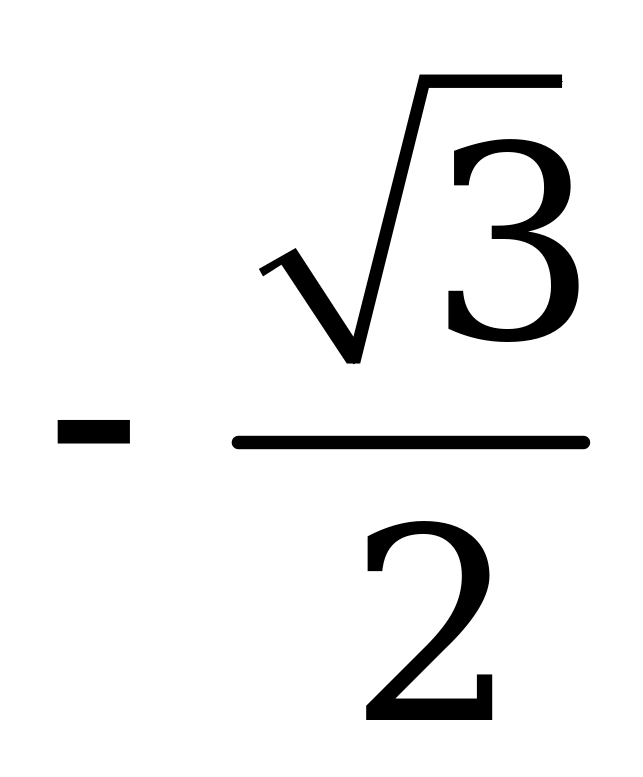 | С |
| В4.9 Найдите наименьшее значение функции y = 3cos23x - 3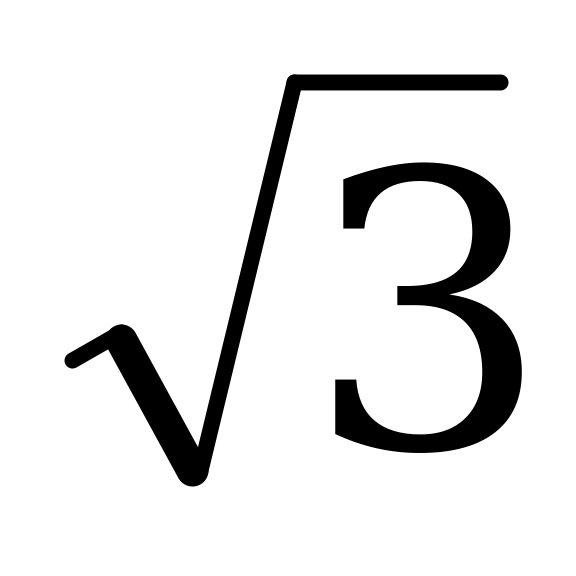 cos3x – sin23x + 4 cos3x – sin23x + 4 A) 1,545 B) 1,2325 C) 2,1413 D) 1,3125 E) 2,125 | Д |
| В4.10 Если y = x3 + 1 и -1 x y? A) (-1: ) B) (0; 9) C) (1; 8) D) (-1; 9) E) (2; 9) | В |
| В5. Уравнение касательной функции | Ответы |
| В5.1 Чему равно расстояние до начала координат от точки, в которой касательная к кривой 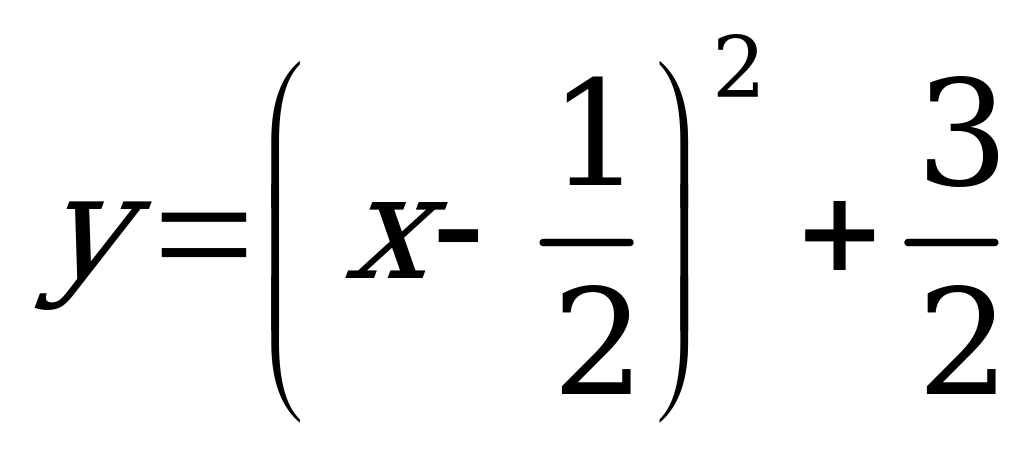 параллельна прямой y = 3x + 7? параллельна прямой y = 3x + 7? A) 5,5 B) 3,75 C) 4,25 D) 6,85 E) 4,75 | С |
| В5.2 Найдите уравнение касательной к кривой y = -x2 – 2, которая параллельна прямой y = 4x + 1. A) y = 4x + 6 B) y = 4x - 6 C) y = 4x - 2 D) y = 4x + 2 E) y = 4x +10 | Д |
| В5.3 Под каким углом график функции 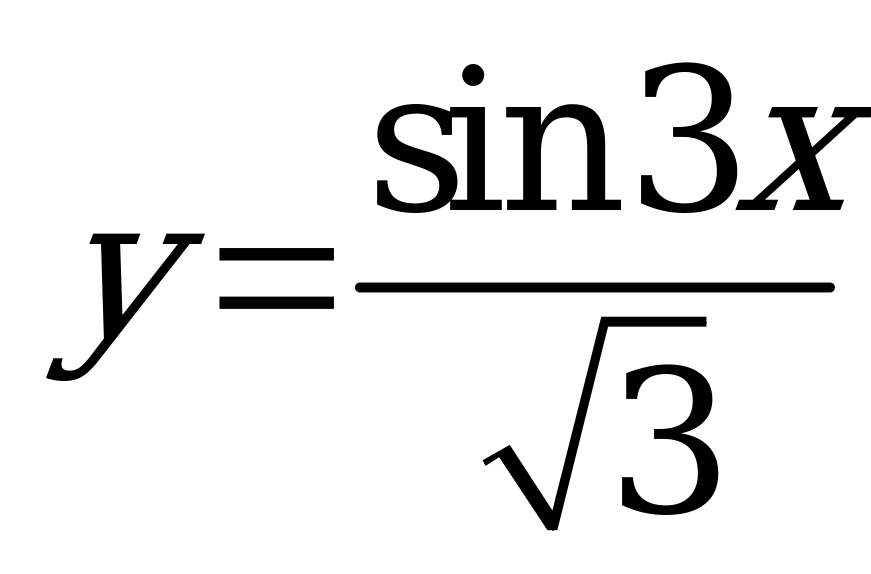 пересекает в начале координат ось абсцисс? пересекает в начале координат ось абсцисс? A) 300 B) 600 C) 750 D) 800 E) 500 | В |
| В5.4 Чему равны абсциссы точек, в которых касательная к графику функции 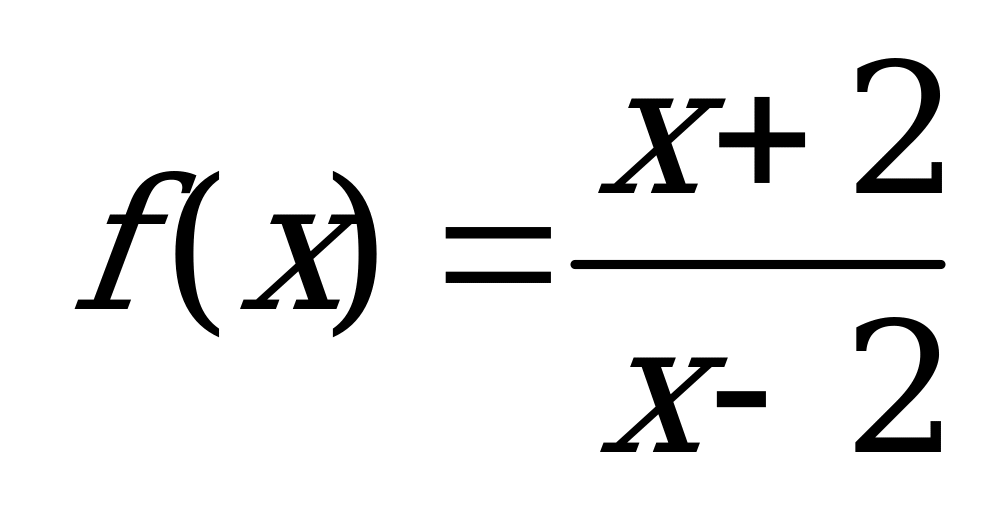 образует с положительными направлением оси Ox угол в 1350? образует с положительными направлением оси Ox угол в 1350? A) 1 и 4 B) 2 и 3 C) 0 и 5 D) 1 и 5 E) 0 и 4 | Е |
| В5.5 Определите уравнение касательной к кривой 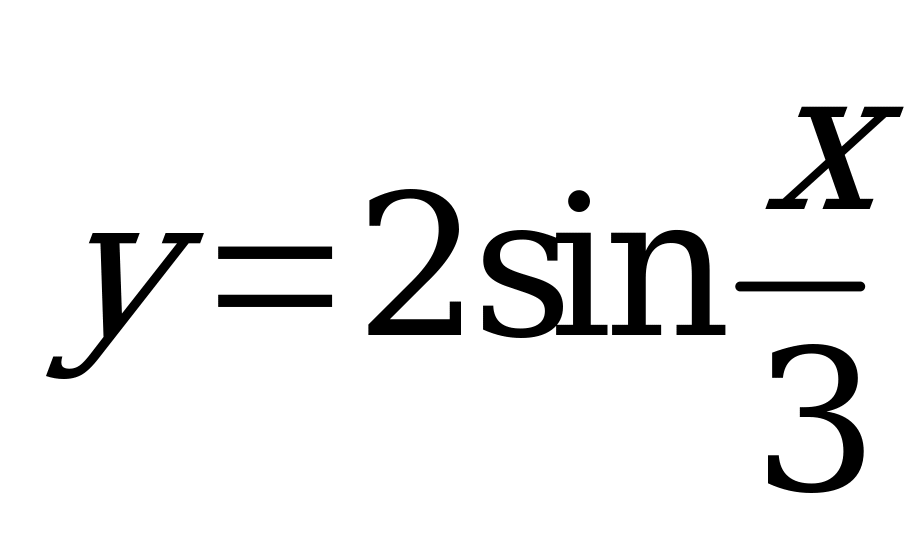 , проведённой в точке , проведённой в точке 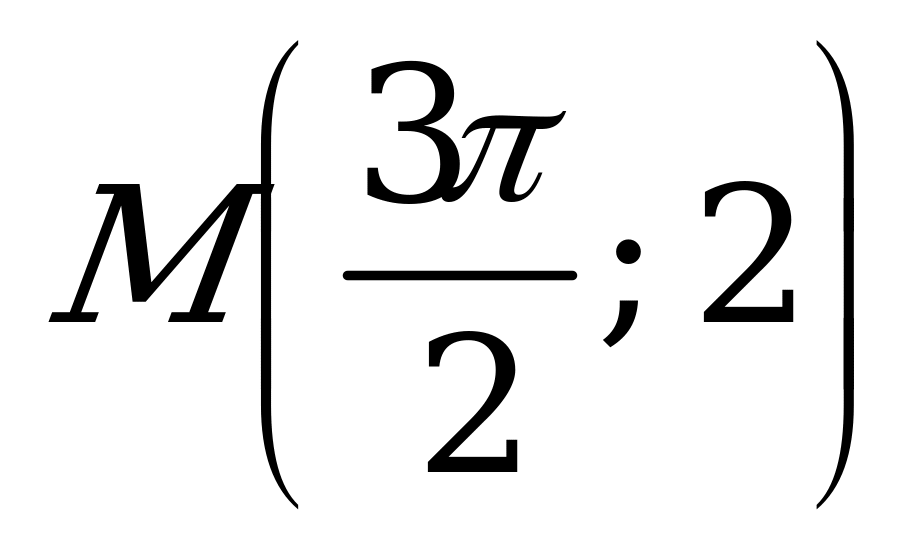 A) y = 2 B) y - 1 = 0 C) y = x D) y = x – 2 E) y = -2x | А |
| В5.6 Укажите уравнение касательной, проведенной к кривой f(x) = cos2x в точке 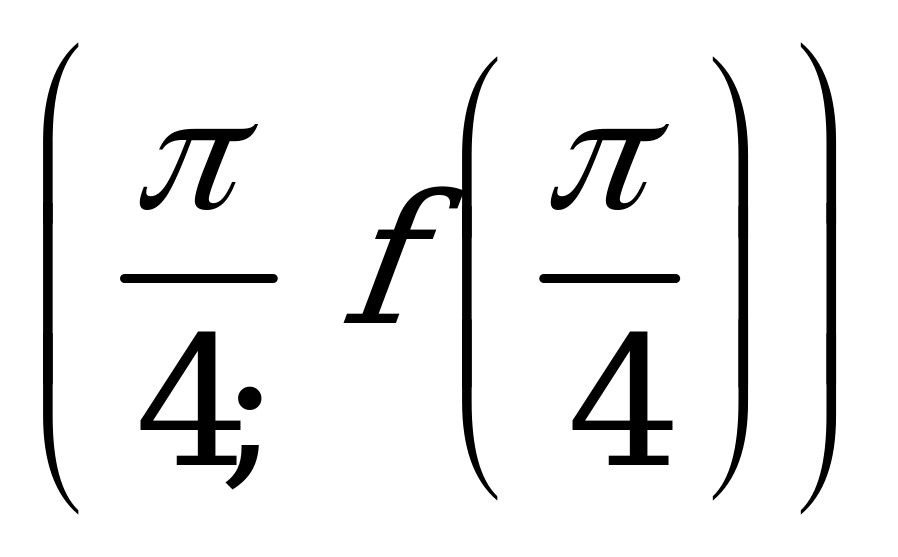 . . A) 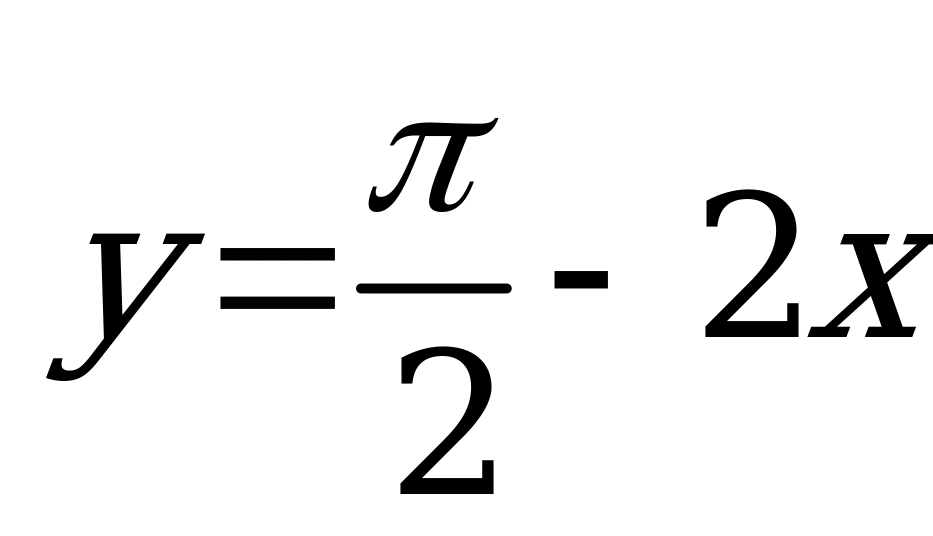 B) B) 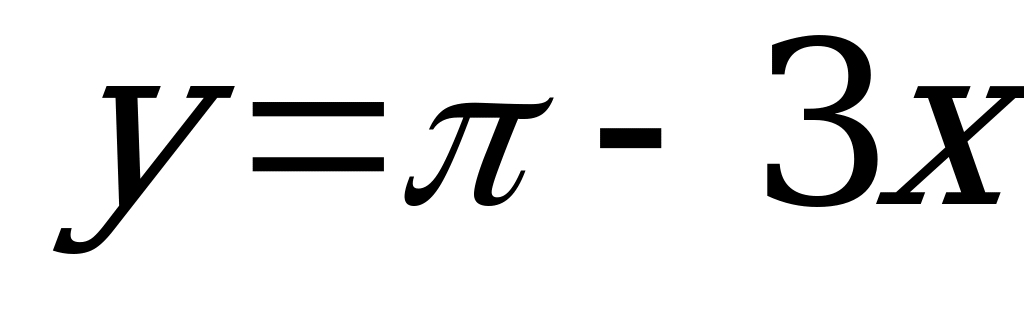 C) C) 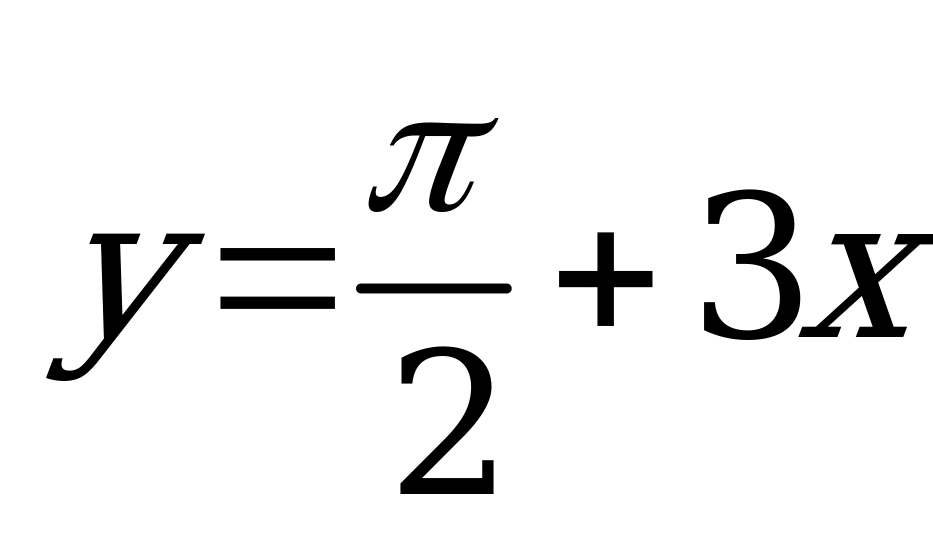 D) 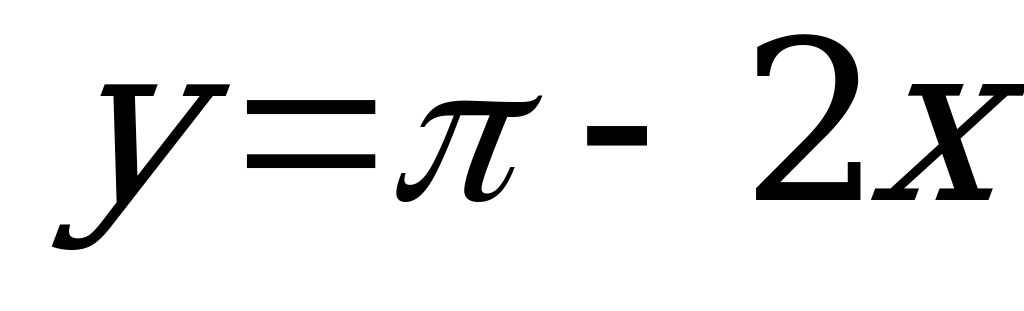 E) E) 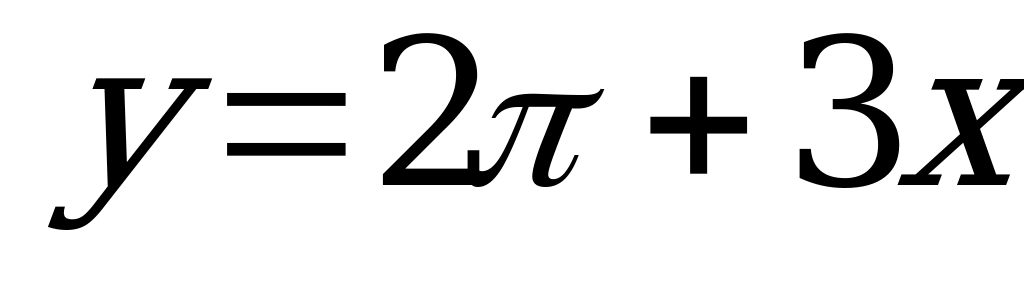 | А |
| В5.7 Определите уравнение касательной к графику функции f(x) = 4 - x2 , проведенной в точке пересечения этого графика с положительным направлением оси абсцисс. A) y = -4x + 8 B) y = 4x + 8 C) y = 2x – 3 D) y = -2x + 5 E) y = -4x | А |
| В5.8 К графику функции y = x2 + 3x + 2 в точке с абсциссой x = 0 проведена касательная. Найдите ординату точки касания, абсцисса которой x = 11. A) 36 B) 33 C) 35 D) 32 E) 34 | С |
| В5.9 К параболе y = 4 - x2 в точке с абсциссой x0 = 1 проведена касательная. Найдите координаты точки пересечения этой касательной с осью OY. A) (0; 5) B) (0; 1) C) (0; -5) D) (0; -1) E) (0; 2) | А |
| В5.10 Через точку М(1; 8) к графику функции 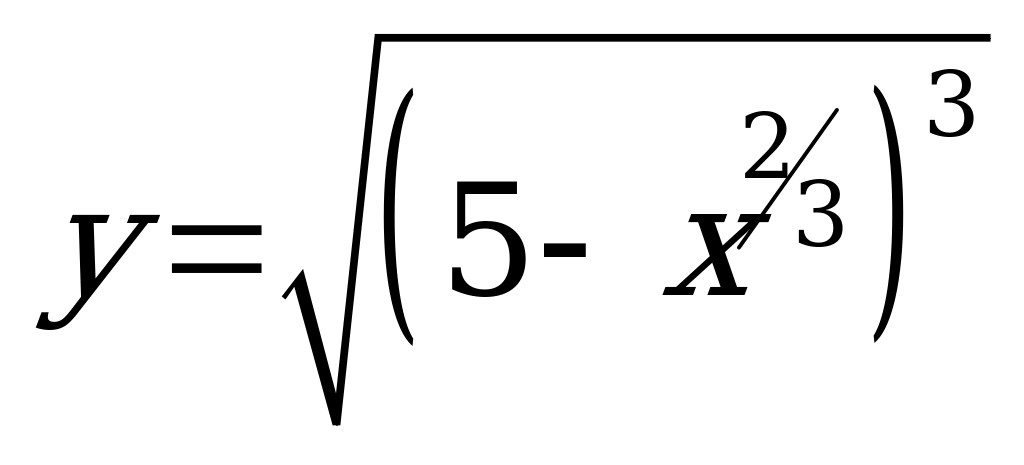 проведена касательная. Найдите длину, лежащего между координатными осями отрезка этой касательной. проведена касательная. Найдите длину, лежащего между координатными осями отрезка этой касательной. A) 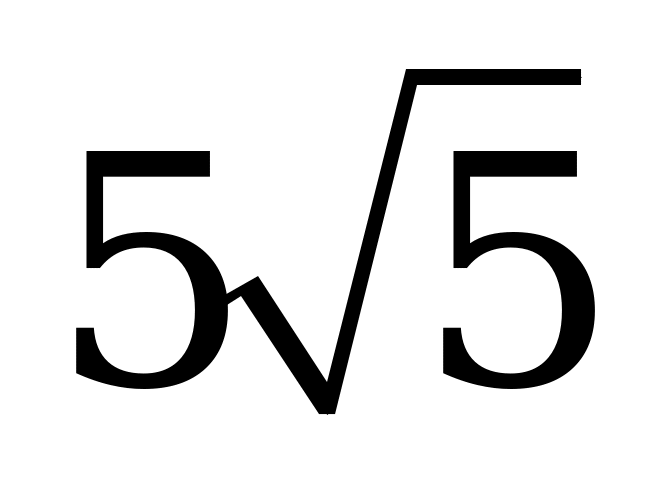 B) 10 C) 5 D) B) 10 C) 5 D) 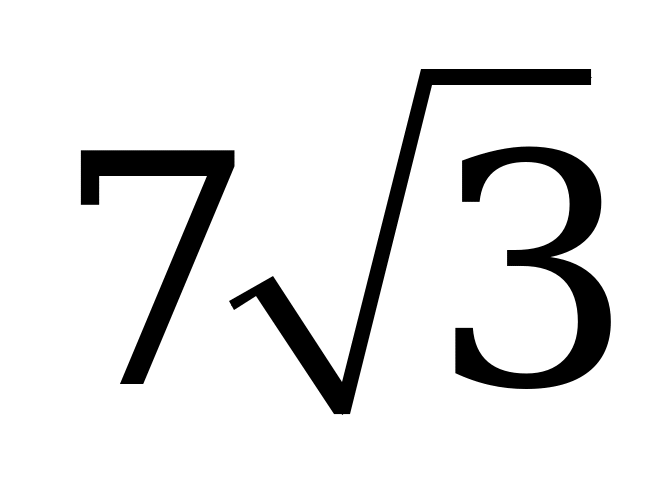 E) E) 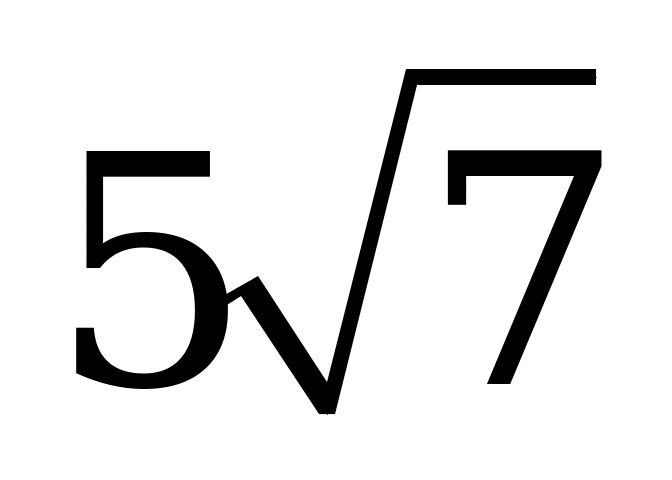 | А |
| В6. Уравнения движения материальной точки | Ответы |
| В6.1 Материальная точка движется по прямой согласно закону S(t) = 6t2 - 2t3 +5. Чему была равна мгновенная скорость, когда ускорение было равно 0 ? A) 8 B) 6 C) 7 D) 9 E) 6,5 | В |
| В6.2 Материальная точка движется согласно закону s(t) = t4 (км). Чему будет равна ее скорость, когда пройденный путь будет равен 16 км (время измеряется в часах)? A) 28 км/ч B) 30 км/ч C) 34 км/ч D) 32 км/ч E) 26 км/ч | Д |
| В6.3 Материальная точка движется прямолинейно. Ее скорость изменяется согласно закону 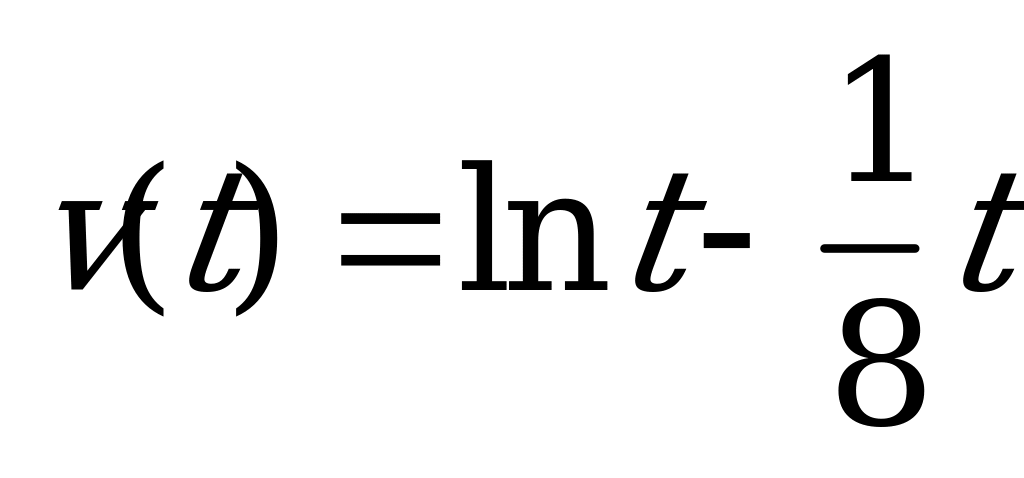 (м/с). В какой момент времени (сек) ее ускорение будет равно 0? A) 6 B) 7 C) 8 D) 9 E) 5 (м/с). В какой момент времени (сек) ее ускорение будет равно 0? A) 6 B) 7 C) 8 D) 9 E) 5 | С |
| В6.4 Сколько метров проедет машина за первые 6 с, если она движется прямолинейно со скоростью v(t) = (t2 + t) m/c? A) 80 B) 85 C) 90 D) 96 E) 94 | С |
| В6.5 Сколько метров пройдет материальная точка за первые 6 с, если она движется прямолинейно со скоростью v(t) = (t2 - t + 1) м/с ? A) 54 B) 64 C) 56 D) 62 E) 60 | Е |
| В6.6 Материальная точка движется прямолинейно. Ее скорость определяется уравнением: V(t) = 3t2 - 2t + 2 (м/с). Чему равен путь (м), пройденный этой точкой от начала движения до 3с ? A) 24 B) 26 C) 22 D) 20 E) 25 | А |
| В6.7 Материальная точка движется прямолинейно согласно закону 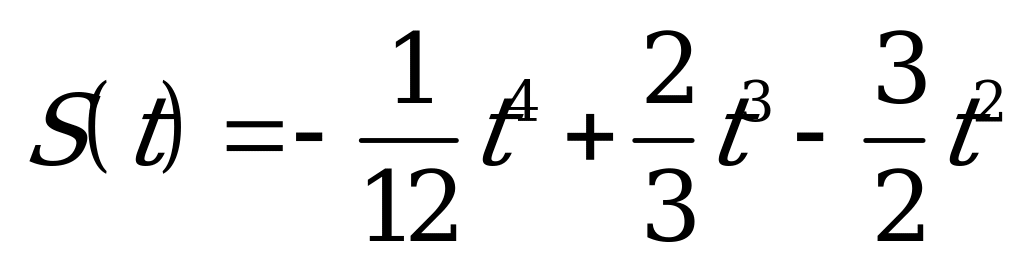 (м). В какой момент времени (с) ее ускорение будет наибольшим? (м). В какой момент времени (с) ее ускорение будет наибольшим? A) 1,5 B) 2,5 C) 3 D) 1,75 E) 2 | Е |
| В6.8 Найдите наибольшую скорость тела, движущего по закону S(t)=4t2 - t3/3 A) 16 B) 20 C) 12 D) 24 Е) 36 | А |
|
| Ответы |
| С1 Найдите x из уравнения 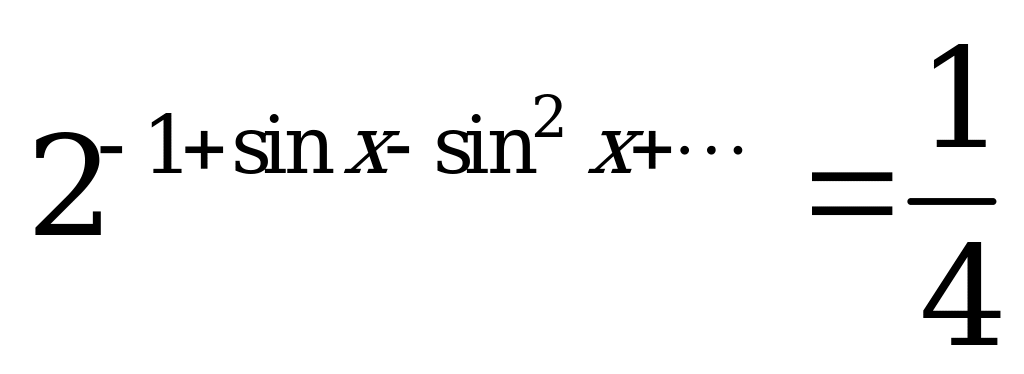 A) 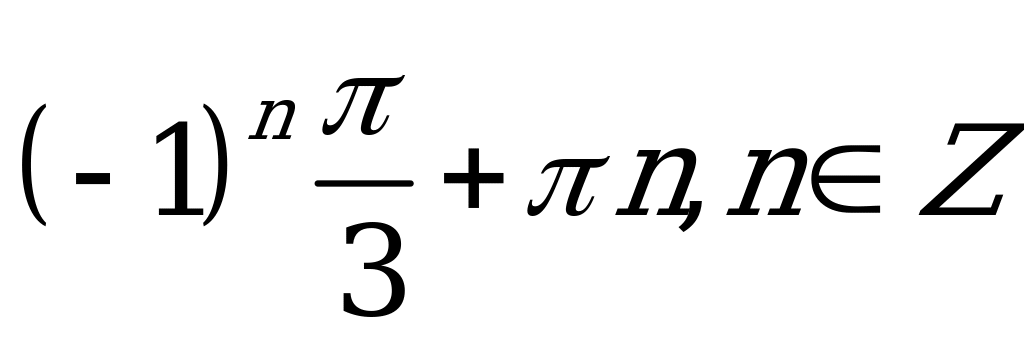 B) B) 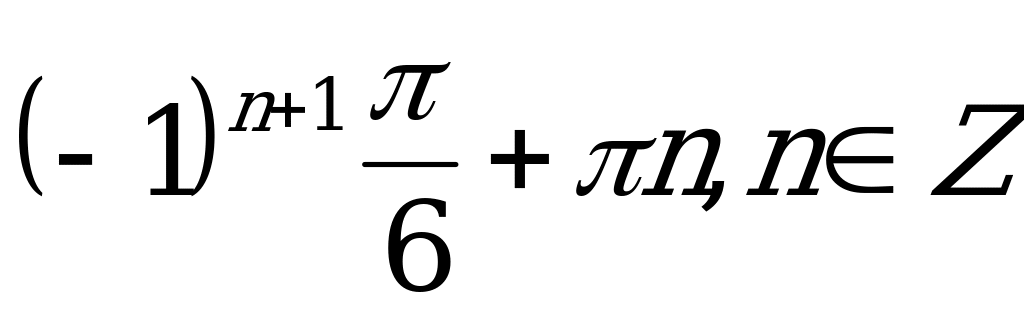 C) 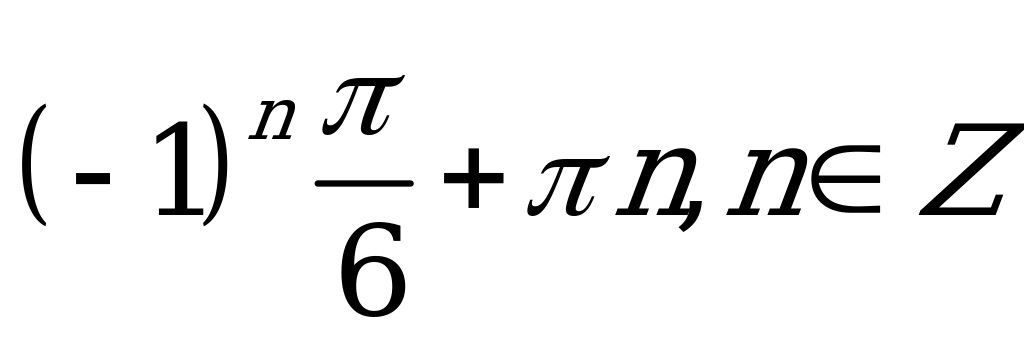 D) D) 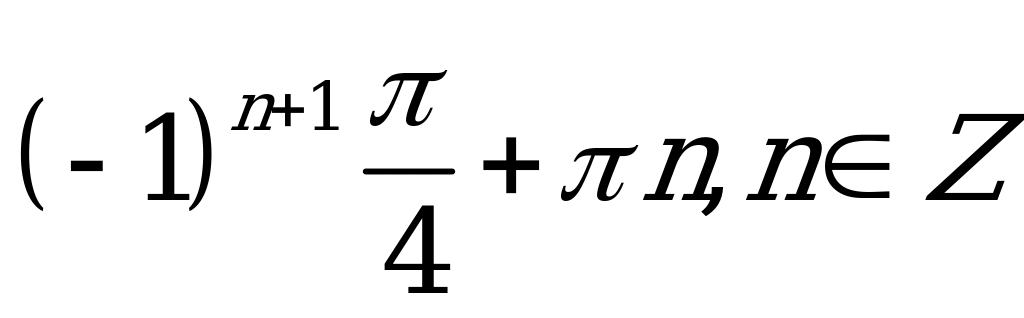 E) 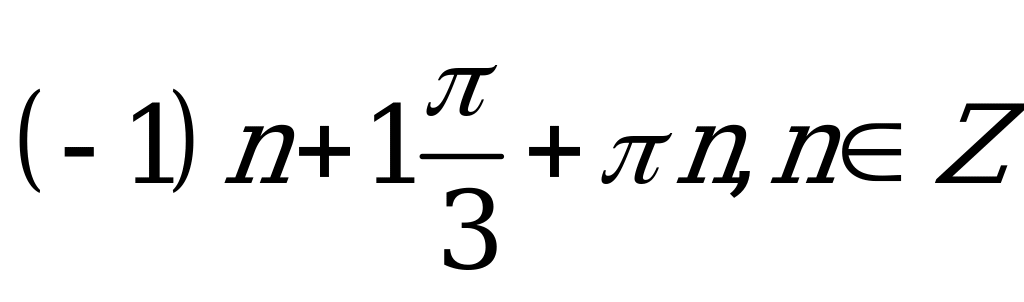 | В |
| С2 При каких значениях x для функций f(x) = sinx и g(x) = 5x + 3 выполняется неравенство f '(x) g '(x) A) (- ; 5) B) ; 5) B) 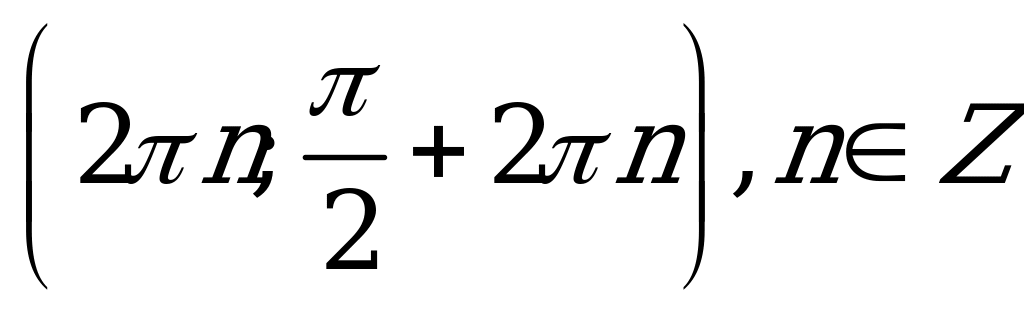 C) (- C) (- ; ; ) ) D) (0;  ) E) (- ) E) (- ; 0) ; 0) | С |
| С3 Даны две функции 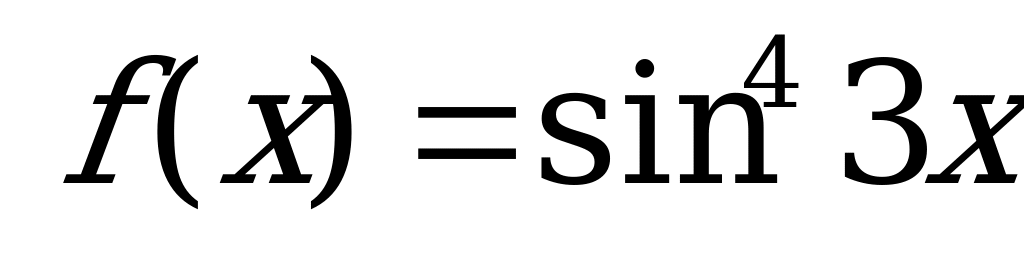 и и 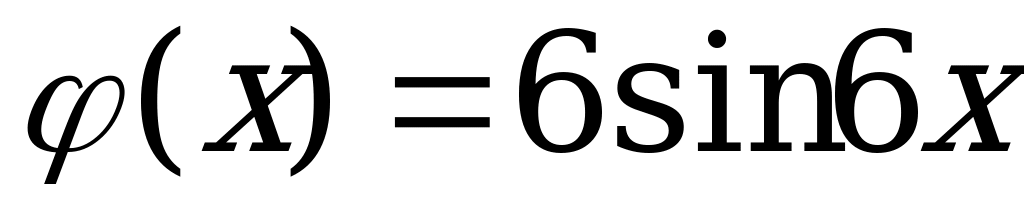 . Найдите все x, для которых . Найдите все x, для которых 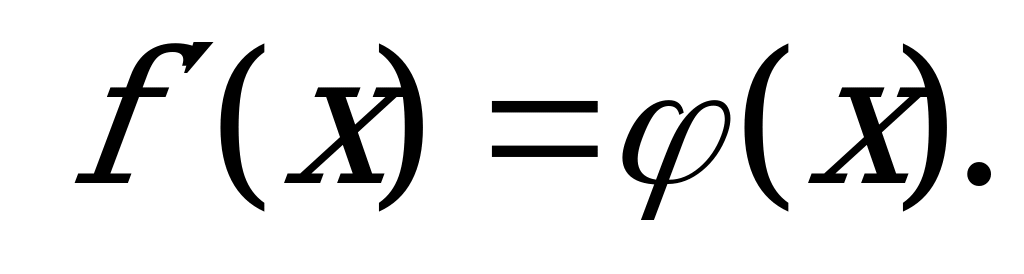 A) 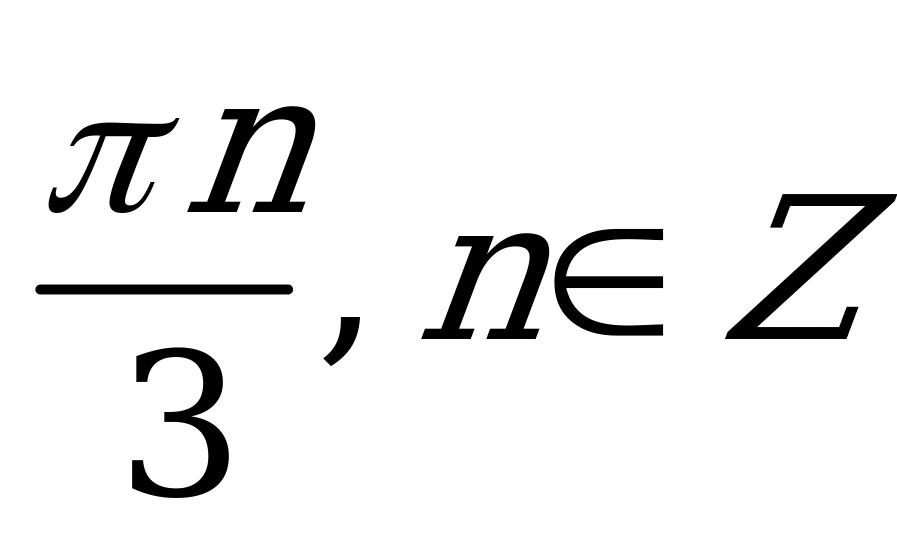 B) B) 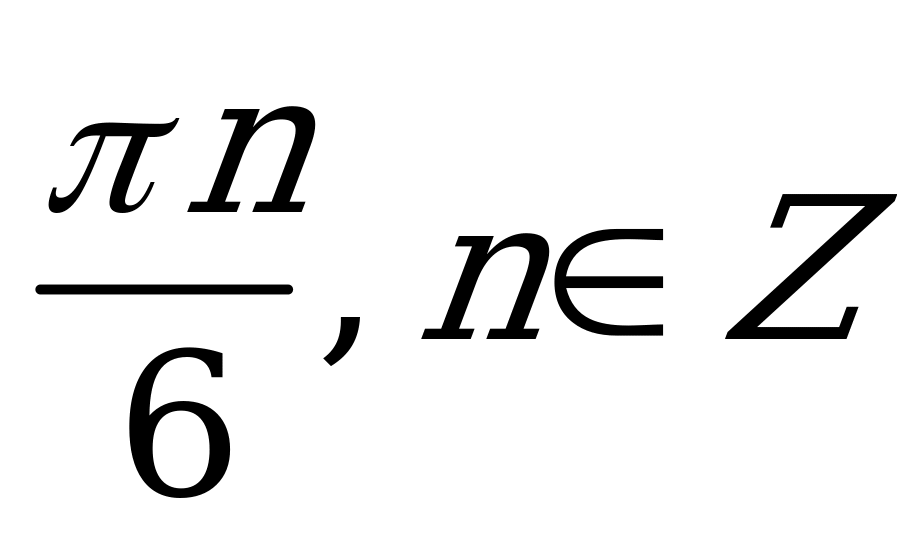 C) C) 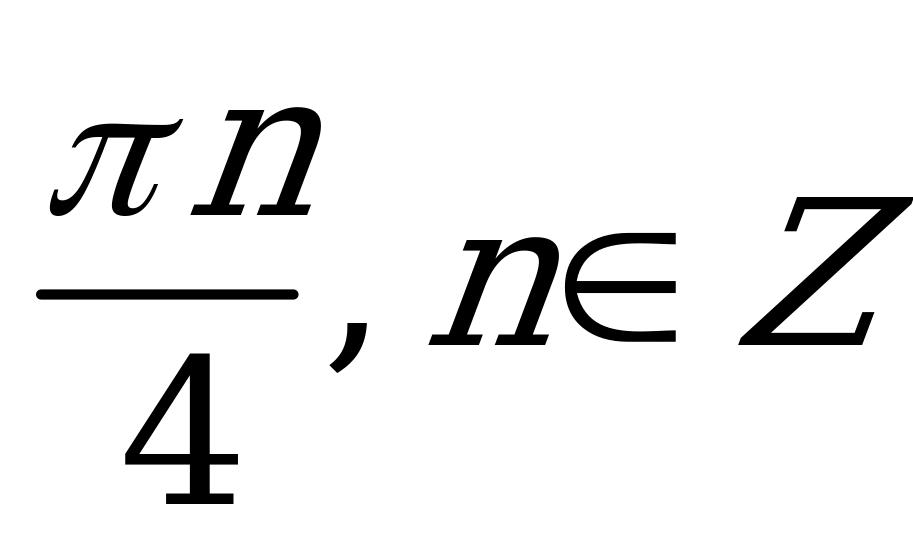 D) 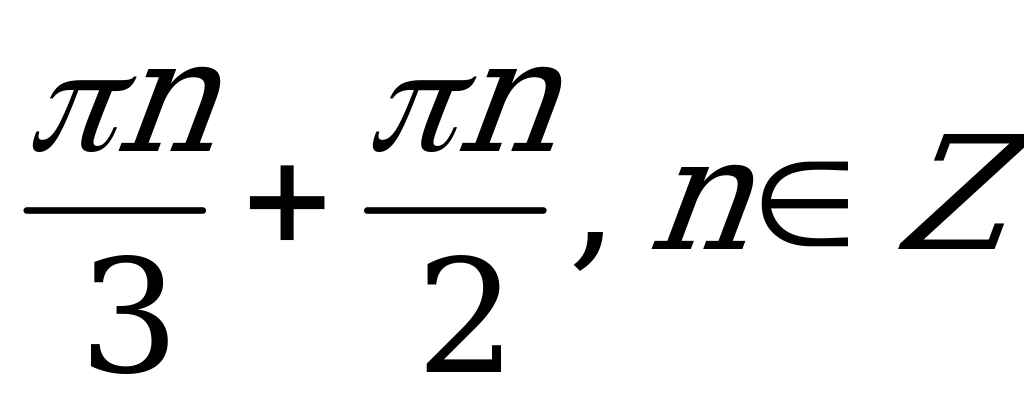 E) E) 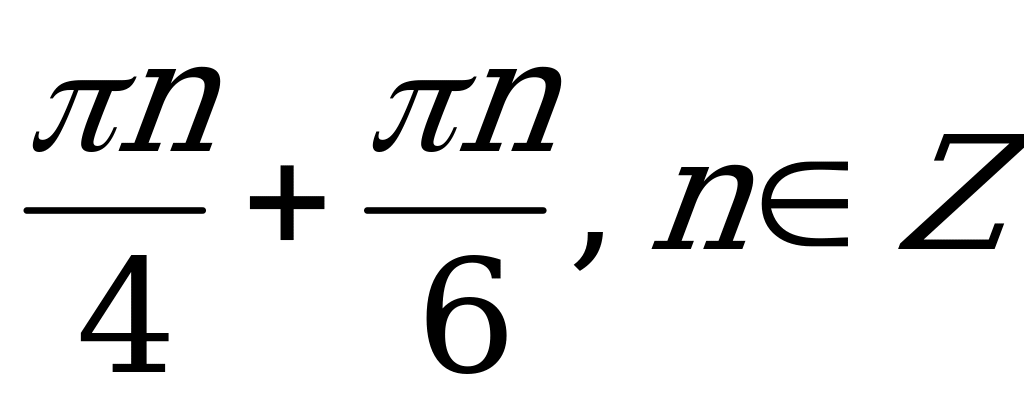 | В |
| С4 Найдите 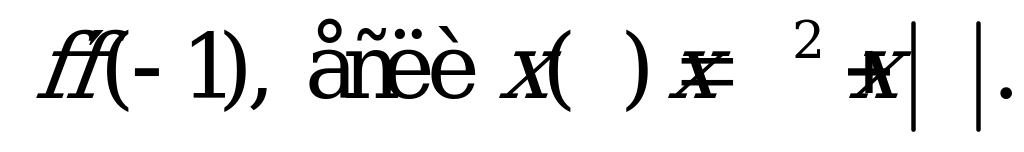 A) -3 B) 3 C) 2 D) -2 E) 0 | А |
| С5 Найдите f (6), если 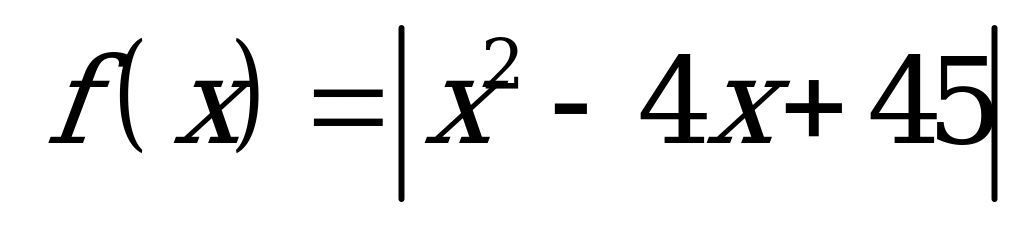 . . A) 0 B) 5 C) 2 D) 7 E) не существует | С |
| С6 Найдите производную функции y=|x+1| A) 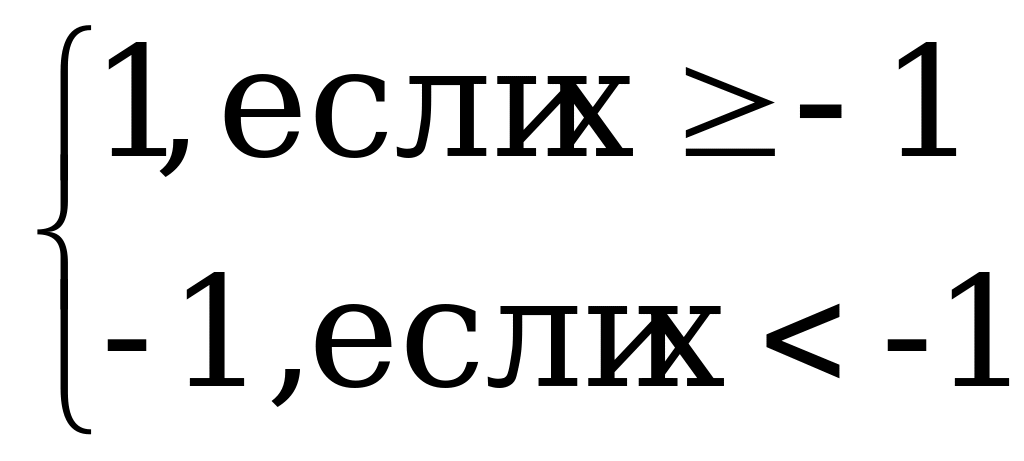 B) B) 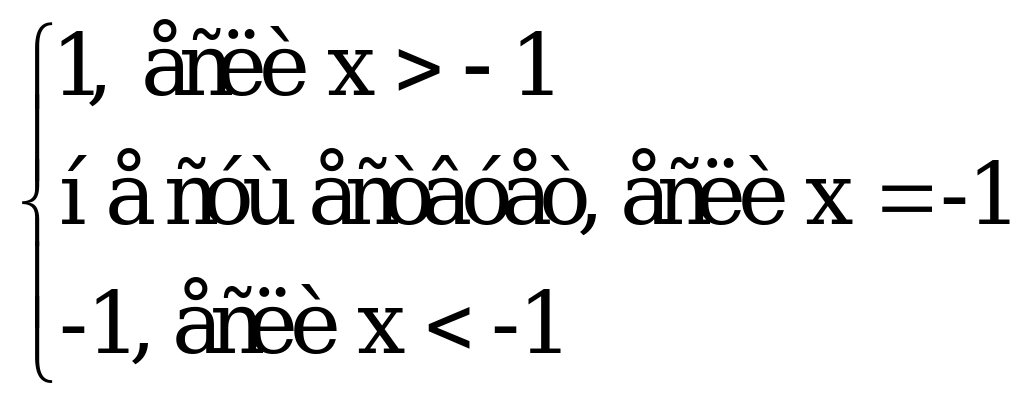 С) 2 D) 1 E) -1 | В |
| С7 Найдите производную функции y = x + 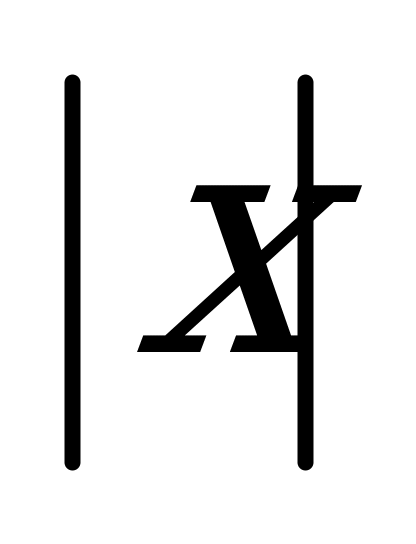 A) 0 B) 2 E) не существует C)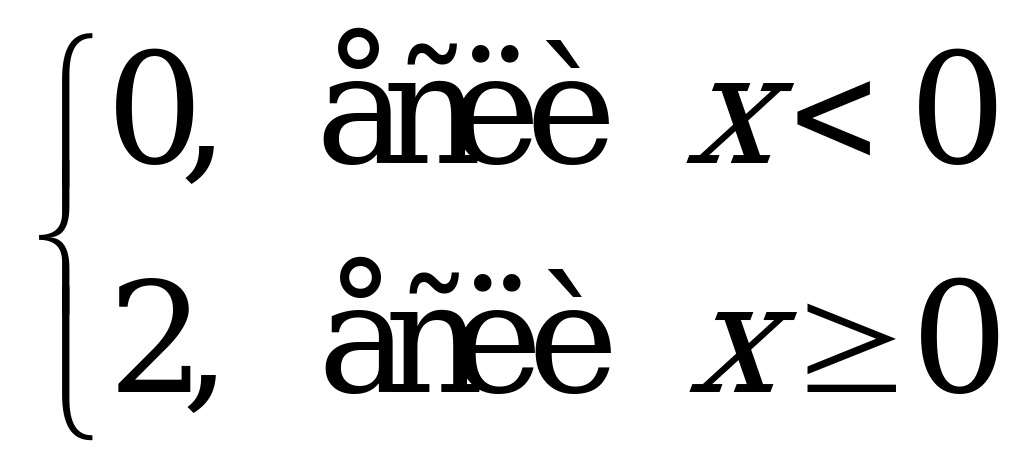 D) D) 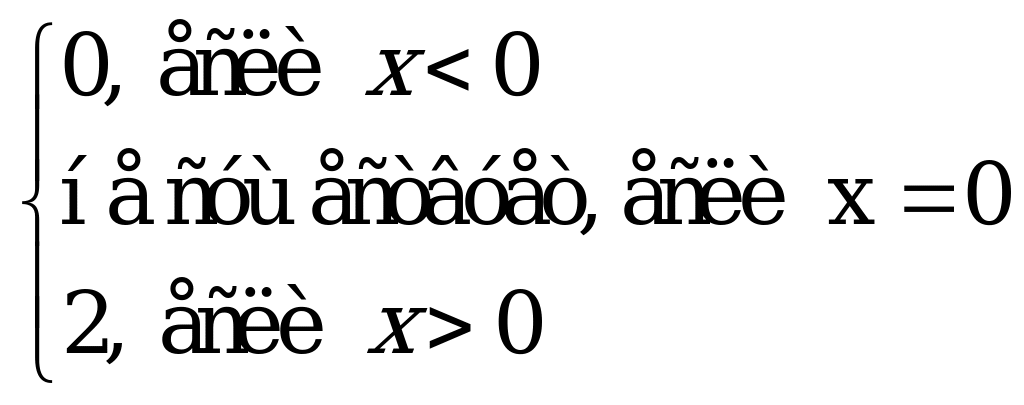 | Д |
| С8 Найдите промежуток возрастания функции y = sin2x – x (x[0;  ]). ]). A) 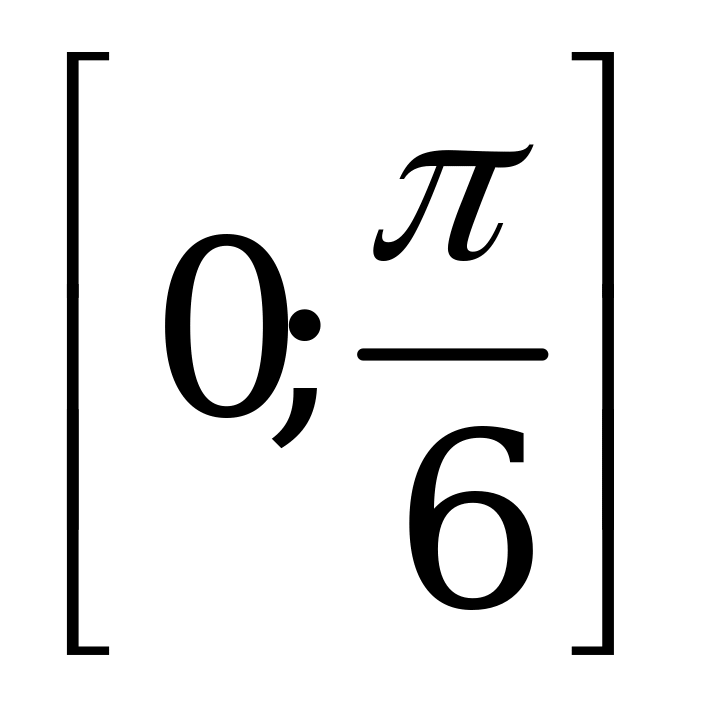 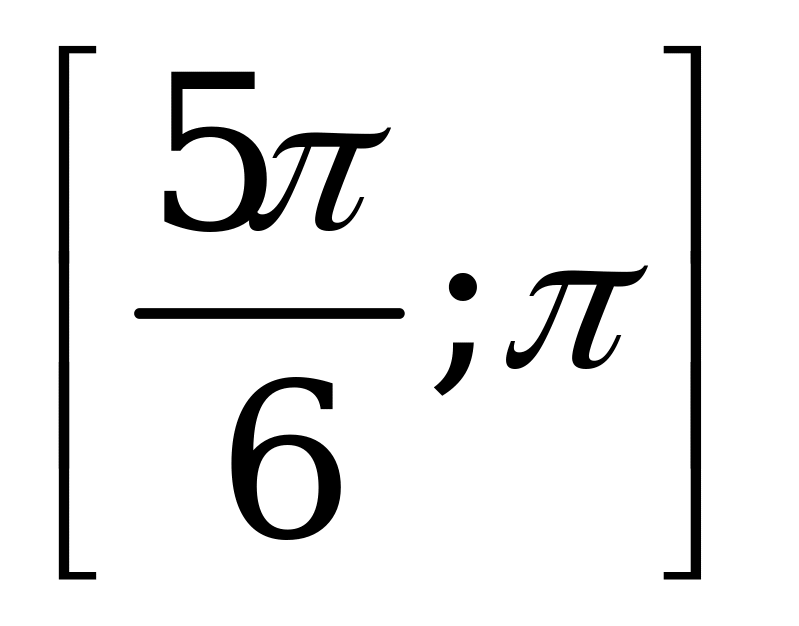 B) B) 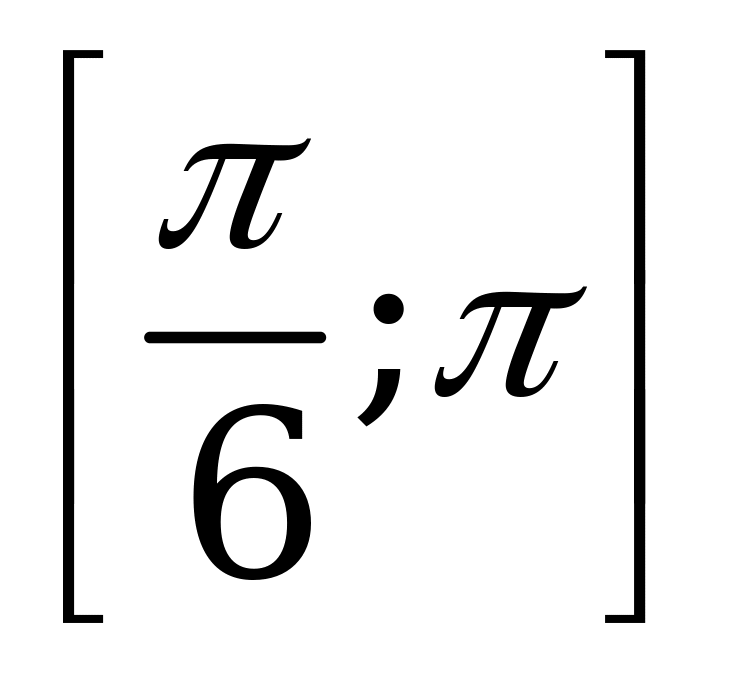 C) C) 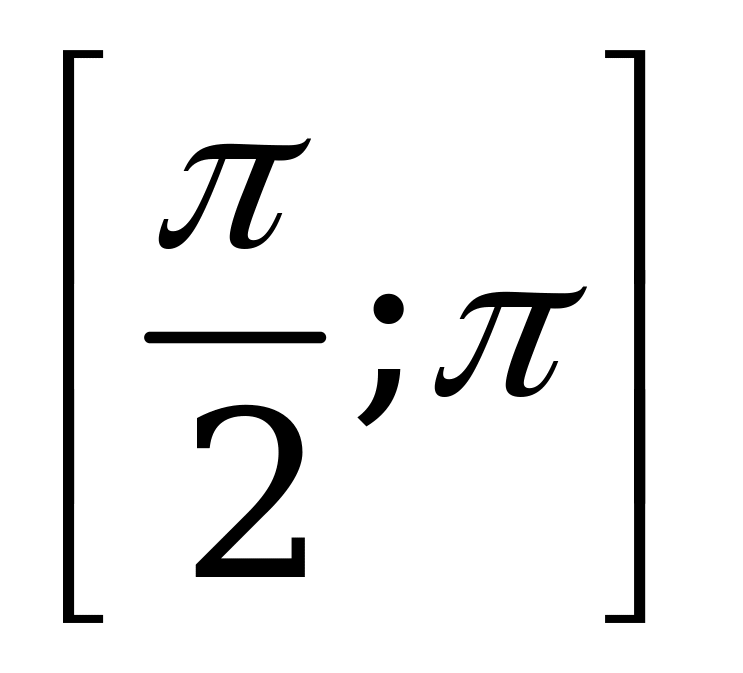 D) 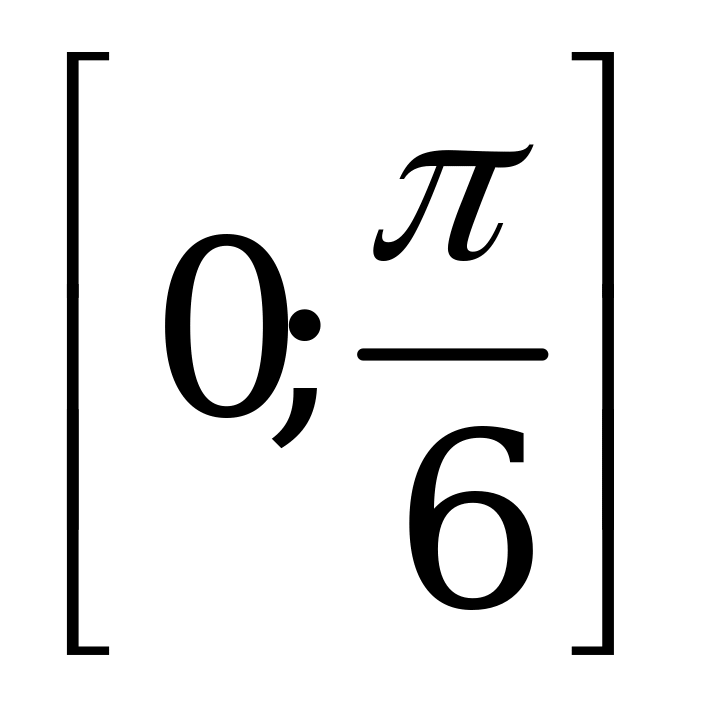 E) E) 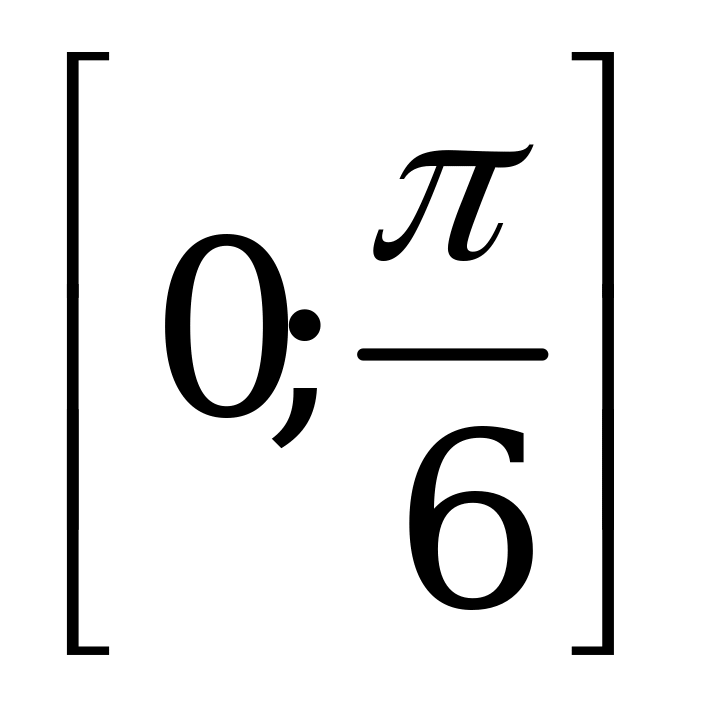 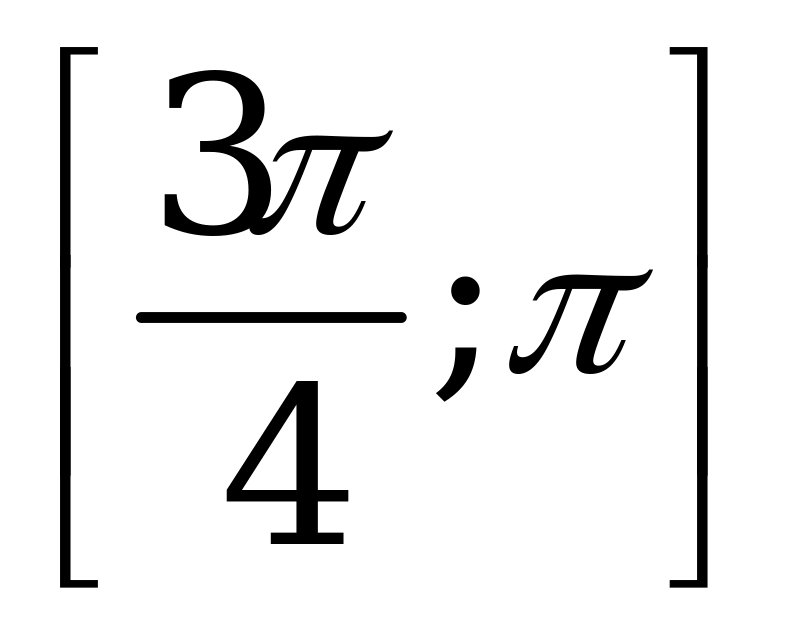 | А |
| С9 Какая из функций является возрастающей при любых значениях x из области ее определения? A) y = sinx B) 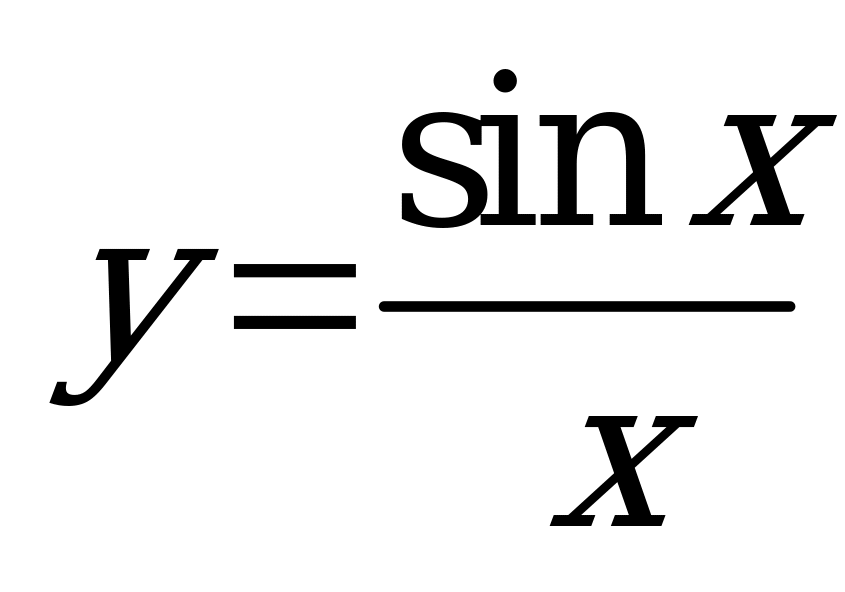 C) C) 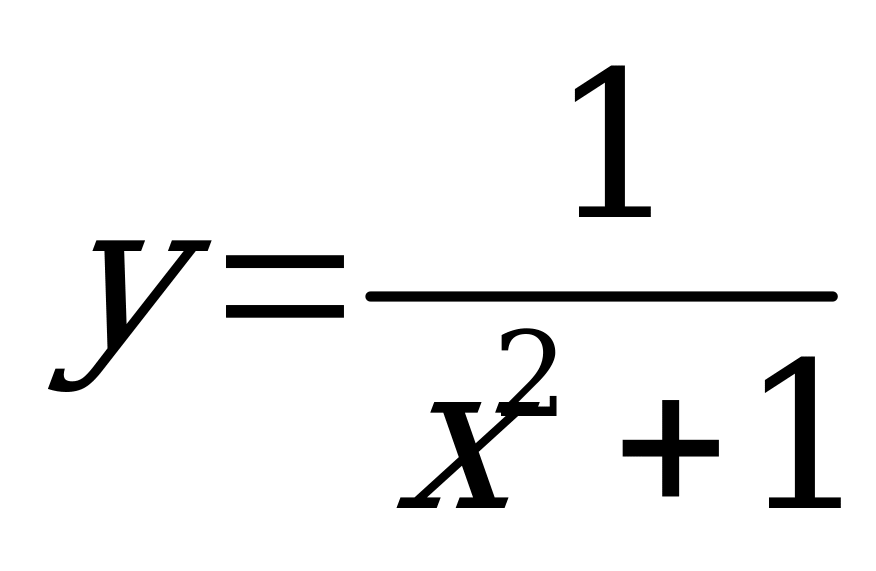 D) y = x2 + 4 E) y = 2x7 - 8 | Е |
| С10 Найдите наибольшее значение функции y = |x – 2| + 2x – 3x2 A) 2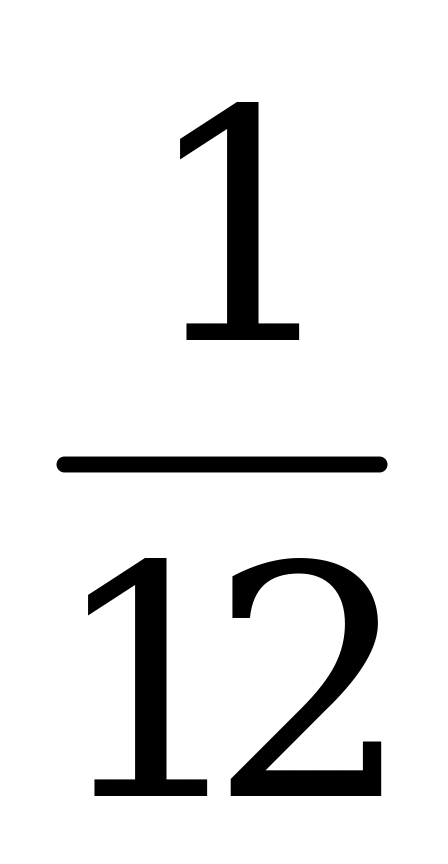 B) 10 C) -1 B) 10 C) -1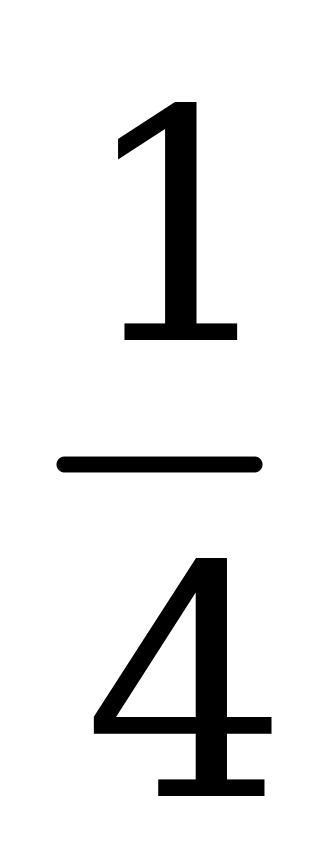 D) D) 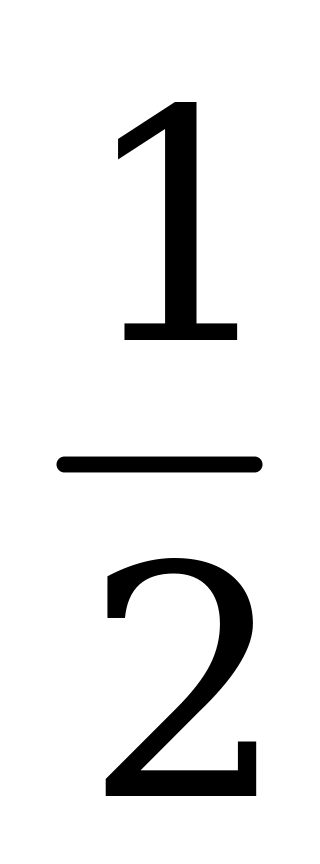 E) - E) -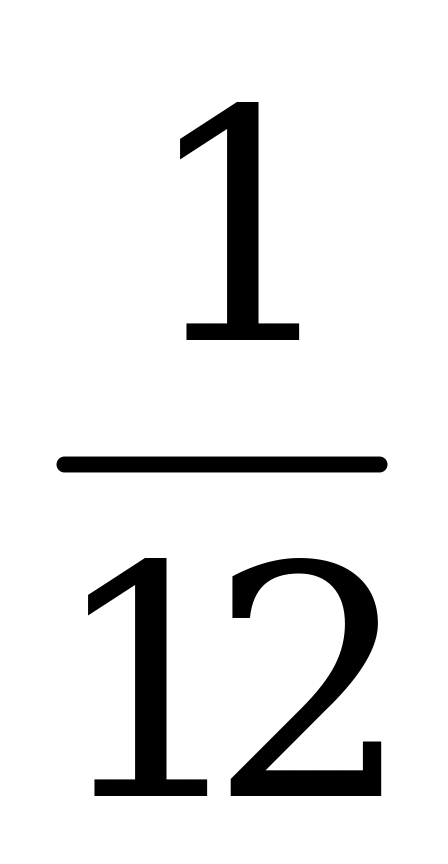 | А |
| С11 Найдите множество значений функции 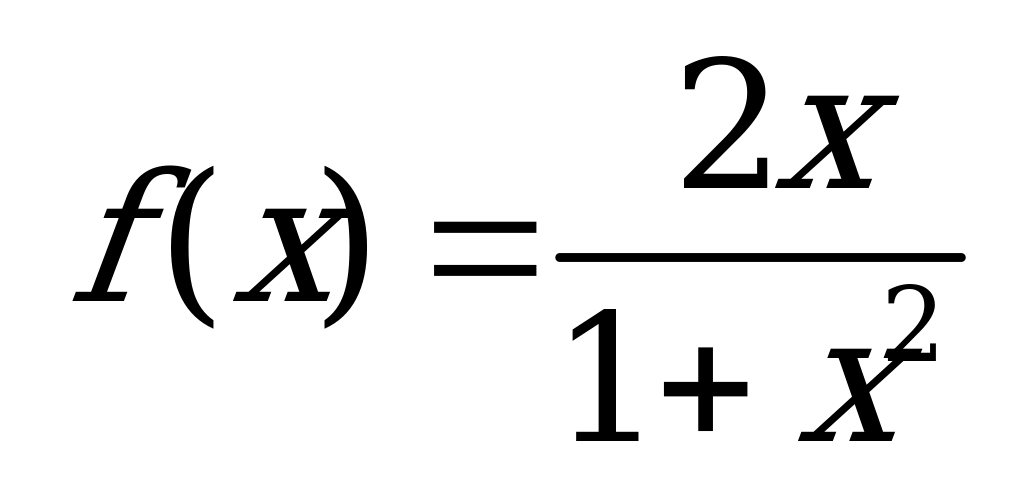 A) [-1; 1] B) [0; 1] C) R D) [-1; 0] E) [0; ) | А |
| С12 Напишите уравнение прямой, проходящей через точку (3; 4) и параллельной касательной, проведенной к параболе y=x2 в точке с абсциссой 3. A) y = 6x - 14 B) y = 3x - 8 C) y = 6x + 14 D) y = 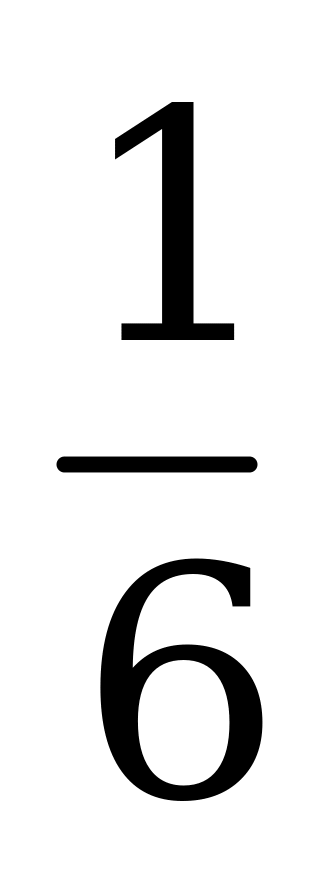 x - 14 E) y = - x - 14 E) y = -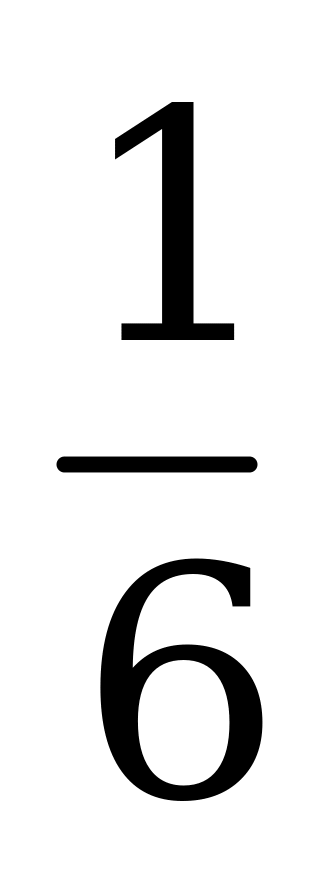 x + 12 x + 12 | А |
| С13 Прямая y = 2 - 3x является касательной к параболе 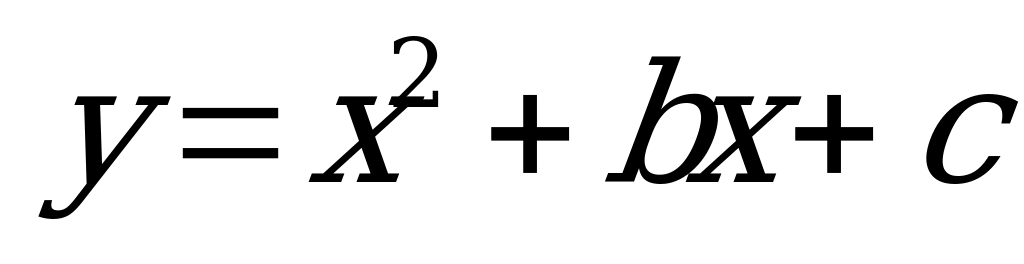 в точке с абсциссой x = 0. в точке с абсциссой x = 0. Найдите 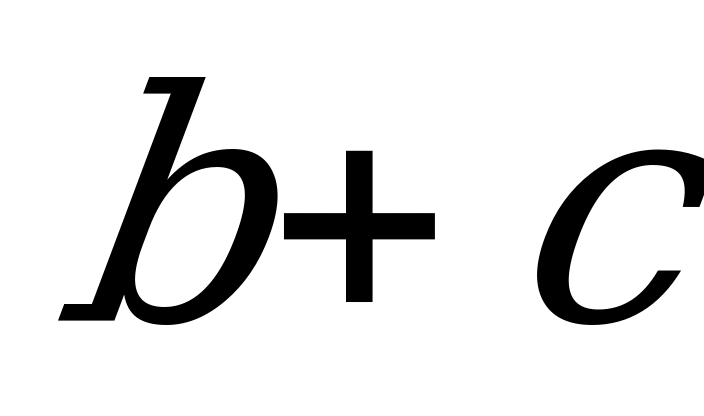 . A) 2 B) -2 C) 3 D) -3 E) -1 . A) 2 B) -2 C) 3 D) -3 E) -1 | Е |
| С14 При каком значении m прямая y = 1, будет касательной к параболе y = x2 - 2x + m ? A) 4 B) 1 C) 3 D) 2 E) 5 | Д |
| С15 Уравнение касательной, проведенной в точке x0 = 2 к графику функции f(x), имеет вид 2x - 3y = 6. Найдите f '(2). A) 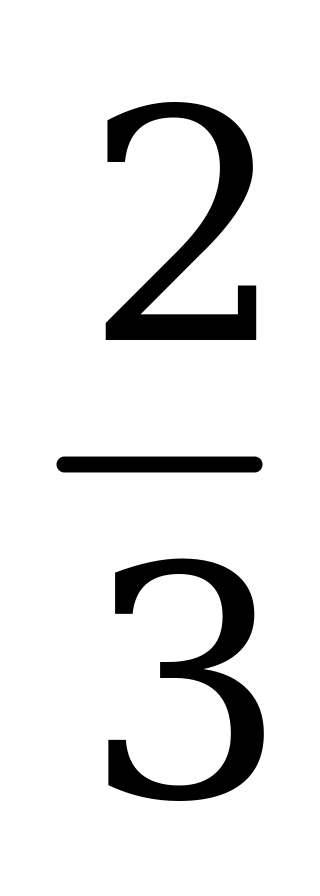 B) B) 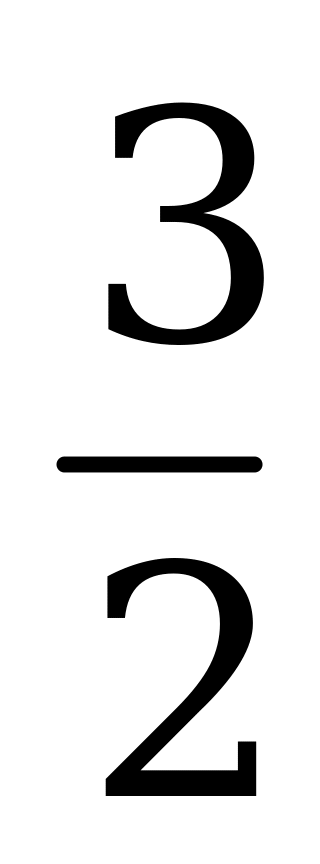 C) 2 D) 3 E) 4 C) 2 D) 3 E) 4 | А |
| С16 Касательная, проведенная к графику функции y = f(x), образует с осью Ox угол в 450. Напишите уравнение этой касательной, если известно, что абсцисса точки касания равна 2 и f(2) = 18. A) y = x + 16 B) y = x - 16 C) y = x + 18 D) y = x -18 E) y = x + 14 | А |
| С17 Решите неравенство cosx (-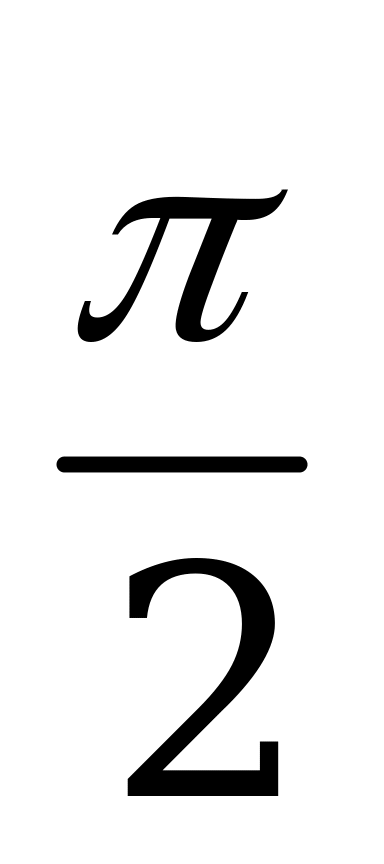 x) x) A) нет решений B) [- + 2n; + 2n], n Z C) [-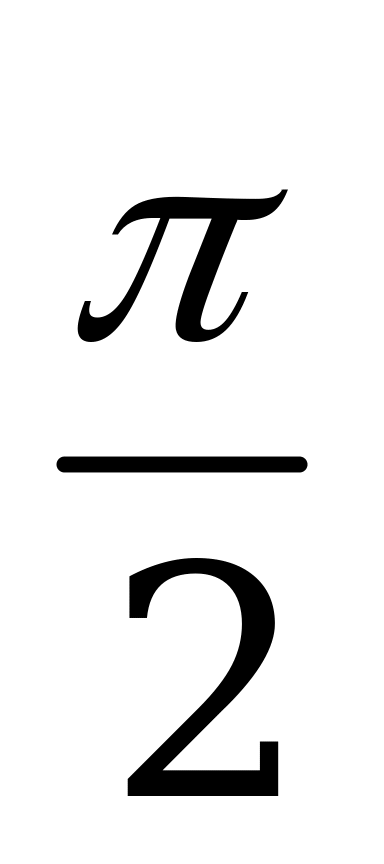 + 2n; + 2n; 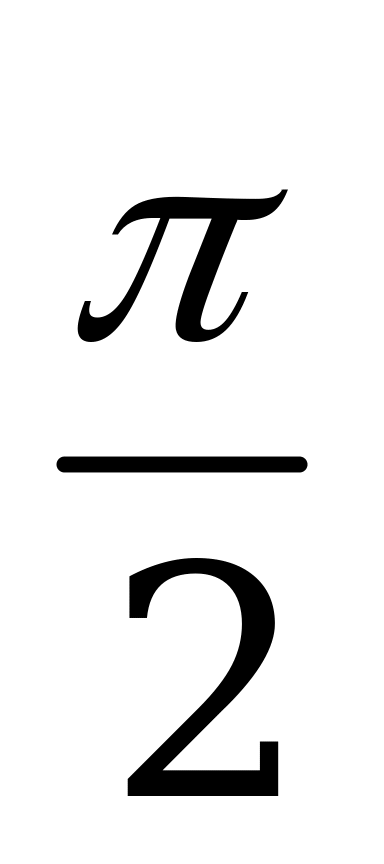 + 2n], n Z + 2n], n Z D) [-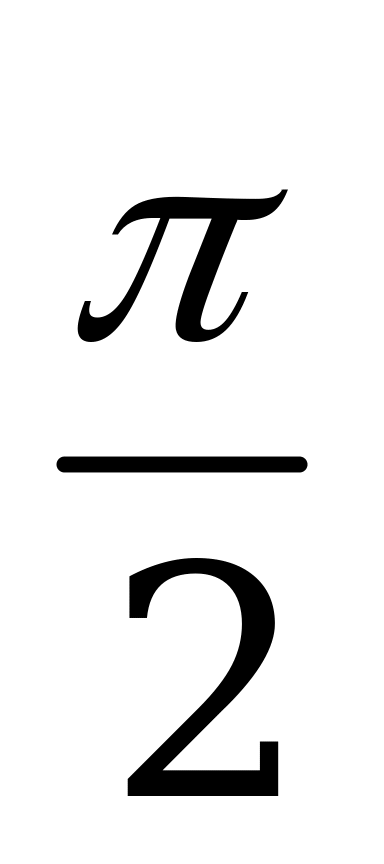 + n; + n; 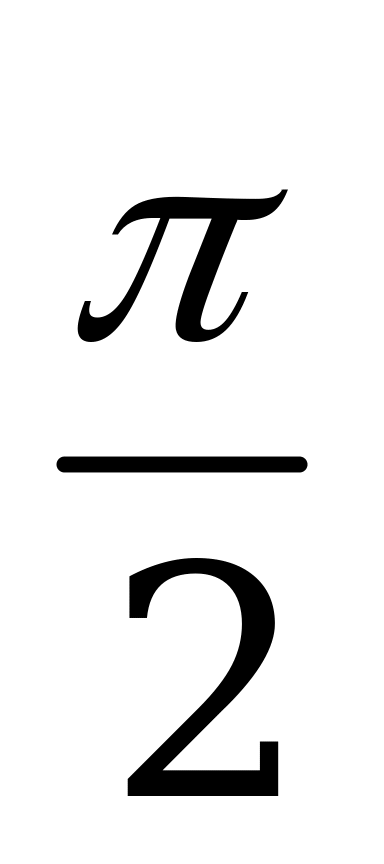 + n], n Z E) (- ; ) + n], n Z E) (- ; ) | Е |
| С18 Какое число будучи сложенным со своим квадратом дает наименьшую сумму? A) -1 B) -0,4 C) -0,8 D) -0,5 E) -0,6 | Д |







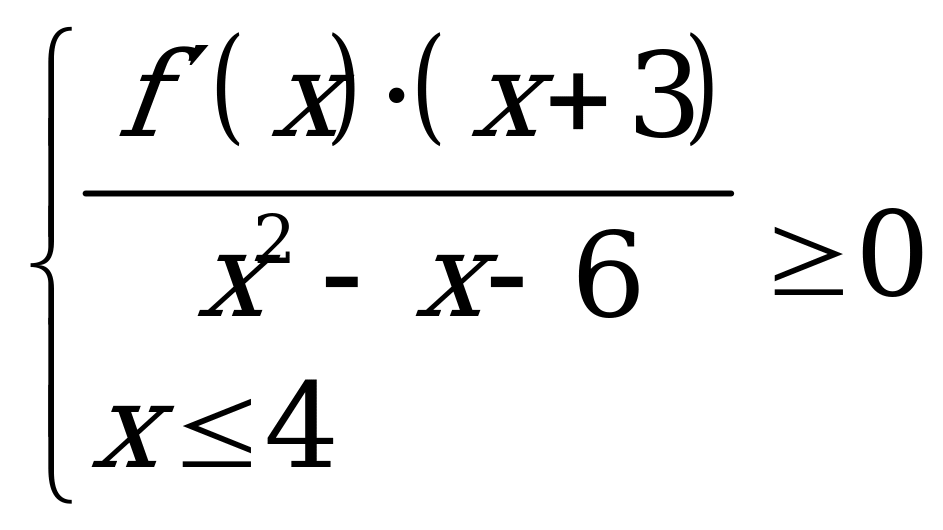 если
если