Повторение. Параллельные прямые в пространстве. Параллельность трёх прямых

Дата:

Тема: Параллельные прямые в пространстве. Параллельность трёх прямых

Цели: обобщить и систематизировать знания и навыки учащихся по теме; закрепить в ходе решения задач.

Ход урока.

1. АКТУАЛИЗАЦИЯ ЗНАНИЙ

Вспомним необходимый теоретический материал.

Определение. Две прямые в пространстве называются параллельными, если лежат в одной плоскости и не пересекаются.

Параллельность прямых a и b обозначается так: a∥b или b∥a.

Teорема 1.  Через две параллельные прямые можно провести плоскость, и притом только одну.

Теорема 2.  Через любую точку пространства вне данной прямой можно провести прямую, параллельную данной прямой, и притом только одну.

Теорема 3.  Если одна из двух параллельных прямых пересекает данную плоскость, то и другая прямая пересекает эту плоскость.

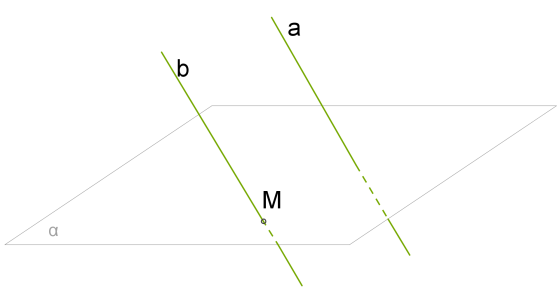
Теорема 4.  Две прямые, параллельные третьей прямой, параллельны.

1. ПРАКТИЧЕСКАЯ ЧАСТЬ

Откройте рабочие тетради и запишите сегодняшнее число и тему урока. И письменно выполняем решение приведенных ниже задач.

Задача № 16. Дано: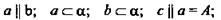 

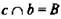
Доказать: с ⊂ α.

Доказательство: По условию а ∩ с = А; b ∩ с = В, значит А ∈ α и В ∈ α, так как а ⊂ α и b ⊂ α, по А₂ с ⊂ α, что и требовалось доказать.

Задача № 17. Дано: М - середина BD; N - середина CD; Q - середина АС; Р - середина АВ; AD = 12 см; ВС = 14 см.

Найти: P_MNQP-?

Решение:

Т.к. М - середина BD; N - середина CD, то отрезок MN – средняя линия треугольника BDC.

Т.к. Q - середина АС; Р - середина АВ, то отрезок PQ – средняя линия треугольника АВС.

Аналогично, MP и NQ – средние линии треугольников ABD и ACD соответственно.

А это значит:

MN || BC по определению средней линии ⇒ MN || PQ; PQ || BC.

РМ || AD по определению средней линии ⇒ PM || QN; NQ || DA.

По определению MNQP - параллелограмм.

PQ = 7; РМ = 6 ⇒ РMNQP = 2(7 + 6) = 26.

Ответ: 26 см.

Задача № 22. Дано: A ∈ α, В ∈ α, С ∈ α; AM = МС; BN = NC.

Доказать: MN || α.

Доказательство: MN || АВ (по свойству средней линии), АВ ∈ α; MN || α по теореме.

Что и требовалось доказать.

Задача № 18(б). Дано:

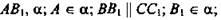
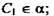   АС : СВ = 3 : 2; ВВ₁ = 20 см.

Найти: СС₁.

Решение:

1. Докажем, что точки А, С₁, В₁ лежат на одной прямой. Точка А и ВВ₁ определяют плоскость β (треугольник АВВ₁). β∩α=АВ₁. Докажем, что С₁ ∈ АВ₁. Предположим противное, пусть С₁ ∉ β, тогда

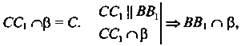
что противоречит BB₁ ∈ β. СС₁ ∩ β. Следовательно, С₁ ∈ АВ₁.

2. Так как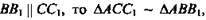  

 тогда 

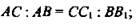
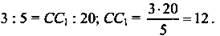
Ответ: 12 см.

1. ПОДВЕДЕНИЕ ИТОГОВ УРОКА. РЕФЛЕКСИЯ

Домашнее задание: №18(а), 29 стр. 13, 14.