Повторение. Решение задач на движение по воде

Задачи на движение по воде. Повторение 5 класс Истомина Т.Г.

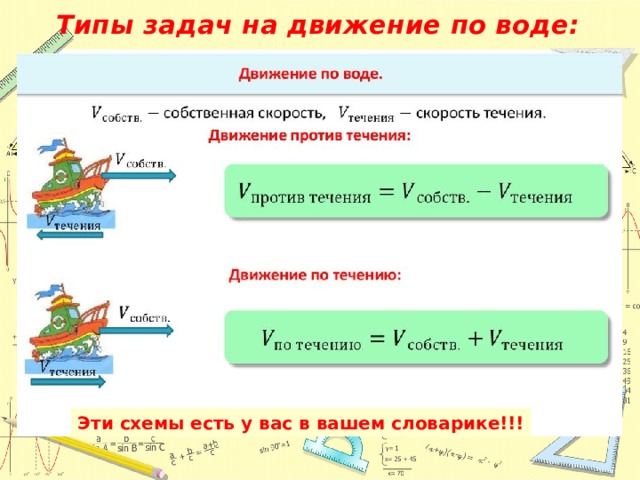
Типы задач на движение по воде:

Эти схемы есть у вас в вашем словарике!!!

Задача на движение по реке

Суда двигаются по реке с различной скоростью. При этом они могут двигаться, как по течению реки, так и против течения. В зависимости от того, как они двигаются (по или против течения), скорость будет меняться.

Предположим, что скорость реки составляет 3 км/ч. Если спустить лодку на реку, то река унесет лодку со скоростью 3 км/ч.

Если спустить лодку на стоячую воду, в которой отсутствует течение, то и лодка будет стоять. Скорость движения лодки в этом случае будет равна нулю.

Если лодка плывет по стоячей воде, в которой отсутствует течение, то говорят, что лодка плывет с  собственной скоростью .

Например, если моторная лодка плывет по стоячей воде со скоростью 40 км/ч, то говорят что  собственная скорость моторной лодки  составляет 40 км/ч.

Если судно плывет по течению реки, то к собственной скорости судна нужно прибавить скорость течения реки.

Например, если моторная лодка плывет со скоростью 30 км/ч  по течению   реки , и скорость течения реки составляет 2 км/ч, то к собственной скорости моторной лодки (30 км/ч) необходимо прибавить скорость течения реки (2 км/ч)

30 + 2 = 32 км/ч – V по течению   реки

Течение реки можно сказать помогает моторной лодке дополнительной скоростью равной двум километрам в час.

Если судно плывет против течения реки, то из собственной скорости судна нужно вычесть скорость течения реки.

Например, если моторная лодка плывет со скоростью

30 км/ч  против течения   реки , и скорость течения реки составляет 2 км/ч, то из собственной скорости моторной лодки (30 км/ч) необходимо вычесть скорость течения реки (2 км/ч)

30 − 2 = 28 км/ч –V против течения   реки

Течение реки в этом случае препятствует моторной лодке свободно двигаться вперед, снижая её скорость на два километра в час.

Задача 1 . Скорость катера 40 км/ч, а скорость течения реки 3 км/ч. С какой скоростью катер будет двигаться по течению реки? Против течения реки?

40 км/ч,

V по течения   реки - ?

3 км/ч

40 км/ч,

V против течения   реки - ?

Решение:

3 км/ч

Если катер будет двигаться по течения реки, то скорость его движения составит

• 40 + 3 = 43 (км/ч) – V по течению

Если катер будет двигаться против течения реки, то скорость его движения составит

2) 40 − 3 = 37 (км/ч) - V против течения

Ответ: 43 км/ч, 37 км/ч

Задача 2 . Скорость теплохода в стоячей воде — 23 км/ч. Скорость течения реки — 3 км/ч. Какой путь пройдет теплоход за 3 часа по течению реки? Против течения?

23 км/ч

t = 3 ч

23 км/ч

t = 3 ч

3 км/ч

S - ?

S - ?

3 км/ч

Решение

Если теплоход будет двигаться по течению реки, то скорость его движения составит

• 23 + 3 = 26 (км/ч) - V по течения реки .

За три часа он пройдет в три раза больше

2) 26 × 3 = 78 (км) - S за 3 часа

Если теплоход будет двигаться против течения реки, то скорость его движения составит

3) 23 − 3 =20 (км/) - V против течения реки .

За три часа он пройдет в три раза больше

4) 20 × 3 = 60 (км ) S за 3 часа

Ответ : 78 км, 60 км

Задача 3 . За какое время при движении против течения реки теплоход пройдет 204 км, если его собственная скорость 15 км/ч, а скорость течения в 5 раз меньше собственной скорости теплохода?

t = ? ч

15 км/ч

?, в 5 раз

S = 204 км

Решение

В условии сказано, что скорость течения реки в 5 раз меньше собственной скорости теплохода, поэтому сначала определим скорость течения реки. Для этого уменьшим 15 км/ч в пять раз

1) 15 : 5 = 3 (км/ч) - V течения реки .

Скорость течения реки составляет 3 км/ч. Вычтем эту скорость из скорости движения теплохода

2) 15 − 3 = 12 (км/ч) - V против течения реки .

Теперь определим время за которое теплоход пройдет 204 км при скорости 12 км/ч. В час теплоход проходит 12 километров. Чтобы узнать за сколько часов он пройдет 204 километра, нужно определить сколько раз 204 километра содержит по 12 километров

3) 204 : 12 = 17 (ч)

Ответ : теплоход пройдет 204 километра за 17 часов

Задача 4 . Двигаясь по течению реки, за 6 часов лодка прошла 102 км. Определите собственную скорость лодки, если скорость течения – 4 км/ч.

– ? км/ч

t = 6 ч

S = 102 км

– 4 км/ч

Решение

Узнаем с какой скоростью лодка двигалась по реке. Для этого пройденное расстояние (102км) разделим на время движения (6ч)

• 102 : 6 = 17 (км/ч) - V по течения реки .

Определим собственную скорость лодки. Для этого из скорости по которой она двигалась по реке (17 км/ч) вычтем скорость течения реки (4 км/ч)

2) 17 − 4 = 13 (км/ч) – собственная V лодки

Ответ: 13 км/ч

Задача 5 . Двигаясь против течения реки, за 5 часов лодка прошла 110 км. Определите собственную скорость лодки, если скорость течения – 4 км/ч.

t = 5 ч

- ? км/ч

- 4 км/ч

S = 110 км

Решение

Узнаем с какой скоростью лодка двигалась по реке. Для этого пройденное расстояние (110км) разделим на время движения (5ч)

• 110 : 5 = 22 (км/ч) - V против течения реки

Определим собственную скорость лодки. В условии сказано, что она двигалась против течения реки. Скорость течения реки составляла 4 км/ч. Это значит, что собственная скорость лодки была уменьшена на 4. Наша задача прибавить эти 4 км/ч и узнать собственную скорость лодки

2) 22 + 4 = 26 (км/ч) – собственная V лодки

Ответ : 26 км/ч

Задача 6.  Двигаясь против течения реки, расстояние в 72 км теплоход проходит за 4ч, а плот такое же расстояние проплывает за 36 ч. За сколько часов теплоход проплывет расстояние 110 км, если будет плыть по течению реки?

t плота = 36 ч

S = 72 км

- ? км/ч

t тепл = 4 ч

- ? км/ч

S = 72 км

- ? км/ч

S = 110 км

- ? км/ч

t тепл = ? ч

Решение

Найдем скорость течения реки. В условии сказано, что плот может проплыть 72 километра за 36 часов. Плот не может двигаться против течения реки. Значит скорость плота с которой он преодолевает эти 72 километра и является скоростью течения реки. Чтобы найти эту скорость, нужно 72 километра разделить на 36 часов

1) 72 : 36 = 2 (км/ч) - V плота или она же V течения

Найдем собственную скорость теплохода. Сначала найдем скорость его движения против течения реки. Для этого разделим 72 километра на 4 часа

2) 72 : 4 = 18 (км/ч) – V против течения

Если против течения реки скорость теплохода составляет 18 км/ч, то

3) 18+2 = 20 (км/ч) - собственная V теплохода

4) 20+2 = 22 (км/ч) - V теплохода по течению реки

Разделив 110 километров на скорость движения теплохода по течению реки (22 км/ч), можно узнать за сколько часов теплоход проплывет эти 110 километров

5) 110 : 22 = 5 (ч)

Ответ:  по течению реки теплоход проплывет 110 километров за 5 часов.

Задача 7. Катер проплывает против течения реки 24 км за 5 ч. Его скорость по течению реки - 8,2 км/ч. Найдите собственную скорость катера и скорость течения реки.

Против течения

S

t

24 км

По течению

Найти :

V

5 ч

? км/ч

8,2 км/ч

? Катера

? течения

При решении таких задач можно вывести формулы самим из того, что

V по течению = V катера + V течения

V против течения = V катера - V течения

А можно воспользоваться уже готовой формулой, у кого она не записана в словарик, запишите:

Решение:

Для начала найдем V катера против течения реки, зная что он проплыл 24 км за 5 ч

• 24:5=4,8 (км/ч) - V катера против течения

Теперь воспользуемся первой формулой ( формулу писать обязательно)

2) (8,2 – 4,8) :2 = 3,4 : 2= 1,7 (км/ч) - V течения реки

Теперь воспользуемся второй формулой и найдем скорость катера, но это можно сделать и не применяя формулу.

3) (8,2 + 4,8) :2 = 13 : 2= 6,5 (км/ч) - V катера

Или 3) 4,8 + 1,7 = 6,5 (км/ч) - V катера

Ответ: 6,5 км/ч, 1,7 км/ч

Устно: повторить теорию из словарика.

Письменно:

Задача 1. Теплоход плыл 5ч по озеру, а потом 4 ч - вниз по реке. Какое расстояние проплыл теплоход за это время, если его собственная скорость 56 км/ч, а скорость течения реки 3 км/ч?

Задача 2. Лодка проплывает по течению реки 36,6 км за 6 ч. Скорость лодки против течения реки 2,5 км/ч. Найдите собственную скорость лодки и скорость течения реки.

Задача 3. Туристы проплыли на плоту 48 км за 16 ч. Обратно они вернулись на моторной лодке, собственная скорость которой - 15 км/ч. Сколько времени затратили туристы на обратный путь?  

Домашнее задание: