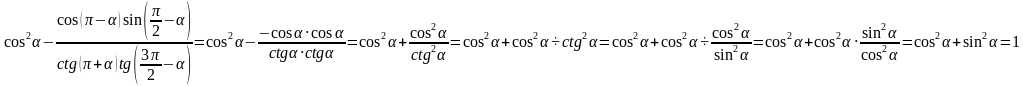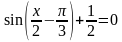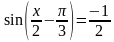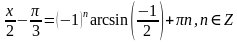Дата
Тема урока: Повторение. Тригонометрические формулы и функции. Тригонометрические уравнения и неравенства.
Цели: обобщить и систематизировать знания учащихся по теме.
Ход урока
-
АКТУАЛИЗАЦИЯ ЗНАНИЙ
Вспомним основные формулы
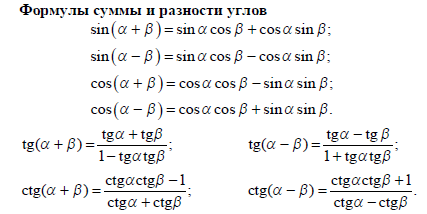
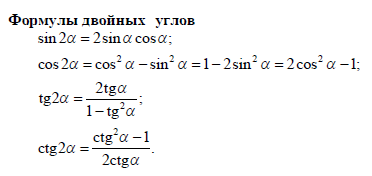

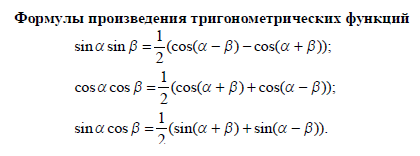
-
ПРАКТИЧЕСКАЯ ЧАСТЬ
Откройте тетради и запишите сегодняшнее число и тему урока. Выполняем письменно предложенные примеры.
Пример 1. Найти значение выражения 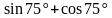 .
.
Решение. Чтобы воспользоваться формулой суммы тригонометрических функций, преобразуем выражение 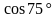 с помощью формулы приведения:
с помощью формулы приведения:
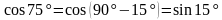 .
.
Тогда
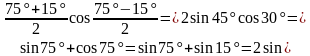
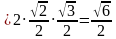
Ответ: 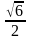
Пример 2. Найти значение выражения
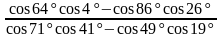
Решение. Воспользуемся формулами приведения:
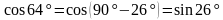
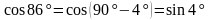
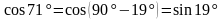
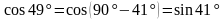
Подставим в выражение:
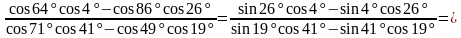
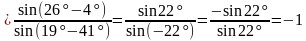
Пример 3. Упростите выражения:
а) 
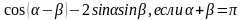 ;
;
б) 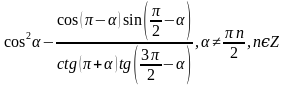 .
.
Решение:
а) 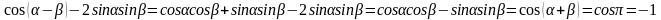 .
.
б) 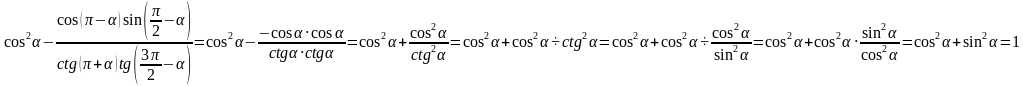
Ответ: а) -1, б) 1.
Пример 4. Решить уравнение
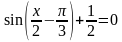
Решение. Перепишем уравнение в виде
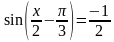
Воспользуемся формулой корней общего вида, получим:
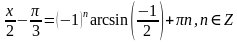
Применим нечетность функции arcsin x:
Вычислим значение  и перенесем
и перенесем  в правую часть:
в правую часть:
Чтобы найти значения х умножим обе части уравнения на 2, получим:
Ответ: .
Пример 5. Решить уравнение
Решим в общем виде, применив частный случай:
Разделим обе части уравнения на 3, получим:
Ответ:
Пример 6. Решить уравнение
Решение. Данное уравнение является квадратным относительно функции  и решается с помощью замены.
и решается с помощью замены.
Замена:  . При введении замены помним про ограничения для функции косинус, не может быть больше 1 и меньше -1.
. При введении замены помним про ограничения для функции косинус, не может быть больше 1 и меньше -1.
Получим и решим уравнение

Его корни  . Возвращаемся к замене:
. Возвращаемся к замене:

Вспоминаем про ограничения на переменную и понимаем, что корень  не подходит, т.е. уравнение
не подходит, т.е. уравнение  не имеет решений.
не имеет решений.
Остается решить  . Снова применим частный случай, получим:
. Снова применим частный случай, получим:


Ответ:  .
.
Пример 7. Решить уравнение:

Решение. Применим формулу синуса двойного угла  , получим:
, получим:

Вынесем общий множитель за скобку:

Решим распадающееся уравнение, запишем в виде совокупности:
Ответ:  ; .
; .
Пример 8. Решить уравнение:
Решение. Используем формулу приведения для  , чтобы уравнение было относительно одной функции:
, чтобы уравнение было относительно одной функции:
Перепишем уравнение в виде:
Далее применим формулу суммы косинусов, получим:
Снова пришли к распадающемуся уравнению, решим его:
Ответ: ; .
Пример 9. Решить уравнение:
Решение. Применим формулу синуса двойного угла, получим:
Уравнение пока еще зависит от двух функций, поэтому применим к косинусу основное тригонометрическое тождество, получим:
Тогда исходное уравнение примет вид:
Раскроем скобку, приведем подобные и умножим на « -1 »:
Получили квадратное уравнение относительно  . Выполним замену:
. Выполним замену: 


Оба значения подходят. Вернемся к замене:
Ответ: ; .
-
ПОДВЕДЕНИЕ ИТОГОВ УРОКА. РЕФЛЕКСИЯ
Домашнее задание. Решить уравнение:







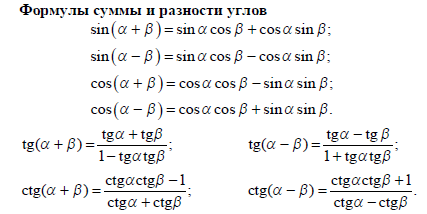
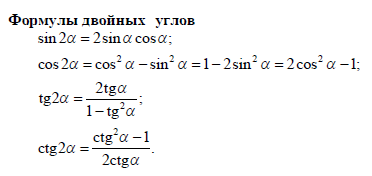

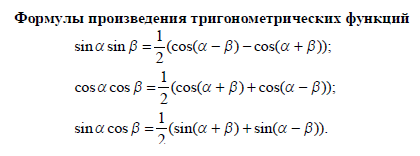
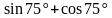 .
.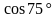 с помощью формулы приведения:
с помощью формулы приведения: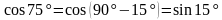 .
.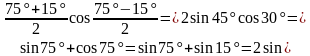
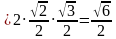
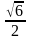
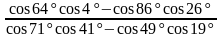
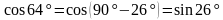
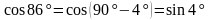
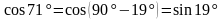
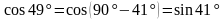
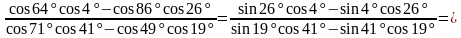
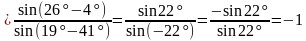

 ;
;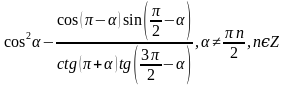 .
.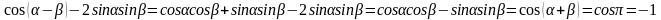 .
.