Практическая работа №42 «Графики элементарных функций»
Цель работы: формировать умения строить графики элементарных функций используя их свойства.
Теоретические сведения к практической работе:
Числовая функция
Числовой функцией с областью определения D называется соответствие, при котором каждому числу х из множества D сопоставляется по некоторому правилу число у, зависящее от х.
Функции обычно обозначают латинскими буквами. Рассмотрим произвольную функцию f. Независимую переменную х называют аргументом функции. Число у, соответствующее числу х, называют значением функции f в точке х и обозначают f(х). Область определения функции f обозначают D(f). Множество, состоящее из всех чисел f(х), таких, что х принадлежит области определения функции f, называют областью значений функции и обозначают Е(f).
Графиком функции f называют множество всех точек (х; у) координатной плоскости, где у=f(х), а х «пробегает» всю область определения функции f.
График линейной функции
Линейная функция задается уравнением у=ах+b. Графиком линейной функций является прямая. Чтобы построить прямую достаточно две точки.
Пример 1. Построить график функции у=2х+1.
найдем две точки. В качестве одной из точек выгодно выбрать нуль. Если х=0, то у=2·0+1=1.
Берем еще какую-нибудь точку, например, 1. Если х=1, то у=2·1+1=3.
При оформлении заданий координаты точек обычно сводятся в таблицу:
Д ве точки найдены, выполним чертеж:
ве точки найдены, выполним чертеж:
При оформлении чертежа всегда подписываем графики.
Частные случаи линейной функции
1 ) Линейная функция вида у=ах (а≠0) называется прямой пропорциональностью. Например,
) Линейная функция вида у=ах (а≠0) называется прямой пропорциональностью. Например, 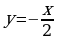 . График прямой пропорциональности всегда проходит через начало координат. Таким образом, построение прямой упрощается – достаточно найти всего одну точку.
. График прямой пропорциональности всегда проходит через начало координат. Таким образом, построение прямой упрощается – достаточно найти всего одну точку.
2) Уравнение вида у=b задает прямую, параллельную оси Ох, в частности, сама ось Ох задается уравнением у=0.
3) Уравнение вида х=b задает прямую, параллельную оси Оу, в частности, сама ось Оу задается уравнением х=0.
График квадратичной, кубической функции
П арабола. График квадратичной функции у=ax2+bx+c (а≠0) представляет собой параболу. Рассмотрим канонический случай: у=x2. Область определения – любое действительное число. Функция у=x2 является чётной. Если функция является чётной, то ее график симметричен относительно оси Оу.
арабола. График квадратичной функции у=ax2+bx+c (а≠0) представляет собой параболу. Рассмотрим канонический случай: у=x2. Область определения – любое действительное число. Функция у=x2 является чётной. Если функция является чётной, то ее график симметричен относительно оси Оу.
Пример 2 Построить график функции у=-х2+2х.
сначала находим вершину параболы:  ,
, 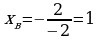 . Рассчитываем соответствующее значение «игрек»: у=-12+2·1=-1+2=1. Таким образом, вершина находится в точке (1; 1).
. Рассчитываем соответствующее значение «игрек»: у=-12+2·1=-1+2=1. Таким образом, вершина находится в точке (1; 1).
Теперь находим другие точки, при этом пользуемся симметричностью параболы.
| х | -2 | -1 | 0 | 1 | 2 | 3 | 4 |
| у | -8 | -3 | 0 | 1 | 0 | -3 | -8 |
Выполним чертеж:

Для квадратичной функции у=ax2+bx+c (а≠0) справедливо следующее: Если a0, то ветви параболы направлены вверх. Если a
Кубическая парабола
К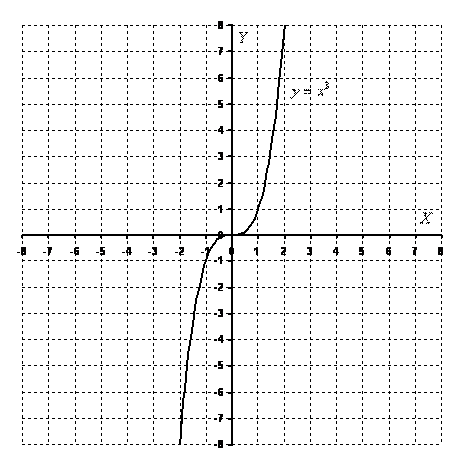 убическая парабола задается функцией у=х3. Область определения, область значений – любое действительное число. Функция является нечётной. График строим по точкам:
убическая парабола задается функцией у=х3. Область определения, область значений – любое действительное число. Функция является нечётной. График строим по точкам:
| х | -2 | -1 | 0 | 1 | 2 |
| у | -8 | -1 | 0 | 1 | 8 |
Гипербола
О бщий вид
бщий вид 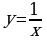 . Область определения: D(y): (-∞; 0) и (0; +∞). Область значений: E(y): (-∞; 0) и (0; +∞). Функция является нечётной, гипербола симметрична относительно начала координат.
. Область определения: D(y): (-∞; 0) и (0; +∞). Область значений: E(y): (-∞; 0) и (0; +∞). Функция является нечётной, гипербола симметрична относительно начала координат.
Выполним чертеж:График функции вида 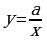 (а≠0) представляют собой две ветви гиперболы.
(а≠0) представляют собой две ветви гиперболы.
Если а0, то гипербола расположена в первой и третьей координатных четвертях. Если а, то гипербола расположена во второй и четвертой координатных четвертях.
Пример 3. Построить правую ветвь гиперболы  .
.
значения х выгодно подбираем так, чтобы делилось нацело:
Выполним чертеж:

Задания для самостоятельного решения:
Построить графики функций:
| 1 вариант 1) у=x2+2x+3; 2)  ; ; 3) 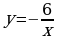 . . | 2 вариант 1) у=x2-4x; 2)  ; ; 3)  . . | 3 вариант 1) у=-x2+2x-1; 2)  ; ; 3) 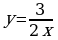 . . |
Контрольные вопросы:
-
Что называется функцией?
-
Что является графиком линейной, квадратичной функций?







 ве точки найдены, выполним чертеж:
ве точки найдены, выполним чертеж: ) Линейная функция вида у=ах (а≠0) называется прямой пропорциональностью. Например,
) Линейная функция вида у=ах (а≠0) называется прямой пропорциональностью. Например, 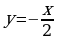 . График прямой пропорциональности всегда проходит через начало координат. Таким образом, построение прямой упрощается – достаточно найти всего одну точку.
. График прямой пропорциональности всегда проходит через начало координат. Таким образом, построение прямой упрощается – достаточно найти всего одну точку. арабола. График квадратичной функции у=ax2+bx+c (а≠0) представляет собой параболу. Рассмотрим канонический случай: у=x2. Область определения – любое действительное число. Функция у=x2 является чётной. Если функция является чётной, то ее график симметричен относительно оси Оу.
арабола. График квадратичной функции у=ax2+bx+c (а≠0) представляет собой параболу. Рассмотрим канонический случай: у=x2. Область определения – любое действительное число. Функция у=x2 является чётной. Если функция является чётной, то ее график симметричен относительно оси Оу. ,
, 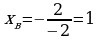 . Рассчитываем соответствующее значение «игрек»: у=-12+2·1=-1+2=1. Таким образом, вершина находится в точке (1; 1).
. Рассчитываем соответствующее значение «игрек»: у=-12+2·1=-1+2=1. Таким образом, вершина находится в точке (1; 1).
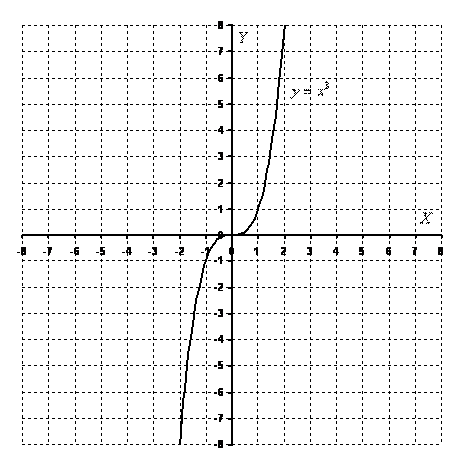 убическая парабола задается функцией у=х3. Область определения, область значений – любое действительное число. Функция является нечётной. График строим по точкам:
убическая парабола задается функцией у=х3. Область определения, область значений – любое действительное число. Функция является нечётной. График строим по точкам: бщий вид
бщий вид 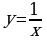 . Область определения: D(y): (-∞; 0) и (0; +∞). Область значений: E(y): (-∞; 0) и (0; +∞). Функция является нечётной, гипербола симметрична относительно начала координат.
. Область определения: D(y): (-∞; 0) и (0; +∞). Область значений: E(y): (-∞; 0) и (0; +∞). Функция является нечётной, гипербола симметрична относительно начала координат.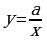 (а≠0) представляют собой две ветви гиперболы.
(а≠0) представляют собой две ветви гиперболы. .
.
 ;
;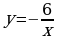 .
. ;
; .
. ;
;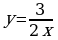 .
.


















