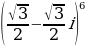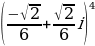Практическая работа № 2
Тема: Действия над комплексными числами, заданными в тригонометрической формах.
1. Краткие теоретические сведения
Комплексные числа
Комплексными числами называются числа вида 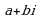 , где a и b - действительные числа, а число
, где a и b - действительные числа, а число 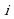 , определяемое равенством
, определяемое равенством 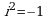 , называется мнимой единицей.
, называется мнимой единицей.
Действительное число 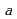 называется действительной частью комплексного числа
называется действительной частью комплексного числа 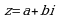 , а действительное число
, а действительное число 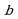 - мнимой частью.
- мнимой частью.
Запись комплексного числа в виде 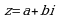 называется алгебраической формой записи комплексного числа.
называется алгебраической формой записи комплексного числа.
Модулем комплексного числа 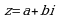 называется число
называется число 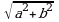 :
: 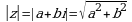
Угол между положительной действительной осью Ох и вектором называется аргументом комплексного числа.
Значение аргумента комплексного числа 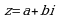 можно найти так:
можно найти так:
1) определить четверть, в которой находится комплексное число;
2) найти в этой четверти угол по формуле:
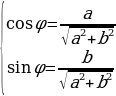 (1) или
(1) или 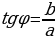
3) найти все значения аргумента по формуле:
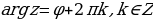
Пусть 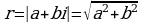 - модуль, а
- модуль, а 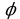 - одно из значений аргумента комплексного числа
- одно из значений аргумента комплексного числа 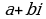 . Так как из соотношений (1) вытекает, что
. Так как из соотношений (1) вытекает, что 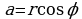 ,
, 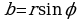 , тогда
, тогда
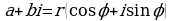 (2)
(2)
Таким образом, любое комплексное число 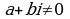 можно записать по формуле (2), где
можно записать по формуле (2), где 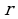 - модуль, а
- модуль, а 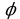 - одно из значений аргумента этого числа.
- одно из значений аргумента этого числа.
Верно и обратное утверждение: если комплексное число 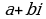 представлено в виде (2), где
представлено в виде (2), где 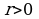 , то
, то 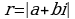 ,
, 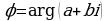 .
.
Представление комплексного числа в виде
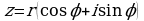 ,
,
где 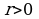 , называется тригонометрической формой записи комплексного числа.
, называется тригонометрической формой записи комплексного числа.
Для представления комплексного числа 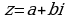 в тригонометрической форме необходимо найти: 1) модуль этого числа; 2) одно из значений аргумента этого числа. В силу многозначности
в тригонометрической форме необходимо найти: 1) модуль этого числа; 2) одно из значений аргумента этого числа. В силу многозначности 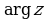 тригонометрическая форма комплексного числа также неоднозначна.
тригонометрическая форма комплексного числа также неоднозначна.
Действия над комплексными числами,
заданными в тригонометрической форме
1. Произведение комплексных чисел 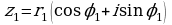 и
и 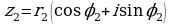 находится по формуле
находится по формуле
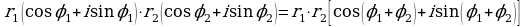 , т.е.
, т.е.
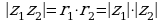 ,
, 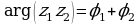 .
.
Таким образом, при умножении двух комплексных чисел, заданных в тригонометрической форме, их модули перемножаются, а аргументы складываются.
2. Частное комплексных чисел 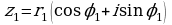 и
и 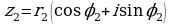 находится по формуле
находится по формуле
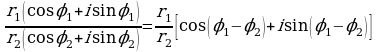 , т.е.
, т.е.
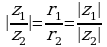 ,
, 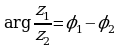 .
.
Таким образом, при делении комплексных чисел, заданных в тригонометрической форме, их модули делятся, а аргументы вычитаются.
3. Для возведения комплексного числа 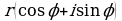 в n-ю степень используется формула
в n-ю степень используется формула
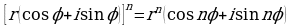 ,
, 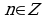 ,
,
которая называется формулой Муавра.
Для извлечения корня n-й степени из комплексного числа 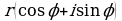 используется формула
используется формула
 ,
,
где 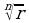 - арифметический корень,
- арифметический корень, 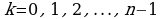 .
.
|
| ВАРИАНТ I | ВАРИАНТ II |
| 1. | Даны два комплексных числа 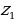 и и 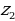 . . Выполните указанные действия. |
|
| 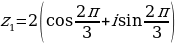 ; ;
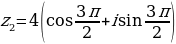
| 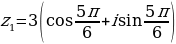 ; ;
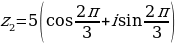
|
|
| а) 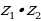 ; ; б) 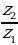 . . | а) 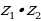 ; ; б) 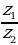 . . |
| 2. | Даны два комплексных числа 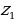 и и 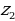 . Представьте их в тригонометрической форме и выполните указанные действия. . Представьте их в тригонометрической форме и выполните указанные действия. |
|
| 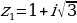 ; ; 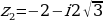
| 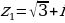 ; ; 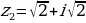
|
|
| а) 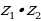 ; ; б) 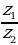 ; ; в) 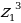 ; ; г) 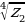 . . | а) 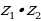 ; ; б) 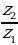 ; ; в) 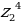 ; ; г) 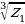 . . |
| 3. | Возведите в степень по формуле Муавра. |
|
| 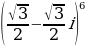
| 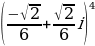
|
Контрольные вопросы
Дайте определение комплексного числа (алгебраическая форма записи).
Что такое мнимая единица, действительная и мнимая часть комплексного числа?
Что такое модуль и аргумент комплексного числа, как их найти?
Тригонометрическая форма записи комплексного числа.
Операции над комплексными числами в тригонометрической форме.
Запишите формулы Муавра.







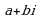 , где a и b - действительные числа, а число
, где a и b - действительные числа, а число 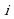 , определяемое равенством
, определяемое равенством 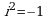 , называется мнимой единицей.
, называется мнимой единицей.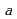 называется действительной частью комплексного числа
называется действительной частью комплексного числа 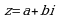 , а действительное число
, а действительное число 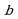 - мнимой частью.
- мнимой частью.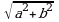 :
: 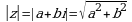
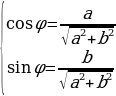 (1) или
(1) или 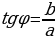
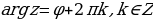
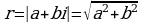 - модуль, а
- модуль, а 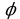 - одно из значений аргумента комплексного числа
- одно из значений аргумента комплексного числа 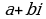 . Так как из соотношений (1) вытекает, что
. Так как из соотношений (1) вытекает, что 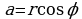 ,
, 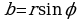 , тогда
, тогда 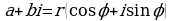 (2)
(2)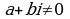 можно записать по формуле (2), где
можно записать по формуле (2), где 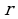 - модуль, а
- модуль, а 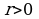 , то
, то 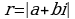 ,
, 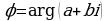 .
.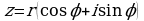 ,
,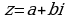 в тригонометрической форме необходимо найти: 1) модуль этого числа; 2) одно из значений аргумента этого числа. В силу многозначности
в тригонометрической форме необходимо найти: 1) модуль этого числа; 2) одно из значений аргумента этого числа. В силу многозначности 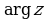 тригонометрическая форма комплексного числа также неоднозначна.
тригонометрическая форма комплексного числа также неоднозначна.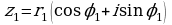 и
и 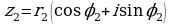 находится по формуле
находится по формуле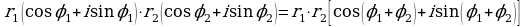 , т.е.
, т.е.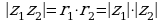 ,
, 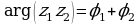 .
.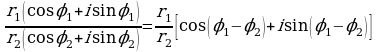 , т.е.
, т.е. 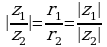 ,
, 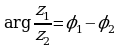 .
.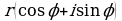 в n-ю степень используется формула
в n-ю степень используется формула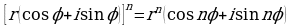 ,
, 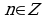 ,
,  ,
, 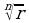 - арифметический корень,
- арифметический корень, 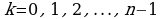 .
.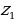 и
и 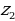 .
. 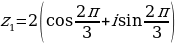 ;
;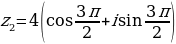
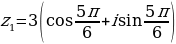 ;
;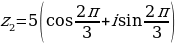
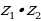 ;
;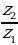 .
.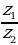 .
.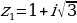 ;
; 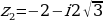
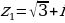 ;
; 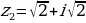
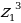 ;
;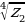 .
.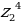 ;
;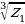 .
.