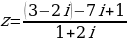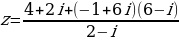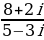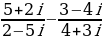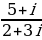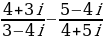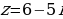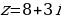Просмотр содержимого документа
«Практическая работа "Действия над комплексными числами в алгебраической форме записи".»
Практическая работа № 1
Тема: Действия над комплексными числами
в алгебраической форме записи
1. Краткие теоретические сведения
Комплексные числа
Комплексными числами называются числа вида 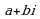 , где
, где 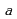 и
и 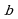 - действительные числа, а число
- действительные числа, а число 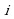 , определяемое равенством
, определяемое равенством 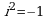 , называется мнимой единицей.
, называется мнимой единицей.
Действительное число 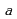 называется действительной частью комплексного числа
называется действительной частью комплексного числа 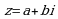 , а действительное число
, а действительное число 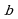 - мнимой частью.
- мнимой частью.
Запись комплексного числа в виде 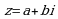 называется алгебраической формой записи комплексного числа.
называется алгебраической формой записи комплексного числа.
Два комплексных числа 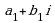 и
и 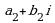 называются равными, если
называются равными, если 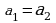 и
и 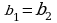 .
.
Комплексные числа вида 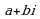 и
и 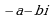 называются противоположными.
называются противоположными.
Комплексное число 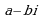 называется комплексно сопряженным с числом
называется комплексно сопряженным с числом 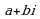 и обозначается
и обозначается 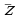 , т.е.
, т.е. 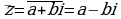 .
.
Любое действительное число 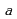 содержится в множестве комплексных чисел, его можно записать так:
содержится в множестве комплексных чисел, его можно записать так: 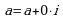 . Числа 0, 1 и
. Числа 0, 1 и 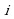 записываются соответственно в виде
записываются соответственно в виде 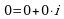 ,
, 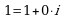 и
и 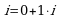 .
.
При 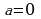 комплексное число
комплексное число 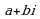 обращается в чисто мнимое число
обращается в чисто мнимое число 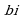 .
.
Модулем комплексного числа 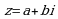 называется число
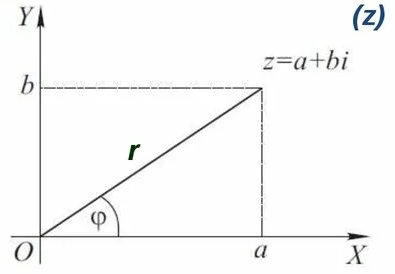
называется число 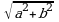 :
:
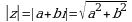
Комплексное число 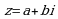 можно изображать точкой на плоскости с координатой (a;b). При этом ось Ох называется действительной осью, а ось Оу – мнимой. Каждой такой точке соответствует единственный вектор с началом координат и концом в точке (a;b).
можно изображать точкой на плоскости с координатой (a;b). При этом ось Ох называется действительной осью, а ось Оу – мнимой. Каждой такой точке соответствует единственный вектор с началом координат и концом в точке (a;b).
Угол между положительной действительной осью Ох и вектором называется аргументом комплексного числа.
Значение аргумента комплексного числа 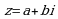 можно найти так:
можно найти так:
1) определить четверть, в которой находится комплексное число;
2) найти в этой четверти угол по формуле:
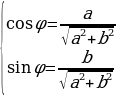 или
или 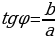
3) найти все значения аргумента по формуле:
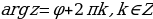
Действия над комплексными числами,
заданными в алгебраической форме
суммой двух комплексных чисел 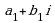 и
и 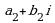 называется комплексное число
называется комплексное число 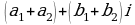 ;
;
разностью двух комплексных чисел 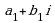 и
и 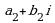 называется комплексное число
называется комплексное число 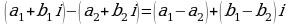 ;
;
произведением двух комплексных чисел 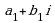 и
и 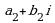 называется комплексное число
называется комплексное число 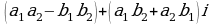 .
.
правила деления двух комплексных чисел 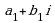 и
и 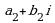 называется комплексное число:
называется комплексное число:
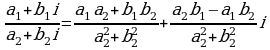 .
.
2. Задание.
| пп | ВАРИАНТ I | ВАРИАНТ II |
| 1. | Для данных комплексных чисел найдите: а) 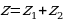 ; б) ; б) 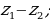 в) в) 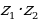 ; г) ; г) 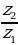 ; ; |
|
| 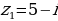 и и 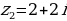 . .
| 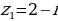 и и 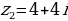 . .
|
| 2. | Вычислите: |
|
| 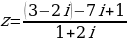
| 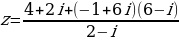
|
| 3. | Найдите модуль и аргумент числа: |
|
| а) 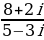 б) 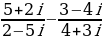 | а) 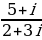 б) 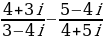 |
| 4. | Построите геометрическую модель квадрата комплексного числа |
|
| 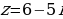
| 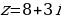
|
| 5. | Решите квадратные уравнения: |
|
| x2 – 2x + 8 = 0; x2 – 4x + 5 = 0; x2 + 6x + 69 = 0; | x2 + 6x + 25 =0; x2-2x+2=0; x2 -4x +16 = 0; |
Контрольные вопросы
Дайте определение комплексного числа (алгебраическая форма записи).
Что такое мнимая единица, действительная и мнимая часть комплексного числа?
Дайте определение комплексной плоскостью? Почему комплексное число называют вектором или точкой на комплексной плоскости?
Что такое модуль и аргумент комплексного числа, как их найти?
Дайте определение противоположному и комплексно-сопряженному числу.
Операции над комплексными числами в алгебраической форме.







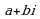 , где
, где 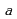 и
и 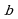 - действительные числа, а число
- действительные числа, а число 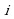 , определяемое равенством
, определяемое равенством 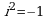 , называется мнимой единицей.
, называется мнимой единицей.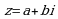 , а действительное число
, а действительное число 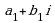 и
и 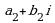 называются равными, если
называются равными, если 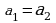 и
и 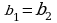 .
.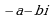 называются противоположными.
называются противоположными.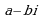 называется комплексно сопряженным с числом
называется комплексно сопряженным с числом 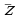 , т.е.
, т.е. 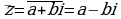 .
.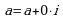 . Числа 0, 1 и
. Числа 0, 1 и 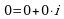 ,
, 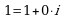 и
и 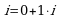 .
.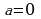 комплексное число
комплексное число 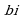 .
.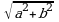 :
:
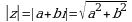
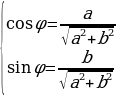 или
или 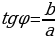
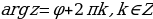
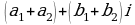 ;
;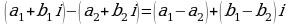 ;
;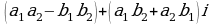 .
.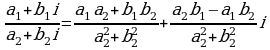 .
.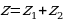 ; б)
; б) 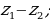 в)
в) 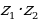 ; г)
; г) 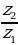 ;
; 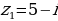 и
и 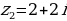 .
.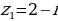 и
и 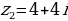 .
.