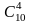Просмотр содержимого документа
«Практическая работа по теме : Размещения, сочетания, перестановки»
Практическое занятие Приложение 8
Размещения, сочетания и перестановки. История развития комбинаторики, теории вероятностей и статистики и их роль в различных сферах человеческой жизнедеятельности. Правила комбинаторики. Решение комбинаторных задач. Бином Ньютона и треугольник Паскаля. Прикладные задачи.
Теоретический этап.
Опорный конспект.
Определение.
Произведение всех натуральных чисел от 1 до n включительно называют
n – факториалом и пишут  .
.
0!=1 1!=1
| Перестановки | Размещения | Сочетания |
| n элементов n мест | n элементов m мест | n элементов m мест |
| порядок имеет значение | порядок имеет значение | порядок не имеет значение |
| P = n! | 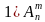 = = 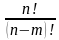
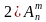 = n = n (n – 1) (n – 1) (n – 2) (n – 2)  … … (n – m +1) (n – m +1)
| 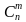 = = 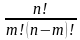
|
2) Подготовительный этап.
Перепишите и заполните пропуски:
Пример 1. За столом пять мест. Сколькими способами можно расставить пятерых гостей?
Решение: Р5 = 5! = 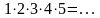 способов
способов
Ответ: 120 способов.
Пример 2. а) Сколько трехзначных чисел можно записать, используя цифры 1,3,6,7,9, если каждая их них может быть использована в записи только один раз?
Решение: Искомое число вариантов равно числу размещений из 5 элементов по 3 элемента, т.е. по формуле получаем: 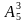 = 5
= 5  4
4  3 = … чисел.
3 = … чисел.
Ответ: 60 чисел.
б) Из 20 студентов надо выбрать старосту, его заместителя и редактора газеты. Сколькими способами это можно сделать?
Решение: Искомое число вариантов равно числу размещений из 20 элементов по 3 элемента, т.е. по формуле получаем: 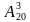 = 20
= 20  19
19  18 = … способов.
18 = … способов.
Ответ: 6840 способов.
Пример 3. а) Из 15 членов туристической группы надо выбрать трех дежурных. Сколькими способами можно сделать этот выбор?
Решение: каждый выбор отличается от другого хотя бы одним дежурным. Значит, здесь речь идет о сочетаниях из 15 элементов по 3. Следовательно, по формуле получаем 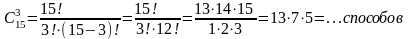
Ответ: 455 способов.
б) Студентам дали список из 10 книг, которые рекомендуется прочитать во время каникул. Сколькими способами студент может выбрать из них 6 книг?
Решение: Выбор 6 из 10 без учёта порядка: 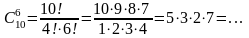 способов.
способов.
Ответ: 210 способов.
3) Практический этап.
За столом семь мест. Сколькими способами можно расставить семерых гостей?
а) Сколько трехзначных чисел можно записать, используя цифры 1,2,4,6,7,9, если каждая их них может быть использована в записи только один раз?
б) Из 15 учащихся надо выбрать старосту, его заместителя и редактора газеты. Сколькими способами это можно сделать?
3. а) Из 25 членов туристической группы надо выбрать трех дежурных. Сколькими способами можно сделать этот выбор?
б) Учащимся дали список из 10 книг, которые рекомендуется прочитать во время каникул. Сколькими способами ученик может выбрать из них 7 книг?
Пример 4. Вычислить 
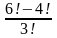
Пример 5. Упростить 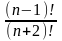
Пример 6. Вычислить 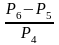
Пример 7. Вычислить 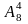 ;
; 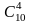
4) Дополнительные задания*.
Вариант 1
1.Вычислить 
2.Упростить 
3.Вычислить 
4.Вычислить  ;
; 
Вариант 2
1.Вычислить 
2.Упростить 
3.Вычислить 
4.Вычислить  ;
; 







 .
.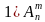 =
= 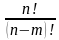
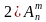 = n
= n (n – 1)
(n – 1)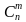 =
= 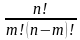
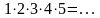 способов
способов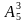 = 5
= 5 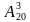 = 20
= 20 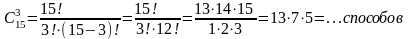
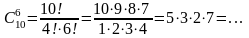 способов.
способов.
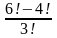
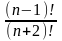
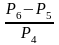
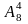 ;
;